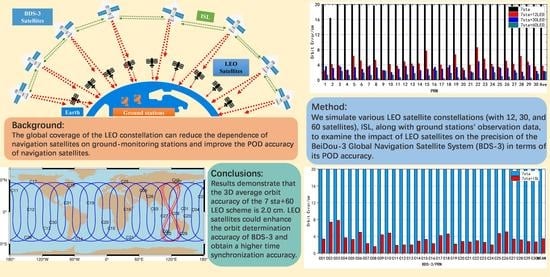
Analysis on BDS-3 Autonomous Navigation Performance Based on the LEO Constellation and Regional Stations
Abstract
:1. Introduction
2. BDS-3 Satellites POD Method
2.1. Satellite Equations of Motion and Observation Models
2.2. Processing Strategy
| Project | Parameters and Models |
|---|---|
| Elevation Angle Threshold | 5° for the ground station and 1° for LEO |
| Earth Gravity Field | EIGEN6C (12 × 12) for BDS-3 and EIGEN6C (120 × 120) for LEO [33] |
| N-body Perturbation | JPL DE405 [34] |
| SRP | ECOM 5 model for BDS-3 and macro-model for LEO [24] |
| Atmospheric drag | DTM94 [35] for LEO |
| BDS-3 Phase Center Offset (PCO) and Phase Center Variation (PCV) | igs14.atx |
| Station PCO and PCV | igs14.atx |
| LEO PCO and PCV | None |
| Solid tide and Pole tide | IERS 2010 [36] |
| Relativity | IERS 2010 |
| Ocean tide | FES 2004 [37] |
| Earth rotation parameters | One set per arc |
3. Results
3.1. BDS3 Joint POD Results Based on Ground Monitoring Stations and ISL
3.2. BDS-3 Joint POD Results Based on Ground-Monitoring Stations and LEO Satellites
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Jiao, W.; Ding, Q.; Li, J.; Lu, X.; Feng, L.; Ma, J.; Chen, G. Monitoring and assessment of GNSS open services. J. Navig. 2011, 64, S19–S29. [Google Scholar] [CrossRef]
- Capuano, V.; Botteron, C.; Farine, P.-A. Gnss Performances for Meo, Geo and Heo; Springer: Singapore, 2013. [Google Scholar]
- Lv, Y.; Geng, T.; Zhao, Q.; Xie, X.; Zhang, F.; Wang, X. Evaluation of BDS-3 Orbit Determination Strategies Using Ground-Tracking and Inter-Satellite Link Observation. Remote Sens. 2020, 12, 2647. [Google Scholar] [CrossRef]
- Ke, M.; Lv, J.; Chang, J.; Dai, W.; Tong, K.; Zhu, M. Integrating GPS and LEO to accelerate convergence time of precise point positioning. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar]
- Opromolla, R.; Vela, C.; Nocerino, A.; Lombardi, C. Monocular-Based Pose Estimation Based on Fiducial Markers for Space Robotic Capture Operations in GEO. Remote Sens. 2022, 14, 4483. [Google Scholar] [CrossRef]
- Dai, X.; Ge, M.; Lou, Y.; Shi, C.; Wickert, J.; Schuh, H. Estimating the yaw-attitude of BDS IGSO and MEO satellites. J. Geod. 2015, 89, 1005–1018. [Google Scholar] [CrossRef]
- Geng, J.H.; Shi, C.; Zhao, Q.L.; Ge, M.R.; Liu, J.N. Integrated Adjustment of LEO and GPS in Precision Orbit Determination; Springer: Berlin/Heidelberg, Germany, 2008; pp. 133–137. [Google Scholar]
- Wang, C.; Zhao, Q.; Guo, J.; Liu, J.; Chen, G. The contribution of intersatellite links to BDS-3 orbit determination: Model refinement and comparisons. Navigation 2019, 66, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; Hu, X.; Zhou, S.; Liu, L.; Pan, J.; Chen, L.; Guo, R.; Zhu, L.; Hu, G.; Li, X. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements. J. Geod. 2018, 92, 1155–1169. [Google Scholar] [CrossRef]
- Xie, X.; Geng, T.; Zhao, Q.; Cai, H.; Zhang, F.; Wang, X.; Meng, Y. Precise orbit determination for BDS-3 satellites using satellite-ground and inter-satellite link observations. GPS Solut. 2019, 23, 40. [Google Scholar] [CrossRef]
- Ren, X.; Yang, Y.; Zhu, J.; Xu, T. Orbit determination of the Next-Generation Beidou satellites with Intersatellite link measurements and a priori orbit constraints. Adv. Space Res. 2017, 60, 2155–2165. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Ge, M.; Nie, L.; Shen, Y.; Schuh, H. LEO enhanced Global Navigation Satellite System (LeGNSS) for real-time precise positioning services. Adv. Space Res. 2019, 63, 73–93. [Google Scholar] [CrossRef]
- Cochran, J.E.; Cho, S.; Cheng, Y.M.; Cicci, D.A. Dynamics and Orbit Determination of Tethered Satellite Systems. J. Astronaut. Sci. 1998, 46, 177–194. [Google Scholar] [CrossRef]
- Peng, D.J.; Wu, B. Kinematic Precise Orbit Determination for LEO Satellites Using Space-borne Dual-frequency GPS Measurements. Chin. Astron. Astrophys. 2012, 36, 291–306. [Google Scholar] [CrossRef]
- Montenbruck, O.; van Helleputte, T.; Kroes, R.; Gill, E. Reduced dynamic orbit determination using GPS code and carrier measurements. Aerosp. Sci. Technol. 2005, 9, 261–271. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Verdun, A. Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): Theory and initial results. Manuscr. Geod. 1994, 19, 367–386. [Google Scholar]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial assessment of precise point positioning with LEO enhanced global navigation satellite systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef] [Green Version]
- van den IJssel, J.; Encarnação, J.; Doornbos, E.; Visser, P. Precise science orbits for the Swarm satellite constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, J.; Ge, M.; Shi, C.; Du, R. Precis orbit determination of GPS and CHAMP satellites with PANDA software. Geod. Geodyn. 2005, 25, 113-116+122. [Google Scholar]
- Du, L. A Study on the Precise Orbit Determination of Geostationary Satellites. Ph.D. Thesis, PLA Information Engineering University, Zhengzhou, China, 2006. [Google Scholar]
- Jianghui, G.; Chuang, S.; Qile, Z.; Jingnan, L. Combined ground and satellite-based data for precise GPS satellite orbit determination. Geomatics Inf. Sci. Wuhan Univ. 2007, 32, 906–909. [Google Scholar]
- Ge, H.; Li, B.; Jia, S.; Nie, L.; Wu, T.; Yang, Z.; Shang, J.; Zheng, Y.; Ge, M. LEO enhanced global navigation satellite system (LeGNSS): Progress, opportunities, and challenges. Geo-Spat. Inf. Sci. 2022, 25, 1–13. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Ma, F.; Zhang, W.; Zhang, Q.; Qin, Y.; Zhang, H.; Meng, Y.; Bian, L. Integrated Precise Orbit Determination of Multi-GNSS and Large LEO Constellations. Remote Sens. 2019, 11, 2514. [Google Scholar] [CrossRef] [Green Version]
- Hauschild, A.; Tegedor, J.; Montenbruck, O.; Visser, H.; Markgraf, M. Precise onboard orbit determination for LEO satellites with real-time orbit and clock corrections. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 3715–3723. [Google Scholar]
- Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
- Li, M.; Xu, T.; Ge, H.; Guan, M.; Yang, H.; Fang, Z.; Gao, F. LEO-Constellation-Augmented BDS Precise Orbit Determination Considering Spaceborne Observational Errors. Remote Sens. 2021, 13, 3189. [Google Scholar] [CrossRef]
- Boomkamp, H.; Dow, J. Use of double difference observations in combined orbit solutions for LEO and GPS satellites. Adv. Space Res. 2005, 36, 382–391. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, S. Satellite Availability and Service Performance Evaluation for Next-Generation GNSS, RNSS and LEO Augmentation Constellation. Remote Sens. 2021, 13, 3698. [Google Scholar] [CrossRef]
- Geng, T.; Su, X.; Zhao, Q. MEO and HEO Satellites Orbit Determination Based on GNSS Onboard Receiver; Springer: Berlin/Heidelberg, Germany, 2012; pp. 223–234. [Google Scholar]
- Guo, J.; Chen, G.; Zhao, Q.; Liu, J.; Liu, X. Comparison of solar radiation pressure models for BDS IGSO and MEO satellites with emphasis on improving orbit quality. GPS Solut. 2017, 21, 511–522. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yang, Z.; Jia, Z.; Li, X. Parallel Computation of Multi-GNSS and Multi-Frequency Inter-Frequency Clock Biases and Observable-Specific Biases. Remote Sens. 2023, 15, 1953. [Google Scholar] [CrossRef]
- König, R.; Reigber, C.; Zhu, S. Dynamic model orbits and Earth system parameters from combined GPS and LEO data. Adv. Space Res. 2005, 36, 431–437. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A.; Rizos, C. Integrity monitoring for precise orbit determination of LEO satellites. GPS Solut. 2021, 26, 32. [Google Scholar] [CrossRef]
- Berger, C.; Biancale, R.; Ill, M.; Barlier, F. Improvement of the empirical thermospheric model DTM: DTM94—A comparative review of various temporal variations and prospects in space geodesy applications. J. Geod. 1998, 72, 161–178. [Google Scholar] [CrossRef]
- Xiong, C.; Stolle, C.; Lühr, H. The Swarm satellite loss of GPS signal and its relation to ionospheric plasma irregularities. Space Weather 2016, 14, 563–577. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean. Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Ma, F.; Lv, H.; Yuan, Y.; Li, X. LEO Precise Orbit Determination with Inter-satellite Links. Remote Sens. 2019, 11, 2117. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Guo, X.; Qu, L.; Zhao, Q. Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites. Remote Sens. 2018, 10, 382. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Yang, J.; Li, G.; Zhou, Y.; Tang, C. Globalization highlight: Orbit determination using BeiDou inter-satellite ranging measurements. GPS Solut. 2017, 21, 1395–1404. [Google Scholar] [CrossRef]
- Jun, W.; Yamin, D.; Hui, P.; Yingyan, C.; Hu, W.; Caiya, Y. Estimation and Analysis of Multi-System Satellite Clock. Bull. Surv. Mapp. 2016, 4, 5–9. [Google Scholar] [CrossRef]
- Ge, M.; Chen, J.; Douša, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2012, 16, 9–17. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Li, Y.; Gao, Y. Impacts of real-time satellite clock errors on GPS precise point positioning-based troposphere zenith delay estimation. J. Geod. 2015, 89, 747–756. [Google Scholar] [CrossRef]
- Leclère, J.; Landry, R.; Botteron, C. Comparison of L1 and L5 Bands GNSS Signals Acquisition. Sensors 2018, 18, 2779. [Google Scholar] [CrossRef] [Green Version]












| Project | Parameters and Models |
|---|---|
| Earth Gravity Field | EIGEN6C (12 × 12) for BDS-3 |
| N-body Perturbation | JPL DE405 |
| SRP | ECOM 5 model for BDS-3 |
| BDS-3 Phase Center Offset (PCO) and | igs14.atx |
| Station PCO and PCV | igs14.atx |
| Solid tide and Pole tide | IERS 2010 |
| Relativity | IERS 2010 |
| Ocean tide | FES 2004 |
| Earth rotation parameters | One set per arc |
| Orbit parameters to be estimated | Satellite initial position, velocity and solar pressure parameters |
| GNSS | BDS-3 Satellites | ||
|---|---|---|---|
| Orbit Type | GEO | IGSO | MEO |
| Satellites number | 3 | 3 | 24 |
| Pseudo-random noise (PRN) number | C01, C02, C03 | C04, C05, C06 | C07–C30 |
| Altitude | 35,786 km | 35,786 km | 21,528 km |
| Inclination | 0° | 55° | 55° |
| Constellation | Located at 80°E, 110.5°E, and 140°E | RAAN of 118°E | Walker (24/3/1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Su, X.; Liu, Z.; Su, M.; Cui, J.; Li, Q.; Xu, Y.; Ma, Z.; Geng, T. Analysis on BDS-3 Autonomous Navigation Performance Based on the LEO Constellation and Regional Stations. Remote Sens. 2023, 15, 3081. https://doi.org/10.3390/rs15123081
Xu B, Su X, Liu Z, Su M, Cui J, Li Q, Xu Y, Ma Z, Geng T. Analysis on BDS-3 Autonomous Navigation Performance Based on the LEO Constellation and Regional Stations. Remote Sensing. 2023; 15(12):3081. https://doi.org/10.3390/rs15123081
Chicago/Turabian StyleXu, Baopeng, Xing Su, Zhimin Liu, Mudan Su, Jianhui Cui, Qiang Li, Yan Xu, Zeyu Ma, and Tao Geng. 2023. "Analysis on BDS-3 Autonomous Navigation Performance Based on the LEO Constellation and Regional Stations" Remote Sensing 15, no. 12: 3081. https://doi.org/10.3390/rs15123081
APA StyleXu, B., Su, X., Liu, Z., Su, M., Cui, J., Li, Q., Xu, Y., Ma, Z., & Geng, T. (2023). Analysis on BDS-3 Autonomous Navigation Performance Based on the LEO Constellation and Regional Stations. Remote Sensing, 15(12), 3081. https://doi.org/10.3390/rs15123081