Evaluating the Performance of PRISMA Shortwave Infrared Imaging Sensor for Mapping Hydrothermally Altered and Weathered Minerals Using the Machine Learning Paradigm
Abstract
:1. Introduction
2. Description of the Study Area
3. Description of Dataset
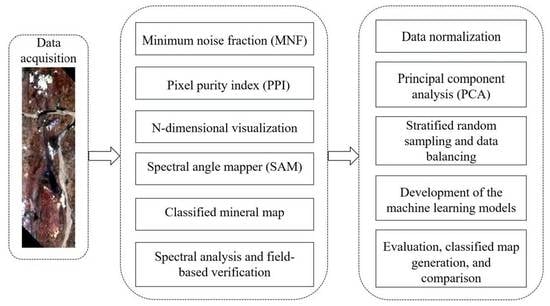
4. Materials and Methods
4.1. Generation of the Reference Mineral Distribution Map
4.2. Field-Based Verification
4.3. Development of ML-Based Predictive Models
4.3.1. Data Normalization
4.3.2. Principal Component Analysis
4.3.3. Development and Evaluation of ML-Based Mapping Models
5. Performance Measures
6. Results and Discussion
6.1. Spectral Absorption Characteristics of the Minerals
6.2. Dimensionality Reduction
6.3. Balancing of the Training Dataset
6.4. Hyper-Parameter Optimization of the Classification Models
6.5. Comparison of Classification Models
6.5.1. Results Obtained with the 30:70 Split
6.5.2. Results Obtained with the 50:50 Split
6.5.3. Results Obtained with the 70:30 Split
7. Conclusions
- The low SNR of the PRISMA dataset does not seem to affect its ability to classify the altered minerals using ML techniques.
- The spectral information associated with the SWIR bands of the PRISMA dataset is sufficient to discriminate the selected minerals.
- The stochastic gradient descent and artificial-neural-network-based multilayer perceptron algorithms are the most efficient ML techniques for the classification of specified mineral using the PRISMA dataset.
- The linear feature transformation technique of PCA can efficiently derive crucial information to map the selected minerals.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Results Obtained with 30:70 Spit Ratio





Appendix B. Results Obtained with 50:50 Spit Ratio





Appendix C. Results Obtained with 70:30 Spit Ratio





References
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced Spectral Classifiers for Hyperspectral Images: A Review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef] [Green Version]
- Mishra, G.; Govil, H.; Srivastava, P.K. Identification of Malachite and Alteration Minerals Using Airborne AVIRIS-NG Hyperspectral Data. Quat. Sci. Adv. 2021, 4, 100036. [Google Scholar] [CrossRef]
- Abdelsalam, M.G.; Stern, R.J.; Berhane, W.G. Mapping Gossans in Arid Regions with Landsat TM and SIR-C Images: The Beddaho Alteration Zone in Northern Eritrea. J. Afr. Earth Sci. 2000, 30, 903–916. [Google Scholar] [CrossRef]
- Qian, S.-E. Hyperspectral Satellites, Evolution, and Development History. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7032–7056. [Google Scholar] [CrossRef]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA Imaging Spectroscopy Mission: Overview and First Performance Analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Loizzo, R.; Daraio, M.; Guarini, R.; Longo, F.; Lorusso, R.; Dini, L.; Lopinto, E. Prisma Mission Status and Perspective. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August; pp. 4503–4506.
- Zuo, R. Machine Learning of Mineralization-Related Geochemical Anomalies: A Review of Potential Methods. Nat. Resour. Res. 2017, 26, 457–464. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef] [Green Version]
- McCoy, J.T.; Auret, L. Machine Learning Applications in Minerals Processing: A Review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Tuşa, L.; Kern, M.; Khodadadzadeh, M.; Blannin, R.; Gloaguen, R.; Gutzmer, J. Evaluating the Performance of Hyperspectral Short-Wave Infrared Sensors for the Pre-Sorting of Complex Ores Using Machine Learning Methods. Miner. Eng. 2020, 146, 106150. [Google Scholar] [CrossRef]
- Kumar, C.; Chatterjee, S.; Oommen, T.; Guha, A. Automated Lithological Mapping by Integrating Spectral Enhancement Techniques and Machine Learning Algorithms Using AVIRIS-NG Hyperspectral Data in Gold-Bearing Granite-Greenstone Rocks in Hutti, India. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102006. [Google Scholar] [CrossRef]
- Lorenz, S.; Ghamisi, P.; Kirsch, M.; Jackisch, R.; Rasti, B.; Gloaguen, R. Feature Extraction for Hyperspectral Mineral Domain Mapping: A Test of Conventional and Innovative Methods. Remote Sens. Environ. 2021, 252, 112129. [Google Scholar] [CrossRef]
- Parakh, K.; Thakur, S.; Chudasama, B.; Tirodkar, S.; Porwal, A.; Bhattacharya, A. Machine Learning and Spectral Techniques for Lithological Classification. In Proceedings of the Multispectral, Hyperspectral, and Ultraspectral Remote Sensing Technology, Techniques and Applications VI, New Delhi, India, 4–7 April 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9880, pp. 456–467. [Google Scholar]
- Pal, M.; Rasmussen, T.; Porwal, A. Optimized Lithological Mapping from Multispectral and Hyperspectral Remote Sensing Images Using Fused Multi-Classifiers. Remote Sens. 2020, 12, 177. [Google Scholar] [CrossRef] [Green Version]
- Lobo, A.; Garcia, E.; Barroso, G.; Martí, D.; Fernandez-Turiel, J.-L.; Ibáñez-Insa, J. Machine Learning for Mineral Identification and Ore Estimation from Hyperspectral Imagery in Tin–Tungsten Deposits: Simulation under Indoor Conditions. Remote Sens. 2021, 13, 3258. [Google Scholar] [CrossRef]
- Eichstaedt, H.; Ho, C.Y.J.; Kutzke, A.; Kahnt, R. Performance Measurements of Machine Learning and Different Neural Network Designs for Prediction of Geochemical Properties Based on Hyperspectral Core Scans. Aust. J. Earth Sci. 2022, 69, 733–741. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Heidari, E.; Beiranvand Pour, A.; Pradhan, B.; Müller, D.; Chandra, R. A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data. Remote Sens. 2022, 14, 819. [Google Scholar] [CrossRef]
- Shayeganpour, S.; Tangestani, M.H.; Gorsevski, P.V. Machine Learning and Multi-Sensor Data Fusion for Mapping Lithology: A Case Study of Kowli-Kosh Area, SW Iran. Adv. Space Res. 2021, 68, 3992–4015. [Google Scholar] [CrossRef]
- Yousefi, B.; Sojasi, S.; Castanedo, C.I.; Maldague, X.P.V.; Beaudoin, G.; Chamberland, M. Comparison Assessment of Low Rank Sparse-PCA Based-Clustering/Classification for Automatic Mineral Identification in Long Wave Infrared Hyperspectral Imagery. Infrared Phys. Technol. 2018, 93, 103–111. [Google Scholar] [CrossRef]
- Lin, N.; Chen, Y.; Liu, H.; Liu, H. A Comparative Study of Machine Learning Models with Hyperparameter Optimization Algorithm for Mapping Mineral Prospectivity. Minerals 2021, 11, 159. [Google Scholar] [CrossRef]
- Guo, X.; Li, P.; Li, J. Lithological Mapping Using EO-1 Hyperion Hyperspectral Data and Semisupervised Self-Learning Method. J. Appl. Remote Sens. 2021, 15, 032209. [Google Scholar] [CrossRef]
- Malhotra, G.; Pandit, M.K. Geology and Mineralization of the Jahazpur Belt, Southeastern Rajasthan. In Crustal Evolution and Metallogeny in the Northwestern Indian Shield: A Festschrift for Asoke Mookherjee; Alpha Science International: Oxford, UK, 2000; pp. 115–125. [Google Scholar]
- Roy, A.B.; Jakhar, S.R. Geology of Rajasthan (Northwest India): Precambrian to Recent; Scientific Publishers: Jodhpur, India, 2002; ISBN 978-81-7233-304-1. [Google Scholar]
- Tripathi, M.K.; Govil, H. Regolith Mapping and Geochemistry of Hydrothermally Altered, Weathered and Clay Minerals, Western Jahajpur Belt, Bhilwara, India. Geocarto International. 2022, 37, 879–895. [Google Scholar] [CrossRef]
- Pandit, M.K.; Sial, A.N.; Malhotra, G.; Shekhawat, L.S.; Ferreira, V.P. C-, O- Isotope and Whole-Rock Geochemistry of Proterozoic Jahazpur Carbonates, NW Indian Craton. Gondwana Res. 2003, 6, 513–522. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Boardmann, J.; Kruse, F.A.; Green, R.O. Mapping Target Signatures via Partial Unmixing of AVIRIS Data. In Proceedings of the Summaries of the 5th Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 23–26 January 1995; Volume 1, pp. 95–101. [Google Scholar]
- Kruse, F.A.; Richardson, L.L.; Ambrosia, V.G. Techniques Developed for Geologic Analysis of Hyperspectral Data Applied to Near-Shore Hyperspectral Ocean Data. In Proceedings of the Fourth International Conference on Remote Sensing for Marine and Coastal Environments: Environmental Research Institute of Michigan (ERIM), Orlando, FL, USA, 17–19 March 1997. [Google Scholar]
- Singh, D.; Singh, B. Investigating the Impact of Data Normalization on Classification Performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a Complex of Statistical Variables into Principal Components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support Vector Machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, X. Multi-Class Support Vector Machine. In Support Vector Machines Applications; Springer International Publishing: Cham, Switzerland, 2014; pp. 23–48. [Google Scholar]
- Quinlan, J.R. Simplifying Decision Trees. Int. J. Hum. Comput. Stud. 1999, 51, 497–510. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Hykin, S. Neural Networks: A Comprehensive Foundation; Printice-Hall: Upper Saddle River, NJ, USA, 1999; pp. 120–134. [Google Scholar]
- Fix, E.; Hodges, J.L. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties. Int. Stat. Rev. Rev. Int. Stat. 1989, 57, 238. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3176. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting. Lect. Notes Comput. Sci. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinforma. 1995, 904, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3147–3155. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. Catboost: Unbiased Boosting with Categorical Features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- Zhang, T. Solving Large Scale Linear Prediction Problems Using Stochastic Gradient Descent Algorithms. In Proceedings of the Twenty-First International Conference on Machine Learning, ICML 2004, New York, NY, USA, 4–8 July 2004; pp. 919–926. [Google Scholar]
- Murphy, K.P. Naive Bayes Classifiers. Univ. Br. Columbia 2006, 18, 1–8. [Google Scholar]
- Balakrishnama, S.; Ganapathiraju, A. Linear Discriminant Analysis—A Brief Tutorial. Compute 1998, 18, 1–8. [Google Scholar]
- Srivastava, S.; Gupta, M.R.; Frigyik, B.A. Bayesian Quadratic Discriminant Analysis. J. Mach. Learn. Res. 2007, 8, 1277–1305. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]








| Orbit Altitude | 615 km | Spectral Range | VNIR—0.400–1.01 µm (66 bands) SWIR—0.92–2.5 µm (173 bands) PAN—0.4–0.7 µm |
| Swath Width | 30 km | Spectral Resolution | ≤12 nm |
| Field of View (FOV) | 2.77° | Radiometric Resolution | 12 bits |
| Spatial Resolution | Hyperspectral—30 m Panchromatic—5 m | Signal-to-Noise Ratio (SNR) | VNIR—>200:1 SWIR—>100:1 PAN—>240:1 |
| Pixel Size | Hyperspectral—30 µm × 30 µm PAN—6.5 µm × 6.5 µm | Lifetime | 5 years |
| Measure | Equation |
|---|---|
| Average Accuracy | |
| Recall (TPR) | |
| Precision | |
| F1-score | |
| Kappa Coefficient |
| Class—Id | Mineral Class | Total Pixels |
|---|---|---|
| 1 | Montmorillonite | 35 |
| 2 | Talc | 383 |
| 3 | Kaolinite and Kaosmec | 120 |
| S. No. | MLA Name | Optimized Hyper Parameters | Range |
|---|---|---|---|
| 1 | SVM | Regularization parameter or ‘C’ | [10−1–103] |
| ‘kernel’ | [‘linear’, ‘poly’, ‘rbf’] | ||
| Kernel coefficient or ‘gamma’ | [10−3–1] | ||
| 2 | DT | ‘criterion’ | [‘gini’, ‘entropy’] |
| ‘max_depth’ | [1–10] | ||
| ‘min_samples_split’ | [1–5] | ||
| ‘max_features’ | [‘auto’, ‘sqrt’, ‘log2’] | ||
| 3 | Bagging Classifier | ‘n_estimators’ | [1–30] |
| ‘max_samples’ | [1–5] | ||
| 4 | RF | ‘n_estimators’ | [1–30] |
| ‘criterion’ | [‘gini’, ‘entropy’] | ||
| ‘max_depth’ | [1–10] | ||
| ‘min_samples_split’ | [1–5] | ||
| 5 | ET | ‘n_estimators’ | [1–30] |
| ‘criterion’ | [‘gini’, ‘entropy’] | ||
| ‘max_depth’ | [1–10] | ||
| ‘min_samples_split’ | [1–50] | ||
| 6 | k-NN | ‘n_neighbors’ | [1–30] |
| 7 | GPC | ‘multi_class’ | [‘one_vs_rest’, ‘one_vs_one’] |
| 8 | AdaBoost | ‘n_estimators’ | [1–30] |
| 9 | GBC | ‘n_estimators’ | [1–30] |
| ‘learning_rate’ | [0.01, 0.1, 1, 10] | ||
| 10 | XGB | ‘max_depth’ | [1–10] |
| ‘min_samples_split’ | [1–50] | ||
| 11 | LGBM | ‘n_estimators’ | [1–30] |
| 12 | Cat Boost | ‘max_depth’ | [1–10] |
| ‘n_estimators’ | [1–30] | ||
| 13 | HGB | ‘max_depth’ | [1–10] |
| 14 | SGD | ‘penalty’ | [‘l2’, ‘l1’, ‘elasticnet’, None] |
| ‘alpha’ | [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000] | ||
| 15 | GNB | ‘var_smoothing’ | [1 × 10−6, 1 × 10−7, 1 × 10−8, 1 × 10−9, 1 × 10−10, 1 × 10−11] |
| 16 | LDA | ‘solver’ | [‘svd’, ‘lsqr’, ‘eigen’] |
| 17 | QDA | ‘reg_param’ | [0–1] |
| 18 | MLP | ‘hidden_layer_sizes’ | [(5,1), (5,2), (5,3), (10,1), (10,2), (10,3)] |
| ‘activation’ | [‘tanh’, ‘relu’] | ||
| ‘learning_rate’ | [‘constant’, ’adaptive’] |
| MLA Name | OA | AA | K | F1-Score | Precision | Recall | AUC Score | |
|---|---|---|---|---|---|---|---|---|
| 1 | SVM | 0.9602 | 0.9085 | 0.9108 | 0.8844 | 0.8685 | 0.9085 | 0.99 |
| 2 | DT | 0.9072 | 0.8225 | 0.7795 | 0.8144 | 0.8383 | 0.8225 | 0.87 |
| 3 | Bagging Classifier | 0.9151 | 0.8344 | 0.7978 | 0.8348 | 0.8572 | 0.8344 | 0.97 |
| 4 | RF | 0.9523 | 0.8966 | 0.8883 | 0.9124 | 0.9306 | 0.8966 | 0.99 |
| 5 | ET | 0.9655 | 0.9390 | 0.9208 | 0.9231 | 0.9174 | 0.9390 | 1.00 |
| 6 | k-NN | 0.9363 | 0.8743 | 0.8571 | 0.8443 | 0.8348 | 0.8743 | 0.94 |
| 7 | GPC | 0.9337 | 0.8610 | 0.8508 | 0.8431 | 0.8310 | 0.8610 | 0.95 |
| 8 | AdaBoost | 0.9416 | 0.8768 | 0.8696 | 0.8527 | 0.8362 | 0.8768 | 0.99 |
| 9 | GBC | 0.9390 | 0.9169 | 0.8656 | 0.8481 | 0.8403 | 0.9169 | 0.98 |
| 10 | XGB | 0.9629 | 0.9378 | 0.9166 | 0.9001 | 0.8831 | 0.9378 | 1.00 |
| 11 | LGBM | 0.9735 | 0.9603 | 0.9404 | 0.9233 | 0.9048 | 0.9603 | 1.00 |
| 12 | Cat Boost | 0.9363 | 0.8767 | 0.8504 | 0.8679 | 0.8793 | 0.8767 | 0.99 |
| 13 | HGB | 0.9416 | 0.9279 | 0.8719 | 0.8802 | 0.8506 | 0.9279 | 1.00 |
| 14 | SGD | 0.9920 | 0.9787 | 0.9819 | 0.9801 | 0.9814 | 0.9787 | 1.00 |
| 15 | GNB | 0.9469 | 0.8551 | 0.8728 | 0.8893 | 0.9325 | 0.8551 | 1.00 |
| 16 | LDA | 0.9549 | 0.9232 | 0.8991 | 0.8758 | 0.8618 | 0.9232 | 1.00 |
| 17 | QDA | 0.8992 | 0.6244 | 0.7436 | 0.6282 | 0.9295 | 0.6244 | 0.84 |
| 18 | MLP | 0.9602 | 0.9045 | 0.9097 | 0.9045 | 0.9045 | 0.9045 | 0.99 |
| MLA Name | Montmorillonite | Talc | Kaolinite | |
|---|---|---|---|---|
| 1 | SVM | 0.84 | 0.99 | 0.89 |
| 2 | DT | 0.80 | 0.99 | 0.68 |
| 3 | Bagging Classifier | 0.80 | 0.99 | 0.71 |
| 4 | RF | 0.84 | 0.99 | 0.86 |
| 5 | ET | 0.96 | 1.00 | 0.86 |
| 6 | k-NN | 0.80 | 0.98 | 0.85 |
| 7 | GPC | 0.76 | 0.98 | 0.85 |
| 8 | AdaBoost | 0.80 | 0.99 | 0.85 |
| 9 | GBC | 1.00 | 0.99 | 0.76 |
| 10 | XGB | 0.96 | 1.00 | 0.86 |
| 11 | LGBM | 1.00 | 1.00 | 0.88 |
| 12 | Cat Boost | 0.88 | 1.00 | 0.75 |
| 13 | HGB | 0.96 | 0.97 | 0.86 |
| 14 | SGD | 0.96 | 1.00 | 0.98 |
| 15 | GNB | 0.72 | 1.00 | 0.85 |
| 16 | LDA | 0.96 | 1.00 | 0.81 |
| 17 | QDA | 0.04 | 1.00 | 0.83 |
| 18 | MLP | 0.80 | 0.99 | 0.93 |
| MLA Name | OA | AA | K | F1-Score | Precision | Recall | AUC Score | |
|---|---|---|---|---|---|---|---|---|
| 1 | SVM | 0.9926 | 0.9759 | 0.9832 | 0.9759 | 0.9759 | 0.9759 | 1.00 |
| 2 | DT | 0.9740 | 0.9481 | 0.9415 | 0.9228 | 0.9070 | 0.9481 | 0.97 |
| 3 | Bagging Classifier | 0.9591 | 0.9244 | 0.9071 | 0.9206 | 0.9174 | 0.9244 | 1.00 |
| 4 | RF | 0.9963 | 0.9815 | 0.9916 | 0.9877 | 0.9945 | 0.9815 | 1.00 |
| 5 | ET | 0.9926 | 0.9630 | 0.9831 | 0.9749 | 0.9892 | 0.9630 | 1.00 |
| 6 | k-NN | 0.9703 | 0.9708 | 0.9341 | 0.9298 | 0.9049 | 0.9708 | 1.00 |
| 7 | GPC | 0.9851 | 0.9648 | 0.9664 | 0.9536 | 0.9443 | 0.9648 | 1.00 |
| 8 | AdaBoost | 0.7732 | 0.6649 | 0.5235 | 0.4579 | 0.4095 | 0.6649 | 0.94 |
| 9 | GBC | 0.9963 | 0.9944 | 0.9916 | 0.9882 | 0.9825 | 0.9944 | 1.00 |
| 10 | XGB | 0.9814 | 0.9722 | 0.9582 | 0.9449 | 0.9275 | 0.9722 | 1.00 |
| 11 | LGBM | 0.9851 | 0.9778 | 0.9665 | 0.9552 | 0.9394 | 0.9778 | 1.00 |
| 12 | Cat Boost | 0.9888 | 0.9704 | 0.9746 | 0.9722 | 0.9741 | 0.9704 | 1.00 |
| 13 | HGB | 0.9814 | 0.9593 | 0.9581 | 0.9430 | 0.9307 | 0.9593 | 1.00 |
| 14 | SGD | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.00 |
| 15 | GNB | 0.9665 | 0.8852 | 0.9211 | 0.9252 | 0.9808 | 0.8852 | 1.00 |
| 16 | LDA | 0.9814 | 0.9593 | 0.9581 | 0.9430 | 0.9307 | 0.9593 | 1.00 |
| 17 | QDA | 0.9405 | 0.7296 | 0.8599 | 0.7500 | 0.9384 | 0.7296 | 0.87 |
| 18 | MLP | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.00 |
| MLA Name | Montmorillonite | Talc | Kaolinite | |
|---|---|---|---|---|
| 1 | SVM | 0.94 | 1.00 | 0.98 |
| 2 | DT | 0.94 | 1.00 | 0.90 |
| 3 | Bagging Classifier | 0.89 | 0.98 | 0.90 |
| 4 | RF | 0.94 | 1.00 | 1.00 |
| 5 | ET | 0.89 | 1.00 | 1.00 |
| 6 | k-NN | 1.00 | 0.98 | 0.93 |
| 7 | GPC | 0.94 | 1.00 | 0.95 |
| 8 | AdaBoost | 1.00 | 0.99 | 0.00 |
| 9 | GBC | 1.00 | 1.00 | 0.98 |
| 10 | XGB | 1.00 | 1.00 | 0.92 |
| 11 | LGBM | 1.00 | 1.00 | 0.93 |
| 12 | Cat Boost | 0.94 | 1.00 | 0.97 |
| 13 | HGB | 0.94 | 1.00 | 0.93 |
| 14 | SGD | 1.00 | 1.00 | 1.00 |
| 15 | GNB | 0.72 | 1.00 | 0.93 |
| 16 | LDA | 0.94 | 1.00 | 0.93 |
| 17 | QDA | 0.22 | 1.00 | 0.97 |
| 18 | MLP | 1.00 | 1.00 | 1.00 |
| MLA Name | OA | AA | K | F1-Score | Precision | Recall | AUC Score | |
|---|---|---|---|---|---|---|---|---|
| 1 | SVM | 0.9938 | 0.9907 | 0.9861 | 0.9808 | 0.9722 | 0.9907 | 1.00 |
| 2 | DT | 0.9691 | 0.8969 | 0.9299 | 0.9124 | 0.9337 | 0.8969 | 0.94 |
| 3 | Bagging Classifier | 0.9815 | 0.9512 | 0.9582 | 0.9424 | 0.9349 | 0.9512 | 1.00 |
| 4 | RF | 0.9877 | 0.9604 | 0.9721 | 0.9604 | 0.9604 | 0.9604 | 1.00 |
| 5 | ET | 0.9877 | 0.9394 | 0.9720 | 0.9577 | 0.9825 | 0.9394 | 1.00 |
| 6 | k-NN | 0.9630 | 0.9572 | 0.9177 | 0.9143 | 0.8929 | 0.9572 | 0.99 |
| 7 | GPC | 0.9753 | 0.9630 | 0.9436 | 0.9497 | 0.9430 | 0.9630 | 1.00 |
| 8 | AdaBoost | 0.7716 | 0.6638 | 0.5206 | 0.4569 | 0.4084 | 0.6638 | 0.94 |
| 9 | GBC | 0.9877 | 0.9815 | 0.9722 | 0.9627 | 0.9487 | 0.9815 | 1.00 |
| 10 | XGB | 0.9753 | 0.9630 | 0.9446 | 0.9291 | 0.9111 | 0.9630 | 1.00 |
| 11 | LGBM | 0.9938 | 0.9907 | 0.9861 | 0.9808 | 0.9722 | 0.9907 | 1.00 |
| 12 | Cat Boost | 0.9753 | 0.9419 | 0.9439 | 0.9360 | 0.9318 | 0.9419 | 1.00 |
| 13 | HGB | 0.9938 | 0.9907 | 0.9861 | 0.9808 | 0.9722 | 0.9907 | 1.00 |
| 14 | SGD | 0.9938 | 0.9697 | 0.9860 | 0.9796 | 0.9910 | 0.9697 | 1.00 |
| 15 | GNB | 0.9815 | 0.9301 | 0.9573 | 0.9545 | 0.9850 | 0.9301 | 1.00 |
| 16 | LDA | 0.9877 | 0.9604 | 0.9721 | 0.9604 | 0.9604 | 0.9604 | 1.00 |
| 17 | QDA | 0.9444 | 0.7694 | 0.8697 | 0.8051 | 0.9415 | 0.7694 | 0.98 |
| 18 | MLP | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.00 |
| MLA Name | Montmorillonite | Talc | Kaolinite | |
|---|---|---|---|---|
| 1 | SVM | 1.00 | 1.00 | 0.97 |
| 2 | DT | 0.73 | 0.99 | 0.97 |
| 3 | Bagging Classifier | 0.91 | 1.00 | 0.94 |
| 4 | RF | 0.91 | 1.00 | 0.97 |
| 5 | ET | 0.82 | 1.00 | 1.00 |
| 6 | k-NN | 1.00 | 0.98 | 0.89 |
| 7 | GPC | 1.00 | 1.00 | 0.89 |
| 8 | AdaBoost | 1.00 | 0.99 | 0.00 |
| 9 | GBC | 1.00 | 1.00 | 0.94 |
| 10 | XGB | 1.00 | 1.00 | 0.89 |
| 11 | LGBM | 1.00 | 1.00 | 0.97 |
| 12 | Cat Boost | 0.91 | 1.00 | 0.92 |
| 13 | HGB | 1.00 | 1.00 | 0.97 |
| 14 | SGD | 0.91 | 1.00 | 1.00 |
| 15 | GNB | 0.82 | 1.00 | 0.97 |
| 16 | LDA | 0.91 | 1.00 | 0.97 |
| 17 | QDA | 0.36 | 1.00 | 0.94 |
| 18 | MLP | 1.00 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrawal, N.; Govil, H.; Mishra, G.; Gupta, M.; Srivastava, P.K. Evaluating the Performance of PRISMA Shortwave Infrared Imaging Sensor for Mapping Hydrothermally Altered and Weathered Minerals Using the Machine Learning Paradigm. Remote Sens. 2023, 15, 3133. https://doi.org/10.3390/rs15123133
Agrawal N, Govil H, Mishra G, Gupta M, Srivastava PK. Evaluating the Performance of PRISMA Shortwave Infrared Imaging Sensor for Mapping Hydrothermally Altered and Weathered Minerals Using the Machine Learning Paradigm. Remote Sensing. 2023; 15(12):3133. https://doi.org/10.3390/rs15123133
Chicago/Turabian StyleAgrawal, Neelam, Himanshu Govil, Gaurav Mishra, Manika Gupta, and Prashant K. Srivastava. 2023. "Evaluating the Performance of PRISMA Shortwave Infrared Imaging Sensor for Mapping Hydrothermally Altered and Weathered Minerals Using the Machine Learning Paradigm" Remote Sensing 15, no. 12: 3133. https://doi.org/10.3390/rs15123133
APA StyleAgrawal, N., Govil, H., Mishra, G., Gupta, M., & Srivastava, P. K. (2023). Evaluating the Performance of PRISMA Shortwave Infrared Imaging Sensor for Mapping Hydrothermally Altered and Weathered Minerals Using the Machine Learning Paradigm. Remote Sensing, 15(12), 3133. https://doi.org/10.3390/rs15123133