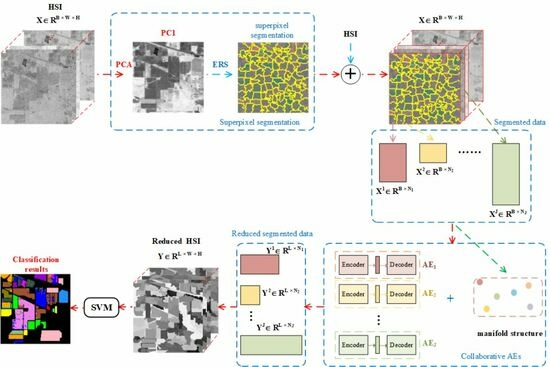
A Collaborative Superpixelwise Autoencoder for Unsupervised Dimension Reduction in Hyperspectral Images
Abstract
:1. Introduction
2. Related Works
2.1. Entropy Rate Superpixel Segmentation Model
2.2. Locally Linear Embedding Model
2.3. Auto-Encoder Model
3. Collaborative Superpixelwise Auto-Encoder
3.1. Superpixel Segmentation
3.2. Collaborative AEs
3.2.1. Learning the Manifold Structure among Superpixels
3.2.2. AE Model with Manifold Constraints
3.3. Computational Analysis of ColAE
| Algorithm 1 Procedures of ColAE. |
| Input: An HSI , the number of superpixels J, the number of nearest neighbors K in LLE, the balancing weight , the dimensionality L for the code, the number of iteration T. Output: The output . 1: Reshape into 2D form, which is . Use PCA to reduce the dimensionality of to 1, and reshape it into the image with three channels; 2: Apply ERS algorithm to segment the image into J non-overlapped regions; 3: Use Equation (7) to compute the mean vector for each superpixel. Then, calculate the weights for each mean vector according to Equation (2); 4: Use Xavier initialization to initial the parameters in ; 5: for to T do 6: Calculate the loss by Equation (11); 7: Calculate the gradient of using existing optimizer, and update the parameters by ; 8: end for 9: Compute the code by , then reshape the code into . 10: return . |
4. Experimental Results
4.1. Data Sets
- (1)
- Indian Pines. The Indian Pines data set was collected by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor over an agricultural area in Indiana, USA. It consists of pixels and 224 spectral bands, covering a wide range of wavelengths from 400 to 2500 nm. In this paper, 24 bands covering the region of water absorption are removed, and a total of 200 bands are used. The data set contains 16 different classes, including various crops, bare soil, and human-made structures. Approximately 10,249 samples with labels are from the ground-truth map.
- (2)
- University of Pavia. The University of Pavia data set was acquired by the Reflective Optics System Imaging Spectrometer (ROSIS) sensor over an agricultural area in Pavia, Italy. It consists of pixels and 115 spectral bands, covering wavelengths from 430 to 860 nm. A total of 12 noisy and water bands are removed, and a total of 103 bands are preserved. The data set contains nine different classes, including various crops, bare soil, and meadows. Approximately 42,776 samples with labels are from the ground-truth map.
- (3)
- Salinas. The Salinas data set was collected by the AVIRIS sensor over an agricultural area in Salinas Valley, California, USA. It consists of pixels and 224 spectral bands, covering wavelengths from 400 to 2500 nm. A total of 20 bands are removed for noisy and water bands, and 204 bands are used in our experiments. The data set contains 16 different classes, including various crops, bare soil, and human-made structures. A total of 53,129 labeled samples are used in our experiments.
4.2. Experimental Setup
4.3. Comparisons with Other Algorithms
4.4. Parameter Analyses
4.4.1. The Effect of the Dimensionality of the Code
4.4.2. The Effects of the Number of Superpixels, Number of Nearest Neighbors, and Balance Weight
4.4.3. Execution Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature extraction for hyperspectral imagery: The evolution from shallow to deep: Overview and toolbox. IEEE Geosci. Remote Sens. Mag. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Jia, X.; Kuo, B.C.; Crawford, M.M. Feature mining for hyperspectral image classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Schwaller, M.R. A geobotanical investigation based on linear discriminant and profile analyses of airborne thematic mapper simulator data. Remote Sens. Environ. 1987, 23, 23–34. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Du, Q. Modified Fisher’s linear discriminant analysis for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 503–507. [Google Scholar] [CrossRef]
- Fabiyi, S.D.; Murray, P.; Zabalza, J.; Ren, J. Folded LDA: Extending the linear discriminant analysis algorithm for feature extraction and data reduction in hyperspectral remote sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12312–12331. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E.; Bruce, L.M. Locality-preserving discriminant analysis in kernel-induced feature spaces for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2011, 8, 894–898. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Q.; Li, X. Discriminant analysis with graph learning for hyperspectral image classification. Remote Sens. 2018, 10, 836. [Google Scholar] [CrossRef]
- Luo, F.; Zhang, L.; Du, B.; Zhang, L. Dimensionality reduction with enhanced hybrid-graph discriminant learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5336–5353. [Google Scholar] [CrossRef]
- Ly, N.H.; Du, Q.; Fowler, J.E. Sparse graph-based discriminant analysis for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3872–3884. [Google Scholar]
- Luo, F.; Zhang, L.; Zhou, X.; Guo, T.; Cheng, Y.; Yin, T. Sparse-adaptive hypergraph discriminant analysis for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1082–1086. [Google Scholar] [CrossRef]
- Lim, S.; Sohn, K.H.; Lee, C. Principal component analysis for compression of hyperspectral images. In Proceedings of the IGARSS 2001, Sydney, NSW, Australia, 9–13 July 2001; Volume 1, pp. 97–99. [Google Scholar]
- Rodarmel, C.; Shan, J. Principal component analysis for hyperspectral image classification. Surv. Land Inf. Sci. 2002, 62, 115–122. [Google Scholar]
- Machidon, A.L.; Del Frate, F.; Picchiani, M.; Machidon, O.M.; Ogrutan, P.L. Geometrical approximated principal component analysis for hyperspectral image analysis. Remote Sens. 2020, 12, 1698. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Zhu, X.X. Learning a robust local manifold representation for hyperspectral dimensionality reduction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2960–2975. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, M.; Shen, Y. Learning a local manifold representation based on improved neighborhood rough set and LLE for hyperspectral dimensionality reduction. Signal Process. 2019, 164, 20–29. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Marsheva, T.V.B.; Zhou, D. Semi-supervised graph-based hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3044–3054. [Google Scholar] [CrossRef]
- Liao, W.; Pizurica, A.; Scheunders, P.; Philips, W.; Pi, Y. Semisupervised local discriminant analysis for feature extraction in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2012, 51, 184–198. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L. Sparse dimensionality reduction of hyperspectral image based on semi-supervised local Fisher discriminant analysis. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 122–129. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Zhou, P.; Han, J.; Cheng, G.; Zhang, B. Learning compact and discriminative stacked autoencoder for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4823–4833. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, L.; Zhu, L.; Yokoya, N.; Jia, X. Fine-grained classification of hyperspectral imagery based on deep learning. Remote Sens. 2019, 11, 2690. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature extraction with multiscale covariance maps for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 755–769. [Google Scholar] [CrossRef]
- Fang, L.; He, N.; Li, S.; Plaza, A.J.; Plaza, J. A new spatial–spectral feature extraction method for hyperspectral images using local covariance matrix representation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3534–3546. [Google Scholar] [CrossRef]
- Li, N.; Zhou, D.; Shi, J.; Wu, T.; Gong, M. Spectral-locational-spatial manifold learning for hyperspectral images dimensionality reduction. Remote Sens. 2021, 13, 2752. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, X.; Jiang, J.; Zhang, Y.; Liu, X.; Cai, Z. Spectral–spatial and superpixelwise PCA for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Zhang, A.; Pan, Z.; Fu, H.; Sun, G.; Rong, J.; Ren, J.; Jia, X.; Yao, Y. Superpixel nonlocal weighting joint sparse representation for hyperspectral image classification. Remote Sens. 2022, 14, 2125. [Google Scholar] [CrossRef]
- Zhang, L.; Su, H.; Shen, J. Hyperspectral dimensionality reduction based on multiscale superpixelwise kernel principal component analysis. Remote Sens. 2019, 11, 1219. [Google Scholar] [CrossRef]
- Liang, M.; Jiao, L.; Meng, Z. A superpixel-based relational auto-encoder for feature extraction of hyperspectral images. Remote Sens. 2019, 11, 2454. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the ICCV 2015, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- He, X.; Niyogi, P. Locality preserving projections. Adv. Neural Inf. Process. Syst. 2003, 16, 186–197. [Google Scholar]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. In International Conference on Artificial Neural Networks; Springer: Berlin, Germany, 1997; pp. 583–588. [Google Scholar]
- He, L.; Chen, X.; Li, J.; Xie, X. Multiscale superpixelwise locality preserving projection for hyperspectral image classification. Appl. Sci. 2019, 9, 2161. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Geng, Y.; Zhang, Z.; Li, X.; Du, Q. Unsupervised spatial-spectral feature learning by 3D convolutional autoencoder for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6808–6820. [Google Scholar] [CrossRef]
- Cao, Z.; Li, X.; Feng, Y.; Chen, S.; Xia, C.; Zhao, L. ContrastNet: Unsupervised feature learning by autoencoder and prototypical contrastive learning for hyperspectral imagery classification. Neurocomputing 2021, 460, 71–83. [Google Scholar] [CrossRef]
- Bakır, G.H.; Weston, J.; Schölkopf, B. Learning to find pre-images. Adv. Neural Inf. Process. Syst. 2004, 16, 449–456. [Google Scholar]








| Indian Pines | University of Pavia | Salinas | ||||
|---|---|---|---|---|---|---|
| Class Name | Numbers | Class Name | Numbers | Class Name | Numbers | |
| c1 | Alfalfa | 46 | Asphalt | 6631 | Broccoli green weeds 1 | 2009 |
| c2 | Corn-notill | 1428 | Meadows | 18,649 | Broccoli green weeds 2 | 3726 |
| c3 | Corn-mintill | 830 | Gravel | 2099 | Fallow | 1976 |
| c4 | Corn | 237 | Tress | 3064 | Fallow rough plow | 1394 |
| c5 | Grass-pasture | 483 | Mental sheets | 1345 | Fallow smooth | 2678 |
| c6 | Grass-tress | 730 | Bare soil | 5029 | Stubble | 3959 |
| c7 | Grass-pasture-mowed | 28 | Bitumen | 1330 | Celery | 2579 |
| c8 | Hay-windrowed | 478 | Bricks | 3682 | Grapes untrained | 11271 |
| c9 | Oats | 20 | shadow | 947 | Soil vineyard develop | 6203 |
| c10 | Soybean-nottill | 972 | Corn senesced green seed | 3278 | ||
| c11 | Soybean-mintill | 2455 | Lettuce romaine 4wk | 1068 | ||
| c12 | Soybean-clean | 593 | Lettuce romaine 5wk | 1927 | ||
| c13 | Wheat | 205 | Lettuce romaine 6wk | 916 | ||
| c14 | Woods | 1265 | Lettuce romaine 7wk | 1070 | ||
| c15 | Buildings-grass-trees-dirves | 386 | Vineyard untrained | 7268 | ||
| c16 | Stone-steel-towers | 93 | Vineyard vertical trellis | 1807 | ||
| Total number | 10,249 | Total number | 42,776 | Total number | 54,129 | |
| Layer | Output Shape | ||
|---|---|---|---|
| Indian Pines | University of Pavia | Salinas | |
| input | [−1, 200] | [−1, 103] | [−1, 203] |
| Linear | [−1, 100] | [−1, 75] | [−1, 100] |
| Tanh | [−1, 100] | [−1, 75] | [−1, 100] |
| Linear | [−1, L] | [−1, L] | [−1, L] |
| Linear | [−1, 100] | [−1, 75] | [−1, 100] |
| Tanh | [−1, 100] | [−1, 75] | [−1, 100] |
| Linear | [−1, 200] | [−1, 103] | [−1, 203] |
| Data Set | T.N.s/C | Metric | Raw | PCA | LPP | KPCA | AE | Super PCA | Super LPP | Super KPCA | Contrast Net | CAE | SuperAE | ColAE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Indian Pines | 3 | OA(%) | 40.89 | 40.89 | 45.01 | 40.81 | 40.37 | 54.55 | 58.28 | 48.28 | 55.20 | 54.50 | 67.78 | 68.81 |
| AA(%) | 44.30 | 44.21 | 45.60 | 43.97 | 44.00 | 74.69 | 71.32 | 53.78 | 55.31 | 54.06 | 70.15 | 66.41 | ||
| kappa | 0.3455 | 0.3455 | 0.3870 | 0.3451 | 0.3404 | 0.4837 | 0.5276 | 0.4415 | 0.4977 | 0.4942 | 0.6397 | 0.6518 | ||
| 5 | OA(%) | 47.41 | 46.98 | 53.56 | 47.52 | 47.72 | 69.84 | 65.86 | 64.30 | 67.88 | 64.28 | 77.20 | 77.72 | |
| AA(%) | 48.60 | 48.38 | 52.23 | 48.43 | 48.65 | 80.91 | 76.43 | 61.22 | 60.73 | 60.81 | 77.49 | 74.79 | ||
| kappa | 0.4156 | 0.4115 | 0.4818 | 0.4158 | 0.4190 | 0.6560 | 0.6149 | 0.6061 | 0.6364 | 0.5992 | 0.7429 | 0.7493 | ||
| 7 | OA(%) | 51.38 | 50.84 | 58.47 | 51.46 | 50.65 | 77.01 | 75.00 | 77.62 | 73.36 | 70.20 | 81.34 | 82.03 | |
| AA(%) | 51.53 | 50.77 | 55.71 | 50.92 | 50.54 | 86.13 | 81.14 | 90.35 | 66.80 | 65.16 | 80.78 | 80.18 | ||
| kappa | 0.4578 | 0.4516 | 0.5351 | 0.4566 | 0.4509 | 0.7378 | 0.7178 | 0.7364 | 0.6995 | 0.6651 | 0.7892 | 0.7969 | ||
| 10 | OA(%) | 54.68 | 53.98 | 61.31 | 54.44 | 53.71 | 83.19 | 83.80 | 73.91 | 76.60 | 75.83 | 85.09 | 85.10 | |
| AA(%) | 54.00 | 53.46 | 58.90 | 53.66 | 52.98 | 85.31 | 80.25 | 87.48 | 70.11 | 69.57 | 82.84 | 81.96 | ||
| kappa | 0.4943 | 0.4867 | 0.5669 | 0.4908 | 0.4840 | 0.8084 | 0.8092 | 0.7055 | 0.7369 | 0.7278 | 0.8311 | 0.8312 | ||
| 15 | OA(%) | 58.83 | 57.60 | 64.56 | 58.29 | 56.86 | 87.81 | 86.23 | 87.82 | 80.02 | 80.96 | 87.69 | 88.02 | |
| AA(%) | 56.67 | 55.70 | 60.88 | 55.80 | 54.66 | 86.81 | 80.64 | 89.99 | 70.17 | 73.07 | 83.38 | 82.04 | ||
| kappa | 0.5401 | 0.5267 | 0.6034 | 0.5328 | 0.5190 | 0.8611 | 0.8442 | 0.8620 | 0.7803 | 0.7852 | 0.8603 | 0.8640 | ||
| 20 | OA(%) | 61.57 | 60.53 | 67.26 | 61.26 | 59.83 | 89.13 | 88.24 | 87.93 | 84.44 | 84.46 | 89.18 | 89.20 | |
| AA(%) | 57.39 | 56.48 | 60.89 | 56.98 | 56.35 | 85.17 | 83.61 | 89.66 | 75.13 | 74.89 | 81.28 | 80.98 | ||
| kappa | 0.5694 | 0.5578 | 0.6326 | 0.5654 | 0.5503 | 0.8765 | 0.8726 | 0.8631 | 0.8237 | 0.8241 | 0.8771 | 0.8773 | ||
| University of Pavia | 3 | OA(%) | 60.50 | 60.55 | 54.40 | - | 61.03 | 78.48 | 67.41 | 81.83 | 79.71 | 70.52 | 83.66 | 84.04 |
| AA(%) | 64.73 | 64.62 | 56.80 | - | 65.25 | 73.94 | 72.72 | 73.99 | 81.67 | 74.61 | 83.54 | 84.01 | ||
| kappa | 0.5154 | 0.5157 | 0.4341 | - | 0.5203 | 0.7222 | 0.5736 | 0.7615 | 0.7333 | 0.6239 | 0.7911 | 0.7957 | ||
| 5 | OA(%) | 65.77 | 65.73 | 58.22 | - | 65.03 | 82.02 | 71.49 | 85.06 | 83.49 | 78.89 | 87.21 | 87.40 | |
| AA(%) | 68.53 | 68.49 | 59.97 | - | 68.56 | 78.94 | 75.25 | 80.49 | 85.11 | 81.10 | 86.40 | 86.70 | ||
| kappa | 0.5731 | 0.5727 | 0.4788 | - | 0.5671 | 0.7675 | 0.6297 | 0.8061 | 0.7813 | 0.7300 | 0.8366 | 0.8390 | ||
| 7 | OA(%) | 70.36 | 70.34 | 60.02 | - | 69.01 | 84.40 | 74.98 | 86.92 | 87.81 | 84.75 | 88.83 | 89.43 | |
| AA(%) | 72.03 | 71.92 | 61.92 | - | 70.70 | 82.89 | 79.18 | 83.32 | 86.66 | 84.79 | 87.24 | 87.65 | ||
| kappa | 0.6253 | 0.6247 | 0.5016 | - | 0.6107 | 0.7988 | 0.6714 | 0.8305 | 0.8393 | 0.8033 | 0.8564 | 0.8638 | ||
| 10 | OA(%) | 72.66 | 72.48 | 63.43 | - | 71.46 | 89.01 | 80.24 | 91.09 | 91.95 | 88.83 | 92.53 | 92.74 | |
| AA(%) | 74.12 | 73.95 | 64.54 | - | 72.85 | 87.22 | 83.33 | 89.87 | 90.37 | 87.97 | 90.94 | 91.10 | ||
| kappa | 0.6553 | 0.6532 | 0.5450 | - | 0.6414 | 0.8577 | 0.7387 | 0.8836 | 0.8939 | 0.8545 | 0.9031 | 0.9057 | ||
| 15 | OA(%) | 77.90 | 78.26 | 65.48 | - | 76.26 | 91.86 | 81.26 | 92.30 | 94.38 | 92.03 | 94.76 | 94.93 | |
| AA(%) | 77.03 | 77.13 | 66.57 | - | 75.32 | 89.56 | 83.74 | 91.29 | 92.70 | 90.55 | 93.10 | 93.29 | ||
| kappa | 0.7169 | 0.7210 | 0.5734 | - | 0.6975 | 0.8938 | 0.7549 | 0.8982 | 0.9257 | 0.8957 | 0.9314 | 0.9337 | ||
| 20 | OA(%) | 80.57 | 80.66 | 70.13 | - | 79.35 | 92.60 | 82.48 | 91.37 | 95.01 | 94.08 | 95.16 | 95.39 | |
| AA(%) | 78.84 | 78.84 | 69.32 | - | 77.40 | 90.79 | 85.38 | 89.52 | 93.34 | 92.49 | 93.29 | 93.61 | ||
| kappa | 0.7497 | 0.7512 | 0.6254 | - | 0.7346 | 0.9034 | 0.7714 | 0.8865 | 0.9343 | 0.9222 | 0.9365 | 0.9396 | ||
| Salinas | 3 | OA(%) | 79.13 | 79.15 | 78.22 | - | 80.86 | 70.21 | 75.30 | 76.84 | 80.21 | 80.84 | 88.14 | 89.46 |
| AA(%) | 83.48 | 83.48 | 83.38 | - | 86.34 | 73.75 | 79.16 | 89.20 | 81.93 | 84.38 | 90.91 | 92.43 | ||
| kappa | 0.7687 | 0.7688 | 0.7598 | - | 0.7877 | 0.6729 | 0.7217 | 0.7435 | 0.7808 | 0.7874 | 0.8681 | 0.8828 | ||
| 5 | OA(%) | 81.13 | 81.09 | 82.21 | - | 82.48 | 80.67 | 80.97 | 80.46 | 84.98 | 87.12 | 90.97 | 91.97 | |
| AA(%) | 85.86 | 85.88 | 87.55 | - | 87.96 | 84.59 | 87.58 | 78.96 | 86.78 | 89.04 | 94.29 | 94.77 | ||
| kappa | 0.7906 | 0.7901 | 0.8035 | - | 0.8056 | 0.7859 | 0.7871 | 0.7835 | 0.8330 | 0.8570 | 0.8997 | 0.9108 | ||
| 7 | OA(%) | 83.68 | 83.66 | 83.58 | - | 84.63 | 88.20 | 90.21 | 87.46 | 87.18 | 89.92 | 93.25 | 94.01 | |
| AA(%) | 87.79 | 87.74 | 88.09 | - | 89.47 | 90.75 | 93.69 | 90.28 | 88.62 | 91.18 | 95.94 | 96.21 | ||
| kappa | 0.8188 | 0.8186 | 0.8176 | - | 0.8293 | 0.8692 | 0.8906 | 0.8602 | 0.8576 | 0.8883 | 0.9251 | 0.9334 | ||
| 10 | OA(%) | 85.45 | 85.27 | 84.71 | - | 85.94 | 91.38 | 90.59 | 89.58 | 88.71 | 91.98 | 94.53 | 94.83 | |
| AA(%) | 89.15 | 89.09 | 89.30 | - | 90.34 | 94.45 | 93.99 | 93.03 | 90.26 | 92.91 | 96.51 | 96.61 | ||
| kappa | 0.8382 | 0.8362 | 0.8305 | - | 0.8437 | 0.9036 | 0.8948 | 0.8892 | 0.8747 | 0.9109 | 0.9392 | 0.9426 | ||
| 15 | OA(%) | 86.89 | 86.77 | 86.04 | - | 87.28 | 95.26 | 92.69 | 92.36 | 91.59 | 94.10 | 96.06 | 96.14 | |
| AA(%) | 90.63 | 90.55 | 90.68 | - | 91.45 | 96.10 | 94.32 | 94.66 | 92.48 | 94.69 | 97.18 | 97.27 | ||
| kappa | 0.8543 | 0.8530 | 0.8450 | - | 0.8587 | 0.9471 | 0.9174 | 0.9146 | 0.9066 | 0.9345 | 0.9562 | 0.9571 | ||
| 20 | OA(%) | 88.14 | 88.16 | 88.39 | - | 88.16 | 97.06 | 94.62 | 94.25 | 92.84 | 95.52 | 97.06 | 97.20 | |
| AA(%) | 91.44 | 91.48 | 91.80 | - | 92.09 | 96.89 | 93.43 | 94.38 | 93.70 | 95.91 | 97.55 | 97.63 | ||
| kappa | 0.8680 | 0.8682 | 0.8809 | - | 0.8666 | 0.9633 | 0.9403 | 0.9359 | 0.9204 | 0.9503 | 0.9673 | 0.9687 |
| Raw | PCA | LPP | KPCA | AE | Super PCA | Super LPP | Super KPCA | Contrast Net | CAE | SuperAE | ColAE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | 34.70 | 35.91 | 40.57 | 31.72 | 31.17 | 100.00 | 100.00 | 100.00 | 53.45 | 64.65 | 100.00 | 98.81 |
| c2 | 47.50 | 45.38 | 54.40 | 46.80 | 44.93 | 78.82 | 75.48 | 58.02 | 78.22 | 72.38 | 78.10 | 78.89 |
| c3 | 36.87 | 34.91 | 42.88 | 36.10 | 38.18 | 91.56 | 99.53 | 96.23 | 68.63 | 75.18 | 87.41 | 83.61 |
| c4 | 32.52 | 30.66 | 40.47 | 31.64 | 28.79 | 82.44 | 69.10 | 86.56 | 48.66 | 58.29 | 69.31 | 65.46 |
| c5 | 66.76 | 65.47 | 67.28 | 66.76 | 63.60 | 98.55 | 97.01 | 99.76 | 91.74 | 85.49 | 97.31 | 96.12 |
| c6 | 89.97 | 89.40 | 88.21 | 89.38 | 88.07 | 99.80 | 99.43 | 100.00 | 93.11 | 90.27 | 99.76 | 99.89 |
| c7 | 22.17 | 20.98 | 23.44 | 21.52 | 20.77 | 50.80 | 39.39 | 34.21 | 26.00 | 45.89 | 59.74 | 51.95 |
| c8 | 98.39 | 98.32 | 96.91 | 98.33 | 98.41 | 98.57 | 98.72 | 100.00 | 97.68 | 94.95 | 99.98 | 100.00 |
| c9 | 8.25 | 7.54 | 14.74 | 7.51 | 5.97 | 45.59 | 10.20 | 100.00 | 22.73 | 16.52 | 35.19 | 21.74 |
| c10 | 50.52 | 48.54 | 59.45 | 47.62 | 48.85 | 90.91 | 95.05 | 95.83 | 79.52 | 80.00 | 83.84 | 85.78 |
| c11 | 70.36 | 72.25 | 80.06 | 70.02 | 73.29 | 87.94 | 95.61 | 98.71 | 87.54 | 89.22 | 93.54 | 94.20 |
| c12 | 43.09 | 39.19 | 54.22 | 41.98 | 33.23 | 85.07 | 87.76 | 88.77 | 68.76 | 72.79 | 70.46 | 76.54 |
| c13 | 82.80 | 81.65 | 83.30 | 80.81 | 82.05 | 100.00 | 100.00 | 100.00 | 81.66 | 84.36 | 99.79 | 100.00 |
| c14 | 92.84 | 92.56 | 93.84 | 92.36 | 92.28 | 92.49 | 71.27 | 98.42 | 93.62 | 94.81 | 98.56 | 98.56 |
| c15 | 36.92 | 35.50 | 42.04 | 37.32 | 33.08 | 97.51 | 91.96 | 99.46 | 66.97 | 71.13 | 92.72 | 92.18 |
| c16 | 93.10 | 92.98 | 92.32 | 93.00 | 91.87 | 88.96 | 59.69 | 83.87 | 64.46 | 73.20 | 68.31 | 68.88 |
| AA | 56.67 | 55.70 | 60.88 | 55.80 | 54.66 | 86.81 | 80.64 | 89.99 | 70.17 | 73.07 | 83.38 | 82.04 |
| OA | 58.83 | 57.60 | 64.56 | 58.29 | 56.86 | 87.81 | 86.23 | 87.82 | 80.20 | 80.96 | 87.69 | 88.02 |
| Raw | PCA | LPP | AE | Super PCA | Super LPP | Super KPCA | Contrast Net | CAE | SuperAE | ColAE | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | 93.94 | 93.93 | 92.52 | 93.55 | 92.42 | 93.51 | 89.13 | 96.12 | 95.21 | 97.53 | 97.68 |
| c2 | 91.48 | 90.93 | 88.97 | 91.67 | 98.33 | 86.62 | 97.58 | 99.08 | 98.87 | 98.88 | 98.85 |
| c3 | 59.62 | 59.37 | 46.08 | 55.17 | 94.71 | 89.98 | 98.53 | 93.16 | 90.39 | 93.60 | 93.63 |
| c4 | 70.22 | 69.52 | 65.85 | 69.50 | 69.54 | 80.28 | 76.85 | 84.02 | 81.28 | 77.95 | 78.38 |
| c5 | 95.80 | 96.01 | 74.25 | 96.43 | 98.00 | 96.95 | 96.61 | 99.98 | 98.94 | 99.86 | 99.86 |
| c6 | 62.08 | 63.36 | 44.53 | 62.07 | 99.02 | 54.54 | 98.56 | 96.53 | 95.06 | 98.00 | 99.16 |
| c7 | 57.60 | 57.69 | 45.10 | 51.67 | 78.53 | 75.68 | 77.10 | 89.19 | 90.38 | 80.96 | 82.28 |
| c8 | 57.60 | 57.69 | 45.10 | 51.67 | 78.53 | 75.68 | 71.89 | 83.61 | 84.28 | 80.96 | 82.28 |
| c9 | 99.94 | 99.95 | 99.99 | 99.95 | 99.81 | 99.46 | 99.43 | 98.30 | 97.98 | 99.84 | 99.88 |
| AA | 78.84 | 78.84 | 69.32 | 77.40 | 90.79 | 85.38 | 89.52 | 93.34 | 92.49 | 93.30 | 93.61 |
| OA | 80.57 | 80.66 | 70.13 | 79.35 | 92.60 | 82.48 | 91.37 | 95.02 | 94.08 | 95.16 | 95.39 |
| Raw | PCA | LPP | AE | Super PCA | Super LPP | Super KPCA | Contrast Net | CAE | SuperAE | ColAE | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | 97.70 | 97.70 | 99.38 | 98.74 | 99.97 | 100.00 | 100.00 | 97.07 | 98.84 | 100.00 | 100.00 |
| c2 | 98.46 | 98.43 | 98.37 | 99.07 | 99.85 | 99.17 | 100.00 | 96.31 | 99.00 | 99.88 | 99.88 |
| c3 | 91.23 | 91.16 | 89.20 | 91.73 | 98.52 | 98.23 | 96.05 | 95.95 | 96.08 | 99.99 | 99.79 |
| c4 | 96.92 | 96.93 | 98.76 | 97.25 | 96.70 | 95.86 | 97.23 | 93.71 | 82.88 | 96.57 | 96.57 |
| c5 | 96.71 | 96.69 | 95.07 | 96.58 | 95.67 | 77.29 | 95.76 | 91.82 | 98.68 | 98.29 | 98.14 |
| c6 | 99.78 | 99.78 | 99.72 | 99.95 | 99.18 | 100.00 | 99.82 | 99.68 | 99.72 | 100.00 | 100.00 |
| c7 | 98.41 | 98.35 | 98.66 | 99.03 | 99.70 | 99.68 | 99.83 | 94.04 | 99.39 | 99.76 | 99.80 |
| c8 | 78.45 | 77.98 | 78.25 | 78.54 | 98.33 | 99.92 | 91.29 | 90.08 | 95.41 | 98.04 | 97.18 |
| c9 | 98.89 | 98.84 | 99.24 | 99.23 | 98.05 | 98.04 | 90.32 | 98.61 | 99.67 | 99.13 | 99.12 |
| c10 | 84.89 | 85.56 | 81.05 | 86.07 | 94.58 | 88.31 | 88.43 | 95.29 | 95.48 | 91.68 | 91.85 |
| c11 | 78.10 | 77.99 | 75.48 | 80.91 | 88.41 | 62.57 | 89.76 | 77.67 | 89.15 | 98.79 | 98.68 |
| c12 | 95.79 | 95.82 | 96.70 | 96.69 | 94.39 | 97.79 | 83.71 | 96.75 | 97.50 | 98.79 | 98.82 |
| c13 | 94.76 | 94.65 | 98.99 | 96.43 | 98.21 | 99.55 | 96.10 | 93.98 | 98.56 | 98.63 | 98.12 |
| c14 | 86.24 | 86.06 | 92.66 | 89.05 | 90.93 | 88.71 | 85.20 | 97.68 | 97.78 | 91.63 | 92.63 |
| c15 | 68.46 | 69.54 | 69.06 | 66.18 | 98.57 | 90.82 | 99.87 | 84.75 | 87.41 | 90.34 | 92.32 |
| c16 | 98.22 | 98.28 | 98.16 | 98.01 | 99.15 | 98.99 | 96.77 | 95.85 | 98.99 | 99.29 | 99.25 |
| AA | 91.44 | 91.48 | 91.80 | 92.09 | 96.89 | 93.43 | 94.38 | 93.70 | 95.91 | 97.55 | 97.63 |
| OA | 88.14 | 88.16 | 88.39 | 88.16 | 97.06 | 94.62 | 94.25 | 92.84 | 95.52 | 97.06 | 97.20 |
| PCA | LPP | KPCA | AE | SuperPCA | SuperLPP | SuperKPCA | SuperAE | ColAE | |
|---|---|---|---|---|---|---|---|---|---|
| Indian Pines | 0.09 | 85.12 | 628.87 | 53.23 | 1.03 | 90.64 | 524.66 | 58.34 | 58.45 |
| University of Pavia | 0.91 | 104.21 | - | 214.12 | 1.22 | 277.22 | 1245.12 | 158.58 | 160.10 |
| Salinas | 0.73 | 102.12 | - | 198.72 | 1.47 | 232.98 | 1862.23 | 132.43 | 134.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, C.; Zheng, L.; Feng, L.; Yang, F.; Guo, Z.; Ma, M. A Collaborative Superpixelwise Autoencoder for Unsupervised Dimension Reduction in Hyperspectral Images. Remote Sens. 2023, 15, 4211. https://doi.org/10.3390/rs15174211
Yao C, Zheng L, Feng L, Yang F, Guo Z, Ma M. A Collaborative Superpixelwise Autoencoder for Unsupervised Dimension Reduction in Hyperspectral Images. Remote Sensing. 2023; 15(17):4211. https://doi.org/10.3390/rs15174211
Chicago/Turabian StyleYao, Chao, Lingfeng Zheng, Longchao Feng, Fan Yang, Zehua Guo, and Miao Ma. 2023. "A Collaborative Superpixelwise Autoencoder for Unsupervised Dimension Reduction in Hyperspectral Images" Remote Sensing 15, no. 17: 4211. https://doi.org/10.3390/rs15174211
APA StyleYao, C., Zheng, L., Feng, L., Yang, F., Guo, Z., & Ma, M. (2023). A Collaborative Superpixelwise Autoencoder for Unsupervised Dimension Reduction in Hyperspectral Images. Remote Sensing, 15(17), 4211. https://doi.org/10.3390/rs15174211