A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression
Abstract
:1. Introduction
2. Methods
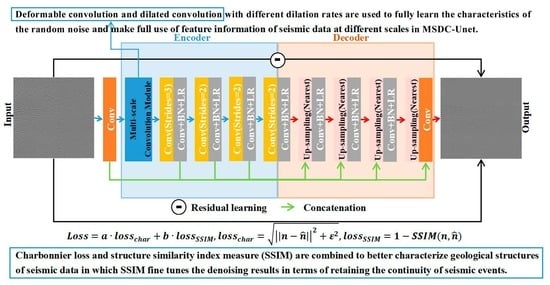
2.1. Network Architecture
2.2. Multi-Scale Convolution Module
2.3. Loss Function
2.4. Synthetic Dataset
2.5. Selection of Parameters and Quantitative Analysis of Denoising Performance
3. Results
3.1. Synthetic Examples
3.2. Field Examples
4. Discussion
4.1. Parameters Selection in Multi-Scale Convolution Module
4.2. Loss Function Parameters Selection
4.3. Strategy of Modifying the Network Structure
4.4. Future Works
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, G.; Yang, W.; Liu, Y.; Wang, H.; Huang, X. Salt Structure Elastic Full Waveform Inversion Based on the Multiscale Signed Envelope. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Chen, G.; Yang, W.; Wang, H.; Zhou, H.; Huang, X. Elastic Full Waveform Inversion Based on Full-Band Seismic Data Reconstructed by Dual Deconvolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yang, L.; Fomel, S.; Wang, S.; Chen, X.; Chen, W.; Saad, O.M.; Chen, Y. Denoising of distributed acoustic sensing data using supervised deep learning. Geophysics 2023, 88, WA91–WA104. [Google Scholar] [CrossRef]
- Abma, R.; Claerbout, J. Lateral prediction for noise attenuation by t-x and f-x techniques. Geophysics 1995, 60, 1887–1896. [Google Scholar] [CrossRef]
- Chen, T.; Ma, K.K.; Chen, L.H. Tri-state median filter for image denoising. IEEE Trans. Image Process. 1999, 8, 1834–1838. [Google Scholar] [CrossRef]
- Andrews, H.; Patterson, C. Singular value decompositions and digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 26–53. [Google Scholar] [CrossRef]
- Bi, W.; Zhao, Y.; An, C.; Hu, S. Clutter Elimination and Random-Noise Denoising of GPR Signals Using an SVD Method Based on the Hankel Matrix in the Local Frequency Domain. Sensors 2018, 18, 3422. [Google Scholar] [CrossRef]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Hyperspectral Image Denoising via Noise-Adjusted Iterative Low-Rank Matrix Approximation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3050–3061. [Google Scholar] [CrossRef]
- Huang, W.; Wang, R.; Chen, Y.; Li, H.; Gan, S. Damped multichannel singular spectrum analysis for 3D random noise attenuation. Geophysics 2016, 81, V261–V270. [Google Scholar] [CrossRef]
- Zhuang, L.; Bioucas-Dias, J.M. Fast Hyperspectral Image Denoising and Inpainting Based on Low-Rank and Sparse Representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 730–742. [Google Scholar] [CrossRef]
- Feng, J.; Li, X.; Liu, X.; Chen, C. Multigranularity Feature Fusion Convolutional Neural Network for Seismic Data Denoising. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Li, P.; Ren, P.; Zhang, X.; Wang, Q.; Zhu, X.; Wang, L. Region-Wise Deep Feature Representation for Remote Sensing Images. Remote Sens. 2018, 10, 871. [Google Scholar] [CrossRef]
- He, C.; Shi, Z.; Qu, T.; Wang, D.; Liao, M. Lifting Scheme-Based Deep Neural Network for Remote Sensing Scene Classification. Remote Sens. 2019, 11, 2648. [Google Scholar] [CrossRef]
- Tao, Y.; Muller, J.P. Super-Resolution Restoration of MISR Images Using the UCL MAGiGAN System. Remote Sens. 2019, 11, 52. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Zhang, C.; Atkinson, P.M.; Tan, X.; Jian, X.; Zhou, X.; Li, Y. Two-Phase Object-Based Deep Learning for Multi-Temporal SAR Image Change Detection. Remote Sens. 2020, 12, 548. [Google Scholar] [CrossRef]
- Pei, J.; Huo, W.; Wang, C.; Huang, Y.; Zhang, Y.; Wu, J.; Yang, J. Multiview Deep Feature Learning Network for SAR Automatic Target Recognition. Remote Sens. 2021, 13, 1455. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep Learning for Geophysics: Current and Future Trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, N.; Lu, W.; Wang, J. Deep-learning-based seismic data interpolation: A preliminary result. Geophysics 2019, 84, V11–V20. [Google Scholar] [CrossRef]
- Liu, D.; Wang, W.; Wang, X.; Wang, C.; Pei, J.; Chen, W. Poststack Seismic Data Denoising Based on 3-D Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1598–1629. [Google Scholar] [CrossRef]
- Sang, W.; Yuan, S.; Yong, X.; Jiao, X.; Wang, S. DCNNs-Based Denoising with a Novel Data Generation for Multidimensional Geological Structures Learning. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1861–1865. [Google Scholar] [CrossRef]
- Wu, B.; Meng, D.; Zhao, H. Semi-Supervised Learning for Seismic Impedance Inversion Using Generative Adversarial Networks. Remote Sens. 2021, 13, 909. [Google Scholar] [CrossRef]
- Yu, J.; Wu, B. Attention and Hybrid Loss Guided Deep Learning for Consecutively Missing Seismic Data Reconstruction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–8. [Google Scholar] [CrossRef]
- Zhao, H.; Bai, T.; Wang, Z. A Natural Images Pre-Trained Deep Learning Method for Seismic Random Noise Attenuation. Remote Sens. 2022, 14, 263. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Yang, X.; Li, S.; Chen, Z.; Chanussot, J.; Jia, X.; Zhang, B.; Li, B.; Chen, P. An attention-fused network for semantic segmentation of very-high-resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2021, 177, 238–262. [Google Scholar] [CrossRef]
- Gui, Y.; Li, W.; Xia, X.G.; Tao, R.; Yue, A. Infrared Attention Network for Woodland Segmentation Using Multispectral Satellite Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhu, W.; Mousavi, S.M.; Beroza, G.C. Seismic Signal Denoising and Decomposition Using Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9476–9488. [Google Scholar] [CrossRef]
- Kaur, H.; Fomel, S.; Pham, N. Seismic ground-roll noise attenuation using deep learning. Geophys. Prospect. 2020, 68, 2064–2077. [Google Scholar] [CrossRef]
- Dong, X.; Wang, H.; Zhong, T.; Li, Y. PDN: An effective denoising network for land prestack seismic data. J. Appl. Geophys. 2022, 199, 104558. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, M.; Zhao, Y.; Wu, N. Distributed Acoustic Sensing Vertical Seismic Profile Data Denoising Based on Multistage Denoising Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Liu, D.; Deng, Z.; Wang, C.; Wang, X.; Chen, W. An Unsupervised Deep Learning Method for Denoising Prestack Random Noise. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhong, T.; Cheng, M.; Lu, S.; Dong, X.; Li, Y. RCEN: A Deep-Learning-Based Background Noise Suppression Method for DAS-VSP Records. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Saad, O.M.; Chen, Y. A fully unsupervised and highly generalized deep learning approach for random noise suppression. Geophys. Prospect. 2021, 69, 709–726. [Google Scholar] [CrossRef]
- Dong, X.; Li, Y.; Zhong, T.; Wu, N.; Wang, H. Random and Coherent Noise Suppression in DAS-VSP Data by Using a Supervised Deep Learning Method. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Hu, Z. Deep Learning for Simultaneous Seismic Image Super-Resolution and Denoising. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, S.; Cai, J.; Hong, L.; Zheng, J. Research on Deep Convolutional Neural Network Time-Frequency Domain Seismic Signal Denoising Combined With Residual Dense Blocks. Front. Earth Sci. 2021, 9, 681869. [Google Scholar] [CrossRef]
- Bai, T.; Zhao, H.; Wang, Z. A U-Net Based Deep Learning Approach for Seismic Random Noise Suppression. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 6165–6168. [Google Scholar]
- Zhao, H.; Bai, T.; Chen, Y. Background Noise Suppression for DAS-VSP Records Using GC-AB-Unet. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zhao, Q.; Miao, Z.; Xu, W.; Song, S. A multi-scale adaptive feature enhancement network for image denoising. In Proceedings of the Thirteenth International Conference on Signal Processing Systems (ICSPS 2021), Shanghai, China, 12–15 November 2021; Li, Q., Mao, K., Xie, Y., Eds.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2022; Volume 12171, p. 1217117. [Google Scholar]
- Ganley, D.C. A method for calculating synthetic seismograms which include the effects of absorption and dispersion. Geophysics 1981, 46, 1100–1107. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, J.; Peng, J. Extended reflectivity method for modelling the propagation of diffusive–Viscous wave in dip-layered media. Geophys. Prospect. 2017, 65, 246–258. [Google Scholar] [CrossRef]
- Martin, G.; Wiley, R.; Marfurt, K. Marmousi2: An elastic upgrade for Marmousi. Lead. Edge 2006, 25, 156–166. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, W.; Zhang, D.; Chen, W. An open-source Matlab code package for improved rank-reduction 3D seismic data denoising and reconstruction. Comput. Geosci. 2016, 95, 59–66. [Google Scholar] [CrossRef]
- Guo, L.; Luo, R.; Li, X.; Zhou, Y.; Juanjuan, T.; Lei, C. Seismic Random Noise Removal Based on a Multiscale Convolution and Densely Connected Network for Noise Level Evaluation. IEEE Access 2022, 10, 13911–13925. [Google Scholar] [CrossRef]




















| Datasets | The Training Datasets | The Test Datasets |
|---|---|---|
| VSP data | 800 | 139 |
| Reflection seismic data | 800 | 35 |
| Marmousi2 data | 800 | 180 |
| Bpvelanal2004 | 700 | - |
| Total | 3100 | 354 |
| Dataset | VSP Data | Reflection Seismic Data | Marmousi2 Data | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Evaluation indexes | SNR/dB | MSE | SSIM | SNR/dB | MSE | SSIM | SNR/dB | MSE | SSIM |
| Initial value | 9.31 | 0.938 | 5.16 | 0.01 | 0.849 | −0.92 | 0.629 | ||
| f-x filtering | 14.26 | 0.97 | 12.93 | 0.954 | 13.24 | 0.949 | |||
| DRR | 15.69 | 0.985 | 16.24 | 0.987 | 13.34 | 0.974 | |||
| DnCNN | 23.77 | 0.996 | 20.92 | 0.989 | 14.25 | 0.949 | |||
| U-Net | 24.54 | 0.987 | 22 | 0.93 | 14.82 | 0.941 | |||
| MSDC-Unet | |||||||||
| Number of Convolution Layers | Dilation Rate | Convolution Kernel | SNR/dB | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Branch1 | Branch2 | Branch3 | Branch1 | Branch2 | Branch3 | Branch1 | Branch2 | Branch3 | |
| 1 | 1 | 1 | 1 | 3 | 5 | 3 × 3 | 3 × 3 | 3 × 3 | 15.23 |
| , | , | ||||||||
| 2 | 2 | 2 | 1 | 3 | 5 | 3 × 3 | 3 × 3 | 3 × 3 | 14.82 |
| 3 | 3 | 3 | 1 | 3 | 5 | 3 × 3 | 3 × 3 | 3 × 3 | 13.74 |
| 1 | 2 | 3 | 1 | 2 | 2 | 1 × 1 | 1 × 1, 3 × 3 | 1 × 1, 3 × 3 | 15.13 |
| a | b | MSE | SNR/dB | |
|---|---|---|---|---|
| - | - | 0.0175 | 17.52 | |
| - | - | 0.0125 | 16.81 | |
| - | - | 0.0113 | 18.12 | |
| 0.9 | 0.1 | 0.0085 | 17.57 | |
| 0.99 | 0.01 | 0.0098 | 17.67 | |
| 0.995 | 0.005 | 0.0079 | 17.62 | |
| MFE | ✓ | ✓ | ||
| DC | ✓ | |||
| CS | ✓ | ✓ | ✓ | |
| SNR/dB | 12.51 | 14.93 | 16.08 | 17.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhou, Y.; Bai, T.; Chen, Y. A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression. Remote Sens. 2023, 15, 4569. https://doi.org/10.3390/rs15184569
Zhao H, Zhou Y, Bai T, Chen Y. A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression. Remote Sensing. 2023; 15(18):4569. https://doi.org/10.3390/rs15184569
Chicago/Turabian StyleZhao, Haixia, You Zhou, Tingting Bai, and Yuanzhong Chen. 2023. "A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression" Remote Sensing 15, no. 18: 4569. https://doi.org/10.3390/rs15184569
APA StyleZhao, H., Zhou, Y., Bai, T., & Chen, Y. (2023). A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression. Remote Sensing, 15(18), 4569. https://doi.org/10.3390/rs15184569