Enhancing Spatial Resolution of GNSS-R Soil Moisture Retrieval through XGBoost Algorithm-Based Downscaling Approach: A Case Study in the Southern United States
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Cyclone Global Navigation Satellite System
2.3. Soil Moisture Active Passive Data
2.4. International Soil Moisture Network
2.5. Auxiliary Data
3. Soil Moisture Downscaling Framework
3.1. Random Forest (RF)
3.2. eXtreme Gradient Boosting (XGBoost)
3.3. Light Gradient Boosting Machine (LGBM)
3.4. Genetic Algorithm, Back Propagation (GA-BP)
3.5. Performance Metrics and Evaluation
3.6. Downscaling Process
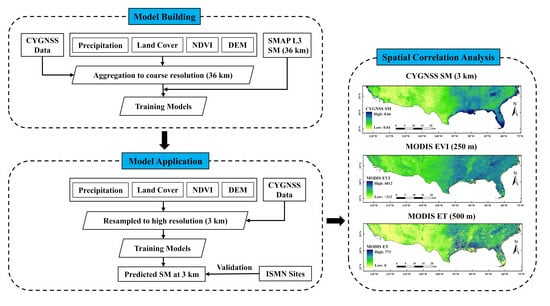
- Aggregation: The training procedure is carried out on the 36-km grid of SMAP SM. To maintain consistency with the spatial resolution of SMAP SM, the high-resolution CYGNSS observables and auxiliary variables (i.e., predictive factors) are aggregated to a 36 km scale using a simple arithmetic averaging method. It is worth noting that the theoretical resolution of the CYGNSS dataset used in this study is 7 × 0.5 km, while the SMAP product resolution is 36 km. This means that multiple CYGNSS observation points inevitably exist within the same SMAP grid. To address this, we average the CYGNSS sample points within the SMAP grid during the spatial matching process. Figure 3 presents the daily count of CYGNSS sampling points within the study area, as well as the counts after matching with SMAP. Specifically, from January to August, the counts correspond to the match with SMAP’s 36-km grid; from September to December, the counts result from matching with the resampled 3-km grid of SMAP.
- Model building: The aggregated data is divided into 70% for training and 30% for testing. SMAP SM is used as the response variable, and CYGNSS observables and auxiliary variables are used as input variables to train the four models: RF, XGBoost, LGBM, and GA-BP.
- Resampling: The CYGNSS observables and auxiliary variables are resampled to a high resolution of 3 km using the nearest neighbor method. Subsequently, a spatial connection is established between them.
- Model application: The resampled 3-km high-resolution CYGNSS observables and auxiliary variables were input to the downscaling models to obtain the downscaled CYNGSS SM with a spatial resolution of 3 km.
- Model evaluation: Once the most optimal downscaling models were determined based on the lowest RMSE as a benchmark, these models were then evaluated for accuracy using the testing set. Then, the 3-km downscaled SM obtained was validated using in situ data. Spatial analysis of the downscaled CYGNSS SM is conducted using MODIS EVI and MODIS EV products.
4. Results
4.1. Models Evaluation
4.2. Assessing the Accuracy of Downscaled Soil Moisture Using In Situ Observations
4.3. Graphical Assessment of Spatial Distribution of Downscaled Soil Moisture
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Yan, Q.; Gao, M.; Zafar, Z.; Li, A. Ground based GNSS-R observations for soil moisture. Chin. J. Geophys. 2011, 54, 2735–2744. [Google Scholar]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Crow, W.T.; Wood, E.F.; Dubayah, R. Potential for downscaling soil moisture maps derived from spaceborne imaging radar data. J. Geophys. Res. Atmos. 2000, 105, 2203–2212. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Hall, C.; Cordey, R. Multistatic Scatterometry. In Proceedings of the International Geoscience and Remote Sensing Symposium, ‘Remote Sensing: Moving Toward the 21st Century’, Edinburgh, UK, 12–16 September 1988; pp. 561–562. [Google Scholar]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.-W.; Judge, J. Sensitivity of GNSS-R spaceborne observations to soil moisture and vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Masters, D. Utilizing calibrated GPS reflected signals to estimate soil reflectivity and dielectric constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Description of the UCAR/CU Soil Moisture Product. Remote Sens. 2020, 12, 1558. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Soil moisture sensing using spaceborne GNSS reflections: Comparison of CYGNSS reflectivity to SMAP soil moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Ruf, C. Cyclone Global Navigation Satellite System (CYGNSS) Observations and Applications—Part I. In Proceedings of the 99th American Meteorological Society Annual Meeting, Washington, DC, USA, 6–10 January 2019. [Google Scholar]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-series retrieval of soil moisture using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Eroglu, O.; Kurum, M.; Boyd, D.; Gurbuz, A.C. High spatio-temporal resolution CYGNSS soil moisture estimates using artificial neural networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef]
- Senyurek, V.; Lei, F.; Boyd, D.; Kurum, M.; Gurbuz, A.C.; Moorhead, R. Machine learning-based CYGNSS soil moisture estimates over ISMN sites in CONUS. Remote Sens. 2020, 12, 1168. [Google Scholar] [CrossRef]
- Jia, Y.; Jin, S.; Chen, H.; Yan, Q.; Savi, P.; Jin, Y.; Yuan, Y. Temporal-spatial soil moisture estimation from CYGNSS using machine learning regression with a preclassification approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4879–4893. [Google Scholar] [CrossRef]
- Zhan, X.; Miller, S.; Chauhan, N.; Di, L.; Ardanuy, P. Soil Moisture Visible/Infrared Radiometer Suite Algorithm Theoretical Basis Document; Raytheon Systems Company: Lanham, MD, USA, 2002. [Google Scholar]
- Chauhan, N.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Panciera, R.; Rudiger, C.; Kerr, Y.H.; Walker, J. Downscaling SMOS-derived soil moisture using MODIS visible/infrared data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Choi, M.; Hur, Y. A microwave-optical/infrared disaggregation for improving spatial representation of soil moisture using AMSR-E and MODIS products. Remote Sens. Environ. 2012, 124, 259–269. [Google Scholar] [CrossRef]
- Peischl, S.; Walker, J.P.; Rüdiger, C.; Ye, N.; Kerr, Y.H.; Kim, E.; Bandara, R.; Allahmoradi, M. The AACES field experiments: SMOS calibration and validation across the Murrumbidgee River catchment. Hydrol. Earth Syst. Sci. 2012, 16, 1697–1708. [Google Scholar] [CrossRef]
- Piles, M.; Sánchez, N.; Vall-llossera, M.; Camps, A.; Martínez-Fernández, J.; Martínez, J.; González-Gambau, V. A downscaling approach for SMOS land observations: Evaluation of high-resolution soil moisture maps over the Iberian Peninsula. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3845–3857. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards improved spatio-temporal resolution soil moisture retrievals from the synergy of SMOS and MSG SEVIRI spaceborne observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, S.; Piles, M.; Sánchez, N.; Martínez-Fernández, J.; Vall-llossera, M.; Camps, A. Combining SMOS with visible and near/shortwave/thermal infrared satellite data for high resolution soil moisture estimates. J. Hydrol. 2014, 516, 273–283. [Google Scholar] [CrossRef]
- Zhao, W.; Li, A. A downscaling method for improving the spatial resolution of AMSR-E derived soil moisture product based on MSG-SEVIRI data. Remote Sens. 2013, 5, 6790–6811. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Njoku, E.G.; Shi, J.J.; Johnson, J.T.; Colliander, A. Tests of the SMAP combined radar and radiometer algorithm using airborne field campaign observations and simulated data. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2018–2028. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Merlin, O.; Molero, B.; Rüdiger, C.; Bacon, S. DisPATCh as a tool to evaluate coarse-scale remotely sensed soil moisture using localized in situ measurements: Application to SMOS and AMSR-E data in Southeastern Australia. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 221–234. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Merlin, O.; Gascoin, S.; Gastellu, J.P.; Mattar, C.; Olivera-Guerra, L.; Khabba, S.; Jarlan, L. Normalizing land surface temperature data for elevation and illumination effects in mountainous areas: A case study using ASTER data over a steep-sided valley in Morocco. Remote Sens. Environ. 2017, 189, 25–39. [Google Scholar] [CrossRef]
- Gleason, S.; Ruf, C.S.; O’Brien, A.J.; McKague, D.S. The CYGNSS level 1 calibration algorithm and error analysis based on on-orbit measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 37–49. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Podest, E.; Jensen, K.; McDonald, K.C. Classifying inundation in a tropical wetlands complex with GNSS-R. Remote Sens. 2019, 11, 1053. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Lowe, S.; Zuffada, C.; Esterhuizen, S.; Oveisgharan, S. Spaceborne GNSS-R from the SMAP mission: First assessment of polarimetric scatterometry over land and cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar] [CrossRef]
- Van Dijk, A.I.; Brakenridge, G.R.; Kettner, A.J.; Beck, H.E.; De Groeve, T.; Schellekens, J. River gauging at global scale using optical and passive microwave remote sensing. Water Resour. Res. 2016, 52, 6404–6418. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Dorigo, W.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiova, A.; Sanchis-Dufau, A.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global automated quality control of in situ soil moisture data from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 1–21. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Zwieback, S.; Xaver, A.; Wagner, W. Characterizing coarse-scale representativeness of in situ soil moisture measurements from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
- Hu, F.; Wei, Z.; Zhang, W.; Dorjee, D.; Meng, L. A spatial downscaling method for SMAP soil moisture through visible and shortwave-infrared remote sensing data. J. Hydrol. 2020, 590, 125360. [Google Scholar] [CrossRef]
- Ranney, K.J.; Niemann, J.D.; Lehman, B.M.; Green, T.R.; Jones, A.S. A method to downscale soil moisture to fine resolutions using topographic, vegetation, and soil data. Adv. Water Resour. 2015, 76, 81–96. [Google Scholar] [CrossRef]
- Busch, F.A.; Niemann, J.D.; Coleman, M. Evaluation of an empirical orthogonal function–based method to downscale soil moisture patterns based on topographical attributes. Hydrol. Process. 2012, 26, 2696–2709. [Google Scholar] [CrossRef]
- Coleman, M.L.; Niemann, J.D. Controls on topographic dependence and temporal instability in catchment-scale soil moisture patterns. Water Resour. Res. 2013, 49, 1625–1642. [Google Scholar] [CrossRef]
- Mascaro, G.; Vivoni, E.R.; Deidda, R. Soil moisture downscaling across climate regions and its emergent properties. J. Geophys. Res. Atmos. 2011, 116, D22114. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Sidhu, N.; Pebesma, E.; Wang, Y.-C. Usability study to assess the IGBP land cover classification for Singapore. Remote Sens. 2017, 9, 1075. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Q.; Zhang, Y.; Wang, H.; Du, X. Normalized NDVI valley area index (NNVAI)-based framework for quantitative and timely monitoring of winter wheat frost damage on the Huang-Huai-Hai Plain, China. Agric. Ecosyst. Environ. 2020, 292, 106793. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 1–9. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
- Mirjalili, S. Evolutionary algorithms and neural networks. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; Volume 780. [Google Scholar]
- Mao, T.; Shangguan, W.; Li, Q.; Li, L.; Zhang, Y.; Huang, F.; Li, J.; Liu, W.; Zhang, R. A Spatial Downscaling Method for Remote Sensing Soil Moisture Based on Random Forest Considering Soil Moisture Memory and Mass Conservation. Remote Sens. 2022, 14, 3858. [Google Scholar] [CrossRef]
- Wakigari, S.A.; Leconte, R. Enhancing Spatial Resolution of SMAP Soil Moisture Products through Spatial Downscaling over a Large Watershed: A Case Study for the Susquehanna River Basin in the Northeastern United States. Remote Sens. 2022, 14, 776. [Google Scholar] [CrossRef]
- Wei, X.; Zhou, Q.; Cai, M.; Wang, Y. Effects of vegetation restoration on regional soil moisture content in the humid karst areas—A case study of Southwest China. Water 2021, 13, 321. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Liu, M.; Jiang, Y.; Peng, Z. A moisture-based triangle approach for estimating surface evaporative fraction with time-series of remotely sensed data. Remote Sens. Environ. 2022, 280, 113212. [Google Scholar] [CrossRef]
- Nadeem, A.A.; Zha, Y.; Shi, L.; Ali, S.; Wang, X.; Zafar, Z.; Afzal, Z.; Tariq, M.A.U.R. Spatial downscaling and gap-filling of SMAP soil moisture to high resolution using MODIS surface variables and machine learning approaches over ShanDian River Basin, China. Remote Sens. 2023, 15, 812. [Google Scholar] [CrossRef]
- Lei, F.; Senyurek, V.; Kurum, M.; Gurbuz, A.C.; Boyd, D.; Moorhead, R.; Crow, W.T.; Eroglu, O. Quasi-global machine learning-based soil moisture estimates at high spatio-temporal scales using CYGNSS and SMAP observations. Remote Sens. Environ. 2022, 276, 113041. [Google Scholar] [CrossRef]
- Kim, H.; Lakshmi, V. Use of cyclone global navigation satellite system (CyGNSS) observations for estimation of soil moisture. Geophys. Res. Lett. 2018, 45, 8272–8282. [Google Scholar] [CrossRef]
- Calabia, A.; Molina, I.; Jin, S. Soil moisture content from GNSS reflectometry using dielectric permittivity from fresnel reflection coefficients. Remote Sens. 2020, 12, 122. [Google Scholar] [CrossRef]











| Datasets | Variables | Temporal Resolution (Day) | Spatial Resolution | Time |
|---|---|---|---|---|
| MOD09GQ | NDVI | 1 | 250 m | 1 January–31 December 2019 |
| MCD12Q1 | Land cover | - | 500 m | 2019 |
| SRTM | DEM | - | 30 m | 2019 |
| CHIRPS | Precipitation | 1 | 0.5° | 1 January–31 December 2019 |
| - | Lon, Lat | 1 | - | 1 January–31 December 2019 |
| - | Doy | 1 | - | 1 January–31 December 2019 |
| Model | Hyperparameters |
|---|---|
| GA-BP | popu = 50, learning_rate = 0.001, epochs = 100, n_hidden layer = 10 |
| RF | n_estimators = 100, max_depth = 6, max_leaf_nodes = None, min_samples_leaf = 1, min_samples_split = 2 |
| XGBoost | booster = tree, max_depth = 8, min_child_weight = 1, leaing_rate = 0.25, n_estimators = 100, subsample = 0.9, colsaple_bytree = 0.6, gamma = 0 |
| LGBM | learning_rate = 0.09, n_estimators = 100, min_samples_gain = 0.1, max_depth = 6, num_leaves = 50, subsample = 0.8, colsample bytree = 0.8 |
| Name | Time | Model Training | Model Testing | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | R | RMSE | MAE | R | ||
| - | - | ||||||
| GA-BP | 46.16 | 0.071 | 0.055 | 0.834 | 0.072 | 0.055 | 0.831 |
| RF | 5712.91 | 0.011 | 0.007 | 0.996 | 0.031 | 0.021 | 0.969 |
| XGBoost | 25.90 | 0.037 | 0.027 | 0.958 | 0.038 | 0.028 | 0.955 |
| LGBM | 6.85 | 0.045 | 0.033 | 0.937 | 0.045 | 0.034 | 0.935 |
| Evaluation Index | Ranges | Number of In Situ Site | Average Value |
|---|---|---|---|
| MAE | <0.04 | 38 | 0.051 |
| 0.04–0.06 | 10 | ||
| 0.06–0.08 | 20 | ||
| >0.08 | 10 | ||
| RMSE | <0.06 | 48 | 0.062 |
| 0.06–0.07 | 10 | ||
| 0.07–0.08 | 11 | ||
| >0.08 | 9 | ||
| R | <0.60 | 22 | 0.813 |
| 0.60–0.70 | 6 | ||
| 0.70–0.80 | 10 | ||
| >0.80 | 40 |
| Evaluation Index | Ranges | Number of In Situ Site | Average Value |
|---|---|---|---|
| MAE | <0.04 | 24 | 0.058 |
| 0.04–0.06 | 18 | ||
| 0.06–0.08 | 19 | ||
| >0.08 | 17 | ||
| RMSE | <0.06 | 37 | 0.065 |
| 0.06–0.07 | 5 | ||
| 0.07–0.08 | 11 | ||
| >0.08 | 25 | ||
| R | <0.60 | 29 | 0.712 |
| 0.60–0.70 | 9 | ||
| 0.70–0.80 | 7 | ||
| >0.80 | 33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Liang, Y.; Guo, Y.; Liang, X.; Ren, C.; Yue, W.; Zhu, B.; Jiang, X. Enhancing Spatial Resolution of GNSS-R Soil Moisture Retrieval through XGBoost Algorithm-Based Downscaling Approach: A Case Study in the Southern United States. Remote Sens. 2023, 15, 4576. https://doi.org/10.3390/rs15184576
Luo Q, Liang Y, Guo Y, Liang X, Ren C, Yue W, Zhu B, Jiang X. Enhancing Spatial Resolution of GNSS-R Soil Moisture Retrieval through XGBoost Algorithm-Based Downscaling Approach: A Case Study in the Southern United States. Remote Sensing. 2023; 15(18):4576. https://doi.org/10.3390/rs15184576
Chicago/Turabian StyleLuo, Qidi, Yueji Liang, Yue Guo, Xingyong Liang, Chao Ren, Weiting Yue, Binglin Zhu, and Xueyu Jiang. 2023. "Enhancing Spatial Resolution of GNSS-R Soil Moisture Retrieval through XGBoost Algorithm-Based Downscaling Approach: A Case Study in the Southern United States" Remote Sensing 15, no. 18: 4576. https://doi.org/10.3390/rs15184576
APA StyleLuo, Q., Liang, Y., Guo, Y., Liang, X., Ren, C., Yue, W., Zhu, B., & Jiang, X. (2023). Enhancing Spatial Resolution of GNSS-R Soil Moisture Retrieval through XGBoost Algorithm-Based Downscaling Approach: A Case Study in the Southern United States. Remote Sensing, 15(18), 4576. https://doi.org/10.3390/rs15184576