A Remote Sensing Image Fusion Method Combining Low-Level Visual Features and Parameter-Adaptive Dual-Channel Pulse-Coupled Neural Network

Abstract

Remote sensing image fusion can effectively solve the inherent contradiction between spatial resolution and spectral resolution of imaging systems. At present, the fusion methods of remote sensing images based on multi-scale transform usually set fusion rules according to local feature information and pulse-coupled neural network (PCNN), but there are problems such as single local feature, as fusion rule cannot effectively extract feature information, PCNN parameter setting is complex, and spatial correlation is poor. To this end, a fusion method of remote sensing images that combines low-level visual features and a parameter-adaptive dual-channel pulse-coupled neural network (PADCPCNN) in a non-subsampled shearlet transform (NSST) domain is proposed in this paper. In the low-frequency sub-band fusion process, a low-level visual feature fusion rule is constructed by combining three local features, local phase congruency, local abrupt measure, and local energy information to enhance the extraction ability of feature information. In the process of high-frequency sub-band fusion, the structure and parameters of the dual-channel pulse-coupled neural network (DCPCNN) are optimized, including: (1) the multi-scale morphological gradient is used as an external stimulus to enhance the spatial correlation of DCPCNN; and (2) implement parameter-adaptive representation according to the difference box-counting, the Otsu threshold, and the image intensity to solve the complexity of parameter setting. Five sets of remote sensing image data of different satellite platforms and ground objects are selected for experiments. The proposed method is compared with 16 other methods and evaluated from qualitative and quantitative aspects. The experimental results show that, compared with the average value of the sub-optimal method in the five sets of data, the proposed method is optimized by 0.006, 0.009, 0.009, 0.035, 0.037, 0.042, and 0.020, respectively, in the seven evaluation indexes of information entropy, mutual information, average gradient, spatial frequency, spectral distortion, ERGAS, and visual information fidelity, indicating that the proposed method has the best fusion effect.

1. Introduction

Remote sensing image fusion is the basis of information extraction, target recognition, and ground object classification, which plays an important role in remote sensing applications [1]. Panchromatic (PAN) and multispectral (MS) image fusion can effectively solve the inherent contradiction between spatial resolution and spectral resolution of imaging system, so it has attracted extensive attention in the field of remote sensing image fusion. How to combine the advantages of the two types of data to the greatest extent to achieve redundancy control and complementary advantages of remote sensing data, thereby improving its interpretation ability and application value, is a hot topic in the field of remote sensing image processing [2].

The four main categories of panchromatic and multispectral image fusion methods include component replacement methods, multi-scale transform methods, model-based methods, and hybrid methods. [3]. The classical methods of component replacement include intensity–hue–saturation (IHS) [4], principal component analysis (PCA) [5] and Gram–Schmidt (GS) [6], etc. These methods have high computational efficiency and good retention effect on spatial details, but there are different degrees of spectral distortion [7]. Multi-scale transform usually decomposes the image into sub-bands of different scales, and then makes corresponding fusion rules according to the characteristics of different sub-bands, so as to accurately extract the features of each sub-band, which can effectively reduce aliasing artifacts and has better spectral domain advantages [8]. Multi-scale transform methods include discrete wavelet transform (DWT) [9], dual-tree complex wavelet transform (DTCWT) [10], curvelet transform [11], non-subsampled contourlet transform (NSCT) [12], and non-subsampled shearlet transform (NSST) [13]. In addition, the fusion performance of the multi-scale transform method largely depends on the setting of different sub-band fusion rules [14]. These fusion rules can be roughly divided into pixel level, block level, and region level, and different activity measures are usually used to measure the active degree of pixels, blocks, and regions [15]. The pixel level fusion rules mainly include taking the largest absolute value and weighted average, which are simple and efficient to calculate based on a single pixel but easily affected by noise. The block-level fusion rules take into account the correlation between pixels and measure image features in the form of blocks. The region-level fusion rule divides different sub-bands into several regions and selects the optimal region measured by the activity measure to construct the fusion sub-band. Therefore, activity measure construction, as the key to fusion rule setting, has attracted the attention of most researchers. Popular activity measures include spatial frequency (SF) [16], sum modified-laplacian (SML) [17], and multi-scale morphological gradient (MSMG) [18].

The main model-based methods are variational optimization models and sparse representations. The variational model-based methods mainly include two steps: the construction of the energy function and the optimal solution of the model function. For example, Khademi et al. combined Markov’s priori model and the Bayesian framework to enhance the fusion effect [19]. Wang et al. constructed a posteriori model to improve the preservation of spatial and spectral information based on the spatial consistency prior, spectral consistency prior, and similarity assumptions [20]. Sparse representation theory uses linear arrangement of a small number of atoms to approximate the image, in which the acquisition of dictionaries is important for the performance of the algorithm. Liu et al. obtained a set of compact sub-dictionaries based on a large number of high-quality trained images and selected a sub-dictionary for sparse representation based on the gradient information of the image blocks [21]. Deng et al. proposed a fusion method based on tensor-based nonconvex sparse modeling [22]. Although some scholars have improved the sparse representation model, sparse encoding and dictionary construction are still challenging problems. In recent years, the Pulse-Coupled Neural Network (PCNN) model has gained wide attention as a third-generation artificial neural network with the advantages of pulse synchronization, global coupling, and strong adaptability. It can effectively extract useful information in complex environment without learning and training [23]. However, traditional PCNN cannot process two images at the same time, with complex structure and low efficiency. In order to make up for the shortcomings of PCNN, a model of a dual-channel pulse-coupled neural network (DCPCNN) which can simultaneously use the pixels of two images as external stimuli is developed. Some improved DCPCNN models have also emerged. Yin et al. took edge energy as the external stimulus of DCPCNN, and stimulated DCPCNN according to the edge information of the image [24]. Liu et al. took the average gradient as the linking strength of DCPCNN to enhance the feature extraction ability [25]. Cheng et al. proposed triple linking strength DCPCNN, which took local structure information, direction gradient, and Laplacian energy as the linking strength of DCPCNN, and consolidated the stability of the linking strength value [26].

Hybrid methods are usually the combined forms of the previous types of fusion methods and combine the advantages of each fusion methods. Therefore, in this paper, the IHS transform of the component combination method, the NSST of the multiscale transform method, and the PCNN model are mixed, and the advantages of the IHS transform, NSST, and PCNN in each aspect are combined. Among them, although NSST can effectively suppress the loss of spectral information, the fusion rules of different sub-bands need to be reasonably designed to obtain excellent fusion results. At present, the fusion rules of multi-scale transform methods are usually designed based on local feature information, such as local energy, local spatial frequency, and local Laplacian. This local feature information focuses on a single image feature and cannot extract the feature information of the image effectively. Meanwhile, pulse-coupled neural network models are widely used for the design of high-frequency sub-band fusion rules due to their pulse synchronization and global coupling properties, but the parameters of these models need to be set artificially. Although some of the models have adaptive modulation of link strength, other parameters are selected as empirical values. In addition, using only image grayscale or simple measures as the external stimulus of the model will result in poor spatial correlation of the fused images.

In order to solve the above problems, a method of remote sensing image fusion combining low-level visual features (LLVF) and parameter-adaptive dual-channel pulse-coupled neural network (PADCPCNN) in the NSST domain, namely the NSST-LLVF-PADCPCNN method, is proposed in this paper. The main contributions and advantages of this paper can be concluded as follows.

(1)

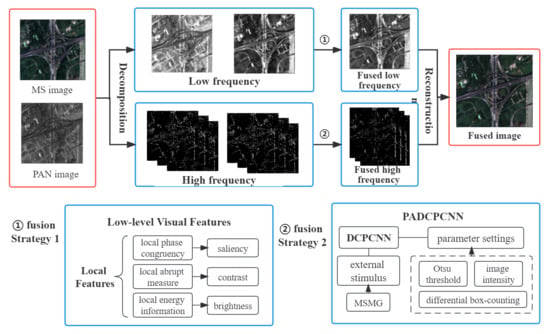
Low-frequency sub-band fusion based on LLVF. In the process of low-frequency sub-band fusion, the fusion rules are constructed only based on a single local feature, which cannot effectively extract the feature information of the image. To this end, according to the principle of the human visual system to understand the image through the underlying visual features such as the saliency, contrast, and brightness of the image, a fusion rule which is more in line with the visual characteristics of the human eye is constructed by combining the three local features of local phase congruency, local abrupt measure, and local energy information.

(2)

High-frequency sub-band fusion based on PADCPCNN. Based on the advantage that MSMG can integrate gradient information at multiple scales, it is used as an external stimulus for DCPCNN, thereby enhancing the spatial correlation of DCPCNN. The parameters of DCPCNN are adaptively represented by differences in the box dimension, the Otsu threshold, and the image intensity to solve the complexity of parameter setting.

(3)

A remote sensing image fusion method combining LLVF and PADCPCNN. By combining the fusion strategies proposed above, a novel NSST domain fusion method is proposed, which more fully considers the energy preservation and detail extraction of remote sensing images. In order to verify the effectiveness of the method, five sets of remote sensing image data from different platforms and ground objects are selected to conduct comparative experiments between the proposed method and 16 other methods, and the experimental results are compared and analyzed from qualitative and quantitative aspects.

The paper is organized as follows: in Section 2, the fusion rules and steps of the proposed method are introduced in detail. The experimental design, including the experimental data, comparative experiments, and the selection of evaluation indexes are described in Section 3. In Section 4, the experimental results are evaluated and analyzed. Finally, some conclusions are made in Section 5.

2. Methodology

The proposed method improves the fusion rules of low-frequency sub-bands and high-frequency sub-bands, mainly including low-level visual features and PADCPCNN. The framework of the proposed NSST-LLVF-PADCPCNN method is shown in Figure 1.

2.1. Low-Level Visual Features

The human visual system understands images mainly based on underlying visual features such as saliency, contrast, and brightness, and the local phase congruency, local abrupt measure, and local energy information are used to reflect the three features, respectively.

• Phase congruency is a dimensionless measure, often used in image edge detection, which can better measure the saliency of image features. The phase congruency at position $(i,j)$ can be expressed as

  $$PC\left(i,j\right)=\frac{{\displaystyle {\sum }_k\sqrt{{\left({\displaystyle {\sum }_n{e}_{n,{\theta }_k}\left(i,j\right)}\right)}^2+{\left({\displaystyle {\sum }_n{o}_{n,{\theta }_k}\left(i,j\right)}\right)}^2}}}{\epsilon +{\displaystyle {\sum }_n{\displaystyle {\sum }_k{A}_{n,{\theta }_k}\left(i,j\right)}}}$$

  (1)

  where $\epsilon =0.001$ is the positive constant, ${\theta }_k$ is the orientation angle at $k$, and $A_{n,{\theta }_k}$ is the amplitude and angle of the n-th Fourier component. $e_{n,{\theta }_k}\left(i,j\right)=I\left(i,j\right)\ast M_n^e$ and $o_{n,{\theta }_k}\left(i,j\right)=I\left(i,j\right)\ast M_n^o$ are the convolution results of the input image at $\left(i,j\right)$, where $I(i,j)$ represents the pixel value at $\left(i,j\right)$, and $M_n^e$ and $M_n^o$ are two-dimensional Log-Gabor even symmetric and odd symmetric filters with scale $n$, respectively.
• Local abrupt measure mainly reflects the contrast information of the image, which can overcome the difficulty that phase congruency is insensitive to the image contrast information. The expression of the abrupt measure $SCM$ is

  $$SCM\left(i,j\right)={{\displaystyle \sum _{\left(i_0,j_0\right)\in {\Omega }_0}\left(I\left(i,j\right)-I\left(i_0,j_0\right)\right)}}^2$$

  (2)

  where ${\Omega }_0$ represents a local region of size 3 × 3, and $\left(i_0,j_0\right)$ is the pixel value in local region ${\Omega }_0$. In order to calculate the contrast of $\left(i,j\right)$ in the neighborhood range $\left(2M+1\right)\times \left(2N+1\right)$, the local abrupt measure $LSCM$ is proposed, and its expression is

  $$LSCM\left(i,j\right)={\displaystyle \sum _{a=-M}^M{\displaystyle \sum _{b=-N}^{N}SCM(i+a,j+b)}}$$

  (3)
• Local energy information $LE$ can reflect the intensity of image brightness variation, and its equation can be expressed as

  $$LE\left(i,j\right)={{\displaystyle \sum _{a=-M}^M{\displaystyle \sum _{b=-N}^N\left(I(i+a,j+b)\right)}}}^2$$

  (4)

By combining three local features, $PC$, $LSCM$, and $LE$, a new activity measure $NAM$, which can fully reflect the saliency of image features, is constructed [27]. Its expression is

$$NAM\left(i,j\right)=\left(PC\left(i,j\right)\right)·{\left(LSCM\left(i,j\right)\right)}^2·{\left(LE\left(i,j\right)\right)}^2$$

(5)

2.2. PADCPCNN

DCPCNN consists of three parts: a receptive field, a modulation field, and a pulse generator. The architecture of the model is shown in Figure 2, and its mathematical expression is

$$\{\begin{array}{c}\begin{array}{c}{F}_{ij}{}^A\left(n\right)=S_{ij}{}^A,F_{ij}{}^B\left(n\right)=S_{ij}{}^B\\ \begin{array}{l}{L}_{ij}\left(n\right)=V_L{\displaystyle {\sum }_{kl}{\mathit{W}}_{ijkl}{Y}_{kl}\left(n-1\right)}\\ U_{ij}{}^A\left(n\right)=F_{ij}{}^A\left(n\right)\left[1+{\beta }^A{L}_{ij}\left(n\right)\right]\\ U_{ij}{}^B\left(n\right)=F_{ij}{}^B\left(n\right)\left[1+{\beta }^B{L}_{ij}\left(n\right)\right]\end{array}\end{array}\\ U_{ij}\left(n\right)=e^{-{\alpha }_f}{U}_{ij}\left(n-1\right)+\max \left\{U_{ij}{}^A\left(n\right),U_{ij}{}^B\left(n\right)\right\}\\ Y_{ij}\left(n\right)=\{\begin{array}{cc}1,& if U_{ij}\left(n\right)>E_{ij}\left(n-1\right)\\ 0,& otherwise\end{array}\\ E_{ij}\left(n\right)=e^{-{\alpha }_e}{E}_{ij}\left(n-1\right)+V_E{Y}_{ij}\left(n\right)\end{array}$$

(6)

where $F_{ij}{}^X\left(n\right)$, $L_{ij}\left(n\right)$, $U_{ij}{}^X\left(n\right)$, $Y_{ij}\left(n\right)$, and $E_{ij}\left(n\right)$ are the feeding input, linking input, internal activity, output, and dynamic threshold of the neuron at position $\left(i,j\right)$ at the n-th iteration, respectively, and $X\in \left(A,B\right)$; $S_{ij}{}^A$ and $S_{ij}{}^B$ are the external input of image A and image B at position $\left(i,j\right)$, that is, the gray value of the relative position of image; $V_L$ and ${\mathit{W}}_{ijkl}$ are the amplitude coefficient and synaptic weight coefficient matrix of linking input, respectively, and ${\mathit{W}}_{ijkl}=\left[\begin{array}{ccc}0.5& 1& 0.5\\ 1& 0& 1\\ 0.5& 1& 0.5\end{array}\right]$; ${\alpha }_f$ is the attenuation coefficient of the internal activity; ${\beta }^A$ and ${\beta }^B$ are the linking strengths corresponding to $S_{ij}{}^A$ and $S_{ij}{}^B$, respectively; and ${\alpha }_e$ and $V_E$ are the attenuation coefficient and amplitude coefficient of the dynamic threshold.

Due to the weak spatial correlation and complex parameter setting of the traditional DCPCNN model, the external stimulus and free parameters of the model are optimized, respectively. MSMG can achieve multi-scale expansion by changing the size of morphological gradient operator structure elements and can integrate the gradient information extracted from different scales into an effective sharpness measure [28]. MSMG with high-frequency sub-bands is selected as the external stimulus signal of the model, which can better quantify the image sharpness and enhance the spatial correlation of the image [28]. Its expression is

$$F_{ij}{}^A\left(n\right)=MSM{G}_A,F_{ij}{}^B\left(n\right)=MSM{G}_B$$

(7)

where $MSM{G}_A$ and $MSM{G}_B$ are multi-scale morphological gradients of input images A and B. Equation (5) shows that DCPCNN mainly has six free parameters, namely $V_L$, ${\beta }^A$, ${\beta }^B$, ${\alpha }_f$, ${\alpha }_e$, and $V_E$. Because ${\beta }^A$, ${\beta }^B$, and $V_L$ are all coefficients of ${\displaystyle {\sum }_{kl}{\mathit{W}}_{ijkl}{Y}_{kl}\left(n-1\right)}$, they are integrated into weight-linking coefficients ${\gamma }^A={\beta }^A{V}_L$ and ${\gamma }^B={\beta }^B{V}_L$. Because differential box-counting can measure the contrast of a specific grid and reflect the intensity variation on a specific grid through the number of boxes, ${\gamma }^A$ and ${\gamma }^B$ are expressed adaptively according to the idea of differential box-counting and normalized by the Sigmoid function [29]. Its expression is

$${\gamma }^X=\frac{1}{1+e^{-\eta ·{\left(g_{ij,\max }-g_{ij,\min }\right)}^X}}$$

(8)

where $g_{ij,\max }$ and $g_{ij,\min }$ represent the maximum and minimum gray levels within the window size $3\times 3$, respectively, with the pixel point at $\left(i,j\right)$ of image $X\in \left(A,B\right)$ as the center. $\eta =0.01$ is a constant. Parameters ${\alpha }_f$, $V_E$, and ${\alpha }_e$ are set according to the image intensity and the Otsu threshold, and the weights are allocated through the differential box-counting. The setting rule is

$$\{\begin{array}{c}\begin{array}{l}{\alpha }_f=\log \left(1/\left(w_1{\sigma }^A\left(S\right)+w_2{\sigma }^B\left(S\right)\right)\right)\\ V_E=e^{-{\alpha }_f}+\lambda \end{array}\\ {\alpha }_e=\ln \left(\frac{V_E/\left(w_1{S}_{otsu}^A+w_2{S}_{otsu}^B\right)}{\left(1-e^{-3{\alpha }_f}\right)/\left(1-e^{-{\alpha }_f}\right)+\left(\lambda -1\right)e^{-{\alpha }_f}}\right)\end{array}$$

(9)

$$\lambda =w_1{S}_{\max }^A/S_{otsu}^A+w_2{S}_{\max }^B/S_{otsu}^B$$

(10)

$$w_1=w_A/\left(w_A+w_B\right),w_2=w_B/\left(w_A+w_B\right)$$

(11)

where ${\sigma }^A\left(S\right)$ and ${\sigma }^B\left(S\right)$ represent the standard deviation of image A and image B, respectively; $S_{otsu}^A$ and $S_{otsu}^B$ represent the optimal histogram threshold of image A and image B determined by the Otsu method, respectively [30,31]; $S_{\max }^A$ and $S_{\max }^B$ represent the maximum intensity of image A and image B, respectively; and $w_A$ and $w_B$ represent the differential box-counting of image A and image B, respectively [32].

2.3. NSST-LLVF-PADCPCNN Method

The proposed method mainly consists of NSST decomposition, low frequency sub-bands fusion, high-frequency sub-bands fusion, and NSST reconstruction. Before NSST decomposition, a luminance component $Y$ and two chromaticity components $U$ and $V$ are obtained by YUV space transform of multispectral image $I_{MS}$. NSST is mainly composed of a non-subsampled pyramid filter bank (NSPFB) and a shearlet filter bank (SFB). The function of NSPFB is to realize the multi-scale decomposition of the image, and the function of SFB is to realize the multi-direction decomposition of the image. The NSST transform is used to decompose the luminance component $Y$ obtained by YUV space transform and the panchromatic image $I_{Pan}$ obtained by preprocessing to obtain $\left\{H_{Pan}^{l,k},L_{Pan}\right\}=nsst\_de\left(I_{Pan}\right)$ and $\left\{H_{MS}^{l,k},L_{MS}\right\}=nsst\_de\left(Y\right)$, where $l$ and $k$ represent the decomposition series and direction, respectively, and $nsst\_de$ is the NSST decomposition function. The corresponding low-frequency component $\left\{L_{Pan},L_{MS}\right\}$ and high-frequency component $\left\{H_{Pan}^{l,k},H_{MS}^{l,k}\right\}$ are obtained, and then the corresponding fusion rules are designed according to the characteristics of different sub-bands.

The low-frequency sub-band coefficient reflects the whole structure of the image and contains most of the energy of the image. Traditional low-frequency sub-bands fusion methods usually use local energy to measure activity levels of the image. However, an image contains rich visual information, and the local energy can only reflect the brightness information of the image, which lacks the representation of other low-level visual features. In order to overcome this defect, a fusion strategy based on low-level visual features is adopted in this paper. It can fully consider the saliency of image features, image contrast information, and image brightness information, which is more consistent with human visual features. The new activity measure $NAM$ is used to fuse the low-frequency sub-band coefficients $L_{Pan}$ and $L_{MS}$, and the fused low-frequency sub-band coefficients can be expressed as

$$L_F\left(i,j\right)=\{\begin{array}{cc}{L}_{Pan}\left(i,j\right)& if \lceil S_i\left(i,j\right)\rceil >\frac{\overline{M}\times \overline{N}}{2}\\ L_{MS}\left(i,j\right)& otherwise\end{array}$$

(12)

$$S_i\left(i,j\right)=\left\{\left(i_0,j_0\right)\in {\Omega }_1|NA{M}_i\left(i_0,j_0\right)\ge \max \left(NA{M}_1\left(i_0,j_0\right),\dots ,NA{M}_{i-1}\left(i_0,j_0\right),NA{M}_{i+1}\left(i_0,j_0\right),\dots ,NA{M}_K\left(i_0,j_0\right)\right)\right\}$$

(13)

where $\lceil ·\rceil$ represents the cardinality of the set, ${\Omega }_1$ represents the sliding window with size $\overline{M}\times \overline{N}$ centered on $\left(i,j\right)$, and $K$ is the number of low-frequency sub-bands images.

The high-frequency sub-band coefficient contains a lot of texture details and edge information, which directly reflects the sharpness of the image. DCPCNN is a commonly used method in high-frequency sub-band fusion, but its performance in high-frequency sub-band fusion is limited by the weak spatial correlation and complex parameter settings. Therefore, the external stimulus and free parameters of the model are optimized, respectively, to enhance the fusion performance of high-frequency sub-bands. The MSMG is able to better express the clarity of the image due to its large dispersion [28]. MSMG can also provide a higher normalized value for the image, thus having a higher prediction rate than other activity measures [28]. Therefore, MSMG is chosen as an external stimulus for DCPCNN to enhance spatial correlation. In addition, the parameters of DCPCNN are set in combination with the difference box-counting, the Otsu threshold, and the image intensity to achieve adaptive representation. The proposed PADCPCNN method is obtained by improving it and fusing the high-frequency sub-band coefficients $H_{Pan}^{l,k}$ and $H_{MS}^{l,k}$. The activity degree of the high-frequency coefficient is evaluated by comparing the internal activity $U_{Pan,ij}^{l,k}\left(N\right)$ and $U_{MS,ij}^{l,k}\left(N\right)$ of the high-frequency sub-band $H_{Pan}^{l,k}$ and $H_{MS}^{l,k}$, where $N$ is the total number of iterations. The fusion high-frequency sub-bands $H_F^{l,k}$ is obtained according to the following equation:

$$H_F^{l,k}\left(i,j\right)=\{\begin{array}{cc}{H}_{Pan}^{l,k}\left(i,j\right),& if U_{Pan,ij}^{l,k}\left(N\right)\ge U_{MS,ij}^{l,k}\left(N\right)\\ H_{MS}^{l,k}\left(i,j\right),& otherwise\end{array}$$

(14)

Finally, the NSST inverse transform is performed on the fused high- and low-frequency fusion coefficients to obtain the new luminance component $Y^{\prime }$, namely $Y^{\prime }=nsst\_re\left\{H_F^{l,k},L_F\right\}$, where $nsst\_re$ is the NSST reconstruction function. Then the new fused image is obtained by YUV space inverse transform of the new luminance component $Y^{\prime }$ and chromaticity component $U$ and $V$.

2.4. Steps

The procedure of the proposed method is shown in Figure 3, and the specific steps are as follows:

• One luminance component $Y$ and two chromaticity components $U$ and $V$ are obtained by YUV space transform of multispectral image $I_{MS}$.
• The luminance component $Y$ obtained by YUV space transform and panchromatic image $I_{Pan}$ obtained by preprocessing are multi-scale decomposed by NSST transform, and the low-frequency sub-bands $\left\{L_{Pan},L_{MS}\right\}$ and high-frequency sub-bands $\left\{H_{Pan}^{l,k},H_{MS}^{l,k}\right\}$ are obtained, respectively, where $l$ and $k$ represent decomposition series and direction, respectively.
• The fusion strategy of low-level visual features is used, the low frequency sub-bands are fused according to Equations (6)–(8), and the fused low-frequency sub-band coefficient $L_F$ is obtained.
• PADCPCNN model is performed on the high-frequency sub-bands through Equations (9)–(14), and the fused high-frequency sub-band coefficient $H_F^{l,k}$ is obtained.
• The new luminance component $Y^{\prime }$ is obtained by NSST inverse transform of the fused low-frequency and high-frequency fusion coefficients.
• Then the new fused image is obtained by YUV space inverse transform of the new luminance component $Y^{\prime }$ and chromaticity component $U$ and $V$.

3. Experimental Design

3.1. Experimental Data

In order to verify the adaptability and effectiveness of the proposed method on remote sensing data of different satellite platforms, five sets of remote sensing images of different satellite platforms and ground objects are selected for experiments. The first set of experimental data is QuickBird data with 0.61 m panchromatic resolution and 2.44 m multispectral resolution, respectively, as shown in Figure 4(a1,a2). The second set of experimental data is SPOT-6 data with 1.5 m panchromatic resolution and 6 m multispectral resolution, respectively, as shown in Figure 4(b1,b2). The third set of experimental data is WorldView-2 data with 0.5 m panchromatic resolution and 1.8 m multispectral resolution, respectively, as shown in Figure 4(c1,c2). The fourth set of experimental data is WorldView-3 data with 0.31 m panchromatic resolution and 1.24 m multispectral resolution, respectively, as shown in Figure 4(d1,d2). The fifth set of experimental data is Pleiades data with 0.5 m panchromatic resolution and 2 m multispectral resolution, respectively, as shown in Figure 4(e1,e2). The size of multispectral image is 256 × 256, and the size of panchromatic image is 1024 × 1024. Pre-processing operations such as noise reduction and registration are performed on the original image to suppress the effects of factors such as noise and spatial location on image fusion [33,34].

3.2. Compared Methods

In order to better illustrate the experimental effect, the proposed method is compared with 16 other fusion methods, namely, Curvelet [35], dual-tree complex wavelet transform (DTCWT) [35], convolutional neural network (CNN) [36], contrast and structure extraction (CSE) [37], Total Variational Model (TVM) [38], Relative Total Variational Decomposition (RTVD) [39], adaptive sparse representation (ASR) [22], convolutional sparse representation (CSR) [40], convolution sparsity and morphological component analysis (CSMCA) [41], rolling guide filter (RGF) [42], multi-level Gaussian curvature filtering (MLGCF) [43], visual saliency map and weighted least square (VSM-WLS) [44], the NSST domain fusion method combining energy attribute (EA) and DCPCNN (EA-DCPCNN) [45], the NSST domain fusion method combining EA and PAPCNN (EA-PAPCNN) [46], and the NSST domain fusion method combing weighted local energy (WLE) and PAPCNN (WLE-PAPCNN) [30]. The NSST domain fusion method combs LLVF and PAPCNN (LLVF-PAPCNN) [47]. These compared methods can be divided into five main categories, among which Curvelet and DTCWT are classical multi-scale transform methods; TVM and RTVD are variational model-based methods; ASR, CSR, and CSMCA are sparse representation-based methods; RGF, MLGCF, and VSM-WLS are edge-preserving filter-based methods; EA-DCPCNN, EA-PAPCNN, WLE-PAPCNN, and LLVF-PAPCNN are methods combining multi-scale transform and PCNN models; and CNN and CSE are other methods. In order to ensure the rigor of the experiment, the same experimental environment is selected for the proposed method and compared methods. In addition, all parameters in these compared methods are set to the default values given by their authors. In this paper, the decomposition filter is maxflat, the decomposition degree is 4, and the iteration number of PADCPCNN is set to 110 [15,30,46,47].

3.3. Evaluation Indexes

Qualitative evaluation is mainly based on the observation of the human visual system. According to the expert knowledge base, the visual effect, texture details, color information, spatial structure, and other aspects of the fused image are compared and analyzed, and the subjective evaluation of each set of fusion results is made. Quantitative evaluation is an objective evaluation of experimental results through evaluation indexes. In the experiment, two information abundance evaluation indexes, Information Entropy (IE) and Mutual information (MI), are selected. Average Gradient (AG), Spatial Frequency (SF), and Spatial Correlation Coefficient (SCC) are selected as spatial information evaluation indexes. Spectral Distortion (SD), Spectral Angle Mapper (SAM), and Erreur Relative Globale Adimensionnelle de Synthese (ERGAS) are selected as spectral information evaluation indexes. Two overall quality evaluation indexes, Q4 [48] and Visual Information Fidelity for Fusion (VIFF) [49], are used. Details for the used indexes are shown below.

• IE: It is an evaluation index to measure the amount of information contained in the fused image, and the greater the information entropy, the richer the information. The mathematical expression of IE is

  $$IE=-{\displaystyle \sum _{i=0}^{L-1}{Z}_i\log (Z_i)}$$

  (15)

  where $L$ is the gray level of the image and $Z_i$ is the statistical probability of the gray histogram.
• MI: It measures the extent to which the fused image acquires information from the original image. A larger MI indicates that more information is retained from the original image. The mathematical expression of MI is

  $$MI={\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{h}_{I_A{I}_B}(i,j)}}\times {\log }_2\left(\frac{h_{I_A{I}_B}(i,j)}{h_{I_A}(i,j)h_{I_B}(i,j)}\right)$$

  (16)

  where $I_A$ and $I_B$ are the fused image and the reference image, respectively; $M$ and $N$ are the length and width of the image, respectively; and $M\times N$ denotes the resolution of the image. $h_{I_A{I}_B}$ is the joint grayscale histogram of $I_A$ and $I_B$.
• AG: It measures the clarity of the image, and the greater the AG, the higher the clarity and the better the quality of the fusion. The mathematical expression of AG is

  $$AG=\frac{1}{MN}{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N\sqrt{\frac{\nabla F_x{}^2\left(i,j\right)+\nabla F_y{}^2\left(i,j\right)}{2}}}}$$

  (17)

  where $\nabla F_x{}^2\left(i,j\right)$ and $\nabla F_y{}^2\left(i,j\right)$ represent the first-order differences of the image $F$ in the x- and y-directions, respectively.
• SF: It reflects the grayscale rate of change of the image and reflects the active level of the image. A larger SF indicates clearer and higher fusion quality. The mathematical expression of SF is

  $$SF=\sqrt{R{F}^2+C{F}^2}$$

  (18)

  $RF$ and $CF$ represent the row space frequency and column space frequency of image $F$, respectively. It can be expressed as

  $$RF=\sqrt{\frac{1}{MN}{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left(F\left(i,j\right)-F\left(i,j-1\right)\right)}^2}}}$$

  (19)

  $$CF=\sqrt{\frac{1}{MN}{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left(F\left(i,j\right)-F\left(i-1,j\right)\right)}^2}}}$$

  (20)
• SCC: It reflects the spatial correlation between the two images, and the larger the correlation coefficient, the better the fusion effect. It can be expressed as

  $$SCC(I_A,I_B)=\frac{{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N\left(I_A(i,j)-{\overline{I}}_A\right)\left(I_B(i,j)-{\overline{I}}_B\right)}}}{\sqrt{{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left(I_A(i,j)-{\overline{I}}_A\right)}^2\times {\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left(I_B(i,j)-{\overline{I}}_B\right)}^2}}}}}}$$

  (21)
• SD: It measures the spectral difference between the fused image and the reference image. The larger the SD, the more severe the spectral distortion. The mathematical expression of SD is

  $$SD=\frac{1}{MN}{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N\left(I_A\left(i,j\right)-I_B\left(i,j\right)\right)}}$$

  (22)
• SAM: It measures the similarity between spectra by calculating the inclusion angle between two vectors. The smaller the inclusion angle is, the more similar the two spectra are. The mathematical expression of SAM is

  $$SAM(v,\widehat{v})=\arccos \left(\frac{\langle v,\widehat{v}\rangle }{{\Vert v\Vert }_2·{\Vert \widehat{v}\Vert }_2}\right)$$

  (23)

  where $v$ is the spectral pixel vector of the original image, and $\widehat{v}$ is the spectral pixel vector of the fused image.
• ERGAS: It reflects the degree of spectral distortion between the fused image and the reference image. The larger the ERGAS, the more severe the spectral distortion. The mathematical expression of ERGAS is

  $$ERGAS=100\frac{h}{l}\sqrt{\frac{1}{K}{\displaystyle \sum _{k=1}^K\frac{RMSE\left(I_A,I_B\right)}{{\mu }_{I_A}}}}$$

  (24)

  $$RMSE\left(I_A,I_B\right)=\frac{1}{MN}\sqrt{{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left(I_A\left(i,j\right)-I_B\left(i,j\right)\right)}^2}}}$$

  (25)

  where $\frac{h}{l}$ is the ratio of the resolution of the ASR image to that of the multispectral image, $K$ denotes the number of bands, and $\mu$ denotes the mean value of the image.
• Q4: It is a global evaluation index based on the calculation of the hypercomplex correlation coefficient between the reference image and the fused image, which jointly measure the spectral and spatial distortion. Its specific definition is detailed in reference [43].
• VIFF: It is a newly proposed index that measures the fidelity of visual information between the fused image and each source image by measuring the fidelity of the visual information based on the Gaussian scale mixture model, the distortion model, and the HVS model. Its specific definition is detailed in reference [44].

4. Experimental Results and Analysis

In order to comprehensively evaluate the experimental results, all the fusion results of the five sets of data are compared and analyzed from two aspects of subjective qualitative evaluation and objective quantitative evaluation, respectively.

4.1. Qualitative Evaluation

The fusion results of QuickBird images are shown in Figure 5, and the corresponding SAM error images are shown in Figure 6. Through comparative analysis, it can be seen that the spatial structure of TVM and RTVD based on variational models as well as ASR, CSR, and CSMCA based on sparse representation theory is relatively fuzzy, and there are obvious artifacts, among which TVM, RTVD, and ASR have the most serious artifacts. The fusion method of CNN and CSE has serious spectral distortion, which is quite different from the original multispectral image. The proposed method can clearly show the contours of buildings and the edge structure of roads and better retain the spatial and spectral information of the original image. Other fusion methods such as Curvelet, DTCWT, MLGCF, RGF, VSM-WLS, EA-DCPCNN, EA-PAPCNN, and WLE-PAPCNN are suboptimal.

The fusion results of SPOT-6 images are presented in Figure 7, and the corresponding SAM error images are shown in Figure 8. The comparative analysis shows that the spatial information of TVM and RTVD based on variational models as well as ASR, CSR, and CSMCA fusion methods based on sparse representation theory is poor, especially the blurred degree of farmland boundary, and the road edge structure is high. The fusion result of CNN is brighter than that of the original multispectral image, whereas the fusion result of RGF is lighter than that of the original multispectral image. Seven methods of Curvelet, DTCWT, CSE, MLGCF, VSM-WLS, EA-DCPCNN, and EA-PAPCNN have no obvious spatial blur and spectral distortion. The fusion results of WLE-PAPCNN and the proposed method have high sharpness, high retention of spectral information, and good overall visual effect.

It can be seen that the sharpness of TVM and RTVD based on variational models as well as ASR and CSR based on sparse representation theory is obviously low, and the overall structure is fuzzy from the fusion results of WorldView-2 images shown in Figure 9 and the corresponding SAM error images in Figure 10. The spectral fidelity of CNN, CSE, and RGF fusion methods is poor, and the color of vegetation in the fusion results is obviously lighter than that of the original multispectral images. The color of vegetation in the valley of the seven fusion methods of Curvelet, DTCWT, CSMCA, MLGCF, VSM-WLS, EA-DCPCNN, and EA-PAPCNN is slightly lighter than that of the original multispectral image. WLE-PAPCNN and the proposed method can clearly show the texture information of ridgelines and mountains, and the overall effect is good.

Figure 11 presents the fusion results of WorldView-3 images, and Figure 12 shows the corresponding SAM error images. It shows that TVM, RTVD, ASR, CSR, and CSMCA fusion methods have poor retention ability of spatial information, and the water edge is blurred. The two fusion methods of CNN and CSE have different degrees of spectral distortion, and the color of vegetation and shallow water is brighter. The proposed method can clearly show the details of water shoreline and pond edge, and the overall color of water body and vegetation is not significantly different from the original multispectral image. The overall colors of Curvelet, DTCWT, RGF, MLGCF, VSM-WLS, EA-DCPCNN, and EA-PAPCNN fusion methods are slightly brighter, whereas the overall color of WLE-PAPCNN is slightly darker.

It can be found that the spatial resolution of TVM, RTVD, ASR, CSR, and CSMCA fusion methods is low; in particular, ASR cannot identify the contours of some small vehicles from the fusion results of Pleiades image shown in Figure 13 and the corresponding SAM error images in Figure 14. The overall color of CSE is brighter than that of the original multispectral image, and the overall color of RGF is redder than that of the original multispectral image. The proposed method performs better on the texture details of roads, bridges, and vehicles, and the colors of vegetation, water, and bare land are not significantly different from the original multispectral images. Curvelet, DTCWT, CNN, MLGCF, VSM-WLS, EA-DCPCNN, EA-PAPCNN, and WLE-PAPCNN retained the spatial and spectral information of the original image to a certain extent, and the comprehensive visual effect is suboptimal.

4.2. Quantitative Evaluation

Table 1. Objective evaluation of 5 sets of image data.

Image	Method	IE↑	MI↑	AG↑	SF↑	SCC↑	SD↓	SAM↓	ERGAS↓	Q4↑	VIFF↑
QuickBird	Curvelet	3.988	7.977	1.505	3.208	0.894	2.338	2.747	10.673	0.853	0.587
	DTCWT	4.005	8.010	1.541	3.318	0.893	2.438	2.870	11.224	0.870	0.591
	CNN	3.812	7.625	1.524	3.288	0.865	4.214	7.550	24.836	0.923	0.444
	CSE	3.739	7.479	1.495	3.284	0.849	4.338	7.096	26.453	0.719	0.332
	ASR	3.799	7.599	0.822	2.025	0.881	2.297	2.430	10.998	0.899	0.470
	CSR	3.944	7.888	1.149	2.632	0.900	2.268	2.572	10.363	0.861	0.561
	CSMCA	4.019	8.037	1.330	2.962	0.888	2.385	2.903	10.626	0.398	0.631
	TVM	3.704	7.408	0.948	1.918	0.870	4.131	6.561	24.153	0.720	0.348
	RTVD	3.109	6.217	0.734	1.560	0.858	5.120	4.057	38.677	0.883	0.182
	RGF	4.051	8.102	1.558	3.318	0.862	2.049	1.841	8.213	0.749	0.559
	MLGCF	4.017	8.026	1.521	3.228	0.895	2.284	2.734	10.099	0.881	0.631
	VSM-WLS	4.042	8.085	1.583	3.401	0.896	2.439	2.909	10.687	0.801	0.655
	EA-DCPCNN	3.977	7.954	1.451	3.122	0.892	2.517	2.691	11.469	0.864	0.620
	EA-PAPCNN	4.007	8.015	1.524	3.322	0.888	2.560	2.940	12.127	0.884	0.520
	WLE-PAPCNN	4.262	8.514	1.552	3.359	0.884	1.720	1.746	7.025	0.892	0.715
	LLVF-PAPCNN	4.308	8.616	1.598	3.382	0.884	1.268	1.857	5.442	0.860	0.899
	Proposed	4.319	8.639	1.633	3.487	0.899	1.242	1.637	5.396	0.938	0.948
SPOT-6	Curvelet	3.620	7.200	0.763	1.562	0.964	2.001	2.890	11.129	0.861	0.550
	DTCWT	3.622	7.213	0.787	1.666	0.965	2.036	3.089	11.415	0.869	0.564
	CNN	3.273	6.546	0.776	1.631	0.929	3.526	5.881	16.812	0.837	0.337
	CSE	3.601	5.931	0.677	1.447	0.957	1.991	3.133	10.730	0.734	0.641
	ASR	3.600	7.202	0.350	0.925	0.952	1.920	2.799	10.650	0.851	0.461
	CSR	3.533	7.066	0.475	1.194	0.963	1.937	2.452	10.985	0.816	0.501
	CSMCA	3.584	7.168	0.590	1.398	0.963	1.970	2.720	11.010	0.804	0.609
	TVM	3.038	6.076	0.436	0.999	0.937	3.227	4.933	29.552	0.561	0.260
	RTVD	2.736	5.472	0.355	0.845	0.957	4.550	6.344	44.935	0.280	0.192
	RGF	3.468	6.937	0.792	1.655	0.926	2.222	3.403	12.057	0.658	0.452
	MLGCF	3.625	7.251	0.772	1.579	0.964	1.919	2.839	10.160	0.842	0.589
	VSM-WLS	3.632	7.264	0.794	1.664	0.966	1.944	3.060	10.343	0.777	0.581
	EA-DCPCNN	3.618	7.235	0.709	1.541	0.967	1.741	3.037	10.340	0.698	0.604
	EA-PAPCNN	3.638	7.276	0.779	1.661	0.965	1.969	3.109	8.625	0.718	0.541
	WLE-PAPCNN	4.002	8.004	0.799	1.695	0.966	0.848	2.108	3.883	0.815	0.842
	LLVF-PAPCNN	4.021	8.042	0.809	1.712	0.967	0.630	1.965	3.441	0.814	0.958
	Proposed	4.023	8.047	0.813	1.712	0.968	0.601	1.903	3.328	0.878	0.954
WorldView-2	Curvelet	5.385	10.771	2.667	4.778	0.920	8.608	0.704	4.095	0.781	0.563
	DTCWT	5.409	10.818	2.802	5.040	0.917	8.707	0.736	4.146	0.792	0.594
	CNN	5.209	10.417	2.796	5.037	0.869	16.035	1.629	6.942	0.727	0.519
	CSE	5.083	10.166	2.784	5.019	0.823	16.337	1.379	9.168	0.731	0.471
	ASR	5.685	11.370	1.362	2.961	0.875	7.203	0.787	3.273	0.801	0.723
	CSR	5.360	10.720	1.977	3.804	0.876	8.605	0.700	4.047	0.795	0.530
	CSMCA	5.386	10.771	2.450	4.560	0.918	8.786	0.744	4.116	0.792	0.553
	TVM	4.935	9.869	1.202	2.309	0.846	16.284	1.318	9.156	0.711	0.360
	RTVD	4.234	8.469	1.208	2.167	0.911	38.444	0.615	41.154	0.413	0.120
	RGF	5.116	10.234	2.799	5.041	0.827	8.729	0.868	4.081	0.754	0.474
	MLGCF	4.413	10.820	2.627	4.709	0.921	8.433	0.690	3.975	0.817	0.580
	VSM-WLS	5.439	10.878	2.742	4.914	0.919	8.735	0.751	4.109	0.804	0.629
	EA-DCPCNN	5.456	10.912	2.619	4.754	0.920	10.205	0.478	4.995	0.783	0.635
	EA-PAPCNN	5.435	10.873	2.809	5.057	0.916	8.629	0.743	3.590	0.807	0.635
	WLE-PAPCNN	5.735	11.470	2.823	5.079	0.916	2.898	0.451	1.969	0.884	0.594
	LLVF-PAPCNN	5.758	11.516	2.839	5.102	0.909	3.059	0.464	1.482	0.879	0.809
	Proposed	5.760	11.521	2.839	5.103	0.923	3.020	0.458	1.441	0.893	0.833
WorldView-3	Curvelet	3.870	7.740	0.777	1.631	0.979	2.407	9.160	14.849	0.641	0.535
	DTCWT	3.874	7.748	0.788	1.661	0.978	2.124	9.257	14.891	0.632	0.546
	CNN	3.277	6.555	0.651	1.534	0.956	4.683	22.300	49.153	0.357	0.383
	CSE	3.290	6.793	0.632	1.455	0.959	4.632	21.682	49.419	0.341	0.205
	ASR	3.564	7.129	0.418	1.103	0.970	3.531	13.961	26.933	0.501	0.370
	CSR	3.774	7.548	0.531	1.331	0.978	2.340	7.571	14.489	0.695	0.534
	CSMCA	3.790	7.579	0.609	1.525	0.975	2.333	7.758	13.868	0.756	0.683
	TVM	3.229	6.459	0.449	1.180	0.963	4.640	23.004	49.765	0.409	0.283
	RTVD	3.049	6.097	0.398	0.993	0.962	4.846	6.014	43.436	0.395	0.258
	RGF	4.062	8.123	0.846	1.808	0.966	1.473	3.908	6.551	0.627	0.826
	MLGCF	3.887	7.774	0.792	1.695	0.978	2.241	8.799	12.765	0.668	0.618
	VSM-WLS	3.876	7.751	0.804	1.742	0.977	2.219	8.674	12.388	0.726	0.644
	EA-DCPCNN	3.674	7.528	0.680	1.582	0.975	2.558	5.498	14.371	0.706	0.645
	EA-PAPCNN	3.857	7.715	0.767	1.590	0.977	2.289	8.698	13.656	0.628	0.504
	WLE-PAPCNN	4.092	8.185	0.805	1.659	0.972	0.807	2.735	4.078	0.691	0.488
	LLVF-PAPCNN	4.094	8.188	0.850	1.815	0.972	0.614	2.495	3.570	0.758	0.929
	Proposed	4.101	8.202	0.851	1.855	0.981	0.518	2.484	2.574	0.759	0.943
Pleiades	Curvelet	4.089	8.177	1.276	2.582	0.822	2.484	2.030	8.004	0.579	0.453
	DTCWT	4.116	8.231	1.330	2.720	0.824	2.571	2.121	8.206	0.827	0.458
	CNN	4.522	9.043	1.350	2.732	0.756	1.932	2.806	6.370	0.830	0.657
	CSE	3.586	7.172	1.265	2.608	0.736	4.707	3.529	16.998	0.561	0.148
	ASR	3.929	7.858	0.679	1.773	0.784	2.341	1.954	8.183	0.807	0.446
	CSR	4.037	8.073	0.911	2.120	0.820	2.416	1.953	7.875	0.826	0.454
	CSMCA	4.191	8.383	1.094	2.343	0.812	2.384	2.069	7.477	0.752	0.611
	TVM	3.478	6.956	0.704	1.424	0.746	4.532	3.349	16.335	0.713	0.163
	RTVD	3.194	6.388	0.616	1.318	0.766	6.873	2.668	35.893	0.699	0.158
	RGF	4.048	8.096	1.367	2.719	0.772	3.817	3.471	9.207	0.728	0.488
	MLGCF	4.135	8.271	1.282	2.587	0.821	2.344	1.979	7.241	0.764	0.508
	VSM-WLS	4.157	8.314	1.345	2.727	0.827	2.567	2.191	7.670	0.825	0.504
	EA-DCPCNN	4.195	8.390	1.242	2.620	0.814	2.209	1.950	7.369	0.810	0.600
	EA-PAPCNN	4.135	8.269	1.309	2.688	0.819	2.608	2.174	8.162	0.836	0.408
	WLE-PAPCNN	4.408	8.818	1.349	2.753	0.785	2.008	2.321	5.020	0.840	0.641
	LLVF-PAPCNN	4.523	9.047	1.427	2.872	0.791	1.404	1.941	3.907	0.864	0.915
	Proposed	4.532	9.064	1.433	2.911	0.832	1.404	1.930	3.901	0.867	0.931

lists the quantitative evaluation results of the proposed method and 16 compared methods corresponding to five different sets of image data. All values are the average values of R, G, and B bands of the fused image on the corresponding evaluation indexes. The symbol “↑” indicates that a larger value is better, the symbol “↓” indicates that a smaller value is better, bold indicates the optimal value, and underscore indicates the suboptimal value.

As can be seen from Table 1, the two classical multi-scale transformation methods, Curvelet and DTCWT, perform relatively similarly in all indexes, and the spectral distortion phenomenon on SPOT-6 data is more obvious, such that the SD and ERGAS indexes both exceed 2 and 11, respectively. The CNN and CSE methods perform poorly on all indexes. Although the CNN method achieves good results on the Pleiades data, it still performs poorly on the other four sets of data. The three sparse representation-based methods ASR, CSR, and CSMCA are significantly worse than other methods in the three spatial information-based indexes of AG, SF, and SCC, so that the ambiguity is the most serious, and they are not prominent in the other five indexes. Both TVM and RTVD methods based on variational models show extremely poor spatial information retention and spectral information fidelity, with severe spatial blurring and spectral distortion. RGF, MLGCF, and VSM-WLS based on edge-preserving filtering have no obvious advantages in all indexes. Among them, the stability of RGF is very poor, and all indexes show good results in WorldView-3 data, but there are general deviations in SPOT-6 data. EA-DCPCNN, EA-PAPCNN, WLE-PAPCNN, and LLVF-PAPCNN are the hybrid methods of NSST and improved PCNN, of which EA-DCPCNN is the worst method among the four methods, and EA-PAPCNN does not perform well in various indexes. The WLE-PAPCNN and LLVF-PAPCNN methods are the two best methods among all the comparison methods, especially showing obvious advantages on the three spectral information-based indexes SD, SAM, and ERGAS. However, the proposed method has been significantly optimized in all aspects, the performance on all indexes is almost the best, and the sub-optimal values basically appear in the LLVF-PAPCNN method.

Comparing all fusion methods, all four methods, CNN, CSE, TVM, and RTVD, have poor spectral quality in spatial quality, with the two methods based on variational models, TVM and RTVD, being somewhat worse than the CNN and CSE methods. The three sparse representation-based methods, ASR, CSR, and CSMCA, have good spectral fidelity, but their spatial clarity is poor. The two classical multiscale transformation methods, Curvelet and DTCWT, are better for the representation of spatial information, but not for the spectral information. The three edge-preserving filtering-based methods, RGF, MLGCF, and VSM-WLS, perform more generally in all evaluation indexes without significant advantages. The four hybrid methods based on NSST and improved PCNN, EA-DCPCNN, EA-PAPCNN, WLE-PAPCNN, and LLVF-PAPCNN, have some advantages over several other types of comparative methods in terms of overall effectiveness and can better extract spatial and spectral information.

Compared to the average value of the LLVF-PAPCNN methods in the five sets of data, the proposed method optimized the 10 evaluation indexes of IE, MI, AG, SF, SCC, SD, SAM, ERGAS, Q4, and VIFF by 0.006, 0.009, 0.009, 0.035, 0.016, 0.037, 0.062, 0.042, 0.030, and 0.020, respectively. It shows that the proposed method has the best fusion effect. Among all the indexes, the proposed method performs well in IE and MI, two evaluation indexes based on information content, indicating that the proposed method can remove redundant information and retain complementary information to a large extent. The results of AG and SF, two evaluation indexes based on spatial information, show that the proposed method can effectively extract the detailed texture and edge information of the image and enhance the image sharpness. At the same time, the proposed method can better retain the spectral information of the original multispectral image and greatly reduce the spectral distortion, which is confirmed by SD and ERDAS, two evaluation indexes based on spectral information. In addition, the excellent performance of the proposed method on VIFF reveals that the design of the proposed method conforms to the essential features of the human visual system and can obtain better visual effects.

5. Conclusions

In this paper, a remote sensing image fusion method combining low-level visual features and PADCPCNN in the non-subsampled shearlet transform domain is proposed. Three local features are combined to solve the singleness of activity measure construction in low-frequency sub-bands fusion. In the high-frequency sub-bands fusion, the parameter settings and external inputs of the DCPCNN model are optimized, and the spatial correlation is enhanced while the model realizes the adaptive parameter selection. By selecting five sets of remote sensing image data of different satellite platforms and ground objects for experiment, the fusion results are evaluated qualitatively and quantitatively and show the effectiveness and universality of the proposed method. The experimental results show that, compared with the other 16 methods, the proposed method is significantly better than the other methods in all evaluation indexes, indicating that the proposed method improves the spatial resolution and spectral resolution of remote sensing images to a large extent.