Local Differential Privacy Based Membership-Privacy-Preserving Federated Learning for Deep-Learning-Driven Remote Sensing

Abstract

With the development of deep learning, image recognition based on deep learning is now widely used in remote sensing. As we know, the effectiveness of deep learning models significantly benefits from the size and quality of the dataset. However, remote sensing data are often distributed in different parts. They cannot be shared directly for privacy and security reasons, and this has motivated some scholars to apply federated learning (FL) to remote sensing. However, research has found that federated learning is usually vulnerable to white-box membership inference attacks (MIAs), which aim to infer whether a piece of data was participating in model training. In remote sensing, the MIA can lead to the disclosure of sensitive information about the model trainers, such as their location and type, as well as time information about the remote sensing equipment. To solve this issue, we consider embedding local differential privacy (LDP) into FL and propose LDP-Fed. LDP-Fed performs local differential privacy perturbation after properly pruning the uploaded parameters, preventing the central server from obtaining the original local models from the participants. To achieve a trade-off between privacy and model performance, LDP-Fed adds different noise levels to the parameters for various layers of the local models. This paper conducted comprehensive experiments to evaluate the framework’s effectiveness on two remote sensing image datasets and two machine learning benchmark datasets. The results demonstrate that remote sensing image classification models are susceptible to MIAs, and our framework can successfully defend against white-box MIA while achieving an excellent global model.

1. Introduction

Remote sensing is a technology that uses sensors (e.g., satellites, airplanes) to detect physical features in a non-contact, long-distance manner [1,2]. In recent years, with the increasing deployment of remote sensing satellites, the magnitude of remote sensing data has also grown dramatically. To analyze and utilize these remote sensing image data, more scholars apply state-of-the-art deep learning techniques for remote sensing image data analysis, such as scene classification [3,4] and object detection [5]. As we know, deep learning models significantly benefit from the size and quality of the training dataset. However, in practice, on the one hand, remote sensing data need to be collected from different companies [6]. On the other hand, remote sensing data cannot directly be shared because they are usually sensitive and contain trade secrets, which may leak information about sensitive infrastructure or military facilities [7]. This is one of the major problems affecting the practical application of deep learning algorithms in remote sensing. To solve this problem, federated learning has been researched and applied to remote sensing [8,9,10,11].

Federated learning allows participants to collaboratively train an efficient global model by sharing the parameters of a local model instead of sensitive data. However, in recent years, scholars have found that federated learning is vulnerable to various inference attacks launched against model parameters, such as adversarial attacks [12,13], backdoor attacks [14], and membership inference attacks [15]. In this paper, we focus on the membership inference attack, the goal of which is to infer whether a specific data point is participating in the model’s training process. Suppose an attacker successfully launches a membership inference attack against a participant, the attacker can infer the location, time, and equipment type of the company’s remote sensing equipment from these membership data. This will be a serious secret disclosure for a remote sensing company.

Recently, scholars have proposed some approaches to defend against MIAs, which can be summarized as confidence score masking [16,17,18] (hiding the target model’s true confidence scores), regularization [16,18,19,20,21] (reducing the overfitting of the target model), knowledge distillation [22,23] (transferring the private large model’s knowledge to the small one through an unlabeled public dataset), and differential privacy [15,24,25] (adding noise to parameters during the model training). For defending against white-box MIAs in FL, researchers have mainly focused on regularization and differential privacy [15,26,27,28,29]. However, the majority of them struggle to balance the privacy preservation and model utility for the deep neural network with high dimensional parameters. Some scholars attempt to encrypt the model parameters with homomorphic encryption [11], which can guarantee the model’s effectiveness while taking into account the privacy and security of the model. However, for complex remote sensing images and classification models, it leads to huge computational and communication costs.

To solve the abovementioned problems, we propose local differential privacy federated learning (LDP-Fed) in this paper. It is a private FL system that allows participants to train DNN models jointly under the protection of LDP. The main inspiration for our LDP-Fed is that adversaries launch membership inference attacks by collecting a set of local or global model parameters in FL. Based on this point, it is different from the central differential privacy, which adds noise during local model training [24]. We perform a piecewise mechanism (PM) on the local model parameters before they are delivered to the central server so that participants satisfy local privacy guarantees. As far as we know, there have been some works [28,29] that applied LDP mechanisms to FL to protect local model parameters. They added the same level of LDP noise to the parameters of each dimension separately. Hence, to improve the model performance, they must either increase the overall privacy budget or the number of federal learning participants, which may reduce the framework usability or raise the risk of privacy disclosure. To show the effectiveness of LDP-Fed, we evaluated LDP-Fed on various datasets. The experimental results demonstrate that LDP-Fed could defend against white-box MIAs while having a minor impact on the utility of complex DNN models. The contributions are summarized as follows:

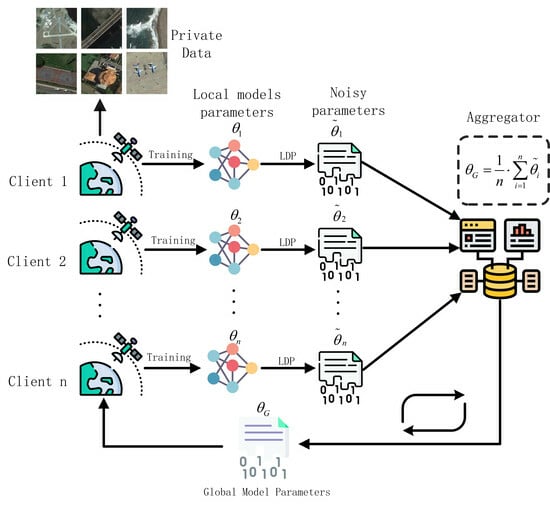
• We propose and implement LDP-Fed to defend against white-box MIAs in the federated learning system on remote sensing, especially for global attacks launched from the central server. It allows participants to collaboratively train DNN models with formal LDP guarantees.
• To achieve optimal privacy-utility trade-offs, we optimize the noise addition method according to the characteristics of white-box MIAs and apply the piecewise mechanism (PM) that is more suitable for the parameters of the DNN models in LDP-Fed. It gives our framework more utility than others while resisting white-box membership inference attacks.
• We extensively evaluate LDP-Fed on various datasets to show the advanced trade-offs of the local participants’ privacy and model utility. For the remote sensing image dataset NWPU-RESISC45 with VGG, it reduced the adversary advantage Adv of global attacks from 46.2% to 10.6% while decreasing the model accuracy by 5.0%.

The rest of our paper is organized as follows: Section 2 presents some related works and background techniques related to the subject of this paper, then an overview of the LDP-Fed framework and details of the LDP-Fed framework are presented in Section 3. Section 4 and Section 5 present the experimental setup and experimental results with analysis and comparison. Section 6 concludes this paper.

2. Related Works and Background Techniques

2.1. Related Works

The development of deep learning algorithms, especially image recognition algorithms, has led to their application in remote sensing, such as scene recognition and object detection. With the increase in remote sensing equipment, the distribution of remote sensing data has become decentralized, with multiple entities (remote sensing companies) holding a small volume of data. To enhance the model’s effectiveness while guaranteeing the security of remote sensing data, scholars have widely used federated learning in remote sensing [30,31,32]. However, it still suffers from some security issues, such as adversarial attacks, backdoor attacks, and especially membership inference attacks. These attacks target the model’s parameters and pose serious security problems for federated learning. There are some typical works on traditional FL applications for these attacks but less research on remote sensing. Therefore, we propose the LDP-Fed framework for MIA in FL on remote sensing. We will describe related work in three aspects: the application of machine learning in remote sensing, membership inference attacks, and defense against membership inference attacks.

2.1.1. Machine Learning in Remote Sensing

The research on remote sensing image data classification using state-of-the-art machine learning models has been studied by scholars for many years [33,34]. Geiß et al. [35] followed the idea of learning invariant decisions function to address the problem of the efficient classification of remote sensing images under sparse data. They proposed a virtual support vector machine based on self-learning (VSVM-SL). In the same period, Wang et al. [36] used the efficient random forest (RF) algorithm to classify remote sensing image data, and the results showed that RF can achieve a superior and more stable classification performance than SVM on the land-cover dataset. With the development of deep learning algorithms, convolutional neural networks (CNN) have emerged as the most promising technique for remote sensing image classification. Zhang et al. [37] proposed the model architecture named CNN-CapsNet to improve the performance of the scene classification model for remote sensing images. Their model utilizes the convolutional layer of a pre-trained convolutional model for feature extraction from the image and then uses CapsNet to classify the intermediate features. In contrast, Li et al. [38] used a convolutional neural network for remote sensing image multi-target scene classification tasks. They proposed MLRSSC-CNN-GNN. The main idea is to generate high-level representation features with the CNN model and combine them with the graph attention network model to fully exploit the scene graph’s spatial-topological relationship. Tang et al. [39] proposed a new CNN model attentional consistent network (ACNet), which can improve the model classification performance by emphasizing the local features of an image. Chen et al. [40] proposed CNSPN, a method that better solves the problem of few-shot remote sensing image classification by combining the semantic information of image class names. Along with the successful applications of deep neural networks in remote sensing image recognition, some scholars have focused on the security concerns posed by the models, such as backdoor attacks [11,14] and adversarial attacks [12,13].

2.1.2. Membership Inference Attack

We categorize membership inference attacks into white-box and black-box MIAs according to the attacker’s information obtained from the target model.

Black-box membership inference attack. Shokri et al. [16] first presented the study of MIAs on the classification model. They trained an inference attack model based on the difference in model prediction between trained and untrained data. With the black box setting, they need to train a series of shadow models to simulate the target model, significantly impacting the attack model. Additionally, it is shown in [16] that overfitting was highly correlated with MIAs, and the techniques that can mitigate over-fittings, such as L2 regularization and dropout, could weaken the effect of an MIA. Yeom et al. [41] proposed another inference attack model based on quantitatively analyzing the difference in the model’s loss between the training and the testing dataset to simplify the MIA. Salem et al. [21] attempted to decrease the shadow model’s number in [16] and proposed a lighter-weight MIA strategy. These schemes rely on black-box features of the target model, such as model prediction, to launch the attack.

White-box membership inference attack. Unlike the previous works, Nasr et al. [27] proposed a comprehensive white-box MIA framework. They assumed that attackers held some knowledge about the training dataset. To obtain the training dataset for the attack model, they use forward and backward propagation to obtain all the model outputs at the data points (e.g., gradients of the data, neuron outputs, and model losses). A one-hot value is added, representing whether the data point participates in the target model training. Their attacks achieve a better performance than the black-box setting. Nasr et al. [27] pointed out that the MIA effect is improved in the FL scenario due to the frequent communication enabling the attacker to acquire more helpful knowledge.

2.1.3. Defense Mechanism against Membership Inference Attack

As MIAs have demonstrated efficiency on various DNN models, researchers have proposed many protection solutions to defend against MIAs. Here, we summarize the existing schemes into four categories, i.e., confidence score masking, regularization, knowledge distillation, and differential privacy. We introduce them separately. In

Table 1. Comparison summary.

Function/Method	[16]	[20]	[22]	[24]	LDP-Fed
Data Type	Arbitrary	Image	Arbitrary	Arbitrary	Arbitrary
Federated Learning	✕	✓	✓	✓	✓
Defend against white-box MIA	✕	✕	✓	✓	✓
Defend against black-box MIA	✓	✓	✓	✓	✓
Defense Mechanism	Confidence Masking	Mixup Regularization	Knowledge Distillation	DP-SGD	LDP
Model Performance	High	High	High	Low	High
Efficiency of Training	High	Low	Low	High	High

, we compare various aspects of the existing schemes with those of LDP-Fed.

Confidence score masking. The motivation for confidence score masking is that defenders could hide some prediction information from the attacked model to mitigate black-box MIAs. Shokri et al. [16] proposed sharing the top-k confidence scores with the attacker instead of providing the complete prediction vector. Jia et al. [17] proposed a defense method called MemGuard using the adversarial machine learning technique. However, follow-up works [23,42] proved that neither could completely defend against membership inference attacks.

Regularization. The overfitting problem of machine learning is an important cause of membership inference attacks [16,43,44], and regularization can effectively mitigate overfitting. Therefore, many scholars have analyzed the effectiveness of various regularization methods to defend against MIA (e.g., L2-norm regularization, dropout, early stopping, and label smoothing [45]). Apart from that, regularization methods are specifically used to defend against MIAs. Nasr et al. [19] proposed adversarial regularization. Li et al. [20] proposed Mixup+MMD (Maximum Mean Discrepancy) to mitigate MIAs. Kaya et al. [45] applied data augmentation to machine learning and compared it with classical regularization methods to demonstrate that data augmentation can effectively defend against MIA experimentally.

Knowledge distillation. Knowledge distillation is often applied as an efficient model compression and acceleration technique in machine learning model deployment. It trains a small “student model” that is transferable by extracting the knowledge from an extensive deep neural network “teacher mode” with high generalization ability since the output vector of the teacher model may contain much potential information about itself [46]. Based on knowledge distillation, Shejwalkar et al. [22] proposed the DMP (Distillation for Membership Privacy) method to defend against MIAs. Unlike the conventional model training process, DMP first trains an unprotected teacher model on their private dataset and then uses the teacher model to classify an unlabeled public dataset as their soft labels. Finally, training the student model with a portion of the soft-labeled dataset. Because DMP requires additional public datasets, Zheng et al. [47] proposed complementary knowledge distillation (CKD) and pseudo complementary knowledge distillation (PCKD) that allows the process of knowledge distillation without the need for additional public datasets.

Differential privacy. Differential privacy [48] is an excellent privacy protection framework that strictly quantifies privacy by the privacy budget $ϵ$ and provides different mechanisms to suit all data types. Since Abadi et al. [24] proposed DP-SGD (differential privacy stochastic gradient descent) for DL, DP has been widely employed in DL. The main idea of DP-SGD is to clip the gradients to obtain a bounded local sensitivity and add Gaussian noise to it. Abadi et al. [24] calculated the privacy cost by applying “moments accountant” to reduce the maximum privacy upper bound. DNN models trained with DP-SGD can effectively defend against MIAs but suffer a significant loss of model utility.

2.2. Background Techniques

2.2.1. Federated Learning

FL was proposed in the form of collaborative learning by Google in 2017 [49]. The importance of FL is that it enables participants to train high-quality machine learning models without sharing the original dataset directly, which may pose privacy concerns. First, N participants with the same private dataset structure agree on training a typical machine learning model with the same architecture. At each iteration, local participants receive the weights from the central server, perform local training with their private dataset, and finally submit their gradients or local model weights to the server. After that, the central server gathers and averages the gradients or model weights from clients. Afterward, the global model’s parameters are distributed to the participants again, and the next iteration starts. This process will iterate until the global model converges or completes a predetermined number of iterations.

2.2.2. Local Differential Privacy

As a variant of DP, local differential privacy [50] aims to enhance the privacy protection of local participants. It allows each participant to perturb sensitive data before being uploaded to the central server. Consequently, the aggregator has no access to the original dataset from the participants. It provides better privacy protection for the participants. The definition of $ϵ$-LDP is given below:

Definition 1.

($ϵ$-Local Differential Privacy). A randomized algorithm $\mathcal{M}$ satisfies ϵ-LDP, if and only if for any two input values v and $v^{\prime }$ in the domain of $\mathcal{M}$, and any possible output Y of $\mathcal{M}$, we have:

$$Pr[\mathcal{M}\left(v\right)\in Y]\le e^{ϵ}·Pr[\mathcal{M}\left(v^{\prime }\right)\in Y],$$

(1)

where $ϵ$ is the privacy budget, which controls the privacy guarantee of mechanism $\mathcal{M}$, a smaller $ϵ$ means stronger privacy protection, and $Pr[·]$ denotes probability.

In addition, similar to DP, LDP also holds two widely-used properties [51]: post-processing and sequential composition. The former property states that it is always privacy-guaranteed to perform arbitrary computations on the output of a differentially private mechanism. The latter property offers the ability to bound the total privacy cost of releasing multiple results of differentially private mechanisms on the same input data.

Theorem 1.

(Posting-Processing). Let $\mathcal{M}\left(x\right)$ be a ϵ-LDP mechanism, where x is the input of $\mathcal{M}$, then for any (deterministic or randomized) function G, $G\left(\mathcal{M}\right(x\left)\right)$ satisfies ϵ-LDP.

Theorem 2.

(Sequential Composition). Given n mechanisms {${\mathcal{M}}_1\left(x\right),{\mathcal{M}}_2\left(x\right),\dots ,{\mathcal{M}}_n\left(x\right)$} satisfy ${ϵ}_i$-LDP, respectively, where x is the same input to all of the mechanisms, then for a new mechanism $\mathcal{A}\left(x\right)=({\mathcal{M}}_1\left(x\right),{\mathcal{M}}_2\left(x\right),\dots ,{\mathcal{M}}_n\left(x\right))$ satisfies ${\sum }_{i=1}^n{ϵ}_i$-LDP.

2.2.3. Piecewise Mechanism

Piecewise mechanism (PM) [50] is a random algorithm that privately analyzes user data’s mean value and frequency estimate. Meanwhile, it also ensures that the user side satisfies the $ϵ$-LDP. An aggregator will calculate the mean value over all n users in this setting. However, instead of raw data t, users send the data $t^{\ast }$ perturbed by PM, and PM guarantees that t is an unbiased estimate of $t^{\ast }$.

Theorem 3.

Let $S=\frac{1}{n}{\sum }_{i=1}^n{t}_i^{\ast }$ and $\overline{S}=\frac{1}{n}{\sum }_{i=1}^n{t}_i^{}$, with at least $1-\beta$ probability,

$$\left|S-\overline{S}\right|=O(\frac{\sqrt{log(1/\beta )}}{ϵ\sqrt{n}}).$$

(2)

Different from the Laplace mechanism [52] and Duchi et al.’s method [53] for one-dimensional data, PM will adjust the probability destiny function according to the input value, which leads to a lower worst-case variance $\frac{4e^{ϵ/2}}{3{(e^{ϵ/2}-1)}^2}$ compared to Duchi et al.’s $\frac{{(e^{ϵ}+1)}^2}{{(e^{ϵ}-1)}^2}$ and Laplace mechanism’s $\frac{8}{{ϵ}^2}$. It is easy to prove that the PM has a lower variance than Duchi et al.’s method when $ϵ>1.29$. Additionally, the worst-case variance of the Laplace mechanism and PM will decrease dramatically as $ϵ$ increases. However, PM’s worst-case variance is still lower than that of the Laplace mechanism, as illustrated in Figure 1.

2.2.4. Membership Inference Attack in Federated Learning

As for the MIA, the primary goal of the attack is to detect whether a data point $(x,y)$ belongs to the training dataset of the target model $f(x,\omega )$. We separate this type of attack into white-box and black-box MIAs depending on the attacker’s information about the attacked model [27]. For the white-box setting, an attacker can obtain all information (i.e., model parameters, model architecture, loss function) about the target model and use these features to train its attack model. However, an attack can only access the model through queries for the black-box attack. This paper focuses on the white-box MIA due to the FL setting.

Unfortunately, federated learning is easily attacked by MIAs. As shown in Figure 2, the adversary may be one of the participants or the CS. In this paper, we set a curious parameter server that can receive the gradients or parameters from each participant and perform a passive white-box MIA on all the local participants, respectively. The local side attacker can only observe a fraction of updated global models, so it achieves a lower attack accuracy than the global attacker. Meanwhile, MIA accuracy declines as the number of participants decreases [27].

3. Methodology

3.1. Overview of LDP-Fed

The rapid development of machine learning techniques has motivated the broad application of deep learning-based image recognition in remote sensing. To improve the model’s effectiveness while ensuring the security of remote sensing data, federated learning has also been widely used in remote sensing. However, frequent transmission of local model parameters in federated learning can lead to membership inference attacks on participants’ remote sensing data, which are launched against the parameters of a model. Suppose an attacker launches membership attacks on a remote sensing company participating in federated learning. In that case, it can infer the location, type, and time information about the company’s satellites through the membership information, resulting in a severe security risk to their satellites. Therefore, this paper proposes LDP-Fed, which aims to train an excellent global model while guaranteeing the security of participants’ sensitive data.

3.1.1. Main Motivation of LDP-Fed

The target model’s generalization gap (i.e., loss gap) between the model on the training dataset and the test dataset is the fundamental reason for the membership inference attack [22,54,55], which is due to the continuous fitting of the training dataset by the deep learning model during the training process. However, in the FL scenario, attackers can obtain more information about the model, enhancing the MIA’s effectiveness. Hence, the methods generally used in the black-box MIA scenario for a defender cannot apply to FL. Local differential privacy is the best option to solve this problem. Participants use local differential privacy algorithms to perturb the parameters of the local model during interaction to reduce the privacy risk. However, the direct use of LDP brings a huge model utility loss, so we designed LDP-Fed for MIA attacks. We chose more appropriate LDP algorithms and allocated a reasonable privacy budget to achieve a better trade-off between member privacy and model utility, and we improved the practicality of the LDP-Fed framework.

3.1.2. Framework of LDP-Fed

As shown in Figure 2, our LDP-Fed mainly contains two parts: (1) Central Server (CS) and (2) Participants. We apply the local differential privacy to FL to protect the parameters of local models and prevent attackers from obtaining information about the local models’ training dataset through parameters.

(1) CS is responsible for communicating with local participants to collect and aggregate local models’ parameters. After aggregating the local models into a global model, CS releases the model information to the chosen participants to perform local training and start the next iteration.

(2) Participants are remote sensing companies involved in federated learning. These companies collect remote sensing image data via private satellites and intend to train a more efficient global model collaboratively. At the beginning of FL, participants initialize their local model based on the parameters distributed by the CS (i.e., global model parameters). Then, the participants start to perform local training using their private remote sensing dataset. Then, participants perturb their local model’s parameters through the LDP algorithm, upload the perturbation parameters to CS, and wait for the next iteration.

Different from the traditional FL framework, which transfers local models’ parameters directly, we perturb the parameters by PM that make the FL process satisfy local differential privacy and can defend against white-box MIAs effectively.

3.1.3. Adversary Model

This paper assumes that the CS and participants are honest but curious. Even though they strictly perform local model training, they remain interested in obtaining the private training dataset of other remote sensing companies to infer the private information of their satellites. Under this assumption, we present the passive adversary $\mathcal{A}$, which has auxiliary data points; a part of that is sampled from the training dataset of the victims. The remaining parts have the same distribution as the training dataset but have not been involved in the model training and launch a white-box MIA to infer whether a data point appears in the training dataset of participants. $\mathcal{A}$ has the following capabilities:

(1) $\mathcal{A}$ can compromise CS to spy on the participants’ local training process, collect all the local models from any participants, and launch the passive white-box MIA.

(2) $\mathcal{A}$ can compromise one remote sensing company, different from the CS situation. It can only observe a series of global models and launch a white-box MIA.

3.1.4. Privacy Requirement

In LDP-Fed, we attempt to protect the private data in each participant’s private remote sensing data from disclosure. In this paper, we mainly focus on the MIA, which is a highly prevalent and efficient attack in federated learning. Therefore, we require our LDP-Fed framework to be defensible against passive white-box MIA launched from the CS and the participant sides during the process of FL training. It means that the adversary fails to distinguish whether a specific data point belongs to the training dataset of a local participant.

3.2. Details of LDP-Fed

Here, we first describe the steps of LDP-Fed illustrated in Algorithm 1, and we presente key details of LDP-Fed as shown in Figure 3.

3.2.1. Federated Learning with LDP

In federated learning, we consider K participants with the same remote sensing data structure who want to train a remote sensing scene classification model collaboratively. During the training process of FL, each participant performs the local model training by its private remote sensing image dataset and shares the local model’s weights with the CS. However, to defend against membership inference attacks, we apply PM to FL and propose LDP-Fed. As shown in Algorithm 1, we present our LDP-Fed training process from the perspective of the central server and the local participants separately.

Cloud update. The central server side is similar to the traditional FL framework. First, it generates the target model with the initial parameters ${\theta }_0$ and sends it to each client with a privacy budget $ϵ$. Then, the server waits for responses from the clients selected by the k-clients selection module. At every iteration in FL, the k-clients selection module will select $k(k\le n)$ clients with probability $q=k/n$, where n is the total number of the local clients. Upon getting responses, the central server aggregates and averages all the updated parameters from the local clients and sends the results back to the clients. After that, the central server moves on to the next iteration.

Clients Update. For the clients, they are participants in federated learning, and each client is a remote sensing company with a private image dataset. At each communication round r, the selected clients will update their local models using weights ${\theta }_r$ sent from the central server. Next, they will use their private remote sensing dataset to perform the local training by the SGD (stochastic gradients descent) [56] in parallel. Then, the clients will send the updated local models’ weights ${\theta }_r^{\prime }$ back to the central server and wait for the next iteration. However, they integrate the PM into this process for client-level security concerns. Before the clients send the updated models’ weights back to the central server, each parameter will be clipped and then perturbed ${\theta }_r^{\prime }$ by PM with the privacy budget $ϵ$ as shown in Algorithm 2. They allocate privacy budgets based on the model’s different layers, unlike the previous methods [28,29] of allocating privacy budgets equally. The privacy budget allocation is described in Section 3.2.4.

Algorithm 1: LDP-Fed.

Algorithm 2: PM_Perturbation.

This process between the central server and local clients will continue until the target model converges or reaches maximum communication rounds (iterations).

3.2.2. Parameter Norm Clipping

Considering the LDP-Fed system’s overall privacy budget and communication costs, we transfer the local model’s weights, which the local private dataset has trained for three epochs. Therefore, the input value of Algorithm 2 is likely not in the range of [−1,1] compared with the FL system, which transfers the model gradients. To satisfy the local differential privacy of Algorithm 1, we have to bound the perturbed local model weights ${\omega }_r$ into [−1,1]. Thus, in Algorithm 1, we have to clip each parameter $\theta$ in ${\omega }_r$ before they are perturbed by Algorithm 2, i.e., for a parameter $\theta$ replaced by $\theta /max(1,|\theta \left|\right)$. The clipping ensures that if $\left|\theta \right|\le 1$, then the parameter $\theta$ is preserved, whereas if $\left|\theta \right|>1$ gets scaled down to be 1 or −1.

3.2.3. Parameter Perturbation

After norm clipping, we subject the parameters to perturbation based on the PM. Specifically, Given a weight ${\omega }_i$ of local model ${\omega }_i\in [-1,1]$ from local client $n_i$, PM outputs a perturbed value ${\omega }_i^{\ast }\in [-C,C]$, where

$$C=\frac{e^{ϵ/2}+1}{e^{ϵ/2}-1}$$

and the PM’s probability density function (pdf) is a piecewise constant function as follows:

$$pdf({\omega }_i^{\ast }=x|{\omega }_i)\left\{\begin{array}{cc}p,\hfill & x\in [l\left({\omega }_i\right),r\left({\omega }_i\right)],\\ \frac{p}{e^{\epsilon }},\hfill & x\in [-C,l\left({\omega }_i\right))\cup (r\left({\omega }_i\right),C].\end{array}\right.$$

(3)

where

$$p=\frac{e^{ϵ}-e^{ϵ/2}}{2e^{ϵ/2}+2},$$

$$l\left({\omega }_i\right)=\frac{C+1}{2}\ast {\omega }_i-\frac{C-1}{2},$$

$$r\left({\omega }_i\right)=l\left({\omega }_i\right)+C-1.$$

In Algorithm 2, we show the pseudo-code of PM. We apply PM in our LDP-Fed because, compared with previous mechanisms (the Laplace mechanism and Duchi et al.’s method), PM performs better when dealing with neural network parameters, which have high precision (5–10 digits after decimal points). Given numeric data t to the LDP mechanism, the algorithm returns perturbed data $t^{\ast }$, and $t^{\ast }$ is the unbiased estimator of the original data t. However, different LDP mechanisms have variances for $t^{\ast }$. The variances of PM, Duchi’s solution, and the Laplace mechanism are $\frac{t^2}{e^{ϵ/2}-1}+\frac{e^{ϵ/2}+3}{3{(e^{ϵ/2}-1^{})}^2}$, ${\left(\frac{e^{ϵ}+1}{e^{ϵ}-1}\right)}^2-t^2$,$\frac{8}{{ϵ}^2}$, respectively. PM has a smaller variance when dealing with smaller values, while Duchi et al. ’s has a larger variance.

3.2.4. Privacy Budget Allocation of LDP-Fed

The privacy budget allocation is vital for applying PM to the FL system. PM is a design for the single numerical attribute collection, so we have to use PM for each parameter of the target model. As shown in Algorithm 1, we assume the FL system has a total of E iterations, n clients, and an overall privacy budget $ϵ$. At each iteration, randomly select k clients for target model updating. Based on the composition property of LDP [57], to guarantee $ϵ$-LDP, Truex et al. [28] and Sun et al. [29] split the privacy budget $ϵ$ into E small pieces and hold $ϵ={\sum }_{i=0}^{E-1}{ϵ}_i$. At each iteration $i<E$, the small piece of the privacy budget ${ϵ}_i$ will be allocated equally to every dimension of the model parameters, just as ${ϵ}_p=\frac{{ϵ}_i}{\left|\theta \right|}$, where the $\left|\theta \right|$ represents the total numbers of the model parameter uploaded to the central server. However, this type of privacy budget allocation assumes that the parameters are identically sensitive to LDP noise. This may lead to a less accurate DNN model or be ineffective in defending against white-box MIAs in FL. Our experiments found that the DNN model’s former layers are more noise-sensitive. As the layers increase, the robustness of the parameters increases. This is due to the former layers extracting features from the training dataset and generalizing better than the later layers. Thus, a slight change could be reflected in the DNN model’s accuracy. Another important point is that, in [27], their experiments showed that among the layers of the target model, the latter leak more information about the training dataset than the former layers, especially for the last layer. As shown in Theorem 3, the asymptotically optimal error bound of PM is $O(\frac{\sqrt{log(1/\beta )}}{ϵ\sqrt{n}})$. To increase the target model utility, it has to increase the privacy budget $ϵ$ for each parameter when we fix clients’ number k, which may result in privacy leakage from the later layers’ parameters when k is small.

Combining the twofold, we suggest that the defender allocates more privacy budget to the former layers of their model when using LDP to defend against white-box MIAs in FL. Specifically, given a total privacy budget $ϵ$ in our LDP-Fed, we allocate it equally to each iteration. In each iteration, we allocate the privacy budget for all parameters in the last layer as ${ϵ}_L$. Moreover, for the parameters of layer l, we allocate the privacy budget ${ϵ}_L+(L-l)\ast s$. In our experiments, we set $s=1$ uniformly.

4. Experimental Setup

In this section, we briefly introduce the experimental setup. It contains the dataset information, the target model’s architecture and hyperparameters in FL, the white-box inference attack model setup, and the metrics for model performance.

4.1. Datasets

To evaluate our experiments, we used four datasets: two famous remote sensing image datasets, EuroSAT and NWPU-RESISC45, and two standard image recognition benchmark datasets, Fashion-MNIST and CIFAR10.

EuroSAT was proposed by Helber et al. [58], which is a satellite image dataset based on Sentinel-2. EuroSAT provides 27,000 non-overlapping $64\times 64$ color pixels images and is classified into ten categories, as shown in Figure 4. Researchers often use it as a benchmark dataset for land use and land cover issues in remote sensing image recognition.

NWPU-RESISC45 [59] was created by Northwestern Polytechnical University (NWPU) as a benchmark dataset for remote sensing image scene classification. It consists of 31,500 remote sensing images that cover 45 scene categories, with 700 images in each category. Due to its large-scale scene categories and data quantity, it is widely used in remote sensing image classification tasks. In Figure 5, we present part of the scene images of NWPU-RESISC45.

Fashion-MNIST [60] contains 60,000 training images and 10,000 testing images containing $28\times 28$ pixels gray-level (0 to 255). A classification task is trained to recognize the ten clothing labels of the input images (e.g., t-shirt, trousers, and dress).

CIFAR10 [61] is a popular benchmark dataset used to evaluate image recognition algorithms. The dataset consists of 32 × 32 color pixels and contains 50,000 training and 10,000 validation images drawn from 10 classes.

4.2. Target Model Setting

We investigated LDP-Fed on the datasets mentioned previously. For EuroSAT, we used a three convolutional layers and a two fully connected layers convolutional neural network (CNN). As for Fashion-MNIST, we used a six-layer (1024,512,256,128) fully connected neural network (FCN), which had been used by Nasr et al. [27] for a target model to be attacked. The features and label size of the dataset determine the size of the input and output layers. For the CIFAR10 and NWPU-RESISC45, we used the Alexnet [62] and VGG [63] models, respectively. We trained our model with the Adam [64] optimizer with a 0.001 learning rate.

We used two federated learning settings to verify the robustness of the LDP-Fed and the effectiveness against the white-box MIA. Specifically, we chose the parameters averaging the aggregation method in FL. At every iteration in FL, each selected participant sends the updated local model’s parameter to the central server after training three epochs. We uniformly used the same dataset size for all the participants. For the former, we used four datasets, and the sizes are shown in

Table 2. The size of the dataset used to train and test the LDP-Fed classification models and the architecture of the models.

Dataset	Architecture	Training Size	Testing Size
EuroSAT	Convolutional Neural Network	15,000	12,000
NWPU-RESISC45	Convolutional Neural Network(VGG)	20,000	10,000
Fashion-MNIST	Fully Connected Network	60,000	10,000
CIFAR10	Convolutional Neural Network(Alexnet)	50,000	10,000

. We averaged all the data points for all of the participants, which do not overlap between various participants. We continued the experiment’s setup in [27] for the latter. We set four participants in FL, and the sizes of the datasets are shown in

Table 3. Datasets sizes of the target and attack models in FL experiments.

Datesets	Client’s Datasets Size		Attack Model Datasets Size
	Training	Testing	Training Member	Training Non-Member	Testing Member	Testing Non-Member
EuroSAT	5000	5000	2500	2500	2500	2500
NWPU-RESISC45	10,000	10,000	5000	5000	5000	5000
Fashion-MNIST	5000	10,000	2500	2500	2500	2500
CIFAR10	15,000	10,000	10,000	5000	5000	5000

.

4.3. Threat Model Setting

We implemented the MIA with TensorFlow and Keras. The architecture of our threat model is the same as Nasr et al.’s [27] supervised learning part. When a global attacker launches a white-box MIA against a participant, the attacker first actively collects the local models uploaded by the participant. Then, it obtains all the helpful information, just like the model’s output, hidden layers’ output, and the gradients of the loss to the parameters by forward and backward passes as the input features of the attack model. Finally, a binary classification attack model is trained by supervised learning. However, the target model is changed to the global model when the attacker is a local participant. An attacker can launch an MIA at any epoch during the FL training process. In this paper, we uniformly set it to 120, which may lead to a better attack performance [27].

4.4. Metrics

To quality the model’s utility in FL, we used its top-1 accuracy on the testing dataset, $\mathit{Acc}$. We tested our attack model’s accuracy on a dataset consisting of half members and half non-members. However, on the dataset, a random guessing strategy has an accuracy of 50%. Thus, to quantify the performance of the attack model, we followed [20,41,45] to use the adversary advantage metric $\mathit{Adv}$, defined as its accuracy over a balanced 1/2 as a percentage, i.e., $Adv=(Acc-50\%)\ast 2$.

5. Experimental Results and Discussion

Here, we present our experimental results for the LDP-Fed defense effectiveness to the white-box MIA in remote sensing, followed by results for analyzing the effect of parameters in LDP-Fed on its performance.

5.1. Defende against White-Box MIA

Unconstrained attack. We presented the performance of the membership inference attack without deployment defense in

Table 4. Performance of applying LDP in FL against white-box MIA on EuroSAT, CIFAR10, NWPU-RESISC45, and Fashion-MNIST.

Defense	Dateset	Privacy Budget $\mathit{ϵ}$	Acc.	Global Att.$\mathit{Adv}$	Local Att.$\mathit{Adv}$
No Defense	EuroSAT	-	89.2%	46.4%	25.8%
	CIFAR10	-	62.1%	44.6%	26.3%
	NWPU-RESISC45	-	83.5%	46.2%	28.4%
	Fashion-MNIST	-	86.5%	24.5%	12.5%
Defense with LDP	EuroSAT	3.0	82.5%	13.8%	17.6%
	CIFAR10	2.0	59.6%	12.2%	18.4%
	NWPU-RESISC45	5.0	77.9%	10.6%	18.6%
	Fashion-MNIST	2.0	83.6%	4.6%	8.2%

. All four datasets suffered from white-box MIAs to varying degrees, especially for the more complex remote sensing image datasets EuroSAT and NWPU-RESISC45. It indicates that remote sensing image classification models are more vulnerable to membership inference attacks. Further, we can conclude that a global attacker is more effective than a local attacker (e.g., 46.4% vs. 25.8% attack $Adv$ on EuroSAT and 44.6% vs. 26.3% on CIFAR10). This is because the model updated by the local clients contains more information about the clients’ training data than the averaged model in an iteration of the FL.

LDP against white-box MIAs in FL. We first have to provide good utility for the FL model when $n=4$. Thus, we chose different $ϵ$ values for the four datasets based on the results of the previous experiment. As shown in Table 4, we set $ϵ=3.0$ for EuroSAT, $ϵ=2.0$ for CIFAR10, $ϵ=5.0$ for NWPU-RESISC45, and $ϵ=3.0$ for Fashion-MNIST. They achieved $Acc=82.5\%$, $Acc=59.6\%$, $Acc=77.9\%$, and $Acc=83.6\%$, respectively. Our LDP-Fed can significantly reduce the white-box MIA’s effectiveness while maintaining a high testing accuracy on global models. Under this LDP setting, a passive global attacker $Adv$ is decreased dramatically for all four datasets. For EuroSAT, CIFAR10, and NWPU-RESISC45, LDP reduced attack $Adv$ by more than 70% over the baseline attack $Adv$, and for Fashion-MNIST, by almost 82%. In Table 4, we also presented the results of the LDP defending against a local passive attacker. We observed that LDP reduces the risk slightly compared to a global attacker: on EuroSAT, CIFAR10, Fashion-MNIST, and NWPU-RESISC45, it reduced the attack $Adv$ by nearly 30%. Fortunately, the efficiency of local attackers decreases quickly and naturally as the number of participants increases, because averaging in the FL scenario may decrease the effects of each party [27].

Why does LDP-Fed work? In Figure 6, we recorded the performance of the local and global models on four datasets during LDP-Fed’s training process. Specifically, we recorded the updated local models’ training and testing accuracy, the testing accuracy of the local models after LDP perturbation, and the testing accuracy of the aggregated global models at 30, 60, 90, 120, and 150 epochs, respectively. The experimental results showed that the local and global models converge after 30 epochs, and the perturbation effect of LDP on the local models is evident. It seriously reduced the testing accuracy of the local models by around 40–50 percentage points for all datasets, while the aggregated global model still performs well after aggregation. LDP perturbation caused dramatic changes in the local models’ parameters, leading to significant inaccuracies in a global attacker’s training dataset. That is why the LDP-Fed is so effective in defending against attacks launched from the global side. The global model received by the client still maintained a good performance, resulting in LDP-Fed being less effective than the global attacker in defending against the local attackers.

5.2. Hyperarameter of LDP-Fed Analysis

As shown in Figure 7, to evaluate the relationship between the client’s number n and the global model testing accuracy in FL, we fixed the privacy budget $ϵ$. We changed the client’s number n in four different datasets. We observed that the LDP-Fed models perform better with the increase of n, even as close as the undefended models. However, after $n=10$, they almost hold the same performance distance between LDP-Fed and undefended models no matter the change of n. This is because, as shown in Theorem 3, the error between the mean of the original data and the perturbed data by PM is constrained by the privacy budget $ϵ$ and the number of participants n. The error decreases rapidly as the number of participants increases. In practice, the number of clients n still should be ten or more to get an acceptable model performance in our LDP-Fed.

Another important hyperparameter to the LDP-Fed is the privacy budget $ϵ$. As shown in Figure 8, we analyzed the effect of $ϵ$ on model performance. Specifically, we set n to 20 in FL and presented the accuracy results with $ϵ$ from 1 to 7 for all four datasets. It showed that the accuracy would increase as $ϵ$ increases. We observed four different $ϵ$ as an inflection point on EuroSAT $(ϵ=3.0)$, Fashion-MNIST $(ϵ=2.0)$, CIFAR10 $(ϵ=3.0)$, and NWPU-RESISC45 $(ϵ=5.0)$. The model’s accuracy dropped rapidly when $ϵ$ was less than the point. On the contrary, the accuracy increased slowly and was close to the undefended model’s performance. Furthermore, more complex datasets or DNN models require more privacy costs. This is because of the more sophisticated neural network and more model weights.

In addition, we evaluated the model convergence rate, which determines the communication costs between clients and the central server in LDP-Fed. As shown in Figure 9, for Fashion-MNIST, the models converged within ten communication rounds. For the rest of the dataset, limited by model complexity and sensitivity, they need more than 15 communication rounds to achieve a better performance. Our LDP-Fed is convenient for training an excellent model within an acceptable communication cost.

5.3. Performance Comparison

Comparison with DP-SGD. As a gold standard, DP provides theoretical privacy guarantees. Abadi et al. [24] proposed DP-SGD to protect against privacy leakage in machine learning. Essentially, DP-SGD clipped and added Gaussian noise to the gradients computed on the private dataset during model training to limit the influence of a single sample on the target model. In this paper, we followed the method of Naseri et al. [15], which applied the DP-SGD to the local models training process of the FL. We compared LDP-Fed and DP-SGD using the empirically observed trade-offs between membership privacy and global model accuracy.

We used CIFAR10 with Alexnet and chose two different privacy budgets for the DP-SGD, $ϵ=2.0$ (same with LDP-Fed privacy budget setting), $ϵ=8.6$ (suggested by [15]), and $\delta ={10}^{-5}$ in both cases. We presented the experimental results in

Table 5. Compare the performance of different defense mechanisms against a white-box MIA in FL using Alexnet on CIFAR10.

Defense Method	Privacy Budget $\mathit{ϵ}$	Model Acc.	Global Att.$\mathit{Adv}$	Local Att.$\mathit{Adv}$
No Defense	-	62.1%	44.6%	26.3%
LDP-Fed	2.0	59.6%	12.2%	18.4%
DP-SGD	2.0	42.3%	5.8%	4.2%
	8.6	54.6%	13.6%	12.8%

. As shown in Table 5, our LDP-Fed and DP-SGD did mitigate the white-box MIA for a global attacker. However, LDP-Fed could achieve a better defensive performance while obtaining a target model with higher testing accuracy. When we set the privacy budget of DP-SGD to 2.0, both global and local attackers were almost ineffective. However, this accompanied a loss of more than 31% of model accuracy. As we anticipated, DP-SGD performed better against the local attackers. Unlike DP-SGD, which adds noise during local model training, LDP-Fed-aggregated perturbed parameters were unbiased estimates of the original parameters, meaning the global LDP-Fed models have much less noise compared with DP-SGD.

Comparison with other LDP-FL. In Figure 8, we set $n=20$ for all the datasets. Our LDP-Fed achieved 73.4% accuracy with $ϵ=3.0$, 77.9% accuracy with $ϵ=5.0$, 83.8% accuracy with $ϵ=2.0$, and 59.3% accuracy with $ϵ=2.0$ on EuroSAT, NWPU-RESISC45, Fashion-MNIST, and CIFAR10, respectively. To our knowledge, the results are very competitive with previous works. Geyer et al. [65] first applied DP under Gaussian Mechanism to federated learning to preserve clients’ level privacy. While they only achieved 78%,92%, and 96% accuracy with $(ϵ,m,n)=(8,11,100),(8,54,1000),(8,12,10,000)$ on MNIST with differential privacy, where $(ϵ,m,n)$ represented the privacy budget, communication rounds, and clients number, respectively. LDP was first exploited for federated learning by Bhowmick et al. [66]. However, due to the high variance of their LDP algorithm, to improve the convolutional neural network model’s accuracy to 10 percent of the original value, they required a relatively large privacy budget and communication rounds, i.e., CIFAR10 $(ϵ=1000,CR=200)$. Truex et al. [28] utilized condensed local differential privacy (CLDP) to FL and up to $Acc=86.93\%$ for Fashion-MNIST. Unlike the DP privacy budget $ϵ$, $\alpha$-CLDP’s privacy budget is controlled by the parameter $\alpha$. However, $\alpha$-CLDP achieved the accuracy by requiring a high privacy budget $ϵ=\alpha ·2c·p$ (e.g., $\alpha =1,c=1,p=10$), which may cause a weak LDP guarantee. Meanwhile, they did not apply $\alpha$-CLDP to a more complex DNN model or dataset. Sun et al. [29] proposed an advanced LDP-Fed recently, which obtained high accuracy while protecting the privacy of the model, i.e., Fashion-MNIST $(ϵ=4,Acc=86.26\%,n=200)$, CIFAR10 $(ϵ=10,Acc=61.46\%,n=500)$. However, they need more than 100 clients in FL because they added the same noise to all parameters. Thus, the number of clients must be constantly increased to reduce the noise’s impact on model performance. In our LDP-Fed, we designed a special noise addition method against MIAs. We can efficiently train excellent complex DNN models with fewer clients than in previous works.

6. Conclusions

As the most promising solution for remote sensing institutions to maximize the potential of data-driven models, FL has been widely used in remote sensing, such as in FL-based image scene classification. However, FL is vulnerable to white-box MIAs, which may lead to the serious disclosure of the participants’ secret satellite sensitive information when we apply FL in remote sensing. To solve the problem, we presented LDP-Fed, a federated learning framework with LDP to defend against white-box MIAs in FL. Unlike conventional federated learning, our system does not require a trusted aggregation server due to local participants perturbing their model parameters with LDP to provide privacy protection. To efficiently train a complex DNN model with LDP guaranteed, we have allocated a reasonable privacy budget according to the network layers. We conducted comprehensive experiments on four datasets, including two benchmark datasets for remote sensing scene classification. Our experimental results demonstrate that remote sensing image classification models are susceptible to MIAs. Furthermore, our framework can defend against membership inference attacks while guaranteeing the utility of the models.