A Modified Version of the Direct Sampling Method for Filling Gaps in Landsat 7 and Sentinel 2 Satellite Imagery in the Coastal Area of Rhone River
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. Applied Methodology
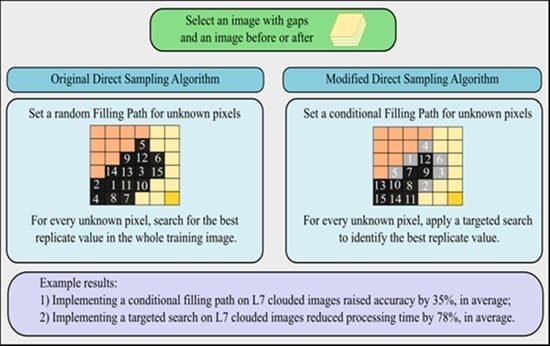
2.2.1. Modified Direct Sampling Method
2.2.2. Experimental Setting
2.3. Performance Assessment
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Robert, E.; White, J.C. Forest Monitoring Using Landsat Time Series Data: A Review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Jamshidi, S.; Zand-parsa, S.; Niyogi, D. Assessing Crop Water Stress Index of Citrus Using In-Situ Measurements, Landsat, and Sentinel-2 Data. Int. J. Remote Sens. 2021, 42, 1893–1916. [Google Scholar] [CrossRef]
- Du, Y.; Song, K.; Liu, G.; Wen, Z.; Fang, C.; Shang, Y.; Zhao, F.; Wang, Q.; Du, J.; Zhang, B. Quantifying total suspended matter (TSM) in waters using Landsat images during 1984–2018 across the Songnen Plain, Northeast China. J. Environ. Manag. 2020, 262, 110334. [Google Scholar] [CrossRef]
- Jamshidi, S.; Zand-parsa, S.; Pakparvar, M.; Niyogi, D. Evaluation of Evapotranspiration over a Semi-Arid Region using Multi-Resolution Data Sources. J. Hydrometeorol. 2019, 20, 947–964. [Google Scholar] [CrossRef]
- Naghdyzadegan Jahromi, M.; Zand-parsa, S.; Razzaghi, F.; Jamshidi, S.; Didari, S.; Doosthosseini, A.; Reza Pourghasemi, H. Developing machine learning models for wheat yield prediction using ground-based data, satellite-based actual evapotranspiration and vegetation indices. Eur. J. Agron. 2023, 146, 126820. [Google Scholar] [CrossRef]
- Bannari, A.; Al-ali, Z.M. Assessing Climate Change Impact on Soil Salinity Dynamics between 1987–2017 in Arid Landscape Using Landsat TM, ETM+ and OLI Data. Remote Sens. 2020, 12, 2794. [Google Scholar] [CrossRef]
- Cammarano, D.; Jamshidi, S.; Hoogenboom, G.; Ruane, A.C.; Niyogi, D.; Ronga, D. Processing tomato production is expected to decrease by 2050 due to the projected increase in temperature. Nat. Food 2022, 3, 437–444. [Google Scholar] [CrossRef]
- Amani, M.; Member, S.; Ghorbanian, A.; Ahmadi, S.A.; Moghimi, A.; Mirmazloumi, S.M.; Member, S.; Hamed, S.; Moghaddam, A.; Mahdavi, S.; et al. Google Earth Engine Cloud Computing Platform for Remote Sensing Big Data Applications: A Comprehensive Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5326–5350. [Google Scholar] [CrossRef]
- Shao, Z.; Fu, H.; Li, D.; Altan, O.; Cheng, T. Remote sensing monitoring of multi-scale watersheds impermeability for urban hydrological evaluation. Remote Sens. Environ. 2019, 232, 111338. [Google Scholar] [CrossRef]
- Weiss, D.J.; Atkinson, P.M.; Bhatt, S.; Mappin, B.; Hay, S.I.; Gething, P.W. An effective approach for gap-filling continental scale remotely sensed time-series. ISPRS J. Photogramm. Remote Sens. 2014, 98, 106–118. [Google Scholar] [CrossRef]
- Belda, S.; Pipia, L.; Morcillo-pallarés, P.; Rivera-caicedo, J.P.; Amin, E.; De Grave, C.; Verrelst, J. Europe PMC Funders Group DATimeS: A machine learning time series GUI toolbox for gap-filling and vegetation phenology trends detection. Environ. Model. Softw. 2022, 127, 104666. [Google Scholar] [CrossRef]
- Freyr, A.; Baum, A.; Vicente-serrano, S.M.; Stockmarr, A. Gap-Filling of NDVI Satellite Data Using Tucker Decomposition: Exploiting Spatio-Temporal Patterns. Remote Sens. 2021, 13, 4007. [Google Scholar]
- Li, M.; Zhu, X.; Li, N.; Pan, Y. Gap-Filling of a MODIS Normalized Difference Snow Index Product Based on the Similar Pixel Selecting Algorithm: A Case Study on the Qinghai–Tibetan Plateau. Remote Sens. 2020, 12, 1077. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM + SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations–application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Henn, B.; Raleigh, M.S.; Fisher, A.; Lundquist, J.D. A Comparison of Methods for Filling Gaps in Hourly Near-Surface Air Temperature Data. Am. Meteorol. Soc. 2013, 14, 929–945. [Google Scholar] [CrossRef]
- Noor, N.M.; Mustafa, M.; Bakri, A.; Yahaya, A.S.; Ramli, N.A. Comparison of Linear Interpolation Method and Mean Method to Replace the Missing Values in Environmental Data Set. Mater. Sci. Forum 2015, 803, 278–281. [Google Scholar] [CrossRef]
- Rezaee, H.; Mariethoz, G.; Koneshloo, M.; Asghari, O. Multiple-point geostatistical simulation using the bunch-pasting direct sampling method. Comput. Geosci. 2013, 54, 293–308. [Google Scholar] [CrossRef]
- Aitokhuehi, I.; Durlofsky, L.J. Optimizing the performance of smart wells in complex reservoirs using continuously updated geological models. J. Pet. Sci. Eng. 2005, 48, 254–264. [Google Scholar] [CrossRef]
- Hoffman, B.T.; Caers, J. History matching by jointly perturbing local facies proportions and their spatial distribution: Application to a North Sea reservoir. J. Pet. Sci. Eng. 2007, 57, 257–272. [Google Scholar] [CrossRef]
- Huysmans, M.; Dassargues, A. Application of multiple-point geostatistics on modelling groundwater flow and transport in a cross-bedded aquifer (Belgium). Hydrogeol. J. 2009, 17, 1901–1911. [Google Scholar] [CrossRef]
- Yin, G.; Mariethoz, G.; McCabe, M.F. Gap-filling of landsat 7 imagery using the direct sampling method. Remote Sens. 2017, 9, 12. [Google Scholar] [CrossRef]
- Guardiano, F.B.; Srivastava, R.M. Multivariate Geostatistics: Beyond Bivariate Moments; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Strebelle, S. Conditional Simulation of Complex Geological Structures Using Multiple-Point Statistics 1. Math. Geol. 2002, 34, 1–21. [Google Scholar] [CrossRef]
- Zhang, T.; Switzer, P.; Journel, A. Filter-Based Classification of Training Image Patterns for Spatial Simulation. Int. Assoc. Math. Geol. 2006, 38, 62–80. [Google Scholar] [CrossRef]
- Gloaguen, E.; Dimitrakopoulos, R. Two-dimensional Conditional Simulations Based on the Wavelet Decomposition of Training Images. Math. Geosci. 2009, 41, 679–701. [Google Scholar] [CrossRef]
- Honarkhah, M.; Caers, J. Stochastic Simulation of Patterns Using Distance-Based Pattern Modeling Distance-based Method. Math. Geosci. 2010, 42, 487–517. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. Multiple-point geostatistical modeling based on the cross-correlation functions. Comput. Geosci. 2012, 16, 779–797. [Google Scholar] [CrossRef]
- Straubhaar, J.; Renard, P.; Mariethoz, G.; Froidevaux, R.; Besson, O. An Improved Parallel Multiple-point Algorithm Using a List Approach. Math. Geosci. 2011, 43, 305–328. [Google Scholar] [CrossRef]
- Straubhaar, J.; Walgenwitz, A.; Renard, P. Parallel Multiple-Point Statistics Algorithm Based on List and Tree Structures. Math. Geosci. 2013, 45, 131–147. [Google Scholar] [CrossRef]
- Mariethoz, G.; Renard, P. Reconstruction of Incomplete Data Sets or Images Using Direct Sampling. Math. Geosci. 2010, 42, 245–268. [Google Scholar] [CrossRef]
- Abdollahifard, M.J.; Faez, K. Fast direct sampling for multiple-point stochastic simulation. Arab. J. Geosci. 2013, 15, 1927–1939. [Google Scholar] [CrossRef]
- Feng, W.; Wu, S.; Yin, Y.; Zhang, J.; Zhang, K. A training image evaluation and selection method based on minimum data event distance for multiple-point geostatistics. Comput. Geosci. 2017, 104, 35–53. [Google Scholar] [CrossRef]
- Zuo, C.; Pan, Z.; Gao, Z.; Gao, J. Correlation-driven direct sampling method for geostatistical simulation. Am. Phys. Soc. 2019, 99, 053310. [Google Scholar] [CrossRef]
- Soltan Mohammadi, H.; Javad Abdollahifard, M.; Doulati Ardejani, F. CHDS: Conflict handling in direct sampling for stochastic simulation of spatial variables. Stoch. Environ. Res. Risk Assess. 2020, 4, 23. [Google Scholar] [CrossRef]
- Zuo, C.; Yin, Z.; Pan, Z.; Mackie, E.J.; Jef, C. A Tree-Based Direct Sampling Method for Stochastic Surface and Subsurface Hydrological Modeling. Water Resour. Res. 2020, 56, 20. [Google Scholar] [CrossRef]
- Antonelli, C.; Eyrolle, F.; Rolland, B.; Provansal, M.; Sabatier, F. Suspended sediment and 137Cs fluxes during the exceptional December 2003 flood in the Rhone River, southeast France. Geomorphology 2008, 95, 350–360. [Google Scholar] [CrossRef]
- Delile, H.; Masson, M.; Miège, C.; Le Coz, J.; Poulier, G.; Le Bescond, C.; Radakovitch, O.; Coquery, M. Hydro-climatic drivers of land-based organic and inorganic particulate micropollutant fluxes: The regime of the largest river water inflow of the Mediterranean Sea. Water Res. 2020, 185, 116067. [Google Scholar] [CrossRef] [PubMed]
- Comby, E.; Le Lay, Y.F.; Piégay, H. How chemical pollution becomes a social problem. Risk communication and assessment through regional newspapers during the management of PCB pollutions of the Rhône River (France). Sci. Total Environ. 2014, 482, 100–115. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, W.; Meybeck, M. Riverine Transport of Water, Sediments and Pollutants to the Mediterranean Sea, UNEP/MAP/MED POL, MAP Technical Reports Series; No. 141; UNEP/MAP: Athens, Greece, 2003. [Google Scholar]
- UNESCO Parc Naturel Régional de Camargue. Available online: https://en.unesco.org/biosphere/eu-na/camargue (accessed on 23 October 2023).
- Mariethoz, G.; Renard, P.; Straubhaar, J. The direct sampling method to perform multiple-point geostatistical simulations. Water Resour. Res. 2010, 46, 1–14. [Google Scholar] [CrossRef]
- Meerschman, E.; Pirot, G.; Mariethoz, G.; Straubhaar, J.; Van Meirvenne, M.; Renard, P. A practical guide to performing multiple-point statistical simulations with the Direct Sampling algorithm. Comput. Geosci. 2013, 52, 307–324. [Google Scholar] [CrossRef]
- Farhat, L. A Set of Algorithms for Preprocessing and Gap Filling of Landsat 7 and Sentinel 2 Imagery Using a Modified Direct Sampling Approach. Available online: https://github.com/farhatlokmen/GapFilling.jl (accessed on 23 October 2023).
- Huang, T.; Li, X.; Zhang, T.; Lu, D. GPU-accelerated Direct Sampling method for multiple-point statistical simulation. Comput. Geosci. 2013, 57, 13–23. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Beckers, J.M.; Weisberg, R.H. Multivariate reconstruction of missing data in sea surface temperature, chlorophyll, and wind satellite fields. J. Geophys. Res. 2007, 112, 1–11. [Google Scholar] [CrossRef]
- Hilborn, A.; Costa, M. Applications of DINEOF to Satellite-Derived Chlorophyll-a from a Productive Coastal Region. Remote Sens. 2018, 10, 1449. [Google Scholar] [CrossRef]
- Sarafanov, M.; Kazakov, E.; Nikitin, N.O.; Kalyuzhnaya, A.V. A Machine Learning Approach for Remote Sensing Data Gap-Filling with Open-Source Implementation: An Example Regarding Land Surface Temperature, Surface Albedo and NDVI. Remote Sens. 2020, 12, 3865. [Google Scholar] [CrossRef]





| Imagery Series | Spectral Band Designation | Description | Central Wavelength (nm) | Resolution (m) |
|---|---|---|---|---|
| L7 | B01 | Blue | 450–520 | 30 |
| B02 | Green | 520–600 | 30 | |
| B03 | Red | 630–690 | 30 | |
| B04 | Near Infrared | 770–900 | 30 | |
| B05 | Shortwave Infrared | 1550–1750 | 30 | |
| B07 | Shortwave Infrared | 2080–2350 | 30 | |
| S2 | B02 | Blue | 433–453 | 10 |
| B03 | Green | 458–523 | 10 | |
| B04 | Red | 543–578 | 10 | |
| B05 | Vegetation Red Edge | 650–680 | 20 | |
| B06 | Vegetation Red Edge | 698–713 | 20 | |
| B07 | Vegetation Red Edge | 733–748 | 20 | |
| B08 | Near Infrared (NIR) | 785–900 | 10 | |
| B8A | Near NIR | 855–875 | 20 | |
| B11 | Shortwave Infrared | 1565–1655 | 20 | |
| B12 | Shortwave Infrared | 2100–2280 | 20 |
| D1 | D2 | D3 | |||
|---|---|---|---|---|---|
| Date | Gap (%) | Date | Gap (%) | Date | Gap (%) |
| 20010126 | 0 | 20010126 | 0 | 20210328 | 0 |
| 20051207 | 10.70 | 20020419 | 34.76 | 20210726 | 3.19 |
| 20051223 | 8.94 (P1) | 20020428 | 100 | 20210728 | 12.47 (P1) |
| 20050630 | 9.96 | 20020505 | 11.79 (P1) | 20210731 | 51.51 |
| 20050716 | 14.23 (P2) | 20020514 | 100 | 20211021 | 81.86 |
| 20050801 | 66.94 | 20020521 | 0.12 | 20211024 | 18.57 (P2) |
| 20020113 | 19.25 | 20211026 | 0.48 | ||
| 20020129 | 15.93 (P2) | 20210221 | 2.71 | ||
| 20020318 | 2.5 | 20210223 | 26.63 (P3) | ||
| 20030201 | 0 | 20210226 | 100 | ||
| 20030217 | 27.26 (P3) | 20210820 | 0.22 | ||
| 20030305 | 0.05 | 20210822 | 31.06 (P4) | ||
| 20020318 | 2.5 | 20210825 | 100 | ||
| 20020419 | 34.76 (P4) | ||||
| 20020428 | 100 | ||||
| Parameter | Cases |
|---|---|
| n1 | 8–14–20–24 |
| n2 | 1–50–100–150–200 |
| t | 0.005–0.007–0.01 |
| f | 1 |
| minNx | 0–2–4–6 |
| (w1; w2) | (0.25; 0.75)–(0.5; 0.5)–(0.75; 0.25) |
| (a) Overall Accuracy (%) When Imposing a Conditional Filling Path | (b) Processing Time (%) When Applying a Targeted Search | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| n2 | minNx | ||||||||
| Gap (%) | Band | 50 | 100 | 150 | 200 | 0 | 2 | 4 | 6 |
| 11.8 | B01 | 62.95 | 77.60 | 82.03 | 87.56 | −17.78 | −1.32 | 10.68 | 5.48 |
| B02 | 78.39 | 86.65 | 90.04 | 91.10 | −10.65 | 22.23 | 34.72 | 27.42 | |
| B03 | 68.99 | 78.59 | 84.44 | 85.66 | −4.95 | 34.6 | 41.09 | 39.19 | |
| B04 | 82.75 | 88.35 | 89.86 | 88.96 | −7.41 | 67.07 | 68.23 | 68.43 | |
| B05 | 82.20 | 84.92 | 85.73 | 85.19 | −5.93 | 50.88 | 59.88 | 55.99 | |
| B07 | 65.16 | 75.38 | 80.11 | 79.78 | −6.87 | 47.46 | 49.13 | 52.73 | |
| 15.94 | B01 | 46.54 | 62.02 | 69.81 | 78.19 | 35.93 | 57.54 | 58.94 | 58.04 |
| B02 | 55.71 | 67.43 | 70.17 | 80.52 | 54.03 | 77.83 | 78.53 | 78.27 | |
| B03 | 40.93 | 53.36 | 61.29 | 70.63 | 59.16 | 79.41 | 80.66 | 81.47 | |
| B04 | 57.41 | 61.88 | 65.12 | 74.69 | 70.01 | 93.71 | 93.95 | 94.35 | |
| B05 | 44.02 | 50.36 | 52.03 | 51.91 | 64.52 | 87.67 | 87.83 | 88.12 | |
| B07 | 34.40 | 41.95 | 42.64 | 41.95 | 59.97 | 80.91 | 81.11 | 81.01 | |
| 27.26 | B01 | 55.74 | 72.02 | 79.33 | 86.25 | −3.16 | 18.85 | 14.44 | 12.84 |
| B02 | 68.32 | 80.58 | 83.24 | 88.76 | 0.43 | 42.54 | 43.4 | 38.23 | |
| B03 | 56.28 | 68.37 | 75.01 | 81.74 | 0.67 | 49.1 | 47.2 | 46.7 | |
| B04 | 75.19 | 80.78 | 86.37 | 83.54 | −6.74 | 61.35 | 64.01 | 64.03 | |
| B05 | 58.96 | 65.11 | 68.52 | 68.81 | −5.3 | 47.39 | 43.87 | 44.55 | |
| B07 | 51.49 | 60.93 | 60.04 | 60.26 | −4.5 | 40.8 | 38.82 | 38.74 | |
| 34.76 | B01 | 75.33 | 89.61 | 92.07 | 93.76 | −27.7 | −12.94 | −12.69 | −10.01 |
| B02 | 75.37 | 84.52 | 88.72 | 92.17 | −30.52 | −18.69 | −19.51 | −17.81 | |
| B03 | 60.97 | 75.14 | 81.89 | 86.43 | −26.67 | −22.84 | −20.79 | −22.3 | |
| B04 | 39.96 | 65.83 | 68.34 | 76.45 | −33.56 | −31.86 | −29.97 | −29.46 | |
| B05 | 16.63 | 25.54 | 39.01 | 44.75 | −28.09 | −26.34 | −25.4 | −26.41 | |
| B07 | 43.41 | 39.08 | 40.41 | 44.12 | −25.52 | −25.99 | −25.42 | −24.62 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhat, L.; Manakos, I.; Sylaios, G.; Kalaitzidis, C. A Modified Version of the Direct Sampling Method for Filling Gaps in Landsat 7 and Sentinel 2 Satellite Imagery in the Coastal Area of Rhone River. Remote Sens. 2023, 15, 5122. https://doi.org/10.3390/rs15215122
Farhat L, Manakos I, Sylaios G, Kalaitzidis C. A Modified Version of the Direct Sampling Method for Filling Gaps in Landsat 7 and Sentinel 2 Satellite Imagery in the Coastal Area of Rhone River. Remote Sensing. 2023; 15(21):5122. https://doi.org/10.3390/rs15215122
Chicago/Turabian StyleFarhat, Lokmen, Ioannis Manakos, Georgios Sylaios, and Chariton Kalaitzidis. 2023. "A Modified Version of the Direct Sampling Method for Filling Gaps in Landsat 7 and Sentinel 2 Satellite Imagery in the Coastal Area of Rhone River" Remote Sensing 15, no. 21: 5122. https://doi.org/10.3390/rs15215122
APA StyleFarhat, L., Manakos, I., Sylaios, G., & Kalaitzidis, C. (2023). A Modified Version of the Direct Sampling Method for Filling Gaps in Landsat 7 and Sentinel 2 Satellite Imagery in the Coastal Area of Rhone River. Remote Sensing, 15(21), 5122. https://doi.org/10.3390/rs15215122