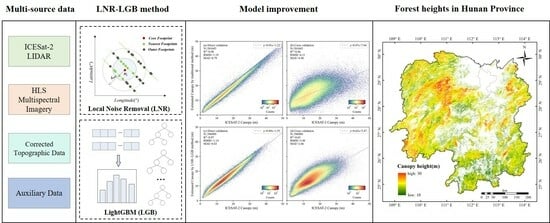
Improved Mapping of Regional Forest Heights by Combining Denoise and LightGBM Method
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. ICESat-2 Data
2.2.2. Landsat-8 Data
2.2.3. Sentinel-2 Data
2.2.4. Ancillary Data
| Data Type | Variables Name | Description |
|---|---|---|
| Topographic Metrics (Corrected SRTM-DEM [68]) | DEM | Mean of topographic elevation |
| Slope | Slope extracted from DEM | |
| Surface Reflectance (Landsat-8 Data [53]) | Blue | 0.45~0.51 µm band reflectivity |
| Green | 0.53~0.59 µm band reflectivity | |
| Red | 0.64~0.67 µm band reflectivity | |
| NIR | 0.85~0.88 µm band reflectivity | |
| SWIR | 2.11~2.29 µm band reflectivity | |
| Vegetation Index (Landsat-8 Data [53]) | RVI | NIR/Red |
| GLI | (2 × Green − Red − Blue)/(2 × Green + Red + Blue) | |
| RGVI | (Red − Green)/(Red + Green) | |
| ARVI | (NIR – 2 × Red + Blue)/(NIR + 2 × Red − Blue) | |
| NDII | (NIR − SWIR)/(NIR + SWIR) | |
| MSAVI | (2 × NIR + 1 − )/2 | |
| Red-edge Vegetation Index (Sentinel-2 Data [53]) | NDVI58a | (NIR2 − RE1)/(NIR2 + RE1) |
| NDVI56 | (RE2– RE1)/(RE2 + RE1) | |
| NDVI47 | (RE3 − Red)/(RE3 + Red) | |
| RECI | RE3/RE1 − 1 | |
| PSRI | (Red − Green)/RE2 | |
| Biophysical Features (MODIS Product [69,70]) | VCF | Percentage of vegetation cover |
| LAI | Leaf area index | |
| Climatic Metrics (WorldClim Data [71]) | AMT | Annual mean temperature |
| TQ | Temperature seasonality | |
| PQ | Precipitation seasonality | |
| PHQ | Precipitation of hottest quarter | |
| PCQ | Precipitation of coldest quarter |
2.2.5. Compared Products
2.3. Forest Canopy Height Estimation
2.3.1. Local Noise Removal (LNR) Method
- Search for k nearest points in the two-dimensional plane within the given maximum range dmax with the current point O as the center, and calculate the average value of the absolute difference between the heights of all nearest points and the center point
- 2.
- When the average value of height difference is greater than the given threshold (here, the neighborhood standard deviation is taken), the point is considered as a noise point and removed, otherwise it is kept as a valid point.
2.3.2. LightGBM
2.3.3. Accuracy Evaluation
3. Results
3.1. Forest Canopy Height Model Accuracy
3.2. Spatial Distribution of Canopy Height
3.3. Comparison with Other Height Products
4. Discussion
4.1. Uncertainty of ATL08 Canopy Height Estimation
4.2. Discussion of Model for Canopy Height Extrapolation
4.3. Limitations and Prospects
5. Conclusions
- Topography, vegetation cover, temperature, and precipitation could be considered important variables for canopy height estimation;
- In contrast to the traditional model, the accuracy of the model was significantly increased by using the LNR-LGB method, in which R2 increased from 0.46 to 0.65 and RMSE decreased from 6.11 m to 3.48 m, reducing the error by about 50%;
- Based on the LNR-LGB model generating 30 m forest canopy height maps of Hunan Province, the forest height ranged from 2.53 to 50.79 m with the mean value of 18.34 m, and its spatial distribution was closely correlated with the topographic conditions;
- Through comparison with two existing forest canopy height products, our model exhibited a lower error, and the accuracy of the output forest height products demonstrated high reliability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Tang, S.; Min, M.; Veroustraete, F.; Cheng, J. Aboveground forest biomass based on OLSR and an ANN model integrating LiDAR and optical data in a mountainous region of China. Int. J. Remote Sens. 2019, 40, 6059–6083. [Google Scholar] [CrossRef]
- Hao, J.; Gao, F.; Fang, X.; Nong, X.; Zhang, Y.; Hong, F. Multi-factor decomposition and multi-scenario prediction decoupling analysis of China’s carbon emission under dual carbon goal. Sci. Total Environ. 2022, 841, 156788. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.; Guo, J.; Li, H.; Jin, S.; Ma, Y.; Gong, W. Estimating hub-height wind speed based on a machine learning algorithm: Implications for wind energy assessment. Atmos. Chem. and Physics. 2023, 23, 3181–3193. [Google Scholar] [CrossRef]
- Peng, S.; Wen, D.; He, N.; Yu, G.; Ma, A.; Wang, Q. Carbon storage in China’s forest ecosystems: Estimation by different integrative methods. Ecol. Evol. 2016, 6, 3129–3145. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yang, J.; Shi, S.; Song, S.; Luo, Y.; Du, L. The rising impact of urbanization-caused CO2 emissions on terrestrial vegetation. Eco. Indicators. 2023, 148, 110079. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef]
- Asner, G.P.; Powell, G.V.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E. High-resolution forest carbon stocks and emissions in the Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 16738–16742. [Google Scholar] [CrossRef]
- Hill, R.A.; Hinsley, S.A. Airborne lidar for woodland habitat quality monitoring: Exploring the significance of lidar data characteristics when modelling organism-habitat relationships. Remote Sens. 2015, 7, 3446–3466. [Google Scholar] [CrossRef]
- Zhang, J.; Nielsen, S.E.; Mao, L.; Chen, S.; Svenning, J.C. Regional and historical factors supplement current climate in shaping global forest canopy height. J. Ecol. 2016, 104, 469–478. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A. Remote sensing of terrestrial plant biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote Sensing of Above-Ground Biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, J.; Zhao, N.; Liu, Y.; Wang, Y.; Wilson, J.P.; Yue, T. Estimation of China’s forest stand biomass carbon sequestration based on the continuous biomass expansion factor model and seven forest inventories from 1977 to 2013. For. Ecol. Manag. 2019, 448, 528–534. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Wheeler, J.; Louis, V.; Tansey, K.; Balzter, H. Quantifying forest biomass carbon stocks from space. Curr. For. Rep. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.W. The importance of consistent global forest aboveground biomass product validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed–A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; He, J.; Jin, Z.; Wang, N. Spatially continuous mapping of hourly ground ozone levels assisted by Himawari-8 short wave radiation products. GISci. Remote Sens. 2023, 60, 2174280. [Google Scholar] [CrossRef]
- Pei, Z.; Han, G.; Mao, H.; Chen, C.; Shi, T.; Yang, K.; Ma, X.; Gong, W. Improving quantification of methane point source emissions from imaging spectroscopy. Remote Sens. Environ. 2023, 295, 113652. [Google Scholar] [CrossRef]
- Pascual, C.; Garcia-Abril, A.; Cohen, W.B.; Martin-Fernandez, S. Relationship between LiDAR-derived forest canopy height and Landsat images. Int. J. Remote Sens. 2010, 31, 1261–1280. [Google Scholar] [CrossRef]
- Ni, W.; Sun, G.; Pang, Y.; Zhang, Z.; Liu, J.; Yang, A.; Wang, Y.; Zhang, D. Mapping three-dimensional structures of forest canopy using UAV stereo imagery: Evaluating impacts of forward overlaps and image resolutions with LiDAR data as reference. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3578–3589. [Google Scholar] [CrossRef]
- Li, C.; Song, J.; Wang, J. New approach to calculating tree height at the regional scale. For. Ecosyst. 2021, 8, 1–19. [Google Scholar] [CrossRef]
- McCombs, J.W.; Roberts, S.D.; Evans, D.L. Influence of fusing lidar and multispectral imagery on remotely sensed estimates of stand density and mean tree height in a managed loblolly pine plantation. For. Sci. 2003, 49, 457–466. [Google Scholar]
- Su, Y.; Ma, Q.; Guo, Q. Fine-resolution forest tree height estimation across the Sierra Nevada through the integration of spaceborne LiDAR, airborne LiDAR, and optical imagery. Int. J. Digit. Earth 2017, 10, 307–323. [Google Scholar] [CrossRef]
- Chopping, M.; Moisen, G.G.; Su, L.; Laliberte, A.; Rango, A.; Martonchik, J.V.; Peters, D.P. Large area mapping of southwestern forest crown cover, canopy height, and biomass using the NASA Multiangle Imaging Spectro-Radiometer. Remote Sens. Environ. 2008, 112, 2051–2063. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Zhang, Z.; Ni, W.; Sun, G.; Huang, W.; Ranson, K.J.; Cook, B.D.; Guo, Z. Biomass retrieval from L-band polarimetric UAVSAR backscatter and PRISM stereo imagery. Remote Sens. Environ. 2017, 194, 331–346. [Google Scholar] [CrossRef]
- Qi, W.; Lee, S.-K.; Hancock, S.; Luthcke, S.; Tang, H.; Armston, J.; Dubayah, R. Improved forest height estimation by fusion of simulated GEDI Lidar data and TanDEM-X InSAR data. Remote Sens. Environ. 2019, 221, 621–634. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W. Estimating forest stock volume in Hunan Province, China, by integrating in situ plot data, Sentinel-2 images, and linear and machine learning regression models. Remote Sens. 2020, 12, 186. [Google Scholar] [CrossRef]
- Huang, W.; Min, W.; Ding, J.; Liu, Y.; Hu, Y.; Ni, W.; Shen, H. Forest height mapping using inventory and multi-source satellite data over Hunan Province in southern China. For. Ecosyst. 2022, 9, 100006. [Google Scholar] [CrossRef]
- Sharifi, A.; Amini, J. Forest biomass estimation using synthetic aperture radar polarimetric features. J. Appl. Remote Sens. 2015, 9, 097695. [Google Scholar] [CrossRef]
- Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S.D. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ. 2002, 79, 305–319. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Almeida, D.d.; Broadbent, E.N.; Zambrano, A.M.A.; Wilkinson, B.E.; Ferreira, M.E.; Chazdon, R.; Meli, P.; Gorgens, E.; Silva, C.A.; Stark, S.C. Monitoring the structure of forest restoration plantations with a drone-lidar system. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 192–198. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Xie, D.; Li, G.; Wang, J.; Guo, J.; Jiaqi, M.; Yang, C. An Overview of the Application Prospect of New Laser Altimetry Satellite ICESat-2 in Geoscience. Geomat. Spat. Inf. Technol. 2020, 43, 38–42+45. [Google Scholar]
- Magruder, L.A.; Brunt, K.M. Performance Analysis of Airborne Photon-Counting Lidar Data in Preparation for the ICESat-2 Mission. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2911–2918. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and terrain height retrievals with ICESat-2: A first look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Narine, L.; Malambo, L.; Popescu, S. Characterizing canopy cover with ICESat-2: A case study of southern forests in Texas and Alabama, USA. Remote Sens. Environ. 2022, 281, 113242. [Google Scholar] [CrossRef]
- Mulverhill, C.; Coops, N.C.; Hermosilla, T.; White, J.C.; Wulder, M.A. Evaluating ICESat-2 for monitoring, modeling, and update of large area forest canopy height products. Remote Sens. Environ. 2022, 271, 112919. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the forest canopy height in Northern China by synergizing ICESat-2 with Sentinel-2 using a stacking algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Zhu, X. Forest Height Retrieval of China with a Resolution of 30 m Using ICESat-2 and GEDI Data. Ph.D. Thesis, Aerospace Information Research Institute, Chinese Academy of Sciences (CAS), Beijing, China, 2021. [Google Scholar]
- Potapov, P.; Hansen, M.C.; Kommareddy, I.; Kommareddy, A.; Turubanova, S.; Pickens, A.; Adusei, B.; Tyukavina, A.; Ying, Q. Landsat analysis ready data for global land cover and land cover change mapping. Remote Sens. 2020, 12, 426. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, C.; Nie, S.; Pan, F.; Xi, X.; Hu, Z. Mapping forest height using photon-counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA. Ecol. Indic. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, F. Mapping Forest Canopy Height at Large Scales using ICESat-2 and Landsat: An Ecological Zoning Random Forest Approach. IEEE Trans. Geosci. Remote Sens. 2022, 61, 1–16. [Google Scholar] [CrossRef]
- Lang, N.; Schindler, K.; Wegner, J.D. Country-wide high-resolution vegetation height mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef]
- Nandy, S.; Srinet, R.; Padalia, H. Mapping forest height and aboveground biomass by integrating ICESat-2, Sentinel-1 and Sentinel-2 data using Random Forest algorithm in northwest Himalayan foothills of India. Geophys. Res. Lett. 2021, 48, e2021GL093799. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, D. Mapping 30m Boreal Forest Heights Using Landsat and Sentinel Data Calibrated by ICESat-2. Authorea Prepr. 2022. [Google Scholar] [CrossRef]
- Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest canopy height mapping by synergizing icesat-2, sentinel-1, sentinel-2 and topographic information based on machine learning methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Shang, R.; Zhu, Z. Harmonizing Landsat 8 and Sentinel-2: A time-series-based reflectance adjustment approach. Remote Sens. Environ. 2019, 235, 111439. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Liu, T.; Abd-Elrahman, A.; Morton, J.; Wilhelm, V.L. Comparing fully convolutional networks, random forest, support vector machine, and patch-based deep convolutional neural networks for object-based wetland mapping using images from small unmanned aircraft system. GIScience Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the agreement of ICESat-2 terrain and canopy height with airborne lidar over US ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Pang, S.; Li, G.; Jiang, X.; Chen, Y.; Lu, Y.; Lu, D. Retrieval of forest canopy height in a mountainous region with ICESat-2 ATLAS. For. Ecosyst. 2022, 9, 100046. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Guenther, E.; White, J.C.; Duncanson, L.; Montesano, P. Validation of ICESat-2 terrain and canopy heights in boreal forests. Remote Sens. Environ. 2020, 251, 112110. [Google Scholar] [CrossRef]
- Moudrý, V.; Gdulová, K.; Gábor, L.; Šárovcová, E.; Barták, V.; Leroy, F.; Špatenková, O.; Rocchini, D.; Prošek, J. Effects of environmental conditions on ICESat-2 terrain and canopy heights retrievals in Central European mountains. Remote Sens. Environ. 2022, 279, 113112. [Google Scholar] [CrossRef]
- Sun, T.; Qi, J.; Huang, H. Discovering forest height changes based on spaceborne lidar data of ICESat-1 in 2005 and ICESat-2 in 2019: A case study in the Beijing-Tianjin-Hebei region of China. For. Ecosyst. 2020, 7, 1–12. [Google Scholar] [CrossRef]
- Dong, J.; Ni, W.; Zhang, Z.; Sun, G. Performance of ICESat-2 ATL08 product on the estimation of forest height by referencing to small footprint LiDAR data. Natl. Remote Sens. Bull 2021, 25, 1294–1307. [Google Scholar] [CrossRef]
- Chen, L.-C.; Guan, X.; Li, H.-M.; Wang, Q.-K.; Zhang, W.-D.; Yang, Q.-P.; Wang, S.-L. Spatiotemporal patterns of carbon storage in forest ecosystems in Hunan Province, China. For. Ecol. Manag. 2019, 432, 656–666. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Magruder, L.; Guenther, E.; Hancock, S.; Purslow, M. Radiometric assessment of ICESat-2 over vegetated surfaces. Remote Sens. 2022, 14, 787. [Google Scholar] [CrossRef]
- Zhao, X.; Su, Y.; Hu, T.; Chen, L.; Gao, S.; Wang, R.; Jin, S.; Guo, Q. A global corrected SRTM DEM product for vegetated areas. Remote Sens. Lett. 2018, 9, 393–402. [Google Scholar] [CrossRef]
- Carroll, M.; Townshend, J.; Hansen, M.; DiMiceli, C.; Sohlberg, R.; Wurster, K. MODIS vegetative cover conversion and vegetation continuous fields. Land Remote Sens. Glob. Environ. Chang. 2011, 11, 725–745. [Google Scholar]
- Yang, W.Z.; Tan, B.; Huang, D.; Rautiainen, M.; Shabanov, N.V.; Wang, Y.; Privette, J.L.; Huemmrich, K.F.; Fensholt, R.; Sandholt, I.; et al. MODIS leaf area index products: From validation to algorithm improvement. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1885–1898. [Google Scholar] [CrossRef]
- Tao, S.; Guo, Q.; Li, C.; Wang, Z.; Fang, J. Global patterns and determinants of forest canopy height. Ecology 2016, 97, 3265–3270. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Chen, X.; Gao, Y.; Xie, S.; Mi, J. GLC_FCS30: Global land-cover product with fine classification system at 30 m using time-series Landsat imagery. Earth Syst. Sci. Data 2021, 13, 2753–2776. [Google Scholar] [CrossRef]
- Zhang, Z.; Jung, C. GBDT-MO: Gradient-boosted decision trees for multiple outputs. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3156–3167. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhu, X.; Nie, S.; Xi, X.; Li, D.; Zheng, W.; Chen, S. Ground elevation accuracy verification of ICESat-2 data: A case study in Alaska, USA. Opt. Express 2019, 27, 38168–38179. [Google Scholar] [CrossRef]
- Huang, X.; Cheng, F.; Wang, J.L.; Duan, P.; Wang, J.S. Forest Canopy Height Extraction Method Based on ICESat-2/ATLAS Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Zhang, L.P.; Zhang, L.F.; Du, B. Deep Learning for Remote Sensing Data A technical tutorial on the state of the art. Ieee Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Sothe, C.; Gonsamo, A.; Lourenço, R.B.; Kurz, W.A.; Snider, J. Spatially Continuous Mapping of Forest Canopy Height in Canada by Combining GEDI and ICESat-2 with PALSAR and Sentinel. Remote Sens. 2022, 14, 5158. [Google Scholar] [CrossRef]











| Attribute | Description |
|---|---|
| Longitude | Center longitude of each 100 m segment |
| Latitude | Center latitude of each 100 m segment |
| h_te_best_fit | Best fit terrain height at the regional center of each 100 m segment |
| h_te_uncertainty | Uncertainty of terrain height estimation |
| h_canopy | 98% relative canopy height of each 100 m segment |
| h_canopy_uncertainty | Uncertainty of relative canopy height estimation |
| segment_landcover | Land cover classification of each 100 m segment |
| night_flag | Data acquisition time (0 for day and 1 for night) |
| cloud_flag_atm | Cloud confidence flag of ATL09 |
| sc_orient | Spacecraft flight direction |
| ID | Variable Combination | Traditional Method | LNR-LGB Method | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (m) | MAE (m) | R2 | RMSE (m) | MAE (m) | ||
| 1 | TM; SR; VI; CM | 0.41 | 6.49 | 4.62 | 0.57 | 3.78 | 3.25 |
| 2 | TM; RVI; CM | 0.43 | 6.34 | 4.57 | 0.56 | 3.85 | 3.37 |
| 3 | TM; SR; VI; BF | 0.38 | 6.84 | 5.04 | 0.61 | 3.68 | 2.94 |
| 4 | TM; RVI; BF | 0.44 | 6.30 | 4.47 | 0.63 | 3.57 | 2.76 |
| 5 | TM; SR; VI; RVI; CM | 0.45 | 6.28 | 4.42 | 0.63 | 3.56 | 2.73 |
| 6 | TM; SR; VI; RVI; BF | 0.39 | 6.34 | 4.67 | 0.65 | 3.52 | 2.72 |
| 7 | TM; SR; VI; RVI; BF; CM | 0.46 | 6.11 | 4.48 | 0.65 | 3.48 | 2.66 |
| Product | Coverage | Data Source | Res | Training Method | Accuracy Verification | Forest Height (m) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Validation | Num | Range | Mean | Std | |||||||
| Potapov et al. [57] | Global | Landsat ARD SRTM DEM * GEDI RH95 | 30 m | Regression tree | Set-aside GEDI | ~3 × 106 | 0.62 | 6.60 m | [3.0, 37.0] | 12.72 | 4.15 |
| ALS data | ~106 | 0.61 | 9.07 m | ||||||||
| Liu et al. [59] | China | Corrected SRTM Sentinel-2 WorldClim 2.1 * GEDI RH100 * ICESat-2 RH98 | 30 m | Neural network guided interpolation | Set-aside GEDI | ~106 | 0.55 | 5.32 m | [0.4, 57.1] | 13.52 | 4.71 |
| ALS data | 65,600 | 0.58 | 4.93 m | ||||||||
| Field data | 59,780 | 0.60 | 4.88 m | ||||||||
| This study | Hunan, China | HLS Corrected SRTM MOD44, MOD15 WorldClim 2.1 * ICESat-2 RH98 | 30 m | Light Gradient Boosting Machine | Training data (10-fold cross validation) | 396,989 | 0.65 | 3.48 m | [2.5, 50.8] | 18.34 | 5.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, M.; Xiao, H.; Jin, Z.; He, J.; Wang, N.; Wang, W. Improved Mapping of Regional Forest Heights by Combining Denoise and LightGBM Method. Remote Sens. 2023, 15, 5436. https://doi.org/10.3390/rs15235436
Sang M, Xiao H, Jin Z, He J, Wang N, Wang W. Improved Mapping of Regional Forest Heights by Combining Denoise and LightGBM Method. Remote Sensing. 2023; 15(23):5436. https://doi.org/10.3390/rs15235436
Chicago/Turabian StyleSang, Mengting, Hai Xiao, Zhili Jin, Junchen He, Nan Wang, and Wei Wang. 2023. "Improved Mapping of Regional Forest Heights by Combining Denoise and LightGBM Method" Remote Sensing 15, no. 23: 5436. https://doi.org/10.3390/rs15235436
APA StyleSang, M., Xiao, H., Jin, Z., He, J., Wang, N., & Wang, W. (2023). Improved Mapping of Regional Forest Heights by Combining Denoise and LightGBM Method. Remote Sensing, 15(23), 5436. https://doi.org/10.3390/rs15235436