Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions
Abstract
:1. Introduction
2. Physical and Spectral Characterization of Snowpack in Microwave Wavelength Region for Snow Depth Inversion and PMW Missions
2.1. Physical Characterization of Snow
2.2. Spectral Characterisation of Snow
2.3. Passive Microwave Remote Sensing Missions
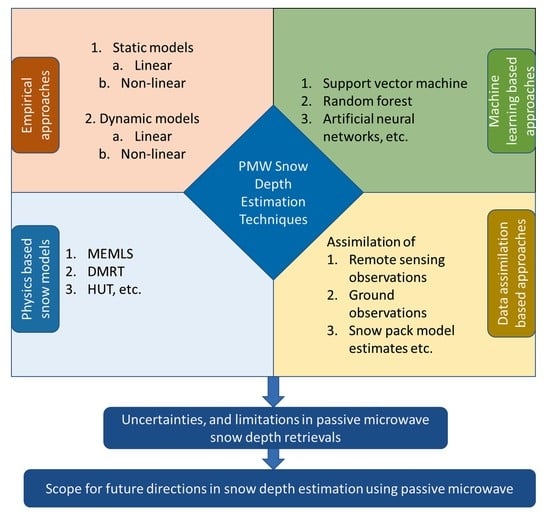
3. Snow Depth Estimation from PMW Observations
3.1. Static Linear and Non-Linear Inversion Algorithms
| S. No. | Type of Model | Modelling Approach | Studies | Observations |
|---|---|---|---|---|
| 1 | Static Empirical models (Linear and Non-linear) | Static models use a fixed relationship between snow depth and model variables. | [22,23,65,72,73,74] | Linear and non-linear models are used for representing the relationship between snow depth and PMW TB, with other factors. Many models used static values of snow density, grainsize while formulating the snow depth model. The performance of models is mainly constrained to study region. |
| 2 | Dynamic models | Dynamic models use a varying relationship between snow depth and model parameters. | [66,75,76,77]; | These models adopted dynamic values of different model parameters such as regression coefficient, snow grain size, snow density, etc., for estimation of snow depth. Look-up tables are developed for dynamic approaches in few studies. |
| 3 | Semi-empirical and physically based models | The physical relation between various snowpack characteristics is taken into account using different snow emission models such as MEMLS, HUT, DMRT. | [64,78,79,80]; | Depending on data availability, requirements, either semi-empirical or fully physical snow emission models are used for forward simulation of TB, and estimating snow depth. |
| 4 | Non-linear models based on machine learning | PMW data and other various observations used for training the models using different machine learning and deep learning frameworks. | [26,27,81,82,83,84,85]; | Due to naive representation of relationship between snowpack characteristics, the transferability and reliability of developed models is always a concern. |
| 5 | Data assimilation models | Assimilation models use or provide a framework for integrating variety of data such as in-situ, remote sensing, model simulations data, etc., from different sources. | [86,87,88,89,90,91,92,93] | Different types of snowpack parameters are assimilated into LSM models such as CLSM, SSiB for snow depth estimations. The estimates rely mainly on the forcing parameters of LSM. The limitation of these approaches is: the observed climatological and weather forcing parameters are often not available in many places and not consistent on varying scales. |
3.2. Dynamic Models
3.2.1. Dynamic Models Built upon the Empirical Methods or Statistical Analysis
3.2.2. Dynamic Models Based on Semi-Empirical, and Physical Models
3.3. Models Based on Data Assimilation
3.4. Non-Linear Models Based on Machine Learning
3.4.1. ANN-Based Snow Depth Estimation
3.4.2. SVM-Based Snow Depth Estimation
3.4.3. Random Forest-Based Snow Depth Estimation
3.5. Downscaling Snow Depth from PMW Observations
4. PMW Global Snow Depth Products
4.1. GlobSnow Product
4.2. AMSR-E Product
4.3. AMSR-2 Product
5. Causes of Uncertainties in Estimated Snow Depths from PMW
5.1. Effect of Vegetation
5.2. Effect of Snow Grain Dimension and Snow Density
5.3. Saturation of PMW Signals
5.4. Effect of Wet Snow
5.5. Effect of Water Bodies
5.6. Effect of the Atmosphere
5.7. Other Factors
6. Summary, Conclusions and Future Directions
Scope for Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMSR-E | Advanced Microwave Scanning Radiometer for Earth observation |
| AMW | Active Microwave |
| ANN | Artificial Neural Network |
| BTD | Brightness Temperature Difference |
| CLSM | Catchment Land Surface Model |
| DEM | Digital Elevation Model |
| DMRT | Dense Media Radiative Transfer |
| DMSP | Defense Meteorological Satellite Program |
| EnKF | Ensemble Kalman Filter |
| ESA | European Space Agency |
| ESMR | Electronically Scanning Microwave Radiometer |
| GCOM-W | Global Change Observation Mission for Water |
| HUT | Helsinki University of Technology |
| LSM | Land Surface Model |
| LWC | Liquid Water Content |
| MEMLS | Microwave Emission Model for Layered Snowpacks |
| MWRI | Microwave Radiation Imager |
| NSIDC | National Snow and Ice Data Center |
| PMW | Passive Microwave |
| RF | Random Forest |
| SAST | Snow Atmosphere Soil Transfer |
| SCP | Snow Cover Probability |
| SMMR | Scanning Multichannel Microwave Radiometer |
| SPD | Spectral Polarization Difference |
| SSiB | Simplified Simple Biosphere |
| SSM/I | Special Sensor Microwave/Imager |
| SSMI/S | Special Sensor Microwave Imager/Sounder |
| SVM | Support Vector Machine |
| SWE | Snow Water Equivalent |
| TB | Brightness temperature |
| TGI | Temperature Gradient Index |
| UAV | Unmanned Aerial Vehicle |
Appendix A
| Platform | Operational Period | Sensor | Frequency (GHz) | Polarization | Foot Print (km × km) | Swath Width (km) | Incidence Angle |
|---|---|---|---|---|---|---|---|
| Nimbus-7 | (1978–1987) | SMMR | 6.6 | H and V | 95 × 148 | 780 | 50.2 |
| 10.69 | 70 × 109 | ||||||
| 18 | 43 × 68 | ||||||
| 21 | 36 × 56 | ||||||
| 37 | 18 × 27 | ||||||
| DMSP F8–F15 | (1987–ongoing) | SSM/I | 19.35 | H and V | 45 × 68 | 1400 | 53.1 |
| 22.235 * | 40 × 60 | ||||||
| 37 | 24 × 36 | ||||||
| 85.5 | 11 × 16 | ||||||
| AQUA | (2002–2011) | AMSR-E | 6.925 | H and V | 43 × 74 | 1450 | 55 |
| 10.65 | 30 × 51 | ||||||
| 18.7 | 16 × 27 | ||||||
| 23.8 | 18 × 31 | ||||||
| 36.5 | 9 × 14 | ||||||
| 89 | 4 × 6 | ||||||
| DMSP F16–F20 | (2003–ongoing) | SSMIS | 21 frequencies including below | H and V | 1700 | 53.1 | |
| 19.35 | 42.4 × 70.1 | ||||||
| 22.235 | 42.4 × 70.1 | ||||||
| 37 | 27.5 × 4 4.2 | ||||||
| 91.655 | 13.1 × 14.4 | ||||||
| FY3-B/C | (2010–ongoing) | MWRI | 10.65 | H and V | 51 × 85 | 1400 | 53.1 |
| 18.7 | 30 × 50 | ||||||
| 23.8 | 27 × 45 | ||||||
| 36.5 | 18 × 30 | ||||||
| 89 | 9 × 15 | ||||||
| GCOM-W1 | (2012–ongoing) | AMSR-2 | 6.925 | H and V | 35 × 62 | 1450 | 55 |
| 7.3 | 34 × 58 | ||||||
| 10.65 | 24 × 42 | ||||||
| 18.7 | 14 × 22 | ||||||
| 23.8 | 15 × 26 | ||||||
| 36.5 | 7 × 12 | ||||||
| 89 | 3 × 5 | ||||||
| GOSAT-GW | Planned (2023) | AMSR-3 | 12 frequencies including below | H and V | 1450 | 55 | |
| 10.65 | 22 × 69 | ||||||
| 18.7 | 12 × 21 | ||||||
| 23.8 | 14 × 24 | ||||||
| 36.5 | 7 × 11 | ||||||
| 89 | 3 × 5 |

References
- Aguirre, F.; Carrasco, J.; Sauter, T.; Schneider, C.; Gaete, K.; Garín, E.; Adaros, R.; Butorovic, N.; Jaña, R.; Casassa, G. Snow Cover Change as a Climate Indicator in Brunswick Peninsula, Patagonia. Front. Earth Sci. 2018, 6, 130. [Google Scholar] [CrossRef]
- Bender, E.; Lehning, M.; Fiddes, J. Changes in Climatology, Snow Cover, and Ground Temperatures at High Alpine Locations. Front. Earth Sci. 2020, 8, 100. [Google Scholar] [CrossRef]
- ul Shafiq, M.; Ahmed, P.; ul Islam, Z.; Joshi, P.K.; Bhat, W.A. Snow Cover Area Change and Its Relations with Climatic Variability in Kashmir Himalayas, India. Geocarto Int. 2019, 34, 688–702. [Google Scholar] [CrossRef]
- Estilow, T.W.; Young, A.H.; Robinson, D.A. A Long-Term Northern Hemisphere Snow Cover Extent Data Record for Climate Studies and Monitoring. Earth Syst. Sci. Data 2015, 7, 137–142. [Google Scholar] [CrossRef] [Green Version]
- Lemke, P.; Ren, J.; Alley, R.B.; Allison, I.; Carrasco, J.; Flato, G.; Fujii, Y.; Kaser, G.; Mote, P.; Thomas, R.H.; et al. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; ISBN 978-0521705967. [Google Scholar]
- Yang, F.; Kumar, A.; Wang, W.; Juang, H.M.H.; Kanamitsu, M. Snow-Albedo Feedback and Seasonal Climate Variability over North America. J. Clim. 2001, 14, 4245–4248. [Google Scholar] [CrossRef]
- Liu, X.; Chen, R.; Liu, J.; Wang, X.; Zhang, B.; Han, C.; Liu, G.; Guo, S.; Liu, Z.; Song, Y.; et al. Effects of Snow-Depth Change on Spring Runoff in Cryosphere Areas of China. Hydrol. Sci. J. 2019, 64, 789–797. [Google Scholar] [CrossRef]
- Stigter, E.M.; Wanders, N.; Saloranta, T.M.; Shea, J.M.; Bierkens, M.F.P.; Immerzeel, W.W. Assimilation of Snow Cover and Snow Depth into a Snow Model to Estimate Snow Water Equivalent and Snowmelt Runoff in a Himalayan Catchment. Cryosphere 2017, 11, 1647–1664. [Google Scholar] [CrossRef] [Green Version]
- Schweizer, J.; Jamieson, J.B.; Schneebeli, M. Snow Avalanche Formation. Rev. Geophys. 2003, 41, 1016. [Google Scholar] [CrossRef] [Green Version]
- Beniston, M. Variations of Snow Depth and Duration in the Swiss Alps Over the Last 50 Years: Links to Changes in Large-Scale Climatic Forcings. In Climatic Change at High Elevation Sites; Springer: Dordrecht, The Netherlands, 1997; pp. 49–68. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent Increase in High Asia’s Runoff Due to Increasing Glacier Melt and Precipitation. Nat. Clim. Change 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Kirkham, J.D.; Koch, I.; Saloranta, T.M.; Litt, M.; Stigter, E.E.; Møen, K.; Thapa, A.; Melvold, K.; Immerzeel, W.W. Near Real-Time Measurement of Snow Water Equivalent in the Nepal Himalayas. Front. Earth Sci. 2019, 7, 177. [Google Scholar] [CrossRef] [Green Version]
- Kinar, N.J.; Pomeroy, J.W. Measurement of the Physical Properties of the Snowpack. Rev. Geophys. 2015, 53, 481–544. [Google Scholar] [CrossRef]
- Singh, K.K.; Kumar, A.; Kulkarni, A.V.; Datt, P.; Dewali, S.K.; Kumar, V.; Chauhan, R. Snow Depth Estimation in the Indian Himalaya Using Multi-Channel Passive Microwave Radiometer. Curr. Sci. 2015, 108, 942–953. [Google Scholar] [CrossRef]
- Dong, C. Remote Sensing, Hydrological Modeling and in Situ Observations in Snow Cover Research: A Review. J. Hydrol. 2018, 561, 573–583. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fassnacht, S.R.; Beguería, S.; Latron, J.B.P. Variability of Snow Depth at the Plot Scale: Implications for Mean Depth Estimation and Sampling Strategies. Cryosphere 2011, 5, 617–629. [Google Scholar] [CrossRef] [Green Version]
- Meromy, L.; Molotch, N.P.; Link, T.E.; Fassnacht, S.R.; Rice, R. Subgrid Variability of Snow Water Equivalent at Operational Snow Stations in the Western USA. Hydrol. Process. 2013, 27, 2383–2400. [Google Scholar] [CrossRef]
- Kongoli, C.; Key, J.; Smith, T.M. Mapping of Snow Depth by Blending Satellite and In-Situ Data Using Two-Dimensional Optimal Interpolation-Application to AMSR2. Remote Sens. 2019, 11, 3049. [Google Scholar] [CrossRef] [Green Version]
- Woody, J.; Lu, Q.Q.; Livsey, J. Statistical Methods for Forecasting Daily Snow Depths and Assessing Trends in Inter-Annual Snow Depth Dynamics. Environ. Ecol. Stat. 2020, 27, 609–628. [Google Scholar] [CrossRef]
- Buhler, Y.; Adams, M.S.; Bosch, R.; Stoffel, A. Mapping Snow Depth in Alpine Terrain with Unmanned Aerial Systems (UASs): Potential and Limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef] [Green Version]
- Maier, K.; Nascetti, A.; van Pelt, W.; Rosqvist, G. Direct Photogrammetry with Multispectral Imagery for UAV-Based Snow Depth Estimation. ISPRS J. Photogramm. Remote Sens. 2022, 186, 1–18. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K. Nimbus-7 SMMR Derived Global Snow Cover Parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Foster, J.L.; Chang, A.T.C.; Hall, D.K. Comparison of Snow Mass Estimates from a Prototype Passive Microwave Snow Algorithm, a Revised Algorithm and a Snow Depth Climatology. Remote Sens. Environ. 1997, 62, 132–142. [Google Scholar] [CrossRef]
- Kelly, R. The AMSR-E Snow Depth Algorithm: Description and Initial Results. J. Remote Sens. Soc. Jpn. 2009, 29, 307–317. [Google Scholar] [CrossRef]
- Lee, J.-E.; Lee, G.W.; Earle, M.; Nitu, R. Uncertainty Analysis for Evaluating the Accuracy of Snow Depth Measurements. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 4157–4190. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Shao, W.; Li, X. Support Vector Regression Snow-Depth Retrieval Algorithm Using Passive Microwave Remote Sensing Data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Yang, J.W.; Jiang, L.M.; Lemmetyinen, J.; Pan, J.M.; Luojus, K.; Takala, M. Improving Snow Depth Estimation by Coupling HUT-Optimized Effective Snow Grain Size Parameters with the Random Forest Approach. Remote Sens. Environ. 2021, 264, 112630. [Google Scholar] [CrossRef]
- Shi, L.; Qiu, Y.; Lemmetyinen, J.; Shi, J. Atmospheric Correction of Passive Microwave Brightness Temperature on the Estimation of Snow Depth. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 3982–3985. [Google Scholar] [CrossRef]
- Bühler, Y.; Marty, M.; Egli, L.; Veitinger, J.; Jonas, T.; Thee, P.; Ginzler, C. Snow Depth Mapping in High-Alpine Catchments Using Digital Photogrammetry. Cryosphere 2015, 9, 229–243. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Kelly, R.E.; Foster, J.L.; Chang, A.T. Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; Chapter 55; pp. 812–830. ISBN 9780471491033. [Google Scholar]
- Nolin, A.W. Recent Advances in Remote Sensing of Seasonal Snow. J. Glaciol. 2010, 56, 1141–1150. [Google Scholar] [CrossRef] [Green Version]
- Prokop, A. Assessing the Applicability of Terrestrial Laser Scanning for Spatial Snow Depth Measurements. Cold Reg. Sci. Technol. 2008, 54, 155–163. [Google Scholar] [CrossRef]
- Bernier, P.Y. Microwave Remote Sensing of Snowpack Properties: Potential and Limitations. Hydrol. Res. 1987, 18, 1–20. [Google Scholar] [CrossRef]
- Hallikainen, M.; Lemmetyinen, J.; Jiang, L. Snow Properties from Passive Microwave. Compr. Remote Sens. 2018, 4, 224–236. [Google Scholar] [CrossRef]
- Leinss, S.; Parrella, G.; Hajnsek, I. Snow Height Determination by Polarimetric Phase Differences in X-Band SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3794–3810. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; He, G.; Man, W. Estimating Snow Depth and Snow Water Equivalence Using Repeat-Pass Interferometric SAR in the Northern Piedmont Region of the Tianshan Mountains. J. Sens. 2017, 2017, 8739598. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Demuzere, M.; Marshall, H.P.; Reichle, R.H.; Brucker, L.; Brangers, I.; de Rosnay, P.; Dumont, M.; Girotto, M.; Immerzeel, W.W.; et al. Snow Depth Variability in the Northern Hemisphere Mountains Observed from Space. Nat. Commun. 2019, 10, 4629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahmoodzada, A.B.; Varade, D.; Shimada, S. Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peakwinter and Early Melt Season. Remote Sens. 2020, 12, 2788. [Google Scholar] [CrossRef]
- Patil, A.; Singh, G.; Rüdiger, C. Retrieval of Snow Depth and Snow Water Equivalent Using Dual Polarization SAR Data. Remote Sens. 2020, 12, 1183. [Google Scholar] [CrossRef] [Green Version]
- Patil, A.; Mohanty, S.; Singh, G. Snow Depth and Snow Water Equivalent Retrieval Using X-Band PolInSAR Data. Remote Sens. Lett. 2020, 11, 817–826. [Google Scholar] [CrossRef]
- Maass, N.; Kaleschke, L.; Tian-Kunze, X.; Tonboe, R.T. Snow Thickness Retrieval from L-Band Brightness Temperatures: A Model Comparison. Ann. Glaciol. 2015, 56, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Rignot, E.; Echelmeyer, K.; Krabill, W. Penetration Depth of Interferometric Synthetic-Aperture Radar Signals in Snow and Ice. Geophys. Res. Lett. 2001, 28, 3501–3504. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Stiles, W.H. Microwave response of snow. Adv. Space Res 1981, 1, 131–149. [Google Scholar] [CrossRef]
- Tsai, Y.L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Remote Sensing of Snow Cover Using Spaceborne SAR: A Review. Remote Sens. 2019, 11, 1456. [Google Scholar] [CrossRef] [Green Version]
- Amlien, J. Remote Sensing of Snow with Passive Microwave Radiometers. A Review of Current Algorithms; Report no 1019, Norsk Regnesentral, 2008. ISBN 978-82-539-0529-7. Available online: https://vdocuments.mx/remote-sensing-of-snow-with-passive-microwave-radiometers-6-remote-sensing-of-snow.html?page=1 (accessed on 1 November 2022).
- Awasthi, S.; Varade, D. Recent Advances in the Remote Sensing of Alpine Snow: A Review. GIScience Remote Sens. 2021, 58, 852–888. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote Sensing of Snow—A Review of Available Methods. Int. J. Remote Sens. 2011, 33, 4094–4134. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R.; Flemming, M.; Li, Q. Review of Snow Water Equivalent Retrieval Methods Using Spaceborne Passive Microwave Radiometry. Int. J. Remote Sens. 2019, 41, 996–1018. [Google Scholar] [CrossRef]
- Cho, E.; Tuttle, S.; Jacobs, J. Evaluating Consistency of Snow Water Equivalent Retrievals from Passive Microwave Sensors over the North Central U.S.: SSM/I vs. SSMIS and AMSR-E vs. AMSR2. Remote Sens. 2017, 9, 465. [Google Scholar] [CrossRef] [Green Version]
- Lemmetyinen, J.; Derksen, C.; Rott, H.; Macelloni, G.; King, J.; Schneebeli, M.; Wiesmann, A.; Leppänen, L.; Kontu, A.; Pulliainen, J. Retrieval of Effective Correlation Length and Snow Water Equivalent from Radar and Passive Microwave Measurements. Remote Sens. 2018, 10, 170. [Google Scholar] [CrossRef] [Green Version]
- Clifford, D. Global Estimates of Snow Water Equivalent from Passive Microwave Instruments: History, Challenges and Future Developments. Int. J. Remote Sens. 2010, 31, 3707–3726. [Google Scholar] [CrossRef]
- Vuyovich, C.; Jacobs, J.M. Snowpack and Runoff Generation Using AMSR-E Passive Microwave Observations in the Upper Helmand Watershed, Afghanistan. Remote Sens. Environ. 2011, 115, 3313–3321. [Google Scholar] [CrossRef]
- Merkouriadi, I.; Lemmetyinen, J.; Liston, G.E.; Pulliainen, J. Solving Challenges of Assimilating Microwave Remote Sensing Signatures with a Physical Model to Estimate Snow Water Equivalent. Water Resour. Res. 2021, 57, e2021WR030119. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, J.; Zhang, C.; Wu, S.; Li, Z.; Dai, L.; Li, X.; Qiu, Y. Daily Snow Water Equivalent Product with SMMR, SSM/I and SSMIS from 1980 to 2020 over China. Big Earth Data 2022, 6, 420–434. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Koskinen, J.; Bojkov, B. Estimating Northern Hemisphere Snow Water Equivalent for Climate Research through Assimilation of Space-Borne Radiometer Data and Ground-Based Measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating Snow Water Equivalent Using Snow Depth Data and Climate Classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Denoth, A. Snow Dielectric Measurements. Adv. Space Res. 1989, 9, 233–243. [Google Scholar] [CrossRef]
- Mätzler, C.; Wegmüller, U. Dielectric Properties of Fresh-Water Ice at Microwave Frequencies. J. Phys. D Appl. Phys. 1988, 21, 1660. [Google Scholar] [CrossRef]
- Chang, T.C.; Gloersen, P.; Schmugge, T.; Wilheit, T.T.; Zwally, H.J. Microwave Emission from Snow and Glacier Ice. J. Glaciol. 1976, 16, 23–39. [Google Scholar] [CrossRef] [Green Version]
- Lakhankar, T.; Azar, A.E.; Shahroudi, N.; Powell, A.; Khanbilvardi, R. Analysis of the Effects of Snowpack Properties on Satellite Microwave Brightness Temperature and Emissivity Data. J. Remote Sens. GIS 2012, 1, 1–6. [Google Scholar] [CrossRef]
- Saraf, A.K.; Tarafdar, S.; Foster, J.L.; Singh, P. Passive Microwave Data for Snow-Depth and Snow-Extent Estimations in the Himalayan Mountains. Int. J. Remote Sens. 1999, 20, 83–95. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Hall, D.K.; Foster, J.L.; Rango, A.; Schmugge, T.J. Studies of Snowpack Properties by Passive Microwave Radiometry. 1979. Available online: https://ntrs.nasa.gov/citations/19790008308 (accessed on 15 November 2022).
- Matzler, C. Microwave Properties of Ice and Snow. In Solar System Ices. Astrophysics and Space Science Library; Schmitt, B., De Bergh, C., Festou, M., Eds.; Springer: Dordrecht, The Netherlands, 1998; Volume 227, pp. 241–257. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Microwave Emission Model of Layered Snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Foster, J.L.; Sun, C.; Walker, J.P.; Kelly, R.; Chang, A.; Dong, J.; Powell, H. Quantifying the Uncertainty in Passive Microwave Snow Water Equivalent Observations. Remote Sens. Environ. 2005, 94, 187–203. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow Depth Derived from Passive Microwave Remote-Sensing Data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Kutuza, B.G. Cosmos-243 as the Starting Point for the Development of Microwave Radiometry Methods of the Earth’s Atmosphere and Surface. Izv. Atmos. Ocean. Phys. 2018, 54, 275–281. [Google Scholar] [CrossRef]
- Kunzi, K.F.; Rott, H.; Patil, S. Snow-Cover Parameters Retrieved from Nimbus-7 Scanning Multichannel Microwave Radiometer (SMMR) Data. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 452–467. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K.; Rango, A.; Hartline, B.K. Snow Water Equivalent Estimation by Microwave Radiometry. Cold Reg. Sci. Technol. 1982, 5, 259–267. [Google Scholar] [CrossRef]
- Jiang, L.M.; Wang, P.; Zhang, L.X.; Yang, H.; Yang, J.T. Improvement of Snow Depth Retrieval for FY3B-MWRI in China. Sci. China Earth Sci. 2014, 57, 1278–1292. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Yu, H. Snow Depth Estimation Using a Lookup Table Method Based on MEMLS. Gaojishu Tongxin/Chin. High Technol. Lett. 2014, 24, 915–921. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K.; Goodison, B.E.; Walker, A.E.; Metcalfe, J.R.; Harby, A. Snow Parameters Derived from Microwave Measurements during the BOREAS Winter Field Campaign. J. Geophys. Res. Atmos. 1997, 102, 29663–29671. [Google Scholar] [CrossRef]
- Wang, J.; Huang, X.; Wang, Y.; Liang, T. Retrieving Snow Depth Information from AMSR2 Data for Qinghai-Tibet Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 752–768. [Google Scholar] [CrossRef]
- Wei, P.; Zhang, T.; Zhou, X.; Yi, G.; Li, J.; Wang, N.; Wen, B. Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau. Remote Sens. 2021, 13, 657. [Google Scholar] [CrossRef]
- Josberger, E.G.; Mognard, N.M. A Passive Microwave Snow Depth Algorithm with a Proxy for Snow Metamorphism. Hydrol. Process. 2002, 16, 1557–1568. [Google Scholar] [CrossRef]
- Kelly, R.E.J.; Chang, A.T.C. Development of a Passive Microwave Global Snow Depth Retrieval Algorithm for Special Sensor Microwave Imager (SSM/I) and Advanced Microwave Scanning Radiometer-EOS (AMSR-E) Data. Radio Sci. 2003, 38, 8076. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Xie, H.; Wu, X. Estimation of Snow Depth over the Qinghai-Tibetan Plateau Based on AMSR-E and MODIS Data. Remote Sens. 2018, 10, 1989. [Google Scholar] [CrossRef] [Green Version]
- Pulliainen, J.T.; Grandeil, J. HUT Snow Emission Model and Its Applicability to Snow Water Equivalent Retrieval. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1378–1390. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, C.-T.; Chang, A.T.C.; Guo, J.; Ding, K.H. Dense Media Radiative Transfer Theory Based on Quasicrystalline Approximation with Applications to Passive Microwave Remote Sensing of Snow. Radio Sci. 2000, 35, 731–749. [Google Scholar] [CrossRef]
- Picard, G.; Brucker, L.; Roy, A.; Dupont, F.; Fily, M.; Royer, A.; Harlow, C. Simulation of the Microwave Emission of Multi-Layered Snowpacks Using the Dense Media Radiative Transfer Theory: The DMRT-ML Model. Geosci. Model Dev. 2013, 6, 1061–1078. [Google Scholar] [CrossRef] [Green Version]
- Tedesco, M.; Jeyaratnam, J. A New Operational Snow Retrieval Algorithm Applied to Historical AMSR-E Brightness Temperatures. Remote Sens. 2016, 8, 1037. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Forman, B.A. Comparison of Passive Microwave Brightness Temperature Prediction Sensitivities over Snow-Covered Land in North America Using Machine Learning Algorithms and the Advanced Microwave Scanning Radiometer. Remote Sens. Environ. 2015, 170, 153–165. [Google Scholar] [CrossRef]
- Liang, J.; Liu, X.; Huang, K.; Li, X.; Shi, X.; Chen, Y.; Li, J. Improved Snow Depth Retrieval by Integrating Microwave Brightness Temperature and Visible/Infrared Reflectance. Remote Sens. Environ. 2015, 156, 500–509. [Google Scholar] [CrossRef]
- Nikraftar, Z.; Hasanlou, M.; Esmaeilzadeh, M. Novel Snow Depth Retrieval Method Using Time Series SSMI Passive Microwave Imagery. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives, Prague, Czech Republic, 12–19 July 2016; Volume 41. [Google Scholar]
- Hu, Y.; Che, T.; Dai, L.; Xiao, L. Snow Depth Fusion Based on Machine Learning Methods for the Northern Hemisphere. Remote Sens. 2021, 13, 1250. [Google Scholar] [CrossRef]
- Durand, M.; Margulis, S.A. Feasibility Test of Multifrequency Radiometric Data Assimilation to Estimate Snow Water Equivalent. J. Hydrometeorol. 2006, 7, 443–457. [Google Scholar] [CrossRef]
- Tedesco, M.; Reichle, R.; Löw, A.; Markus, T.; Foster, J.L. Dynamic Approaches for Snow Depth Retrieval from Spaceborne Microwave Brightness Temperature. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1955–1967. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Kontu, A.; Kärnä, J.P.; Vehviläinen, J.; Takala, M.; Pulliainen, J. Correcting for the Influence of Frozen Lakes in Satellite Microwave Radiometer Observations through Application of a Microwave Emission Model. Remote Sens. Environ. 2011, 115, 3695–3706. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Huang, C. Assimilating Passive Microwave Remote Sensing Data into a Land Surface Model to Improve the Estimation of Snow Depth. Remote Sens. Environ. 2014, 143, 54–63. [Google Scholar] [CrossRef]
- Kwon, Y.; Yang, Z.L.; Hoar, T.J.; Toure, A.M. Improving the Radiance Assimilation Performance in Estimating Snow Water Storage across Snow and Land-Cover Types in North America. J. Hydrometeorol. 2017, 18, 651–668. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Liljedahl, A.K.; Dafflon, B.; Ulrich, C.; Peterson, J.E.; Gusmeroli, A.; Hubbard, S.S. Mapping Snow Depth within a Tundra Ecosystem Using Multiscale Observations and Bayesian Methods. Cryosphere 2017, 11, 857–875. [Google Scholar] [CrossRef] [Green Version]
- Kwon, Y.; Forman, B.A.; Ahmad, J.A.; Kumar, S.V.; Yoon, Y. Exploring the Utility of Machine Learning-Based Passive Microwave Brightness Temperature Data Assimilation over Terrestrial Snow in High Mountain Asia. Remote Sens. 2019, 11, 2265. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Huang, C.; Chen, W.; Zhang, Y. Improving Snow Estimates Through Assimilation of MODIS Fractional Snow Cover Data Using Machine Learning Algorithms and the Common Land Model. Water Resour. Res. 2021, 57, e2020WR029010. [Google Scholar] [CrossRef]
- Das, I.; Sarwade, R.N. Snow Depth Estimation over North-Western Indian Himalaya Using AMSR-E. Int. J. Remote Sens. 2008, 29, 4237–4248. [Google Scholar] [CrossRef]
- de Sève, D.; Bernier, M.; Fortin, J.P.; Walker, A. Preliminary Analysis of Snow Microwave Radiometry Using the SSM/I Passive-Microwave Data: The Case of La Grande River Watershed (Quebec). Ann. Glaciol. 1997, 25, 353–361. [Google Scholar] [CrossRef]
- Derksen, C. The Contribution of AMSR-E 18.7 and 10.7 GHz Measurements to Improved Boreal Forest Snow Water Equivalent Retrievals. Remote Sens. Environ. 2008, 112, 2701–2710. [Google Scholar] [CrossRef]
- Schanda, E.; Kunzi, C.M. & K. Microwave Remote Sensing of Snow Cover. Int. J. Remote Sens. 1983, 4, 149–158. [Google Scholar] [CrossRef]
- Aschbacher, J.; Rott, H. Microwave Emission of Snow-Covered and Snow-Free Terrain from Satellite Measurements. Adv. Space Res. 1989, 9, 289–295. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Wang, J.; Zhou, M.; Liang, T. AMSR2 Snow Depth Downscaling Algorithm Based on a Multifactor Approach over the Tibetan Plateau, China. Remote Sens. Environ. 2019, 231, 111268. [Google Scholar] [CrossRef]
- Grippa, M.; Mognard, N.; le Toan, T.; Josberger, E.G. Siberia Snow Depth Climatology Derived from SSM/I Data Using a Combined Dynamic and Static Algorithm. Remote Sens. Environ. 2004, 93, 30–41. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Pulliainen, J.; Rees, A.; Kontu, A.; Qiu, Y.; Derksen, C. Multiple-Layer Adaptation of HUT Snow Emission Model: Comparison with Experimental Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2781–2794. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Wang, J.; Zhang, P. Snow Depth and Snow Water Equivalent Estimation from AMSR-E Data Based on a Priori Snow Characteristics in Xinjiang, China. Remote Sens. Environ. 2012, 127, 14–29. [Google Scholar] [CrossRef]
- Wu, L.; Li, X.; Zhao, K.; Zheng, X. Snow Depth Inversion Using the Localized HUT Model Based on FY-3B MWRI Data in the Farmland of Heilongjiang Province, China. J. Indian Soc. Remote Sens. 2017, 45, 89–100. [Google Scholar] [CrossRef]
- Gu, L.; Fan, X.; Li, X.; Wei, Y. Snow Depth Retrieval in Farmland Based on a Statistical Lookup Table from Passive Microwave Data in Northeast China. Remote Sens. 2019, 11, 3037. [Google Scholar] [CrossRef] [Green Version]
- Kelly, R.; Li, Q.; Saberi, N. ’The AMSR2 Satellite-Based Microwave Snow Algorithm (SMSA): A New Algorithm for Estimating Global Snow Accumulation. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 5606–5609. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R.; Pan, J.; Durand, M.; Goh, J.; Scott, K.A. The Use of a Monte Carlo Markov Chain Method for Snow-Depth Retrievals: A Case Study Based on Airborne Microwave Observations and Emission Modeling Experiments of Tundra Snow. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1876–1889. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R. An Evaluation of DMRT-ML for AMSR2 Estimates of Snow Depth. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1943–1946. [Google Scholar] [CrossRef]
- Tedesco, M.; Kim, E.J. Retrieval of Dry-Snow Parameters from Microwave Radiometric Data Using a Dense-Medium Model and Genetic Algorithms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2143–2151. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.J.; Margulis, S.A. Radiance Assimilation Shows Promise for Snowpack Characterization. Geophys. Res. Lett. 2009, 36, 2503. [Google Scholar] [CrossRef]
- Piazzi, G.; Thirel, G.; Campo, L.; Gabellani, S. A Particle Filter Scheme for Multivariate Data Assimilation into a Point-Scale Snowpack Model in an Alpine Environment. Cryosphere 2018, 12, 2287–2306. [Google Scholar] [CrossRef] [Green Version]
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating Remotely Sensed Snow Observations into a Macroscale Hydrology Model. Adv. Water Resour. 2006, 29, 872–886. [Google Scholar] [CrossRef]
- Graf, T.; Koike, T.; Li, X.; Hirai, M.; Tsutsui, H. Assimilating Passive Microwave Brightness Temperature Data into a Land Surface Model to Improve the Snow Depth Predictability. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006; pp. 710–713. [Google Scholar] [CrossRef]
- Liu, Y.; Peters-Lidard, C.D.; Kumar, S.; Foster, J.L.; Shaw, M.; Tian, Y.; Fall, G.M. Assimilating Satellite-Based Snow Depth and Snow Cover Products for Improving Snow Predictions in Alaska. Adv. Water Resour. 2013, 54, 208–227. [Google Scholar] [CrossRef]
- Helmert, J.; Şorman, A.Ş.; Montero, R.A.; de Michele, C.; de Rosnay, P.; Dumont, M.; Finger, D.C.; Lange, M.; Picard, G.; Potopová, V.; et al. Review of Snow Data Assimilation Methods for Hydrological, Land Surface, Meteorological and Climate Models: Results from a COST Harmosnow Survey. Geosciences 2018, 8, 489. [Google Scholar] [CrossRef] [Green Version]
- Hedrick, A.R.; Marks, D.; Havens, S.; Robertson, M.; Johnson, M.; Sandusky, M.; Marshall, H.; Kormos, P.R.; Bormann, K.J.; Painter, T.H. Direct Insertion of NASA Airborne Snow Observatory-Derived Snow Depth Time Series Into the ISnobal Energy Balance Snow Model. Water Resour. Res. 2018, 54, 8045–8063. [Google Scholar] [CrossRef]
- Xu, J.; Shu, H. Assimilating MODIS-Based Albedo and Snow Cover Fraction into the Common Land Model to Improve Snow Depth Simulation with Direct Insertion and Deterministic Ensemble Kalman Filter Methods. J. Geophys. Res. Atmos. 2014, 119, 10684–10701. [Google Scholar] [CrossRef]
- Revuelto, J.; Vionnet, V.; López-Moreno, J.I.; Lafaysse, M.; Morin, S. Combining Snowpack Modeling and Terrestrial Laser Scanner Observations Improves the Simulation of Small Scale Snow Dynamics. J. Hydrol. 2016, 533, 291–307. [Google Scholar] [CrossRef]
- Liston, G.E.; Hiemstra, C.A. A Simple Data Assimilation System for Complex Snow Distributions (SnowAssim). J. Hydrometeorol. 2008, 9, 989–1004. [Google Scholar] [CrossRef]
- Avanzi, F.; Zheng, Z.; Coogan, A.; Rice, R.; Akella, R.; Conklin, M.H. Gap-Filling Snow-Depth Time-Series with Kalman Filtering-Smoothing and Expectation Maximization: Proof of Concept Using Spatially Dense Wireless-Sensor-Network Data. Cold Reg. Sci. Technol. 2020, 175, 103066. [Google Scholar] [CrossRef]
- Yang, J.; Li, C. Assimilation of D-InSAR Snow Depth Data by an Ensemble Kalman Filter. Arab. J. Geosci. 2021, 14, 505. [Google Scholar] [CrossRef]
- Magnusson, J.; Winstral, A.; Stordal, A.S.; Essery, R.; Jonas, T. Improving Physically Based Snow Simulations by Assimilating Snow Depths Using the Particle Filter. Water Resour. Res. 2017, 53, 1125–1143. [Google Scholar] [CrossRef] [Green Version]
- Smyth, E.J.; Raleigh, M.S.; Small, E.E. Particle Filter Data Assimilation of Monthly Snow Depth Observations Improves Estimation of Snow Density and SWE. Water Resour. Res. 2019, 55, 1296–1311. [Google Scholar] [CrossRef]
- Kim, R.S.; Durand, M.; Li, D.; Baldo, E.; Margulis, S.A.; Dumont, M.; Morin, S. Estimating Alpine Snow Depth by Combining Multifrequency Passive Radiance Observations with Ensemble Snowpack Modeling. Remote Sens. Environ. 2019, 226, 1–15. [Google Scholar] [CrossRef]
- Tedesco, M.; Narvekar, P.S. Assessment of the NASA AMSR-E SWE Product. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 141–159. [Google Scholar] [CrossRef]
- Pulliainen, J. Mapping of Snow Water Equivalent and Snow Depth in Boreal and Sub-Arctic Zones by Assimilating Space-Borne Microwave Radiometer Data and Ground-Based Observations. Remote Sens. Environ. 2006, 101, 257–269. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Arsenault, K.R.; Getirana, A.; Mocko, D.; Liu, Y. Quantifying the Added Value of Snow Cover Area Observations in Passive Microwave Snow Depth Data Assimilation. J. Hydrometeorol. 2015, 16, 1736–1741. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Hoar, T.J.; Yang, Z.L.; Anderson, J.L.; Toure, A.M.; Rodell, M. Assimilation of MODIS Snow Cover through the Data Assimilation Research Testbed and the Community Land Model Version 4. J. Geophys. Res. Atmos. 2014, 119, 7091–7103. [Google Scholar] [CrossRef]
- Kumar, S.V.; Dong, J.; Peters-Lidard, C.D.; Mocko, D.; Gómez, B. Role of Forcing Uncertainty and Background Model Error Characterization in Snow Data Assimilation. Hydrol. Earth Syst. Sci. 2017, 21, 2637–2647. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Zhang, Y.; Wang, J.; Tian, W.; Liu, Q.; Ma, G.; Kan, X.; Chu, Y. Downscaling Snow Depth Mapping by Fusion of Microwave and Optical Remote-Sensing Data Based on Deep Learning. Remote Sens. 2021, 13, 584. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, X.; Zhu, X. Retrieval Snow Depth by Artificial Neural Network Methodology from Integrated AMSR-E and in-Situ Data—A Case Study in Qinghai-Tibet Plateau. Chin. Geogr. Sci. 2008, 18, 356–360. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Abyaneh, H.Z.; Sharifi, M.R. Comparison of Artificial Neural Network and Combined Models in Estimating Spatial Distribution of Snow Depth and Snow Water Equivalent in Samsami Basin of Iran. Neural. Comput. Appl. 2010, 19, 625–635. [Google Scholar] [CrossRef]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial Neural Network-Based Techniques for the Retrieval of SWE and Snow Depth from SSM/I Data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
- Zaerpour, A.; Adib, A.; Motamedi, A. Snow Depth Retrieval from Passive Microwave Imagery Using Different Artificial Neural Networks. Arab. J. Geosci. 2020, 13, 696. [Google Scholar] [CrossRef]
- Davis, D.T.; Chen, Z.; Tsang, L.; Hwang, J.N.; Chang, A.T.C. Retrieval of Snow Parameters by Iterative Inversion of a Neural Network. IEEE Trans. Geosci. Remote Sens. 1993, 31, 842–852. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, Z.; Oh, S.; Marks, R.J.; Chang, A.T.C. Inversion of Snow Parameters from Passive Microwave Remote Sensing Measurements by a Neural Network Trained with a Multiple Scattering Model. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1015–1024. [Google Scholar] [CrossRef]
- Kang, D.H.; Tan, S.; Kim, E.J. Evaluation of Brightness Temperature Sensitivity to Snowpack Physical Properties Using Coupled Snow Physics and Microwave Radiative Transfer Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10241–10251. [Google Scholar] [CrossRef]
- Karystinos, G.N.; Pados, D.A. On Overfitting, Generalization, and Randomly Expanded Training Sets. IEEE Trans Neural Netw 2000, 11, 1050–1057. [Google Scholar] [CrossRef]
- Ahmad, J.A.; Forman, B.A.; Kwon, Y. Analyzing Machine Learning Predictions of Passive Microwave Brightness Temperature Spectral Difference Over Snow-Covered Terrain in High Mountain Asia. Front. Earth Sci. 2019, 7, 212. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Forman, B.A. Integration of Satellite-Based Passive Microwave Brightness Temperature Observations and an Ensemble-Based Land Data Assimilation Framework to Improve Snow Estimation in Forested Regions. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 311–314. [Google Scholar] [CrossRef]
- Revuelto, J.; Billecocq, P.; Tuzet, F.; Cluzet, B.; Lamare, M.; Larue, F.; Dumont, M. Random Forests as a Tool to Understand the Snow Depth Distribution and Its Evolution in Mountain Areas. Hydrol. Process. 2020, 34, 5384–5401. [Google Scholar] [CrossRef]
- Zhang, J.; Pohjola, V.A.; Pettersson, R.; Norell, B.; Marchand, W.-D.; Clemenzi, I.; Gustafsson, D. Improving the Snowpack Monitoring in the Mountainous Areas of Sweden from Space: A Machine Learning Approach. Environ. Res. Lett. 2021, 16, 84007. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Luojus, K.; Pan, J.; Lemmetyinen, J.; Takala, M.; Wu, S. Snow Depth Estimation and Historical Data Reconstruction over China Based on a Random Forest Machine Learning Approach. Cryosphere 2020, 14, 1763–1778. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Pan, J.; Shi, J.; Wu, S.; Wang, J.; Pan, F. Comparison of Machine Learning-Based Snow Depth Estimates and Development of a New Operational Retrieval Algorithm over China. Remote Sens. 2022, 14, 2800. [Google Scholar] [CrossRef]
- Luojus, K.; Pulliainen, J.; Takala, M.; Lemmetyinen, J.; Mortimer, C.; Derksen, C.; Mudryk, L.; Moisander, M.; Hiltunen, M.; Smolander, T.; et al. GlobSnow v3.0 Northern Hemisphere Snow Water Equivalent Dataset. Sci. Data 2021, 8, 163. [Google Scholar] [CrossRef] [PubMed]
- Xiong, C.; Yang, J.; Pan, J.; Lei, Y.; Shi, J. Mountain Snow Depth Retrieval from Optical and Passive Microwave Remote Sensing Using Machine Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2001705. [Google Scholar] [CrossRef]
- Yan, D.; Ma, N.; Zhang, Y. Development of a Fine-Resolution Snow Depth Product Based on the Snow Cover Probability for the Tibetan Plateau: Validation and Spatial–Temporal Analyses. J. Hydrol. 2021, 604, 127027. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; DIng, Y.; Hao, X. Evaluation of Snow Cover and Snow Depth on the Qinghai-Tibetan Plateau Derived from Passive Microwave Remote Sensing. Cryosphere 2017, 11, 1933–1948. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Zhang, X.; Liang, T.; Xie, H.; Wang, X.; Feng, Q.; Chen, Q. A New Approach of Dynamic Monitoring of 5-Day Snow Cover Extent and Snow Depth Based on MODIS and AMSR-E Data from Northern Xinjiang Region. Hydrol. Process. 2012, 26, 3052–3061. [Google Scholar] [CrossRef]
- Wei, Y.; Li, X.; Li, L.; Gu, L.; Zheng, X.; Jiang, T.; Li, X. An Approach to Improve the Spatial Resolution and Accuracy of AMSR2 Passive Microwave Snow Depth Product Using Machine Learning in Northeast China. Remote Sens. 2022, 14, 1480. [Google Scholar] [CrossRef]
- Brown, R.D.; Braaten, R.O. Spatial and Temporal Variability of Canadian Monthly Snow Depths, 1946–1995. Atmos. -Ocean 2010, 36, 37–54. [Google Scholar] [CrossRef]
- Sturm, M.; Holmgren, J.; Liston, G.E. A Seasonal Snow Cover Classification System for Local to Global Applications. J. Clim. 1995, 8, 1261–1283. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Li, X. Spatiotemporal Variation of Snow Depth in the Northern Hemisphere from 1992 to 2016. Remote Sens. 2020, 12, 2728. [Google Scholar] [CrossRef]
- Girotto, M.; Musselman, K.N.; Essery, R.L.H. Data Assimilation Improves Estimates of Climate-Sensitive Seasonal Snow. Curr. Clim. Change Rep. 2020, 6, 81–94. [Google Scholar] [CrossRef]
- Hedstrom, N.R.; Pomeroy, J.W. Measurements and Modelling of Snow Interception in the Boreal Forest. Hydrol. Process. 1998, 12, 1611–1625. [Google Scholar] [CrossRef]
- Kurvonen, L.; Hallikainen, M. Influence of Land-Cover Category on Brightness Temperature of Snow. IEEE Trans. Geosci. Remote Sens. 1997, 35, 367–377. [Google Scholar] [CrossRef]
- Vuyovich, C.M.; Jacobs, J.M.; Daly, S.F. Comparison of Passive Microwave and Modeled Estimates of Total Watershed SWE in the Continental United States. Water Resour. Res. 2014, 50, 9088–9102. [Google Scholar] [CrossRef] [Green Version]
- Che, T.; Dai, L.; Zheng, X.; Li, X.; Zhao, K. Estimation of Snow Depth from Passive Microwave Brightness Temperature Data in Forest Regions of Northeast China. Remote Sens. Environ. 2016, 183, 334–349. [Google Scholar] [CrossRef]
- Markus, T.; Powell, D.C.; Wang, J.R. Sensitivity of Passive Microwave Snow Depth Retrievals to Weather Effects and Snow Evolution. IEEE Trans. Geosci. Remote Sens. 2006, 44, 68–77. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fassnacht, S.R.; Heath, J.T.; Musselman, K.N.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small Scale Spatial Variability of Snow Density and Depth over Complex Alpine Terrain: Implications for Estimating Snow Water Equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Good, W.; Schanda, E. Towards the Definition of Optimum Sensor Specifications for Microwave Remote Sensing of Snow. IEEE Trans. Geosci. Remote Sens. 1982, 20, 57–66. [Google Scholar] [CrossRef]
- Kang, D.H.; Barros, A.P.; Déry, S.J. Evaluating Passive Microwave Radiometry for the Dynamical Transition from Dry to Wet Snowpacks. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3–15. [Google Scholar] [CrossRef]
- Vuyovich, C.M.; Jacobs, J.M.; Hiemstra, C.A.; Deeb, E.J. Effect of Spatial Variability of Wet Snow on Modeled and Observed Microwave Emissions. Remote Sens. Environ. 2017, 198, 310–320. [Google Scholar] [CrossRef]
- Stiles, W.H.; Ulaby, F.T. The Active and Passive Microwave Response to Snow Parameters: 1. Wetness. J. Geophys. Res. Ocean. 1980, 85, 1037–1044. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Abdelrazik, M. Dielectric Properties of Snow In the 3 to 37 GHz Range. IEEE Trans. Antennas Propag. 1986, AP-34, 1329–1340. [Google Scholar] [CrossRef]
- Walker, A.E.; Goodison, B.E. Discrimination of a Wet Snow Cover Using Passive Microwave Satellite Data. Ann. Glaciol. 1993, 17, 307–311. [Google Scholar] [CrossRef]
- Grody, N.C.; Basist, A.N. Global Identification of Snowcover Using Ssm/i Measurements. IEEE Trans. Geosci. Remote Sens. 1996, 34, 237–249. [Google Scholar] [CrossRef]
- Rees, A.; Derksen, C.; English, M.; Walker, A.; Duguay, C. Uncertainty in Snow Mass Retrievals from Satellite Passive Microwave Data in Lake-Rich High-Latitude Environments. Hydrol. Process. 2006, 20, 1019–1022. [Google Scholar] [CrossRef]
- Gunn, G.E.; Duguay, C.R.; Derksen, C.; Lemmetyinen, J.; Toose, P. Evaluation of the HUT Modified Snow Emission Model over Lake Ice Using Airborne Passive Microwave Measurements. Remote Sens. Environ. 2011, 115, 233–244. [Google Scholar] [CrossRef]
- Duguay, C.; English, M.C.; Profile, S.; Rees, A. Preliminary Assessment of the Impact of Lakes on Passive Microwave Snow Retrieval Algorithms in the Arctic. In Proceedings of the 62nd Eastern Snow Conference Proceedings, Waterloo, ON, Canada, 7–10 June 2005; pp. 223–228. [Google Scholar]
- Tedesco, M.; Wang, J.R. Atmospheric Correction of AMSR-E Brightness Temperatures for Dry Snow Cover Mapping. IEEE Geosci. Remote Sens. Lett. 2006, 3, 320–324. [Google Scholar] [CrossRef]
- Wang, J.R.; Tedesco, M. Identification of Atmospheric Influences on the Estimation of Snow Water Equivalent from AMSR-E Measurements. Remote Sens. Environ. 2007, 111, 398–408. [Google Scholar] [CrossRef]
- Gu, L.; Ren, R.; Li, X. Snow Depth Retrieval Based on a Multifrequency Dual-Polarized Passive Microwave Unmixing Method from Mixed Forest Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7279–7291. [Google Scholar] [CrossRef]
- Gu, L.; Ren, R.; Li, X.; Zhao, K. Snow Depth Retrieval Based on a Multifrequency Passive Microwave Unmixing Method for Saline-Alkaline Land in the Western Jilin Province of China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2210–2222. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Wang, G.; Hao, S.; Chen, Z. Using a Linear Unmixing Method to Improve Passive Microwave Snow Depth Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4414–4429. [Google Scholar] [CrossRef]
- Dong, J.; Walker, J.P.; Houser, P.R. Factors Affecting Remotely Sensed Snow Water Equivalent Uncertainty. Remote Sens. Environ. 2005, 97, 68–82. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Dai, L.; Pan, J.; Wu, S.; Wang, G. The Consistency of SSM/I vs. SSMIS and the Influence on Snow Cover Detection and Snow Depth Estimation over China. Remote Sens. 2019, 11, 1879. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.J.; Margulis, S.A.; Molotch, N.P. A First-Order Characterization of Errors from Neglecting Stratigraphy in Forward and Inverse Passive Microwave Modeling of Snow. IEEE Geosci. Remote Sens. Lett. 2011, 8, 730–734. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, J.; Du, J.; Fu, X. Evaluation of Terrain Effect on Microwave Radiometer Measurement and Its Correction. Int. J. Remote Sens. 2011, 32, 8899–8913. [Google Scholar] [CrossRef]
- Mätzler, C.; Standley, A.; Ma¨tzler, C.; Ma¨tzler, M. Technical Note: Relief Effects for Passive Microwave Remote Sensing Technical Note Relief EOE Ects for Passive Microwave Remote Sensing. Int. J. Remote Sens. 2000, 21, 2403–2412. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, L.; Zhang, L.; Guo, Y. Impact of Terrain Topography on Retrieval of Snow Water Equivalence Using Passive Microwave Remote Sensing. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1757–1760. [Google Scholar] [CrossRef]
- Jin, R.; Li, X.; Che, T. A Decision Tree Algorithm for Surface Soil Freeze/Thaw Classification over China Using SSM/I Brightness Temperature. Remote Sens. Environ. 2009, 113, 2651–2660. [Google Scholar] [CrossRef]
- Armstrong, R.L.; Brodzik, M.J. Hemispheric-Scale Comparison and Evaluation of Passive-Microwave Snow Algorithms. Ann. Glaciol. 2002, 34, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Deschamps-Berger, C.; Gascoin, S.; Berthier, E.; Deems, J.; Gutmann, E.; Dehecq, A.; Shean, D.; Dumont, M. Snow Depth Mapping from Stereo Satellite Imagery in Mountainous Terrain: Evaluation Using Airborne Laser-Scanning Data. Cryosphere 2020, 14, 2925–2940. [Google Scholar] [CrossRef]
- Lievens, H.; Brangers, I.; Marshall, H.P.; Jonas, T.; Olefs, M.; de Lannoy, G. Sentinel-1 Snow Depth Retrieval at Sub-Kilometer Resolution over the European Alps. Cryosphere 2022, 16, 159–177. [Google Scholar] [CrossRef]
- He, S.; Ohara, N.; Miller, S.N. Understanding Subgrid Variability of Snow Depth at 1-Km Scale Using Lidar Measurements. Hydrol. Process. 2019, 33, 1525–1537. [Google Scholar] [CrossRef]
- Hou, Y.; Huang, X.; Zhao, L. Point-to-Surface Upscaling Algorithms for Snow Depth Ground Observations. Remote Sens. 2022, 14, 4840. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanniru, S.; Ramsankaran, R. Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions. Remote Sens. 2023, 15, 1052. https://doi.org/10.3390/rs15041052
Tanniru S, Ramsankaran R. Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions. Remote Sensing. 2023; 15(4):1052. https://doi.org/10.3390/rs15041052
Chicago/Turabian StyleTanniru, Srinivasarao, and RAAJ Ramsankaran. 2023. "Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions" Remote Sensing 15, no. 4: 1052. https://doi.org/10.3390/rs15041052
APA StyleTanniru, S., & Ramsankaran, R. (2023). Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions. Remote Sensing, 15(4), 1052. https://doi.org/10.3390/rs15041052