Study on the Backscatter Differential Phase Characteristics of X-Band Dual-Polarization Radar and its Processing Methods

Abstract

The differential propagation phase (Φ_DP) of X-band dual-polarization weather radar (including X-band dual-polarization phased-array weather radar, X-PAR) is important for estimating precipitation and classifying hydrometeors. However, the measured differential propagation phase contains the backscatter differential phase (δ), which poses difficulties for the application of the differential propagation phase from X-band radars. This paper presents the following: (1) the simulation and characteristics analysis of the backscatter differential phase based on disdrometer DSD (raindrop size distribution) measurement data; (2) an improved method of the specific differential propagation phase (K_DP) estimation based on linear programming and backscatter differential phase elimination; (3) the effect of backscatter differential phase elimination on the specific differential propagation phase estimation of X-PAR. The results show the following: (1) For X-band weather radar, the raindrop equivalent diameters D > 2 mm may cause a backscatter differential phase between 0 and 20°; in particular, the backscatter differential phase varies sharply with raindrop size between 3.2 and 4.5 mm. (2) Using linear programming or smoothing filters to process the differential propagation phase could suppress the backscatter differential phase, but it is hard to completely eliminate the effect of the backscatter differential phase. (3) Backscatter differential phase correction may improve the calculation accuracy of the specific differential propagation phase, and the optimization was verified by the improved self-consistency of polarimetric variables, correlation between specific differential propagation phase estimations from S- and X-band radar and the accuracy of quantitative precipitation estimation. The X-PAR deployed in Shenzhen showed good observation performance and the potential to be used in radar mosaics with S-band weather radar.

1. Introduction

By transmitting and receiving horizontal and vertical electromagnetic waves simultaneously or alternately, dual-polarization radar not only detects the reflectivity (Z) but also observes the differential reflectivity factor (Z_DR), differential propagation phase (Φ_DP), specific differential propagation phase (K_DP), and correlation coefficient (ρ_HV). These polarimetric variables are related to the size and phase state of precipitation particles and can improve radar quantitative precipitation estimation (QPE) and achieve raindrop size distribution (DSD) retrieval and classification of the three-dimensional structure of hydrometeors [1,2,3].

The X-band dual-polarization radar is intended to obtain the detailed spatial variation in precipitation systems and reduce the QPE errors caused by the vertical variation of raindrops, while also improving the QPE, based on its improved spatial and temporal resolution and observation ability at low altitudes. For the applications of X-band dual-polarization radar, Φ_DP and K_DP play important roles in attenuation correction, QPE, hydrometeor classification, and DSD retrieval [4,5,6,7,8,9]. However, the total measured differential phase Φ_DP is affected by radar sampling errors and beam non-uniformity [10,11]. In addition, for short-wavelength dual-polarization radar, the backscatter differential phase (δ) due to Mie scattering is one of the causes of the local variation in Φ_DP and the deviation of ρ_HV from 1.0, while the influence of δ on Φ_DP is also non-negligible. The effects of δ show that the Φ_DP of heavy precipitation containing large raindrops suddenly increases and decreases [10,11,12,13]. To eliminate the effects of noise (including δ) on Φ_DP and K_DP, Φ_DP could be filtered through cyclic iterative low-pass FIR filters to eliminate the effects of local variations caused by random noise and δ [14,15]. Based on the internal self-consistency of the polarimetric variables, some adaptive methods were proposed to estimate K_DP, which internally include the suppression or elimination of δ [16,17,18]. To ensure the monotonicity of Φ_DP (i.e., K_DP is nonnegative while the electromagnetic waves pass through liquid precipitation), a linear programming (LP) method with physical constraint was proposed to reconstruct Φ_DP, and then obtain a reasonable K_DP [19,20]. The LP method had been applied in the data quality control of an X-band dual-polarization radar network in Beijing, and the results showed that this method could effectively weaken the influence of δ on the K_DP calculation [21]. The comparative analysis of K_DP estimation algorithms showed that the published methods have apparent strengths and weaknesses, and the LP algorithm has good performance in accuracy and general applicability [22,23].

However, the LP algorithm mitigates the abrupt variation in Φ_DP by spatial smoothing and reconstruction, rather than direct δ calculation and elimination. It is effective to suppress δ as random noise, but hard to completely eliminate the effect of δ. According to the published research, δ and Z_DR have a good fitting relationship [16,24,25], which is helpful to calculate δ quantitatively. Separating the δ-elimination from random noise elimination makes the pre-processing of Φ_DP more realistic, because δ has a definite physical meaning, rather than random noise.

Previous studies have proven that an X-band radar network can greatly enrich the observation information of the current S-band-based operational radar networks; in particular, it could provide low-level observation information with high spatial and temporal resolution, which is of great significance to the observation, assimilation, short-term forecast, and QPE of strong convective weather. At present, an X-band dual-polarization phased-array weather radar (X-PAR) network has been built or is under construction over a large area in China. However, the non-negligible δ caused by short-wavelength observations restricted the application of K_DP. After verifying the observation accuracy of X-PAR in Guangdong taking S-band weather radar as the standard, although Φ_DP trends were essentially the same for both radars, the random jitter of the X-PAR K_DP calculated by median filtering and least squares was very sharp, and the Φ_DP-processing and the K_DP calculation method still needed to be improved [26].

In order to explore and reduce the influence of δ on the K_DP estimation, and to further eliminate δ to obtain more accurate K_DP for X-PAR observation applications, we used DSD measurement, avoiding uncertain parameters in the gamma hypothesis, to calculate polarimetric variables and fit the equations between δ and Z_DR for X- and C-band dual-polarization radars. Through a space–time transformation approach, we simulated and constructed radial data to analyze the impact of δ on K_DP estimation, QPE, and attenuation correction. The improved effect of δ correction on K_DP calculations was further analyzed using X-PAR deployed in Shenzhen via the case study and statistical analysis from three aspects: the self-consistency of radar polarimetric variables, the consistency of X-PAR and S-POL observation, and the accuracy of QPE. This paper proposes an improved method for K_DP estimation, and shows the performance of X-PARs in South China in Φ_DP measurement and K_DP estimation.

2. Data and Methods

For this article, the main contributions are as follows: (1) An analysis of the characteristics of δ, the effect of δ on quality control, and the effect of δ correction on K_DP calculation, based on DSD measurements. (2) Provide an improved algorithm for K_DP estimation based on LP and δ-correction. (3) Test the effects of the δ-correction method on K_DP calculation based on X-PAR data. Therefore, we used DSD and radar observation to analyze the characteristics and processing methods of δ with the perspectives of theory and application, respectively.

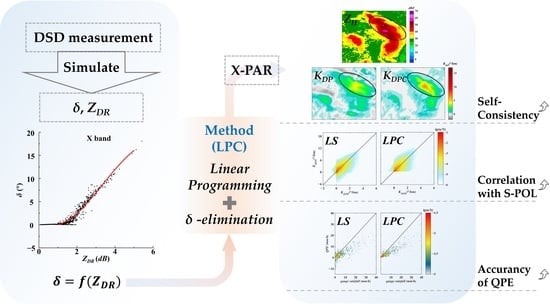
2.1. Simulation and Correction Methods Based on DSD Data

For a single hydrometeor, the backscattering matrix of the radar wave can be expressed as:

$$\left[\begin{array}{c}{E}_H^r\\ E_V^r\end{array}\right]=\frac{e^{-jkr}}{r}\left[\begin{array}{cc}{S}_{HH}& S_{HV}\\ S_{VH}& S_{VV}\end{array}\right]\left[\begin{array}{c}{E}_H^i\\ E_V^i\end{array}\right]$$

(1)

where $E_H^i$ and $E_V^i$ are the incident electric field intensities of the horizontally and vertically polarized waves, respectively; $E_H^r$ and $E_V^r$ are the electric field intensities of the particle scattering; S_HH, S_HV, S_VH, and S_VV are the four complex scattering functions of the scattering matrix. The forward and backward scattering is denoted by 0° and 180°, respectively, while the DSD is denoted by N(D). Then, the δ of a single hydrometeor can be expressed as:

$$\delta \left(D\right)=arg\left(S_{HH}^{*}\left(180\right)S_{VV}\left(180\right)\right)$$

(2)

where * denotes the conjugate of the complex number. For a rain area with a DSD of N(D), the δ, Z_V, Z_H, Z_DR, K_DP, and specific attenuation A can be calculated by [27]

$$\delta =\arg \left[\underset{0}{\overset{D_{max}}{{\displaystyle \int }}}N\left(D\right)\left|S_{HH}\left(180,D\right) S_{VV}\left(180,D\right)\right|e^{j\left[\delta \left(D\right)\right]}dD\right]$$

(3)

$$Z_{H,V}=\frac{{\lambda }^4}{{\pi }^5{\left|U\right|}^2}\underset{0}{\overset{D_{max}}{{\displaystyle \int }}}4\pi {\left|S_{HH,VV}\left(180,D\right)\right|}^{2}N\left(D\right)dD$$

(4)

$$Z_{DR}=10.0lo{g}_{10}\left(\frac{Z_H}{Z_V}\right)$$

(5)

$$K_{DP}=\frac{180\lambda }{\pi }\underset{0}{\overset{D_{max}}{{\displaystyle \int }}}Re\left(S_{HH}\left(0,D\right)-S_{VV}\left(0,D\right)\right)N\left(D\right)dD$$

(6)

$$A_{H,V}=0.4343\frac{4\pi }{k}\underset{0}{\overset{D_{max}}{{\displaystyle \int }}}{I}_m\left(S_{HH,VV}\left(0,D\right)\right)N\left(D\right)dD$$

(7)

where $U=\frac{\epsilon -1}{\epsilon +2}$, and ε is the complex relative dielectric constant,$k=\frac{2\pi }{\lambda }$.

In this way, the total measured differential phase Φ_DP and K_DPR calculated by Φ_DP can be expressed by Equations (8) and (9), respectively:

$${\Phi }_{DP}\left(r\right)=\delta \left(r\right)+2.0\underset{0}{\overset{r}{{\displaystyle \int }}}{K}_{DP}\left(s\right)ds$$

(8)

$$K_{DPR}=K_{DP}+\frac{{\delta }_2-{\delta }_1}{2\left(r_2-r_1\right)}$$

(9)

The definition of δ shows that it is related to the raindrops’ size, rather than their numerical density, similar to Z_DR. The effect of δ on K_DP is only related to its variation with distance.

The backscattering cross-section of raindrops was calculated using the extended boundary condition method [28]. The quality-controlled data from an OTT Particle Size Velocity (PARSIVEL) disdrometer [29] at the Longmen Observatory in Guangdong Province in 2020 were used to calculate Z_H, Z_DR, K_DP, and δ and to fit their relationships. For the 1 min resolution DSD data, the data with precipitation intensity less than 0.5 mm/h and fewer than 50 total raindrops were first removed [30], followed by the removal of data that deviated from the terminal velocity of the falling raindrops [31].

To simulate the effect of δ on the radar polarimetric variables and attenuation correction, we assumed that the precipitation system was a rigid body in uniform motion and that the precipitation parameters were homogeneous within the radar observation volume; in this way, the variation in the DSD over time could be transformed into spatial variation, and the polarimetric variables along a propagation path of the radar observations could be simulated and used to analyze the effects of δ on the K_DP and correction effect.

It is known that δ and Z_DR depend on the particles size and are independent of the absolute particle number density; thus, the following method for δ correction using quality-controlled Z_DR was proposed:

• Firstly, based on the local DSD data, the fitted relationship between δ and Z_DR was calculated.
• Based on this relationship, the threshold of Z_DR for δ correction was determined; i.e., δ was only calculated when Z_DR was larger than this threshold.
• The elimination of δ from the filtered Φ_DP was carried out:

$${\Phi }_{DPC}={\Phi }_{DPR}-\delta \left(Z_{DR}\right)$$

(10)

where ${\Phi }_{DPR}$ and ${\Phi }_{DPC}$ represent the differential propagation phase before and after the δ elimination, respectively, and δ(Z_DR) is the δ calculated using Z_DR.

2.2. The X-PAR Data

The X-PAR data used in this paper were taken from the Qiuyutan station in Shenzhen, Guangdong (22.65°N, 113.85°E). This radar network was completed by the end of 2019. The X-PAR was X-band fully coherent pulsed doppler dual-polarization phased-array radar. Its peak power is 256 W, and it provides a range resolution of 30 m, 12 elevation angles, and a temporal resolution of 92 s; its 3D scan data contain polarimetric variables such as reflectivity Z_H (unit: dB), correlation coefficient ρ_hv, differential reflectivity Z_DR (unit: dB), differential propagation phase Φ_DP (unit: °), and specific differential propagation phase K_DP (unit: °/km). The radar data from March to September 2020 (a total of 17,863 volume scans) were processed with attenuation correction (including Z_H and Z_DR) based on the quasi-linear relation between path integral attenuation (PIA) and ΔΦ_DP (PIA = γΔΦ_DP). Usually, S-band dual-polarization Doppler weather radar (S-POL) undergoes rigorous calibration during the upgrade process to increase the data reliability, and the S-band signal is weakly affected by attenuation when the electromagnetic wave passes through the rain. Because of the high reliability and the same location as the X-PAR, S-POL data were used to verify the accuracy of X-PAR data. The key parameters of the two radars are listed in

Table 1. X-PAR and S-POL radar parameters.

Radar Parameters	X-PAR	Shenzhen S-POL
Frequency	9.3~9.5 GHz	2.8 GHz
Peak power	256 W	≥650 kW
Update time	92 s	360 s
Range coverage	42 km	230 km
Range resolution	30 m	250 m
Elevation scan range	0.9°~20.7° with 1.8° step	0.5~19.5°, 9 layers
Beamwidths	Horizontal: 3.6°; vertical: 1.8°	Horizontal: <1°; vertical: <1°
Array plane normal angle	15°	/
Scan mode	Volume range height indicator scan	Volume plan position indicator scan

.

2.3. K_DP Calculation Methods

The Φ_DP and Z_DR based on the DSD simulation data do not take other noise information from the actual radar observations into account. However, there is a large amount of random noise in the actual radar-observed Φ_DP, in addition to the effect of δ, and the noise information from the Z_DR is also brought into Φ_DP due to δ correction. Therefore, in the process of calculating the K_DP, δ correction and further denoising are required. Since filtering and denoising can also suppress the effects of δ, two filtering and denoising schemes were used to preprocess Φ_DP and then calculate the K_DP in order to analyze the effect of δ correction.

2.3.1. K_DP Calculation Based on Low-Pass Filtering and Least Squares (LS)

K_DP can be calculated directly from filtered Φ_DP via the least-squares method, which is common and efficient. In this study, a 3 km moving average was used to denoise the Φ_DP. This method set a low-pass filter with filter coefficients equal to the reciprocal of the span. Least-squares linear regression was then fitted to Φ_DP within a total of 1 km window of each gate of the ray path, using the slope obtained from the fit to calculate the K_DP for that gate.

2.3.2. K_DP Calculation Based on SG Smoothing Filters and LP Method

The LP method proposed by [19] with good performance was chosen to calculate Φ_DP, and the K_DP consistent with the physical characteristics of the precipitation system could be obtained. The objective of LP is to minimize the difference between reconstructed ${\phi }_{DPfit}$ and observed Φ_DP within the constraint that the K_DP corresponding to ${\phi }_{DPfit}$ is within the interval between K_DPmin and K_DPmax. This objective was achieved by an LP scheme designed as follows:

Minimize c· x_c

Subject to A_AUG x_c ≥ b_AUG

$x_c\equiv {\left\{z,x\right\}}^{\mathrm{T}}\ge 0$

of which

$$A_{\mathrm{AUG}}=\left(\begin{array}{c}\begin{array}{cc}{I}_n& -I_n\end{array}\\ \begin{array}{cc}{I}_n& I_n\end{array}\\ \begin{array}{cc}{Z}_{n-m+1,n}& M_{n-m+1,n}\end{array}\\ \begin{array}{cc}{Z}_{n-m+1,n}& -M_{n-m+1,n}\end{array}\end{array}\right)$$

(11)

where I_n is the n × n identity matrix, while Z_n−m+1,n is an (n − m + 1) × n matrix of zeros. The range resolution of the X-PAR is 30 m, m = 33 (i.e., 1 km), and n is the length of Φ_DP.

$$M_{n-m+1,n}=\left(\begin{array}{c}{d}_1 d_2\dots d_m 0_1\dots 0_{n-m} \\ \dots \\ 0_1 \dots 0_{n-m} d_1 d_2\dots d_m\end{array}\right)$$

(12)

$$d_i=\frac{6\left(2i-m-1\right)}{m\left(m+1\right)\left(m-1\right)}$$

(13)

$$b_{\mathrm{AUG}}=\left(\begin{array}{c}-{\Phi }_{DP}\\ {\Phi }_{DP}\\ 2s{K}_{DPmin}\\ -2s{K}_{DPmax}\end{array}\right)$$

(14)

where ${\Phi }_{DP}$ is the observational radial ${\Phi }_{DP}$ data array, s is the range resolution of X-PAR, while K_DPmin and K_DPmax are set as the weak physical constraints for ${\phi }_{DPfit}$, and they are 1/4 and 4 times the K_DPZ calculated from Z_H after attenuation correction by using the fitting formula based on DSD, respectively. Since the K_DP is calculated from Φ_DP by a 33-point Savitzky–Golay (SG) derivative filter, the physical constraint here is weak, which is only to avoid some extremely unreasonable Φ_DP jitter.

$$c=\left(t_{1 }{t}_{2 }\dots t_{n }{0}_{1 }{0}_{2 }\dots 0_{n }\right)$$

(15)

$$t_i=\left\{\begin{array}{c} 1 ,QC\left(i\right)=1 \\ 0.3 , QC\left(i\right)=0\end{array}\right.$$

(16)

The weight integral of z represents the difference between ${\Phi }_{DP}$ and ${\phi }_{DPfit}$; ${\Phi }_{DP}$ should be continuous within the precipitation zone, but due to observation or signal processing error, ${\Phi }_{DP}$ occasionally has missing measurements or abnormal jitter at some gates. For this area of poor-quality ${\Phi }_{DP}$, linear interpolation was used to supplement it. Since these data were interpolated, a smaller weight was set in the cost function, where t_i is the weight factor of z.

Finally, an LP scheme is solved to obtain x_c as a 2n × 1 column matrix, where rows 1 to n are z and rows (n + 1) to 2n are x. The vector x satisfies the constraints of the LP scheme for ${\phi }_{DPfit}$, but there are still some high-frequency fluctuations, and the vector x can be filtered by the SG smoothing filter corresponding to the SG derivative filter to obtain a smooth ${\phi }_{DPfit}$. K_DP can be calculated from ${\phi }_{DPfit}$ using the SG derivative filter.

$$s_i=\left\{\begin{array}{c}-\raisebox{1ex}{$d_1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. , i=1 \\ -\frac{d_i}{2}-{\displaystyle \sum _1^{i-1}}{d}_j ,i\in \left[2,\frac{m+1}{2}\right] \\ s_{m-i+1} , i\in \left[\frac{m+1}{2}+1,m\right] \end{array}\right.$$

(17)

$$N_{n-m+1,n}=\left(\begin{array}{c}{s}_1 s_2\dots s_m 0_1\dots 0_{n-m} \\ \dots \\ 0_1 \dots 0_{n-m} s_1 s_2\dots s_m\end{array}\right)$$

(18)

$${\phi }_{DPfit}=Nx$$

(19)

2.3.3. K_DP Calculation Schemes for X-PAR

In order to test the effect of the δ-correction method, four sets of K_DP calculation schemes of X-PAR were designed based on the two different K_DP calculation methods mentioned above:

Exp1: A low-pass filter is applied to Φ_DP to remove some of the random noise, and then the least-squares method is used to calculate K_DP1.

Exp2: Based on the δ–Z_DR statistical relationship, δ is calculated using the attenuation-corrected Z_DR. After subtracting δ from the observed Φ_DP to obtain Φ_DP2, K_DP2 is calculated using the method of Exp1.

Exp3: Based on the DSD measurement and fitting calculation, an equation between K_DP and Z_H is obtained, and then the K_DPZ based on the radar-observed Z_H (after attenuation correction) is calculated. The K_DPZ is used as a weak physical constraint, and the LP method is used to calculate the processed Φ_DP3, as well as to calculate the K_DP3 [19].

Exp4: Based on the δ–Z_DR statistical relationship, δ is calculated using the attenuation-corrected Z_DR. After subtracting δ from the observed Φ_DP to obtain Φ_DP2, Φ_DP4, and K_DP4 are calculated using the method of Exp3.

3. Results

3.1. The Relationship of δ with Raindrops’ Size and Temperature

Firstly, the analysis shows the relationship between δ and the equivalent diameter of the raindrops at different temperatures in S-, C-, and X-bands (Figure 1). For S-, C-, and X-bands, an obvious change in the δ exists only when the equivalent diameter D of the raindrops is greater than 6 mm, 4 mm, and 2 mm, respectively. The conditions for generating δ in precipitation are easily satisfied for X-band. It is noted that δ shows a nonmonotonic change with diameter causing resonance effects at higher temperatures at C-band. In addition, there is a range of diameters that δ varies most strongly with D for each band (near 6 mm for C-band and near 4 mm for X-band). Since the effect of δ on K_DP is mainly based on the variation in δ with distance, a change in the DSD in these ranges may produce a significant change in Φ_DP and affect the calculation of K_DP. The variation trend of δ with D is in accordance with the previous studies [7], but the amplitude of δ calculated in this paper is about 1/4 higher, which may be related to different assumptions of the raindrops shape.

The scatterplot of the distribution of δ with Z_DR was calculated using DSD measurement from the Longmen observatory in Guangdong in May–June 2019 (Figure 2). Only the C- and X-band cases are given in Figure 2, considering that δ has little effect on the Φ_DP and K_DP of the S-band radar. The time resolution of DSD measurement is 1 min, the sample size of valid data is 85,265, with 10,001 samples with simulated reflectivity greater than 10 dBZ. According to Figure 2, δ is very small at Z_DR < 1.0 dB. For this reason, we suggest that this case (Z_DR < 1.0 dB) should not be processed with δ elimination for Φ_DP. For X-band, the number of points with simulated Z_DR > 1.0 dB is 3358, while the number of points with δ > 1.0° is 1239. In contrast, for C-band, there are 572 points with Z_DR > 1.0 dB and 72 points with δ > 1.0°.

In order to compare the differences between the DSD measurement and the simulations in other articles [24], we used the gamma model, where the simulations of C- and X-band radar are given in Figure 2c,d, respectively. The gamma distribution equation is:

$$N\left(D\right)=N_w{D}^{m}exp\left(\frac{-3.67D}{D_0}\right)$$

(20)

The m values were in the range from −1 to 4, while D₀ took values in the range from 0.5 to 2.5 mm. Noted that δ has no relation with N_W.

Comparing the two DSD sources, they have a consistent trend for Z_DR > 2.0 dB, and the C-band results from the DSD measurement are more dispersed than the gamma model’s DSD values. The DSD measurement often deviates from the gamma parameter distribution, leading to weak correlation between the X-band δ and Z_DR for Z_DR < 2.0 dB. Considering the uncertainty of the parameters in the gamma distribution hypothesis, the simulation based on the DSD measurement is more accurate to the statistics of the polarimetric variables in the research area. Compare with previous studies, the fitting relationship between δ and Z_DR at X-band is basically consistent with the fitting curve of [12] and δ = Z_DR^1.8 proposed by [25].

According to the above results, the fitting equations for X- and C-band Z_DR and δ were obtained:

X-band:

$$\delta =0.962-3.16Z_{DR}+2.44Z_{DR}^2-0.241Z_{DR}^3$$

(21)

C-band:

$$\delta =0.536-1.170Z_{DR}+0.499Z_{DR}^2+0.0334Z_{DR}^3$$

(22)

To analyze the effects of δ on QPE and attenuation correction, the X-band radar QPE equations and attenuation correction equations were obtained through fitting.

$$R=0.023Z_H^{0.694}$$

(23)

$$R=sign\left(K_{DP}\right)12.7{\left|K_{DP}\right|}^{0.85}$$

(24)

$$A_H=sign\left(K_{DP}\right)0.16{\left|K_{DP}\right|}^{0.96}$$

(25)

$$A_{DR}=sign\left(K_{DP}\right)0.0247{\left|K_{DP}\right|}^{1.18}$$

(26)

Notably, it may seem unreasonable to calculate negative attenuation and rain intensity when the K_DP is negative in Equations (24) and (25), but, in fact, this approach is justified because negative K_DP is often caused by a variety of factors, especially the effects of δ and radar sampling errors, but such errors are local or random. While the negative values of K_DP may match some overestimated positive K_DP, when such negative rain intensity or attenuation is calculated by distance-averaging or time-averaging, these unreasonable values will be smoothed out by the accumulation to give a relatively reasonable average.

3.2. The δ-Correction Effect Based on Simulated Data

3.2.1. Simulating the Effects of δ on Ф_DP and K_DP

Using the disdrometer DSD measurements from 12:12 to 15:58 on 10 June 2019, the polarimetric variables of an X-band radar were simulated for a 40 km radar’s radial data, with the assumption that the movement speed is 18 km/h. Figure 3 shows the variation in Z_H, Z_DR, Ф_DP1, and K_DP1 (without the effect of δ), as well as that of Ф_DP2 and K_DP2 (affected by δ, which represents actually the result of the actual radar observation), with distance for these simulated radial data. Among these radial data, Z_H varies from 10 to 50 dBZ, with a Z_DR range of 0–3.0 dB. It can be seen that with sudden changes in Z_DR, δ can cause local variations of ±8.0° in Ф_DP and ±25.0°/km in K_DP, far exceeding the reasonable range, overestimating K_DP in areas of sudden Z_DR increase and underestimating K_DP in areas of Z_DR decrease, sometimes even resulting in significantly negative K_DP. The local mutation of Φ_DP and K_DP produced by δ is not negligible. For the effect of δ on QPE (Figure 3c), without the δ elimination, QPE is significantly locally underestimated and overestimated. Although the effect of δ on cumulative precipitation estimates can be mostly offset by space–time integration, its effect on rainfall intensity estimates is very severe.

3.2.2. The Effects of δ on Attenuation Correction

Under the assumption that the precipitation system is moving at a constant speed, the variation in Z_H, Z_DR, A_H, A_DR, and δ with distance of a ray path can be obtained using the time series of these polarimetric variables calculated from the DSD measurement. Using the calculated A_H and A_DR, the Z_H and Z_DR after attenuation can be obtained—that is, the simulated radar measurements’ Z_H and Z_DR. Additionally, based on Equations (25) and (26), the K_DP can be used to calculate the A_H and A_DR for correction, and we can obtain the Z_H and Z_DR after attenuation correction and further compare them with the Z_H and Z_DR calculated from the DSD data to analyze the correction effect.

Figure 4 shows the Z_H, Z_DR, and PIA (calculated directly from the DSD and calculated from K_DP affected by δ). The difference between the PIA calculated from the two datasets is the correction error. In this case, as shown in Figure 4, the attenuation causes an underestimation of Z_H and Z_DR by 5.2 dB and 0.78 dB, respectively, which is sufficient to cause significant errors in precipitation estimation and hydrometeor classification; e.g., Z_DR may become negative after a distance of 20 km. The PIA calculated from K_DP results in a smaller correction than that calculated from DSD; the magnitude of this error is distance-dependent and is mainly related to the characteristics of the DSD in the region, but the errors are all within the 1.0 dB detection error for Z_H and the 0.2 dB detection error for Z_DR—much smaller than the actual attenuation. Noted that the observation error of the K_DP was not considered in this simulation.

3.2.3. The Effects of δ-Elimination on K_DP Calculation

In order to analyze the effect of δ elimination on the K_DP calculation, the Z_DR calculated from DSD without attenuation effect (Test A) and the Z_DR after attenuation correction (Test B) were used to calculate the δ using Equation (11), and then the δ was eliminated from Ф_DPR to obtain Ф_DP1 (Test A) and Ф_DP2 (Test B), and to calculate K_DP1 (Test A) and K_DP2 (Test B), which were compared with the Ф_DP and K_DP calculated by DSD simulation, respectively; finally, the rain intensity was calculated using K_DP, K _DP1 and K_DP2 to analyze the effects of δ elimination on the rain intensity. Test A focused on the effect of the error of the δ (Z_DR) fitting relation, while Test B focused on the effect of the Z_DR attenuation correction error. Figure 5 shows the simulated K_DP (unaffected by δ) and K_DPδ (affected by δ), along with the δ-corrected K_DP1 and K_DP2 obtained from Test A and Test B, as well as the rain intensity calculated from these data. The calculated K_DPδ (affected by δ) could be considered equivalent to the actual radar observation. As shown in Figure 5a, the local variability of K_DPδ is increased due to δ, significantly, with extreme values and negative values occurring in the Z_DR mutation region. Comparing Figure 5b,c reveals that the δ correction modifies the K_DP error in the Z_DR mutation region but also adds additional K_DP local variation in the region of slow change in Z_DR, which indicates the necessity of denoising after δ correction.

Based on DSD data from the Longmen Observatory in Guangdong for May–June 2019, the simulated K_DP (unaffected by δ) and the simulated K_DPδ (affected by δ) were calculated, along with the corrected K_DP1, which was calculated based on the δ-elimination using Z_DR (Figure 6b). The results show that the δ produces too many negative values of K_DP as well as overestimation of K_DP, especially in low-value K_DP (weak rainfall) areas, and that the δ correction reduces the negative effect of δ on the K_DP calculation, but there are still some errors.

3.3. The Effect of δ Correction on X-PAR K_DP Calculation

3.3.1. Case Analysis on Radial Data

Taking the results of the radial data processed at 10:32 a.m. on 13 September 2020—with an elevation angle of 4.5° and an azimuth angle of 293.4°—as an example (see Figure 7), there are obvious high values of Z_H and Z_DR, as well as the strong fluctuations of the corresponding Φ_DP, with an obvious δ characteristic near 26 km of the ray path. The δ calculated from Z_DR reaches a maximum of 7.2°. The δ-eliminated Φ_DP shows a relatively significant decrease in the range of 24–27 km. The Φ_DP3 calculated by LP is shown in Figure 7b. Due to the physical constraints that ensure a monotonically non-negative trend of Φ_DP3 with distance in the liquid precipitation, the δ- eliminated Φ_DP4 differs from Φ_DP3 mainly in the weak fluctuations at 24 km and the backward shift of the steeply rising section (corresponding to the region of large K_DP values). K_DP and Z_H are mainly related to the scale and number of large oblate spherical raindrops, while the target of observation is liquid precipitation. The trends of K_DP calculated by LS and LP are essentially the same, with both peaking around 25 km, but the δ-corrected K_DP is more consistent with the trend of Z_H. This is because δ increases Φ_DP in the large raindrops zone and, thus, causes an overestimation of K_DP at the front of the large raindrops zone, while δ decreases after the large raindrops zone, which also causes an underestimation of K_DP at the back of the large raindrops zone. After the δ correction, the K_DP values calculated by both LS and LP were more consistent with the Z_H trend. On the other hand, despite the filtering process, the K_DP calculated by LS still had some negative values in the liquid precipitation, which was inconsistent with the non-negative K_DP corresponding to the oblate spherical characteristics of raindrops, while the K_DP calculated by LP—due to the physical constraints—ensured the non-negative characteristics.

3.3.2. Case Analysis on PPI

Taking a strong convective weather process as an example, in the northeast direction of the X-PAR at 01:20 on 8 June 2020. To analyze the performance of K_DP estimation to fine structures, we selected a small research area with only 15 km. Thanks to the high spatial resolution, X-PAR has observed a hook echo structure of the convective cell, while S-POL was difficult to show such detailed characteristics.

Because there is a time difference (≤1 min) between the two radars’ measurements, and the position of the same echo is slightly mismatched, the relative position of each polarimetric variable was the main focus of the analysis. In terms of S-POL observation, the high-value positions of Z_H, Z_DR, and K_DP of A and B cells were basically consistent; although, the detailed characteristics of K_DP were insufficient due to the low resolution.

For Exp1 (Figure 8f) and Exp3 (Figure 8h) without δ correction, the high value centers of K_DP of cell A are shifted southward relative to the Z_H high value, which was improved with δ correction of Exp2 (Figure 8g) and Exp4 (Figure 8i), and the K_DP of cell B with δ non-corrected has a similar situation. This problem is manifested in the relative expansion of the high-value range, the underestimation of high value, and the poor self-consistence with Z_H and Z_DR. After δ correction, the maximum value of K_DP of cell B was more reasonable (consistent with S-POL), and the structure of K_DP was also more consistent with Z_H and Z_DR. In addition, the false increase in Φ_DP caused by δ will also result in an unreasonable negative value (Figure 8f) behind the K_DP peak by the LS method. Through δ correction, the negative values of K_DP at the back side (north side) of cell A and B were significantly improved (Figure 8g). The LP method with physical constraints solves this problem more strictly than the LS method. In a word, through smoothing filtering, Exp1 and Exp3 can obtain relatively stable K_DP estimation. However, the δ, which was not completely eliminated, still affected the magnitude, position, and structure of K_DP around the large particle area, which is unfavorable for the detailed analysis of cloud physical characteristics. δ correction can be helpful to solve this problem.

3.3.3. Statistical Analysis

Furthermore, the effect of δ elimination on the calculation of X-PAR K_DP was tested statistically by S-POL K_DP and the X-PAR attenuation-corrected Z_H and Z_DR. By fitting the DSD data, the statistical relation between K_DP of S-band and X-band radar was obtained, and the standard value of K_DP for X-PAR could be calculated from the S-POL observations via the fitting equation. In addition, there is internal self-consistency of the polarimetric variables. Z_H, Z_DR, and K_DP are related to the scale, shape, and number of spherical raindrops, with nonlinear correlation (K_DP = aZ_H^bZ_DR^c). Therefore, the determination coefficient of the nonlinear correlation between Z_H, Z_DR, and K_DP can also be used to test the effect of δ correction on the accuracy of K_DP estimation.

In order to reduce the errors caused by inaccurate gate-matching, only the gates with a time difference of less than 30 s between the two radar observations were selected for calculation and comparison, from which a total of 4,578,385 points with Z_DR ≥ 1 dB were selected. The statistical results of four experiments are shown in

Table 2. Accuracy and error statistics of K_DP obtained from four tests.

	S-POL Test			Self-Consistency Test
Test	MAE	RMSE	CC	R2	RMSE
Exp1	0.74	1.14	0.73	0.60	0.96
Exp2	0.71	1.11	0.75	0.64	0.94
Exp3	0.73	1.16	0.73	0.62	0.95
Exp4	0.71	1.13	0.75	0.66	0.92

. These δ-corrected K_DPs obtained from both the LS and LP are more consistent with the S-POL K_DP. The self-consistent analysis shows a similar result; the determination coefficient of three polarimetric variables (Z_H, Z_DR, and K_DP) was improved after δ correction for both LS and LP—mainly due to the δ result in the overestimated K_DP at the front of the large raindrops region and the underestimated K_DP behind the large raindrops region. This effect was mitigated by the δ correction, and the accuracy of K_DP in the large raindrops region was improved.

Figure 9 shows the calculation results of Exp2 and Exp4, mainly showing the difference between the calculation of K_DPX by the LS method and LP method. Although the statistical errors of the two groups are close (as shown in Table 2), there are obvious differences in their distribution. Especially for the part of weak precipitation (low K_DP value), the random noise of Φ_DP may bring serious errors in the calculation of K_DP, which is reflected in the weak consistency between calculated K_DPX and low K_DPS, as well as K_DPX and low K_DPM, as shown in Figure 9a,c. By contrast, the weak physical constraints of LP ensure the non-negativity of K_DPX in the liquid precipitation, which is an important reason for the more accurate low K_DP than using LS (as shown in Figure 9b,d).

3.3.4. QPE Test

One of the important applications of K_DP is QPE; however, the noise of Φ_DP makes it difficult to accurately calculate K_DP in weak rainfall areas. Therefore, K_DP is generally not used to calculate the precipitation intensity in the weak rainfall area [32,33]. Theoretically, the noise of Φ_DP should be well suppressed via the δ correction and LP processing, and then the accurate K_DP in the weak rainfall area can be obtained. In this paper, we calculated QPE based on the R-K_DP relationship fitted by DSD, and then tested the accuracy of K_DP of four experiments based on the local rainfall gauges (874 sets of 1 h rainfall).

In order to test the accuracy of QPE for different precipitation intensities, the errors of weak rainfall cases with precipitation intensity ≤5 mm and moderate and strong rainfall cases with precipitation intensity >5 mm are tested, respectively. On the whole, the R(K_DP) calculated by LP combined with δ correction is the best (as shown in

Table 3. Error statistics of QPE by R (K_DP).

	Test	MAE (mm/h)	RMSE (mm/h)	RMAE (%)	CC
All cases	Exp1	4.51	7.02	59.18	0.78
	Exp2	4.51	6.98	59.19	0.79
	Exp3	3.61	6.32	47.37	0.89
	Exp4	3.60	6.27	47.19	0.89
Rainfall ≤5 mm/h	Exp1	2.20	3.35	96.44	0.31
	Exp2	2.19	3.33	96.22	0.32
	Exp3	0.98	1.33	43.12	0.58
	Exp4	0.97	1.31	42.57	0.59
Rainfall >5 mm/h	Exp1	7.50	9.92	51.65	0.77
	Exp2	7.51	9.86	51.70	0.78
	Exp3	7.00	9.44	48.23	0.82
	Exp4	6.99	9.37	48.12	0.83

).

Affected by noise, the relative mean absolute error (RMAE = 96.4) from the LS method in weak rainfall areas is far larger than its RMAE (51.7%) in the rainfall area above 5 mm/h. In comparison, the RMAE (42.6%) of the LP method in weak rainfall areas is even slightly better than that in moderate and strong rainfall areas (48.1%). The LP method can obtain a more accurate estimation of K_DP in weak rainfall areas and improve the application ability of K_DP in QPE (as shown in Figure 10).

With the δ correction, the accuracy of K_DP estimation was improved, and the error of QPE was reduced. The improvement in K_DP accuracy in weak rainfall areas was better than that in strong rainfall areas. However, for the LS method, in the part of the rainfall > 5 mm/h, Exp2 is slightly higher than Exp1 in RMAE. The reason is that strong rainfall is often accompanied by a large δ estimation, and the errors of Z_DR and calculation errors of δ would be brought into the estimation of K_DP. The LP method with physical constraints can better suppress these errors.

4. Discussion

The δ observed by S-, C-, and X-band weather radar at different temperatures for various raindrop sizes was simulated using the OTT PARSIVEL laser disdrometer. For comparison, in the liquid precipitation region, S-band radar was less affected by δ, and the δ in C- and X-bands varied sharply with raindrop sizes of 6 mm and 4 mm. Due to the influence of δ on K_DP calculation—mainly as a result of the variation in δ with radial distance—the Φ_DP of X-band weather radar observations is susceptible to δ during heavy precipitation, which further affects the K_DP calculations.

Based on the analysis of the physical properties of the polarimetric variables, both δ and Z_DR are highly correlated with the precipitation’s particle size, while they are insensitive to the particle number concentration. It is feasible to calculate and fit Z_DR and δ using DSD data. For X-band weather radar, the value of δ is small (about zero) at Z_DR < 1 dB, and there is a positive correlation between Z_DR and δ at Z_DR > 1 dB. The fitting result is basically consistent with δ = Z_DR^1.8 proposed by [25].

By simulating the radar-sounding data from disdrometer DSD measurements, it was found that for Z_DR within a 3 dB variation, there was local variation with a maximum of ±8° to Φ_DP and ±25.0°/km to K_DP. While this effect can be suppressed in cumulative precipitation, it has a large impact on local estimates of rain intensity. As the specific attenuation has a quasilinear relationship with K_DP—which is often used for attenuation correction of reflectivity—the δ may cause errors in K_DP, as well as having a negative effect on the attenuation correction. However, δ is not an integral variable, and its effect on the attenuation correction is local. Based on the polarimetric variables simulated from DSD, the effect of δ on the attenuation correction is not very significant in the holistic radial observation. The estimation of K_DP without δ correction shows excessive fluctuations in the Z_DR mutation region, which could be suppressed by fitting the Z_DR–δ relationship and δ elimination.

K_DP was calculated based on different calculation schemes using the observations of X-PAR deployed in Shenzhen, China. The Ф_DP preprocessing is generally achieved via filtering or reconstruction. Even if the expected value of K_DP is used as a physical constraint, the LP method for Φ_DP preprocessing can only be used as a weak constraint to avoid unreasonable jitter of K_DP. Although these methods have inhibitory effects on the jitter of Φ_DP due to δ, the influence of δ still exists, causing overestimation of Φ_DP at the front of the large raindrop area of the ray path, along with further overestimation and underestimation of K_DP in this region. With δ correction and subsequent filtering, the effects of δ could be better eliminated than with that of simple filtering. Both the estimation of K_DP via LS and LP could benefit from δ correction. This optimization was verified by the improved self-consistency of polarimetric variables, the correlation between K_DP calculations from S and X-band radar and the accuracy of QPE. These improvements are beneficial to the application of K_DP in fine analysis of cloud physics and QPE. Notably, the δ correction may introduce errors, and the statistical results of QPE show that the LP method is better than the simple filtering method in suppressing such errors.

The positive effect of δ correction on K_DP calculation was demonstrated by comparative test and analysis. Moreover, the comparison with S-POL shows that even though the beam width of X-PAR is wider, it still has a good detection performance, and the observation of X-PAR and S-POL are highly consistent, indicative of the relatively high potential for applications in radar network observations and radar mosaic.