Present-Day Surface Deformation in North-East Italy Using InSAR and GNSS Data
Abstract
:1. Introduction


Geological Setting
2. Materials and Methods
2.1. InSAR Processing
2.2. GNSS-InSAR Calibration
- (1)
- GPS phase reduction and generation of loosely constrained sub-networks solutions using GAMIT [106];
- (2)
- Combination of daily subnet solutions and realization of positions in specific reference frames using GLOBK [106];
- (3)
- Analysis of time-series using QOCA (URL: http://qoca.jpl.nasa.gov (accessed on 20 March 2023)).
- InSAR-GNSS temporal coverage overlapping;
- GNSS data continuity;
- InSAR-GNSS spatial colocation;
- Low spatial variability underlying the deformation field.
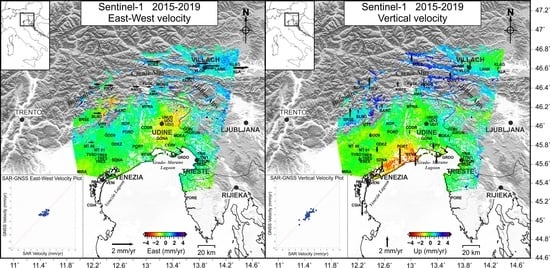
3. Results
4. Discussion
4.1. Tectonic Signals
4.2. Non-Tectonic Signals
5. Conclusions
- A positive vertical gradient of 1 mm/yr is observed between the Montello and the Prealps due to strain accumulation of the deepest portion of the thrusts. Specifically, we suggested the Bassano-Valdobbiandene thrust as the main one responsible for the interseismic signal detected in the area.
- The eastward (1 mm/yr) and upward (1–2 mm/yr) interseismic signals are accommodated by the Friulian Alpine-Dinaric faults (i.e., thrusts and strike-slip faults) in the area.
- The westward signal of 1 mm/yr recorded near Udine might be related to transcurrent-transpressive systems and buried thrusts, although further investigations and analysis are required.
- The velocity profiles traced across the Dinaric dextral strike-slip faults show an uplift and an eastward motion (about 1 mm/yr) that can be attributed to the tectonic activity of the Raša, Predjama, and Idrija faults.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grandin, R.; Doin, M.-P.; Bollinger, L.; Pinel-Puysségur, B.; Ducret, G.; Jolivet, R.; Sapkota, S.N. Long-term growth of the Himalaya inferred from interseismic InSAR measurement. Geology 2012, 40, 1059–1062. [Google Scholar] [CrossRef] [Green Version]
- Pezzo, G.; Tolomei, C.; Atzori, S.; Salvi, S.; Shabanian, E.; Bellier, O.; Farbod, Y. New kinematic constraints of the western Doruneh fault, northeastern Iran, from interseismic deformation analysis. Geophys. J. Int. 2012, 190, 622–628. [Google Scholar] [CrossRef] [Green Version]
- Karimzadeh, S.; Cakir, Z.; Osmanoğlu, B.; Schmalzle, G.; Miyajima, M.; Amiraslanzadeh, R.; Djamour, Y. Interseismic strain accumulation across the North Tabriz Fault (NW Iran) deduced from InSAR time series. J. Geodyn. 2013, 66, 53–58. [Google Scholar] [CrossRef]
- Liu, C.; Ji, L.; Zhu, L.; Zhao, C. InSAR-Constrained Interseismic Deformation and Potential Seismogenic Asperities on the Altyn Tagh. Remote Sens. 2018, 10, 943. [Google Scholar] [CrossRef] [Green Version]
- Fialko, Y. Interseismic strain accumulation and the earthquake potential on the southern San Andreas fault system. Nature 2006, 441, 968–971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, X.; Sandwell, D.T.; Smith-Konter, B. High-resolution interseismic velocity data along the San Andreas Fault from GPS and InSAR. J. Geophys. Res. Solid Earth 2013, 118, 369–389. [Google Scholar] [CrossRef] [Green Version]
- Chaussard, E.; Johnson, C.W.; Fattahi, H.; Bürgmann, R. Potential and limits of InSAR to characterize interseismic deformation independently of GPS data: Application to the southern San Andreas Fault system. Geochem. Geophys. Geosyst. 2016, 17, 1214–1229. [Google Scholar] [CrossRef] [Green Version]
- Wright, T.; Parsons, B.; Fielding, E. Measurement of interseismic strain accumulation across the North Anatolian Fault by satellite radar interferometry. Geophys. Res. Lett. 2001, 28, 2117–2120. [Google Scholar] [CrossRef]
- Walters, R.J.; Holley, R.J.; Parsons, B.; Wright, T.J. Interseismic strain accumulation across the North Anatolian Fault from Envisat InSAR measurements. Geophys. Res. Lett. 2011, 38, L05303. [Google Scholar] [CrossRef] [Green Version]
- Hussain, E.; Hooper, A.; Wright, T.J.; Walters, R.J.; Bekaert, D.P.S. Interseismic strain accumulation across the central North Anatolian Fault from iteratively unwrapped InSAR measurements. J. Geophys. Res. Solid Earth 2016, 121, 9000–9019. [Google Scholar] [CrossRef] [Green Version]
- Weiss, J.R.; Walters, R.J.; Morishita, Y.; Wright, T.J.; Lazecky, M.; Wang, H.; Hussain, E.; Hooper, A.J.; Elliott, J.R.; Rollins, C.; et al. High-Resolution Surface Velocities and Strain for Anatolia From Sentinel-1 InSAR and GNSS Data. Geophys. Res. Lett. 2020, 47, e2020GL087376. [Google Scholar] [CrossRef]
- Cheloni, D.; D’Agostino, N.; Selvaggi, G. Interseismic coupling, seismic potential, and earthquake recurrence on the southern front of the Eastern Alps (NE Italy). J. Geophys. Res. Solid Earth 2014, 119, 4448–4468. [Google Scholar] [CrossRef]
- Pezzo, G.; Merryman Boncori, J.P.; Visini, F.; Carafa, M.M.C.; Devoti, R.; Atzori, S.; Kastelic, V.; Berardino, P.; Fornaro, G.; Riguzzi, F.; et al. Interseismic Ground Velocities of the Central Apennines from GPS and SAR Measurements and Their Contribution to Seismic hazard Modelling: Preliminary Results of the ESA CHARMING Project. Misc. INGV 2015.
- Pezzo, G.; Petracchini, L.; Devoti, R.; Maffucci, R.; Anderlini, L.; Antoncecchi, I.; Billi, A.; Carminati, E.; Ciccone, F.; Cuffaro, M.; et al. Active Fold-Thrust Belt to Foreland Transition in Northern Adria, Italy, Tracked by Seismic Reflection Profiles and GPS Offshore Data. Tectonics 2020, 39, e2020TC006425. [Google Scholar] [CrossRef]
- Serpelloni, E.; Vannucci, G.; Anderlini, L.; Bennett, R.A. Kinematics, seismotectonics and seismic potential of the eastern sector of the European Alps from GPS and seismic deformation data. Tectonophysics 2016, 688, 157–181. [Google Scholar] [CrossRef]
- Anderlini, L.; Serpelloni, E.; Tolomei, C.; Marco De Martini, P.; Pezzo, G.; Gualandi, A.; Spada, G. New insights into active tectonics and seismogenic potential of the Italian Southern Alps from vertical geodetic velocities. Solid Earth 2020, 11, 1681–1698. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Wegmüller, U.; Rizzetto, F. Mapping regional land displacements in the Venice coastland by an integrated monitoring system. Remote Sens. Environ. 2005, 98, 403–413. [Google Scholar] [CrossRef]
- Tosi, L.; Teatini, P.; Strozzi, T.; Carbognin, L.; Brancolini, G.; Rizzetto, F. Ground surface dynamics in the northern Adriatic coastland over the last two decades. Rend. Lince 2010, 21, 115–129. [Google Scholar] [CrossRef]
- Tosi, L.; Teatini, P.; Strozzi, T. Natural versus anthropogenic subsidence of Venice. Sci. Rep. 2013, 3, 2710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osmanoğlu, B.; Dixon, T.H.; Wdowinski, S.; Cabral-Cano, E.; Jiang, Y. Mexico City subsidence observed with persistent scatterer InSAR. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 1–12. [Google Scholar] [CrossRef]
- Da Lio, C.; Tosi, L. Science of the Total Environment Land subsidence in the Friuli Venezia Giulia coastal plain, Italy: 1992–2010 results from SAR-based interferometry. Sci. Total Environ. 2018, 633, 752–764. [Google Scholar] [CrossRef]
- Del Soldato, M.; Farolfi, G.; Rosi, A.; Raspini, F.; Casagli, N. Subsidence Evolution of the Firenze–Prato–Pistoia Plain (Central Italy) Combining PSI and GNSS Data. Remote Sens. 2018, 10, 1146. [Google Scholar] [CrossRef] [Green Version]
- Polcari, M.; Albano, M.; Montuori, A.; Bignami, C.; Tolomei, C.; Pezzo, G.; Falcone, S.; La Piana, C.; Doumaz, F.; Salvi, S.; et al. InSAR Monitoring of Italian Coastline Revealing Natural and Anthropogenic Ground Deformation Phenomena and Future Perspectives. Sustainability 2018, 10, 3152. [Google Scholar] [CrossRef] [Green Version]
- Farolfi, G.; Bianchini, S.; Casagli, N. Integration of GNSS and Satellite InSAR Data: Derivation of Fine-Scale Vertical Surface Motion Maps of Po Plain, Northern Apennines, and Southern Alps, Italy. IEEE Trans. Geosci. Remote Sens. 2019, 57, 319–328. [Google Scholar] [CrossRef]
- Farolfi, G.; Del Soldato, M.; Bianchini, S.; Casagli, N. A procedure to use GNSS data to calibrate satellite PSI data for the study of subsidence: An example from the north-western Adriatic coast (Italy). Eur. J. Remote Sens. 2019, 52, 54–63. [Google Scholar] [CrossRef] [Green Version]
- Floris, M.; Fontana, A.; Tessari, G.; Mulè, M. Subsidence Zonation Through Satellite Interferometry in Coastal Plain Environments of NE Italy: A Possible Tool for Geological and Geomorphological Mapping in Urban Areas. Remote Sens. 2019, 11, 165. [Google Scholar] [CrossRef] [Green Version]
- Žibret, G.; Komac, M.; Jemec, M. PSInSAR displacements related to soil creep and rainfall intensities in the Alpine foreland of western Slovenia. Geomorphology 2012, 175–176, 107–114. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GPS/GNSS and radar interferometric data for a 3D surface displacement monitoring of landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Notti, D.; Calò, F.; Cigna, F.; Manunta, M.; Herrera, G.; Berti, M.; Meisina, C.; Tapete, D.; Zucca, F. A User-Oriented Methodology for DInSAR Time Series Analysis and Interpretation: Landslides and Subsidence Case Studies. Pure Appl. Geophys. 2015, 172, 3081–3105. [Google Scholar] [CrossRef] [Green Version]
- Aslan, G.; Foumelis, M.; Raucoules, D.; De Michele, M.; Bernardie, S.; Cakir, Z. Landslide Mapping and Monitoring Using Persistent Scatterer Interferometry (PSI) Technique in the French Alps. Remote Sens. 2020, 12, 1305. [Google Scholar] [CrossRef] [Green Version]
- Busetti, A.; Calligaris, C.; Forte, E.; Areggi, G.; Mocnik, A.; Zini, L. Non-Invasive Methodological Approach to Detect and Characterize High-Risk Sinkholes in Urban Cover Evaporite Karst: Integrated Reflection Seismics, PS-InSAR, Leveling, 3D-GPR and Ancillary Data. A NE Italian Case Study. Remote Sens. 2020, 12, 3814. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Atmos. 2007, 112, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Pezzo, G.; Palano, M.; Tolomei, C.; De Gori, P.; Calcaterra, S.; Gambino, P.; Chiarabba, C. Flank sliding: A valve and a sentinel for paroxysmal eruptions and magma ascent at Mount Etna, Italy. Geology 2020, 48, 1077–1082. [Google Scholar] [CrossRef]
- Beccaro, L.; Tolomei, C.; Gianardi, R.; Sepe, V.; Bisson, M.; Colini, L.; De Ritis, R.; Spinetti, C. Multitemporal and Multisensor InSAR Analysis for Ground Displacement Field Assessment at Ischia Volcanic Island (Italy). Remote Sens. 2021, 13, 4253. [Google Scholar] [CrossRef]
- Perski, Z.; Hanssen, R.; Wojcik, A.; Wojciechowski, T. InSAR analyses of terrain deformation near the Wieliczka Salt Mine, Poland. Eng. Geol. 2009, 106, 58–67. [Google Scholar] [CrossRef]
- Klemm, H.; Quseimi, I.; Novali, F.; Ferretti, A.; Tamburini, A. Monitoring horizontal and vertical surface deformation over a hydrocarbon reservoir by PSInSAR. First Break. 2010, 28, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Ab Latip, A.S.; Matori, A.; Aobpaet, A.; Din, A.H.M. Monitoring of offshore platform deformation with stanford method of Persistent Scatterer (StaMPS). Int. Conf. Sp. Sci. Commun. Iconsp. 2015, 2015, 79–83. [Google Scholar] [CrossRef]
- Gama, F.F.; Mura, J.G.; Paradella, W.R.; De Oliveira, C.G. Deformations Prior to the Brumadinho Dam Collapse Revealed by Sentinel-1 InSAR Data Using SBAS and PSI Techniques. Remote Sens. 2020, 12, 3664. [Google Scholar] [CrossRef]
- Kumar Maurya, V.; Dwivedi, R.; Ranjan Martha, T. Site scale landslide deformation and strain analysis using MT-InSAR and GNSS approach—A case study. Adv. Space Res. 2022, 70, 3932–3947. [Google Scholar] [CrossRef]
- Yalvac, S. Validating InSAR-SBAS results by means of different GNSS analysis techniques in medium- and high-grade deformation areas. Environ. Monit. Assess. 2020, 192, 120. [Google Scholar] [CrossRef]
- Li, Y. Analysis of GAMIT/GLOBK in high-precision GNSS data processing for crustal deformation. Earthq. Res. Adv. 2021, 1, 100028. [Google Scholar] [CrossRef]
- Nof, R.N.; Abelson, M.; Raz, E.; Magen, Y.; Atzori, S.; Salvi, S.; Baer, G. SAR Interferometry for Sinkhole Early Warning and Susceptibility Assessment along the Dead Sea, Israel. Remote Sens. 2019, 11, 89. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Jiang, W.; Zhang, J.; Li, B.; Yan, R.; Wang, X. Sentinel-1 SAR-Based coseismic deformation monitoring service for rapid geodetic imaging of global earthquakes. Nat. Hazards Res. 2021, 1, 11–19. [Google Scholar] [CrossRef]
- Castellarin, A.; Vai, G.B.; Cantelli, L. The Alpine evolution of the Southern Alps around the Giudicarie faults: A Late Cretaceous to Early Eocene transfer zone. Tectonophysics 2006, 414, 203–223. [Google Scholar] [CrossRef]
- Aoudia, A.; Saraò, A.; Bukchin, B.; Suhadolc, P. The 1976 Friuli (NE Italy) thrust faulting earthquake: A reappraisal 23 years later. Geophys. Res. Lett. 2000, 27, 577–580. [Google Scholar] [CrossRef]
- Pondrelli, S.; Ekström, G.; Morelli, A. Seismotectonic re-evaluation of the 1976 Friuli, Italy, seismic sequence. J. Seism. 2001, 5, 73–83. [Google Scholar] [CrossRef]
- Carulli, G.B.; Slejko, D. The 1976 Friuli, Italy, Earthquake. G. Geol. Appl. 2005, 1, 147–156. [Google Scholar] [CrossRef]
- Anselmi, M.; Govoni, A.; De Gori, P.; Chiarabba, C. Seismicity and velocity structures along the south-Alpine thrust front of the Venetian Alps (NE-Italy). Tectonophysics 2011, 513, 37–48. [Google Scholar] [CrossRef]
- Danesi, S.; Pondrelli, S.; Salimbeni, S.; Cavaliere, A.; Serpelloni, E.; Danecek, P.; Lovati, S.; Massa, M. Active deformation and seismicity in the Southern Alps (Italy): The Montello hill as a case study. Tectonophysics 2015, 653, 95–108. [Google Scholar] [CrossRef]
- Bressan, G.; Ponton, M.; Rossi, G.; Urban, S. Spatial organization of seismicity and fracture pattern in NE Italy and W Slovenia. J. Seism. 2016, 20, 511–534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. The Italian earthquake catalogue CPTI15. Bull. Earthq. Eng. 2020, 18, 2953–2984. [Google Scholar] [CrossRef]
- Carbognin, L.; Teatini, P.; Tomasin, A.; Tosi, L. Global change and relative sea level rise at Venice: What impact in term of flooding. Clim. Dyn. 2009, 35, 1055–1063. [Google Scholar] [CrossRef]
- D’Agostino, N.; Cheloni, D.; Mantenuto, S.; Selvaggi, G.; Michelini, A.; Zuliani, D. Strain accumulation in the southern Alps (NE Italy) and deformation at the northeastern boundary of Adria observed by CGPS measurements. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Vrabec, M.; Prešeren, P.P.; Stopar, B. GPS study (1996–2002) of active deformation along the Periadriatic fault system in northeastern Slovenia: Tectonic model. Geol. Carpathica 2006, 57, 57–65. [Google Scholar]
- Bechtold, M.; Battaglia, M.; Tanner, D.C.; Zuliani, D. Constraints on the active tectonics of the Friuli/NW Slovenia area from CGPS measurements and three-dimensional kinematic modeling. J. Geophys. Res. Solid Earth. 2009, 114, B03408. [Google Scholar] [CrossRef] [Green Version]
- Moulin, A.; Benedetti, L.; Rizza, M.; Jamšek Rupnik, P.; Gosar, A.; Bourlès, D.; Keddadouche, K.; Aumaître, G.; Arnold, M.; Guillou, V.; et al. The Dinaric fault system: Large-scale structure, rates of slip, and Plio-Pleistocene evolution of the transpressive northeastern boundary of the Adria microplate. Tectonics 2016, 35, 2258–2292. [Google Scholar] [CrossRef] [Green Version]
- Rossi, G.; Zuliani, D.; Fabris, P. Tectonophysics Long-term GNSS measurements from the northern Adria microplate reveal fault-induced fluid mobilization. Tectonophysics 2016, 690, 142–159. [Google Scholar] [CrossRef]
- Rossi, G.; Fabris, P.; Zuliani, D. Overpressure and Fluid Diffusion Causing Non-hydrological Transient GNSS Displacements. Pure Appl. Geophys. 2018, 175, 1869–1888. [Google Scholar] [CrossRef]
- Rossi, G.; Pastorutti, A.; Nagy, I.; Braitenberg, C.; Parolai, S. Recurrence of Fault Valve Behavior in a Continental Collision Area: Evidence From Tilt/Strain Measurements in Northern Adria. Front. Earth Sci. 2021, 9, 641416. [Google Scholar] [CrossRef]
- Stocchi, P.; Spada, G.; Cianetti, S. Isostatic rebound following the Alpine deglaciation: Impact on the sea level variations and vertical movements in the Mediterranean region. Geophys. J. Int. 2005, 162, 137–147. [Google Scholar] [CrossRef] [Green Version]
- Devoti, R.; Zuliani, D.; Braitenberg, C.; Fabris, P.; Grillo, B. Hydrologically induced slope deformations detected by GPS and clinometric surveys in the Cansiglio Plateau, southern Alps. Earth Planet. Sci. Lett. 2015, 419, 134–142. [Google Scholar] [CrossRef]
- Serpelloni, E.; Pintori, F.; Gualandi, A.; Scoccimarro, E.; Cavaliere, A.; Anderlini, L.; Belardinelli, M.E.; Todesco, M. Journal of Geophysical Research: Solid Earth Hydrologically Induced Karst Deformation: Insights From GPS Measurements in the Adria-Eurasia Plate Boundary Zone. J. Geophys. Res. Solid Earth 2018, 123, 4413–4430. [Google Scholar] [CrossRef]
- Pintori, F.; Serpelloni, E.; Longuevergne, L.; Garcia, A.; Faenza, L.; D’Alberto, L.; Gualandi, A.; Belardinelli, M.E. Mechanical Response of Shallow Crust to Groundwater Storage Variations: Inferences From Deformation and Seismic Observations in the Eastern Southern Alps, Italy. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020586. [Google Scholar] [CrossRef]
- Bock, Y.; Wdowinski, S.; Ferretti, A.; Novali, F.; Fumagalli, A. Recent subsidence of the Venice Lagoon from continuous GPS and interferometric synthetic aperture radar. Geochem. Geophys. Geosyst. 2012, 13, Q03023. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef] [Green Version]
- Vecchio, A.; Anzidei, M.; Serpelloni, E.; Florindo, F. Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100. Water 2019, 11, 1480. [Google Scholar] [CrossRef] [Green Version]
- Asch, K. IGME 5000:1:5 Million International Geological Map of Europe and Adjacent Areas -final version for the internet- BGR, Hannover. 2005. Available online: https://services.bgr.de/geologie/igme5000 (accessed on 15 March 2023).
- Nicolich, R.; Della Vedova, B.; Giustiniani, M.; Fantoni, R. Carta del sottosuolo Della Pianura Friulana. 2004. Available online: https://www.regione.fvg.it/rafvg/export/sites/default/RAFVG/ambiente-territorio/geologia/FOGLIA16/allegati/note_illustrative.pdf (accessed on 15 March 2023).
- Fantoni, R.; Franciosi, R. Tectono-sedimentary setting of the Po Plain and Adriatic foreland. Rend. Fis. Acc. Lincei. 2010, 21, 197–209. [Google Scholar] [CrossRef]
- Masetti, D.; Fantoni, R.; Romano, R.; Sartorio, D.; Trevisani, E. Tectonostratigraphic evolution of the Jurassic extensional basins of the eastern southern Alps and Adriatic foreland based on an integrated study of surface and subsurface data. Am. Assoc. Pet. Geol. Bull. 2012, 96, 2065–2089. [Google Scholar] [CrossRef]
- Mellere, D.; Stefani, C.; Angevine, C. Polyphase Tectonics through subsidence analysis: The Oligo-Miocene Venetian and Friuli Basin, north-east Italy. Basin Res. 2000, 12, 159–182. [Google Scholar] [CrossRef]
- Toscani, G.; Marchesini, A.; Barbieri, C.; Di Giulio, A.; Fantoni, R.; Mancin, N.; Zanferrari, A. The Friulian-Venetian Basin I: Architecture and sediment flux into a shared foreland basin. Ital. J. Geosci. 2016, 135, 444–459. [Google Scholar] [CrossRef]
- Bosellini, A.; Masetti, D.; Sarti, M. A Jurassic “Tongue of the Ocean” infilled with oolitic sands: The Belluno Trough, Venetian Alps, Italy. Mar. Geol. 1981, 44, 59–95. [Google Scholar] [CrossRef]
- Placer, L.; Vrabec, M.; Celarc, B. The bases for understanding of the NW Dinarides and Istria Peninsula tectonics. Geologija 2010, 53, 55–86. [Google Scholar] [CrossRef]
- Doglioni, C.; Bosellini, A. Eoalpine and mesoalpine tectonics in the Southern Alps. Geol. Rundsch. 1987, 76, 735–754. [Google Scholar] [CrossRef]
- Castellarin, A.; Cantelli, L. Neo-Alpine evolution of the Southern Eastern Alps. J. Geodyn. 2000, 30, 251–274. [Google Scholar] [CrossRef]
- Bressan, G.; Bragato, P.L.; Venturini, C. Stress and Strain Tensors Based on Focal Mechanisms in the Seismotectonic Framework of the Friuli-Venezia Giulia Region (Northeastern Italy). Bull. Seism. Soc. Am. 2003, 93, 1280–1297. [Google Scholar] [CrossRef]
- Vrabec, M.; Fodor, L. Late Cenozoic tectonics of Slovenia: Structural styles at the northeastern corner of the Adriatic microplate. In The Adria Microplate: GPS Geodesy, Tectonics and Hazards; Springer: Dordrecht, The Netherlands, 2006; pp. 151–168. [Google Scholar] [CrossRef]
- Galadini, F.; Poli, M.E.; Zanferrari, A. Seismogenic sources potentially responsible for earthquakes with M≥ 6 in the eastern Southern Alps (Thiene-Udine sector, NE Italy). Geophys. J. Int. 2005, 161, 739–762. [Google Scholar] [CrossRef] [Green Version]
- Burrato, P.; Poli, M.E.; Vannoli, P.; Zanferrari, A.; Basili, R.; Galadini, F. Sources of Mw 5+ earthquakes in northeastern Italy and western Slovenia: An updated view based on geological and seismological evidence. Tectonophysics 2008, 453, 157–176. [Google Scholar] [CrossRef]
- Bressan, G.; Barnaba, C.; Bragato, P.; Ponton, M.; Restivo, A. Revised seismotectonic model of NE Italy and W Slovenia based on focal mechanism inversion. J. Seism. 2018, 22, 1563–1578. [Google Scholar] [CrossRef]
- Atanackov, J.; Jamšek Rupnik, P.; Jež, J.; Celarc, B.; Novak, M.; Milanič, B.; Markelj, A.; Bavec, M.; Kastelic, V. Database of Active Faults in Slovenia: Compiling a New Active Fault Database at the Junction Between the Alps, the Dinarides and the Pannonian Basin Tectonic Domains. Front. Earth Sci. 2021, 9, 604388. [Google Scholar] [CrossRef]
- DISS Working Group Database of Individual Seismogenic Sources (DISS), Version 3.3.0: A Compilation of Potential Sources for Earthquakes Larger than M 5.5 in Italy and Surrounding Areas. 2021. Available online: https://diss.ingv.it/ (accessed on 15 March 2023).
- Bajc, J.; Aoudia, A.; Saraò, A.; Suhadolc, P. The 1998 Bovec-Krn Mountain (Slovenia) Earthquake Sequence. Geophys. Res. Lett. 2001, 28, 1839–1842. [Google Scholar] [CrossRef]
- Poli, M.E.; Peruzza, L.; Rebez, A.; Slejko, D. New seismotectonic evidence from the analysis of the 1976–1977 and 1977–1999 seismicity in Friuli (NE Italy). Boll. Geofis. Teor. Appl. 2002, 43, 53–78. [Google Scholar]
- Bressan, G.; Gentile, G.F.; Perniola, B.; Urban, S. The 1998 and 2004 Bovec-Krn (Slovenia) seismic sequences: Aftershock pattern, focal mechanisms and static stress changes. Geophys. J. Int. 2009, 179, 231–253. [Google Scholar] [CrossRef] [Green Version]
- Poli, M.E.; Zanferrari, A. The Seismogenic Sources of the 1976 Friuli Earthquakes: A new seismotectonic model for the Friuli area. Boll. Geofis. Teor. Appl. 2018, 59, 463–480. [Google Scholar] [CrossRef]
- Tosi, L.; Teatini, P.; Carbognin, L.; Brancolini, G. Using high resolution data to reveal depth-dependent mechanisms that drive land subsidence: The Venice coast, Italy. Tectonophysics 2009, 474, 271–284. [Google Scholar] [CrossRef]
- Brambati, A.; Carbognin, L.; Quaia, T.; Teatini, P.; Tosi, L. The Lagoon of Venice: Geological setting, evolution and land subsidence. Episodes 2003, 26, 264–265. [Google Scholar] [CrossRef]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Foumelis, M.; Blasco, J.M.D.; Desnos, Y.L.; Engdahl, M.; Fernández, D.; Veci, L.; Lu, J.; Wong, C. ESA SNAP—Stamps integrated processing for Sentinel-1 persistent scatterer interferometry. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1364–1367. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear Subsidence Rate Estimation Using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatters in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Doin, M.-P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Farolfi, G.; Piombino, A.; Catani, F. Fusion of GNSS and Satellite Radar Interferometry: Determination of 3D Fine-Scale Map of Present-Day Surface Displacements in Italy as Expressions of Geodynamic Processes. Remote Sens. 2019, 11, 394. [Google Scholar] [CrossRef] [Green Version]
- Del Soldato, M.; Confuorto, P.; Bianchini, S.; Sbarra, P.; Casagli, N. Review of Works Combining GNSS and InSAR in Europe. Remote Sens. 2021, 13, 1684. [Google Scholar] [CrossRef]
- Cigna, F.; Ramírez, R.E.; Tapete, D. Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data. Remote Sens. 2021, 13, 4800. [Google Scholar] [CrossRef]
- Serpelloni, E.; Cavaliere, A.; Martelli, L.; Pintori, F.; Anderlini, L.; Borghi, A.; Randazzo, D.; Bruni, S.; Devoti, R.; Perfetti, P.; et al. Surface Velocities and Strain-Rates in the Euro-Mediterranean Region From Massive GPS Data Processing. Front. Earth Sci. 2022, 10, 907897. [Google Scholar] [CrossRef]
- Devoti, R.; D’Agostino, N.; Serpelloni, E.; Pietrantonio, G.; Riguzzi, F.; Avallone, A.; Cavaliere, A.; Cheloni, D.; Cecere, G.; D’Ambrosio, C.; et al. A Combined Velocity Field of the Mediterranean Region. Ann. Geophys. 2017, 60, S0217. [Google Scholar] [CrossRef] [Green Version]
- Herring, T.A.; King, R.W.; Mcclusky, S.C.; Sciences, P. Introduction to GAMIT/GLOBK, Release 10.6; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015. [Google Scholar]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-11. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Solid Earth. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P. On the derivation of coseismic displacement fields using differential radar interferometry: The Landers earthquake. In Proceedings of the 1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 286–288. [Google Scholar] [CrossRef]
- Feng, G.; Ding, X.; Li, Z.; Mi, J.; Zhang, L.; Omura, M. Calibration of an InSAR-Derived Coseimic Deformation Map Associated With the 2011 Mw-9.0 Tohoku-Oki Earthquake. IEEE Geosci. Remote Sens. Lett. 2012, 9, 302–306. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, Q01007. [Google Scholar] [CrossRef]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef] [Green Version]
- Mehrabi, H.; Voosoghi, B.; Motagh, M.; Hanssen, R.F. Three-Dimensional Displacement Fields from InSAR through Tikhonov Regularization and Least-Squares Variance Component Estimation. J. Surv. Eng. 2019, 145, 4019011. [Google Scholar] [CrossRef] [Green Version]
- Merlini, S.; Doglioni, C.; Fantoni, R.; Ponton, M. Analisi strutturale lungo un profilo geologico tra la linea Fella-Sava e l’avampaese adriatico (Friuli Venezia Giulia-Italia). Mem. Della Soc. Geol. Ital. 2002, 57, 293–300. [Google Scholar]
- Sternai, P.; Sue, C.; Husson, L.; Serpelloni, E.; Becker, T.W.; Willett, S.D.; Faccenna, C.; Di Giulio, A.; Spada, G.; Jolivet, L.; et al. Present-day uplift of the European Alps: Evaluating mechanisms and models of their relative contributions. Earth-Sci. Rev. 2019, 190, 589–604. [Google Scholar] [CrossRef]
- Barba, S.; Finocchio, D.; Sikdar, E.; Burrato, P. Modelling the interseismic deformation of a thrust system: Seismogenic potential of the Southern Alps. Terra Nova 2013, 25, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Brancolini, G.; Civile, D.; Donda, F.; Tosi, L.; Zecchin, M.; Volpi, V.; Rossi, G.; Sandron, D.; Ferrante, G.M.; Forlin, E. New insights on the Adria plate geodynamics from the northern Adriatic perspective. Mar. Pet. Geol. 2019, 109, 687–697. [Google Scholar] [CrossRef]
- Benedetti, L.; Tapponnier, P.; King, G.C.P.; Meyer, B.; Manighetti, I. Growth folding and active thrusting in the Montello region, Veneto, northern Italy. J. Geophys. Res. Solid Earth 2000, 105, 739–766. [Google Scholar] [CrossRef]
- Delacourt, C.; Briole, P.; Achache, J. Tropospheric corrections of SAR interferograms with strong topography. Application to Etna. Geophys. Res. Lett. 1998, 25, 2849–2852. [Google Scholar] [CrossRef]
- Patricelli, G.; Poli, M.E.; Cheloni, D. Structural Complexity and Seismogenesis: The Role of the Transpressive Structures in the 1976 Friuli Earthquakes (Eastern Southern Alps, NE Italy). Geosciences 2022, 12, 227. [Google Scholar] [CrossRef]
- Viscolani, A.; Grützner, C.; Diercks, M.; Reicherter, K.; Ustaszewski, K. Late Quaternary Tectonic Activity of the Udine-Buttrio Thrust, Friulian Plain, NE Italy. Geosciences 2020, 10, 84. [Google Scholar] [CrossRef] [Green Version]
- Kastelic, V.; Vrabec, M.; Cunningham, D.; Gosar, A. Neo-Alpine structural evolution and present-day tectonic activity of the eastern Southern Alps: The case of the Ravne Fault, NW Slovenia. J. Struct. Geol. 2008, 30, 963–975. [Google Scholar] [CrossRef]
- Kastelic, V.; Carafa, M.M.C. Fault slip rates for the active External Dinarides thrust-and-fold belt. Tectonics 2012, 31, TC3019. [Google Scholar] [CrossRef] [Green Version]
- Vičič, B.; Aoudia, A.; Javed, F.; Foroutan, M.; Costa, G. Geometry and mechanics of the active fault system in western Slovenia. Geophys. J. Int. 2019, 217, 1755–1766. [Google Scholar] [CrossRef]
- Grützner, C.; Aschenbrenner, S.; Jamšek Rupnik, P.; Reicherter, K.; Saifelislam, N.; Vičič, B.; Vrabec, M.; Welte, J.; Ustaszewski, K. Holocene surface-rupturing earthquakes on the Dinaric Fault System, western Slovenia. Solid Earth 2021, 12, 2211–2234. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Cecconi, G.; Rosselli, R.; Libardo, S. Resolving land subsidence within the Venice Lagoon by persistent scatterer SAR interferometry. Phys. Chem. Earth 2012, 40–41, 72–79. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef] [Green Version]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Areggi, G.; Pezzo, G.; Merryman Boncori, J.P.; Anderlini, L.; Rossi, G.; Serpelloni, E.; Zuliani, D.; Bonini, L. Present-Day Surface Deformation in North-East Italy Using InSAR and GNSS Data. Remote Sens. 2023, 15, 1704. https://doi.org/10.3390/rs15061704
Areggi G, Pezzo G, Merryman Boncori JP, Anderlini L, Rossi G, Serpelloni E, Zuliani D, Bonini L. Present-Day Surface Deformation in North-East Italy Using InSAR and GNSS Data. Remote Sensing. 2023; 15(6):1704. https://doi.org/10.3390/rs15061704
Chicago/Turabian StyleAreggi, Giulia, Giuseppe Pezzo, John Peter Merryman Boncori, Letizia Anderlini, Giuliana Rossi, Enrico Serpelloni, David Zuliani, and Lorenzo Bonini. 2023. "Present-Day Surface Deformation in North-East Italy Using InSAR and GNSS Data" Remote Sensing 15, no. 6: 1704. https://doi.org/10.3390/rs15061704
APA StyleAreggi, G., Pezzo, G., Merryman Boncori, J. P., Anderlini, L., Rossi, G., Serpelloni, E., Zuliani, D., & Bonini, L. (2023). Present-Day Surface Deformation in North-East Italy Using InSAR and GNSS Data. Remote Sensing, 15(6), 1704. https://doi.org/10.3390/rs15061704