Next Article in Journal
A Partial Reconstruction Method for SAR Altimeter Coastal Waveforms Based on Adaptive Threshold Judgment
Next Article in Special Issue
Accuracy Enhancement and Feature Extraction for GNSS Daily Time Series Using Adaptive CEEMD-Multi-PCA-Based Filter
Previous Article in Journal
Breach Progression Observation in Rockfill Dam Models Using Photogrammetry
Previous Article in Special Issue
Research on the Performance of an Active Rotating Tropospheric and Stratospheric Doppler Wind Lidar Transmitter and Receiver
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 6
10.3390/rs15061716
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Weakening the Flicker Noise in GPS Vertical Coordinate Time Series Using Hybrid Approaches

by
Bing Yang
,
Zhiqiang Yang
*,
Zhen Tian
and
Pei Liang
College of Geological Engineering and Geomatics, Chang’an University, Xi’an 710054, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(6), 1716; https://doi.org/10.3390/rs15061716
Submission received: 14 January 2023 / Revised: 18 March 2023 / Accepted: 20 March 2023 / Published: 22 March 2023
(This article belongs to the Special Issue Remote Sensing in Space Geodesy and Cartography Methods)
Browse Figures
Review Reports Versions Notes

Abstract

:
Noises in the GPS vertical coordinate time series, mainly including the white and flicker noise, have been proven to impair the accuracy and reliability of GPS products. Various methods were adopted to weaken the white and flicker noises in the GPS time series, such as the complementary ensemble empirical mode decomposition (CEEMD), wavelet denoising (WD), and variational mode decomposition (VMD). However, a single method only works at a limited frequency band of the time series, and the corresponding denoising ability is insufficient, especially for the flicker noise. Hence, in this study, we try to build two combined methods: CEEMD & WD and VMD & WD, to weaken the flicker noise in the GPS positioning time series from the Crustal Movement Observation Network of China. First, we handled the original signal using CEEMD or VMD with the appropriate parameters. Then, the processed signal was further denoised by WD. The results show that the average flicker noise in the time series was reduced from 19.90 mm/year0.25 to 2.8 mm/year0.25. This relates to a reduction of 86% after applying the two methods to process the GPS data, which indicates our solutions outperform CEEMD by 6.84% and VMD by 16.88% in weakening the flicker noise, respectively. Those apparent decreases in the flicker noises for the two combined methods are attributed to the differences in the frequencies between the WD and the other two methods, which were verified by analyzing the power spectrum density (PSD). With the help of WD, CEEMD & WD and VMD & WD can identify more flicker noise hidden in the low-frequency signals obtained by CEEMD and VMD. Finally, we found that the two combined methods have almost identical effects on removing the flicker noise in the time series for 226 GPS stations in China, testified by the Wilcoxon rank sum test.

Graphical Abstract

1. Introduction

In the past two decades, the Global Positioning System (GPS) has produced a dense and accurate set of observations for crustal motion and provided essential constraints on tectonics, rheological structure, and geodynamics (e.g., plate motion [1,2,3], crustal deformation [4,5,6]). The daily coordinate time series from a reprocessing of GPS measurements are also helpful for refining the terrestrial reference frame [7,8] and better understanding surface mass loading [9,10,11] and water storage [12,13]. However, the millimeter-level flicker and white noises in the GPS coordinate time series (see Appendix A) are detrimental to the estimations of velocity and their uncertainties [14,15]. The noise is usually caused by the environment (e.g., the surrounding topography, upper atmosphere conditions) of the GPS site and the processing (e.g., the employed models) of the GPS data [16,17,18]. Therefore, weakening the noise in the GPS time series is essential to improving data reliability and can further provide substantial constraints on regional tectonics and rheology.
The non-linear and non-stationary noises involved in the GPS time series can be detected and weakened by various approaches. Empirical Mode Decomposition (EMD), a data-driven approach, decomposes the non-stationary and non-linear signals adaptively into a finite number of intrinsic mode function (IMF) components using all the local extrema [19]. Based on the EMD, Montillet et al. [20] proposed an algorithm to estimate the white noise in the GPS time series and demonstrated its efficiency. However, EMD constructs the envelopes by utilizing all the local extremes, causing a mode mixing problem that an IMF includes incorporates signals with multiple scales [21]. To overcome this shortcoming, the ensemble EMD (EEMD) and complementary EEMD (CEEMD) were proposed by adding the white noises [21,22]. Peng et al. [23] and Li et al. [24] used EEMD and CEEMD to decompose the GPS time series into IMFs and focus on the extraction of seasonal signals not involving noise characteristics. The second method, Wavelet Denoising (WD), usually decomposes the signal into the wavelet coefficients of multiple high-frequency components and a low-frequency component, then performs a thresholding operation on the high-frequency coefficients, and finally reconstructs the threshold coefficients with the low-frequency coefficients to obtain a denoising signal [25,26,27]. Due to multiresolution decomposition, WD was applied to remove white noise and assist the maximum likelihood estimate (MLE) method in estimating the GPS coordinate time series [28]. Wu et al. [16] proposed a wavelet algorithm, merging Shannon entropy and wavelet thresholding, to remove white noise and flicker noise from the GPS position time series, and proved the comprehension of hybrid thresholding in removing white noise and flicker noise. Kaczmarek and Kontny [29] used the inverse continuous wavelet transform to model the GPS measurements and proved that the nature of noise could be analyzed by the wavelet algorithm. Those studies all indicate that the WD can be an efficient tool for removing noise from the GPS time series. The third method, Variational Mode Decomposition (VMD), decomposes the original signals robustly into IMF components with a specified center frequency by a partially variational approach, which avoids the mode mixing problem during the EMD iterations [30]. For the GPS signals, Sivavaraprasad et al. [31] investigated the application of VMD on GPS signals to research the influences of ionospheric scintillations and its potentiality in mitigating the ionospheric amplitude scintillation effects. Shen et al. [32] further confirmed the ability of VMD to extract seasonal signals from GPS and GRACE data. Those studies only focus on the decomposition ability of VMD and ignore its denoising performance for the GPS observations.
Overall, previous studies indicate that the three decomposition methods, CEEMD, VMD, and WD, are feasible for removing white noise and partial flicker noise from the GPS data [16,24,33]. However, the non-stationary nature of the flicker noise leads to residual flicker noises still hidden in the signal components decomposed by the CEEMD or VMD methods and the low-frequency signal obtained by the WD method [16,33]. Studies have suggested that it is challenging to eliminate the flicker noise from the GPS data by a single denoising approach [16,33]. With the help of the multi-scale feature, WD can decompose the low-frequency signal components obtained by VMD or CEEMD to extract low-frequency flicker noise. Hence, combining the above different methods may be a reasonable and effective way to extract the flicker noise in the GPS data [33,34]. Additionally, the VMD was usually used to estimate the GPS seasonal signals rather than the observation noises [32]. It is necessary to investigate its denoising ability for the GPS time series.
In this study, we propose two hybrid algorithms based on the wavelet denoising approach to reduce flicker noise in the GPS time series. We first introduce the three decomposition methods, CEEMD, VMD, and WD, and obtain their optimal denoising parameters. Secondly, the two WD-based combined algorithms, CEEMD & WD and VMD & WD, are proposed to remove the noises in the GPS data. Finally, the two hybrid approaches to reduce flicker noise are further assessed by the 226 GPS stations from the Crustal Movement Observation Network of China (CMONOC).

2. Methods

In this section, we introduce the principles and processes of the three decomposition methods: CEEMD, VMD, and WD. Then, the two combined methods, CEEMD & WD and VMD &WD, are presented in detail. For assessing and comparing the abilities of the combined methods, we also build an indicator, the level of the flicker noises, derived from the trajectory model based on the study of Bos et al. [35] and Klos et al. [36].

2.1. The Principles of CEEMD, WD, and VMD

2.1.1. Complementary Ensemble Empirical Mode Decomposition (CEEMD)

CEEMD is an enhanced EMD method assisted by a pair of white noise, which is proposed to solve the mode mixing problem for EMD and to remove the residual white noise in the EEMD algorithm [22]. The denoising steps of CEEMD are the following [24]: (1) the positive and negative white noise are added to the original data; (2) EMD is applied to decompose the two new signals, and the positive and negative ensemble intrinsic mode functions (IMFs) are achieved; (3) the IMFs of the original signal are calculated by averaging the corresponding positive and negative modes; and (4) a criterion is used to determine the noise components from IMFs.

2.1.2. Wavelet Denoising (WD)

Wavelet denoising (WD) is an essential application of wavelet analysis, in which the wavelet coefficients are handled by a threshold rule in the decomposition and reconstruction of the signal through the wavelet transform. The procedure of WD can be accomplished in three stages [16,37,38]: firstly, the noisy signal is decomposed by applying the wavelet transform with orthogonal scaling functions and wavelet functions to obtain a sequence of wavelet coefficients comprising high-frequency and low-frequency components. Then, a thresholding rule is used for high-frequency coefficients. Finally, the denoised signal is derived by reconstructing the coefficients using the inverse wavelet transform operation.

2.1.3. Variational Mode Decomposition (VMD)

Following a non-recursive method, the variational mode decomposition (VMD) could adaptively decompose a multi-frequency signal into a number of IMFs, which are limited to a band in the spectral domain [30]. VMD can decompose the GPS coordinate time series into several modes u k K = 1 , 2 … K around their respective center frequencies w k [31,32]. In searching for u k and w k , a constrained variational problem needs to be resolved by a quadratic penalty and Lagrangian multipliers [39]. Note that the number K is set in advance. A detailed principle of the VMD algorithm can be found in Dragomiretskiy and Zosso [30]. Similar to CEEMD, the denoising procedure of VMD utilizes a criterion to differentiate the components from signal and noise.

2.2. Parameters of CEEMD, VMD, and WD

We selected the vertical time series at an IGS station, BJSH, with a lower flicker noise (18.85 mm/year0.25) as the test sample to find the optimal settings for the denoising methods for the CEEMD, VMD, and WD. In addition, the components, decomposed by CEEMD and VMD, require a criterion to define the noise and signal components as mentioned above. We also introduce the Hausdorff distance as the filtering criterion (see Appendix B), which was proved to be an efficient and robust criterion [40].
For CEEMD, β could be a critical element in the denoising process; we thus varied β from 0.1 to 1 to obtain the best values (Figure 1). We found that both the original and added white noise were removed, which is consistent with the conclusion of Yeh et al. [22]. The amplitude of flicker noise of the denoised coordinate time series of the BJSH station achieved a minimum of 1.85 mm/year0.25 with β being equal to 4 (Figure 1a). Therefore, a value of 0.4 was adopted in this research.
In the VMD, a key parameter, the number of decomposition modes ( K ) usually needs to be determined before the processing. We conducted a test varying K from 3 to 11 following the study of Liu et al. [41]. The amplitude of flicker noise for the denoised coordinate time series of BJSH station using VMD with different K are shown in Figure 1b. We discovered that K = 4 resulted in a minimum amplitude of flicker noise of 6.14 mm/year0.25. Therefore, 4 was employed as an appropriate decomposition mode for VMD.
In addition, the performance of the WD method usually depends on the wavelet, decomposed level, and thresholding selection rule [25,26,42]. Therefore, we investigated various combinations of factors that were widely used in the wavelets, including bior3.5, db4, coif3, and sym5, and the decomposed levels ranging from 1 to 20, and the thresholding selection rules such as Rigrsure, Sqtwolog, Heursure, and Minimaxi [38]. As shown in Figure 1c, the amplitude of the semi-annual signals in the denoised time series ranges from 1.30 mm to 1.60 mm when the level is less than 7 but drops sharply to a maximum of 0.40 mm with increasing levels. It suggests that a larger decomposition level causes an unreasonable removal of the seasonal signals in GPS measurement. Meanwhile, with the determined thresholding selection rule and the wavelet, the amplitude of flicker noise decreases as the number of decomposition layers grows. Hence, the superlative decomposed level is set to 6. In terms of threshold selection (Figure 1d), the average noise amplitudes for Sqtwolog and Heursure are 2.59 mm/year0.25 and 2.78 mm/year0.25, which are substantially lower than those for Rigrsure (8.00 mm/year0.25) and Minimaxi (4.73 mm/year0.25). This is mainly due to the differences that Sqtwolog and Heursure are applied to all wavelet coefficients, unlike the partial thresholds of the others [38]. When the threshold method is identical, coif3 yields a smaller noise amplitude than other wavelets (Figure 1d). Hence, we adopted coif3 wavelet, 6 for decomposition level and Sqtwolog for the thresholding selection in the following denoising process.

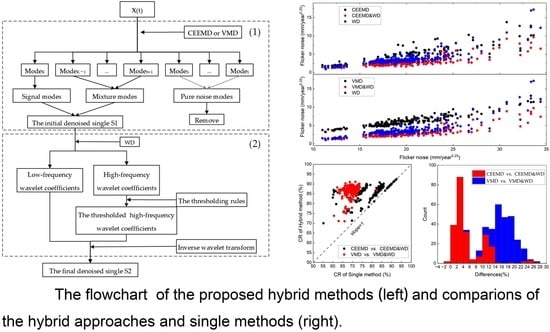
2.3. Proposed Mixture Methods

The two combined methods proposed in this study, CEEMD & WD and VMD & WD, are performed in two steps: (1) CEEMD or VMD is first used to decompose the GPS coordinate time series into noise modes and signal modes with the help of the Hausdorff distance; (2) then, the WD is used to further denoise the signal modes.
The detailed procedure of the hybrid approaches for the denoising process can be described as follows (Figure 2):
i.
The coordinate time series of a GPS station, X t , is decomposed into K modes by CEEMD or VMD.
ii.
Based on the criterion of the Hausdorff distance, the modes are classified into two types, including pure noise modes and signal modes.
iii.
The pure noise modes are eliminated directly and signal modes are reconstructed to obtain the initial denoised signal S 1 .
iv.
WD is performed to decompose the signal S 1 , then the high-frequency and low-frequency wavelet coefficients are obtained by wavelet transform.
v.
The thresholding rules are applied to high-frequency wavelet coefficients.
vi.
The thresholded high-frequency wavelet coefficients and low-frequency wavelet coefficients are reconstructed by the inverse wavelet transform to obtain the final denoised signal S 2 .

2.4. The Trajectory Model of the GPS Time Series

The GPS time series is the sum of a trend term, a seasonal term, and stochastic noise [43,44]. Their trajectory model can be described as follows [43]:
y t = a + v t − t R + ∑ k = 1 n F s k cos ω k t + φ k + ε t
where y t is the position at time t ; a and t R are the reference position and epoch; v is the station velocity; n F is the number of frequencies used to model the nonlinear variations cycle, s k and φ k are amplitude and phase of the frequency, annual ( k = 1 ) and semi-annual ( k = 2 ) variations are considered in this study; ε t is random noise.
In this study, MLE was used to accurately estimate the parameters with a noise model [35]. The combination of the white noise and flicker noise was proved to be a better description for the noise in the GPS time series [16,45,46]. Therefore, we adopt this model to calculate the amplitudes of the flicker noise in the vertical components before and after the noise reduction, based on the maximum likelihood estimation.

3. Data and Experimental Design

3.1. GPS Data

In this study, the daily vertical coordinate time series of 226 CMONOC GPS stations (Figure 3), spanning from 2010 to 2020, are employed. Among these, the tracking data of 19 stations are available until September 2019, while for 200 more stations, observations could be retrieved until December 2020, corresponding to a mean duration of 10.35 and 7.75 years, respectively. The observation spans of the remaining 7 stations range from 4.57 years to 9.98 years. Long observations ensure reliable estimations of parameters in the trajectory model of GPS stations [35,47]. The detailed strategies of GPS data processing can be found in the study by Hao et al. [9].
Due to the observation environments (e.g., instruments and earthquakes) and data processing, there are inevitable outliers and gaps in the GPS coordinate time series, affecting the denoising process. Therefore, before denoising the 226 GPS time series, a pre-processing procedure was conducted to eliminate the outliers and gaps. Firstly, in order to eliminate the outliers induced by numerous causes, the interquartile range (IQR) approach was applied [18,35]. Then, considering the constraints of denoising methods, missing data were interpolated using segment cubic Hermite interpolation, which was typically performed to cover the gaps [48,49]. Figure 4. represents the vertical time series of three typical GPS sites before and after conducting the pre-processing procedure.

3.2. Experimental Design

A series of experiments were designed to evaluate the improvement in the new hybrid methods on denoising GPS coordinate time series. To start, two hybrid algorithms, CEEMD & WD and VMD & WD, were utilized to denoise the coordinate time series of 226 GPS sites. In order to compare the capabilities of the mixed methods, CEEMD, VMD, and WD methods were also applied. All parameters of the subsequent methods involved in this process were obtained from the previous parts. Then, the maximum likelihood estimation method was used to estimate the noise amplitudes, and the variations in the levels of flicker noise were quantified and analyzed.
In order to facilitate the subsequent analysis, the denoised results are represented using corresponding methods. The result obtained before denoising is referred to as Raw.

4. Results

4.1. Flicker Noises in the GPS Time Series

The scatter plot in Figure 5 illustrates the geographical distribution and magnitudes of flicker noise at the 226 investigated GPS sites evaluated using six strategies. The results indicate that the minimal and maximal amplitudes of flicker noise are 10.99 mm/year0.25 and 34.38 mm/year0.25, respectively, with an average of 19.90 mm. Most stations in northwest, south, and northeast of China, as well as locations adjacent to the South China Sea, have amplitudes between 15.00 mm/year0.25 and 30.00 mm/year0.25. By comparison, those of stations in eastern and mid-China range from 10.00 mm/year0.25 to 15.00 mm/year0.25, and the poorer observing environments around eight stations resulted in flicker noise exceeding 30 mm/year0.25. Additionally, 207 stations, accounting for 91.6% of total stations, are characterized by an amplitude of flicker noise more significant than 15 mm/year0.25. Among these, the number of stations with an amplitude of 15–20 mm/year0.25 is 111, whereas 75 stations experience an amplitude of 20–25 mm/year0.25. The amplitudes of 19 and 8 stations range between the amplitudes of 10–15 mm/year0.25 and 30–35 mm/year0.25, respectively.
Figure 5 exhibits that the distribution of flicker noise for the four strategies is similar to Raw, but with significantly lower amplitude after subtracting the bouncing noise from the GPS coordinate time series. The averages of flicker noise for 226 GPS stations are 3.92 mm/year0.25 for CEEMD, 2.78 mm/year0.25 for CEEMD & WD, 6.1 mm/year0.25 for VMD, 2.82 mm/year0.25 for VMD & WD, and 3.84 mm/year0.25 for WD, respectively, all of which are notably lower than the Raw. For CEEMD, 104 stations have flicker noise of less than 3 mm/year0.25, 76 stations have flicker noise between 3 and 5 mm/year0.25, and 45 stations have flicker noise more remarkable than 5 mm/year0.25 at a level of 5–8 mm/year0.25. All stations for VMD have a flicker noise level of 3–12 mm/year0.25. There are 48 stations with amplitudes between 3 and 5 mm/year0.25, and 163 GPS stations have results between 5 mm/year0.25 and 9 mm/year0.25, accounting for about 72.12% of the stations. For both hybrid methodologies, amplitudes of flicker noise are limited to 10 mm/year0.25, and 211 stations, representing almost 93.36% of total sites, do not exceed 5 mm/year0.25. In detail, 138 stations show a flicker noise between 3 and 4 mm/year0.25 after denoising with CEEMD & WD, while 144 stations show a noise in this range after denoising with VMD & WD.
We discovered that the levels and geographic distributions of flicker noise are analogous after applying CEEMD and WD, CEEMD & WD, and VMD & WD. In order to verify the difference in results between the mentioned methods, the Wilcoxon rank sum test was performed. According to the favorable response, the two denoising methods are not significantly different. It demonstrates that CEEMD and WD may have the same denoising ability for the employed stations. The conclusion applies to the two hybrid methods.

4.2. Correction Rate of Flicker Noise

The correction rate (CR) of flicker noise was introduced to assess the effects of the denoising methods on the flicker noise in the vertical time series. The CR was calculated as follows:
C R = P b e f o r e − P a f t e r P b e f o r e
in which P b e f o r e and P a f t e r are the flicker noise, which were estimated from the model of GPS height time series before and after denoising processes with different methods, respectively. Positive CR indicates that the denoising algorithm decreases the flicker noise of the GPS time series.
We calculated the CRs of several denoising methods for each GPS station to compare their ability to denoise (Figure 6). In general, the averages of CRs for 226 GPS stations, after utilizing five denoising approaches, are 80.93% for CEEMD, 86.47% for CEEMD & WD, 69.39% for VMD, 86.27% for VMD & WD, and 81.49% for WD, respectively. In order to compare the denoising ability of different methods, this study further categorized the 226 GPS coordinate time series with different noise levels into five groups. This is based on research concerning the influence of flicker noise with 1 mm/year0.25,10 mm/year0.25, and 25 mm/year0.25 on the extraction of seasonal signals from GPS coordinate time series [36] and the number of employed stations with varying flicker noise. The five groups are designated as follows: 10–15 mm/year0.25 comprises 19 stations,15–20 mm/year0.25 comprises 111 stations,20–25 mm/year0.25 comprises 75 stations,25–30 mm/year0.25 comprises 13 stations, and 30–35 mm/year0.25 comprises 8 stations.
Figure 7 exhibited the differences in CRs between CEEMD & WD and VMD & WD. We found that 189 stations, accounting for 83.6% of total stations, are characterized by a difference of 1% between CEEMD & WD and VMD & WD. The stations with a difference of 1–2% and 2–6% are 27 and 9, respectively. The results indicate that the difference in denoising ability between CEEMD & WD and VMD & WD is within 2% for 83.6% of the employed stations. In conclusion, the two hybrid methods have the same ability to weaken the flicker noise.
As seen in Figure 6 and Table 1, the CRs for the first two groups of CEEMD surpass 80%, while the CRs for the latter three groups are 78.97%, 76.71%, and 70.12% on average, respectively, and are accompanied by more than 6% for standard deviation of the 226 CRs. For the WD method, the first two groups have an average CR of more than 80% with a standard deviation of less than 5%, whereas the average CRs of the latter two groups are 77.82% ± 7.13% and 62.77% ± 10.45%, respectively. Although CEEMD and WD were statistically indistinguishable for the flicker noise levels of 226 stations, their CRs differed for groups of 10–15 mm/year0.25, 20–25 mm/year0.25, and especially 30–35 mm/year0.25 with a difference of 7.35%. The CRs of the other two groups for CEEMD are comparable to those for WD. These indicate that CEEMD is superior to WD for denoising GPS time series with lower and higher levels of flicker noise. Concerning the VMD method, the CRs of the first four groups are around 69.89%, which is about 4% higher than that of the fifth group. The standard deviation of each group for VMD is smaller than that of other methods, demonstrating that VMD is insensitive to the levels of flicker noise compared to other methods. For both hybrid methods, the average CRs of the five groups are higher than that for the other methods. Among them, the average CRs of the first four groups are all higher than 83%, whereas those of the 30–35 mm/year0.25 were 77.63% ± 5.42% for CEEMD & WD and 76.60% ± 5.18% for VMD & WD, respectively.
Judging from the standard deviations of the correction rates of the five groups, the standard deviations of the latter three groups are significantly larger than those of the two groups. It indicates that the denoising capability of each method is more stable for GPS stations with small levels of flicker noise than those with significant levels of flicker noise.

4.3. Comparison of Hybrid Algorithms and Single Algorithms

Figure 8 presents the amplitudes and disparities of CRs for flicker noise after applying CEEMD and VMD and their hybrid methods. After flicker noise was subtracted by CEEMD and CEEMD & WD, the average CRs of flicker noise for 226 GPS stations were 80.93% and 86.47%, respectively. Compared to CEEMD, the mean CR for 226 GPS stations shows a superiority of 5.51% when CEEMD & WD was applied. There are 39 and 120 GPS stations with CR improvement at 0–2% and 2–6%, respectively. Of the 226 stations, 57 showed a bigger superiority, ranging between 6% and 14%, and 46 out of the 57 stations showed an advance higher than 10%. The largest differences in CR for 8 stations ranged between 14% and 26%, which includes a maximal station of 26.58%, three stations of 24–26%, two stations of 22–24%, a station of 18.01%, and a station of 14.78%. Two disadvantages were noticed for stations SCPZ and SCTQ located in Sichuan province, with differences of 0.1% and 0.2%, respectively. The difference in average CRs of flicker noise was 16.88% between VMD and VMD & WD when we subtracted the noise from the vertical GPS position time series of 226 GPS stations. We found an ascendancy arises from the VMD & WD algorithm in correction rates. In detail, the differences in 153 stations vary from 14% to 20%, followed by 39 stations, for which the differences fluctuate from 20 to 28% and 26 stations with a difference of 12–14%. Only eight out of 226 stations showed an increase of less than 10%: six stations of 8–10% and two stations of 4–6%. After comparing the differences in CRs of flicker noise for 226 stations, we found that the hybrid algorithms, CEEMD & WD and CEEMD & WD, exhibited a superiority of 5.54% and 16.88% compared to the single CEEMD and VMD, respectively.

5. Discussions

5.1. The Comparisons of the Power Spectral Density

As stated previously, the hybrid approaches were more efficient in removing flicker noise. We attempted to deduce the reasons for the advantages of hybrid algorithms in the frequency domain. Figure 9 presents the power spectral density (PSD) of several denoised vertical coordinate time series for the BJSH station.
In comparison to the CEEMD and WD approaches, CEEMD & WD removes the power compared to CEEMD between 3 and 7 cpy and the power retained by WD between 8–13 cpy and 36–182 cpy, respectively, leading to a decrease in the amplitude of the flicker noise of about 1 mm/year0.25. Compared to CEEMD and VMD, VMD & WD primarily liberates the power between 3 and 50 cpy reserved by VMD, which explains the level of flicker noise of 3.29 mm/year0.25. VMD & WD still deviates from CEEMD & WD at some frequencies (e.g.,15–30 cpy), although this difference has little bearing on the estimation of flicker noise. Simultaneously, CEEMD and WD have differences in frequency, and the powers of those frequencies are identical, resulting in similar flicker noise levels. While VMD outperforms WD between 73 and 180 cpy, the reduced power is insufficient to compensate for the disadvantages of VMD.
The perspective of PSD suggests that CEEMD and VMD work better on high-frequency signals of 3–7 cpy, while WD works on low-frequency signals larger than 36 cpy. The advantage of the two hybrid algorithms is that they can combine the characteristics of two approaches to decrease flicker noise across a more comprehensive frequency range.

5.2. The Adaptability of Optimal Parameters

In this paper, we utilized the height time series at BJSH with a lower level of flicker noise to determine the optimal parameters of CEEMD, VMD, and WD and apply them to all stations. Although this strategy considers the workload of ascertaining the optimal parameters of each denoising method for each GPS time series, it also increases the uncertainty in the denoising effect of the above methods. Therefore, we evaluate the adaptability of the applied methods in this section.
After denoising methods are applied, the CRs of flicker noise are 80.91% for CCEMD, 69.37% for VMD, and 81.51% for WD, respectively. A total of 146 CCEMD stations, 215 VMD stations, and 142 WD stations were selected, which represented 64.6%, 85.1%, and 62.8% of all stations with CRs higher than those of the BJFS station. It proves that the three algorithms have a significant denoising effect on over 60% of the stations. In addition, we discuss the adaptability of the parameters of each method from the point of CRs of the five groups (Figure 6). For the 15–20 mm/year0.25 group to which the BJFS station belongs, the average CRs of flicker noise for each method are congenial relative to the results of the BJFS station and have slight disadvantages in standard deviation. Nevertheless, it is still shown that the parameters are applicable to the 15–20 mm/year0.25 group. Compared to the results of the BJFS station, for CEEMD, the average CRs of the first two groups are higher, while the average of the latter two groups are slightly lower. The average CRs for the first four groups are comparable regarding VMD. For WD, the average CRs are greater for the first three groups, while the average for the latter group is slightly lower. The average CRs of the three algorithms for the 30–35 mm/year0.25 group are significantly smaller than the test results, accompanied by large fluctuations. Thus, it is worth researching whether the parameters determined by the 30–35 mm/year0.25 group have the best correction effect. The mean CRs of the first four groups for CEEMD & WD and VMD & WD are superior to the test results, with a standard deviation of less than 4%, respectively. The above fact indicates that the two hybrid methods are beneficial for denoising coordinate time series of stations with a flicker noise level of 10–30 mm/year0.25.
The above analysis reveals that the strategy of determining the parameters of the noise reduction algorithm for single station data can significantly reduce the complexity and time of the test while also being effective for the majority of stations, which has important implications.

5.3. Analysis of the Performance of the Vmd Method

In the preliminary explorations of the VMD method for denoising GPS coordinate time series, it was found that VMD reduces flicker noise by an average CR of 69.39% when the optimal parameter, k = 4 , was determined by the criterion of Hausdorff distance. The CR of VMD has a disadvantage of 11.53% compared to that of CEEMD, which is inconsistent with the conclusion of Sivavaraprasad, Padmaja, and Ratnam [31]. Although the data characteristics are distinct, it is critical to analyze the disadvantages of VMD in denoising GPS coordinate time series.
There are two potential reasons for the poor performance of VMD. To begin, k = 4 is smaller than the value of 6 in Sivavaraprasad, Padmaja, and Ratnam [31]. A smaller k indicates fewer modal components, which may cause flicker noise in the signal components determined by the Hausdorff distance or other criteria. On the contrary, since a larger k increases the likelihood that flicker noise would be distributed in different modes, an excellent criterion (such as the detrended fluctuation analysis) may be used to filter out the modal components that contain more flicker noise. Secondly, the results in this paper seem to prove that the Hausdorff distance is not very effective at identifying noise components for VMD. The primary reason for utilizing the Hausdorff distance in this paper is to mitigate the impact of the criterion when compared to CEEMD. The above analysis demonstrates that when studying the noise reduction results of VMD with different k , particular attention should be given to the criteria.

6. Conclusions

In this study, we develop two hybrid algorithms, CEEMD & WD and VMD & WD, for denoising the GPS time series to mitigate the flicker noise. Compared with the single methods, our hybrid algorithms are proved to be a more advantageous way to weaken the flicker noise, based on the vertical time series of 226 GPS sites from the CMONOC.
The new methods, CEEMD & WD and VMD & WD, significantly decrease the magnitude of flicker noise from 19.90 mm/year0.25 to 2.77 mm/year0.25 and 2.84 mm/year0.25 on average, respectively. Moreover, the CRs of flicker noise for CEEMD & WD and VMD & WD are estimated to be 86.47% and 86.27%. Compared to the single method, the two hybrid algorithms reveal improvements of 6.84% to CEEMD and 16.88% to VMD, respectively.
The hybrid approaches remove flicker noise from GPS signals larger than 3 cpy in more comprehensive bands than the single methods. The improvements are attributed to the integrations of CEEMD or VMD and WD, which reduce the power held by CEEMD between 3 and 7 cpy, the power between 8–13 cpy and 36–182 cpy retained by WD, and primarily liberates power between 3 and 50 cpy reserved by VMD, respectively. VMD & WD still varies from CEEMD & WD at some frequencies, but this has a negligible influence on the estimate of flicker noise.
Despite the achievements of this study, the influence of parameters on the denoising method needs to be further examined, especially the criterion of VMD. We cannot rule out the possibility of improving the hybrid algorithm by changing other parameters. In addition, to mitigate the complex noise in global GPS time series, it is necessary to investigate the parameters to further improve the ability to remove flicker noise for the hybrid method.

Author Contributions

Conceptualization, B.Y. and Z.T.; methodology, B.Y.; software, B.Y.; validation, B.Y. and P.L.; formal analysis, B.Y.; investigation, B.Y.; resources, Z.Y.; data curation, P.L.; writing—original draft preparation, B.Y.; writing—review and editing, Z.Y. and Z.T.; visualization, B.Y.; supervision, Z.T.; project administration, Z.Y.; funding acquisition, Z.Y. and Z.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of China under grant number 42174054. This work was also supported by the Natural Science Foundation of China (Grant No. 42104003), and the China Postdoctoral Science Foundation (Grant No. 2022M710012).

Data Availability Statement

The data that support the findings of this study are available from ftp://58.48.77.29/products/ (accessed on 3 April 2021).

Acknowledgments

We thank the Crustal Movement Observation Network of China (CMONOC) for providing GPS time series (ftp://58.48.77.29/products/, accessed on 3 April 2021) in this study. We appreciate Machiel Bos and Rui Fernandes for providing useful software tool: Hector.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

For the noise in the geophysics signals, the power spectrum is a useful tool. The power spectrum of noise is represented by a power law process as follows:
P f = P 0 f − α
in which P f is the spectrum at the frequency f . α is the spectrum index. P 0 is a constant.
The spectral index is not always an integer, and most geophysical phenomena have a spectral index value of 1 < α < 3 , called ‘fractal random walk’; and when the spectral index − 1 < α < 2 , called fractal white noise. In particular, the white noise is defined as   α = 0 and flicker noise is defined as   α = 1 .

Appendix B

The principle of the Hausdorff distance can be described as below.
To separate pure noise modes and signal modes, x t is first decomposed into intrinsic mode function (IMF) components arranged from high-frequency to low-frequency. In order to classify the noise modes and the signal modes, the Hausdorff distance, proposed by Komaty et al., is introduced to represent the relationship between the signal and each component using the probability density functions (PDF). The Hausdorff distance is described defined as follows:
For two signals, A = a 1 , ⋯ , a m and B = b 1 , ⋯ , b n , the Hausdorff distance is defined as:
HD A , B = max { h A , B , h B , A } h A , B = m a x a ∈ A d a , B = m a x a ∈ A m i n b ∈ B d a , b = m a x a ∈ A m i n b ∈ B ‖ a − b ‖ h B , A = m a x b ∈ B d b , A = m a x b ∈ B m i n a ∈ A d b , a = m a x b ∈ B m i n a ∈ A ‖ b − a ‖
where HD A , B is Hausdorff distance of A and B . Here, h A , B and h B , A are the one-way distance from A to B and B to A , respectively. The d a , b = ‖ a − b ‖ and d b , a = ‖ b − a ‖ represent the Euclidean distance of a and b , respectively.
Furthermore, the steps of Hausdorff distance to classify the IMFs are described defined as follows:
L i = HD pdf x , pdf ( IMF i i = 1 ,   2 ⋯ n
In which L i is the i-th Hausdorff distance of x and IMF i the i-th IMF component. M is the maximum point of the L i , which can be defined by
l = arg m a x i L i
Therefore, starting the IMF with a high frequency, the first l IMF components are the pure noise modes. The residual IMF components are the signal models. The noise component, N , and signal component, S , are calculated as follows:
N = ∑ i = 1 l IMF i S = ∑ i = l + 1 n IMF i

References

  1. Prawirodirdjo, L.; Bock, Y. Instantaneous global plate motion model from 12 years of continuous GPS observations. J. Geophys. Res. Solid Earth 2004, 109, 2944. [Google Scholar] [CrossRef]
  2. Wang, Q.; Zhang, P.-Z.; Freymueller, J.T.; Bilham, R.; Larson, K.M.; Lai, X.a.; You, X.; Niu, Z.; Wu, J.; Li, Y. Present-day crustal deformation in China constrained by global positioning system measurements. Science 2001, 294, 574–577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Wallace, L.M.; Beavan, J.; McCaffrey, R.; Berryman, K.; Denys, P. Balancing the plate motion budget in the South Island, New Zealand using GPS, geological and seismological data. Geophys. J. Int. 2007, 168, 332–352. [Google Scholar] [CrossRef] [Green Version]
  4. Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
  5. Hao, M.; Li, Y.; Zhuang, W. Crustal movement and strain distribution in East Asia revealed by GPS observations. Sci. Rep. 2019, 9, 16797. [Google Scholar] [CrossRef] [Green Version]
  6. Tian, Z.; Freymueller, J.T.; Yang, Z. Spatio-temporal variations of afterslip and viscoelastic relaxation following the Mw 7.8 Gorkha (Nepal) earthquake. Earth Planet. Sci. Lett. 2020, 532, 116031. [Google Scholar] [CrossRef]
  7. Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
  8. Collilieux, X.; Métivier, L.; Altamimi, Z.; van Dam, T.; Ray, J. Quality assessment of GPS reprocessed terrestrial reference frame. GPS Solut. 2011, 15, 219–231. [Google Scholar] [CrossRef]
  9. Hao, M.; Freymueller, J.T.; Wang, Q.; Cui, D.; Qin, S. Vertical crustal movement around the southeastern Tibetan Plateau constrained by GPS and GRACE data. Earth Planet. Sci. Lett. 2016, 437, 1–8. [Google Scholar] [CrossRef]
  10. Li, W.; Shum, C.K.; Li, F.; Zhang, S.; Ming, F.; Chen, W.; Zhang, B.; Lei, J.; Zhang, Q. Contributions of Greenland GPS Observed Deformation from Multisource Mass Loading Induced Seasonal and Transient Signals. Geophys. Res. Lett. 2020, 47, e2020GL088627. [Google Scholar] [CrossRef]
  11. Mémin, A.; Boy, J.-P.; Santamaría-Gómez, A. Correcting GPS measurements for non-tidal loading. GPS Solut. 2020, 24, 45. [Google Scholar] [CrossRef]
  12. Borsa, A.A.; Agnew, D.C.; Cayan, D.R. Ongoing drought-induced uplift in the western United States. Science 2014, 345, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
  13. Carlson, G.; Werth, S.; Shirzaei, M. Joint Inversion of GNSS and GRACE for Terrestrial Water Storage Change in California. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023135. [Google Scholar] [CrossRef] [PubMed]
  14. Amiri-Simkooei, A.R. Noise in multivariate GPS position time-series. J. Geod. 2009, 83, 175–187. [Google Scholar] [CrossRef] [Green Version]
  15. Klos, A.; Gruszczynska, M.; Bos, M.S.; Boy, J.-P.; Bogusz, J. Estimates of Vertical Velocity Errors for IGS ITRF2014 Stations by Applying the Improved Singular Spectrum Analysis Method and Environmental Loading Models. Pure Appl. Geophys. 2018, 175, 1823–1840. [Google Scholar] [CrossRef]
  16. Wu, H.; Li, K.; Shi, W.; Clarke, K.C.; Zhang, J.; Li, H. A wavelet-based hybrid approach to remove the flicker noise and the white noise from GPS coordinate time series. GPS Solut. 2015, 19, 511–523. [Google Scholar] [CrossRef]
  17. Klos, A.; Bos, M.S.; Fernandes, R.M.S.; Bogusz, J. Noise-Dependent Adaption of the Wiener Filter for the GPS Position Time Series. Math. Geosci. 2019, 51, 53–73. [Google Scholar] [CrossRef] [Green Version]
  18. Langbein, J. Noise in GPS displacement measurements from Southern California and Southern Nevada. J. Geophys. Res. Solid Earth 2008, 113, 5247. [Google Scholar] [CrossRef]
  19. Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
  20. Montillet, J.; Tregoning, P.; McClusky, S.; Yu, K. Extracting White Noise Statistics in GPS Coordinate Time Series. IEEE Geosci. Remote Sens. Lett. 2013, 10, 563–567. [Google Scholar] [CrossRef]
  21. Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
  22. Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
  23. Peng, W.; Dai, W.; Santerre, R.; Cai, C.; Kuang, C. GNSS Vertical Coordinate Time Series Analysis Using Single-Channel Independent Component Analysis Method. Pure Appl. Geophys. 2017, 174, 723–736. [Google Scholar] [CrossRef]
  24. Li, Y.; Xu, C.; Yi, L.; Fang, R. A data-driven approach for denoising GNSS position time series. J. Geod. 2018, 92, 905–922. [Google Scholar] [CrossRef]
  25. Liu, L.; Hsu, H.; Grafarend, E.W. Normal Morlet wavelet transform and its application to the Earth’s polar motion. J. Geophys. Res. Solid Earth 2007, 112, 4895. [Google Scholar] [CrossRef] [Green Version]
  26. Souza, E.M.d.; Monico, J.F.G. The wavelet method as an alternative for reducing ionospheric effects from single-frequency GPS receivers. J. Geod. 2007, 81, 799–804. [Google Scholar] [CrossRef]
  27. Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
  28. Wornell, G.W.; Oppenheim, A.V. Estimation of fractal signals from noisy measurements using wavelets. IEEE Trans. Signal Process. 1992, 40, 611–623. [Google Scholar] [CrossRef]
  29. Kaczmarek, A.; Kontny, B. Identification of the Noise Model in the Time Series of GNSS Stations Coordinates Using Wavelet Analysis. Remote Sens. 2018, 10, 1611. [Google Scholar] [CrossRef] [Green Version]
  30. Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
  31. Sivavaraprasad, G.; Padmaja, R.S.; Ratnam, D.V. Mitigation of Ionospheric Scintillation Effects on GNSS Signals Using Variational Mode Decomposition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 389–393. [Google Scholar] [CrossRef]
  32. Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H. Feature Extraction Algorithm Using a Correlation Coefficient Combined with the VMD and Its Application to the GPS and GRACE. IEEE Access 2021, 9, 17507–17519. [Google Scholar] [CrossRef]
  33. Xu, H.; Lu, T.; Montillet, J.-P.; He, X. An Improved Adaptive IVMD-WPT-Based Noise Reduction Algorithm on GPS Height Time Series. Sensors 2021, 21, 8295. [Google Scholar] [CrossRef] [PubMed]
  34. Anusha, S.; Sriram, A.; Palanisamy, T. A Comparative Study on Decomposition of Test Signals Using Variational Mode Decomposition and Wavelets. Int. J. Electr. Eng. Inform. 2016, 8, 886–896. [Google Scholar]
  35. Bos, M.S.; Fernandes, R.; Williams, S.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef] [Green Version]
  36. Klos, A.; Bos, M.S.; Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut. 2017, 22, 21. [Google Scholar] [CrossRef] [Green Version]
  37. Mallat, S.G. Multiresolution approximations and wavelet orthonormal bases of. Trans. Am. Math. Soc. 1989, 315, 69–87. [Google Scholar] [CrossRef]
  38. Han, M.; Liu, Y.; Xi, J.; Guo, W. Noise Smoothing for Nonlinear Time Series Using Wavelet Soft Threshold. IEEE Signal Process. Lett. 2007, 14, 62–65. [Google Scholar] [CrossRef]
  39. Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
  40. Komaty, A.; Boudraa, A.O.; Augier, B.; Dare-Emzivat, D. EMD-Based Filtering Using Similarity Measure between Probability Density Functions of IMFs. IEEE Trans. Instrum. Meas. 2013, 63, 27–34. [Google Scholar] [CrossRef] [Green Version]
  41. Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
  42. Ji, K.; Shen, Y.; Wang, F. Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis. Remote Sens. 2020, 12, 992. [Google Scholar] [CrossRef] [Green Version]
  43. Bevis, M.; Brown, A. Trajectory models and reference frames for crustal motion geodesy. J. Geod. 2014, 88, 283–311. [Google Scholar] [CrossRef] [Green Version]
  44. Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG9-1–ETG9-16. [Google Scholar] [CrossRef] [Green Version]
  45. Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. Solid Earth 2004, 109, 2741. [Google Scholar] [CrossRef] [Green Version]
  46. Teferle, F.N.; Williams, S.D.P.; Kierulf, H.P.; Bingley, R.M.; Plag, H.-P. A continuous GPS coordinate time series analysis strategy for high-accuracy vertical land movements. Phys. Chem. Earth Parts A/B/C 2008, 33, 205–216. [Google Scholar] [CrossRef] [Green Version]
  47. Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
  48. ElGharbawi, T.; Tamura, M. Measuring deformations using SAR interferometry and GPS observables with geodetic accuracy: Application to Tokyo, Japan. ISPRS J. Photogramm. Remote Sens. 2014, 88, 156–165. [Google Scholar] [CrossRef] [Green Version]
  49. Montenbruck, O.; Ramos-Bosch, P. Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut. 2008, 12, 187–198. [Google Scholar] [CrossRef]
Remotesensing 15 01716 g001 550
Figure 1. The variation of flicker noise with different options for CEEMD (a), VMD (b) and WD (c,d).
Figure 1. The variation of flicker noise with different options for CEEMD (a), VMD (b) and WD (c,d).
Remotesensing 15 01716 g001
Remotesensing 15 01716 g002 550
Figure 2. Flowchart of the two proposed methods for denoising GPS coordinate time series.
Figure 2. Flowchart of the two proposed methods for denoising GPS coordinate time series.
Remotesensing 15 01716 g002
Remotesensing 15 01716 g003 550
Figure 3. Spatial locations and time spans of selected 226 continuous GPS stations from CMONOC. The color declares the observation days of each station.
Figure 3. Spatial locations and time spans of selected 226 continuous GPS stations from CMONOC. The color declares the observation days of each station.
Remotesensing 15 01716 g003
Remotesensing 15 01716 g004 550
Figure 4. The vertical time series before and after conducting the pre-processing procedure of three typical GPS sites (BJFS: 115.89°E, 39.61°N, YNCX: 101.49°E, 25.05°N and XJRQ: 88.17°E, 39.02°N) are shown. Good measurements (black points) plus outliers (red points) present the raw time series. Good measurements (black points) plus gaps (blue points) present the input time series to our investigations.
Figure 4. The vertical time series before and after conducting the pre-processing procedure of three typical GPS sites (BJFS: 115.89°E, 39.61°N, YNCX: 101.49°E, 25.05°N and XJRQ: 88.17°E, 39.02°N) are shown. Good measurements (black points) plus outliers (red points) present the raw time series. Good measurements (black points) plus gaps (blue points) present the input time series to our investigations.
Remotesensing 15 01716 g004
Remotesensing 15 01716 g005 550
Figure 5. The estimations of flicker noise of GPS vertical coordinate time series with six strategies for the 226 CMONOC stations employed in this study.
Figure 5. The estimations of flicker noise of GPS vertical coordinate time series with six strategies for the 226 CMONOC stations employed in this study.
Remotesensing 15 01716 g005
Remotesensing 15 01716 g006 550
Figure 6. The CRs of flicker noise for different methods. Mean and std represent the average and standard deviation of CRs for each group, respectively. (Unit: %).
Figure 6. The CRs of flicker noise for different methods. Mean and std represent the average and standard deviation of CRs for each group, respectively. (Unit: %).
Remotesensing 15 01716 g006
Remotesensing 15 01716 g007 550
Figure 7. The differences of CRs between CEEMD & WD and VMD & WD.
Figure 7. The differences of CRs between CEEMD & WD and VMD & WD.
Remotesensing 15 01716 g007
Remotesensing 15 01716 g008 550
Figure 8. The CRs (left) and their differences (right) of flicker noise for single and hybrid methods.
Figure 8. The CRs (left) and their differences (right) of flicker noise for single and hybrid methods.
Remotesensing 15 01716 g008
Remotesensing 15 01716 g009 550
Figure 9. The power spectral density (PSD) of residual vertical coordinate time series after applying different methods for BJSH station.
Figure 9. The power spectral density (PSD) of residual vertical coordinate time series after applying different methods for BJSH station.
Remotesensing 15 01716 g009
Table
Table 1. The averages of CRs of flicker noise for different methods with five groups. (Unit: %).
Table 1. The averages of CRs of flicker noise for different methods with five groups. (Unit: %).
GroupCEEMDCEEMD & WDVMDCEEMD & WDWD
10–15 mm/year0.2584.11 ± 2.8388.85 ± 1.5568.77 ± 1.5888.90 ± 1.4087.22 ± 1.47
15–20 mm/year0.2582.98 ± 5.0087.30 ± 1.5969.67 ± 2.3187.13 ± 1.2582.51 ± 2.32
20–25 mm/year0.2578.97 ± 6.9585.98 ± 3.1769.71 ± 2.9685.77 ± 2.8481.17 ± 4.35
25–30 mm/year0.2576.71 ± 8.8784.05 ± 5.4568.89 ± 3.0883.89 ± 5.0877.82 ± 7.13
30–35 mm/year0.2570.12 ± 8.8677.63 ± 5.4264.95 ± 2.1376.60 ± 5.1862.77 ± 10.45
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Yang, B.; Yang, Z.; Tian, Z.; Liang, P. Weakening the Flicker Noise in GPS Vertical Coordinate Time Series Using Hybrid Approaches. Remote Sens. 2023, 15, 1716. https://doi.org/10.3390/rs15061716

AMA Style

Yang B, Yang Z, Tian Z, Liang P. Weakening the Flicker Noise in GPS Vertical Coordinate Time Series Using Hybrid Approaches. Remote Sensing. 2023; 15(6):1716. https://doi.org/10.3390/rs15061716

Chicago/Turabian Style

Yang, Bing, Zhiqiang Yang, Zhen Tian, and Pei Liang. 2023. "Weakening the Flicker Noise in GPS Vertical Coordinate Time Series Using Hybrid Approaches" Remote Sensing 15, no. 6: 1716. https://doi.org/10.3390/rs15061716

APA Style

Yang, B., Yang, Z., Tian, Z., & Liang, P. (2023). Weakening the Flicker Noise in GPS Vertical Coordinate Time Series Using Hybrid Approaches. Remote Sensing, 15(6), 1716. https://doi.org/10.3390/rs15061716

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop