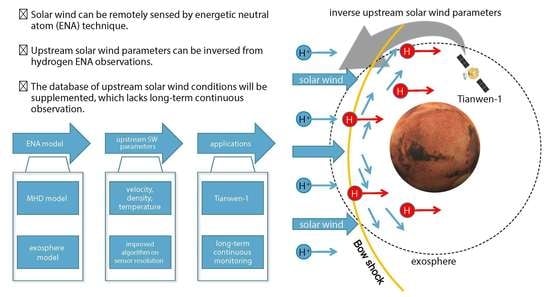
Inversion of Upstream Solar Wind Parameters from ENA Observations at Mars

Abstract

An algorithm has been developed to invert the solar wind parameters from the hydrogen energetic neutral atom (H-ENA) measured in near-Mars space. Supposing the H-ENA is produced by change exchange collision between protons that originated in the solar wind and neutrals in the exosphere, an H-ENA model is established based on the magnetohydrodynamic (MHD) simulation of the solar wind interaction with Mars, to study the H-ENA characteristics. It is revealed that the solar wind H-ENAs are high-speed, low-temperature beams, just like the solar wind, while the magnetosheath H-ENAs are slower and hotter, with broader energy distribution. Assuming Maxwellian velocity distribution, the solar wind H-ENA flux is best fitted by a Gaussian function, from which the solar wind velocity, density, and temperature can be retrieved. Further investigation, based on the ENA flux simulated by the H-ENA model, reveals that the accuracy of inversed solar wind parameters is related to the angular and energy resolutions of the ENA detector. Finally, the algorithm is verified using the H-ENA observations from the Tianwen-1 mission. The upstream solar wind velocity when inversed is close to that of the in situ plasma measurement. Our result suggests the solar wind parameters inversed from H-ENA observation could be an important supplement to the dataset supporting studies on the Martian space environment, where long-term continuous monitoring of the upstream SW condition is lacking.

1. Introduction

The energetic neutral atom (ENA) is a type of neutral atom with substantial energy. When an energetic ion collides with a neutral particle, the ion gains an electron, neutralizing its own electricity, and thus forms an ENA. The neutral species has a relatively low velocity and can be considered as stationary. When the energy of the ion is greater than 10 (100) eV, the newborn H-ENAs fly almost in the same way as the original ion, with a deviation less than 4° (1°) [1]. The ENA is then no longer restricted by magnetic or electric fields and moves almost in a straight line, which can be detected by remote sensors. According to the ENA particle species, velocity, temperature, density, etc., the space plasma information at its source can be deduced. Compared with in situ particle detection, remote sensing of ENAs can provide a complete picture of the planetary magnetosphere instantaneously [2,3].

Due to the lack of a global magnetic field, the radial position of Mars’ bow shock at the subsolar point is only about 1.64 R_M (radius of Mars, 1 R_M = 3396 km) [4]. Mars’ exosphere is widely distributed outside the bow shock and is directly exposed to the solar wind (SW). The charge exchange of the SW protons with the exosphere neutrals produces SW hydrogen ENAs (SW H-ENAs) across a vast space, carrying the SW plasma information, which can be remotely sensed.

Thus far, the only two missions that have carried out ENA exploration at Mars are Mars Express and Tianwen-1. Results show [5,6,7,8,9,10,11,12] the SW H-ENAs have a typical flux of 10⁹–10¹⁰ m⁻² sr⁻¹ s⁻¹; magnetosheath (MS) hydrogen ENAs (MS H-ENAs), produced by interaction between the shocked solar wind and the exosphere, have a typical flux of (4–7) × 10⁹ m⁻² sr⁻¹ s⁻¹. Limited by insufficient ENA observations, details about ENA are drawn from modeling works, which simulate ENA production from charge exchange collisions. Based on a model study, Kallio et al. [13] found that 1–3% of the SW protons are converted into hydrogen ENAs (H-ENAs) in front of the bow shock, which precipitate into the magnetosphere with an energy flux of 3 × 10¹³ eVm⁻² s⁻¹. Wang et al. [14,15] pointed out that during solar minimum, about 2% of the SW protons are converted into ENAs, and the ENA production rate increases when the SW dynamic pressure increases. Holmstrom et al. [16] found that the temperature of the H atom at the critical height of the exosphere plays a major role in determining the ENA distribution. Ramstad et al. [17] calculated the global distribution of ENAs at Mars and found a SW H-ENA flux of 3 × 10⁹ m⁻² s⁻¹, based on the ion observations by MAVEN.

Due to its nature of remote sensing, ENA sounding could be used as a method to study the interaction between the planetary atmosphere and the solar wind, to monitor the density of planetary upper atmosphere [18], and to invert the distribution of the solar wind ions. For example, deriving from the ENA data on board the TC-2 spacecraft, Lu et al. [19] inversed the distribution of ring current ions during a magnetic storm. The inversion was constrained by the ENA model, based on an empirical ring current ion flux model and an adjusted Chamberlain exosphere model. By fitting the modeled ENA with the observed ENA, the ion distribution was retrieved. A similar scheme was also applied to inverse the flux of protons in the magnetosphere using the ENA observations by IBEX [20].

The space environment varies with the upstream solar wind conditions. However, unlike Earth, Mars has few missions to continuously monitor the solar wind, which has hampered the scientific research for a long time. To overcome this difficulty, different solar wind proxies have been developed, based on models or previous observations [21]. The SW plasma information retrieved from SW H-ENA provides direct and simultaneous information on the upstream solar wind condition. In this paper, based on the SW H-ENA observations at Mars, inversion of the SW parameters is studied. Quantitative analysis and comparison with observations are also carried out on the basis of modeling work.

2. Modeling H-ENA

The Martian H-ENAs are mainly generated by the following three processes [14,15,16,22]:

• H⁺ + H → H + H⁺;
• H⁺ + O → H + O⁺;
• H⁺ + H₂ → H + H₂⁺.

The production rate p_ENA of ENAs is determined by

$$p_{ENA}\approx nu{\displaystyle \sum }_i{n}_i{\sigma }_i\left(u\right)$$

(1)

where n and u are the solar wind density and magnitude of bulk velocity, respectively; $n_i$ and ${\sigma }_i$ are the densities and charge exchange cross-sections of neutral species, respectively; and H, O, and H₂ are denoted by subscript i = 1, 2, and 3, respectively. Secondary collision and other loss mechanisms are ignored here. The charge exchange cross-sections are derived from experimental curves [23,24]. The ion and neutral parameters are highly variable, depending on the SW, Mars atmosphere, and their interactions.

Here, we use a single-fluid multi-species MHD model [25] to describe the SW interaction with Mars, including the large-scale structure of the induced magnetosphere [26]. In the MHD model, the plasma is treated as fluid, the magnetic field is frozen into the fluid, and an isotropic velocity distribution is assumed. The single-fluid MHD model has only one momentum equation and thus all ion species have the same velocity. The specific, normalized equations solved are

$$\frac{\partial }{\partial t}\left(\begin{array}{c}\begin{array}{c}{\rho }_i\\ \left({\displaystyle {\displaystyle \sum }_{i=1}^4}{\rho }_i\right)u\end{array}\\ B\\ \epsilon \end{array}\right)+{\left\{\nabla ·\left(\begin{array}{c}\begin{array}{c}{\rho }_i\mathrm{u}\\ \left({\displaystyle {\displaystyle \sum }_{i=1}^4}{\rho }_i\right)uu+\left(p+\frac{1}{2}{B}^2\right)I-BB\end{array}\\ uB-Bu\\ u\left(\epsilon +p+\frac{1}{2}{B}^2\right)-\left(B·u\right)B\end{array}\right)\right\}}^T=Q$$

(2)

where the total energy density $\epsilon$ is defined as

$$\epsilon =\frac{1}{2}\left({\displaystyle \sum }_{i=1}^4{\rho }_i\right)u^2+\frac{1}{\gamma -1}p+\frac{B^2}{2}$$

(3)

where ${\rho }_{i }$ (i = 1, 2, 3, and 4) represent the mass densities of H⁺, O₂⁺, O⁺, and CO₂⁺, respectively; p is the total thermal pressure; $\gamma$ is the ratio of specific heat of the plasma; u is the bulk velocity of plasma; B is the magnetic field; and Q represents the source term. The undisturbed upstream SW conditions are shown in

Table 1. Parameters for the MHD model.

Parameter	Value
SW density	1.8 cm−3
SW velocity	(500, 0, 0) km/s
SW proton temperature	1.5 × 105 K
SW magnetic field	(−1.6, 2.5, 0) nT

.

Figure 1 shows the distribution of the proton density and velocity simulated by the MHD model. When the SW encounters the obstacle of Mars, it slows down and forms boundaries and regions such as the bow shock and the MS. Protons are mainly distributed in two regions, the MS and upstream, where charge exchange with the exosphere will produce the SW H-ENA and the MS H-ENA.

The global distributions of neutral species are described by the exosphere and thermosphere models. The exosphere model used in this paper is the Chamberlain exosphere model [27]. In the exosphere model, all particles are assumed to have originated in the atmosphere below the exobase, following ballistic trajectories under the gravitational pull of the planet in the absence of an incident source of external particles. The exosphere model gives the density of neutral species at radial distance r:

$$N \left(r\right)=N_c{e}^{\lambda -{\lambda }_c}\xi \left(\lambda \right)$$

(4)

where $\xi \left(\lambda \right)$ is Chamberlain’s partition function; $\lambda =\frac{GMm}{k{T}_{c}r}$; ${\lambda }_c=\frac{GMm}{k{T}_c{r}_c}$; G is the gravitational constant; k is the Boltzmann constant; m and M are masses of the particle and Mars; and T is the temperature. The subscript C denotes parameters at the critical altitude. Thus, $N \left(r\right)$ is a function of radial distance $r_c$, temperature $T_c$, and density $N_c$ at the critical altitude, which is set to 170 km. Below the critical altitude, the neutral densities are extracted from the thermosphere model adopted by Ma et al. [25,26] in the MHD model, based on the observations of the Viking and Mariner missions. The critical parameters of the exosphere are shown in

Table 2. Parameters of the exosphere model at the critical altitude ¹.

Parameter	Temperature	Density
H	192 K	9.9 × 105 cm−3
H2	192 K	3.8 × 106 cm−3
O (thermal)	173 K	1.4 × 108 cm−3
O (hot)	4.4 × 103 K	5.5 × 103 cm−3

¹ The critical altitude is set to 170 km.

[16,22].

The neutral profiles of the exosphere are illustrated in Figure 2, which can extend to 20 R_M, well above the bow shock (dashed line). H-ENA is produced by the interaction of the proton with the neutral species. According to Equation (1), the production rate of H-ENA is proportional to the density of the exosphere. With the decrease in height, the exosphere density increases, which is conducive to the increase in the H-ENA production rate. The MS and the upstream SW are the main regions producing H-ENA. The extensive exosphere upstream of the bow shock plays an important role in the generation of the SW H-ENAs.

Supposing that protons and neutrals are isotropic, according to the plasma and neutral distributions specified by the models, the H-ENA production rate is calculated according to Equation (1), and its spatial distribution in the MSO X–Z plane is shown in Figure 3.

Figure 3 shows the SW H-ENA generation region; upstream of the bow shock is symmetric, due to the symmetric exosphere model. As the flow decelerates around Mars, the proton flux in the MS increases, and the production rate of the MS H-ENAs is higher than the SW H-ENA production rate upstream of the bow shock. The strongest crustal magnetic fields, located at noon, increase the height of the MS in the southern hemisphere, and thus the MS H-ENA production region, resulting in north–south asymmetry. This is a periodic phenomenon with the rotation of Mars.

Assuming the environment to be “optically” thin to ENAs [16], from the production rate of ENAs p_ENA, the SW H-ENA differential flux and directional flux can be calculated by integration along the line of sight [16]. The images of H-ENA are shown in Figure 4, where the directional flux represents the energy-integrated incoming differential flux in Equation (5).

Figure 4 shows the H-ENA directional flux image in a field of view (FOV) of 2$\pi$, constructed based on the H-ENA model. The images correspond to three observing locations as shown in Figure 3, at 2700 km height, solar zenith angle (SZA) = 20°; at 500 km height, SZA = 20°; and at 3.5 R_M, SZA = 160°. The line of sight points to the opposite direction to SW. The energy integration ranges from 10 eV to 10 keV, and the angular resolution is 3°.

In Figure 4a, the H-ENA fluxes are composed of the SW H-ENAs accumulated over a long distance upstream of the bow shock. The SW H-ENA retains the characteristics of high velocity and low temperature of the SW proton, which is reflected in the image as a concentrated strong incoming beam. The brightness of the image in Figure 4a is a function of the SW parameters. H-ENAs in Figure 4b,c have two components—one is the SW H-ENAs, and the second is the MS H-ENAs. Inside the MS, the bulk velocity of the MS H-ENAs decreases, while the temperature increases, and ENA flux becomes diffusive compared with the SW H-ENA beam in Figure 4a. When the observer moves the magnetotail, the SW H-ENAs are partially blocked by the planet. Here, the absorption and scattering [28] by the Martian atmosphere are not considered.

3. Inversion of Solar Wind Parameters from H-ENA Observation

3.1. Basic Algorithm

If the solar wind proton is thermally isotropic, differential flux j of the SW H-ENA is written as:

$$j\left(r,E,\theta ,\phi \right)=\frac{uvf}{m}{{\displaystyle \int }}_{BS}^{\infty }{\displaystyle \sum }_i{n}_i\left(r^{\prime }\right){\sigma }_i\left(u\right)ds=\frac{uvI}{m}f$$

(5)

where $\theta$ and $\phi$ define the direction of the line of sight; r represents the observation position; E is the ENA energy; v is magnitude of the proton velocity; BS denotes the position of the bow shock along the line of sight; f represents the phase space density; r’ is the position along the line of sight; s is the distance along the line of sight; and I represents the integral term depending on the exosphere condition and the bow shock position, which can be taken as a constant in Equation (5) since the cross-section here changes little. If the SW proton velocity follows the Maxwellian distribution, the ENA differential flux j in Equation (5) can be expressed as follows:

$$\begin{array}{c}j\left(E,\theta ,\phi \right)=\frac{nuvI}{m}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{e}^{-\frac{m}{2kT}{\left|v-u\right|}^2}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{n{u}^{2}I\cos \psi }{m}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{e}^{-\frac{m}{2kT}{\left(u\sin \psi \right)}^2}{e}^{-\frac{m}{2kT}{\left(v-u\cos \psi \right)}^2}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{nuI}{m}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{e}^{-\frac{m}{2kT}{\left(u\sin \psi \right)}^2}\left(v-u\cos \psi \right)e^{-\frac{m}{2kT}{\left(v-u\cos \psi \right)}^2}\end{array}$$

(6)

where ψ is the angle between the proton velocity v and the bulk velocity u. For the solar wind proton, $v-u\cos \psi$ is usually small since the bulk velocity is much higher than the thermal velocity. Since the second term on the right hand of Equation (6) makes little contribution, Equation (6) can be reduced to the form of the Gaussian function $y=a{e}^{-{\left(x-b\right)}^2/c^2}$. If j is given by observation, parameters a, b, and c can be obtained by curve fitting, thus SW parameters are determined according to Equations (7) and (8):

$$\{\begin{array}{c}a=\frac{n{u}^{2}I\cos \psi }{m}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{e}^{-\frac{m}{2kT}{\left(u\sin \psi \right)}^2}\\ b=u\cos \psi \\ c^2=\frac{2kT}{m}\end{array}$$

(7)

$$\{\begin{array}{c}u=\frac{b}{\cos \psi }\\ T=\frac{c^{2}m}{2k}\\ n=\frac{a}{\frac{I{u}^2\cos \psi }{m}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{e}^{-\frac{m}{2kT}{\left(u\sin \psi \right)}^2}}\end{array}$$

(8)

It can also be seen that the mean of the fitted Gaussian function corresponds to the bulk velocity of the SW, and the standard deviation is a function of the temperature. Meanwhile, the height of the peak is related to the density, bulk velocity, and temperature.

3.2. Resolution in Inversion

Figure 5 shows the simulated H-ENA differential flux (blue dotted curves) observed at positions marked in Figure 3. The lines of sight are opposite to the SW direction in Figure 5a,b. Curves in Figure 5a,b reflect different distributions of the beam such as SW H-ENAs and diffusive MS H-ENAs. In Figure 5c, the line of sight deflects 7° away from the SW to simulate possible instrument altitude, which results in a decrease in the SW H-ENA flux. The red curves represent the Gaussian fittings. When the differential fluxes of SW H-ENAs and MS H-ENAs differ by more than two orders of magnitude, single Gaussian fitting gives a good result; when they differ by less than one order of magnitude, double Gaussian fitting seems better. Due to their different distributions, the SW H-ENAs can be separated from the MS H-ENAs to give information on the SW.

In practice, observation represents an integral part of the differential flux with certain angular resolution and energy resolution. Figure 6 shows the simulated H-ENA differential flux observed at the MPR in Figure 4b, and the fitting results with different resolutions. If the angular resolution is lower, the observed peak value of the differential flux will decrease. Accordingly, the height of the fitted Gaussian distribution, and therefore the density of SW, will also be lower. If the energy resolution drops, the observed differential flux exhibits wider distribution; thus, the standard deviation of the fitted Gaussian distribution becomes larger. If it follows the inversed temperature, as well as density, it will be higher. Both resolutions have little effect on the mean of the Gaussian distribution, i.e., on the inversed SW velocity.

3.3. Mitigating the Angular Resolution Effect

The differential flux in an angular bin represents the average differential flux within the bin. According to Figure 6, low angular resolution will reduce height of the SW H-ENA peak. To mitigate this effect, a correction coefficient $K\left(v\right)$ is introduced. $K\left(v\right)$ represents the ratio of the real differential flux to the average differential flux measured in the angular bins:

$$K\left(v\right)=j\left({\Omega }_0,v\right)/\left(\frac{{{\displaystyle \int }}_{{\Omega }_s}^{{\Omega }_t}j\left(\Omega ,v\right)d\Omega }{{{\displaystyle \int }}_{{\Omega }_s}^{{\Omega }_t}d\Omega }\right)=\frac{j\left({\Omega }_0,v\right){{\displaystyle \sum }}_i\mathsf{\Delta }{\Omega }_i}{{{\displaystyle \sum }}_{i}j\left({\Omega }_i,v\right)\mathsf{\Delta }{\Omega }_i}$$

(9)

where $\Omega$ indicates the direction of the line of sight, defined by $\theta$ and $\phi$; ${\Omega }_0$ indicates the direction of the real differential flux; and ${\Omega }_t-{\Omega }_s$ corresponds to the angular bin, which is further decomposed into the sum of several small angular bins. The ith angular bin is $\mathsf{\Delta }{\Omega }_i$ and the differential flux in this bin is $j\left({\Omega }_i,v\right)$. The corrected differential flux is $K\left(v\right)j\left(E\right)$. For the solar wind proton, v can be approximated by $u\cos \psi$. The density of the SW can be written as follows:

$$n=\frac{aK\left(u\cos \psi \right)}{\frac{I{u}^2\cos \psi }{m}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{e}^{-\frac{m}{2kT}{\left(u\sin \psi \right)}^2}}$$

(10)

Under the same solar wind conditions (Table 1), but considering different angular resolutions, inversed results are shown in

Table 3. Inversed SW parameters under different angular resolutions.

Angular Resolution	SW Velocity (km/s)	SW Temperature (×105 K)	SW Density (cm−3) With/Without Correction
real value	502	1.5	1.8
1° × 2°	499	1.54	1.85/1.80
3° × 6°	499	1.55	1.86/1.60
5° × 10°	498	1.56	1.86/1.33
7° × 14°	498	1.57	1.86/1.06
9° × 23°	497	1.60	1.87/0.67

. In the worst case, the SW velocity error is less than 1%, the temperature error is less than 6.7%, and the density error is less than 3.9%.

For different energy resolutions, results are shown in

Table 4. Inversed SW parameters under different energy resolutions.

Energy Resolution ΔE/E	SW Velocity (km/s)	SW Temperature (×105 K)	SW Density (cm−3)
real value	502	1.5	1.8
15%	499	1.54	1.85
33%	499	2.00	2.39
53%	502	2.55	2.98
76%	506	3.27	4.02
102%	509	4.27	4.26

. Energy resolution correction is not included here since usually it is easier for ENA detectors to achieve high energy resolution. When the energy resolution decreases, the inversed SW temperature and density deviate from the real values. In the worst case, the error of the SW velocity is less than 1.4%, but errors in the temperature and density are higher by a factor of about two.

3.4. Application to Tianwen-1 Observation

Mars Ion and Neutral Particle Analyzer (MINPA), carried by Tianwen-1′s orbiter, observes plasma and ENAs [29] along an orbit of 265 km × 12,000 km with an inclination angel of 93°. MINPA has a ring FOV of 360° × 9.7° divided into 16 azimuth sectors for ENA observation. The sun falls into the FOV for about 2/3 of the cycle each orbit. The energy range of the ENA measurements is 50 eV–3 keV.

Figure 7 shows one orbit of H-ENA observation on 31 December 2021. MINPA was in the SW before 3:59 UTC, observing the SW H-ENA at around 1 keV. Thereafter, MINPA observed the hotter MS H-ENAs at lower energy in the MS. Meanwhile, MINPA ion observation gave an average SW velocity of 459 km/s between 3:00 and 3:30 UTC [30].

Figure 8 shows the half-hour averaged count rate of MINPA on 31 December 2021 between 3:00 and 3:30 UTC. The SW H-ENA count rate peak is around 1 keV. From the Gaussian fitting (red line), based on Equation (8), SW velocity is calculated to be 460 ± 27 km/s, with a 95% confidence level. On average, the result is consistent with the SW velocity of 459 km/s. Here, we use count rate instead of different flux because the in-flight G-factor of the ENA detector is still to be further calibrated.

4. Discussion

ENA flux modeling and the SW inversion are carried out based on a single-fluid MHD model [25,26]. The MHD model assumes ions have isotropic distribution. This assumption is suitable for the steady solar wind, which is usually believed to be thermally isotropic. However, observations in the terrestrial MS often exhibit proton anisotropy [31], which might be more pronounced in the Martian MS [32]. Therefore, the MS H-ENA flux predicted by the ENA model under isotropy assumption might deviate from the observations. Regarding the SW H-ENA, considering that the bulk velocity is much greater than the thermal velocity, the model’s predicted distribution should not deviate too much from reality. Inversion of the SW parameters is based on a prior distribution. Appropriate choice of the prior distribution is important to keep the inversion robust. Here, we adopted a Maxwellian thermal velocity distribution to demonstrate inversion using the algorithm. Other distributions, such as Kappa distribution, will be considered in the future to better characterize the solar wind.

Regarding the SW inversion, MS H-ENA is a background component to be separated and eliminated by Gaussian fitting. The quality of the inversion results depends on the strength of the SW H-ENA flux in contrast to the MS H-ENA, which might make a noisier background for the SW H-ENA due to anisotropy. In the future, the ENA observations from Tianwen-1 will be further analyzed to evaluate the consequences of the MS anisotropy quantitatively. Currently, the observation data in Figure 7 are free of the MS H-ENA, since at that time, Tianwen-1 was in the SW and providing plasma measurements of the SW. Therefore, the MS H-ENA did not interfere with the inversion.

5. Conclusions

ENA remote sensing is a new technique to explore the space plasma at Mars. To simulate the ENA observations in the near-Mars space, a H-ENA model was set up, based on the plasma distribution determined by MHD simulation of the solar wind interaction with Mars. Based on the H-ENA model, the relationship between the SW H-ENA differential flux curve and the SW parameters was established. An algorithm to inverse the SW parameters from the H-ENA flux was proposed. The influences of the instrument resolution were discussed, and the inversion approach was verified using the simulated H-ENA flux, along with H-ENA observations by Tianwen-1.

Lack of long-term monitoring of upstream SW at Mars poses an obstacle to the study of the Martian space environment. SW H-ENAs carrying the upstream SW information can be remotely sensed by missions far away from the solar wind. Therefore, real-time monitoring of the upstream SW parameters becomes possible by means of H-ENAs’ inversion.

Furthermore, the time variations of the solar wind and exosphere can also be retrieved from the SW H-ENA observations, to reveal the exosphere seasonal variations, the 3D topology of the bow shock, etc. Further work will be conducted to investigate ENA inversion in the Martian environment.