Target Scattering Feature Extraction Based on Parametric Model Using Multi-Aspect SAR Data
Abstract
:1. Introduction
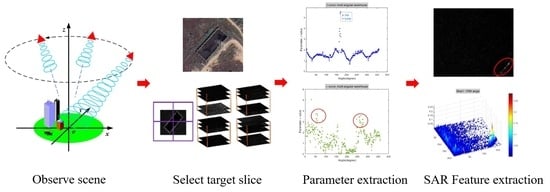
2. Methodology and Experimental Procedures
2.1. Multi-Aspect SAR Observing Model
2.2. Parametric Model
2.2.1. Distribution Function
2.2.2. Estimated Parameters
2.3. Experiment Procedure
3. Dataset and Scattering Analysis
3.1. Dataset
3.2. Scattering and Statistical Analysis
4. Parametric Characterization
4.1. Target Parameter Result I
4.2. Target Parameter Result II
4.2.1. Parameter β
4.2.2. Parameter σ
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ponce, O.; Prats-Iraola, P.; Pinheiro, M.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully Polarimetric High-Resolution 3-D Imaging with Circular SAR at L-Band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]
- Poisson, J.B.; Oriot, H.M.; Tupin, F. Ground Moving Target Trajectory Reconstruction in Single-Channel Circular SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1976–1984. [Google Scholar] [CrossRef] [Green Version]
- Zeng, T.; Yin, W.; Ding, Z.; Long, T. Motion and Doppler Characteristics Analysis Based on Circular Motion Model in Geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1132–1142. [Google Scholar] [CrossRef]
- Shen, W.; Lin, Y.; Yu, L.; Xue, F.; Hong, W. Single Channel Circular SAR Moving Target Detection Based on Logarithm Background Subtraction Algorithm. Remote Sens. 2018, 10, 742. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Lin, Y.; Wang, Y.; Yang, Y.; Shen, W.; Teng, F.; Hong, W. DEM Generation with a Scale Factor Using Multi-Aspect SAR Imagery Applying Radargrammetry. Remote Sens. 2020, 12, 556. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Jiang, X.; Li, Z.; Liu, X.; Zhou, Z. Feature-Enhanced Speckle Reduction via Low-Rank and Space-Angle Continuity for Circular SAR Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7734–7752. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Y.; Hong, W.; Xu, R.; Zhuo, Z.; Yin, Q. Anisotropic Scattering Detection for Characterizing Polarimetric Circular SAR Multi-Aspect Signatures. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4543–4546. [Google Scholar] [CrossRef]
- Xiong, G.; Wang, F.; Zhu, L.; Li, J.; Yu, W. SAR Target Detection in Complex Scene Based on 2-D Singularity Power Spectrum Analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9993–10003. [Google Scholar] [CrossRef]
- Lin, B.; Yang, X.; Wang, J.; Wang, Y.; Wang, K.; Zhang, X. A Robust Space Target Detection Algorithm Based on Target Characteristics. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ding, B.; Wen, G.; Huang, X.; Ma, C.; Yang, X. Data Augmentation by Multilevel Reconstruction Using Attributed Scattering Center for SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 979–983. [Google Scholar] [CrossRef]
- Ishimaru, A.; Chan, T.K.; Kuga, Y. An imaging technique using confocal circular synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1524–1530. [Google Scholar] [CrossRef]
- Soumekh, M. Reconnaissance with slant plane circular SAR imaging. IEEE Trans. Image Process. 1996, 5, 1252–1265. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Hong, W.; Tan, W.; Wang, Y.; Xiang, M. Airborne circular SAR imaging: Results at P-band. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5594–5597. [Google Scholar] [CrossRef]
- Feng, S.; Lin, Y.; Wang, Y.; Teng, F.; Hong, W. 3D Point Cloud Reconstruction Using Inversely Mapping and Voting from Single Pass CSAR Images. Remote Sens. 2021, 13, 3534. [Google Scholar] [CrossRef]
- Ai, J.; Mao, Y.; Luo, Q.; Jia, L.; Xing, M. SAR Target Classification Using the Multikernel-Size Feature Fusion-Based Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Ai, J.; Tian, R.; Luo, Q.; Jin, J.; Tang, B. Multi-Scale Rotation-Invariant Haar-Like Feature Integrated CNN-Based Ship Detection Algorithm of Multiple-Target Environment in SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10070–10087. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, Y.; Wang, Y.P.; Hong, W.; Yu, L. Target multi-aspect scattering sensitivity feature extraction based on Circular-SAR. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2722–2725. [Google Scholar] [CrossRef]
- Teng, F.; Lin, Y.; Wang, Y.; Shen, W.; Feng, S.; Hong, W. An Anisotropic Scattering Analysis Method Based on the Statistical Properties of Multi-Angular SAR Images. Remote Sens. 2020, 12, 2152. [Google Scholar] [CrossRef]
- Yue, X.; Teng, F.; Lin, Y.; Hong, W. A Man-Made Target Extraction Method Based on Scattering Characteristics Using Multiaspect SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11699–11712. [Google Scholar] [CrossRef]
- Kheirandish, A.; Fatehi, A.; Gheibi, M.S. Identification of Slow-Rate Integrated Measurement Systems Using Expectation–Maximization Algorithm. IEEE Trans. Instrum. Meas. 2020, 69, 9477–9484. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Marano, S.; Rosamilia, M. Structured Covariance Matrix Estimation with Missing-(Complex) Data for Radar Applications via Expectation-Maximization. IEEE Trans. Signal Process. 2021, 69, 5920–5934. [Google Scholar] [CrossRef]
- Gao, Y.; Xing, M. A method for extracting amplitude attribute of scattering centers in SAR. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2665–2668. [Google Scholar] [CrossRef]
- Zhou, X. An EM Algorithm Based Maximum Likelihood Parameter Estimation Method for the G0 Distribution. Acta Electron. Sin. 2013, 41, 178–184. [Google Scholar]
- Li, Y.; Zhu, D. The Geometric-Distortion Correction Algorithm for Circular-Scanning SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2010, 7, 376–380. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I.; Gomes, N.R. Stability in Sar Change Detection Results Using Bivariate Rayleigh Distribution for Statistical Hypothesis Test. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 37–40. [Google Scholar] [CrossRef]
- Bian, Y.; Mercer, B. SAR probability density function estimation using a generalized form of K-distribution. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1136–1146. [Google Scholar] [CrossRef]
- Shan, Z.; Wang, C.; Zhang, H.; Wu, F. Change detection in urban areas with high resolution SAR images using second kind statistics based G0 distribution. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4600–4603. [Google Scholar] [CrossRef]
- Da Costa Freitas, C.; Frery, A.C.; Correia, A.H. The polarimetric G distribution for SAR data analysis. Environmetrics 2005, 16, 13–31. [Google Scholar] [CrossRef]
- Yi, W.; Jiang, H.; Kirubarajan, T.; Kong, L.; Yang, X. Track-Before-Detect Strategies for Radar Detection in G0-Distributed Clutter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2516–2533. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, H.; Li, L.; Liu, X. A Novel Statistical Texture Feature for SAR Building Damage Assessment in Different Polarization Modes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 154–165. [Google Scholar] [CrossRef]
- Dempster, A.P. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–22. [Google Scholar]
- Roberts, W.; Furui, S. Maximum likelihood estimation of K-distribution parameters via the expectation-maximization algorithm. IEEE Trans. Signal Process. 2000, 48, 3303–3306. [Google Scholar] [CrossRef] [Green Version]
- Tison, C.; Nicolas, J.M.; Tupin, F.; Maitre, H. A new statistical model for Markovian classification of urban areas in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2046–2057. [Google Scholar] [CrossRef]
- Kumar, S.; Chaudhary, V.; Singh, A.; Chauhan, P. Scattering-based Analysis of South Polar Crater of the Lunar Surface Using L-band SAR Data of Chandrayaan-2 Mission. In Proceedings of the 2021 IEEE International India Geoscience and Remote Sensing Symposium (InGARSS), Virtual Conference, 6–10 December 2021; pp. 459–462. [Google Scholar] [CrossRef]
- Li, Y.; Yin, Q.; Lin, Y.; Hong, W. Anisotropy Scattering Detection From Multiaspect Signatures of Circular Polarimetric SAR. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1575–1579. [Google Scholar] [CrossRef]
- Xu, L.; Yuille, A. Robust principal component analysis by self-organizing rules based on statistical physics approach. IEEE Trans. Neural Netw. 1995, 6, 131–143. [Google Scholar] [CrossRef]
- Yang, D.; Yang, X.; Liao, G.; Zhu, S. Strong Clutter Suppression via RPCA in Multichannel SAR/GMTI System. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2237–2241. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Raman, S. Robust PCA-based solution to image composition using augmented Lagrange multiplier (ALM). Vis. Comput. 2016, 32, 591–600. [Google Scholar] [CrossRef]
- Ulander, L.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef] [Green Version]
- Ponce, O.; Prats, P.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A. Processing of Circular SAR trajectories with Fast Factorized Back-Projection. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3692–3695. [Google Scholar] [CrossRef]
- Liu, J.; He, S.; Zhang, L.; Zhang, Y.; Zhu, G.; Yin, H.; Yan, H. An Automatic and Forward Method to Establish 3-D Parametric Scattering Center Models of Complex Targets for Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8701–8716. [Google Scholar] [CrossRef]
- Jia, L.; Li, M.; Zhang, P.; Wu, Y.; Zhu, H. SAR Image Change Detection Based on Multiple Kernel K-Means Clustering with Local-Neighborhood Information. IEEE Geosci. Remote Sens. Lett. 2016, 13, 856–860. [Google Scholar] [CrossRef]
- Gong, M.; Cao, Y.; Wu, Q. A Neighborhood-Based Ratio Approach for Change Detection in SAR Images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 307–311. [Google Scholar] [CrossRef]
















| Parameters | Value |
|---|---|
| Carrier frequency | 5.4 GHz |
| Bandwidth | 560 MHz |
| PRF | 2358 Hz |
| Flight height | 3 km |
| Flight radius | 5 km |
| Range resolution | 0.27 m |
| Azimuth resolution | 0.3 m |
| Selected Angle | Slice1 | Slice2 | Slice3 | Slice4 |
|---|---|---|---|---|
| 50th | 4.0027 | 2.0413 | 1.7205 | 2.2264 |
| 100th | 3.3064 | 1.8641 | 1.5675 | 1.6111 |
| 150th | 3.7451 | 2.6033 | 2.2140 | 2.6689 |
| 167th | 7.4318 | 9.7013 | 3.8194 | 6.4576 |
| 168th | 4.7545 | 3.0603 | 4.6331 | 9.0546 |
| 169th | 2.8312 | 2.0429 | 5.3442 | 13.1805 |
| 170th | 3.8806 | 2.3414 | 5.6539 | 12.3468 |
| 171st | 3.2174 | 2.1953 | 4.6044 | 8.5438 |
| 172nd | 3.0776 | 2.0824 | 2.0654 | 2.3499 |
| 173rd | 3.2524 | 1.9992 | 1.9934 | 2.0072 |
| 200th | 2.7945 | 2.3107 | 1.7552 | 2.1728 |
| 250th | 3.8236 | 2.1811 | 2.3832 | 2.6348 |
| 300th | 2.9585 | 1.6003 | 1.8814 | 2.5514 |
| 350th | 7.5452 | 2.5207 | 2.3703 | 2.3482 |
| Slice1 | Slice2 | Slice3 | Slice4 | ||||
|---|---|---|---|---|---|---|---|
| 167th | 0.8057 | 167th | 0.08114 | 170th | 0.2568 | 169th | 0.02839 |
| 0.1181 | 0.01625 | 0.02183 | 0.01483 | ||||
| 100th | 1.644 | 100th | 32 | 100th | 18.34 | 100th | 13.27 |
| 0.7367 | 0.4394 | 0.337 | 0.3396 | ||||
| 200th | 21.6 | 200th | 9.943 | 200th | 23.76 | 200th | 4.326 |
| 1.393 | 0.3437 | 0.6441 | 0.2995 | ||||
| 300th | 43.39 | 300th | 29.98 | 300th | 37.44 | 300th | 11.82 |
| 1.163 | 0.4281 | 0.5717 | 0.7429 | ||||
| Selected Angle | Slice1 | Slice2 | Slice3 | Slice4 |
|---|---|---|---|---|
| 50th | 1.7803 | 1.8528 | 0.5084 | 1.9273 |
| 100th | 1.1458 | 1.9270 | 0.8918 | 2.4094 |
| 150th | 1.4322 | 1.2189 | 1.8844 | 2.6954 |
| 167th | 0.0114 | 0.0144 | 0.0056 | 0.0092 |
| 168th | 0.0118 | 0.0086 | 0.0069 | 0.0124 |
| 169th | 0.0114 | 0.0101 | 0.0073 | 0.0183 |
| 170th | 0.0107 | 0.0086 | 0.0077 | 0.0173 |
| 171st | 0.0122 | 0.0119 | 0.0064 | 0.0135 |
| 172nd | 0.1081 | 0.0917 | 0.0120 | 0.0203 |
| 173rd | 0.4637 | 0.3360 | 0.0554 | 0.0809 |
| 200th | 1.2545 | 0.2853 | 1.4792 | 0.7440 |
| 250th | 10.7151 | 2.6559 | 5.3388 | 3.8337 |
| 300th | 4.3230 | 1.6239 | 1.6452 | 1.6228 |
| 350th | 12.3619 | 3.6842 | 2.9505 | 3.0283 |
| Parameters | Slice1: 170th Angle | Slice1: 100th Angle | Slice1: 200th Angle | Slice1: 300th Angle |
|---|---|---|---|---|
| 0.0107 | 1.1458 | 1.2545 | 4.3230 | |
| Maximum Energy | 0.2824 | 66.71 | 1430 | 1.076 × 104 |
| Slice2: 170th angle | Slice2: 100th angle | Slice2: 200th angle | Slice2: 300th angle | |
| 0.0086 | 1.9270 | 0.2853 | 1.6239 | |
| Maximum Energy | 0.4417 | 2.524 × 104 | 459.4 | 5451 |
| Slice3: 170th angle | Slice3: 100th angle | Slice3: 200th angle | Slice3: 300th angle | |
| 0.0077 | 0.8918 | 1.4792 | 1.6452 | |
| Maximum Energy | 0.8304 | 5425 | 5976 | 8.358 × 104 |
| Slice4: 170th angle | Slice4: 100th angle | Slice4: 200th angle | Slice4: 300th angle | |
| 0.0173 | 2.4094 | 0.7440 | 1.6228 | |
| Maximum Energy | 0.1128 | 2.408 × 105 | 430.4 | 597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, X.; Teng, F.; Lin, Y.; Hong, W. Target Scattering Feature Extraction Based on Parametric Model Using Multi-Aspect SAR Data. Remote Sens. 2023, 15, 1883. https://doi.org/10.3390/rs15071883
Yue X, Teng F, Lin Y, Hong W. Target Scattering Feature Extraction Based on Parametric Model Using Multi-Aspect SAR Data. Remote Sensing. 2023; 15(7):1883. https://doi.org/10.3390/rs15071883
Chicago/Turabian StyleYue, Xiaoyang, Fei Teng, Yun Lin, and Wen Hong. 2023. "Target Scattering Feature Extraction Based on Parametric Model Using Multi-Aspect SAR Data" Remote Sensing 15, no. 7: 1883. https://doi.org/10.3390/rs15071883
APA StyleYue, X., Teng, F., Lin, Y., & Hong, W. (2023). Target Scattering Feature Extraction Based on Parametric Model Using Multi-Aspect SAR Data. Remote Sensing, 15(7), 1883. https://doi.org/10.3390/rs15071883