A New Method to Combine Coastal Sea Surface Height Estimates from Multiple Retrackers by Using the Dijkstra Algorithm

Abstract

To increase data availability and accuracy in the coastal zone, especially in the last 5 km to the coast, we present a SCMR (Seamless Combination of Multiple Retrackers) processing strategy to combine sea surface height (SSH) estimates from waveform retrackers of SGDR MLE4, ALES, WLS3 and MB4 for Jason-3 and Saral missions, and of SAMOSA and SAMOSA+ for Sentinel-3A mission in the Australian coastal zone. The SCMR does not require the waveform classification result. It includes two steps: (1) estimating and removing the SSH bias due mainly to the significant wave height (SWH) difference-dependent height differences, and (2) determining the optimal along-track SSH profile by using the Dijkstra algorithm. In the study region, the results show that the SCMR increases the data availability by up to 15% in the last 5 km to the coast and reduces the noise level by 28–34% at the spatial scales < 2.5 km. The validation results against tide gauges show that SCMR-derived SSH estimates achieve a better accuracy than that from any single retracker, with the improvement percentage of 6.26% and 4.94% over 0–10 km and 20–100 km distance bands, respectively.

1. Introduction

Combining sea surface height (SSH) estimates from multiple retrackers is an efficient way to retrieve more high-quality data from altimeters in coastal zones [1,2,3,4,5]. This is because each retracker may well handle certain types of coastal waveforms but cannot deal with all types of waveforms. In addition, the combination of multiple retrackers would result in redundant SSH estimates at a given along-track point, and thus, making it possible to determine the best possible SSH estimate at the point and then to improve the precision and accuracy of the along-track SSH estimates. Previous studies have taken two steps to combine multiple retrackers [1,2,3,4]. The first step is to calculate and remove the systematic bias between SSH estimates from different retrackers. To guarantee the seamless transition of SSH estimates from open oceans to the coast and from one retracker to others, the bias should be reduced to the millimeter level or even smaller [5]. The second step is to select the improved SSH estimate at each along-track point based on waveform classification results or the statistical features of the retracking results [3].

In our previous research, we combined three different retrackers (i.e., ALES, WLS3 and MB4) to process the Jason-2 altimeter data over the Australian coastal zone [4]. These retrackers are selected because they can handle three dominant types of waveforms in Australian coastal zones [4]. The ALES (Adaptive Leading Edge Subwaveform) and WLS3 (3-parameter Weighted Least Squares) retrackers can process coastal waveforms with land contamination observed in the waveform trailing edge or close to the leading edge, respectively [6,7]. The MB4 (4-parameter modified Brown model) retracker can deal with quasi-specular waveforms reflected from the calm waters [8]. A seamless transition of SSH estimates from these three retrackers was achieved by estimating and removing the height differences that depend on the significant wave height (SWH) differences [4]. After that, the improved SSH estimate at each along-track point is selected based on the corresponding waveform type. The performance of the processing strategy is dependent on the accuracy of the waveform classification result, which is limited within a distance of 0–5 km to the coast, due mainly to the wild diversity of waveform types.

The motivation of this study is, therefore, to increase the data availability and accuracy while avoiding the errors caused by the misclassification of coastal waveforms. We present a novel SCMR (Seamless Combination of Multiple Retrackers) strategy that uses the Dijkstra [9] algorithm to obtain the improved along-track SSH estimates derived from multiple retrackers. The Dijkstra algorithm makes use of the edge weight between two arbitrary points to determine the shortest path through minimizing the total edge weights among the start point and all other points in the network [10,11]. Roscher et al. [10] used the Dijkstra algorithm to determine the along-track SSH estimates. They assumed that a waveform has several leading edges and only used the STAR retracker to retrack each leading edge. The Dijkstra algorithm was then used to determine the SSH estimate that is associated to the leading edge best reflecting the ocean surface. However, using a single retracker cannot process all types of waveforms near the coast well [1,3,5], and retracking only the waveform leading edge may miss important information carried in other parts of waveforms. Here, our proposed method differs from that by Roscher et al. [10]. We retrack a waveform using the state-of-art coastal retrackers and combine derived SSH estimates using the Dijkstra algorithm.

Our SCMR strategy is developed by considering the fact that altimeter SSH estimates do not change significantly at the along-track spatial scale of 150–300 m [12]. Therefore, the Dijkstra algorithm can be used to derive the SSH profile for each ground track based on the SSH variation pattern of the profile, which has the potential to improve the precision of the along-track SSH estimates in both open oceans and coastal zones. We also expect that the SCMR will improve the data accuracy in the last 5 km to the coast, where the increasing number of waveform types requires the use of different retrackers to deal with different waveform types [4]. To test the performance of the SCMR strategy, we applied it to multi-altimetry missions, including Jason-3, Saral and Sentinel-3A missions, which represent different altimeter techniques [13,14,15], in the Australian coastal zone. The SSH estimates from the above three retrackers, as well as those from the MLE4 (4-parameter Maximum Likelihood Estimator) retracker provided by the SGDR (Sensor Geophysical Data Record) product, are used for Jason-3 and Saral missions. Note that the latest ALES+ retracker is not adopted in this study because the ALES retracker can achieve better performance in the last 2-8 km to the coast [16]. For Sentinel-3A, our strategy is used to combine the SSH estimates from the SAMOSA (SAR Altimetry Mode Studies and Applications) and SAMOSA+ retrackers, provided by the official product described in Section 2.

The aim of this paper is therefore twofold: (1) testing whether the bias-removing method proposed in our previous research [4] is also applicable for minimizing the bias between the open ocean and dedicated coastal retrackers, as well as for Saral and Sentinel-3A missions and (2) evaluating the improvement in terms of precision and accuracy of SSH estimates brought by the SCMR processing strategy. The rest of the paper is organized as follows. Section 2 presents the data and study region. The methods used for removing bias from SSH estimates, and to assess the accuracy and precision of sea level anomaly (SLA) estimates are shown in Section 3. The performance of the processing scheme (i.e., SCMR) is presented and discussed in Section 4 and Section 5. The conclusions of this study are summarized in Section 6.

2. Data and Study Region

To test the performance of our SCMR processing strategy, the data from multi-altimetry missions are used in this study, including two years of altimeter data from Jason-3 (February 2016–May 2018), Saral (May 2013–May 2015) and Sentinel-3A (April 2016–May 2018). The hourly tide gauge data covering the time span 2013–2018 are also obtained from ABSLMP (Australian Baseline Sea Level Monitoring Project).

2.1. Altimeter Data

The Jason-3 is a follow-on mission to OSTM/Jason-2, which carries a Ku-band (i.e., 13.575 GHz) pulse-limited altimeter. As it flies on the same ground tracks as Topex/Poseidon and Jason-1/2, Jason-3 plays a crucial role in monitoring the long-term sea level changes at both global and regional scales. Compared to the Jason-3, the Saral is a follow-on mission to Envisat, whose main component is a mono-frequency Ka-band (i.e., 35.75 GHz) pulse-limited altimeter. The use of a higher frequency Ka-band Altika altimeter dramatically reduces the diameter of the altimeter footprint size from 15 km for Jason-3 to only 4 km for Saral, leading to a better spatial resolution [17]. Moreover, the enhanced bandwidth (500 MHz for Saral vs. 320 MHz for Jason-3) results in a higher vertical resolution (0.30 m for Saral vs. 0.46 m for Jason-3). As such, the Saral performs better than Jason-3 in avoiding land contamination in the coastal zone [18]. Finally, the Sentinel-3A carries the first altimeter that operates in SAR (Synthetic Aperture Radar) mode over the global ocean. The quality of measurements in coastal zones is also improved due to its smaller footprint size in the along-track direction (i.e., 300 m) and higher signal-to-noise ratio [14].

In this study, we use the Level-2 altimeter dataset, because it contains not only the altimetric waveforms but also the necessary information to calculate the along-track SLA estimates. Of these data products, the Version F SGDR products for both Jason-3 and Saral are distributed by the AVISO+ (Archivage, Validation et Interprétation des données des Satellites Océanographiques plus), which can be downloaded via a registered FTP account (ftp-access.aviso.altimetry.fr). The SAMOSA data for Sentinel-3A are contained in the NTC (Non-Time-Critical) product, which is administered by the EUMETSAT (European Organization for the Exploitation of Meteorological Satellites, https://data.eumetsat.int/search?query= (accessed on 2 February 2023)). The SAMOSA+ data are available in the SARvatore (SAR Versatile Altimetric Toolkit for Ocean Research and Exploitation) data repository, which was used in our previous research [19].

2.2. Tide Gauge Records

The hourly sea levels along the coastline are obtained from 12 tide gauge stations administered by the ABSLMP. The observations from ABSLMP can be freely downloaded through the website (http://www.bom.gov.au/oceanography/projects/abslmp/data/index.shtml (accessed on 2 February 2023)), which have been corrected by vertical land motion associated with Glacial Isostatic Adjustment (GIA) [20]. The name and location of the selected tide gauges are shown in Figure 1. The rate of vertical land motion from present-day GIA models across Australia ranges from −0.20 to 0.03 mm/yr⁻¹ [21]. The impact of vertical land motion associated with GIA on tide gauge data is minimized in this study by using the SLA estimates rather than absolute sea level measurements.

2.3. Study Region

The Australian coastal zone is selected as the study region (Figure 1). The coastal sea levels around Australia are dominated by several major current systems and are highly affected by ENSO-related signals [20]. The sea states in the northern part of Australia are affected by the monsoon and trade winds where the wave heights are smaller than 2 m [19]. The increased wave heights in South Australia are due to westerly winds and Southern Ocean Swell [22].

Note that the Australian coastal zone is highly populated and threatened by the high rate of sea level rise greater than the global mean sea level rise (i.e., ~3 mm yr⁻¹) [20,23]. Therefore, it is of great importance to retrieve high-quality coastal sea levels from multi-altimetry missions in order to better evaluate the negative impact of sea level change. Moreover, the existence of high-quality tide gauge records also makes it convenient for us to validate the accuracy and precision of the reprocessed altimeter datasets.

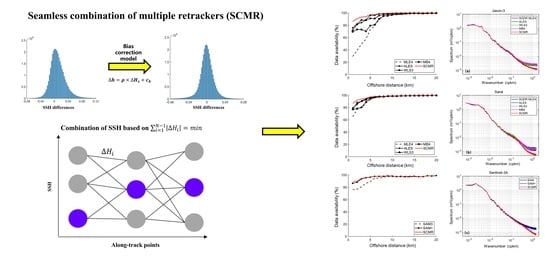
3. Methodology

The SCMR processing strategy proposed in this study aims to achieve the seamless combination of SSH estimates from multiple retrackers at each along-track point. Its flow diagram is shown in Figure 2 for altimetry missions of Jason-3, Saral and Sentinel-3A, respectively.

As illustrated, the SCMR starts from the range estimates derived from different waveform retrackers, and ends with quality-controlled along-track SSH estimates. The main input data source to SCMR is the altimeter range estimates from different waveform retrackers. Waveform retracking is a technique that reprocesses the altimetric waveforms to estimate parameters including the range and SWH. In this study, the retracked ranges are derived from SGDR MLE4, ALES, WLS3, MB4, SAMOSA and SAMOSA+ retrackers. Readers can refer to open literatures in [4,8,24] for detailed information about these retrackers. The SCMR include the following operations:

(1)

To optimize the range and geophysical corrections in the study area. The along-track SSH estimates are obtained as follows,

$$SSH = altitude - retracked\_range - corrections$$

(1)

where the retracked range is derived from the waveform retracker, which is the input as illustrated in Figure 2.The appropriate range and geophysical corrections are selected based on the trade-off between minimum SLA variance criterion and data availability, which will be described in Section 3.1.

(2)

To calculate the temporal-averaged MSS at each along-track point (Section 3.1). The SSH estimates from all repeat cycles are referenced to the Topex ellipsoid and reduced to the nominal points of each reference track by using the nearest neighborhood approach. The reduced SSH estimates are then used to calculate the temporal-averaged MSS at each along-track point following the method in [4]. The along-track MSS can be used to remove the SSH outliers (see Section 3.4).

(3)

To determine and remove the bias of SSH estimates from different retrackers. The SSH bias is estimated with respect to the WLS3 (SAMOSA+) retracker for Jason-3 and Saral missions (Sentinel-3A mission) by the method introduced in Section 3.2.

(4)

To derive the most appropriate along-track SSH profile using the Dijkstra algorithm. This assumes that the high-rate SSH estimates vary insignificantly along the ground track (see Section 3.3). The along-track SLA profile is finally derived as the difference between the along-track SSH and MSS.

Finally, the SCMR results will be validated against independent tide gauges. The methodology used is given in this section.

3.1. Regional Corrections and MSS

In this section, we present the regional optimized wet tropospheric and geocentric ocean tide corrections, along with the comparison of the regional mean SSH profile with the MSS derived from CLS15 (Collecte Localisation Satellites 2015) and DTU21 (Danmarks Tekniske Universitet 2021) global models [25].

In addition to erroneous range estimates, the inaccurate range and geophysical corrections would also cause the degradation of SSH estimates in the coastal zone. Among them, the wet tropospheric correction (WTC) and geocentric ocean tide correction are two terms that can significantly affect the SSH estimates in the coastal zone [12]. Therefore, it is necessary to analyze the performance of these two corrections from different methods. Here, we tested different combinations of WTC and geocentric ocean tide correction provided by the official product. The optimal combination is determined based on the trade-off between SLA variance and data availability [19]. The results are shown in Figure 3.

As we can see from the graph, the FES2014 (Finite Element Solution 2014) ocean tide model is always better than the GOT4.10c (Goddard Ocean Tide) ocean tide model in the study region for all selected altimetry missions. When it comes to the WTC, the situation is quite different. For Jason-3, the WTC from ECMWF (European Center for Medium-range Weather Forecasts), radiometer and GPD+ (Global Navigation Satellite System Derived Path Delay Plus) achieves similar performance in terms of both SLA variance and data availability. For Saral, the best result is the WTC from GPD+ though its SLA variance is higher than that from radiometer. This is a trade-off between SLA variance and data availability, considering that the data availability decreases significantly in the last 5 km to the coast by applying the WTC from radiometer (Figure 3e). For Sentinel-3A, the best result is the WTC from ECMWF model, from which the minimum SLA variance and maximum data availability are achieved. Since the GPD+ WTC correction for Sentinel-3A is not available at present, we cannot conduct the comparison between ECMWF and GPD+ for Sentinel-3A. The above results show that the optimal regional corrections are not only dependent on the study region, but also vary with different altimetry missions.

Previous studies have shown that regional MSS is more accurate than the interpolated values from the global MSS model in coastal zones [4,26]. Here, we compare the along-track mean SSH profile with the two latest global MSS models from CLS15 and DTU21 for all selected altimetry missions. The results of SLA variance as a function of distance to the coast are shown in Figure 4. As illustrated in the graph, the regional MSS always achieves better performance than the global MSS model. The improvement of regional MSS is observed in the distance band of 3–20 km to the coast, where the SLA variance decreases by 0.01–0.02 m². Note that the regional along-track MSS was computed using only two years of reprocessed altimeter data in this study. As such, a more significant improvement in modeling the regional MSS by using longer data records would be expected.

The result also shows that the performance of CLS15 and DTU21 models varies with different altimetry missions. The DTU21 model performs better than CLS15 for Jason-3 and Saral missions, while the CLS15 model outperforms the DTU21 model for the Sentinel-3A mission. To summarize the results, the regional corrections and MSS used in this study are listed in

Table 1. Regional range/geophysical corrections and MSS used in this study. The DTC and WTC represent the dry and wet tropospheric corrections, while the DAC represents the dynamic atmospheric correction.

	Missions	Jason-3	Saral	Sentinel-3A
Corrections
DTC		ECMWF	ERA	ECMWF
WTC		GPD+ [27]		ECMWF
Ionospheric correction		GIM
Sea state bias		Peng and Deng [19]
Geocentric ocean tide		FES2014
DAC		MOG2D
Solid earth tide		Cartwright and Taylor [28] Cartwright and Taylor [29]
Pole tide		Desai et al. [30]
Mean sea surface		Along-track MSS [4]

.

3.2. Removing SSH Bias

As different retrackers adopt different models and fitting algorithms to process altimeter waveforms, there inevitably exists bias between SSH estimates from two arbitrary retrackers [31]. The bias is typically estimated as the average of SSH differences. Its magnitude could vary from several centimeters to meters depending on the retrackers and coastal regions taken for bias estimation [1,2,3,4]. Our recent study [4] has pointed out that the SSH differences derived from two physical retrackers are linearly correlated with the corresponding SWH differences. Based on this knowledge, we have developed a method that removes the SWH-dependent SSH differences and also precisely estimates the SSH bias (i.e., mean SSH differences). For the Jason-2 mission, the SSH bias of a few millimeters has been determined for ALES (and MB4) with respect to WLS3 in [4]. The SSH differences with respect to a reference retracker, ∆h, is presented using a linear regression as follows:

$$∆h=\rho \times ∆H_s+c_b$$

(2)

where $\rho$ and $c_b$ are parameters of the linear regression slope and intercept between SSH differences $∆h$ and SWH differences $∆H_s$. In Equation (2), the first term presents the SWH difference-dependent SSH differences, while the second term $c_b$ is the SSH differences caused mainly by different retracker algorithms. Once parameters $\rho$ and $c_b$ are estimated, the SSH bias between retrackers is computed as the average of SSH differences and is removed. In this paper, the estimated bias is referenced to the WLS3 (SAMOSA+) retracker for conventional (SAR) altimeter missions.

3.3. Combining SSH Estimates by Dijkstra Algorithm

The Dijkstra algorithm [9] is an important component used in the SCMR to determine the seamless combination of the along-track SSH estimates. The algorithm is designed to find the shortest path from the start node to the end node [9,10,11] in the graph based on the distance (i.e., edge weight) between individual connected nodes (Figure 5). In our case, each node represents the SSH estimate from a single retracker (e.g., SGDR MLE4) at a given along-track point. The edge weight between two connected nodes is the absolute SSH difference between them. The most appropriate SSH profile between the point offshore and the point closest to the coast is then derived by applying the Dijkstra algorithm.

As examples, Figure 6 shows the SSH profiles for track 64 of Jason-3 and track 705 of Sentinel-3A, with the location of ground tracks shown in Figure 1. As illustrated in Figure 3, there are four alternatives from SGDR MLE4, ALES, WLS3 and MB4 retrackers for each Jason-3 along-track point and two alternatives from SAMOSA and SAMOSA+ retrackers for each Sentinel-3A along-track point. The SSH estimates along the selected shortest path (red line in Figure 6) satisfy the condition that SSH estimates do not significantly vary at the spatial scale of 150–300 m. They are referred as to the most appropriate SSH estimates along the track, namely the SCMR along-track SSH profile.

3.4. Assessing the Performance of SCMR Strategy

The failure of waveform retracking and degraded geophysical corrections would result in erroneous SSH estimates (hereafter called SSH outliers). Therefore, it is necessary to detect and remove the SSH outliers. Here, we generate the regional MSS following the method proposed in [4]. The SSH estimates, whose absolute differences with respect to the regional MSS are greater than 1.0 m, are considered as outliers and thus removed. The performance of the SCMR strategy is then assessed using quality-controlled SLA estimates in two ways: (1) evaluation of the data precision and availability against the offshore distance and (2) validation of the altimeter SLA time series against tide gauge SLA time series at each along-track point.

Although the scope of this study is to obtain an improved SSH profile in the coastal zone, it is interesting to investigate how the performance of SCMR is over open oceans. Therefore, the data points within 0–20 km nearshore and 20–100 km offshore are evaluated and validated, respectively. For data points within 20 km from the coast, the offshore distance is divided into 20 distance bands with an interval of 1 km, and the number of 20 Hz SLA estimates is calculated and represented as data availability.

The median value of the standard deviation of 20 Hz SLA estimates within 1 s for each distance band is used to evaluate the data precision [12]. As the sampling rate of the Saral mission is 40-Hz, we resampled the SLA estimates at 20 Hz frequency before conducting the evaluation. A similar method is also conducted for the data points within 20–100 km offshore, but with a distance interval of 5 km. Lastly, the power spectral density (PSD) analysis is also conducted to evaluate the spectrum of 20 Hz SLA estimates at different spatial scales.

The validation procedure can be conducted in three steps. First, the SLA estimates from the altimeter and tide gauge are calculated following the method in [4]. Second, the along-track altimeter SLA estimates are referenced to the nominal ground track provided by the Centre for Topographic studies of the Ocean and Hydrosphere (http://ctoh.legos.obs-mip.fr/altimetry/satellites (accessed on 2 February 2023)). Finally, the temporal averages of both altimeter and tide gauge time series are removed and the root mean square error (RMSE) of the differences between SLA time series at each along-track point is calculated and presented. To test the improvement of the SCMR strategy, the result from the SCMR is also compared with that from the selected single retracker.

4. Results

In this section, we assess the performance of the bias-removing method in reducing the SSH bias with respect to the WLS3 retracker for Jason-3 and Saral missions, as well as SSH bias between SAMOSA and SAMOSA+ retrackers for the Sentinel-3A mission. After that, the results in terms of precision and accuracy of quality-controlled SLA estimates are presented.

4.1. SSH Bias between Different Retrackers

In this study, we applied the bias-removing method (cf. Section 3.2) to Jason-3, Saral and Sentinel-3A altimetry missions. The estimated regression coefficients in Equation (2) are listed in

Table 2. Estimated regression coefficients, $\rho$ and $c_b$, in Equation (2) for Jason-3 and Saral missions with respect to WLS3 retracker, as well as those for Sentinel-3A mission with respect to SAMOSA+ retracker. The $\rho$ is dimensionless and $c_b$ is in millimeters. The slash indicates that there are no data available.

	Missions	Jason-3		Saral		Sentinel-3A
Retrackers		$$\mathit{\rho }$$	$${\mathit{c}}_{\mathit{b}}$$	$$\mathit{\rho }$$	$${\mathit{c}}_{\mathit{b}}$$	$$\mathit{\rho }$$	$${\mathit{c}}_{\mathit{b}}$$
SGDR MLE4		−0.0558	16.9	−0.0778	3.7	/	/
ALES		−0.0676	−17.1	−0.0722	−9.6	/	/
MB4		−0.0866	−2.2	−0.0993	−7.3	/	/
SAM		/	/	/	/	0.0136	5.3

, while the mean and root mean square (RMS) of SSH differences before and after removing the bias are summarized in

Table 3. The mean and root mean square of SSH differences (in millimeters) before and after removing the ∆h from Equation (2) for Jason-3 and Saral missions with respect to the WLS3 retracker, as well as those for Sentinel-3A mission with respect to the SAMOSA+ retracker.

	Missions	Jason-3		Saral		Sentinel-3A
Retrackers		Before	After	Before	After	Before	After
SGDR MLE4		22.9	0.6	6.0	0.2	/	/
ALES		−18.6	−2.6	−6.4	−0.4	/	/
MB4		−7.0	−3.0	−7.8	−0.8	/	/
SAM		/	/	/	/	6.8	0.5

and

Table 4. The root mean square of SSH differences (in millimeters) before and after removing the ∆h from Equation (2) for Jason-3 and Saral missions with respect to the WLS3 retracker, as well as those for Sentinel-3A mission with respect to the SAMOSA+ retracker.

	Missions	Jason-3		Saral		Sentinel-3A
Retrackers		Before	After	Before	After	Before	After
SGDR MLE4		57.4	28.7	45.9	42.7	/	/
ALES		43.2	35.5	37.4	33.6	/	/
MB4		36.2	30.5	36.2	32.3	/	/
SAM		/	/	/	/	63.0	62.5

.

It recalls that the SSH bias includes the SWH difference-dependent SSH difference. As illustrated in Table 2, the moderate negative linear regression slopes $\rho$, for both Jason-3 and Saral missions are observed. The ∆H_s typically varies between −0.4 m and −0.3 m in the study area [4], from which the proportion of SSH bias caused by SWH difference-dependent term 𝜌∆H_s ranges from ~19 mm to ~30 mm for Jason-3 and from ~25 mm to ~34 mm for Saral when considering an average ∆H_s of −0.35 m. The results indicate that there is a significant SWH difference-dependent SSH difference for pulse-limited altimeters. It is also noted that the term $c_b$, which represents the SSH bias when ∆h is mainly retracker-related and uncorrelated with ∆H_s, has different magnitudes for Jason-3 and Saral. Overall, both terms need to be considered to minimize the SSH bias.

Thanks to the Delay-Doppler technique, the linear regression slope for Sentinel-3A is much smaller, indicating that the SSH differences are weakly correlated with SWH differences. Our method is still useful is this case by minimizing the SSH bias from 6.8 mm to only 0.5 mm (Table 3). After applying the bias-removing method, the RMS of SSH differences is reduced by about 16–50% for Jaons-3, 6–11% for Saral and about 1% for Sentinel-3A (Table 4). Therefore, the bias-removing method is applicable for both pulse-limited and SAR mode altimeters.

The results from Table 3 and Table 4 also demonstrate that the method used can successfully estimate the SSH bias between official open ocean retrackers (e.g., SGDR MLE4 or SAMOSA) and dedicated coastal retrackers (e.g., WLS3 or SAMOSA+). As such, the seamless transition of SSH estimates from open oceans to coastal zones is feasible, which would significantly contribute to the study of the interaction between coastal and offshore oceanic processes [32]. After removing the ∆h computed from Equation (2), the SSH bias for all selected altimetry missions are reduced to several millimeters or even sub-millimeters. This confirms that using our method to remove the bias is efficient and the seamless combination of SSH estimates from multiple retrackers is feasible.

4.2. Data Availability and Precision

With the outlier-removed SLA estimates, the performance of the SCMR strategy in the study region is evaluated in terms of data availability and precision following the methods described in Section 3.4. Both data availability and precision are represented as a function of distance to the coast because the data quality is normally degraded with decreasing offshore distance.

Figure 7 shows the results of data availability for all selected altimetry missions. As can be seen, the performance of SGDR MLE4 is the worst in the study region. This is expected because the SGDR MLE4 is designed for waveforms over open oceans [33]. However, the performance of the SAMOSA retracker, which is also an open ocean retracker, is much better than the SGDR MLE4. This is mainly because the Sentinel-3A adopts the Delay-Doppler technique and Open Loop mode to remarkably enhance its observation ability in the coastal zone [34]. We can also see from the graph that WLS3 and ALES retrackers achieve similar performance and are superior to the MB4 retracker in the last 10 km to the coast, because the MB4 retracker is designed for the quasi-specular waveforms instead of land-contaminated waveforms [8]. The improvement of SAMOSA+ against SAMOSA in the 0–10 km distance band is also shown in Figure 7c, as the former is a dedicated coastal retracker by using a more accurate leading edge detection method and considering the variation of sea surface roughness [24]. Finally, we can see that the SCMR outperforms all individual coastal retrackers used in this study in the last 5 km to the coast, with the improvement percentage varying between 2–15%. This result suggests that the combination of multiple retrackers would contribute to recovering more reliable data in the nearshore 0–5 km distance band, which is very important for us to analyze the impact of small-scale coastal processes on the variation of sea level trends by comparing the differences between coastal (3–5 km) and offshore (15–20 km) trends [35].

Figure 8 shows the results of data precision for all selected altimetry missions. Three important findings are revealed by the graph. First, the precisions from SGDR MLE4 and WLS3 retrackers are slightly better than that from the ALES retracker. This is because ALES only retracks the sub-waveform, which results in inferior performance when the waveforms are not contaminated [7]. This result suggests the necessity of combining both open ocean and dedicated coastal retrackers to improve the data precision. Second, the data precisions from different altimetry missions are different, which reflects their different capabilities when observing the coastal zone. The best result is observed for the Saral mission (i.e., 3–4 cm), followed by the Sentinel-3A mission (i.e., 4–5 cm). The worst result is found for the Jason-3 mission, with the value ranging between 5–6 cm. Finally, Figure 8 shows that the SCMR achieves the best precision when compared to individual retrackers in both nearshore (0–20 km) and offshore (20–100 km) distance bands. This is because the Dijkstra algorithm [9] would automatically search the most appropriate SSH profile along the ground track when the waveform is not land contaminated (Figure 6b).

The median value of the improvement percentage in terms of data precision is summarized in

Table 5. The median value of improvement percentage (%) in terms of data precision for all selected altimetry missions within nearshore (0–20 km) and offshore (20–100 km) distance bands. The slash indicates that there are no data available.

	Missions	Jason-3		Saral		Sentinel-3A
Retrackers		0–20 km	20–100 km	0–20 km	20–100 km	0–20 km	20–100 km
SCMR vs. MLE4		13.90	10.48	15.60	14.07	/	/
SCMR vs. ALES		24.32	14.67	20.67	14.26	/	/
SCMR vs. WLS3		16.54	10.24	11.74	8.35	/	/
SCMR vs. MB4		21.97	12.69	17.54	12.03	/	/
SCMR vs. SAM		/	/	/	/	25.07	25.07
SCMR vs. SAM+		/	/	/	/	21.18	19.68

. As illustrated in the table, the SCMR significantly improves the data precision by 18.85% and 14.15% on average for 0–20 km and 20–100 km distance bands, respectively. Here, we also investigate to what extent the use of Dijkstra algorithm would remove high-frequency noises due to its filtering characteristics. The power spectral analysis is conducted following the method described in Zanife et al. [36] and Jiang et al. [37]. The spectrum of 20 Hz SLA estimates beyond 5 km off the coast from SCMR and other individual retrackers for all selected altimetry missions are shown in Figure 9.

As shown in Figure 9 and

Table 6. The noise levels of 20 Hz SLA estimates derived from power spectral density analysis for Jason-3, Saral and Sentinel-3A. The unit is in centimeters. The slash indicates that there are no data available.

	Missions	Jason-3	Saral	Sentinel-3A
Retrackers
SGDR MLE4		6.18	4.41	/
ALES		6.61	4.97	/
WLS3		6.34	4.70	/
MB4		6.71	4.57	/
SAM		/	/	5.32
SAM+		/	/	5.04
SCMR		4.65	3.05	3.42

, the SCMR achieves the lower spectral levels at the spatial scales smaller than 2.5 km for all selected altimetry missions. The corresponding noise levels can be calculated from the spectrum for different retrackers and altimetry missions. For Jason-3, the noise level for individual retrackers is at the level around 6.46 cm, while the corresponding value for SCMR is reduced to 4.65 cm with the improvement percentage being 28.02%. We can also see from the graph that the noise level for Saral and Sentinel-3 missions are smaller than that of Jason-3. This is because both missions adopt advanced altimeter technology to improve the altimeter’s performance as described in Section 2.1. The SCMR reduces the noise levels from 4.66 cm to 3.05 cm for Saral, and from 5.18 cm to 3.42 cm for Sentinel-3A, resulting in 34.55% and 33.98% of noise reduction, respectively. This result demonstrates that the SCMR can successfully reduce the high-frequency noise for both pulse-limited and SAR mode altimeters.

The above results show that the main contribution of SCMR lies in that it can increase the data availability in the last 5 km to the coast for both pulse-limited and SAR mode altimeters. This is because the Dijkstra algorithm selects the most accurate SSH estimates from multiple retrackers based on the along-track SSH variation pattern when waveforms are contaminated by land. Beyond 5 km off the coast, the Dijkstra algorithm can reduce the noise levels at the spatial scales smaller than 2.5 km. Considering the pulse-limited altimeter has accumulated nearly 30 years of SSH data, the improvement of up to 15% in the study region is of great value for monitoring long-term coastal sea level trends. As the evaluation of data precision is not enough to demonstrate the feasibility of the SCMR processing strategy, we further assessed the performance of SCMR by validating against tide gauge records in the next section.

4.3. Validation against Tide Gauge Records

To examine the accuracy of SLA estimates from the SCMR processing strategy, the altimeter data at each along-track point is validated against the tide gauge records from 12 stations shown in Figure 1. The results at two stations (i.e., Esperance and Lorne) presented in Figure 10, Figure 11 and Figure 12 are taken as examples to illustrate the performance of SCMR, while the results for all tide gauges in terms of improvement in along-track RMSE values are illustrated in Figure 13, Figure 14 and Figure 15.

As shown in Figure 10, Figure 11 and Figure 12, the left subplots show the percentage of available cycles after removing the SLA outliers, and the right subplots present the along-track RMSE of differences between SLA time series from altimeters and tide gauges. Note that the RMSE values for 20 Hz SLA estimates are typically within the range between 0.05 m and 0.15 m, which is consistent with the results in different coastal oceans for both Jason and Sentinel-3A altimeters [3,38,39]. The percentage of available cycles and along-track RMSE values are presented as a function of distance to the coast, making it easier for us to analyze the results.

As shown in Figure 10, the deterioration of Jason-3 starts from 4 km to the coast, where the RMSE values increase from 0.08 m to 0.2 m. This is expected because the Jason-3 has inferior performance when compared to the other two enhanced satellites. In addition, the satellite flight direction of the satellite, moving away from the coast, is not good for the altimeter to accurately capture the received signal from the ocean surface [31]. The Saral and Sentinel-3A missions, however, can retain low RMSE values (0.05–0.08 m) until 2 km to the coast (Figure 11 and Figure 12), confirming their good ability in reducing land contamination.

The most significant degradation is observed for Saral ground track 477, when the satellite moves towards the coast (Figure 11d). The ALES and SCMR can retrieve much better results than the other three retrackers (i.e., SGDR MLE4, WLS3 and MB4). The reason behind this is that the trailing edge of waveform is significantly contaminated by land topography. Therefore, the full-waveform retracker degrades while the sub-waveform retracker still performs well. Note that the Saral mission operates in the conventional Close Loop mode rather than the advanced Open Loop mode for the other two satellites of Jason-3 and Sentinenl-3A [34]. In this case, the observed waveforms are more likely to be significantly affected by complex coastal topography.

The superior performance of SCMR is mainly observed for pulse-limited altimeter in the last 5 km to the coast (Figure 10 and Figure 11), where the percentage of available cycles increases by up to 15% and the lower RMSE values are obtained. This is because the diversity of waveforms usually appears within a 0–5 km distance band, and thus the advantage of combining multiple retrackers can be fully exploited [4]. The improvement in accuracy for Sentinel-3A is relatively low in a 0–5 km distance band (Figure 12), because SAMOSA cannot deal with land-contaminated waveforms and SAMOSA+ can only handle certain types of coastal waveforms [24]. To further improve the accuracy of altimeter data in the 0–5 km to coast, more coastal retrackers dedicated to the Sentinel-3A or other SAR mode altimeters should be developed, which would be our future work.

To summarize the results, the mean values of improvement percentage in terms of the along-track RMSE within 10 km to the coast and 20–100 km off the coast are presented in Figure 13, Figure 14 and Figure 15. As can be seen, the accuracy of all selected altimetry missions has been, on average, improved by 6.26% within the 0–10 km distance band due to the use of the SCMR. In addition, the SCMR performs better than any single retracker in the 20–100 km distance band though the improvement is relatively small (4.94% on average). Moreover, more than 10% of accuracy improvement has been observed in several tide gauges along the coast. Although there exist negative percentages in a few stations, the corresponding values are small within −2% and 0%. Therefore, we can draw a conclusion that the SCMR improves accuracy of retracked data in coastal zones (0–10 km) and maintains the similar accuracy over open oceans (20–100 km) when compared with ocean (i.e., SGDR MLE4 and SAMOSA) and dedicated coastal retrackers (e.g., WLS3 and SAMOSA+). The results demonstrate that the SCMR is feasible in processing data from both pulse-limited and SAR mode altimeters.

5. Discussions

Previous studies [1,2,3,4,5] have demonstrated that the combination of multiple retrackers can improve the data availability and accuracy in coastal zones and Arctic oceans. The difference between our SCMR processing strategy and previous studies mainly lies in two aspects. First, we combine SSH estimates from different physical retrackers instead of those from both physical and empirical retrackers. This is because the SSH estimates from empirical retrackers lack information about SWH estimates, as they cannot be derived from the empirical retrackers [31]. As discussed in Section 4.1, the SSH bias is mainly caused because the SSH differences ($∆h)$ are negatively correlated with SWH difference ($∆H_s)$. Therefore, it is impossible to minimize the SSH bias between physical and empirical retrackers without the information about SWH differences.

Second, the Dijkstra algorithm is used in this study to combine SSH estimates from multiple retrackers rather than using the inaccurate waveform classification results. This is because the misclassification of coastal waveforms is inevitable due to their complicated shape features [8]. Here, we use the Dijkstra algorithm to search the shortest path between the point offshore and the point closest to the coast, based on the assumption that altimeter along-track SSH estimates vary smoothly at the spatial scales of 150–300 m. Therefore, the waveform classification is not required to derive the optimal along-track SSH profile. Moreover, the results shown in Section 4.2 and Section 4.3 demonstrate the excellent performance of this method, with the data precision and accuracy being improved not only in the last 10 km to the coast, but also over oceans beyond 20 km offshore.

6. Conclusions

In this paper, we present the SCMR processing strategy to increase SSH availability through the combination of multiple retrackers. One of the significant features of SCMR is the use of the Dijkstra algorithm, from which the most accurate SSH estimate at each along-track point can be determined without the help of waveform classification results. The SCMR strategy, including several retrackers (e.g., SGDR MLE4, ALES, WLS3, MB4, SAMOSA and SAMOSA+ retracker), is applied to both conventional and advanced altimetry missions (i.e., Jason-3, Saral and Sentinel-3A). The strategy has been tested in the Australian coastal zone. The validation results against tide gauge records demonstrate that the SCMR strategy is feasible and performs better than any single retracker used in this study. The major findings of this study are summarized as follows.

The analysis of regional corrections and MSS shows that the optimal correction can be determined by a trade-off between the SLA variance and data availability. The DTU21 MSS model outperforms the CLS15 MSS model for Jason-3 and Saral missions in the study region, while the CLS15 MSS has better performance for the Sentinel-3A mission. However, we found that the along-track MSS calculated by using two years of retracked altimeter data is the best MSS in the coastal zone, particularly within distance 3–20 km to the coast where the SLA variance decreases by 0.01–0.02 m². This result implies that the regional MSS model is required to accurately monitor coastal sea levels.

The bias-removing method from our previous research [4] is also applicable to open ocean and dedicated coastal retrackers (i.e., SGDR MLE4 w.r.t WLS3 and SAMOSA w.r.t SAMOSA+), as well as Ka-band and SAR mode altimetry missions (i.e., Saral and Sentinel-3A). The results show that the SSH bias can be reduced from centimeters to the levels of millimeters for Jason-3 mission and from millimeters to sub-millimeters for both Saral and Sentinel-3A missions, which guarantees the seamless combination of SSH estimates from multiple retrackers.

The evaluation and validation results demonstrate that the use of the Dijkstra algorithm to increase data availability near the coast is feasible. The advantage of using the Dijkstra algorithm is that it can determine the improved SSH profile based on the variation pattern of along-track SSHs without the need of external information such as waveform classification results. Therefore, it can avoid errors caused by the misclassification of the coastal waveforms, which is especially important when the waveform shapes become complex [8]. The main contribution brought by the SCMR is the increase of data availability (up to 15%) in the last 5 km to the coast. Although the combination of multiple retrackers is much more time-consuming than using a single retracker, it is important to increase data availability in the last 5 km to the coast because the variation of sea levels nearshore is of great interest in the scientific communities [4,35].

The use of SCMR also improves the data precision, considering that the standard deviation of 20 Hz SLA estimates has been reduced by 18.85% and 14.15% on average for 0–20 km and 20–100 km distance bands, respectively. The power spectral analysis further indicates that the noise reduction by SCMR is mainly observed at the spatial scales smaller than 2.5 km, with the improvement percentage varying between 28% for Jason-3 and 34% for both Saral and Sentinel-3A. In addition, the validation results against tide gauge records show that the altimeter data estimated by SCMR have a better quality/accuracy in the study region when compared to any single retracker, achieving the average improvement percentage by 6.26% and 4.94% over 0–10 km and 20–100 km distance bands, respectively. The results also suggest that the performance of SAR mode altimeters can be further improved by developing and combining more coastal retrackers dedicated to handling land-contaminated SAR waveforms.

Since all retrackers used in this study have been assessed and widely used by researchers [40], the SCMR processing strategy has potential to be used in global coastal zones to precisely retrieve long-term sea level measurements for climate research. We would also like to assess the performance of SCMR over global oceans by using the latest Jason-CS data in the future.