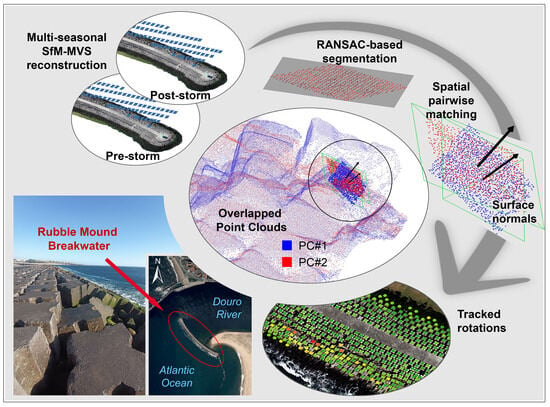
On-Site Stability Assessment of Rubble Mound Breakwaters Using Unmanned Aerial Vehicle-Based Photogrammetry and Random Sample Consensus
Abstract
:1. Introduction
1.1. SfM-MVS Photogrammetry in RMB Inspection
1.2. Change Detection Analysis in RMBs
1.3. The RANSAC Approach
2. Materials and Methods
2.1. Study Site
2.2. Field Campaigns
2.3. Flowchart of the Process
2.4. Photogrammetric Reconstruction
2.5. RANSAC-Based Segmentation
2.6. RMB Change Analysis
3. Results and Discussion
3.1. Photogrammetric Reconstruction
3.2. RANSAC-Based Analysis
3.2.1. PC Segmentation
3.2.2. RMB Stability Assessment
4. Conclusions and Future Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akarsh, P.K.; Chaudhary, B. Review of Literature on Design of Rubble Mound Breakwaters. In Proceedings of the International Conference on Civil Engineering Trends and Challenges for Sustainability, Bapatla, India, 24–25 September 2021; pp. 775–796. [Google Scholar]
- Nguyen, D.V.; Van Gelder, P.H.A.J.M.; Verhagen, H.J.; Vrijling, J.K. Optimal inspection strategy for rubble-mound breakwaters with time-dependent reliability analysis. In Relaibility, Risk and Safety; Taylor & Francis Group: London, UK, 2010; pp. 1409–1415. [Google Scholar]
- Etemad-Shahidi, A.; Bali, M.; van Gent, M.R.A. On the stability of rock armored rubble mound structures. Coast. Eng. 2020, 158, 103655. [Google Scholar] [CrossRef]
- der Meer, J.W. Conceptual design of rubble mound breakwaters. In Advances in Coastal And Ocean Engineering; World Scientific: London, UK, 1995; Volume 1, pp. 221–315. [Google Scholar]
- Puente, I.; Lindenbergh, R.; González-Jorge, H.; Arias, P. Terrestrial laser scanning for geometry extraction and change monitoring of rubble mound breakwaters. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 289–295. [Google Scholar] [CrossRef]
- Campos, Á.; Molina-Sanchez, R.; Castillo, C. Damage in rubble mound breakwaters. Part II: Review of the definition, parameterization, and measurement of damage. J. Mar. Sci. Eng. 2020, 8, 306. [Google Scholar] [CrossRef]
- Musumeci, R.E.; Moltisanti, D.; Foti, E.; Battiato, S.; Farinella, G.M. 3-D monitoring of rubble mound breakwater damages. Meas. J. Int. Meas. Confed. 2018, 117, 347–364. [Google Scholar] [CrossRef]
- Lemos, R.; Peña, E.; Santos, J.; Sande, J.; Figuero, A.; Alvarellos, A.; Laiño, E.; Reis, M.T.; Fortes, C.J.; Kerpen, N.B.; et al. 3D Survey Modelling for Damage Assessment in Rubble-Mound Breakwaters Under Oblique Wave Incidence. Ital. J. Eng. Geol. Environ. 2020, 20, 73–85. [Google Scholar] [CrossRef]
- Lemos, R.; Fortes, C.; Silva, G.; Pinheiro, L. An estimation of the damage of scale models of breakwaters using the time of flight method. Rev. Mecânica Exp. 2022, 35, 49–58. [Google Scholar]
- Lemos, R.; Santos, J.A.; Fortes, C.J.E.M. Damage Evolution Prediction during 2D Scale-Model Tests of a Rubble-Mound Breakwater: A Case Study of Ericeira’s Breakwater. Modelling 2022, 4, 1–18. [Google Scholar] [CrossRef]
- Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. Damage evolution in single-layer cube armoured breakwaters with a regular placement pattern. Coast. Eng. 2021, 169, 103943. [Google Scholar] [CrossRef]
- Lemos, R.; Loja, M.A.R.; Rodrigues, J.; Rodrigues, J.A. Photogrammetric analysis of rubble mound breakwaters scale model tests. AIMS Environ. Sci. 2016, 3, 541–559. [Google Scholar] [CrossRef]
- Fortes, C.J.E.M.; Lemos, R.; Mendonça, A.; Reis, M.T. Damage progression in rubble-mound breakwaters scale model tests, under a climate change storm sequence. Res. Eng. Struct. Mater. 2019, 5, 415–426. [Google Scholar] [CrossRef]
- Marino, S.; Galantucci, R.A.; Saponieri, A. Measuring rock slope damage on rubble mound breakwater through digital photogrammetry. Meas. J. Int. Meas. Confed. 2023, 211, 112656. [Google Scholar] [CrossRef]
- Mishra, V.; Avtar, R.; Prathiba, A.P.; Mishra, P.K.; Tiwari, A.; Sharma, S.K.; Singh, C.H.; Chandra Yadav, B.; Jain, K. Uncrewed Aerial Systems in Water Resource Management and Monitoring: A Review of Sensors, Applications, Software, and Issues. Adv. Civ. Eng. 2023, 2023, 3544724. [Google Scholar] [CrossRef]
- Robin, N.; Levoy, F.; Anthony, E.J.; Monfort, O. Sand spit dynamics in a large tidal-range environment: Insight from multiple LiDAR, UAV and hydrodynamic measurements on multiple spit hook development, breaching, reconstruction, and shoreline changes. Earth Surf. Process. Landforms 2020, 45, 2706–2726. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Stagnitti, M.; Musumeci, R.E.; Foti, E. Surface roughness measurement for the assessment of damage dynamics of existing and upgraded cube-armored breakwaters. Coast. Eng. 2023, 179, 104226. [Google Scholar] [CrossRef]
- King, S.; Leon, J.; Mulcahy, M.; Jackson, L.A.; Corbett, B. Condition survey of coastal structures using UAV and photogrammetry. In Proceedings of the Australasian Coasts & Ports Conference, Twin Waters, Australia, 15–18 August 2017; pp. 704–710. [Google Scholar]
- Rezaldi, M.Y.; Yoganingrum, A.; Hanifa, N.R.; Kaneda, Y.; Kushadiani, S.K.; Prasetyadi, A.; Nugroho, B.; Riyanto, A.M. Unmanned aerial vehicle (Uav) and photogrammetric technic for 3d tsunamis safety modeling in cilacap, indonesia. Appl. Sci. 2021, 11, 11310. [Google Scholar] [CrossRef]
- Layek, S.; Villuri, V.G.K.; Koner, R.; Chand, K. Rainfall & Seismological Dump Slope Stability Analysis on Active Mine Waste Dump Slope with UAV. Adv. Civ. Eng. 2022, 2022, 5858400. [Google Scholar] [CrossRef]
- Kim, K.; Francis, O. Integration of In-Situ, Laboratory and Computer Models for Coastal Risk Assessment, Planning and Development. In Proceedings of the Ocean 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Henriques, M.J.; Lemos, R.; Capitão, R.; Fortes, C.J. The monitoring of rubble mound breakwaters. An assessment of UAV technology. In Proceedings of the 7th International Conference on Engineering Surveying, Lisbon, Portugal, 18–20 October 2017; pp. 1–8. [Google Scholar]
- Gonçalves, D.; Gonçalves, G.; Pérez-Alvávez, J.A.; Andriolo, U. On the 3D Reconstruction of Coastal Structures by Unmanned Aerial Systems with Onboard Global Navigation Satellite System and Real-Time Kinematics and Terrestrial Laser Scanning. Remote Sens. 2022, 14, 1485. [Google Scholar] [CrossRef]
- Gonçalves, D.; Gonçalves, G.; Pérez-Alvárez, J.; Cunha, M.C.; Andriolo, U. Combining Unmanned Aerial Systems and Structure from Motion Photogrammetry To Reconstruct the Geometry of Groins. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2022, 43, 1003–1008. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Queiroz Feitosa, R.; van der Meer, F.; van der Werff, H.; van Coillie, F.; et al. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef]
- Kundal, S.; Chowdhury, A.; Bhardwaj, A.; Garg, P.K.; Mishra, V. GeoBIA-based semi-automated landslide detection using UAS data: A case study of Uttarakhand Himalayas. SPIE Future Sens. Technol. 2023, 12327, 79. [Google Scholar]
- Sharma, S.K.; Jain, K.; Shukla, A.K. A Comparative Analysis of Feature Detectors and Descriptors for Image Stitching. Appl. Sci. 2023, 13, 6015. [Google Scholar] [CrossRef]
- Chen, L.; Rottensteiner, F.; Heipke, C. Feature detection and description for image matching: From hand-crafted design to deep learning. Geo-Spatial Inf. Sci. 2021, 24, 58–74. [Google Scholar] [CrossRef]
- Forero, M.G.; Mambuscay, C.L.; Monroy, M.F.; Miranda, S.L.; Méndez, D.; Valencia, M.O.; Selvaraj, M.G. Comparative analysis of detectors and feature descriptors for multispectral image matching in rice crops. Plants 2021, 10, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Qin, R.; Tian, J.; Reinartz, P. 3D change detection—Approaches and applications. ISPRS J. Photogramm. Remote Sens. 2016, 122, 41–56. [Google Scholar] [CrossRef]
- Williams, R.D. DEMs of difference. Geomorphol. Tech. 2012, 2, 1–17. [Google Scholar]
- Lemos, R.; Capitão, R.; Fortes, C.; Henriques, M.; Silva, L.G.; Martins, T. A methodology for the evaluation of evolution and risk of breakwaters. Application to Portimão harbor and of Faro-Olhão inlet. J. Integr. Coast. Zone Manag. 2020, 20, 103–119. [Google Scholar] [CrossRef]
- Bueno Esposito, M.; Díaz-Vilariño, L.; Martínez-Sánchez, J.; González -Jorge, H.; Arias, P. 3D reconstruction of cubic armoured rubble mound breakwaters from incomplete lidar data. Int. J. Remote Sens. 2015, 36, 5485–5503. [Google Scholar] [CrossRef]
- Xu, Y.; Kanai, S.; Date, H.; Sano, T. Deep-Learning-Based Three-Dimensional Detection of Individual Wave-Dissipating Blocks from As-Built Point Clouds Measured by UAV Photogrammetry and Multibeam Echo-Sounder. Remote Sens. 2022, 14, 5575. [Google Scholar] [CrossRef]
- Shen, Y.; Lindenbergh, R.; Wang, J.; Ferreira, V.G. Extracting individual bricks from a laser scan point cloud of an unorganized pile of bricks. Remote Sens. 2018, 10, 11709. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J.; Puente, I. A Novel Baseline-Based Method to Detect Local Structural Changes in Masonry Walls Using Dense Terrestrial Laser Scanning Point Clouds. IEEE Sens. J. 2020, 20, 6504–6515. [Google Scholar] [CrossRef]
- Choi, S.; Kim, T.; Yu, W. Performance evaluation of RANSAC family. J. Comput. Vision 1997, 24, 271–300. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics; Wiley: Hoboken, NJ, USA, 1981; Volume 1. [Google Scholar]
- Rousseeuw, P.J. Least median of squares regression. J. Am. Stat. Assoc. 1984, 79, 871–880. [Google Scholar] [CrossRef]
- Borrmann, D.; Elseberg, J.; Lingemann, K.; Nüchter, A. The 3d hough transform for plane detection in point clouds: A review and a new accumulator design. 3D Res. 2011, 2, 1–13. [Google Scholar] [CrossRef]
- Mahendran, S.; Ali, H.; Vidal, R. 3D Pose Regression Using Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 494–495. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Gonultas, F.; Atik, M.E.; Duran, Z. Extraction of Roof Planes from Different Point Clouds Using RANSAC Algorithm. Int. J. Environ. Geoinformatics 2020, 7, 165–171. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J. RANSAC-based multi primitive building reconstruction from 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2022, 185, 247–260. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Wang, C.; Zhu, C.; Ren, Y. Multistep rocky slope stability analysis based on unmanned aerial vehicle photogrammetry. Environ. Earth Sci. 2019, 78, 260. [Google Scholar] [CrossRef]
- Giulietti, N.; Allevi, G.; Castellini, P.; Garinei, A.; Martarelli, M. Rivers’ Water Level Assessment Using UAV Photogrammetry and RANSAC Method and the Analysis of Sensitivity to Uncertainty Sources. Sensors 2022, 22, 5319. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, I.; Venâncio, S.; Pinho, J.L.; Avilez-Valente, P.; Vieira, J.M.P. Two models solutions for the Douro estuary: Flood risk assessment and breakwater effects. Estuaries Coasts 2019, 42, 348–364. [Google Scholar] [CrossRef]
- Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; Marcial-Pablo, M.D.J.; Enciso, J. Digital terrain models generated with low-cost UAV photogrammetry: Methodology and accuracy. ISPRS Int. J. Geo-Information 2021, 10, 285. [Google Scholar] [CrossRef]
- Calì, M.; Ambu, R. Advanced 3D photogrammetric surface reconstruction of extensive objects by UAV camera image acquisition. Sensors 2018, 18, 2815. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Sanz, J.; Gil-Docampo, M.; Rego-Sanmartín, T.; Arza-García, M.; Tucci, G. A PBeL for training non-experts in mobile-based photogrammetry and accurate 3-D recording of small-size/non-complex objects. Meas. J. Int. Meas. Confed. 2021, 178, 109338. [Google Scholar] [CrossRef]
- Carrilho, A.C.; Galo, M. Extraction of building roof planes with stratified random sample consensus. Photogramm. Rec. 2018, 33, 363–380. [Google Scholar] [CrossRef]
- Catalão, J.; Sevilla, M.J. Mapping the geoid for Iberia and the Macaronesian Islands using multi-sensor gravity data and the GRACE geopotential model. J. Geodyn. 2009, 48, 6–15. [Google Scholar] [CrossRef]
- Arza-García, M.; Gil-Docampo, M.; Ortiz-Sanz, J. A hybrid photogrammetry approach for archaeological sites: Block alignment issues in a case study (the Roman camp of A Cidadela). J. Cult. Herit. 2019, 38, 195–203. [Google Scholar] [CrossRef]
- Soares, F.; Henriques, M.J.; Rocha, C. Concrete Block Tracking in Breakwater Models Concrete Block Tracking in Breakwater Models. In Proceedings of the FIG Working Week 2017, Helsinki, Finland, 29 May—2 June 2017; pp. 1–14. [Google Scholar]
- Henriques, M.J.; Brás, N.; Roque, D.; Lemos, R.; Fortes, C.J.E.M. Controlling the Damages of Physical Models of Rubble-Mound Breakwaters by Photogrammetric Products-Orthomosaics and Point Clouds. In Proceedings of the Proceedings of the 3rd Joint International Symposium on Deformation Monitoring, Viena, Austria, 30 March–1 April 2016; p. 8. [Google Scholar]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Factor to ROC, Informedness, Markedness & Correlation. Technical Report SIE-07-001. arXiv 2007, arXiv:2010.16061v1. [Google Scholar]
- Kharroubi, A.; Poux, F.; Ballouch, Z.; Hajji, R.; Billen, R. Three Dimensional Change Detection Using Point Clouds: A Review. Geomatics 2022, 2, 457–485. [Google Scholar] [CrossRef]










| Weight | 1388 g |
| Max Wind Speed Resistance | 10 m/s |
| Max Flight Time | Approx. 30 min |
| GNSS Positioning | GPS/GLONASS |
| Hover Accuracy Range | Vertical: 0.5 m (GPS positioning) |
| Horizontal: 1.5 m (GPS positioning) | |
| Camera resolution | 20 megapixels |
| Sensor size | 1-inch CMOS |
| Altitude for Mapping Mission | 30 m |
| Frontlap | 80% |
| Sidelap | 60% |
| Ground Sample Distance | <1 cm |
| Speed of Flight | 2.3 m/s |
| Mission Area | 2.33 ha |
| Image Alignment Method | Adaptive camera model |
| Alignment Accuracy | High (original image size) |
| Key Point Limit | 50,000 |
| Tie Point Limit | 10,000 |
| Depth Maps Quality | High |
| Filtering Mode | Aggressive |
| Flight #1 | Flight #2 | |||
|---|---|---|---|---|
 | # of images | 249 | 237 | |
| Mean flight height (m) | 30.9 | 29.6 | ||
| GSD (mm) | 8.7 | 8.0 | ||
| Key points | 206,882 | 212,619 | ||
| Dense cloud size (points) | 23,119,079 | 23,645,284 | ||
| Residuals from GCPs (mm) | X | 3.8 | 6.5 | |
| Y | 6.1 | 17.8 | ||
| Z | 7.6 | 9.7 | ||
| Accuracy from CPs (mm) | X | 7.2 | 6.8 | |
| Y | 8.9 | 11.4 | ||
| Z | 6.6 | 14.3 | ||
| DEM resolution (mm/pix) | 34.9 | 32.5 | ||
| Predicted Class | ||||||
|---|---|---|---|---|---|---|
| Actual class | True positives | False negatives | Positive | |||
| PC#1 | 932 | PC#1 | 41 | PC#1 | 973 | |
| PC#2 | 882 | PC#2 | 68 | PC#2 | 950 | |
| 1814 | 109 | 1923 | ||||
| False positives | True negatives | Negative | ||||
| PC#1 | 51 | PC#1 | 12 | PC#1 | 63 | |
| PC#2 | 66 | PC#2 | 21 | PC#2 | 87 | |
| 117 | 33 | 150 | ||||
| Positive | Negative | |||||
| PC#1 | 983 | PC#1 | 53 | |||
| PC#2 | 948 | PC#2 | 89 | |||
| 1931 | 142 | |||||
| (3) | |
| (4) | |
| (5) | |
| (6) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arza-García, M.; Gonçalves, J.A.; Ferreira Pinto, V.; Bastos, G. On-Site Stability Assessment of Rubble Mound Breakwaters Using Unmanned Aerial Vehicle-Based Photogrammetry and Random Sample Consensus. Remote Sens. 2024, 16, 331. https://doi.org/10.3390/rs16020331
Arza-García M, Gonçalves JA, Ferreira Pinto V, Bastos G. On-Site Stability Assessment of Rubble Mound Breakwaters Using Unmanned Aerial Vehicle-Based Photogrammetry and Random Sample Consensus. Remote Sensing. 2024; 16(2):331. https://doi.org/10.3390/rs16020331
Chicago/Turabian StyleArza-García, Marcos, José Alberto Gonçalves, Vladimiro Ferreira Pinto, and Guillermo Bastos. 2024. "On-Site Stability Assessment of Rubble Mound Breakwaters Using Unmanned Aerial Vehicle-Based Photogrammetry and Random Sample Consensus" Remote Sensing 16, no. 2: 331. https://doi.org/10.3390/rs16020331
APA StyleArza-García, M., Gonçalves, J. A., Ferreira Pinto, V., & Bastos, G. (2024). On-Site Stability Assessment of Rubble Mound Breakwaters Using Unmanned Aerial Vehicle-Based Photogrammetry and Random Sample Consensus. Remote Sensing, 16(2), 331. https://doi.org/10.3390/rs16020331