1. Introduction
With the rapid development and maturation of unmanned aerial vehicle (UAV) technology and wireless communication network technology, new concepts, such as UAV swarms and manned–unmanned teaming (MUM-T), have gradually been applied and validated [
1,
2,
3,
4]. A UAV swarm refers to the use of multiple UAVs to form a collective group to accomplish tasks, with coordination between them occurring through a wireless communication network. MUM-T refers to the simultaneous control and command of multiple UAVs using a human-piloted aircraft to perform a mission. MUM-T fully leverages the intelligence and experience of a human-piloted aircraft while also utilizing the maneuverability and payload advantages of UAVs. MUM-T can improve efficiency and survivability while reducing the risks of a human-piloted aircraft. These target formations, which are composed of task-oriented groups through wireless communication networks, can be collectively referred to as network-group targets. The collaboration of network-group targets depends on the communication networks. Therefore, analyzing the radiation of network-group targets is expected to improve the state-estimation performance for these targets.
Standard single-target tracking algorithms assume that the target is a point, limiting it to one measurement per target per time only [
5,
6,
7,
8]. Researchers have studied the direct position determination (DPD) of targets using radio signals, including techniques such as time difference of arrival (TDOA), frequency difference of arrival (FDOA), and directions of arrival (DOA) [
9,
10,
11,
12,
13]. Specifically, regarding the moving radiation sources, the estimation of the location by utilizing TDOA and FDOA information was achieved through fixed receiving stations [
10]. Considering the multipath situation, based on the sparsity of locations and velocities, a DPD method for passive radar was proposed to estimate the location and velocity of a moving target in a multipath scenario [
11]. A novel approach to efficiently solve the cost function of DPD was proposed [
12], which requires fewer particles compared with the classical particle filter (PF) to estimate the kinematic state of the moving source. DPD for mobile narrowband sources based on known waveform signals with a Doppler frequency shift was proposed [
13]. The proposed DPD is superior to traditional tracking methods in terms of low signal-to-noise ratio (SNR) and limited quantity of data samples. A system-modeling approach employing cyclic spectrum slices was proposed for directly localizing co-channel signals with distinct cyclic frequencies [
14]. A deep learning model for direct trajectory tracking has been developed [
15], primarily consisting of two main components: a signal-processing component based on convolutional neural networks (CNNs) and a trajectory generation component based on the Transformer architecture. A multi-task learning model designed for joint direct classification and tracking enables the network to further enhance tracking performance by learning the dynamic patterns of different types of targets.
Multi-target tracking (MTT) algorithms, such as multiple hypothesis tracking (MHT) [
16] and the joint probabilistic data association filter (JPDAF) [
17,
18], were designed to solve the problem of tracking targets that may appear and disappear, with the number and trajectories of the targets changing over time. The random finite set (RFS) approach is a novel methodology in MTT that offers a framework for managing multi-target systems while circumventing intricate data association procedures [
19,
20,
21,
22,
23]. An RFS is a random variable whose values are finite sets. The number of points in a random finite set is random, and the values of these points are also random and unordered. Observation sets and state sets can naturally be represented using random finite sets. Compared with the aforementioned traditional association algorithms, the RFS approach holds considerable advantages in scenarios with numerous observations and an uncertain number of targets.
Group targets are usually classified as either unresolved or resolvable based on their distribution of position measurements [
19]. Unresolved targets, which have a larger number of targets that are difficult to differentiate from each other, are not practical to track individually. Hence, collective movements of the entire group were considered. Extended targets can be regarded as a special type of unresolved targets [
24,
25,
26,
27]. These targets have the characteristic that each measurement comes from a single target and each extended target can generate multiple measurements. For instance, a high-resolution radar can detect targets occupying multiple resolution cells, resulting in multiple measurements per time step. Resolvable group targets are defined as a collection of targets with relatively stable formations and similar movement patterns [
28,
29]. In scenarios that involve target tracking with interactive behaviors, various group structure models have emerged as popular choices. These encompass the virtual leader–follower model [
30], Markov random field (MRF) model [
31], evolutionary network model [
32,
33], and social force model [
34]. A novel multigroup target tracking algorithm, which leverages evolutionary networks and the labeled box particle probability hypothesis density (LBP-PHD) filter, was introduced by Cheng et al. [
35] by adding labels to box particles to obtain the trajectory of individual targets within a group and the overall group trajectory, while also avoiding the instability caused by k-means clustering. The group structure is modeled using graph theory, and the cardinality balanced multitarget multi-Bernoulli (CBMeMBer) filtering algorithm is used to estimate the kinematic state of the group targets [
36], which further allows for the estimation of the overall group state based on individual target state estimates within the group. The group structure can be described within the framework of the hypergraph theory, which enhances the performance of data association [
37]. The structure identification and tracking problem of circular formation movement was studied [
38], and a single trajectory was obtained using the labeled multi-Bernoulli (LMB) filter. To address the problem of tracking large-scale multi-structure group targets, a sequential generalized labeled multi-Bernoulli (GLMB) tracking algorithm was proposed by Zhao et al. [
39]. Li et al. derived the single-target state transition function (SSTF) from the direct integral solution of the single-target state stochastic differential equation (SDE) [
40], and integrated the proposed SSTF-MB filter into the sensor control strategy.
To minimize the perceived risks, the networked targets employ their stealth capabilities and radar silence to execute their missions. However, due to the necessity of communication to ensure the synchronization of information, such as location, these signals do not remain disconnected for extended periods. Instead, they maintain intermittent synchronization, and their beam width is relatively wide. Consequently, researching the state of network-group targets and their network topology holds significant importance. Additionally, to the best of the authors’ knowledge, there was no previous study that explored the state estimation of network-group targets.
The purpose of this study was to develop a method to achieve passive state and network topology estimation of network-group targets within the framework of a labeled RFS. Unlike traditional group target definitions, network-group targets are defined not by motion coordination between targets, but by communication links. This method considers the use of received broadband frequency-hopping communication signals containing time delay and Doppler information to determine the location and velocity of the transmitter and considers the coherence between frequency-hopping pulses to further improve the tracking performance. Furthermore, the method draws upon certain concepts from graph theory and utilizes address information to estimate the network topology, which is a crucial means for a comprehensive and accurate understanding of network spaces. The approach is applicable to scenarios where the network-group targets are distinguishable and the communication signals have a relatively high SNR, allowing for the accurate acquisition of the targets’ states.
The main contributions of this study are as follows:
Graph theory is introduced to develop a network-group target-state estimation method that incorporates the network topology.
In order to improve the estimation performance, a likelihood function was established using frequency-hopping communication signals emitted from the network-group targets, including delay and Doppler information.
The remainder of this paper is organized as follows.
Section 2 introduces the network-group target and offers an overview of graph theory and the LMB RFS.
Section 3 presents a model for the state, measurement, and communication signals of a network-group target.
Section 4 proposes an LMB filter specifically designed for network-group targets. The implementation method of the filter, along with track pruning and state extraction methods, is outlined in
Section 5. The simulation results are presented in
Section 6. Finally,
Section 7 provides concluding remarks and summarizes the contributions of this study.
2. Background
2.1. Notation
In this paper, represents the Kronecker- function and represents the Dirac density at . represents the indicator function of the set S, and if , then ; otherwise, . represents the number of elements in the finite set S. is the integral over all state variables. For continuous functions, , and for discrete sequences, . is a multi-objective index. represents all finite subsets of space . indicates all subsets that include n elements.
The state scalar of a single object is represented by a lowercase letter x. The state vector of a single object is represented by lowercase bold letters: . Multiple object states are represented by uppercase letters: X. The corresponding label versions are represented by the regular forms x, x, and X. The spaces are indicated in bold black letters: . The exclusive union of sets X and Y: .
In signal processing, scalar values are represented in lowercase italic letters: a. The vectors are represented by lowercase italic scripts: a. The matrix is represented by the capital italic script . represents the identity matrix, and represents an M-column vector of ones. Here, diag{} represents a diagonal matrix with vector on the main diagonal.
2.2. Introduction to Network-Group Targets
Network-group participants are geographically dispersed, but interconnected through wireless communication networks. They collaborate and work together to accomplish their tasks. The normal operation of a wireless communication network requires communication protocols that address the efficient and reliable interaction of messages. According to the TCP/IP five-layer model [
41], network protocols of wireless communication networks are typically divided into five layers: application, transport, network, data link, and physical. The application layer provides an interface between the user and the network, the transport layer manages the data transmission between two nodes, and the network layer is responsible for routing and forwarding data frames to achieve data transmission between different networks. The data link layer not only divides the bit stream into data frames and performs error detection and correction but is also responsible for the flow control and access control of the data transmitted at the physical layer to ensure reliable data transmission. Finally, the physical layer primarily handles the digital signal transmission. This study primarily involved transport, data link, and physical layers. The following are some of the properties of the wireless communication network investigated in this study.
In the transport layer, a time slot serves as the fundamental unit for accessing a wireless communication network. Each participant is assigned several timeslots for signal transmission and reception. Data can be encapsulated in various formats, such as transmitting the same codeword with two pulses or transmitting one codeword with a single pulse.
The data link layer encapsulates the network layer data by adding the source and destination addresses. The address of each target is unique and fixed. The network topology in our study adopted a decentralized structure, and the sublayer protocol used the time-division multiple access (TDMA) method, in which time is divided into nonoverlapping time slots. Each user is assigned a dedicated time slot for data transmission, with each time slot occupied by at most one user. Generally, to minimize interference with other services, the occupancy factor of the time slots is kept low. In addition, this study assumed that network-group targets adopted a lower update rate (sub-second to multi-second levels) for information transmission to reduce the probability of communication signal interference.
In the physical layer, the network-group targets utilize minimum shift keying (MSK) modulation for signal transmission and the carrier frequency hops in a wideband using a specific method.
Figure 1 shows a time slot diagram of the three sensor platforms and a network-group with three targets. The main graph in the diagram is a two-dimensional plane that shows the geographical locations of the three sensor platforms and the three network-group targets in three time slots. Each target is represented by a pattern, and the straight black arrow beside the pattern indicates the direction of movement of the target in the slot. The targets move in slightly different directions and not in opposite directions. When a target is transmitted in a time slot, it is represented by a solid pattern; otherwise, it is represented by an empty pattern. The blue lightning symbol with an arrow indicates that the target transmits information during that time slot. Targets 1 and 2 transmit information to target 3 in time slots 1 and 3, respectively, whereas no target is transmitted in time slot 2. Above this diagram is a frequency-hopping pattern diagram for the two transmissions in time slots 1 and 3. In this diagram, each transmission consists of five pulses and the pulse frequency changes over time. Each transmission from the target includes the addresses of the transmitter and receiver. Signals containing time delay, Doppler, and address information were intercepted by the three sensor platforms for further processing.
In this scenario, it is assumed that the antennas used to transmit signals between the network-group targets are omnidirectional rather than narrow-beam types, which is a prerequisite for the sensor platform to intercept communication signals. Our aim was to estimate the kinematic state and network topology of network-group targets by processing signals intercepted from three sensor platforms containing time delay, Doppler, and address information.
2.3. Graph Theory
A graph
G consists of a set of vertices
, a set of edges
, and the relationship between them, where two vertices are related by an edge [
42].
The directed graph G comprises a set of vertices , a set of edges , and a mapping function that associates each edge with an ordered vertex pair. Within this pair, the initial vertex represents the edge tail, and the subsequent vertex serves as the edge head. denotes the existence of an edge between u and v. The degree d of a vertex refers to the number of times that the vertex appears at the edge.
The adjacency matrix of G is a matrix of dimensions , where the element is the number of edges ending with vertices and . In the adjacency matrix of directed graph G, the element at is the number of edges from to . The degree matrix of a graph is a diagonal matrix of degrees, that is, .
The induced subgraph consists of a subset of the vertices of the graph and a set of all edges, with both ends in the subset. A dynamic graph is represented by a set of ordered graphs [
43]:
in which
K is the number of time steps.
The network topology of network-group targets can be described using directed graphs from graph theory, where vertices represent targets and edges represent information transfer between targets. As illustrated in
Figure 1, assuming that the addresses of the three targets are 1, 2, and 3, the targets are represented by vertices denoted by
, and the information transfer during the first time slot is represented by edges denoted by
.
2.4. LMB RFS
The state space of the target is represented as
, and the label space can be represented as
, where
represents the set of positive integers, and
is distinct. The labeled multi-target state is represented by X. The characteristics of the LMB RFS X can be entirely encapsulated within a specific set of parameters
, where
is the probability of the existence of the target
ℓ, and
is the probability density of the track when the target
ℓ exists. The LMB RFS density with parameter set
can be written as
where
represents the set of tags in X.
guarantees that the labels of X are distinct. The weight can be written as
Ignoring the target derivation, the multi-target state in the next time step is the union of the surviving and newborn target states. We assumed that the surviving LMB parameter set is
, and the newborn LMB parameter set is
, where
is the label space of the newborn target. The predicted LMB density is the union of the surviving and newborn LMB densities as follows:
and the label space is
, and
.
The predicted LMB parameter set is represented by
, and at this time, there are multiple target measurements
, where
is the measurement space. An LMB parameter set that accurately matches the first moment of the posterior density of multiple targets is
For detailed information on the LMB filter, please refer to the paper written by Reuter et al. [
44].
4. The Proposed Method
Assuming that the distribution of the augmented spatial PDF in the presence of a target is represented by
, the density of the augmented LMB parameter set is represented by
where
is the PDF with the label
ℓ for the target kinematic state, and
and
are the PDFs with the label
ℓ for the transmitter and receiver addresses, respectively.
,
, and
are independent.
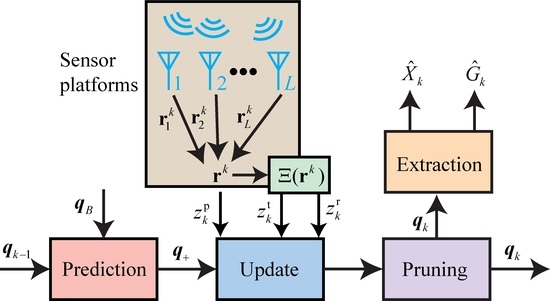
The flowchart of the proposed method is shown in
Figure 4. In the prediction step, the predicted LMB parameter set, denoted as
, is calculated using the prior LMB parameter set, denoted as
, and the birth LMB parameter set, denoted as
. The state transition density function, given by (
7), is used for this calculation. There are
L sensor platforms that listen to signals in time slots of time step
k. The signals captured in the occupied time slots are sent to a platform to form a column vector, denoted as
, as shown in (
22); each signal in the occupied time slots is transmitted to an address recognizer (represented by the confusion matrix in (
9) in this paper) to obtain address measurements
and
for the transmitter and receiver, respectively. The augmented measurement for the occupied time slots is denoted as
, as shown in (
7), and the measurement at time step
k is denoted as
. In the update step, the likelihood function is calculated based on the measurements
. After the update step, track pruning is performed based on the existence probability and addresses. Finally, in the extraction step, the trajectory and network topology structure are extracted.
4.1. Prediction
It was assumed that the prior and newborn target distributions are both LMB.
Proposition 1. Given a set of augmented prior LMB parameters and a set of augmented LMB parameters for births, denoted bythe predicted set of augmented LMB parameters iswith label space (). For the existence part of the augmented LMB:where represents the survival probability and is the survival probability of the target ℓ, which can be expressed as Proof. The survival probability of target
ℓ is represented by
Based on the Markov state transition density in (
7), the predicted LMB has a partially augmented track probability density, which can be expressed as
Then,
,
, and
can be obtained as shown in (
32)–(
34). □
4.2. Update
During the update step of the LMB filter, the predicted LMB density is transformed into the -GLMB form for a full -GLMB update. Subsequently, the -GLMB posterior approximation is reconverted to the closest LMB density.
Proposition 2. Given the augmented predicted LMB parameter set in (26), the LMB posterior parameter set iswhere ,andwhere represents the probability of detection. Proof. can be written as
Therefore, it can be inferred that
. Similar deductions can be made for
and
, thus (
39)–(
41) can be obtained.
can be written as
where
can be written as
where
is given by (
11). The above equation can be decomposed into
, as shown in (
45)–(
47). □
4.3. Likelihood Function of Kinematics
Proposition 3. Given a single-target kinematic measurement , the kinematic likelihood function can be written as The constants
and
were introduced to maintain the stability of the likelihood function, whereas the remaining parameters are described in
Section 3.3.
Proof. is a complex Gaussian random vector with mean
and covariance of
. The unknown vector
is defined as
, where
. The PDF can be written as follows:
The maximum likelihood estimate (MLE) of
is
In the maximum likelihood estimation of
,
is independent of
, and
is related only to the noise covariance. Thus, the maximum likelihood estimation can be simplified to
where
is an unknown vector. To determine the
that maximizes the likelihood function, the complex gradient of the likelihood function with respect to
is set to zero. This yields
By substituting
into the above equation, one can obtain (
56):
Because
, meaning that the first term in the sum is unrelated to
, the equation can be simplified to
In (
57), the phase shift coefficient
exists in the
term. To eliminate the influence of the phase offset, the phase deviation coefficient can be set to one by taking the modulus of (
57), thereby obtaining an approximate MLE of the source position and velocity:
Thus, Equation (
51) can be obtained. □
6. Simulation Results
A simulation was conducted in MATLAB R2023b to evaluate the performance of the proposed method for the state estimation of network-group targets. It was assumed that the time interval was 1 s, and the simulation time was 100 s.
The 2D scenario was assumed to involve three moving sensor platforms and four targets in a network group. The first and second targets were born at
s, whereas the third and fourth targets were born at
s and
s, respectively. The trajectories of the network-group targets and sensor platforms are shown in
Figure 5. The false targets intercepted each time were modeled as a Poisson RFS with a Poisson rate of 5. The false target area was
, that is, the uniform probability density was
. The emission probabilities of the network-group targets were considered to be
. When emitting, target 1 had a probability of 0.3 to transmit signals to target 2 and a probability of 0.7 to transmit signals to target 4. Target 2 had a probability of 1 for transmitting signals to target 1. Target 3 had equal probabilities of 0.5 to transmit signals to both targets 1 and 4. Similarly, target 4 also had equal probabilities of 0.5 to transmit signals to both targets 1 and 4. The survival probability of each individual target was independent and was set at
. The four thresholds were set as follows:
,
,
, and
.
Assuming that the network-group target transmitted 258 hopping patterns in one time slot, the signals hopped between 14 frequency points in the range of 969–1008 MHz, 5 frequency points in the range of 1053–1065 MHz, and 32 frequency points in the range of 1113–1206 MHz. The pulse width was 6.4 s and the pulse period was 13 s. The pulse carried 32 bits of data and modulated the carrier wave using MSK at a rate of 5 Mb/s. Each symbol was transmitted in the form of a double pulse, meaning that the two pulses represent the same symbol but with different carrier frequencies. The SNR was 0 dB and the sampling rate was . In the pulse sequence, one pulse was selected for signal processing every 11 pulses, resulting in 24 pulses at positions [1, 12, ⋯, 254].
Assuming that there were eight candidate addresses, the addresses for the four targets were 1, 2, 3, and 4. The diagonal elements of the recognizer confusion matrix were 0.9, whereas those of the remaining elements were 0.1/7.
The number of particles was set to 600. In addition, the computational cost could be reduced by using a gating approach. The specific method involved establishing a grid for the TDOAs. In this simulation, because there were three sensor platforms used, a two-dimensional grid was created for the TDOAs. Subsequently, the grid position of each particle at the target density was calculated. Finally, the grid position of the measurement was obtained by calculating the two TDOA values using traditional methods, such as the cross ambiguity function (CAF). If there was an overlap between the grid positions of the particle and measurement, the track and measurement were associated.
Since there is no existing literature on research targeting network groups for comparison, the proposed method was compared with the two-step and noncoherent methods. The two-step method involves using the CAF to jointly estimate the TDOA and Doppler velocity difference and then performing state estimation by incorporating both into the likelihood function. The two-step method, which ignores the inherent constraint that the measurements obtained in the first step must be consistent with the target kinematic state determined in the second step, is suboptimal. The difference between the noncoherent and proposed methods lies in the fact that the former does not consider the term
in (
20), which ignores the phase shift caused by variations in the frequency of frequency-hopping pulses and time-varying TDOAs. Therefore, it is expected that the proposed method will outperform the other two.
The actual signal emission from the network-group targets in a single simulation varied over time, as depicted in
Figure 6a, whereas the cardinality estimation of the three methods in a single simulation is illustrated in
Figure 6b. It was evident that the proposed method provided the most accurate cardinality estimation, with only occasional instances of underestimation. The two-step method performed better, whereas the noncoherent method performed the worst, estimating a cardinality of only one after
t = 35 s.
Figure 7 shows the actual and estimated trajectories of the network-group targets in a single simulation, as obtained through (
68). From
Figure 7a, it is evident that the proposed method accurately estimated the trajectories, but there were occasional instances of missed detections, such as at
t = 12 s. By combining
Figure 5 and
Figure 6a, it is apparent that the missed detection was attributed to target 2, which did not emit multiple times. However, at
t = 13 s, the proposed method tracked target 2. The two-step method yielded numerous false trajectories, and the trajectory estimation of target 4 was not detected after
t = 63 s. The trajectory estimation performance of the noncoherent method was even worse, with only one target being tracked at
t = 100 s.
Figure 8 presents comparative network topology estimations from the three different methods within a single simulation trial, as obtained through (
69)–(
71). The initial graph in each row illustrates the actual network topology, along with the observed measurements, with the caveat that false targets are not marked on the graphs. The subsequent trio of graphs on the right displays the network topology estimations derived by the proposed, two-step, and noncoherent methods. At
t = 1 s, both the proposed and two-step methods estimated two vertices in the case of only one target detected; however, only one edge was detected. The noncoherent method detected one target and one edge with the position of the other unknown. At
t = 3 s, the proposed method successfully determined the correct network structure. However, the two-step and noncoherent methods had errors in the target position estimation and missed edge estimation. At
t = 5 s, the actual and recognized network structures remained congruent. The proposed method identified network connections, whereas the two-step method obtained an incorrect position for the target with address 1 and an incomplete edge estimation. The estimation using the noncoherent method was even worse. At
t = 12 s, the system misidentified the address of target 1 as target 4. Despite this error, all the methods managed to accurately assign the correct address number 1 to this target. The two-step method had a poorer position estimation than the proposed method and incorrectly identified a target with address 8. At
t = 86 s, the connections from vertex 2 to vertex 1 were mistakenly read as two to six. In this instance, vertex 6 was incorrectly considered a non-existent target; hence, all methods failed to detect the edge 2 → 1. In addition to missing targets, the two-step and noncoherent methods failed to detect edges. It is evident that the estimation of the network topology tended to be accurate when a set of network-group targets could be reliably tracked and there was sufficient information to ascertain their addresses. However, disruptions or errors in target trajectories could lead to inaccuracies in the assessment of the network topology.
A performance comparison was conducted through 100 Monte Carlo simulations in
Figure 9,
Figure 10 and
Figure 11.
Figure 9 compares the cardinality estimation performances of the three methods. The proposed method provided the most accurate cardinality estimation, whereas the other two methods tended to underestimate the cardinality. This was because with a limited number of particles, the tracked targets in these methods could experience track loss or interruption, making it difficult to maintain stable tracking.
The labeled generalized optimal sub-pattern assignment (LGOSPA) error was utilized to evaluate the performance of the tracking methods. It decomposed the error into four components: the target localization error, missed target, false alarm target, and track switches. The relationship between the LGOSPA and GOSPA is given by the following equation:
where
p is the metric order,
is the switching component,
is the switching penalty, and
is the number of switches. The GOSPA can be found in the study conducted by Abu et al. [
45]. In the simulation, we set
,
, the cutoff distance to 1000, and the alpha parameter to 2.
Figure 10 shows a comparison of the LGOSPA errors and their components for the three methods. From
Figure 10a, it can be observed that the proposed method had the lowest mean and smallest variance of the LGOSPA distance between the three methods, followed by the noncoherent and two-step methods. The proposed method exhibited the lowest false component within the LGOSPA metric, achieving a value of zero at
t = 18 s, which signified the absence of false tracks. In contrast, the two-step method demonstrated a marked inferior performance relative to the proposed method, with higher false and switching components. The noncoherent method incurred the greatest miss component. However, as shown in
Figure 10e, the performance of the incoherent method was lower than that of the proposed method because of the missed detections. Overall, the proposed method outperformed the other methods.
The Jaccard similarity measures the similarity and dissimilarity between finite sets using the Jaccard index. The higher the Jaccard index value, the higher the similarity between the samples. The Jaccard index is calculated as follows:
Figure 11 shows the performance of the vertex and edge estimation, which represents the estimation performance of the addresses and the links in the network topology, respectively. In
Figure 11a, it can be observed that the estimation performance of the proposed method gradually improved before
t = 13 s owing to the accumulation of address information. Ultimately, only the proposed method maintained a high level of accuracy, whereas the performances of the other two methods declined. As illustrated in
Figure 11b, our method stabilized at approximately 80% accuracy in the estimation of opposite edges after
t = 8 s, outperforming the two-step approach. Beyond
t = 44 s, the incoherent method was almost incapable of obtaining correct edge estimations.