On the Critical Behaviour of Observed and Simulated Spatial Soil Moisture Fields during SGP97

Abstract

The aircraft-based ESTAR soil moisture fields from the Southern Great Plains 1997 (SGP97) Hydrology Experiment are compared to the simulated ones obtained by Bertoldi et al. [1] with the GEOtop model [2], with a particular focus on their capability in capturing the critical point behaviour in their space-time dynamics (see [3]). The critical point behaviour should denote the transition of soil moisture spatial patterns from an unorganized to organized appearance, as conditions become wetter. The study region is the Little Washita watershed, located in the southwest Oklahoma, in the Southern Great Plains region of the USA. The case study takes place from June 27 to July 16 and encompasses wetting and drying cycles allowing for exploring the behaviour under transient conditions. Results show that the critical probability value is 0.85 for GEOtop, and 0.80 for ESTAR. The GEOtop patterns appear more fragmented, being more reluctant to organization, as confirmed by the higher value of critical probability. Such behaviour is probably inherited by the model’s parameterization: land use and soil classes impose additional spatial structures to those related to the meteorological forcings and the hillslope morphology, driving to higher degrees of heterogeneity.

1. Introduction

As noted by Western et al. [4], soil moisture can vary in space in an organized way or randomly or in a combination of the two. Soil moisture may exhibit continuity (which is captured statistically by the variogram or the autocorrelation function) and connectivity. Connectivity refers to a feature of spatial fields when interconnected paths into spatial structure exist. It is different from continuity which relates to the smoothness of a spatial pattern. Connectivity is able to capture the extent over which connected features are preserved in a hydrological spatial pattern. The hydrologically connected areas are important because they are deemed to be the main runoff sources [5]. Incorporating connectivity into antecedent moisture patterns has a dramatic effect on simulated runoff, even if the spatial correlation structure is unchanged [6].

The definition of connectivity comes from percolation theory [7]. Percolation processes undergo a phase transition experiencing a switch from a state of local connectedness to one where the connections extend indefinitely. A peculiar quality of a phase transition is a sharp change of one or more physical properties of a system under a slight change of a system state variable. Such transition is defined critical when it is possible to observe a scale-invariant behaviour in the point of coexistence of the phases. The critical point denotes the value of system state variable at which such change occurs. The state variable is the occupation probability, defined in the following.

Since in their seasonal time dynamics, soil moisture spatial patterns show the transition between spatially random to spatially connected appearances, Di Domenico et al. [3] have proposed a novel approach based on percolation theory for investigating whether the soil moisture spatio-temporal dynamics behave as a critical point phenomenon. Thus, the critical point denotes the switching from a state characterized by unorganized soil moisture structures to one where organized structures appear (i.e., the growth of variable source areas), being characterized by scale-invariant behaviour.

In order to assess any organization in soil moisture patterns, it is necessary to process long series of high-resolution data over large areas. Apart from few experimental datasets, e.g., the Tarrawarra one [8], such condition prevents from the use of ground-based measurements. With respect to satellite remote sensing, nowadays the debate on the capability in capturing soil moisture is still open; moreover, spatial resolution and temporal sampling frequency work against each other in operational contexts. Soil moisture fields simulated from distributed hydrological models may be considered as a viable option, provided that they have the ability to reproduce observed spatial organization.

In order to assess whether simulated and observed soil moisture fields present similar connectivity statistics, we investigate their characteristics by means of the algorithms proposed in [3], based on percolation theory and renormalization group method.

The observed soil moisture fields used in this study come from the aircraft-based soil moisture imagery from the Southern Great Plains 1997 (SGP97) Hydrology Experiment [9]. The simulated soil moisture fields are obtained from GEOtop hydrologic model [2]. The case study takes place from June 27 to July 16 and encompasses wetting and drying cycles allowing for exploring the behaviour under transient conditions. Both the datasets are processed by means of the methodology introduced by Di Domenico et al. [3] for assessing the datasets’ capability in capturing the critical point behaviour of the soil moisture space-time dynamics.

2. Data and Method of Analysis

2.1. Study Region

The study region is the Little Washita watershed located in the southwest Oklahoma in the Southern Great Plains region of the USA. The watershed, which has a drainage area of 602 km² upstream of the USGS stream gauge #07327550 near Ninnekah, OK, has been operated as an experimental watershed by the US Department of Agriculture, Agricultural Research Service, since 1961 [10]. The topography is rolling, with minimum elevation of about 300 m and maximum elevation of about 500 m (Figure 1(a)). Soil textures range from fine sand to silty loam, with more than 75% of the watershed having SCS hydrologic soil group B (moderately well to well-drained soils). The more slowly drained soils lie in the western and eastern ends of the watershed, with the more sandy soils in the centre (Figure 1(b)). Soils are 0.5 to 1.5 m thick and are underlain by sedimentary rocks, primarily sandstone. The predominate land uses are grazing and winter wheat production (Figure 1(c)). Climate is considered sub-humid, with 760 mm of annual precipitation. We chose to study the Little Washita watershed because of its dense network of meteorological sites to force simulations and aircraft-based soil moisture imageries to evaluate model performance [11,12]. The study period spans from 27 June to 16 July 1997, which encompasses two dry-down periods interrupted on 11 July by a convective storm with a basin averaged daily precipitation of 53 mm, an amount comparable to the average monthly rainfall in July of 56.4 mm [10].

Figure 1. Little Washita watershed properties: (a) Digital Elevation Model derived from 30-m USGS NED digital elevation model dataset; (b) soil texture obtained from Mohanty et al. [16]; (c) land use obtained from Goddard Earth Sciences Data and Information Services Center.

Figure 1. Little Washita watershed properties: (a) Digital Elevation Model derived from 30-m USGS NED digital elevation model dataset; (b) soil texture obtained from Mohanty et al. [16]; (c) land use obtained from Goddard Earth Sciences Data and Information Services Center.

2.2. Observations

The Southern Great Plains 1997 Hydrology Experiment (SGP97) [9] was a cooperative effort between NASA, USDA, and several other government agencies and universities conducted with the primary goal of collecting a time series of spatial soil moisture data. The core of the experiment involved the deployment of the L-band Electronically Scanned Thinned Array Radiometer (ESTAR) for daily mapping of surface soil moisture. ESTAR is a synthetic aperture, passive microwave radiometer operating at a frequency of 1.413 GHz (21 cm). ESTAR was flown on a P-3B aircraft (at an altitude of 7.5 km) operated by the NASA Wallops Flight Facility. The P-3B flew over Little Washita at approximately 1600 UTC (1000 CST). The footprint of the raw brightness temperature data is 400 m, but the raw data were resampled to 800 m to derive soil moisture maps. Further details on the ESTAR instrument and the inversion of ESTAR brightness temperatures to volumetric soil moisture can be found in LeVine et al. [11], Jackson et al. [12], Jackson and LeVine [13], and Jackson et al. [14]. ESTAR-derived soil moisture estimates were found to be within 3% of estimates of volumetric soil moisture from SGP97 ground samples [14]. The ESTAR soil moisture observations [15] have been used in this study. The observations cover a large strip of approximately 50 km (West-East) by 250 km (North-South), with a pixel size of 800 m × 800 m. We selected a subset of this strip covering Little Washita. The observations represent volumetric soil moisture in absolute percent, i.e., percent of the 800 m × 800 m × 5 cm volume of soil that is occupied by water.

2.3. Simulations

GEOtop [2] is a process-oriented distributed hydrologic model that includes solution of the Richards’ equation in three dimensions for evolution of soil water content and pressure, coupled with one-dimensional simulation of soil heat transport. Spatial variability in the soil moisture distribution is introduced in the model by precipitation, as well as by different evapotranspiration rates, controlled by the vegetation properties (i.e., canopy fraction, root depth, canopy aerodynamic resistance) assigned following the land cover classification [14], and by the soil properties [16]. Further spatial structure is induced by the lateral surface and subsurface water distribution. GEOtop was set up and calibrated for Little Washita at the 200-m scale using observations made during SGP97 [2]. The model showed good skill in reproducing the pointwise energy and water balance and the catchment-scale runoff production during SGP97 [1,2]. The simulations represent relative soil moisture content.

3. Approach Background

Recently Di Domenico et al. [3] have proposed a novel approach dealing with soil moisture organization on the basis of concepts of percolation theory and renormalization group method.

Soil moisture spatial patterns show a behaviour similar to phase transition processes when changing, in their seasonal time dynamics, from spatially random to spatially connected appearances as conditions become wetter. Such a phenomenon is driven by the onset of lateral redistribution, which provides the conditions for the growth of the contributing areas. Soil moisture dynamics may be considered as a system which undergoes a phase transition, consisting of the switch from an unorganized to an organized spatial pattern. Hence, the application of percolation theory to soil moisture fields in principle should be meaningful.

The proposed methodology works in analogy to percolation theory [7], though some differences exist between a percolation system and a watershed. The more evident differences are due to the definition of the system boundaries and of the fluxes exchanged with other systems. A percolation system, for instance, can be represented by a rectangular lattice with two open edges; the exchange fluxes are represented by a fluid injected into a site on one edge and extracted somewhere on the other edge. For our purposes, despite a much more complicated geometry, a watershed can be seen in a similar way: the incoming fluxes, the rainfall, once subtracted of all those components not involved in soil water content redistribution mechanisms, such as evaporation, deep percolation and surface runoff, reach the river network, hence the outlet, as subsurface runoff.

Another distinction between percolation systems and watersheds is that, in the former, the grid cells are randomly filled, whereas, in the latter, certain properties (e.g., soils, topography, meteorological patterns) can generate preferential filling of the soils.

The model consists of four steps, namely Dichotomisation, Individuation of clusters, Scaling transformation, and Critical point assessment, which are further described below. By Dichotomisation the occupation probability or density probability of each map is computed as p = n/N [7], where N is the number of the sites in the map and n is the number of them that are “occupied”. By Individuation of clusters the percolation probability or cluster density of each map is computed as $P_N(p)=\frac{C}{N}$, where C is the number of sites that belong to the “largest cluster” on the map. By Scaling transformation a new occupation probability is computed as the result of the “coarse-graining” procedure, obtaining a new map. In the Critical point assessment phase, the value of the critical occupation probability p_c is determined.

3.1. Dichotomisation

The first issue is related to the need to transform a soil moisture map into a binary map. This can be made considering the definition of preferred states given by Grayson et al. [17]. The switching mechanism between local and non-local control is due to the non-linearity of soil hydraulic conductivity (K). A decrease of soil water content (Θ) causes a decrease in conductivity and thus a reduction in lateral flow.

The switching value has been set taking into account the K(Θ) relation; thus, one assigns zero (i.e., “dry”) to pixels below the switching value and one (i.e., “wet”) to pixels above that value. Once the one pixels (referred as “occupied” in the percolation theory) have been identified, their frequency in each map can be evaluated as p = n/N [7], where N is the number of the sites in the map and n is the number of them that are wet/occupied. The thresholding procedure has been applied to each soil moisture map once the switching value has been chosen.

3.2. Individuation of Clusters

Once the binary map has been generated, the easy up to down percolation scheme controlled by the hydraulic gradient has to be adapted to the river basin scheme. Thus, the second step consists of finding clusters of one pixels.

This can be reached considering the role of the orography in controlling the flow pathways; these are represented on a grid scheme by the flow direction function: two contiguous wet pixels belong to the same cluster if a flow path between them exists.

A recursive algorithm for searching one pixels by stepping from neighbour to neighbour in the whole map has been implemented. As each pixel has eight neighbours, it controls whether (i) at least a one pixel exists in the neighbourhood and (ii) it is along a possible flow path. This process labels pixels that satisfy both the previous conditions with a unique label, involving looping throughout the map. Whenever an unlabeled one pixel is encountered, this latter is labelled with a new label. Finally several clusters are identified.

As discussed, until now the identification of the clusters is due to geometrical and physical considerations. The clusters can be interpreted as partial contributing areas which are responsible for the runoff generation.

A further condition on the cluster aggregation has been modelled for representing the hillslope-channel system. As the time scale of the water flowing through a cluster, considered as an entity related to the sloping processes, is very large with respect to the time scale of the channel flow, it is worth considering all the clusters connected to the channel network as a whole cluster directly connected to the catchment’s outlet.

In a catchment-like system there are no borders to connect, as in a percolation lattice [7]. In our methodology, we assumed that a percolation cluster always exists, being that of greatest size; hence, largest cluster assumes the meaning of percolation cluster. Then, the dimension of largest clusters is evaluated (C) and normalized dividing by N, thus computing the percolation probability $P_N(p)=\frac{C}{N}$ for each map.

3.3. Scaling Transformation

The last task is related to the definition of the scaling method. The percolation cluster, or largest cluster in our case, is statistically self-similar [7], thus looking at it at a lower resolution the details will become blurred, but it will appear similar. The self-similarity leads to scale-invariant behaviour near the critical point, so the percolation cluster of the scaled map is qualitatively the same as the original map. The scaling does not change the occupation probability p, and therefore a system at p_c maintains that condition even after the scaling transformation.

The way the scaling is carried out defines a particular process named coarse-graining. We have chosen to work on three by three cells that will become a zero pixel in the scaled grid if there are no clusters or a one pixel if a cluster is found. The aggregation of the clusters in each group of three by three cells was carried out in the same way throughout the grid map. Finally, the occupation probability of the scaled map p₁ can be computed. Hence, the result of the scaling procedure is a new map with a new concentration of one sites (occupation probability) p₁, and more in general p_n+1, which is a function of p₀ (the subscript 0 denotes the original map occupation probability), and more in general p_n.

3.4. Critical Point Assessment

The critical occupation probability p_c can be determined from the P_N(p) and p_n+1(p_n) curves, being the value of the occupation probability showing an abrupt discontinuity of P_N(p) and the change of concavity at the intersection with the bisecting line of p_n+1(p_n). In Figure 2 the typical trend of P_N(p) and p_n+1(p_n) for percolation processes within a square lattice are reported.

In practice, it is possible to assess in an unambiguous way the critical occupation probability p_c by selecting on the p_n+1(p_n) curve the value of p_n that marks the range of all the points with p_n > p_c falling above the bisecting line (see Figure 2(b)).

Prior to the analysis, the two datasets have been harmonized by transforming the absolute soil moisture values of ESTAR and the relative ones of GEOtop into soil suction (pF). Such representation allows to take into account the hydraulic behaviour of the water into the soil matrix and to avoid problems related to the differences in soil texture (i.e., the value of relative soil moisture at field capacity is different for each soil type, while the pF value is unique).

Figure 2. Relations between (a) the probability P_N(p) of a site belonging to the largest cluster and the occupation probability p, and (b) the occupation probability of an (n+1)th-order cell and the occupation probability of an (n)th-order cell for the percolation process within a square lattice (see [7]). In (a) the solid curve is obtained for a lattice having a side of L = 450, the dash-dot curve for L = 200 and the dotted curve for L = 50; the vertical line indicates p_c = 0.59275, as obtained by numerical simulation. In (b) the critical probability for the appearance of the first percolation cluster is p_c = 0.618, as obtained by renormalization group method.

Figure 2. Relations between (a) the probability P_N(p) of a site belonging to the largest cluster and the occupation probability p, and (b) the occupation probability of an (n+1)th-order cell and the occupation probability of an (n)th-order cell for the percolation process within a square lattice (see [7]). In (a) the solid curve is obtained for a lattice having a side of L = 450, the dash-dot curve for L = 200 and the dotted curve for L = 50; the vertical line indicates p_c = 0.59275, as obtained by numerical simulation. In (b) the critical probability for the appearance of the first percolation cluster is p_c = 0.618, as obtained by renormalization group method.

4. Results and Discussion

We begin the analysis by examining the time series of spatial mean rainfall and soil suction for ESTAR observations and GEOtop simulations (Figure 3). We note that both ESTAR observations and GEOtop simulations respond to the temporal occurrence of rainfall events, with the spatial mean soil suction decreasing after storm events and increasing during dry periods, suggesting that both ESTAR observations and GEOtop simulations represent realistic patterns of temporal variability of soil moisture at the watershed-scale. The correlation between the time-series of spatial mean ESTAR observations and GEOtop simulations is 0.91, confirming agreement in temporal fluctuation behaviour. However, there are differences in the actual values between ESTAR observations and GEOtop simulations. From the limited dataset here available, the ESTAR data seem to react faster than the GEOtop ones, being wetter after rainfall events, then turning through steeper paths to dry conditions afterwards. This behaviour is typical of thin soil layers as compared to deeper layers. This suggests that perhaps ESTAR observations represent soil moisture for a shallower depth compared to the GEOtop simulations, which represent the soil moisture within the first 5 cm of the soil column. This needs to be further verified since the general assumption is that ESTAR observations represent the first 5 cm soil moisture [18,19]. Because of this and other possible inconsistencies between the data and the soil texture map used for the transformation, we also observe that the ESTAR pF sometimes goes below the wilting level.

Figure 3. Time series of watershed averaged soil suction and mean daily rain rate for the Little Washita watershed from June 27 to July 16, 1997. The soil moisture data are from ESTAR observations (squares) and GEOtop simulations (diamonds); the rain rate data are obtained from a dense network of rain gauges.

Figure 3. Time series of watershed averaged soil suction and mean daily rain rate for the Little Washita watershed from June 27 to July 16, 1997. The soil moisture data are from ESTAR observations (squares) and GEOtop simulations (diamonds); the rain rate data are obtained from a dense network of rain gauges.

In order to apply the methodology for assessing the critical behaviour of soil moisture dynamics, it is necessary to determine the two thresholds on soil suction and flow accumulation. The soil suction threshold provides the switching value to transform a soil moisture map into a binary map; the flow accumulation threshold provides the value to discriminate between hillslopes and channel networks. When defining the pF threshold, it is necessary to take into account the need for a thorough spacing of the samples in terms of occupation probability to explore all the possible critical values. Provided that the available data represent rather dry conditions, it has been necessary to select soil suction threshold values of 4 and 4.5 for ESTAR and GEOtop, respectively. In order to obtain a suitable delineation of the river network, we chose a flow accumulation threshold of 25.6 km², which has been used for processing both the ESTAR and GEOtop data.

Using the above soil suction and flow accumulation thresholds, we calculated the time series of percolation probability (P_N(p₀)), (Figure 4) and the occupation probability before (p₀) and after (p₁) the scaling procedure. The (p₀, P_N(p₀)) scatterplots are reported in Figure 5(a) and Figure 6(a), the (p₀, p₁) curves in Figure 5(b) and Figure 6(b). In the curves related to the ESTAR data (Figure 5), five additional samples related to the period from the 18th to the 26th of June have been used. Although the number of available soil moisture maps is limited, the datasets encompass an initially-dry drydown period and an initially-wet drydown period, thus the whole spectrum of p and of P_N(p) is covered.

Figure 4. Time series of occupation probability, percolation probability, and mean daily rain rate for the Little Washita watershed from June 27 to July 16, 1997. The data are related to ESTAR observations (squares) and GEOtop simulations (diamonds).

Figure 4. Time series of occupation probability, percolation probability, and mean daily rain rate for the Little Washita watershed from June 27 to July 16, 1997. The data are related to ESTAR observations (squares) and GEOtop simulations (diamonds).

The typical (p, P_N(p)) relationship of a critical phenomenon shows very low values of percolation probability P_N(p) below p_c and a fast rise with a leap into 1 above p_c. In a watershed the values of the percolation probability are always higher than zero for p < p_c as its spatial organization lets the largest cluster be far from zero also in dry periods. For p > p_c the values of percolation probability are located along a bisecting line, as in Di Domenico et al. [3]. Looking at Figure 5(a), the critical probability for the ESTAR dataset can be estimated as p_c = 0.80. This value seems to be confirmed also by the intersection of the (p₀, p₁) curve and the bisecting line in Figure 5(b)). In the same way, the critical probability for the GEOtop dataset can be estimated as p_c = 0.85 (Figure 6).

Figure 5. Relation between the percolation probability P_N(p) and the occupation probability p (a), and occupation probability values before (p₀) and after the scaling (p₁) for the ESTAR data (b).

Figure 5. Relation between the percolation probability P_N(p) and the occupation probability p (a), and occupation probability values before (p₀) and after the scaling (p₁) for the ESTAR data (b).

Figure 6. Relation between the percolation probability P_N(p) and the occupation probability p (a), and occupation probability values before (p₀) and after the scaling (p₁) for the GEOtop data (b).

Figure 6. Relation between the percolation probability P_N(p) and the occupation probability p (a), and occupation probability values before (p₀) and after the scaling (p₁) for the GEOtop data (b).

By observing together Figure 4, Figure 5, and Figure 6, we notice that the points below p_c indicate the drydown period following the initially dry period (June 29–July 3), while the initially-wet drydown period (July 11–July 14) is located above pc in the upper-right part of the (p₀, P_N(p₀)) and (p₀, p₁) plots.

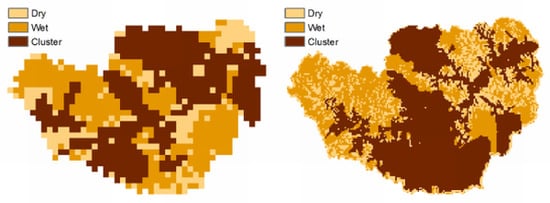
Di Domenico and Laguardia [20], working on a yearly time series of 20 sub-catchments of the Red and Arkansas rivers, found that the critical probability values range between 0.78 and 0.94. Provided that we are dealing with data related to a single catchment, the difference between the ESTAR and GEOtop critical point values should be considered as significant. By observing the maps obtained from the methodology (the samples of the 27th of June and of the 13th of July are reported in Figure 7), the GEOtop patterns appear more fragmented than the ESTAR ones. In previous experiences we observed that the critical point value is partly determined by catchment morphology, which imposes a lower limit to the critical probability, deemed to be the optimal one for that morphological configuration, partly by other perturbing causes occurring at the hillslope scale, which could prevent the system to reach the optimal value. This could be the case of the GEOtop data: the model’s parameterization, e.g., land use, vegetation type, and soil maps, impose additional spatial structures to those related to the meteorological forcings and the hillslope morphology, driving to higher degrees of heterogeneity.

Figure 7. Sample binary maps from the methodology proposed by Di Domenico et al. [3]. “Dry” stands for zero, the other classes for one, with the largest cluster identified as “Cluster”. (a) ESTAR, 27th of June; (b) GEOtop, 27th of June; (c) ESTAR, 13th of July; (d) GEOtop, 13th of July.

Figure 7. Sample binary maps from the methodology proposed by Di Domenico et al. [3]. “Dry” stands for zero, the other classes for one, with the largest cluster identified as “Cluster”. (a) ESTAR, 27th of June; (b) GEOtop, 27th of June; (c) ESTAR, 13th of July; (d) GEOtop, 13th of July.

Recently, Gebremichael et al. [21] compared the ESTAR observations and GEOtop simulations in Little Washita using continuity statistics. They found that ESTAR and GEOtop give contradictory results regarding the relationship between the variogram parameters which measure spatial organization and average soil water content: the drying process was seen to reduce the short-range spatial correlation of the GEOtop simulations while increasing the long-range, while it increased the spatial correlation of the ESTAR observations.

5. Conclusions

GEOtop simulations and ESTAR observations of near-surface soil moisture fields have different degrees of organization in connectivity patterns. The critical probability value is 0.85 for GEOtop, but 0.80 for ESTAR. The GEOtop patterns appear more fragmented, being more reluctant to organization, as confirmed by the higher value of critical probability. Such behaviour is probably inherited by the model’s parameterization: land use and soil classes impose additional spatial structures to those related to the meteorological forcings and the hillslope morphology, driving to higher degrees of heterogeneity. We conclude therefore that soil moisture fields simulated from hydrologic models, which have been calibrated solely on the basis of point observations and streamflow hydrographs at the outlet of the watershed, do not accurately reproduce the connectivity patterns observed in ESTAR. Our results are consistent with Gebremichael et al. [21] who reached at the same conclusion based on continuity patterns. Our results emphasize the need for examining connectivity statistics of spatial soil moisture fields in general, and critical point values in particular, as a more refined means of validating distributed hydrologic models, as compared to the traditional approach of just comparing the streamflow hydrographs.