A Novel Integrated Algorithm for Wind Vector Retrieval from Conically Scanning Scatterometers

Abstract

Due to the lower efficiency and the larger wind direction error of traditional algorithms, a novel integrated wind retrieval algorithm is proposed for conically scanning scatterometers. The proposed algorithm has the dual advantages of less computational cost and higher wind direction retrieval accuracy by integrating the wind speed standard deviation (WSSD) algorithm and the wind direction interval retrieval (DIR) algorithm. It adopts wind speed standard deviation as a criterion for searching possible wind vector solutions and retrieving a potential wind direction interval based on the change rate of the wind speed standard deviation. Moreover, a modified three-step ambiguity removal method is designed to let more wind directions be selected in the process of nudging and filtering. The performance of the new algorithm is illustrated by retrieval experiments using 300 orbits of SeaWinds/QuikSCAT L2A data (backscatter coefficients at 25 km resolution) and co-located buoy data. Experimental results indicate that the new algorithm can evidently enhance the wind direction retrieval accuracy, especially in the nadir region. In comparison with the SeaWinds L2B Version 2 25 km selected wind product (retrieved wind fields), an improvement of 5.1° in wind direction retrieval can be made by the new algorithm for that region.

1. Introduction

A scatterometer is a spaceborne instrument that can simultaneously measure the speed and direction of the ocean surface wind. Since the launch of the SeaSAT-A satellite in 1978, many algorithms have been developed for scatterometer wind vector retrieval [1–9]. The Maximum Likelihood Estimation (MLE) algorithm is regarded as the best one due to its high retrieval accuracy and the complete independence of the Geophysical Model Function; it was operationally used in the data processing of the SeaWinds/QuikSCAT scatterometer [10]. However, the efficiency of the MLE algorithm is relatively low because of its high computational complexity. This problem becomes more prominent when a large amount of data needs to be frequently reprocessed, which usually takes place during the stage of the on-orbit test of a satellite scatterometer. Such a situation was encountered in the China HY-2 scatterometer algorithm testing and validation. In order to solve this problem, we have derived a new fast algorithm for microwave scatterometer data processing [11]. That algorithm adopts wind speed standard deviation as the criterion for searching possible wind vector solutions and has a higher efficiency than that of the traditional MLE algorithm. However, like the MLE algortihm, it also results in relatively lower retrieval accuracy in the nadir and outer regions due to the observing geometry of the conically scanning scatterometer. Stiles proposed a DIR (direction interval retrieval) algorithm to improve the retrieval accuracy of wind direction in the nadir region for SeaWinds scatterometer [12]. Based on the characteristic of the MLE objective function, a modified algorithm for polarimetric scatterometer was derived by Xie et al. by using the simulated backscattered data in full polarization (VV, HH, HV, and VH). The modified algorithm can effectively reduce the wind direction retrieval errors in the nadir and outer regions of the swath [13].

Experiments show that the curve of wind speed standard deviation as a function of wind direction is flatter in the nadir region than those in the middle and outer regions of the swath. Based on this feature, we introduced an algorithm for pencil-beam, conically scanning scatterometer wind vector retrieval to enhance the wind direction retrieval accuracy in the nadir region [14]. However, simulation experiments demonstrate that the uncertainty of wind direction with the traditional WSSD (Wind Speed Standard Deviation) algorithm not only exists in the nadir region, but also exists in the middle and outer regions. Actually, the main difference among these three regions of the swath is the degree of such uncertainty in wind direction retrieval. In spite of relatively lower uncertainty, the ambiguity of wind direction in the middle and outer regions should also be addressed in the wind retrieval in order to further improve the wind direction quality for those regions. The integrated retrieval algorithm generates two segments of possible solutions associated with the first and the second ambiguities by extending the range of wind direction with the change rate of wind speed standard deviation as a criterion. To fit with the integrated retrieval algorithm, a three-step ambiguity removal method is designed. Numerical weather prediction (NWP) wind fields are used for the purpose of initialization and nudging. The NWP wind field we used is the NCEP (the US National Center for Environmental Prediction) forecasting wind product, which was generated by the Global Forecasting System (GFS). The NWP wind data was extracted from the SeaWinds L2B data file and was the same NWP data as used for SeaWinds processing. Three hundred orbits of SeaWinds L2A data (at 25 km resolution) and the co-located buoy data are used to validate and evaluate the integrated algorithm.

This paper is organized as follows. Section 2 describes the principles and steps of the novel integrated algorithm as well as the modified ambiguity removal method designed in this paper. Section 3 covers the method of preparing the SeaWinds L2A and buoy data. Section 4 focuses on the retrieval experiments and the analysis of results to test and evaluate the performance of the new algorithm. Conclusions and comments are summarized in Section 5.

2. Algorithm Description

The purpose of this paper is to apply the wind direction extension method to the wind speed standard deviation retrieval algorithm in order to improve the wind direction retrieval precision.

2.1. Wind Speed Standard Deviation Algorithm

The WSSD algorithm adopts wind speed standard deviation as criterion to search possible wind vector solutions [11]. The standard deviation of wind speed at one given wind direction ϕ can be written as follows:

$$s(\varphi )=\sqrt{\sum _{i=1}^n{\left(w_i(\varphi )-\overline{w}(\varphi )\right)}^2/n}\hspace{1em}\hspace{1em}(i=1,2,\cdots n)$$

(1)

where w_i(ϕ) is wind speed given the i-th observed backscatter coefficient (hereafter denoted as σ⁰) as a function of ϕ, w̄(ϕ) is the average wind speed over all σ⁰ observations at wind direction ϕ, and n is the total number of σ⁰ observations at the current wind vector cell (WVC). A wind vector cell is the basic resolution grid in the swath of a scatterometer, on which the wind field is retrieved.

Just like the MLE algorithm, the baseline WSSD algorithm is also implemented by a two-step method. The first step performs a coarse search for possible wind vector solutions, while the second step makes a fine adjustment for each coarse solution by using a higher wind direction interval resolution.

The baseline WSSD algorithm is implemented by the following procedures:

(1)

Set the wind direction intervals for the coarse search and fine search steps. Let the wind direction be 0 degrees.

(2)

Determine the wind speed for each σ⁰ observation by Geophysical Model Function, and calculate the average and the standard deviation of all the wind speeds at this given wind direction by Equation (1).

(3)

Move to the next wind direction by a coarse direction interval, repeat step (2) until all the average and standard deviation values of wind speeds are calculated for each wind direction position within the range between 0 and 360 degree.

(4)

Search and rank the local minima of Equation (1) along wind direction. Record the local minima and their corresponding wind speed average values and wind directions as ambiguities.

(5)

For each wind vector solution identified by step (4), take its neighboring left (or right) wind direction as the current wind direction and calculate the average and standard deviation of wind speed by Equation (1). A smaller wind direction interval is used in updating the current wind direction. Here, left wind direction refers to the one with smaller value, and right wind direction corresponds to the larger one with respect to the current wind direction.

(6)

Compare the wind speed standard deviation value of the left (or right) wind direction with that of the current wind direction, if the former is smaller, then continue to move the current position to the left (or right) direction, else move the current position to the right (or left) direction.

(7)

Continue to search along the wind direction until the wind speed standard deviation value of the current wind direction is smaller than that of the left (or right) wind direction, or it exceeds the effective range of [0,360]. Take the wind speed standard deviation of the current wind direction as a local minimum.

(8)

Repeat steps (5) to (7) for all the other coarse ambiguities.

(9)

Rank and save up to four precise local minima as the final possible ambiguities.

2.2. New Integrated Wind Vector Retrieval Algorithm

The main reason for lower wind direction accuracy with the traditional WSSD retrieval algorithm in the nadir region is the disadvantageous measurement geometry in which the observation azimuths from one beam are roughly 180° apart. This configuration is usually reflected by the stronger flatness of the wind speed standard deviation curve around each local minimum. Based on this feature of the wind speed standard deviation, the entire swath of the SeaWinds scatterometer can be divided into three regions: (1) nadir region (WVC number 30 to 45); (2) middle regions (WVC number 11 to 30 and 47 to 56); and (3) outer regions (WVC number 1 to10 and 57 to 76). Three examples of wind speed standard deviation curves are illustrated in Figure 1, each showing a curve of a typical wind vector cell located at one of the three regions. From Figure 1, it can be seen that the variation of wind speed standard deviation around the local minimum in the nadir region is comparatively slower than those in the outer and mid regions, which easily leads to higher error in determining the wind direction under the effect of measurement noise.

For the entire swath of SeaWinds scatterometer, the baseline WSSD retrieval algorithm is modified by extending the range of wind direction of the first and second ambiguities. The change rate of the wind speed standard deviation along the wind direction is used as the criterion for wind direction extension. The change rate of the wind speed standard deviation is defined as:

$$k=\frac{\left|s_R-s_L\right|}{2\cdot \Delta d}$$

(2)

where, s_R and s_L are the wind speed standard deviation of the neighboring right and left wind direction with respect to the current wind direction, and Δd is the spacing of wind direction in the wind vector searching.

In wind vector retrieval, the wind direction range for the first and second ambiguities is extended by Equation (2) until the absolute value of the change rate k is larger than the given threshold k₀.

The wind direction extension algorithm consists of left-extension and right-extension components. The left-extension algorithm is given below:

(1)

Take the wind direction of the ambiguity solution as the right wind direction d_r, and calculate the current wind direction d_c by the following equation:

$$d_c=d_r-\Delta d=\{\begin{array}{cc}{d}_c& if\hspace{0.17em}{d}_c\ge 0\\ d_c+360°& \mathit{else}\end{array}$$

(3)

(2)

Calculate the wind speed standard deviation S_c at the current wind direction using Equation (1).

(3)

Similarly, calculate the left wind direction d_l using the following equation:

$$d_l=d_c-\Delta d=\{\begin{array}{cc}{d}_l& if\hspace{0.17em}{d}_l\ge 0\\ d_l+360°& \mathit{else}\end{array}$$

(4)

(4)

Calculate the wind speed standard deviation S_l at the left wind direction.

(5)

Calculate the change rate of wind speed standard deviation for the current wind direction using Equation (2).

(6)

Update the right and current direction with the current and left direction respectively and repeat steps (2) to (6) until the change rate k is larger than the given threshold k₀.

The right-extension algorithm has the similar processing steps. However, the extension wind direction should be computed as follows:

$$d_c=d_l+\Delta d=\{\begin{array}{cc}{d}_c& \mathit{if}\hspace{0.17em}{d}_c<360°\\ d_c-360°& \mathit{else}\end{array}$$

(5)

$$d_r=d_c+\Delta d=\{\begin{array}{cc}{d}_r& \mathit{if}\hspace{0.17em}{d}_r<360°\\ d_r-360°& \mathit{else}\end{array}$$

(6)

2.3. Modified Ambiguity Removal Algorithm

Modifications must also be made for the circle median filter algorithm in order to let it select more possible wind directions in the process of ambiguity removal. In the SeaWinds L2B processor, the NWP product is used to aid in wind direction selection in the ambiguity removal. The NWP product is also used in the modified ambiguity removal algorithm in this paper. It consists of three key steps as follows:

• Step 1: Initialize the wind field by selecting an ambiguity whose direction is closest to that of the NWP wind at each wind vector cell. This procedure is called nudging. It should be noted that the behavior of selecting the closest solution in nudging inevitably assimilates some information of the NWP wind field into the retrieval system. Therefore the quality of the retrieved wind field will partly depend on the quality of the NWP wind field.
• Step 2: Perform the circle median filter over the entire swath until no wind direction is changed in a pass or a maximum iterative time is reached. For the detailed description of the circle median filter, see [15].
• Step 3: Nudge the filtered wind field by the NWP wind direction once again. However, this time, it is a conditional nudging in which only if the difference between the current wind direction and the NWP wind direction is larger than the threshold value, would the operation of nudging be conducted at this wind vector cell. Statistical analysis found that about 95 percent of the co-located buoy and NWP data pairs have a wind direction difference less than 60°. Hence, if a wind direction deviates from the co-located NWP more than 60°, then it can be regarded as a small probability event. Based on this consideration, the threshold value was set to be 60° in this paper.

Note that the filter algorithm should involve additional wind directions beyond the conventional four single directional solutions in step 1 and in step 3. Suppose there are four ambiguities in a wind vector cell, with their directions orderly represented by d₁, d₂, d₃, d₄ respectively. The set of all the possible wind directions to be used in ambiguity removal can be expressed by:

$$d_{ij}^k=\left\{\left[d_{1L},d_{1R}\right],\hspace{0.17em}\left[d_{2L},d_{2R}\right],\hspace{0.17em}{d}_3,\hspace{0.17em}{d}_4\right\}$$

(7)

where [ ] denotes wind direction interval after extension, d_1L and d_1R are the left and the right boundary value of the first ambiguity after extension, and d_2L and d_2R are the corresponding boundaries of the second ambiguity. The directional solution associated with the local minimum of the first ambiguity and that associated with the second ambiguity are contained in the solution interval of [d_1L, d_1R] and [d_2L, d_2R] respectively. Therefore, the directional solution set $d_{ij}^k$ contains the most probable wind directions, which have a potential chance to be the true one. In initialization, we select the direction in the set $d_{ij}^k$ that is nearest to the NWP wind direction $d_{ij}^{\mathit{NWP}}$ at position (i, j) in the wind field.

The purpose of step 3 is to correct the exceptional wind directions which had probably converged to the wrong value due to measurement noise or boundary effects of the filter algorithm.

2.4. Wind Speed Refinement

The wind speed solution determined by the WSSD-based algorithm is generally not very accurate due to the thermal noise from the scatterometer instrument. This problem becomes more serious in the case of low wind speeds where the signal to noise ratio (SNR) is relatively lower. Thus, a wind speed refinement procedure performed following the process of wind vector retrieval and ambiguity removal in order to get a more accurate wind speed for each ambiguity solution. From a wind retrieval perspective, the wind speed uncertainty of the WSSD-based algorithm arises from the method of wind speed determination, which simply calculates the mean value of wind speed and takes it as the possible wind speed solution for a given wind direction (as described in Section 2.1). The probability of the mean wind speed to be the true wind speed solution depends heavily on the noise level of each backscatter observation. If there is no noise, then the mean wind speed will be exactly equal to the true wind speed solution. The wind speed retrieval error goes up as the measurement noise of scatterometer increases.

The contribution of each backscatter observation to the wind vector retrieval can be well characterized by the objective function of MLE according to the measurement variance of each observation, as shown in the following equation:

$$J_{\mathit{MLE}}(w,\Phi )=-\sum _{i=1}^N\left[\frac{{\left(z_i-M(w,\Phi -{\varphi }_i,{\theta }_i,p_i)\right)}^2}{V_{Ri}}+\text{ln}{V}_{Ri}\right]$$

(8)

where J_MLE(w, Φ) is the MLE objective function, z and M represent the backscatter coefficient measurement and model value respectively, V_Ri is the measurement variance, and w, Φ, ϕ, θ, p denote wind speed, wind direction, radar azimuth, incidence angle, polarization respectively. We use Equation (8) to obtain a more precise wind speed by finding the speed that lets J_MLE(w, Φ) reach its maximum at the wind direction of an ambiguity. Since only one peak value exists along the wind speed dimension at a given wind direction, a hill-climbing algorithm is used to search the optimal wind speed. The step of wind speed is set to 0.1 m/s in searching. The rough wind speed solution (the mean value of wind speeds) calculated in the previous wind vector retrieval is taken as the start wind speed. Because the rough wind speed is not far away from the true wind speed to search, the searching times are generally less. In addition, the quadratic function interpolation is applied to precisely locate the wind speed position by using the three adjacent wind speed points with the searched wind speed in the middle. As demonstrated in Section 4, this algorithm has high performance in wind speed refinement.

3. Data Preparation

The purpose of the data preparation is to provide the required data set for the new algorithm validation and evaluation. The main task of data preparing includes: (1) reading and screening; (2) temporal and spatial matching; (3) preprocessing.

3.1. Data Reading and Screening

The Buoy data used in this paper were acquired from the US National Data Buoy Center (NDBC). These data are recorded in F291 format containing the parameters of buoy number, geographical location, height of anemometer, wind speed, wind direction, and measurement time. Due to its high quality and stability, continuous wind measurement data record (record J) in buoy F291 file is used to validate and evaluate the wind retrieval algorithms. A total of 51 NDBC buoys that contain such data records are selected for retrieval performance validation in this paper.

SeaWinds L2A data contains all the parameters that are required in wind vector retrieval, such as data acquiring time, row of wind vector cell, measure times in each wind vector cell, longitude and latitude of each σ⁰ observation, azimuth angle, incidence angle, backscatter coefficient, coefficients of K_p (normalized standard deviation of σ⁰ observation), and atmospheric attenuation [16].

The processing algorithm first reads the buoy data elements, then selectively reads the SeaWinds L2A data according to the longitude and latitude of the buoys. Only the data of the wind vector cells which are no more than 0.3° away from the buoy location are read. This procedure is actually a coarse screening of the SeaWinds L2A data. In addition, the algorithm only reads the data of the wind vector cells which are associated with the surface type of “ocean” and are under the mode of “wind observation”.

3.2. Temporal and Spatial Matching

Precise matching between buoy data and SeaWinds L2A data is performed in this step based on their spatial locations and acquiring times. The temporal and spatial precise matching method is given below:

(1)

Spatial precise matching

Calculate the distance between buoy and wind vector cell. The buoy is matched to the nearest wind vector cell in space.

(2)

Temporal precise matching

For each WVC associated with a buoy in space, find the record of wind speed and direction in the buoy data set where the measurement time deviation between the buoy and the current WVC of scatterometer is the smallest. Here, the buoy wind vector data acquired from record J in F291 data file are 10-min averaged. The intermediate moment of the ten minutes associated with a buoy measurement is taken as the measurement time of that buoy wind data. Time averaging of the buoy data can partially reduce the discrepancy between the point measurement by the buoy and the area average sampling by the scatterometer.

3.3. Data Preprocessing

The data preprocessing covers atmospheric correction of σ⁰ observation, transformation of wind speeds for different heights, and removal of exceptional data points.

(1)

Atmospheric correction of σ⁰

Due to the atmospheric attenuation in microwave band, the measured σ⁰ must be properly corrected for that effect before they are used to retrieve ocean wind. In linear units, the atmospheric correction to the measured σ⁰ can be implemented by the following equation:

$${\sigma }^0={\sigma }_m^0\cdot \mathit{Atten}/\text{cos}\hspace{0.17em}\theta$$

(9)

where ${\sigma }_m^0$ is the measured σ⁰ by the scatterometer in linear units, Atten is the two-way vertical atmospheric attenuation in linear units (contained in SeaWinds L2A data), and θ is the incidence angle of the microwave beam.

(2)

Conversion of wind speed to 10 m height

The anemometers installed on buoys we select are at a height of 5 or 10 m. We converted the winds to neutral stability winds with a uniform height of 10 m. Under neutrally stratified conditions, the wind speed at altitude z in meters can be approximately computed by the following equation:

$$U_z=\frac{u_{*}}{\kappa }\cdot \text{ln}\left(\frac{z}{z_0}\right)$$

(10)

where U_z represents the wind speed at height z above the ocean surface, u_* is the friction velocity, K is the von Karman constant, usually being taken as 0.4, and z₀ is the roughness length, which can be empirically determined by the formula below [17,18]:

$$z_0=\frac{6.84\times {10}^{-5}}{u_{*}}+4.28\times {10}^{-3}\cdot u_{*}^2-4.43\times {10}^{-4}$$

(11)

Using the Equations (10) and (11), we compute u₁₀, the 10 m neutral stability winds, by an iterative method.

(3)

Removal of exceptional data points

The operational empirical model function of Qscat-1 is used to detect and remove the abnormal data points. If the incidence angle, wind speed, and relative azimuth are given, then the corresponding model value of σ⁰ can be expressed by:

$${\sigma }_{\mathit{Qscat}-1}^0=F(\theta (p),\hspace{0.17em}w,\hspace{0.17em}\chi )$$

(12)

where F represents the abstract expression of the Qscat-1 model function, p represents the polarization of the current pulse, θ is the incidence angle, w is wind speed, and χ is relative azimuth, which is defined as the difference angle between wind direction and azimuth angle of radar beam. Suppose the maximum tolerance of the wind speed error is w₀, namely the dynamic range of the wind speed is [w – w₀, w + w₀], the minimum and the maximum reasonable model value of the measured σ⁰ can be written as follows:

$${\sigma }_{\text{min}}^0=F(\theta (p),\hspace{0.17em}w-w_0,\hspace{0.17em}\chi )$$

(13)

$${\sigma }_{\text{max}}^0=F(\theta (p),\hspace{0.17em}w+w_0,\hspace{0.17em}\chi )$$

(14)

Therefore, the range of the reasonable measured σ⁰ is $[{\sigma }_{\text{min}}^0,\hspace{0.17em}{\sigma }_{\text{max}}^0]$. If one of the measured σ⁰s does not fall within the range above, then the wind vector cell associated with it will be detected as an abnormal one. This method is very effective for data quality control in the wind retrieval experiment and result evaluation. The value of 3 m/s for w₀ is applied in the exceptional data removal.

4. Retrieval Experiments

4.1. Experiment Data and Parameters

The new integrated algorithm described in this paper was validated by using 300 orbits of SeaWinds L2A data and the co-located NDBC buoy data. The orbit number of SeaWinds L2A data ranges from 10,158 to 10,472 with a few orbits missing. The wind speed and direction data from buoys are used to evaluate the retrieval accuracy.

The change rate threshold value of wind speed standard deviation k₀ is set to 0.003 (with units in (m/s)/deg) for the entire swath in wind vector retrieval, which is empirically determined by analyzing the feature of the wind speed standard deviation curve and carrying out some retrieval experiments. First, a wide range [0.001, 0.008] of feasible k₀ is obtained based on the average length of the wind direction intervals generated by the extension algorithm. Then, an appropriate value of k₀ is selected from that range by retrieval experiments on another ten orbits of SeaWinds L2A data in terms of their retrieval performance. It is a crucial problem for the integrated algorithm to choose an appropriate value of k₀. If this value is too low, then the integrated algorithm will be nearly equivalent to the baseline of the WSSD algorithm, whereas, a larger threshold value will oversmooth the retrieved wind field. As shown in the following sub-section, the value of 0.003 is appropriate enough to result in a better retrieval performance than those from the traditional WSSD and MLE algorithms. Because the performance of the determined threshold value partially depends on the incremental step in optimization, so the current threshold value is not necessarily optimal. The window size of the circle median filter is set to 7 × 7 for ambiguity removal.

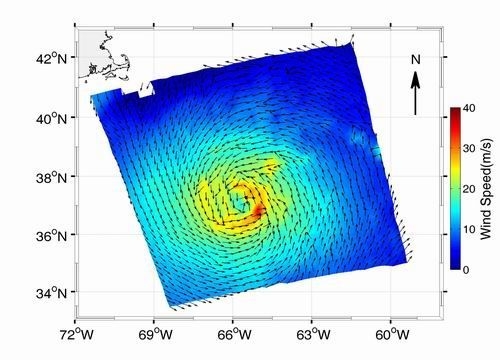
4.2. Experiment Results

To examine the wind direction performance of the new integrated algorithm, the mean absolute errors of wind speed and direction are calculated for each region of the swath as listed in

Table 1. The retrieval errors for each region of the swath.

Error	Region	SeaWinds L2B Data	Traditional WSSD Algorithm	Integrated Algorithm
wind speed mean absolute error (m/s)	nadir	0.764	0.762	0.710
	middle	0.760	0.695	0.696
	outer	0.753	0.684	0.667
wind direction mean absolute error (°)	nadir	20.912	23.881	15.783
	middle	14.601	13.979	12.994
	outer	13.162	13.474	12.095

. In Table 1, the traditional WSSD algorithm refers to the baseline wind speed standard deviation retrieval algorithm without wind direction extension. The total number of wind vector cells co-located with buoy is 141, 411, and 170 in outer, middle, and nadir region respectively. In process of exceptional data removal, 5, 20, and 9 data points are removed in each of three regions. Thus, 136, 391, and 161 co-located data points are respectively left for statistics in outer, middle, and nadir region in Table 1. For comparison, the errors between SeaWinds L2B wind product and the co-located buoy wind data are also given in Table 1. In this paper, all the L2B wind data used to validate the algorithms is the SeaWinds/QuikSCAT Version 2 25 km selected wind product. The results presented in Table 1 reveal that the new integrated algorithm can improve the wind direction retrieval accuracy in the nadir region with respect to the baseline WSSD algorithm and the SeaWinds L2B wind product. Compared with the SeaWinds L2B wind product, the integrated algorithm approximately makes a 5.1° improvement in wind direction retrieval in the nadir region. Slight improvements in direction retrieval are also found in the middle and the outer regions due to the application of wind direction extension algorithm to those regions. It is shown that 1.6° and 1° enhancements of wind direction retrieval accuracy are achieved by the integrated algorithm in the middle and the outer regions respectively. Although the baseline WSSD algorithm performs poorly in wind direction retrieval in the nadir region, its performance is comparable to or slightly better than that of the SeaWinds L2B wind in the middle and outer regions. Moreover, Table 1 clearly shows the lower wind speed retrieval errors of the integrated algorithm compared well against the SeaWinds L2B wind product across the entire swath. The high performance in wind speed retrieval is due to the accurate wind direction input and the effectiveness of the wind speed refinement algorithm in precisely locating the wind speed for a given wind direction.

Figure 2 displays the cumulative distribution function of wind vector cells sorted by wind direction absolute error in the nadir region with comparisons of the new integrated algorithm and the traditional WSSD algorithm, as well as the integrated algorithm and the SeaWinds L2B wind product. As indicated in Figure 2, the new integrated algorithm effectively reduces the wind direction errors in more cases than the Version 2 SeaWinds data processing algorithm in the 10°–120° range, which results in a better performance of wind direction retrieval in the nadir region.

Probability density function of wind vector cells at each wind direction error is another good indicator for the performance of a wind retrieval algorithm. Here, the probability density function is defined as the percentage of wind vector cells which fall into a bin of wind direction errors. Figure 3 presents the variation curves of the probability density function of wind vector cells versus the wind direction error for the nadir region. From Figure 3, it can be seen that the probability density function curve of the integrated algorithm is comparatively narrower and its peak value is higher than that of the traditional WSSD algorithm and the SeaWinds MLE algorithm, implying that the integrated algorithm achieves higher performance in the nadir region than the traditional ones.

Figure 4 illustrates the variations of the wind direction mean absolute error with the wind speed for the three algorithms (WSSD, MLE, and the integrated algorithm) for the nadir region. The wind speed interval is 2 m/s in the statistical analysis. As shown in Figure 4, the wind direction errors of the integrated algorithm are lower than those of the traditional WSSD algorithm at all the wind speed intervals. Obvious improvement is also gained in wind direction by the integrated algorithm in contrast with the L2B wind product at lower (<5 m/s) and higher (>11 m/s) wind speeds. Note that the biggest wind direction absolute error appears at the wind speed of 0–4 m/s for all the three algorithms due to the low SNR (signal to noise ratio) at low wind speed. However, the integrated retrieval algorithm has a notable advantage over the traditional WSSD and the L2B wind product in resisting the measurement noise. This property comes from the ability of the new algorithm to generate and preserve more likely directional solutions by the procedure of wind direction extension across the entire swath.

The wind direction errors at each wind vector cell location in the nadir region are shown in Figure 5 for the traditional WSSD algorithm, the new integrated algorithm and the SeaWinds L2B wind product. Figure 5 indicates that the new integrated algorithm results in lower wind direction errors than the baseline WSSD algorithm at all the wind vector cell locations, as well as than the SeaWinds L2B wind product at most wind vector cell locations (11 of 16 wind vector cells).

For comparisons, some examples of the wind fields retrieved by the traditional WSSD and the integrated algorithm and the corresponding wind field from SeaWinds L2B product are displayed in Figure 6. The wind fields shown in the figures are from orbit 10,163 of the SeaWinds scatterometer with wind vector rows of from 490 to 550. The size of wind vector cell in wind fields is 25 km × 25 km. From Figure 6a, it can be seen that obvious spatial inconsistency of the wind directions occurs in the central parts of the given wind field enclosed by the red rectangular dotted lines, which are located in the nadir and middle region of the swath. Similar phenomena can be found in the L2B wind field as shown in Figure 6c. By contrast, a much more consistent wind field obtained in Figure 6b indicates the capability of the integrated algorithm in reducing the uncertainty of wind direction in the nadir region for conically scanning scatterometer. In Figure 6b, most of the wind directions are coherent with their surroundings except for a few exceptional ones that have abrupt values probably due to the effect of measurement noise.

Furthermore, it can be found that a small red area located in the bottom-right of the L2B wind field (Figure 6c) has the opposite wind directions to the counterparts retrieved by the integrated algorithm and the traditional WSSD algorithm (Figure 6a,b). This inconsistency was clearly exhibited on the images of wind direction difference between the different two wind fields as illustrated in Figure 7. Figure 7 shows that a red area also appears in the bottom-right of Figure 7a,c, which, in shape, is similar to that in Figure 6c. The images indicates that a wind direction difference of about 180° between the L2B wind and the NWP wind, as well as between the L2B wind and the integrated algorithm wind, occurs in that area. In contrast, a smaller difference is found between the integrated algorithm wind and the NWP wind. Thus, if the NWP wind directions are correct in that area, then the L2B wind directions are wrong with a 180° ambiguity. Because about 95% of the NWP wind directions have an error less than 60° compared against the buoy data, the L2B wind directions in the bottom-right of Figure 6c have converged to a wrong result with a high probability.

Another example of a cyclonic system is shown in Figure 8, which is intended to validate the integrated algorithm in correctly resolving a hurricane structure. Hurricane Erin was used to demonstrate the performance of the integrated algorithm in monitoring such a strong storm. It was one of the strongest tropical cyclones during 2001 Atlantic hurricane season. Figure 8 is a snapshot observation of Erin by Seawinds/QuikSCAT at 09:40 UTC, 11 September 2001 (orbit 11612). Besides the wind fields retrieved by the three algorithms (integrated, WSSD, and MLE (L2B)), the NWP wind field and the image of rain probability are also given in Figure 8. The WVC rows of the wind field shown in Figure 8 ranges from 563 to 597, and the columns ranges from 13 to 47, which covers the middle and nadir regions of the swath. The parameter of rain probability is extracted from the SeaWinds L2B data file and its dynamic range of valid value is from 0 to 1, with a higher value indicating a higher probability of rain. A cyclone system is often accompanied by rain, which degrades the wind retrieval accuracy from scatterometer. Figure 8 indicates that a reasonable counterclockwise circulation structure was well retrieved by the integrated algorithm, as well as by the other algorithms (the traditional WSSD and MLE). However, a smoother and more consistent wind field was retrieved by the integrated algorithm. From Figure 8e, it can be seen that most of the area around the circulation center (hurricane eye) has high probability of rain. Therefore, the integrated algorithm has a satisfactory performance even in the region with strong wind and high probability of rain.

The other advantage of the integrated algorithm is that it has higher computational efficiency than the MLE retrieval algorithm. On our current platform (Processor: 2.53 GHz, Memory: 2 GB), the average processing times of the integrated algorithm and the MLE algorithm for one wind vector cell are 0.000478 s and 0.001274 s, respectively. This means that the processing speed of the integrated algorithm is approximately 2.6 times as fast as that of the MLE algorithm.

5. Conclusions

This study presented a novel integrated wind retrieval algorithm from spaceborne conically scanning scatterometer. The new algorithm exhibits some advantages over the existing ones by integrating the wind direction extension method with the traditional WSSD (wind speed standard deviation) algorithm. It retains the respective advantages from these two algorithms and features with lower computational cost and higher wind direction retrieval accuracy. Results showed that the integrated algorithm reduced directional error by 5.1° in wind direction retrieval for the nadir regions in comparison with the standard SeaWinds L2B wind product. In addition, the new algorithm is about 2.6 times as fast as the baseline MLE algorithm in computational speed.

The integrated algorithm provides a new potential approach to further enhancing the wind direction retrieval accuracy and reducing the computational complexity for the conically scanning scatterometer. With some minor modifications and careful parameter tuning, it can be applied to the operational scatterometer data processing due to its better retrieval performance and higher computational speed. However, it is a key point for the new integrated algorithm to select a suitable threshold value of the wind speed standard deviation rate. Therefore, great effort should be made to optimize such a suitable threshold value of the wind speed standard deviation in order to further improve the wind retrieval accuracy.