Unravelling Eastern Pacific and Central Pacific ENSO Contributions in South Pacific Chlorophyll-a Variability through Remote Sensing

Abstract

El Niño—Southern Oscillation (ENSO) is regarded as the main driver of phytoplankton inter-annual variability. Remotely sensed surface chlorophyll-a (Chl-a), has made it possible to examine phytoplankton variability at a resolution and scale that allows for the investigation of climate signals such as ENSO. We provide empirical evidence of an immediate and lagged influence of ENSO on SeaWiFS and MODIS-Aqua derived global Chl-a concentrations. We use 13 years of Chl-a remotely sensed observations along with sea surface temperature (SST) observations across the Tropical and South Pacific to isolate and examine the spatial development of Chl-a anomalies during ENSO: its canonical or eastern Pacific (EP) mode, and El Niño Modoki or central Pacific (CP) mode, using the extended empirical orthogonal function (EEOF) technique. We describe how an EP ENSO phase transition affects Chl-a, and identify an interannual CP mode of variability induced spatial pattern. We argue that when ENSO is analysed as a propagating signal by the EEOF, CP ENSO is found to be more influential on Chl-a interannual to decadal variability than the canonical EP ENSO. Our results cannot confirm the independence of the two ENSO modes but clearly demonstrate that both ENSO flavors manifest a distinct biological response.

1. Introduction

Prior to satellite observations, our understanding of changes in global phytoplankton was relatively poor. Since the advent of satellite remote sensing of surface chlorophyll-a (Chl-a) concentrations in the late 1970s, it has been possible to estimate surface phytoplankton biomass at near global scales. Remote sensing tools have proven to overcome the greatest limitations that classical observational methods suffer by providing global coverage and a continuous temporal sampling rate. Sensors such as the recently terminated SeaWiFS and the on-going MODIS-Aqua are passive ocean color instruments that measure surface water radiance that can be converted into near-surface Chl-a concentrations. Due to the presence of this pigment in all phytoplankton organisms, Chl-a is commonly used as a phytoplankton biomass indicator throughout the water column though the relationship between surface Chl-a and the biomass is indirect and non-linear [1]. The one to two day revisit cycle of the ocean color sensors on board these polar orbiting satellite platforms is ideal for large-scale quantitative studies of the spatial and temporal ocean productivity rates, and its relationship with climate modes of variability.

At the interannual scale, El Niño—Southern Oscillation (ENSO) is not only the dominant global mode of climate variability, but also the determining mode in global ocean productivity [2,3]. As a natural mode of the climate system, ENSO represents the quasi-periodic oscillation that exists due to the “internal” coupling of the atmosphere and ocean on year-to-year time scales. However, recent ENSO discussions have focused on the differences between two El Niño types, the classic canonical (eastern Pacific) El Niño and the central Pacific (CP) El Niño (also known as El Niño “Modoki”) that has been observed more frequently over the past few decades (e.g., [4]). The eastern Pacific (EP) ENSO mode is commonly described in terms of a basin-wide coupling of the ocean and atmosphere across the tropical Pacific that manifests itself as a quasi-periodic variability of the climate system on a time scale of 2–8 years [5]. In the neutral “phase” of ENSO (i.e., neither El Niño nor La Niña conditions), the climatic conditions are characterized by high sea level pressure (SLP) over the central-eastern subtropical Pacific, with strong trade winds pushing the surface waters westward into the Western Pacific Warm Pool (WPWP) [6]. This statistically averaged state of the tropical Pacific climate provides deeper cooler waters to upwell along the eastern and equatorial boundaries creating a cold tongue that extends from the east to central Tropical Pacific. One effect of this cold tongue is to enrich the phytoplankton response around the equator as the upwelling brings nutrient rich waters into the euphotic zone where it is consumed by these organisms [7]. For the composite EP El Niño phase, SLP in the central-eastern subtropical Pacific tends to be reduced, the trade winds are weaker, and the central-eastern equatorial Pacific is anomalously warm and nutrient-depleted due to the reduction in upwelling. EP El Niño events tend to concomitantly show an anomalous decrease of phytoplankton in the Tropical Pacific [8], except in the WPWP region, where the deep nutrient rich waters have a greater chance to surface due to a shoaling thermocline [9]. Conversely the La Niña phase of EP ENSO, which is associated with an enhancement of the trade winds, leads to an anomalous increase of phytoplankton in the central-eastern equatorial Pacific.

The CP El Niño [10]—otherwise known as El Niño “Modoki”—differs from the canonical El Niño in that it is characterized by a SST anomaly at the eastern edge of the WPWP, flanked zonally by two opposite signed anomalies [11]. It is thought that CP El Niño events are excited by anomalous westerly winds in the western Pacific, which push the warm surface layer waters from the off-equatorial western Pacific towards the equator, driving a downwelling equatorial Kelvin wave, which induces a deepening of the thermocline from the central to the eastern Pacific [11]. This is followed by easterly wind anomalies in the eastern Pacific creating convergence in the central Pacific, further deepening the central Pacific thermocline. Thus the SST warming in the central Pacific is further strengthened by downwelling equatorial Kelvin waves from the west, and Rossby waves from the east [11]. CP El Niño displays a strong decadal periodicity [11,12], and has increased in intensity in recent decades, unlike EP El Niño [13]. Recent works reveal that CP El Niño events induce low values of remotely sensed phytoplankton indicators in the eastern part of the WPWP [14–16] while the examination of the strongest CP and EP El Niños to date (i.e., 1997–1998 EP El Niño and 2009–2010 CP El Niño) suggests that horizontal processes (e.g., intrusion of nutrient-deficient warm pool waters) dominate during a CP event while vertical processes (e.g., nutricline suppression) and mixing play a larger role in an EP event [17].

These two ENSO mechanisms have been identified as the leading global Chl-a drivers at interannual time-scales in the past decade using the Empirical Orthogonal Functions (EOF) technique [3,14]. EOF analysis is a commonly used technique in climate and earth sciences, often used to isolate the leading modes of variability in the geo-data that typically relate to forcing climatic mechanisms and processes [18]. However, EOFs do not take into account propagating features [18]. This limitation has the potential to underestimate the importance of the driving mechanisms being examined. Here, we use a variant of this technique, the extended EOF (EEOF) that provides a dynamical expression of the traditional EOF.

In this paper, we aim to describe and interpret the Tropical and South Pacific Chl-a patterns in the context of the dominant and dynamical interannual modes of Pacific and near-global climate variability—specifically the EP and CP ENSO modes. We characterize the variability associated with ENSO changes throughout the South Pacific and the Tropics. Further, we describe and illustrate how an ENSO transition affects Chl-a. Finally, we discuss decadal-scale changes in Chl-a concentrations in the context of recent increases in CP El Niño frequency—a mode with a clear and strong decadal peak. We demonstrate that at least since the late 1990s, the Chl-a signal has been more connected with the CP El Niño structure than with the classical EP ENSO mode—consistent with the increased frequency and intensity of the CP mode over the past 30 years [4,13,16].

2. Data

The primary data investigated in this study are satellite remote sensed Chl-a estimates. These data were retrieved from the Oregon State University Ocean Productivity website [19] originally collected by NASA [20] and are a combination of r2009.1 SeaWiFS and MODIS-Aqua satellite Chl-a products. The dataset comprises of monthly-averaged matrices (maps) of 1080 × 2160 pixels, resolved at 1/6° per pixel, increasing polewards in km resolution at a rate of cosine (latitude). Ocean color data here are only available to 45° latitude, as the lack of sunlight during wintertime limits the remotely sensed observations further poleward. The Chl-a observations were derived from SeaWiFS for the period October 1997–December 2007 after which there were significant gaps in the SeaWiFS dataset. Consequently MODIS-Aqua data were used from January 2008–October 2010. Chl-a observations from the two missions compare very well with correlations of r² > 0.8 while the bias and root-mean-square deviation (RMSD) are within acceptable values (e.g., [21]) allowing for such a merger with minimal artifacts. 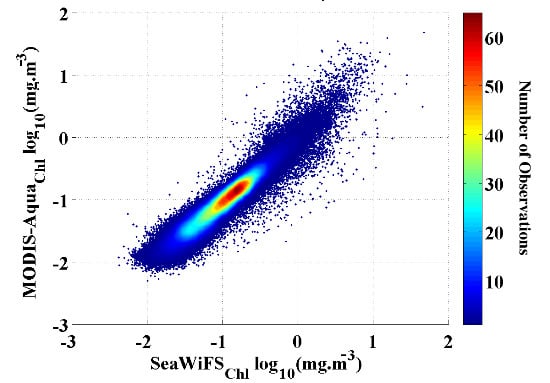Additionally, we have compared the SeaWiFS and MODIS-Aqua Chl-a data between July 2002 and December 2007, when there is overlap between the two missions and full coverage for the spatial domain of this study (Figure 1). We found a strong (r² = 0.93) and significant (p << 0.01) correlation between the two datasets with a low RMSD = 0.10 and standard deviation (STD) < 0.001. Hence, we are confident that our merged Chl-a data set is free of any significant artifacts and that the results of the analysis are not affected by the data transition.

The phases of the EP ENSO are characterized by several available indices derived from several geophysical variables. For the present study, we selected the Multivariate ENSO Index (MEI) since it is the most comprehensive index for basin-scale climate investigations of ENSO. It takes into account six observed atmosphere and ocean physical variables across the tropical Pacific: sea level pressure, zonal and meridional surface wind components, sea surface temperature, surface air temperature and total cloudiness fraction of the sky [22–24]. MEI data were obtained from the US National Oceanic and Atmospheric Administration [25].

The CP (or Modoki) El Niño has only recently been identified as a distinct climatic phenomenon [10,11]. Consequently, there are fewer simple metrics available to diagnose and/or monitor CP ENSO changes. Here we have adopted the Improved El Niño Modoki Index (IEMI) developed by [26], which we calculated using the UK Met Office Hadley Centre SST (HadISST) dataset [27]. We also use the same dataset for the additional SST analysis outlined in the following section.

3. Methods

Before delving into the methodology, we first provide here a justification for the extent of the study domain and choice of analysis by providing some general statistical comparisons of the MEI and Chl-a data (first described in [28]). Figure 2 shows the spatial distribution of statistical significance, correlation coefficient and the time lag of the best correlation coefficient, between the MEI and Chl-a time series from 45°N to 45°S. It can be readily seen here that ENSO (represented by the MEI) has a more significant influence on Chl-a concentrations over the Pacific than in other ocean basins (Figure 2a). Furthermore, significant relationships are found to exist not only in the tropical region of the Pacific but further poleward to 35°N and 45°S. These extra-tropical regions also display high correlation coefficients, albeit with an inverse relationship to that observed throughout the Tropical Pacific, with the exception of the Western Pacific where a positive correlation coefficient is observed (Figure 2b). Direct and highly significant relationships are also found in the subtropical regions while the mid-latitudes of the South Pacific also stand out with a consistently positive relationship. This is in stark contrast to the northern hemisphere equivalent latitudes where correlation coefficients change sign. Most interesting of these results is that while all observed Chl-a regions track well with the MEI, they display different timing with respect to a best fit with the ENSO signal (Figure 2c). The results indicate that the ENSO index is significantly coupled and synchronous with Chl-a patterns that occur off the equatorial belt (shaded in black in Figure 2c) but lagged with the patterns at the equator (shaded in red in same figure). It is also noteworthy that Chl-a variability over the Equatorial Pacific and also at the west coast of Java and Sumatra in the Indian basin (with either a direct or inverse relationship to the MEI) has a positive (leading) best fit to the MEI, and in some regions at three or more months earlier. This best fit is delayed towards the poles.

Based on our focus on ENSO signals, and the above results, we selected the tropical and South Pacific basin-wide area extending meridionally from 20°N to 45°S, zonally from 140°E to 70°W, and coarsened to a 1° grid-scale. The aim of this paper is to study the ENSO related Chl-a propagating patterns in the South Pacific. Hence, we have included both the South Pacific and the Tropical Pacific regions within the study area. The North Pacific to 20° N is included in our analysis in order to ensure that tropical processes are captured including near-equatorial wave dynamics; however our primary focus is the Chl-a variability in the South Pacific. Slow moving mid-latitude Rossby waves are known to play an important role in ENSO dynamics and setting the timing of lagged relationships [29]. We therefore included much of the mid-latitude South Pacific in our domain as we hypothesize that ENSO related Chl-a variability will be found well outside of the tropical region. Also excluding the mid-latitudes of the North Pacific provides the advantage of faster computation without compromising the study domain of interest. Chl-a anomalies (Chl-aA) were calculated by removing the log-normal monthly average at each pixel. That is, we calculate the monthly mean using log values, convert back to normal distribution, and then remove this value from the original monthly data. All data were also de-trended in time, using linear regression. The power spectra for both climate indices (MEI and IEMI) were calculated for the same period as the Chl-a record to determine the periodicity of the ENSO signals. Peaks with maximum power above the mean red noise spectrum, and at the 95% confidence levels [4], corresponded to 28- and 128-month periodicities for the MEI and IEMI respectively (Figure 3a,b). These power spectra maxima indicate the dominant propagating frequencies in the ENSO signal which were taken as the relevant lag (L) periods for an EEOF analysis of Chl-aA to explore whether its propagating variability is well explained by these periodicities. This analysis is described below.

The standard EOF analysis is a commonly used technique in geophysical research since it can summarize large datasets in space and time into only a few distinct modes that may be linked to important mechanisms [30]. A limitation of EOF analysis is that it is unable to account for leads and lags in propagating features, which may be incorrectly identified as two (or more) modes in quadrature, when in fact they are simply part of a single dynamically propagating process [30]. Because the technique yields a standing wave-like pattern, propagating signals are often isolated into different modes with a similar temporal series. Figure 2 and further analysis by [28] demonstrate that propagations and lags exist between ENSO and Chl-a variability and provides the motivation for utilizing a methodology which accounts for this.

The extended EOF technique takes account of lag sequences in the time series, and hence propagation within individual modes—by truncating the data into several subsets of predefined time lengths (also known as “lag-sequence lengths”) and concatenating these prior to applying the EOF analysis. Prior to calculating the anomaly values and reshaping the data into space × time, a time lag (L) is predefined. L represents the cycle of the period of events that the analysis will focus on. Then the matrix is rearranged and concatenated into the following form:

$$F=\left[\begin{array}{llll}{F}_1\left(1\right)\hfill & F_1\left(2\right)\hfill & \cdots \hfill & F_1\left(N-L\right)\hfill \\ F_2\left(1\right)\hfill & F_2\left(2\right)\hfill & \cdots \hfill & F_2\left(N-L\right)\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ F_M\left(1\right)\hfill & F_M\left(2\right)\hfill & \cdots \hfill & F_M\left(N-L\right)\hfill \\ F_1\left(2\right)\hfill & F_1\left(3\right)\hfill & \cdots \hfill & F_1\left(N-L+1\right)\hfill \\ F_2\left(2\right)\hfill & F_2\left(3\right)\hfill & \cdots \hfill & F_2\left(N-L+1\right)\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ F_M\left(2\right)\hfill & F_M\left(3\right)\hfill & \cdots \hfill & F_M\left(N-L+1\right)\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ F_1\left(L+1\right)\hfill & F_1\left(L+2\right)\hfill & \cdots \hfill & F_1\left(N\right)\hfill \\ F_2\left(L+1\right)\hfill & F_2\left(L+2\right)\hfill & \cdots \hfill & F_2\left(N\right)\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ F_M\left(L+1\right)\hfill & F_M\left(L+2\right)\hfill & \cdots \hfill & F_M\left(N\right)\hfill \end{array}\right]$$

Data matrix F, which consists of a time series of geographical locations, has dimensions [M × (L + 1)] × (N − L) where M represents locations, and N time increments. The EOF is then computed as per usual. For a comprehensive explanation of the EOF or EEOF technique, the reader is referred to [18]. Example applications of the technique are also provided by [31–33]. We use the monthly data directly as our time increment for the analysis. The EEOF analysis was then applied using two predefined lag-sequence lengths. These are: lag-sequence length L = 28 months, based on the frequency of maximum power (above red noise) in the MEI that characterizes the EP ENSO (Figure 3a); and L = 128 months, corresponding to the maximum power in the IEMI (Figure 3b). Each EEOF analysis is independent of the other, i.e., the modes yielded by the L28 analysis explain all of the variability in the data, as do the modes produced by the L128 analysis. The sum of all the modes in each analysis adds up to 100% with the first mode explaining the most variance and then less for each subsequent mode thereafter. However, not all modes describe large, coherent structures and generally most of the secondary modes will contain random, stochastic variability explaining a very small percentage (e.g., 1%–2%) of the variance. The aim of an EOF analysis is to utilize only a small (physically meaningful) number of modes, which should explain most of the variance and discard the rest. Because Chl-a variability is strongly dominated by the seasonal cycle and higher frequencies, the individual modes here, even the leading ones, are not expected to explain a large amount of variability (≪20%). In other words, the variance at these timescales makes a much smaller contribution to the total Chl-a variability in the region. The large study area is also likely to contribute to the lower variance in each mode, as smaller scale variability cannot account for the variance in the greater spatial domain.

The EEOF component time series or Principal Components (PCs) and the two ENSO-type climate indices were then comparatively tested for any statistical relationships. Significances of the correlations were determined against the effective number of degrees of freedom according to [34], taking into account the autocorrelation in the time series which provides a more conservative but also more robust result. Finally, the Chl-aA PCs were projected onto SST anomaly (SSTA) fields for the same spatial and temporal domain as the Chl-a, with the aim of characterizing the climate that couples these variables. SSTA is also computed by removing the monthly climatology. The SST data are then concatenated in the same manner as the Chl-a data prior to the EOF analysis, as dictated by the assigned lag. Projecting the PCs onto the concatenated SSTA data yields SST spatial variability maps that complement the Chl-aA modes for each respective EEOF analysis. Since no information regarding ENSO is directly added to this analysis, where the SSTA patterns derived from the Chl-aA PCs resemble ENSO phases provides strong evidence for a connection between Chl-a variability and ENSO. Furthermore, we also compare the correlation with the climate indices and examine the total percentage of variance explained by the first 10 modes in each analysis to determine which ENSO type each analysis relates to, if any.

4. Results

4.1. The Extended Empirical Orthogonal Function (EEOF) L = 28 Month

For the L = 28-month lag-sequence (L28) EEOF analysis, the first 10 modes explain about 30% of the total Chl-aA variance, with the two leading modes (EEOF1 = 7%, and EEOF2 = 5%) being independent [35] (Figure 4). Although this specific lag was chosen to target Chl-a variability related to EP ENSO, the leading mode significantly relates to CP ENSO variability, and EEOF2 to EP ENSO. The EEOF1 time series (PC1) correlates significantly (r² = 0.40, p < 0.01) with the IEMI (Figure 5a). The r² increases to 0.73 (p < 0.01) when compared to a 28 month smoothed index, and to r² = 0.96 (p < 0.01) if PC1 is lagged +9 months when compared to the smoothed IEMI. The correlation between PC1 and the EP ENSO was negligible. In contrast, PC2 is weakly, but not significantly, correlated with the MEI (r² = 0.26, p = 0.94). This increases to r² = 0.77 (p = 0.19) when compared to a 28 month smoothed MEI time series. Note also, that these two time-series are out of phase (MEI leading PC1) by 27 months (Figure 5b) and this is accounted for in the correlation. All results take into account serial correlations according to [34].

One should take caution when interpreting values of the cross correlation, since it possibly results from differences inherent to the nature of both time series. For example, the IEMI is the product of the average of three distinct areas across the Tropical Pacific, which does not necessarily take into account any existing propagation across the basin, while PC1 describes the amplitude of a propagating Chl-a pattern throughout the study region. This discrepancy between the two variables being correlated may partially explain why correlations are optimized at a lag. In addition, IEMI as an SST index, instantaneously reflects climate variability, while chlorophyll is also dependent on other physical variables which vary at a different rate from SST. Finally, the smooth nature of the PC time series from the EEOF as well as the removal of autocorrelations through [34] both act to decrease degrees of freedom and consequently raise p-values, providing a highly conservative estimate of statistical significance.

Figure 6 illustrates the Chl-aA amplitudes from L28 EEOF1. At the basin scale, the most salient features consist of large positive amplitudes in Chl-aA in the western tropical and southern extra-tropics, flanked by weaker negative amplitudes in the WPWP region, eastern equatorial and South Pacific mid-latitudes. There is no discernible equatorial productive region analogous to a SST “cold tongue”. In month 1, large positive Chl-aA amplitudes are observed at the eastern edge of the WPWP which extend eastward through the sequence, then start to dissipate from around month 20. Concurrently, small positive Chl-a amplitudes in the central South Pacific (160°W–100°W) are seen in month 1 that intensify through the 28 month sequence. While this feature mainly remains in the same region throughout the cycle, there is a weak westward extension of the feature over time, which joins with the equatorial anomaly and then dissipates with it. The contour lines in the figure denote the SSTA amplitudes when Chl-aA PC1 is projected onto the SSTA field. It can be readily seen that Chl-aA and SSTA are generally anti-correlated, as might be expected. Negative SSTA amplitudes in the central Pacific, are bounded by positive Chl-aA amplitudes in the WPWP, southwest Pacific and eastern Pacific. The positive SSTA amplitudes in the western Pacific appear to be more stable than in the eastern Pacific—where the region of positive amplitudes contract from month 5 and then expand again between months 20 and 28. However, the anti-correlation between the two variables is not consistent across the entire study domain. For all the timesteps except month 28, in the tropical Pacific, SST anomalies are mostly negative across the Tropical Pacific (between 170°E and 90°W). Conversely, positive anomalies of Chl-aA are more localized in this area and follow a chevron shape with weakly negative anomalies east of 150°W −160°W of the tropical Pacific. Sometimes, strongly negative SST anomalies coincides with strongly negative Chl-aA such as at the front of the chevron while positive Chl-aA anomalies are found within regions of negative SST anomalies such as in month 28.

The L28 EEOF2 Chl-aA spatial pattern sequence is shown in Figure 7. Here, the Chl-aA amplitudes are largely negative in the central and eastern Tropical Pacific and positive in the WPWP region and across the South Pacific in the first month of the cycle. From month 1 to 9, positive amplitudes develop along the equator, while the negative amplitudes persist in the Tropics off the equator. From months 9 to 16, a strong positive Chl-aA pattern develops in the western-central equatorial Pacific (∼170°E), while negative Chl-aA amplitudes along the southern tropical region persist until the final month. From months 16 to 28, the positive Chl-aA pattern in the western-central equatorial Pacific strengthens further and propagates slowly westward in the last six months of the lag sequence.

Projecting PC2 onto the SSTA field yields a similar spatial pattern to Chl-aA, albeit with the sign reversed (Figure 7) implying an anti-correlated relationship between the two variables. The sequence commences with positive SSTA values in the central-eastern equatorial Pacific (between ∼15°N and ∼15°S), while negative SSTAs exist in the subtropical gyre centre, WPWP, and Tasman Sea regions. At the equator, the warm waters cool from the west, eventually reaching the eastern tropical Pacific (in month 11). Meanwhile, a negative anomaly pattern starts to develop in the central equatorial Pacific from month 9 until month 13 of the 28-month sequence, with the lowest minimum values of SSTA, found in the 22–28 month period, slowly propagating westward. This sequence ends with negative SSTAs, flanked by warm anomalies in the northern corner of the Western Tropical Pacific (which developed in month 13), in the central extra-tropical South Pacific (which developed from month 16), and in the eastern tropical and southeast Pacific (which developed northwards from the southeast from month 20).

4.2. The Extended Empirical Orthogonal Function (EEOF) L = 128 Month

In the L128 EEOF analysis, the 10 leading low frequency modes explain twice as much of the interannual Chl-aA variance (∼60%) (Figure 8) compared to the corresponding 10 high frequency EEOFs from the L = 28-month analysis. EEOF1 explains 13% of the total decadal Chl-aA variance and is significantly correlated with the IEMI (r² = 0.36, p < 0.01) but not to the MEI (r² = 0.01, p = 0.27). We note, however, that the leading modes are degenerate, as defined by [35], since the eigenvalue errors overlap (Figure 8). This means that mode 1 is not formally independent from mode 2. This is a consequence of the limited length dataset with respect to the low frequency timescale being investigated, as only one cycle is resolved. However, since both mechanisms, EP and CP ENSO, have a strong decadal component, it is worth reporting that the Chl-a signal also approaches this time scale as suggested by the EEOF L128 analysis though a longer dataset is required to adequately resolve this. Further, PC1 is very smooth compared with the IEMI (Figure 9). This is due to the fact that the EEOF time series represents the 128-month lag-sequence evolution based on several month steps (30) across the complete Chl-a record (n = 157). For consistency with Figure 5, the 128-month smoothed IEMI index is also provided for comparison.

Selected months from the L128 EEOF1 Chl-aA spatial pattern lag sequence are illustrated in Figure 10. The sequence is characterized by high variability within the tropical Pacific region, and is strongest in the western and southern parts. In month 1, the eastern tropical Pacific comprises of negative Chl-aA amplitudes. In the western equatorial Pacific, a pattern of positive Chl-aA amplitudes is evident whereas across most of the South Pacific, there is a mixture of positive and negative amplitudes, being smaller than for the Tropics. Following month 1, the eastern tropical Pacific negative pattern disappears in the first couple of months, and the western tropical Pacific positive amplitude feature extends eastward. At the same time that the eastward positive Chl-aA signature reaches the eastern side of the basin, a positive Chl-aA signature also develops along the eastern Pacific boundary. From month 11 onwards, a pattern of positive amplitudes develops along this eastern boundary and extends westward in the extra-tropics, seemingly joining with the positive feature in the western Pacific (see month 13 in Figure 10). This branched pattern remains for 10 months, until the eastern tropical Pacific feature reaches its maximum positive amplitude. From month 24, in the western tropical Pacific, a negative Chl-aA pattern starts to develop around 170°E and just south of the equator, and intensifies until month 46. Then this negative Chl-aA pattern starts to extend eastward along the latitude 15°N during the following months. At this point in the sequence, the eastern tropical Pacific is characterized by a pattern of small positive Chl-aA amplitudes. From month 56 to 74, two negative Chl-aA quasi-elliptical “cells” are clearly observed—one centered in the western equatorial Pacific between 160°E and 170°E and extending northeastward, and the other centered in the central Pacific extending southeastward from just south of the equator. These patterns have changed sign by about month 110 (see month 115 in Figure 10). Interestingly, the southern Chl-aA pattern is clearly seen to propagate west-northwestward over the period of about 40 months, from around month 59 to month 104.

Projection of L128 EEOF1 onto the SSTA field (contour lines in Figure 10) firstly indicates that the inverse relationship between Ch-aA and SSTA that was found in the L28 results is somewhat maintained here in the low frequency modes as well though not as consistently. Chl-aA amplitudes are also generally weaker than in the L28 results. The lag-sequence of maps shows the largest SSTA oscillating between the west-central and eastern tropical Pacific. The SSTA sequence commences with a cool anomaly in the central equatorial region, flanked by warmer SSTAs in the eastern Tropics, western flank of the South Pacific gyre, and northwest Pacific. As this cooling pattern intensifies and expands eastward along the equator, eventually connecting to the American continent (well visible by month 13 in Figure 10), a positive SST anomaly develops from the western subtropical South Pacific all the way to the southern Chilean coast from months 1 to 13 of the cycle. Both, the equatorial cooling pattern, and the sub-tropical warming pattern intensify until month 15. From month 15 the equatorial cooling pattern fades starting from the western region, and is gone by month 68. The subtropical warmth, however, starts to intensify on the southern east region of the South Pacific. Meanwhile by month 34, a positive SST anomaly in the western region of the equatorial meridian develops, resembling the inverse pattern of the initial month. By month 93, this has intensified and developed eastward along the equatorial line, and also connected with the east side of the basin. From month 96 to month 104, a cool anomaly starts developing in the central equatorial Pacific, flanked by warmer signals in the east and west side. This cooler pattern intensifies until month 109, and propagates westward until the end of the cycle, month 128. Meanwhile the eastern equatorial anomalous warming intensifies and spreads westward.

5. Discussion

5.1. El Niño—Southern Oscillation Quasi-Periodicity

As we are testing the hypothesis that ENSO propagation drives interannual Chl-a variability, we used the spectral peaks from the two ENSO indices time series to set the time scale for the lag in our EEOF analysis. The dominant and significant spectral peaks of the MEI and the IEMI were found to be 28 and 128 months respectively, for the period October 1997 to August 2010. While the literature typically shows that ENSO has a quasi-periodicity of between 2 and 8 years, it is not uncommon for spectral peaks to be in the range of around 3.5–4.5 yr for long time series (e.g., [5,36]). For the shorter record here (1997–2010), the dominant 2.3-yr period in the MEI demonstrates the relatively high frequency that has characterized ENSO in recent years. ENSO quasi-biennial cycles are often treated as noise [37]. “Noise” in the ENSO signal refers to higher frequency forcing and smaller time scale processes, such as Kelvin wave propagation, which can determine, for example, the initialization or termination of an ENSO event [37], and have enormous implications for phytoplankton populations [38]. Indeed a preliminary comparison of our EEOF analysis of Chl-a distribution to sea surface height anomalies (SSHA) (not shown) suggests that zonal phytoplankton communities react in different phases to the shoaling/deepening of the thermocline. We caveat here that our study period commences with the very large 1997/98 El Niño event, and its phase transition, which contributes to the shorter 28-month (2.3-yr) ENSO period. Secondary spectral peaks were also found in the MEI at the 36, 51 and 85-month periodicity (7.1 yr)—but only the 36 month peak was significant against the background red noise and at the 95% confidence level. A more comprehensive comparison of SSHA and the secondary peaks in the Chl-a power spectra is warranted.

5.2. Chl-aA Signature Propagation Induced by El Niño Flavors

Our results confirm that much of the interannual to decadal Chl-aA variance can be (statistically significantly) explained by ENSO propagation and twice as much (∼60%) in the first 10 low frequency modes, with the timing determined by the dominant CP ENSO spectral peak (EEOF L128), than the first 10 higher frequency modes determined by the EP ENSO spectral peak (EEOF L28). The leading modes of Chl-aA correlate with ENSO indices, but more strongly and significantly with the IEMI than the MEI. Projection of the Chl-aA EEOF time series onto SSTA fields confirms, firstly, that the anti-correlated relationship between Chl-a and SST is generally maintained for all analyses, and secondly, that the SSTA patterns associated with the Chl-aA results correspond to descriptions of ENSO induced SST patterns and corroborates previous reports in the literature of specific phases or events. Similarities between the L = 28-month EEOF2 Chl-aA pattern propagation and its projected SSTA field indicate that the spatial patterns are consistent with published studies of the evolution of the classical cold-tongue ENSO [2]. Examples that confirm this are: the strongly negative values of ChlaA from the Costa-Rica Dome in the eastern equatorial Pacific during classical ENSO events [7], the opposite signed Chl-aA in the WPWP; and the substantial projected warm SSTA pattern that corresponds to the cold tongue region in the first month of the sequence.

The influence on Chl-aA of a transition from a canonical eastern Pacific El Niño to a La Niña event was first reported in the literature following the very strong El Niño event transition that occurred in 1997/98 (e.g., [8]). Mode 2 of the EEOF L28 analysis of the Chl-aA fields yielded a spatial pattern sequence (Figure 7) that not only resembles a classical “composite”-like ENSO in the leading month, but by month 8 the evolving spatial pattern is quite similar to reports in the literature describing the difference between the La Niña to El Niño observations [8]. The projected SST pattern of this mode matches the transition from a strong classic El Niño to normal SST conditions. However, after this transition it appears that the SST pattern evolves to a central Pacific type of El Niño (Modoki)/La Niña phase, with the anomalous warm SST in the tropical Pacific flanking a cool pattern. This suggests interdependence between the two ENSO modes at least in this limited dataset, which is dominated in recent years by CP events. This is further discussed in the following section.

The Chl-aA pattern linked to the CP SST pattern in the EEOF L28 analysis is identified as positive amplitudes in the WPWP that extend eastward just north of the equator. We can also see this Chl-aA pattern evolution in the EEOF analysis designed to examine CP ENSO propagation (EEOF1 L128) twice, from month 1 to 15, and from 115 to 128. In between, there is an El Niño phase of CP. A recent study of CP influence on Chl-a distribution is in agreement with our negative amplitude evolution of Chl-aA in the western side of the tropical Pacific [16]. Further, following the pattern described by [14], we observe a propagating negative (positive) Chl-aA pattern, in the case of an El Niño (La Niña) event, linked to the central Pacific and focused on the western and central Tropical Pacific. Differences between the Chl-aA patterns in the ENSO modes suggest that the biological response differs during EP and CP ENSO. This result corroborates previous work [17] suggesting that different underlying mechanisms dominate in the two ENSO types leading to distinct biological signatures. However, further work is required with the inclusion of subsurface data to fully understand the role of ENSO driven propagation and its associated dynamics on interannual phytoplankton variability.

5.3. Eastern Pacific and Central Pacific El Niño—Southern Oscillation Contribution and Modal Independence

It is important to note that while the L28 EEOF2 timing is characteristic of EP ENSO, the pattern sequence also includes CP ENSO characteristics as described above. The authors of [39] argue that the first two modes of tropical Pacific SST do not represent distinct phenomena as has been reported in other studies, i.e., canonical EP ENSO and El Niño Modoki (or CP El Niño), but rather represents the nonlinear evolution of ENSO. Results from our EEOF analysis (keeping in mind that this is an analysis of Chl-a) also cast doubt on an outright independence between EP and CP ENSO—since individual propagating modes contain both of these so-called phenomena, at both the 28-month and 128-month lag-sequence time scales. However, it is not yet clear whether this is actually the case or whether the signals are not well separated due to data limitations. Indeed, the limited length of the dataset (in only being able to resolve one 128 month cycle) does impact on the results here, namely that the analysis cannot confirm the independence of the modes in the L128 EEOF analysis as indicated by [35]. The implications of this is that we cannot confirm the uniqueness of the Chl-a signal to this time span, but we are still able to examine the equivalent projected SST spatial pattern for known mechanisms with distinct characteristics, such as ENSO, that exist at similar frequencies. Since the SST pattern found is corroborated by the ENSO literature, we have some confidence that we are looking at a physically meaningful signal. In the absence of a longer dataset, this is a good reference point and provides direction for future research.

While our analysis has identified a quasi-decadal time scale characteristic of CP El Niño, we also capture a second, higher frequency, spectral maximum in the IEMI time series, which has been previously reported as a CP periodicity [11]. This second peak of 32 months, with >95% confidence above red noise, is close to the dominant peak in the MEI of 28 months. This result further suggests some connection between both modes of variability, and here between both ENSO flavors. Further investigation of this and other secondary peaks is warranted. Finally, it is interesting to note that both EEOF analyses produced modes that were more strongly and significantly linked to CP than to EP ENSO. We interpret this as reflecting the greater influence of CP ENSO during this study period.

6. Conclusions

In the present study, using an Extended Empirical Orthogonal Function (EEOF) analysis approach applied to the most recent 13-yr satellite record of Chl-a, in combination with sea surface temperature (SST) records and El Niño—Southern Oscillation (ENSO) indices based on various climatic parameters, we have shown that ENSO driven propagation can explain interannual Chl-a variability in the South Pacific. This paper demonstrates the usefulness of the EEOF, an underutilized method in the literature, in examining propagating signals. We identified the power spectra maximum periodicity in the Multivariate ENSO Index (MEI) and Improved ENSO Modoki Index from October 1997–October 2010 as being 28 months (L28) and 128 months (L128), respectively. For the recent record that comprised of four central Pacific (CP) El Niño events, the classical eastern Pacific (EP) ENSO, whose influence on phytoplankton is far more widely reported in the literature, explained less Chl-a variability and less significantly (L28 Principal Components (PC) 2 at r² = 0.26, p = 0.94; negligible for L28 and L128 PC1) than the CP mode (L28 PC1 at r² = 0.40, p < 0.01; L128 PC1 at r² = 0.36, p < 0.01).We found that the MEI power spectral maximum of 28 months relates to ENSO high frequency processes, which might represent a transition between phases, and is observed in the EEOF Mode 2 Chl-aA pattern.

The existence and independence of CP ENSO is a highly topical contemporary issue within the ENSO community. Our results add further evidence to the debate and outline some important outcomes: namely that (i) whether the CP mode is independent or not, it also manifests in the South Pacific Chl-a data with real consequences for ocean biology and is not merely a methodological artifact in the SST or sea level pressure (SLP) data, and (ii) there is indeed a low frequency (decadal) signal in the South Pacific Chl-a with CP characteristics, but a longer time series is required to sufficiently test the independence of this signal from EP ENSO. The implications of the differing roles of EP ENSO and CP ENSO on phytoplankton variability is that the prevalence of one flavor of ENSO over another can potentially lead to varied impacts on ocean ecology and ocean carbon fluxes, making this a key issue warranting further investigation as longer datasets and subsurface data become available.