1. Introduction
Vehicular navigation and guidance systems provide vehicle real-time location, communication, and route-guidance services, improving the efficiency of location-based services (LBS) [
1].
The Global Positioning System (GPS) can provide continuous, accurate positioning with lines of sight to more than four satellites. However, the accuracy and availability of GPS-based vehicular navigation systems are subject to the open-sky condition and they will degrade in the presence of signal blockage and reflected signals. The Inertial Navigation System (INS) can fill any GPS gaps to provide continuous navigation solutions including position, velocity, and attitude. An inertial navigator refers to a set of gyroscopes and accelerometers. It provides compensated raw measurements including velocity changes (delta-V) and orientation changes (delta-θ) along the three directions of its body frame. The INS usually refers to a combination of an inertial navigator and an onboard computer that can provide navigation solutions in the chosen navigation frame directly in real-time, in addition to providing compensated raw measurements [
2]. The primary advantage of using the INS is the provision of navigation solutions at high sampling rates. However, the disadvantage is that its accuracy degrades quickly with time because of systematic errors and noises from inertial sensors, including accelerometers and gyros. In particular, low-cost or tactical grade INS can experience large position and attitude errors over short-term duration in comparison with navigation grade INS. Therefore, the tactical inertial navigator is only used in short-term cases if no other navigational aids are available.
The INS was considered the nucleus of the integration system, mainly because it provides the attitudes of the vehicle. Moreover, being a totally autonomous sensor, its performance cannot be degraded by external means. Although an integrated navigation system can work in GPS-denied environments, the high cost of inertial sensors and the length of time that GPS signals are unavailable, for which it can compensate, limit its applicability. In other words, aiding INS with other complementary sensors is critical to improve the accuracy of inertial-based navigation systems. Choosing an appropriate estimation method is a key process in developing an aided INS [
3].
In fact, there are several aiding sources to inertial navigator in military and civil navigation applications. One of them is the Terrain Aided Navigation (TAN) technologies which estimate the position of a moving vehicle by comparing the measured terrain profile under the vehicle to a stored Digital Terrain Model (DTM) [
4]. The process of determining vehicle position by the use of DTM can be described as consisting of data acquisition and data correlation.
On the other hand, Map Matching (MM) is a core component of current vehicular navigation systems and embedded to integrated system for enhancing the sustainability and accuracy. A brief discussion of the earliest conventional MM algorithm, a semi-deterministic method, can be found in [
5]. The Dead Reckoning (DR) sensors are composed of a compass or gyroscope as a heading sensors and an odometer to provide translation. Generally speaking, the 2D navigation solutions provided by a DR are similar to a simplified Inertial Measurement Unit (IMU) that uses one vertical gyroscope and two horizontal accelerometers to calculate the current 2D position with the knowledge of previous position. In technical terms, the coupling relationships between GPS, DR sensors, and MM algorithms can be regarded as uncoupled. To overcome this limitation, several studies have been conducted to develop solid coupling relationships between GPS/DR and MM algorithms [
6]. Certain mechanizations have been implemented to utilize MM results to calibrate DR errors. According to Yu
et al. [
6], MM results can be input into a Kalman Filter (KF) to estimate errors based on DR sensor error models. DR errors can also be corrected by frequently updating new positions from MM results, thus constraining DR predicted position errors during GPS outages.
Several INS/GPS integrated schemes are available for implementing seamless vehicular navigation systems, such as loosely-coupled integration and tightly-coupled integration [
2]. The choice of integration strategy primarily depends on the application. Although tightly-coupled integrations have the advantages of high accuracy and the capacity to update GPS when there are fewer than four satellites, the complexity of computation produces a heavy computation load for processors used in low-cost vehicular navigation applications [
7]. High fault tolerance and a low numerical computation burden make loosely-coupled integration schemes easier to implement [
2]. Therefore, the proposed algorithm is based on the loosely-coupled integration strategy due to its simplicity of implementation and good performance, while INS applies as a central navigation system.
Non-GPS derived references applied in this research are composed of several candidates such as DTM, digital map and waypoint because they can provide position updates to aid INS continuously after certain similarity matching algorithms. In particular, if GPS is not available in military applications, non-GPS derived references can provide reliable position update information using DTM, digital map and waypoint for different platforms. The impact of proposed algorithm on positional errors during GPS outages is shown as
Figure 1. Because the conventional MM only snaps the vehicle position to the most probable 2D location on the map but without using an optimal estimator to estimate the states [
8], the accumulated errors of INS shown in blue dots along with other systematic errors cannot be improved and compensated during the matching process and the mis-matching would occur when the operation time is longer as the INS derived trajectory deviates from reference trajectory. Therefore, the scope of this research is to implement a specific 3D position update strategy by blending non-GPS derived references and navigation solutions derived from INS mechanization with similarity matching strategy then to aid the optimal estimator to provide seamless navigation results in the GPS denied environments where there is intermittent GPS signal reception or no GPS signal reception at all. As shown in
Figure 1, the proposed algorithm utilizes the matched reference information and the optimal estimator—the Extended Kalman Filter (EKF) applied in this study—to reset the INS positional errors whenever matched reference is available. Therefore, the overall performance of the proposed algorithm can be stabilized through frequent error control using reference information.
Generally speaking, instead of using the snapping strategy applied by those similarity matching algorithms that cannot correct any error sources in the INS mechanization, this research adopts matched reference information as pseudo GPS for position update then blends it with the INS navigation solutions using the EKF, thus the proper error control can be implemented to reset the INS positional errors whenever matched reference is available. In addition, conventional MM or TAN algorithms only provide a snapped 2D position while the proposed algorithm provides optimally estimated 3D positions as well as orientations. In other words, a tactical grade IMU is expected to operate less than 10 minutes without any aiding source, however, the proposed algorithm tends to extend the time span of using a tactical grade IMU when GPS is not an option as an aiding source.
Figure 1.
The comparison between conventional Map Matching (MM) and the proposed algorithm.
Figure 1.
The comparison between conventional Map Matching (MM) and the proposed algorithm.
2. The Implementation of the Proposed Aided Algorithm
The KF, which is considered as a special form of Bayesian estimation [
9,
10], has been widely adopted as the standard optimal estimator for the integration system. The KF estimates the instantaneous state of a linear system upset by Gaussian white noise and provides a means of inferring information by the use of measurements. The KF can read the measurements, including associated noise, and then estimates the required states. In this research, the KF relies on a set of position information data from non-GPS derived references and appropriate INS dynamic and stochastic models to provide optimal estimates of the INS error states. If the KF is exposed to input data that does not fit the model, it will not result in reliable estimates. Obviously, the model presentation depends on the
a priori knowledge and the process taking place in the integration system.
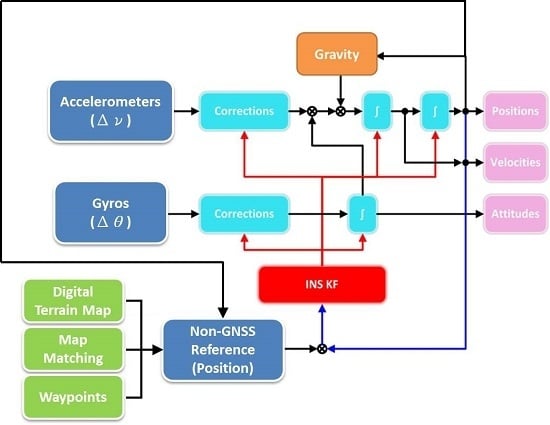
It is common to use an EKF to accomplish the data fusion, and the data flow of the integration navigation system with an EKF is shown in
Figure 2. The linear acceleration and angular rate of the inertial navigator are fed into the INS mechanization to calculate the position, velocity and attitude.
Figure 2.
The architecture of the integration system with Extended Kalman Filter (EKF).
Figure 2.
The architecture of the integration system with Extended Kalman Filter (EKF).
The main advantage of using the EKF is that it estimates the true state directly instead of the deviation of the nominal trajectory. The estimated state is then fed back into the INS to process the nominal trajectory ahead, which is then recursively estimated by the EKF. Thus the nominal trajectory is the estimated state. In order to estimate navigation solutions optimally, the output of the INS mechanization needs to be integrated with the position information from the non-GPS derived reference data model. The EKF is the most popular estimation technique for such integration systems.
In this research, the proposed algorithm uses the EKF to estimate navigation solutions optimally, and the output of the INS mechanization needs to be integrated with the position provided from the non-GPS derived reference data model. A simple form of the mechanization equation in the navigation frame can be written as follows:
where
is the position [
(latitude),
(longitude),
h (height)],
is the velocity [
,
,
],
is the transformation matrix from the inertial navigator body frame to the navigation frame as a function of attitude angles,
is the gravity vector in the navigation frame,
and
are the skew-symmetric matrices of the angular rate vectors
and
respectively, and
is a matrix whose non-zero elements are functions of the vehicle’s latitude and height, as shown in the following:
EKF uses the dynamic error model to determine the navigation solutions by the linearization of the INS mechanization equations and neglect insignificant terms in the resultant linear model. The INS errors are supposed to be the difference between INS solutions and positions from non-GPS derived reference information. There are 21 states of EKF applied in this study including errors of position, velocity, attitude and biases and scale factors of accelerometers and gyroscopes. The basic steps of the computational procedure for EKF are divided into prediction and update, illustrated as
Figure 3.
Figure 3.
The equations of computational procedure for EKF.
Figure 3.
The equations of computational procedure for EKF.
In the prediction part, the predicted states and error covariance at time are computed based on the estimated states at current time . is the optimally estimated state vector, is the state transition matrix, is the covariance matrix, is the covariance matrix of system noise, indicates the estimated value after prediction, and indicates the estimated value after update. Then, in the update part, EKF uses measurement update equations to generate the updated estimate for reducing the INS errors. The Kalman gain matrix can be obtained by utilizing the value from the prediction, then the current state and covariance matrix are acquired based on Kalman gain matrix, priori state estimate and measurement update equations. is the Kalman gain matrix, is the design matrix, is the measurement covariance matrix, and is the updating measurement vector of position.
The prediction and update procedures are implemented recursively at every position from non-GPS derived references, and they update the estimates. To optimize the performance from EKF with the non-GPS derived references, it is necessary to adapt the stochastic model to accommodate for the variable changes in vehicle dynamics. The estimation of multiple measurements is applied in this research and it implements the most reliable measurement as the update for filtering.
Figure 4 illustrates the architecture of proposed algorithm.
In this research, the proposed algorithm is based on the loosely-coupled system, because it is the simplest way of integrating the non-GPS derived reference data processing engine into INS mechanization. The non-GPS derived reference data processing engine calculates the position fixes by performing similarity matching between INS derived states and reference information and then sends the matched information as measurement updates to the INS using INS EKF shown in
Figure 4. By comparing the position of the navigation solutions provided by the INS mechanization with the position provided by non-GPS derived references, the navigation states can be estimated optimally.
Figure 4.
The architecture of proposed algorithm (closed loop).
Figure 4.
The architecture of proposed algorithm (closed loop).
3. Strategy of Non-GPS Derived References Fusion Algorithm
The advantage of the proposed algorithm is that it can be implemented independently and any errors of synchronization can be eliminated. Moreover, all the non-GPS derived references are digitalized to the point segments in this research, because this procedure can improve the performances obviously and avoid incorrect searching; otherwise the accuracy along the vehicle motion cannot be kept at meter-level. Candidates that can provide reference information for the proposed algorithm are discussed below.
3.1. DTM Aiding Algorithm
The basic configuration for DTM aided INS is using altimeter and data processor to correlate the measured terrain contours to acquire the optimal estimate of position. The correlation algorithm is simple but not smart, and a lot of calculations should be performed to have a position fix. The position drift is avoided by combining the integrated system with DTM, and the proposed architecture can provide continuous coordinate updates and implement the seamless navigation mode.
However, the most important issue is that navigation solutions can only be acquired for rough and unique surfaces.
Figure 5 illustrates the DTM aiding algorithm.
Figure 5.
DTM aiding algorithm in use.
Figure 5.
DTM aiding algorithm in use.
The strategy of the DTM aiding algorithm is to search for the corresponding cell where the vehicle is located then to interpolate the position fix. Hence, the interpolated position fix can be fed into the INS EKF as the measurement update in order to obtain the optimal estimates of states aiding INS recursively and accurately determine the actual trajectory of the vehicle.
3.2. Digital Map Aiding Algorithm
The reliability of the digital map has steadily improved and the accuracies are in the order of 1–5 m at a large scale [
11]. In the navigation domain, the positions of a vehicle or person from some sensing system can be used for visualization with a proper display platform that has spatial information. In this respect, a digital map is considered as an interface for drivers to obtain location information and to interact with the LBS; therefore, a high-quality digital map and an accurate positioning module are essential components in vehicular navigation systems [
6].
The MM procedure is based on a presumption that the navigation vehicle travels on a road segment. By utilizing a digital map with meter-level accuracy, the drifts that result from inaccurate aiding information can be minimized by snapping [
8]. The main purpose of MM is to determine the most probable location of the vehicle on the map. Numerous schemes have been proposed to improve the efficiency of MM [
6,
12,
13].
Meanwhile, Cui and Ge [
14] combined a digital map and navigation solutions to find the nearest point to the location of a vehicle that may exist in the digital map to improve the accuracy of navigation solutions. Furthermore, Taylor
et al. [
15] used digital map data and GPS to filter candidate routes on which the vehicle may appear, while Quddus
et al. [
5] utilized the MM algorithm to improve the output from a GPS receiver based on fuzzy logic methodology.
In this research, the MM procedure is divided into five steps: Position Fix, Boundary Setting, Heading Constraint, Nearest Point Constraint and Error Detection.
Figure 6 displays the procedures used for MM.
Figure 6.
Flowchart of MM procedure.
Figure 6.
Flowchart of MM procedure.
In the MM procedure, the predicted positions and headings provided by the EKF are used for MM to derive map-matched positions. Therefore, robust seamless continuous coordinate updates are provided for the EKF to facilitate the measurement update mode. In the update mode, the results from the MM procedure are fed into the proposed algorithm to substitute the original GPS derived positions. Thus, the proposed algorithm provides complementary information by updating the MM results instantaneously without additional cost.
In this research, the Nearest Feature Search (NFS) algorithm is chosen for obtaining the nearest point due to its simple implementation [
15]. The NFS algorithm combines navigation parameters with the digital map, and then finds the nearest point to the coordinates obtained from the navigation parameters on the candidate roads. Taylor
et al. [
15] proposed a vector form of NFS. Based on the type of measurements used in the present study, the NFS algorithm is modified and implemented in point-to-point mode, as shown in the following:
The position calculated from INS mechanization and the coordinates provided from non-GPS derived references are all converted to navigation frame, and is the 3D distance between a vehicle location and the 3D coordinates of the aiding point. , and are the coordinates representing the aiding point in the non-derived reference on north, east and up, respectively. , and are the coordinates representing the search point from INS on north, east and up, respectively. Therefore, the closest matched point can be provided as the update to aid INS and implement the specific 3D position update strategy.
Moreover, this research also utilizes the waypoints set for the Unmanned Aerial Vehicle (UAV) borne mobile mapping application. In fact, it is the route generated for the autopilot and camera trigger for UAV platform as the aiding source for airborne scenarios. Generally, the 3D positioning accuracy of those waypoints is around 5 m [
16].
The fusion algorithm of non-GPS reference information is to consolidate the strategies which are applied during the mission of navigation. When the position is fed into the INS EKF as the measurement update, the measurement covariance matrix is generated simultaneously according to the accuracy of DTM or digital map or the specifications including bias and scale factor of the IMU. Therefore, the proposed algorithm can adopt all the aiding sources of non-GPS derived reference information such as DTM, digital map and waypoint, and then provide the matched position update for INS EKF. Finally, the optimal estimated states are acquired to compensate the navigation solutions from the INS mechanization. In any case, the performance of navigation relies on the accuracy of DTM, digital map, waypoint and the specifications of the IMU.
4. Results and Discussions
In order to validate the performance of the proposed algorithm, two field tests were conducted for detailed analysis, including land scenario in freeway test and airborne scenario with UAV test. The performance evaluation was conducted by comparison between the positions provided by the proposed algorithm and reference system. The reference system is a high-end INS/GNSS integration system from NovAtel, comprising a tactical grade IMU (SPAN-LCI), and a dual-frequency, geodetic grade GNSS receiver (SPAN-SE). The specifications for the SPAN-LCI are shown in
Table 1.
Table 1.
Specifications for testing the tactical inertial navigator.
Table 1.
Specifications for testing the tactical inertial navigator.
![Remotesensing 06 12511 i001]() | System Performance |
| | Gyroscope | Accelerometer |
| Range | ±800 deg/sec | ±40 g |
| Bias | 0.3 deg/hr | 0.5 mg |
| Scale Factor | 100 ppm | 500 ppm |
| Random Walk | 0.05 deg/ | 40 μg/ |
The reference system was generated with its raw IMU measurements and GPS carrier phase measurements processed in the differential mode with commercial software—Inertial Explorer—and sensor fusion was performed in the post-processed tightly-coupled by using the Rauch-Tung-Striebel (RTS) backward smoother [
17]. In general, the accuracy of the reference system was less than 10 cm, which is considered sufficient for this research. The results of the proposed algorithm are analyzed and compared with the INS/GPS integration results processed by RTS smoother.
In the land test, non-GPS derived reference information was applied every minute as the measurement update. For the land test, the road centerline data and terrain data stored in the digital map were the main aiding source. The 3D positioning accuracy of this aiding source is around 1–5 m [
11]. The test system conducted the coarse and fine alignment at the beginning to obtain initial attitudes autonomously since the system used for land test is a high-end tactical grade system and it can provide reliable measurements for the conventional alignment procedure in the static mode.
On the other hand, the waypoints generated at 1 s intervals for the camera trigger were the main aiding source for UAV test and the 3D positioning accuracy is around 5 m. The alignment mode used in the airborne test was the given mode by providing heading angle through a compass reading as well as assuming the platform was leveled by assigning roll and pitch angles as zero.
The initial positions were given using the GPS solutions at the first epoch for both tests. In practical applications where GPS is not available completely, then the vehicle must start at a control point with known coordinates for initialization.
4.1. Land Test
A land test conducted on freeway with an average driving speed of 90 km/h was arranged for the purposes of validating the proposed algorithm for seamless vehicular navigation and comparing with the reference system. The traveled distance was approximately 80 km and the period of the field test was about 60 minutes. The position update rate was set for 1 minute in this test. In this research, the proposed algorithm obtains the update from non-GPS derived references and provides the optimal navigation results in real-time.
Figure 7 illustrates the interface which displays the results of overall trajectory position in the navigation frame.
Figure 7.
The interface of real-time display. (a) Overall position in east, north and height component; (b) Detailed position in horizontal component; (c) Error plots and maximum error of position compared to reference system.
Figure 7.
The interface of real-time display. (a) Overall position in east, north and height component; (b) Detailed position in horizontal component; (c) Error plots and maximum error of position compared to reference system.
Figure 8 shows the reference trajectory which was provided by INS/GNSS integrated RTS smoothed results, the trajectory of the proposed algorithm, and the free navigation (INS only) trajectory. Because of the open-sky conditions and frequent updates from non-GPS reference information, the differences between the reference trajectory and the proposed algorithm are not significant. Therefore, it is not easy to distinguish the differences from
Figure 8 to the scale in use.
Figure 8.
The trajectories of land test.
Figure 8.
The trajectories of land test.
In the land test, long-term navigation solutions are collected in terms of the performce evalution. The error comparison of position in the land test is shown in
Figure 9.
Figure 9.
The error comparison for position in land test.
Figure 9.
The error comparison for position in land test.
In addition,
Table 2 illustrates the statistical analysis in terms of Root Mean Square Errors (RMSE). As shown in
Table 2, the positional errors of the proposed algorithm are improved significantly due to frequent position updates from non-GPS derived references. Because the accuracy of non-GPS derived references could not be consistent at all, the results of proposed algorithm would also be affected accordingly. The degradations are caused by the accuracy of non-GPS derived references and the quality of raw measurements from IMU. Therefore, if the accuracy was further improved, the quality of the non-GPS derived references should be improved.
In general, the 3D position accuracy provided by the proposed algorithm is around 4 meters based on the system and test environment applied in this research, which is limited by the accuracy of the non-GPS derived references.
Table 2.
The statistical analysis of positional errors for land test.
Table 2.
The statistical analysis of positional errors for land test.
| | Positional RMSE (m) |
|---|
| East | North | Up | 3D |
|---|
| INS only | 24464.95 | 1725.98 | 75301.31 | 79194.70 |
| Proposed algorithm | 2.37 | 2.57 | 1.59 | 3.84 |
4.2. Airborne Test
An airborne test was conducted in the suburban area of Tainan, and waypoints generated at 1 s intervals for camera trigger were the main aiding sources. In the airborne test, the UAV designed for medium range applications is applied as the test platform, as illustrated in
Figure 10.
Figure 10.
The UAV platform and setup.
Figure 10.
The UAV platform and setup.
The flight altitude is 600 m above ground and the period of field test is about 50 minutes.
Figure 11 illustrates the proposed algorithm trajectory and the reference trajectory provided by RTS smoother processing with INS and GPS measurements.
Figure 12 illustrates the positional error of the proposed algorithm in the airborne test and the statistical analysis is illustrated in
Table 3. Generally speaking, the performance of proposed algorithm in terms of positional errors is superior to that for free navigation (INS only) results. From the statistical analysis, it is evident that the positional errors were also improved significantly. The 3D positioning accuracy provided by the proposed algorithm in terms of RMSE is approximately 11 m based on the system and test environment applied in this research, which is limited by the accuracy of the non-GPS derived references.
Figure 11.
The trajectories of airborne test.
Figure 11.
The trajectories of airborne test.
Figure 12.
The error comparison for position in airborneland test.
Figure 12.
The error comparison for position in airborneland test.
Table 3.
The statistical analysis of positional errors for airborne test.
Table 3.
The statistical analysis of positional errors for airborne test.
| | Positional RMSE (m) |
|---|
| East | North | Up | 3D |
|---|
| INS/GPS | 4.02 | 10.88 | 2.89 | 11.95 |
| Proposed algorithm | 3.73 | 9.82 | 1.48 | 10.61 |
Although the conditions of the test environments are not the influences in performances, the navigation results would be affected by the procedure of alignment. Therefore, the positional errors might be relatively large and unstable at the commencement of each test. The improvements and the analysis would be focused on the part after alignment. Most of those results presented in this research have proved that the proposed algorithm can provide seamless navigation solutions and improve the performance extensively. Based on the accuracy of non-GPS derived references, the proposed algorithm can provide the navigation results at the meter level, which is about 4–11 m, and the noises in the raw inertial measurements are another reason causing the difference in the accuracies of the tests conducted in this research.
The land and airborne test scenarios can be summed up in a few words. The performances are superior to INS only results based on the scenarios and the hardware applied in this research. On the contrary, the primary limitations of the proposed algorithm are the availability of 3D references including the digital map, terrain model or waypoint, and their accuracies. In addition, since the scenarios applied in this research were implemented by post-processing mode, though the kernel of the proposed algorithm can be easily migrated to the embedded system [
18], the real-time implementation issue might reduce the frequency using aiding information, and thus, this might deteriorate the performance in a real-time environment. These limiting factors will be investigated in future study.
5. Conclusions
This research evaluates the algorithm aided by non-GPS derived references with tactical inertial navigators, and takes advantage of non-GPS derived references as an accurate update for EKF to improve the performance of navigation solutions.
Several issues and test scenarios have been considered in the experiments, and the preliminary results presented in this research illustrate the proposed algorithm with frequent non-GPS derived reference aiding provides seamless, reliable and accurate navigation results.
In addition, the measured performances of the proposed algorithm are mainly superior to those of free navigation (INS only). Based on the performance of non-GPS derived references, the proposed algorithm can provide the navigation results at the meter-level in not only the land test but also the airborne test. On the contrary, the primary limitations of the proposed algorithm are the availability of 3D reference information including digital maps, terrain models or waypoints, and their accuracies.