Next Article in Journal
Phytoplankton Biomass Dynamics in the Strait of Malacca within the Period of the SeaWiFS Full Mission: Seasonal Cycles, Interannual Variations and Decadal-Scale Trends
Previous Article in Journal
Improving Remote Species Identification through Efficient Training Data Collection
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 6
Issue 4
10.3390/rs6042699
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods

by
Xiaoting Peng
1,
Tiezhu Shi
2,
Aihong Song
1,*,
Yiyun Chen
2 and
Wenxiu Gao
3
1
State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
2
School of Resource and Environmental Sciences & Key Laboratory of Geographic Information System of the Ministry of Education, Wuhan University, Wuhan 430079, China
3
School of Architecture & Urban Planning, Shenzhen University, Shenzhen 518060, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2014, 6(4), 2699-2717; https://doi.org/10.3390/rs6042699
Submission received: 13 January 2014 / Revised: 10 March 2014 / Accepted: 17 March 2014 / Published: 25 March 2014
Browse Figures
Versions Notes

Abstract

: With 298 heterogeneous soil samples from Yixing (Jiangsu Province), Zhongxiang and Honghu (Hubei Province), this study aimed to combine a successive projections algorithm (SPA) with a support vector machine regression (SVMR) model (SPA-SVMR model) to improve the estimation accuracy of soil organic carbon (SOC) contents using the laboratory-based visible and near-infrared (VIS/NIR, 350−2500 nm) spectroscopy of soils. The effects of eight spectra pre-processing methods, i.e., Log (1/R), Log (1/R) coupled with Savitzky-Golay (SG) smoothing (Log (1/R) + SG), first derivative with SG smoothing (FD), second derivative with SG smoothing (SD), SG, standard normal variate (SNV), mean center (MC) and multiplicative scatter correction (MSC), on SPA-based informative wavelength selection were explored. The SVMR model (i.e., SVMR without SPA) and SPA-PLSR model (i.e., SPA combined with partial least squares regression (PLSR)) were developed and compared with the SPA-SVMR model in order to evaluate the performance of SPA-SVMR. The results indicated that the variables selected by SPA and their distributions were strongly affected by different pre-processing methods, and SG was the optimal pre-processing method for SPA-SVMR model development; the SPA-SVMR model using SG pre-processing and 28 SPA-selected wavelengths obtained a better result (R2V = 0.73, RMSEV = 2.78 g·kg−1 and RPDV = 1.89) and outperformed the SVMR model (R2V = 0.72, RMSEV = 2.83 g·kg−1 and RPDV = 1.86) and the SPA-PLSR model (R2V = 0.62, RMSEV = 3.23 g·kg−1 and RPDV = 1.63). Most of the spectral bands used by the SPA-SVMR model over the near-infrared region were important wavelengths for SOC content estimation. This study demonstrated that the combination of SPA and SVMR is feasible and reliable for estimating SOC content from the VIS/NIR spectra of soils in regions with multiple soil and land-use types.

Graphical Abstract

1. Introduction

Soil organic carbon (SOC) has considerable influence on soil quality and plant growth, and it governs various physical, chemical and biological processes in the soil environment [1,2]. A rapid and economical method for estimating SOC content can improve environmental monitoring, modeling and precision agriculture [3–5]. However, the traditional laboratory analysis for estimating SOC content is time-consuming, relatively expensive and cannot describe the spatial and temporal dynamics of SOC contents over large areas with sufficient detail [6]. Therefore, there is an urgent need for a rapid and accurate approach for the measurement of SOC content [7].

Visible and near-infrared (VIS/NIR) spectroscopy, known as a rapid, cost-effective, quantitative and eco-friendly technique, can provide hyperspectral data with narrow and numerous wavebands, both in the laboratory and in the field [1,8]. VIS/NIR spectroscopy has great potential for simultaneously estimating a variety of soil properties [1,4]. In recent years, various quantitative methods have been applied to VIS/NIR hyperspectral data to estimate SOC content, such as multiple linear regression (MLR) [9], principal component regression (PCR) [10] and partial least squares regression (PLSR) [9,11]. PLSR, developed by Wold et al. [12], has become the most commonly-used calibration method for SOC estimation, because it can successfully model the linear relationship between spectral data and chemical components, especially when multi-dimension and multi-collinearity exist in raw spectra data. However, nonlinearity between the spectra data and chemical components often exists due to instrument variations (lamp aging and sensor sensitivity) [13] and heterogeneous soil characteristics [14]. Thus, nonlinear calibration methods, such as support vector machine regression (SVMR), can provide a more reasonable solution than linear methods [15].

SVMR utilizes a kernel function to map input variables into a high-dimensional feature space [16], and hence, it can deal with high-dimensional input vectors. Recently, SVMR has been widely applied in VIS/NIR spectroscopy analysis [14,17–19] and generated more accurate calibration results than PLSR in some studies [14,16,18]. Nonetheless, high redundancy, collinearity and sometimes noise existing in full Vis/NIR spectral data may decrease the estimation capability and computing efficiency of the SVMR model [20]. Therefore, the appropriate selection of informative variables (spectral wavelengths) is essential to improve the performance of the SVMR model and/or reduce model complexity [20–22].

Variable selection strategies, like forward selection, backward elimination and stepwise MLR, have been the most commonly used, due to their simple and efficient algorithms (the detailed algorithms can be found in Zou et al. [22]). However, the implementation of these algorithms depends on an ordering or ranking of variables, which often makes them sensitive to the noise distribution. Furthermore, the forward, backward and stepwise selection methods select some neighboring variables easily that contain collinearity, and this may decrease the estimation accuracy. Some other strategies, such as variable importance projection (VIP) and genetic algorithms (GAs), can avoid selecting many collinear variables to some extent. VIP is a combined measure of how much a variable contributes toward describing the dependent and independent variables, and it can reflect how important variables are for PLSR models. Nevertheless, when the spectral information is severely overlapped, VIP may be difficult to interpret [20]. Genetic algorithms inspired by Darwin’s theory of natural selection [22] are a popular heuristic optimization technique that employs a probabilistic, non-local search process, and they have been successfully applied to wavelength selection in soils, especially with PLSR [23,24]. However, apart from their complexity, GAs may also involve a risk of overfitting when there are many (e.g., more than 200) variables [25].

The successive projections algorithm (SPA) designed by Araújo et al. [26] is a novel variable selection algorithm for multivariate calibration analysis. It can effectively decrease the complexity and collinearity of spectral data by performing simple projection operations in a vector space [26,27], compared to relatively complex GA. Thus, SPA combined with various calibration methods has been used to estimate many chemical compositions, such as the soluble solids of beer (with MLR, PLSR and SVMR) [28], the moisture, protein and starch in corn (with MLR) [27] and the Cu, Zn and other heavy metals (with MLR) [29], as well as the nitrogen and carbon (with PLSR) in soils [30]. These studies demonstrate that SPA cannot only simplify calibration models, but also, it can generate better accuracies than full spectrum-based models.

The combination of SPA and SVMR (SPA-SVMR) has also been successfully used in a few studies. For example, Liu et al. [28] applied a SPA-SVMR model to determine the organic acids of plum vinegar, which performed better than full spectrum-based PLSR, SPA-MLR and SPA-PLSR; Goudarzi et al. [31] compared the performance of the SPA-SVMR model and the SPA-MLR model and demonstrated that the former model can dramatically enhance the prediction ability for the electrophoretic mobility of some organic and inorganic compounds. However, to our knowledge, a SPA-SVMR model has not been investigated for the estimation of SOC contents from the VIS/NIR spectra data of soils.

In order to improve the accuracy of SOC calibration models with VIS/NIR spectral data, the raw spectral data are often pre-processed before modeling [9,32,33]. Pre-processing is usually regarded as an integral part of chemometrics modeling with spectral data. The prevailing pre-processing methods for VIS/NIR spectroscopy are scatter-correction and spectral derivatives [34]. Multiplicative scatter correction (MSC) and standard normal variate (SNV) are typical examples of scatter-corrective methods that can remove undesired scatter or particle-size information from reflectance spectra to some extent. Spectral derivatives, including first derivative (FD), second derivative (SD) and Savitzky-Golay (SG) polynomial derivative filters, have the capability to eliminate both additive and multiplicative effects from reflectance spectra. Different pre-processing methods may have different effects on SPA in selecting wavelength variables and further affect the performance of the SVMR model.

This study aimed: (i) to combine the successive projections algorithm (SPA) with the support vector machine regression (SVMR) model (SPA-SVMR model) to estimate soil organic carbon (SOC) contents using the laboratory-based visible and near-infrared (VIS/NIR, 350–2500 nm) spectroscopy of soils; (ii) to compare the performance of the SVMR model without SPA (termed SVMR in the rest of the paper) and SPA-PLSR model with the established SPA-SVMR model; and (iii) to explore the influences of some common pre-processing methods, including Log (1/R), Log (1/R) coupled with SG (Log (1/R) + SG), FD, SD, SG, SNV, mean center (MC) and MSC, on SPA in selecting informative variables.

2. Materials and Methods

2.1. Study Areas

The study areas were located in Yixing (119°31′–120°03′E, 31°07′–31°37′N), Zhongxiang (112°15′–112°30′E, 31°15′–31°30′N) and Honghu (113°07′–114°05′E, 29°39′–30°02′N) (Figure 1). Yixing is located in the south of Jiangsu Province, China, with an annual temperature of 15.7 °C and a mean annual precipitation of 1177 mm [23]. Zhongxiang and Honghu are located in the middle of Hubei Province, China. Their annual temperatures are 15.0 °C and 16.6 °C with mean annual precipitations of 961 mm and 857 mm, respectively. The three areas are typical agricultural regions with various crops under cultivation.

2.2. Soil Samples

A total of 298 soil samples were collected from three study areas: Yixing (Figure 1b, 100 soil samples), Zhongxiang (Figure 1c, 100 soil samples) and Honghu (Figure 1d, 98 soil samples). The 298 soil samples were distributed over a wide range of land-use types, and most of the samples were taken from paddy field and rape field (Table 1). According to the Harmonized World Soil Database (version 1.2) [35], the dominant soil types in Yixing are anthrosols, luvisols, planosols and alisols for different crop cultivations; the soils collected from Zhongxiang mainly belong to anthrosols and leptosols, and those from Honghu belong to anthrosols and gleysols for planting crops (Table 2). For each soil sample, five soil subsamples taken within 1 m2 were collected and thoroughly mixed to get a representative sample. At each sample site, about 1.0–1.5 kg of surface soils from a depth of 0–10 cm were collected after wiping off plant materials, plant residues, roots and stones. The collected soil samples were then kept in a sealed package for later spectral measurements and SOC content analyses in a laboratory.

2.3. Spectra Measurements and SOC Content Analyses

All the soil samples were air-dried at an indoor temperature for three days to standardize the moisture level, and small stones and plant residues were removed. The 298 soil samples were ground with an agate mortar and passed through a 20-mesh grid sieve (<2 mm). The reflectance spectra of all soil samples were measured in a laboratory using an ASD FieldSpec®3 portable spectroradiometer (Analytical Spectral Devices, Inc., St, Boulder, CO, USA) with a wavelength range of 350–2500 nm, and the spectral readings were acquired in 1-nm increments over the wavelength range [36]). Each soil sample was put on a 10-cm diameter petri dish with a thickness of about 15 mm. Considering the optimal values of beam angle, lamp distance and sensor distance recommended by Zhou et al. [37], the spectra of all soil samples were measured in a dark room with a 50-W halogen lamp as the light source, which was positioned 0.3 m away from the soil sample, with a 15° zenith angle; while the optical probe was installed about 0.15 m above the soil sample. The correction with a standardized white Spectralon® panel with 100% reflectance (Labsphere, [38]) was made prior to the first scan and after every six samples. An average value of 10 spectral measurements for each sample was calculated as the final spectral reflectance. After spectral measurements, the SOC contents of all soil samples were determined using the Walkley and Black method [39].

2.4. Data Preparation

The SOC content measurements were combined with the spectra data of soils into a raw dataset. With principal component analysis (PCA) [40], the samples with both a large score distance and a large orthogonal distance were then detected as outliers and eliminated from the raw dataset. A detailed description of PCA can be found in Verboven and Hubert [40].

The reflectance spectra were reduced to 410–2450 nm in order to eliminate the noise at the edges of each spectrum [33]. The dataset of reduced spectra with SOC contents was then sorted based on the SOC content values from low to high, and the samples sorted at n and 2n orders (n ranging from 1 to 96) were selected as the calibration dataset, with 3n order samples as the validation dataset. Such a division ensures that the full range of SOC contents are represented in both the calibration and validation datasets [41].

2.4.1. Spectral Resampling

Hyperspectral data with narrow and numerous wavebands are generally redundant and can decrease computing efficiency. Thus, spectral sampling was used to reduce the volume and the redundancy of hyperspectral data. First, the reflectance spectra were resampled by the means of filtering based on different spacing intervals ranging from 2 to 10 nm. Then, each resampled reflectance spectra were employed to calibrate a SVMR model and a PLSR model. Finally, an optimal resampling interval was determined according to the coefficient of determination between the measured and estimated values of cross-validation (R2CV) and the residual prediction deviation of cross-validation (RPDCV) for the SVMR and PLSR model, respectively. The reflectance spectra generated with the optimal interval were employed for the following analyses.

2.4.2. Pre-Processing Transformations

Eight pre-processing methods were tested in this study, including Log (1/R) (R is the reflectance), Log (1/R) coupled with Savitzky-Golay (SG) smoothing (Log (1/R) + SG), first derivative with SG smoothing (FD), second derivative with SG smoothing (SD), SG with a second order polynomial fit and a window size of 9 data points [42], standard normal variate (SNV), mean center (MC) and multiplicative scatter correction (MSC). The details about these spectral transformations can be found in a review by Rinnan et al. [34]. All the transformations were implemented with MATLAB version R2008b software (The Math Works, Natick, MA, USA). The eight pre-processing methods were used to explore their effects on SPA in selecting informative wavelengths.

2.5. Successive Projections Algorithm (SPA)

The successive projections algorithm (SPA) is a forward selection method, and its purpose is to select wavelengths whose information content is minimally redundant [26]. In the process of SPA, a projection operation in an orthogonal vector space is employed to select subsets of variables with a minimum collinearity. Variable selection by SPA is based on the principle that a new selected variable is the one among all the remaining variables having the maximum projection value on the orthogonal sub-space of the previous selected variable. The spectral data used for SPA wavelength selection are denoted by a matrix, XN × K. Let M = min (N − 1, K) be the maximum number of variables to be selected. There are two sections to variable selection by SPA. The detailed SPA steps in the first section are described for a given initial wavelength, k(0), as follows.

  • Step 1: Before the first iteration (n = 1), let xj be the j-th column of the spectra matrix (XN × K), j = 1,..., K.

  • Step 2: Let S be the set of wavelengths that have not been selected yet. That is,

    S = { j , 1 ≤ j ≤ K , j ∉ { k ( 0 ) , … , k ( n − 1 ) } } .

  • Step 3: Calculate the projection of xj on the sub-space orthogonal to xk(n−1) as:

    P X j = X j − ( X j T X k ( n − 1 ) ) X k ( n − 1 ) ( X k ( n − 1 ) T X k ( n − 1 ) ) − 1

where P is the projection operator.

  • Step 4: Let k(n) = arg (max‖ Pxj‖, j∈S).

  • Step 5: Let xj = Pxj, j∈S.

  • Step 6: Let n = n + 1. If n < M, go back to Step 1.

  • End: The resulting wavelengths are {k(n); n = 0,…, M}.

The second section of SPA is to evaluate the candidate subsets of the variables selected in the first section. A total of M × K subsets of the variables are tested. The best variable subset is selected based on the smallest root mean squared error of prediction in the validation set of the MLR calibration.

In this study, the SPA was implemented using MATLAB version R2008b software (The Math Works, Natick, MA, USA) with a graphical user interface provided by Araújo et al. [43]. The graphical user interface for SPA is available at [44].

2.6. Model Development

Using the calibration dataset, the SPA-selected wavelength variables based on the eight pre-processed spectra were used to calibrate SVMR models, with a Gaussian radial basis function as the kernel function. The parameters, C and γ, of the kernel function were acquired by a grid-searching technique and a leave-one-out cross-validation procedure. The optimal values of these two parameters were selected when the minimal RMSECV was produced. The final SPA-SVMR model with an optimal pre-processing method was chosen.

In order to demonstrate the performance of the final SPA-SVMR model, a SVMR model without SPA operation and a SPA-PLSR model were developed with the same pre-processed spectra as the SPA-SVMR model. Then, these three calibration models were employed to estimate the SOC contents of the validation dataset. All models were implemented using PLS Toolbox 7.0 in MATLAB version R2008b software (The Math Works, Natick, MA, USA).

2.7. Model Evaluation

The coefficients of determination between the measured and estimated values for calibration (R2C) and validation (R2V) datasets, the error statistics root mean square error (RMSE) and the residual prediction deviation (RPD) [9] were used to evaluate the performance of the above models. The six level interpretations of RPD given by Viscarra Rossel et al. [45] were adopted as follows: RPD < 1.0 indicates very poor models/predictions, and their uses are not recommended; 1.0 < RPD < 1.4 indicates poor models/predictions, where only high and low values are distinguishable; 1.4 < RPD < 1.8 indicates fair models/predictions, which may be used for assessment and correlation; 1.8 < RPD < 2.0 indicates good models/predictions, where quantitative predictions are possible; 2.0 < RPD < 2.5 indicates very good, quantitative models/predictions; and RPD > 2.5 indicates excellent models/predictions.

3. Results

3.1. Soil Organic Carbon Contents

According to the score diagnostic results of PCA analysis, a total of 11 samples with a large score distance and orthogonal distance were determined as outliers and were removed from the original 298 samples. Thus, 287 samples were left in the whole dataset, from which 192 samples were chosen as the calibration dataset and 95 samples as the validation dataset. The statistical descriptions of the SOC contents of the whole dataset, the calibration dataset and the validation dataset are presented in Table 3. Compared with the range of SOC content (0.79–30.73 g·kg−1) for both the whole dataset and the calibration dataset, the validation dataset has a narrower range with 1.96–26.23 g·kg−1, due to insufficient soil samples. However, the characteristic statistics of SOC contents in the calibration dataset and validation dataset were similar to those of the whole dataset; thus, the SOC contents of the calibration and validation dataset sufficiently represent those of the whole dataset.

3.2. Resample Intervals

As most wavelength information is redundant in hyperspectral data and the redundant information can decrease the efficiency of variable selection and modeling, proper resampling of hyperspectral data can be useful for rapid analysis and estimation of SOC contents. The resampling performance with 2−10 nm intervals was displayed in Figure 2. Considering the leave-one-out cross-validation results of SVMR and PLSR models calibrated using the calibration dataset, 9 nm was the best resample interval for both SVMR (R2CV = 0.74, RMSECV = 2.78 g·kg−1, RPDCV = 1.95) and PLSR (R2CV = 0.68, RMSECV = 3.12 g·kg−1, RPDCV = 1.74) models. After spectral resampling with 9 nm, only 227 variables were left for the subsequent variable selection.

3.3. Effects of Pre-Processing Methods on SPA and SPA-SVMR

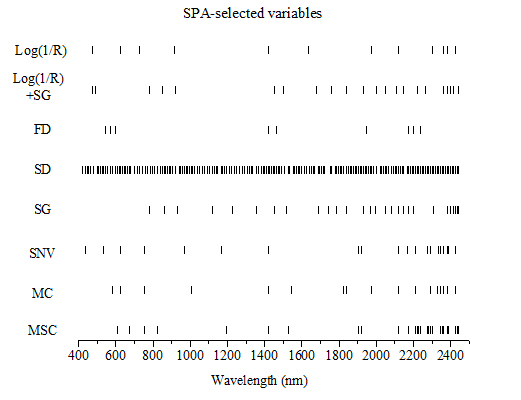
The number of selected wavelengths (ranging from 9 to 186) by SPA and the distribution of these wavelengths varied strongly depending on the different pre-processing methods used in this study (Figure 3, Table 4). For example, SPA with SD selected the maximum number of wavelengths (186), and these wavelengths were located evenly throughout the entire VIS/NIR region, while SG selected 28 wavelengths, which were mainly located beyond the near-infrared region. Thus, these tests indicated that different pre-processing methods had a great influence on the SPA wavelength selection.

As compared with the SPA-SVMR model without pre-processing (Table 4), Log (1/R) + SG, SG, MC and MSC improved the model performance. SG achieved the best model performance (R2V = 0.73, RMSEV = 2.78 g·kg−1 and RPDV = 1.89), followed by Log (1/R) + SG (R2V = 0.70, RMSEV = 2.93 g·kg−1 and RPDV = 1.79). In contrast, the SPA-SVMR models with Log (1/R), FD, SD and SNV resulted in lower estimation accuracies, and Log (1/R) produced the worst performance (R2V = 0.52, RMSEV = 3.68 g·kg−1 and RPDV = 1.43). Comparisons of these tests demonstrate that different pre-processing methods make SPA-SVMR deliver distinctive performance results. Such results can be explained by the fact that several pre-processing methods (e.g., SG, Log (1/R) + SG, MC and MSC) removed noise and enhanced signals and, hence, were beneficial for the selection of feature bands by SPA. Thus, these pre-processing methods can improve the SVMR model accuracy.

3.4. Performance of SPA-SVMR, SVMR and SPA-PLSR Models

Table 5 shows the calibration and validation results of the SPA-SVMR, SVMR and SPA-PLSR models using the same SG-preprocessed dataset. The calibrations of three models achieved RMSEV values ranging from 2.78 to 3.23 g·kg−1. When compared with the SVMR model with 227 wavelengths (R2V = 0.72, RMSEV = 2.83 g·kg−1 and RPDV = 1.86), the SPA-SVMR model with only 28 wavelength variables achieved a similar estimation accuracy (R2V = 0.73, RMSEV = 2.78 g·kg−1 and RPDV = 1.89). The performance of the SPA-SVMR model was much better than that of the SPA-PLSR model, as R2V and RPDV were increased by 17.7% and 16.0%, respectively, while RMSEV was decreased by 0.45 g·kg−1. Therefore, the SPA-SVMR model was optimal for the estimation of SOC contents, since only 12.3% wavelengths were involved to achieve a similar or better estimation accuracy when compared with the SVMR and SPA-PLSR models.

4. Discussion

4.1. Influence of Pre-Processing Methods on SPA and SPA-SVMR

The pre-processing methods used in this study showed considerably different influences on SPA when selecting wavelengths (Figure 3). One possible reason is that the collinearity between wavelengths varied in relation to the different pre-processed reflectance spectra in different degrees (Figure 4). As the main point of SPA is to obtain a subset of variables with minimal collinearity for SOC estimation, SPA with different pre-processing methods had strong differences in the number of selected variables and their distributions (Figure 3, Table 4). For example, after SD processing, collinearities among the wavelengths were considerably lower; therefore, SPA selected 186 variables out of 227 wavelengths. SNV generates similar collinearities for wavelengths as MSC (Figure 4f,h). Thus, the SPA-selected variables for SNV (20 variables) are similar to those of MSC (27 variables), except that there are a few different variables in the visible region (410−700 nm) (Figure 3). Hence, considering the collinearity between wavelengths of different pre-processed reflectance spectra, the variables selected with SPA vary in different degrees.

Based on the wavelengths selected by SPA with the eight pre-processing methods, eight SVMR models were correspondingly calibrated and validated (Table 4). SG can reduce the random noise and improve the quality of raw spectral data [42], which assisted SPA in selecting informative variables. Thus, the corresponding SPA-SVMR model achieved a better accuracy. Log (1/R) + SG also assisted SPA-SVMR to yield a good accuracy, but using Log (1/R) alone made SPA-SVMR deliver the worst performance among the eight pre-processing methods. Log (1/R) can reduce the nonlinearities, which is conflicted with the functionality of SVMR. Comparing with the SPA-SVMR without any pre-processing, SD and SNV obviously decreased the accuracy, because SD potentially generates noise [14] and SNV is sensitive to the noise in the spectrum [34]. Therefore, not all the pre-processing methods are appropriate to improve the accuracy of SPA-SVMR models. In this study, SG was an appropriate pre-processing method for the SPA-SVMR model. Moreover it was also employed and demonstrated to be useful in some other research [9,33,45–49]; for example, Vasques et al. [9] employed SG to improve the estimation accuracy for soil carbon.

4.2. Wavelength Selection

In this study, almost all of the 28 important wavelengths selected by SPA were located in the near-infrared region. Moreover, the eight pre-processing methods shared several wavelengths, particularly near 800, 1000, 1400 and 1900−2450 nm, which confirmed that the wavelengths in the near-infrared spectral region were important for SOC content estimations [4,16,22,24,30,50]. Ge et al. [13] estimated SOC contents with soil VIS/NIR spectra from different instruments/scanning environments. Their results also showed that most of the significant wavebands for SOC content estimation were located in the near-infrared region and shared by all the calibration models in their study. Such a result can be explained by the overtones and combinations of fundamental vibrations related to soil components; the stretching and bending of NH, OH and CH groups is concentrated in the near-infrared region [18,51]. Yang et al. [30] found that the visible range over 600−760 nm could be used to estimate SOC contents. However, this spectral region was not selected by SPA with SG in our study. A possible cause was the stronger influence of water and CH related bands, which overshadowed the influence of visible bands.

The selected wavelengths mainly located in the near-infrared region achieved the optimal estimation accuracy for SOC. Previously, some researchers reported that SOC estimations depend considerably on the spectral information over wavelengths greater than 1200 nm; this information might improve the accuracy of SOC content estimations [24,50,52]. Vohland and Emmerling [24] illustrated that the spectral features over 1900 nm selected by a genetic algorithm were of great significance for SOC content estimations. These results also agreed with the findings in this research, since 24 (85.7%) of the 28 spectral variables selected by SPA with SG pre-processing were located at wavelengths greater than 1200 nm. Specifically, the important wavelengths identified by SPA with SG for SOC coincided with those related to water (e.g., 1915, 1455, 1380, 1135, 940 nm) [16], organics (2381, 2147, 2084, 1967, 1931, 1517, 1454, 860 nm) [16,22], as well as clay minerals (2444, 2201, 2174 nm) [22], with a smaller number of wavelengths coinciding with those related to the iron oxides (e.g., goethite (920 nm), hematite (884 nm)) (Figure 3). These results were consistent with the findings of Viscarra Rossel et al. [16], who reported that most of the important wavelengths for estimating SOC contents were related to the absorptions of iron oxides, water, organics and minerals.

4.3. Comparison of SPA-SVMR, SVMR and SPA-PLSR Models

According to Table 5, when compared with the SVMR model, the SPA-SVMR model only employed 28 wavelength variables, but achieved a similar accuracy for the estimation of SOC contents. Such a result can be attributed to the fact that SPA chooses the informative wavelengths with the minimal collinearity [26] and removes many uninformative spectral variables, which simplifies the SPA-SVMR model and increases its robustness. This simplification of the SVMR model is also helpful in the interpretation of the SVMR model. SVMR, in contrast, may take much time for training samples when there are a large number of spectral variables and samples. In this case, SVMR may not obtain the best results, due to the redundancy in the input spectral data [53].

The SPA-SVMR model was superior to the SPA-PLSR model (Table 5). Our results confirmed the good performance of SVMR for estimating soil properties as compared to other multivariate calibration models [16,54]. The basic reason is that SVMR is more appropriate for dealing with potential nonlinearity from instrument variations (lamp aging and sensor sensitivity) than PLSR [8,16]. In addition, the SVMR model is less sensitive to noise and outliers than PLSR [18]. A similar comparison was also made by Liu and He [21] for determining the organic acids of plum vinegar. Their research also demonstrated that an SPA-SVMR model was better than an SPA-PLSR model. Liu et al. [28] also reported that an SPA-SVMR model outperformed an SPA-PLSR model and other models for the determination of the soluble solids of beer.

When compared with the previous studies in estimating SOC contents by using VIS/NIR spectra (R2V = 0.57–0.91) [9,16,24,30,32,50,51,55–58], the predictive performance of the SPA-SVMR model (R2V = 0.73, RMSEV = 2.78 g·kg−1 and RPDV = 1.89) in this study was moderate according to the evaluation standard of Viscarra Rossel et al. [45]. Stevens et al. [54] used a large-scale EU soil survey of about 20,000 samples belonging to eight land-use types with a greatly wider range of SOC contents (0.0 to 586.8 g·kg−1) to predict SOC contents and reported good prediction results, with R2V values from 0.67 to 0.89 and RPD values ranging from 1.74 to 2.88. Brown et al. [50] achieved a R2V value of 0.87 with a similarly wide range of SOC contents of 0.0–536.8 g·kg−1 from a global scale. With 1011 soil samples and an SOC concentration range of 2.3–55.8 g·kg−1, Shepherd and Walsh [54] obtained a R2V value of 0.80 for SOC content estimation. Moreover, Saiano et al. [7] estimated the soil carbon contents of 89 soils from a small and homogeneous area, Pantelleria Island, and achieved a considerably higher accuracy with a cross-validation R2 value of 0.951 and an RPD value of 4.49.

One basic factor restricting the further improvement in prediction performance of the SPA-SVMR is the range of SOC contents (0.79–30.73 g·kg−1) and the number and representativeness of soil samples (287, Yixing, Zhongxiang and Honghu regions) in our study. Therefore, adequate samples over these regions with a wider range of SOC contents are required to further improve the prediction performance of the SPA-SVMR model. In addition, a range of soil types and land use types (Table 1, Table 2) may be another factor for the SOC content estimation with moderate accuracy in our study. Many studies have shown that the estimation models for soil properties varied to a large extent when considering soils diversity in various soil types and land use types [23,55,59]. That is because soils with different soil types can have considerably different characteristics, such as in compositions and spectra, due to the differences of the parent materials. Meanwhile, various land use types might further result in variations in soil properties, such as variation in observed SOC values. Thus, soil heterogeneity increases and model performance can be affected.

This study was carried out using the ground soil samples and the VIS/NIR spectra under laboratory conditions, and SPA-SVMR obtained good results when estimating SOC contents. These results laid the foundation for quickly estimating SOC contents from in situ field spectroscopy in future studies. However, for the natural soils in the field, the estimation of SOC contents could be affected by some factors, such as soil surface characteristics (e.g., particle size distribution, physical and biogenic crusts), mixed vegetation, atmospheric conditions and the varying moisture contents of natural soils, compared to laboratory-based dried soils. Recently, Minasny et al. [60] successfully utilized an external parameter orthogonalization algorithm to remove the effect of soil moisture from NIR spectra for the calibration of SOC contents and reported improved calibration and prediction of SOC contents. Wu et al. [61] identified a range of wavelengths in the NIR region in which the first derivative of the reflectance spectra seemed independent of the moisture content of the soil samples. They suggested to only use these selected wavelength intervals to obtain moisture-independent estimates of SOC under field conditions. Therefore, we will explore the proper pre-processing and algorithms for field soil samples and spectroscopy in depth to remove the effects of moisture and other environmental factors. The feasible SPA-SVMR model coupled with effective methods for the removal of natural environment effects may facilitate a good method for the rapid estimation of SOC contents from in situ field spectra in the future.

5. Conclusions

The combination of SPA and SVMR was utilized for estimating the SOC contents from laboratory-based VIS/NIR spectroscopy, and the performance was compared with the SVMR model and SPA-PLSR model. SPA can improve the performance of the SVMR model through selecting informative wavelengths and reducing the complexity of SVMR model. Moreover, different spectra pre-processing methods had strong influences on the wavelength selection by SPA and on SPA-SVMR model performance. Overall, SPA-SVMR modeling methods were feasible and reliable for estimating the SOC contents using the VIS/NIR spectra of soils in laboratory conditions, and their application to natural soils in the field is promising and will be explored in future studies.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (grant no. 41171290 and no. 41023001).

Author Contributions

All authors conceived and designed the study. Xiaoting Peng, Tiezhu Shi and Yiyun Chen made substantial contributions to the acquisition, analysis and interpretation of the data. Xiaoting Peng performed the experiments. All authors discussed the basic structure of the manuscript, and Xiaoting Peng finished the first draft. Tiezhu Shi, Aihong Song and Wenxiu Gao reviewed and edited the draft. All authors read and approved the submitted manuscript, agreed to be listed and accepted the version for publication.

Conflict of Interest

The authors declare no conflict of interest.

References

  1. Gomez, C.; Viscarra Rossel, R.A.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field VIS-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar]
  2. Ladoni, M.; Bahrami, H.; Alavipanah, S.; Norouzi, A. Estimating soil organic carbon from soil reflectance: A review. Precis. Agric 2010, 11, 82–99. [Google Scholar]
  3. Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus PLSR method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar]
  4. Sarkhot, D.V.; Grunwald, S.; Ge, Y.; Morgan, C.L.S. Comparison and detection of total and available soil carbon fractions using visible/near infrared diffuse reflectance spectroscopy. Geoderma 2011, 164, 22–32. [Google Scholar]
  5. Bellon-Maurel, V.; McBratney, A. Near-infrared (NIR) and mid-infrared (MIR) spectroscopic techniques for assessing the amount of carbon stock in soils—Critical review and research perspectives. Soil Biol. Biochem 2011, 43, 1398–1410. [Google Scholar]
  6. Reeves, J., Iii; McCarty, G.; Mimmo, T. The potential of diffuse reflectance spectroscopy for the determination of carbon inventories in soils. Environ. Pollut 2002, 116 Suppl. 1, 277–284. [Google Scholar]
  7. Saiano, F.; Oddo, G.; Scalenghe, R.; La Mantia, T.; Ajmone-Marsan, F. DRIFTS sensor: Soil carbon validation at large scale (Pantelleria, Italy). Sensors 2013, 13, 5603–5613. [Google Scholar]
  8. Stevens, A.; Udelhoven, T.; Denis, A.; Tychon, B.; Lioy, R.; Hoffmann, L.; van Wesemael, B. Measuring soil organic carbon in croplands at regional scale using airborne imaging spectroscopy. Geoderma 2010, 158, 32–45. [Google Scholar]
  9. Vasques, G.M.; Grunwald, S.; Sickman, J.O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar]
  10. Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy—Principal components regression analyses of soil properties. Soil Sci. Soc. Am. J 2001, 65, 480–490. [Google Scholar]
  11. Vasques, G.M.; Grunwald, S.; Sickman, J.O. Modeling of soil organic carbon fractions using visible-near-infrared spectroscopy. Soil Sci. Soc. Am. J 2009, 73, 176–184. [Google Scholar]
  12. Wold, S.; Martens, H.; Wold, H. The multivariate calibration problem in chemistry solved by the PLS method. In Matrix Pencils; Proceedings of a Conference Held at Pite Havsbad, Sweden, 22–24 March 1982, Kågström, B., Ruhe, A., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 1983; Volume 973, pp. 286–293. [Google Scholar]
  13. Ge, Y.; Morgan, C.L.S.; Grunwald, S.; Brown, D.J.; Sarkhot, D.V. Comparison of soil reflectance spectra and calibration models obtained using multiple spectrometers. Geoderma 2011, 161, 202–211. [Google Scholar]
  14. Zhu, D.; Ji, B.; Meng, C.; Shi, B.; Tu, Z.; Qing, Z. The performance of ν-support vector regression on determination of soluble solids content of apple by acousto-optic tunable filter near-infrared spectroscopy. Anal. Chim. Acta 2007, 598, 227–234. [Google Scholar]
  15. Walczak, B.; Massart, D.L. The radial basis functions—Partial least squares approach as a flexible non-linear regression technique. Anal. Chim. Acta 1996, 331, 177–185. [Google Scholar]
  16. Viscarra Rossel, R.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar]
  17. Balabin, R.M.; Safieva, R.Z.; Lomakina, E.I. Comparison of linear and nonlinear calibration models based on near infrared (NIR) spectroscopy data for gasoline properties prediction. Chemom. Intell. Lab. Syst 2007, 88, 183–188. [Google Scholar]
  18. Thissen, U.; Pepers, M.; Üstün, B.; Melssen, W.J.; Buydens, L.M.C. Comparing support vector machines to PLS for spectral regression applications. Chem. Intell. Lab. Syst 2004, 73, 169–179. [Google Scholar]
  19. Li, Y.; Shao, X.; Cai, W. A consensus least squares support vector regression (LS-SVR) for analysis of near-infrared spectra of plant samples. Talanta 2007, 72, 217–222. [Google Scholar]
  20. Andersen, C.M.; Bro, R. Variable selection in regression—A tutorial. J. Chem 2010, 24, 728–737. [Google Scholar]
  21. Liu, F.; He, Y. Application of successive projections algorithm for variable selection to determine organic acids of plum vinegar. Food Chem 2009, 115, 1430–1436. [Google Scholar]
  22. Zou, X.; Zhao, J.; Povey, M.J.W.; Holmes, M.; Mao, H. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar]
  23. Wang, J.; Cui, L.; Gao, W.; Shi, T.; Chen, Y.; Gao, Y. Prediction of low heavy metal concentrations in agricultural soils using visible and near-infrared reflectance spectroscopy. Geoderma 2014, 216, 1–9. [Google Scholar]
  24. Vohland, M.; Emmerling, C. Determination of total soil organic C and hot water-extractable C from VIS-NIR soil reflectance with partial least squares regression and spectral feature selection techniques. Eur. J. Soil Sci 2011, 62, 598–606. [Google Scholar]
  25. Leardi, R.; Seasholtz, M.B.; Pell, R.J. Variable selection for multivariate calibration using a genetic algorithm: Prediction of additive concentrations in polymer films from Fourier transform-infrared spectral data. Anal. Chim. Acta 2002, 461, 189–200. [Google Scholar]
  26. Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst 2001, 57, 65–73. [Google Scholar]
  27. Galvão, R.K.H.; Araújo, M.C.U.; Fragoso, W.D.; Silva, E.C.; José, G.E.; Soares, S.F.C.; Paiva, H.M. A variable elimination method to improve the parsimony of MLR models using the successive projections algorithm. Chem. Intell. Lab. Syst 2008, 92, 83–91. [Google Scholar]
  28. Liu, F.; Jiang, Y.; He, Y. Variable selection in visible/near infrared spectra for linear and nonlinear calibrations: A case study to determine soluble solids content of beer. Anal. Chim. Acta 2009, 635, 45–52. [Google Scholar]
  29. Kawakami Harrop Galvão, R.; Fernanda Pimentel, M.; Cesar Ugulino Araujo, M.; Yoneyama, T.; Visani, V. Aspects of the successive projections algorithm for variable selection in multivariate calibration applied to plasma emission spectrometry. Anal. Chim. Acta 2001, 443, 107–115. [Google Scholar]
  30. Yang, H.; Kuang, B.; Mouazen, A.M. Quantitative analysis of soil nitrogen and carbon at a farm scale using visible and near infrared spectroscopy coupled with wavelength reduction. Eur. J. Soil Sci 2012, 63, 410–420. [Google Scholar]
  31. Goudarzi, N.; Goodarzi, M.; Arab Chamjangali, M.; Fatemi, M.H. Application of a new SPA-SVM coupling method for QSPR study of electrophoretic mobilities of some organic and inorganic compounds. Chin. Chem. Lett 2013, 24, 904–908. [Google Scholar]
  32. Brown, D.J.; Bricklemyer, R.S.; Miller, P.R. Validation requirements for diffuse reflectance soil characterization models with a case study of VNIR soil C prediction in Montana. Geoderma 2005, 129, 251–267. [Google Scholar]
  33. Mouazen, A.M.; Kuang, B.; de Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar]
  34. Rinnan, Å.; Berg, F.v.d.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem 2009, 28, 1201–1222. [Google Scholar]
  35. FAO; Freddy, O.N.; Velthuizen, H.T.v.; Verelst, L.; Wiberg, D.; Niels, H.B.; Dijkshoorn, J.A.; Vincent, W.P.v.E.; Gunther, F.; Arywn, J.; et al. Harmonized World Soil Database; Version 1.2; FAO: Rome, Italy; IIASA: Laxenburg, Austria; ISRIC: Wageningen The Netherlands; ISSCAS: Nanjing, China; JRC: Ispra, Italy, 2012. [Google Scholar]
  36. ASD Inc. Available online: http://www.asdi.com (accessed on 23 Augut 2013).
  37. Zhou, Q.; Zhou, B.; Wang, R.C.; Zhang, Y.Z. Effect of geometric conditions on soil hyperspectral data scatter characteristic in laboratory test (in Chinese). J. South China Agric. Univ 2005, 26, 31–35. [Google Scholar]
  38. Labsphere. Available online: www.labsphere.com(accessed on 25 August 2013).
  39. Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Sci 1934, 37, 29–38. [Google Scholar]
  40. Verboven, S.; Hubert, M. LIBRA: A MATLAB library for robust analysis. Chemom. Intell. Lab. Syst 2005, 75, 127–136. [Google Scholar]
  41. Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol 2002, 36, 2742–2747. [Google Scholar]
  42. Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem 1964, 36, 1627–1639. [Google Scholar]
  43. Araújo, H.F.; Galvão, R.K.H.; Pimentel, M.F.; de Barros Neto, B.; Araújo, M.C.U.; de Carvalho, F.R. Robust modeling for multivariate calibration transfer by the successive projections algorithm. Chemom. Intell. Lab. Syst 2005, 76, 65–72. [Google Scholar]
  44. ITA-Instituto Tecnológico de Aeronáutica. Available online: www.ele.ita.br/kawakami/spa/ (accessed on 20 June 2013).
  45. Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV-VIS-NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar]
  46. Wetterlind, J.; Stenberg, B.; Jonsson, A. Near infrared reflectance spectroscopy compared with soil clay and organic matter content for estimating within-field variation in N uptake in cereals. Plant Soil 2008, 302, 317–327. [Google Scholar]
  47. Tian, Y.; Zhang, J.; Yao, X.; Cao, W.; Zhu, Y. Laboratory assessment of three quantitative methods for estimating the organic matter content of soils in China based on visible/near-infrared reflectance spectra. Geoderma 2013, 202–203, 161–170. [Google Scholar]
  48. Honorato, F.A.; Neto, B.d.B.; Pimentel, M.F.; Stragevitch, L.; Galvão, R.K.H. Using principal component analysis to find the best calibration settings for simultaneous spectroscopic determination of several gasoline properties. Fuel 2008, 87, 3706–3709. [Google Scholar]
  49. Stevens, A.; van Wesemael, B.; Bartholomeus, H.; Rosillon, D.; Tychon, B.; Ben-Dor, E. Laboratory, field and airborne spectroscopy for monitoring organic carbon content in agricultural soils. Geoderma 2008, 144, 395–404. [Google Scholar]
  50. Brown, D.J.; Shepherd, K.D.; Walsh, M.G.; Dewayne Mays, M.; Reinsch, T.G. Global soil characterization with VNIR diffuse reflectance spectroscopy. Geoderma 2006, 132, 273–290. [Google Scholar]
  51. Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar]
  52. Cambule, A.H.; Rossiter, D.G.; Stoorvogel, J.J.; Smaling, E.M.A. Building a near infrared spectral library for soil organic carbon estimation in the Limpopo National Park, Mozambique. Geoderma 2012, 183–184, 41–48. [Google Scholar]
  53. Huang, Z.R.; Sha, S.; Rong, Z.Q.; Chen, J.H.; He, Q.L.; Khan, D.M.; Zhu, S.J. Feasibility study of near infrared spectroscopy with variable selection for non-destructive determination of quality parameters in shell-intact cottonseed. Ind. Crop. Prod 2013, 43, 654–660. [Google Scholar]
  54. Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of soil organic carbon at the European scale by visible and near infrared reflectance spectroscopy. PloS One 2013, 8, e66409. [Google Scholar]
  55. Udelhoven, T.; Emmerling, C.; Jarmer, T. Quantitative analysis of soil chemical properties with diffuse reflectance spectrometry and partial least-square regression: A feasibility study. Plant Soil 2003, 251, 319–329. [Google Scholar]
  56. Islam, K.; Singh, B.; McBratney, A. Simultaneous estimation of several soil properties by ultra-violet, visible, and near-infrared reflectance spectroscopy. Soil Res 2003, 41, 1101–1114. [Google Scholar]
  57. Shepherd, K.D.; Walsh, M.G. Development of reflectance spectral libraries for characterization of soil properties. Soil Sci. Soc. Am. J 2002, 66, 988–998. [Google Scholar]
  58. Eisele, A.; Lau, I.; Hewson, R.; Carter, D.; Wheaton, B.; Ong, C.; Cudahy, T.J.; Chabrillat, S.; Kaufmann, H. Applicability of the thermal infrared spectral region for the prediction of soil properties across semi-arid agricultural landscapes. Remote Sens 2012, 4, 3265–3286. [Google Scholar]
  59. Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Chapter five-visible and near infrared spectroscopy in soil science. Adv. Agron 2010, 107, 163–215. [Google Scholar]
  60. Minasny, B.; McBratney, A.B.; Bellon-Maurel, V.; Roger, J.-M.; Gobrecht, A.; Ferrand, L.; Joalland, S. Removing the effect of soil moisture from NIR diffuse reflectance spectra for the prediction of soil organic carbon. Geoderma 2011, 167–168, 118–124. [Google Scholar]
  61. Wu, C.-Y.; Jacobson, A.R.; Laba, M.; Baveye, P.C. Alleviating moisture content effects on the visible near-infrared diffuse-reflectance sensing of soils. Soil Sci 2009, 174, 456–465. [Google Scholar]
Remotesensing 06 02699f1 1024
Figure 1. (a) Study areas and the spatial distributions of soil samples in (b) Yixing, (c) Zhongxiang and (d) Honghu.
Figure 1. (a) Study areas and the spatial distributions of soil samples in (b) Yixing, (c) Zhongxiang and (d) Honghu.
Remotesensing 06 02699f1 1024
Remotesensing 06 02699f2 1024
Figure 2. Resample interval selection based on the leave-one-out cross-validation results of support vector machine regression (SVMR) (a) and partial least squares regression (PLSR); (b) models. R2CV is the coefficient of determination between the measured and estimated values of cross-validation. RPDCV is the residual prediction deviation of cross-validation.
Figure 2. Resample interval selection based on the leave-one-out cross-validation results of support vector machine regression (SVMR) (a) and partial least squares regression (PLSR); (b) models. R2CV is the coefficient of determination between the measured and estimated values of cross-validation. RPDCV is the residual prediction deviation of cross-validation.
Remotesensing 06 02699f2 1024
Remotesensing 06 02699f3 1024
Figure 3. The selected variables (indicated by the | markers) by the successive projections algorithm (SPA) with the eight pre-processing methods (i.e., Log (1/R), Log (1/R) coupled with Savitzky–Golay (SG) smoothing (Log (1/R) + SG), first derivative with SG smoothing (FD), second derivative with SG smoothing (SD), SG, standard normal variate (SNV), mean center (MC) and multiplicative scatter correction (MSC)).
Figure 3. The selected variables (indicated by the | markers) by the successive projections algorithm (SPA) with the eight pre-processing methods (i.e., Log (1/R), Log (1/R) coupled with Savitzky–Golay (SG) smoothing (Log (1/R) + SG), first derivative with SG smoothing (FD), second derivative with SG smoothing (SD), SG, standard normal variate (SNV), mean center (MC) and multiplicative scatter correction (MSC)).
Remotesensing 06 02699f3 1024
Remotesensing 06 02699f4 1024
Figure 4. The correlation coefficient contour plots of different wavelengths of pre-processed spectra ((a) Log (1/R); (b) Log (1/R) + SG; (c) first derivative with SG smoothing (FD); (d) second derivative with SG smoothing (SD); (e) Savitzky-Golay smoothing (SG); (f) standard normal variate (SNV); (g) mean center (MC); and (h) multiplicative scatter correction (MSC)).
Figure 4. The correlation coefficient contour plots of different wavelengths of pre-processed spectra ((a) Log (1/R); (b) Log (1/R) + SG; (c) first derivative with SG smoothing (FD); (d) second derivative with SG smoothing (SD); (e) Savitzky-Golay smoothing (SG); (f) standard normal variate (SNV); (g) mean center (MC); and (h) multiplicative scatter correction (MSC)).
Remotesensing 06 02699f4 1024
Table
Table 1. The number of soil samples (n) and frequency (in percent of the total number of soil samples) occupied by land use type in the Yixing, Zhongxiang and Honghu regions.
Table 1. The number of soil samples (n) and frequency (in percent of the total number of soil samples) occupied by land use type in the Yixing, Zhongxiang and Honghu regions.
Land-Use TypeAreasnFrequency (%)
Paddy fieldYixing, Zhongxiang11438
Sesame landYixing124
Soybean landYixing114
GrasslandYixing133
Arbor landYixing104
Tea gardenYixing114
ShrublandYixing114
CornfieldYixing134
Bare landYixing52
Rape fieldHonghu9833
Table
Table 2. The number of soil samples (n) and frequency (in percent of the total number of soil samples) occupied by soil type in the Harmonized World Soil Database (version 1.2) for the Yixing, Zhongxiang and Honghu regions.
Table 2. The number of soil samples (n) and frequency (in percent of the total number of soil samples) occupied by soil type in the Harmonized World Soil Database (version 1.2) for the Yixing, Zhongxiang and Honghu regions.
Soil TypeAreasnFrequency (%)
AnthrosolsYixing, Zhongxiang, Honghu17157.4
LuvisolsYixing, Zhongxiang4013.4
LeptosolsZhongxiang279.1
GleysolsHonghu279.1
PlanosolsYixing, Zhongxiang175.7
AlisolsYixing165.3
Table
Table 3. Statistical descriptions of the soil organic carbon (SOC) contents (g·kg−1).
Table 3. Statistical descriptions of the soil organic carbon (SOC) contents (g·kg−1).
N aMin bMax cMeanMedianStd. d
Whole dataset2870.7930.7315.3915.245.35
Calibration dataset1920.7930.7315.4015.275.42
Validation dataset951.9626.2315.3715.245.25

asample number;bminimum of SOC;cmaximum of SOC;dstandard deviation.

Table
Table 4. The numbers of wavelength variables selected by the successive projections algorithm (SPA) and the performance of support vector machine regression (SVMR) combined with SPA (i.e., SPA-SVMR model) based on the pre-processed results with the eight methods (i.e., Log (1/R), Log (1/R) coupled with Savitzky-Golay (SG) smoothing (Log (1/R) + SG), first derivative with SG smoothing (FD), second derivative with SG smoothing (SD), SG, standard normal variate (SNV), mean center (MC) and multiplicative scatter correction (MSC)).
Table 4. The numbers of wavelength variables selected by the successive projections algorithm (SPA) and the performance of support vector machine regression (SVMR) combined with SPA (i.e., SPA-SVMR model) based on the pre-processed results with the eight methods (i.e., Log (1/R), Log (1/R) coupled with Savitzky-Golay (SG) smoothing (Log (1/R) + SG), first derivative with SG smoothing (FD), second derivative with SG smoothing (SD), SG, standard normal variate (SNV), mean center (MC) and multiplicative scatter correction (MSC)).
Pre-ProcessingpR2VRMSEPRPDV
No-preprocessing2270.603.311.59
Log (1/R)120.523.681.43
Log (1/R) + SG220.72.931.79
FD90.553.641.47
SD1860.543.591.49
SG280.732.781.89
SNV200.593.381.55
MC170.693.021.74
MSC270.673.111.69

Note: P denotes the number of the selected variables by SPA. R2V is the coefficient of determination between the measured and estimated values of validation. RMSEP is the root mean square error of prediction (g·kg−1). RPDV is the residual prediction deviation of validation.

Table
Table 5. The performance of the SPA-SVMR, SVMR and SPA-PLSR models for SOC contents estimation.
Table 5. The performance of the SPA-SVMR, SVMR and SPA-PLSR models for SOC contents estimation.
Calibration ModelspR2CRMSECR2VRMSEVRPDV
SPA-SVMR280.851.550.732.781.89
SVMR2270.841.660.722.831.86
SPA-PLSR280.722.620.623.231.63

Note: P is the number of variables used in the models. R2C and R2V are the coefficient of determination between the measured and estimated values of calibration and validation, respectively. RMSEC and RMSEV (g·kg−1) are the root mean square error of calibration and validation, respectively. RPDV is the residual prediction deviation of validation.

Share and Cite

MDPI and ACS Style

Peng, X.; Shi, T.; Song, A.; Chen, Y.; Gao, W. Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods. Remote Sens. 2014, 6, 2699-2717. https://doi.org/10.3390/rs6042699

AMA Style

Peng X, Shi T, Song A, Chen Y, Gao W. Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods. Remote Sensing. 2014; 6(4):2699-2717. https://doi.org/10.3390/rs6042699

Chicago/Turabian Style

Peng, Xiaoting, Tiezhu Shi, Aihong Song, Yiyun Chen, and Wenxiu Gao. 2014. "Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods" Remote Sensing 6, no. 4: 2699-2717. https://doi.org/10.3390/rs6042699

APA Style

Peng, X., Shi, T., Song, A., Chen, Y., & Gao, W. (2014). Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods. Remote Sensing, 6(4), 2699-2717. https://doi.org/10.3390/rs6042699

Article Metrics

Back to TopTop