Next Article in Journal
Assessing Long-Term Changes in the Beach Width of Reef Islands Based on Temporally Fragmented Remote Sensing Data
Next Article in Special Issue
1982–2010 Trends of Light Use Efficiency and Inherent Water Use Efficiency in African vegetation: Sensitivity to Climate and Atmospheric CO2 Concentrations
Previous Article in Journal
Decision Fusion Based on Hyperspectral and Multispectral Satellite Imagery for Accurate Forest Species Mapping
Previous Article in Special Issue
Human Land-Use Practices Lead to Global Long-Term Increases in Photosynthetic Capacity
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 6
Issue 8
10.3390/rs6086929
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series

by
Jorge E. Pinzon
1,* and
Compton J. Tucker
2
1
Science Systems and Applications Inc., Biospheric Sciences Laboratory, NASA Goddard Space Flight Center, Code 618, Greenbelt, MD 20771, USA
2
Earth Science Division, NASA Goddard Space Flight Center, Code 610, Greenbelt, MD 20771, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2014, 6(8), 6929-6960; https://doi.org/10.3390/rs6086929
Submission received: 13 December 2013 / Revised: 12 June 2014 / Accepted: 4 July 2014 / Published: 25 July 2014
(This article belongs to the Special Issue Monitoring Global Vegetation with AVHRR NDVI3g Data (1981-2011))
Browse Figures
Versions Notes

Abstract

: The NDVI3g time series is an improved 8-km normalized difference vegetation index (NDVI) data set produced from Advanced Very High Resolution Radiometer (AVHRR) instruments that extends from 1981 to the present. The AVHRR instruments have flown or are flying on fourteen polar-orbiting meteorological satellites operated by the National Oceanic and Atmospheric Administration (NOAA) and are currently flying on two European Organization for the Exploitation of Meteorological Satellites (EUMETSAT) polar-orbiting meteorological satellites, MetOp-A and MetOp-B. This long AVHRR record is comprised of data from two different sensors: the AVHRR/2 instrument that spans July 1981 to November 2000 and the AVHRR/3 instrument that continues these measurements from November 2000 to the present. The main difficulty in processing AVHRR NDVI data is to properly deal with limitations of the AVHRR instruments. Complicating among-instrument AVHRR inter-calibration of channels one and two is the dual gain introduced in late 2000 on the AVHRR/3 instruments for both these channels. We have processed NDVI data derived from the Sea-Viewing Wide Field-of-view Sensor (SeaWiFS) from 1997 to 2010 to overcome among-instrument AVHRR calibration difficulties. We use Bayesian methods with high quality well-calibrated SeaWiFS NDVI data for deriving AVHRR NDVI calibration parameters. Evaluation of the uncertainties of our resulting NDVI values gives an error of ± 0.005 NDVI units for our 1981 to present data set that is independent of time within our AVHRR NDVI continuum and has resulted in a non-stationary climate data set.
Keywords:
Advanced Very High Resolution Radiometer (AVHRR); Normalized Difference Vegetation Index (NDVI); Bayesian analysis; uncertainty; bias; climate variability; non-stationary

Graphical Abstract

1. Introduction

The Normalized Difference Vegetation Index (NDVI) derived from the Advanced Very High Resolution Radiometer (AVHRR) instruments has been crucial to study a variety of global land vegetation processes and how they vary in time [1–8]. The 1981 to present record of AVHRR NDVI data are formed from two AVHRR instruments, the AVHRR/2 that flew from July 1981 to November 2000 and the AVHRR/3 instrument that is flying/has flown since November 2000 to present. These instruments have flown or are flying on fourteen National Oceanic and Atmospheric Administration (NOAA) polar-orbiting platforms in the TIROS-N/NOAA (A-D) series and in the Advanced TIROS-N (ATN)/NOAA (E-N’) series (The National Oceanic and Atmospheric Administration (NOAA) and the National Aeronautics and Space Administration (NASA) have jointly developed this valuable series of polar-orbiting Operational Environmental Satellites (POES). NASA’s Goddard Space Flight Center has managed the development and launch of the mission that encompasses the NOAA (A-N Prime) series of platforms After NASA transferred operational control to NOAA, the name of the satellite changed from NOAA (A-N Prime) to NOAA [6–19] (see Table 1 for renaming). NOAA-B had a launch failure in 29 May 1980) and on two polar-orbiting satellites in the MetOp series operated by the European Organization for the Exploitation of Meteorological Satellites (EUMETSAT) (Table 1). Although AVHRR sensors were not originally intended as a climate mission [1], their early success for vegetation studies was due to a reconfiguration of the instruments to have non-overlapping (“visible”) channel one (0.58–0.68 µm) and (near-infrared) channel two (0.725–1.10 µm) spectral bands [17,18]. The reconfiguration enables the calculation of spectral vegetation indices such as the NDVI which is calculated as: (channel 2 − channel 1)/(channel 2 + channel 1) [19]. Since spectral vegetation indices, reviewed in [20], are a surrogate for photosynthetic potential [19,20], the long record of AVHRR NDVI data has become particularly relevant for continued long-term monitoring of land surface. However, the difficulties in processing AVHRR NDVI data are to properly deal with several limitations of the AVHRR instrument or operation, e.g., vicarious post-launch calibration, atmospheric and cloud correction, and bias correction for the systematic orbital drift during the life of the individual TIROS-N missions. Among-instrument calibration is a prerequisite to observing and documenting the land variability and it is particularly challenging for the AVHRR because, by design, the instrument does not have fully onboard calibration for the visible and near-infrared (VNIR) channels and must rely on external references (i.e., vicariously calibrated). Several sources of radiation have been used as external references for the AVHRR VNIR calibration methods, including stable earth targets such as selected deserts [21–24], molecular scattering from sea surface and reflection from sun glint or clouds [25–27], and glaciers from Antarctica and Greenland [28]. The VNIR channels are sensitive to atmospheric conditions since they are spectrally broad and thus both require additional data for correcting aerosol effects and cloud contamination. Orbital drift of the NOAA-7 to NOAA-14 satellites carrying AVHRR/2 instruments adds to the challenge since the NOAA satellite overpass times drifted from the nominal 1:30 pm overpass time by as much as 4.5 hours toward evening, creating variable illumination and view angles (orbits were stabilized beginning with NOAA-16). The AVHRR global area coverage (GAC) data have a unique sampling method.

In order to reduce on-board global AVHRR data storage circa the late 1970s, the 1.1 km AVHRR spatial resolution data are partially resampled at a 4 km spatial resolution. Within each block of three across-track scan lines by five along-track 1.1 km AVHRR pixels, the first four pixels in the first scan line are averaged and the other eleven pixels are skipped. Thus, the AVHRR GAC data are a 4/15 sampling of every three by five pixel block (that being close to the square of four) and are referred to as “4 km” data. The entire global day and night global area coverage of AVHRR data totals 0.6 GB, a large volume in the late 1970s but trivial today (Table 1).

In the early 1990s, the development of stable long-term data records for land studies became a high priority and several joint NOAA-NASA recalibration efforts emerged to capitalize on the extended temporal coverage of AVHRR/2 data as its primary source [29–34]. Despite some general agreement, global and regional analyses have found important differences between NDVI time series derived from the different methods [35–38]. Therefore, it was and still is important to specify the source of the data processing in each method to certify that the measurements made are traceable and consistent, ensuring thus that potential users can decide whether a given product will suit their needs [39]. Nevertheless, this experience with the AVHRR/2 sensor has led to the design and construction of new coarse resolution global instruments, with better radiometric, spatial, and spectral specifications, that have extended and improved upon the measurements of surface land conditions initiated by the AVHHR/2 instrument series [40]. They include the Sea-Viewing Wide Field-of-view Sensor (SeaWiFS); the Vegetation instruments on SPOT-4, SPOT-5 and Proba-V; the Terra and Aqua Moderate Resolution Imaging Spectro-radiometer (MODIS) instruments on NASA’s Terra and Aqua satellites, and the NOAA Visible Infrared Imaging Radiometer Suite (VIIRS) instrument on the Suomi-NPP satellite (Table 1).

Despite the limitations of the AVHRR/2 design features, the over-riding requirement for data consistency to study potentially varying effects of climate on vegetation can result in their persistence over the lifetime of the instrument series and it could even preclude new ideas to improve the design if they would affect data continuity [38]. However, in the mid-1990s a growing database of accurate and frequent estimates of aerosol optical thickness (AOT) provided by a worldwide sun photometer network [41,42] opened up a new era of improved monitoring of aerosol effects on climate and the validation and improvement of global AOT data sets derived from the new satellite sensors [43–45]. NOAA introduced two new features to the new series carrying the AVHRR/3 instrument [12]. First, orbits for the NOAA/K-N Prime, aka NOAA/15–19, platforms were stabilized to provide consistent scene illumination for the AVHRR VNIR channels. Second, sensitivity at the lower end of the dynamic range of the radiances was increased by using a dual-gain quantization in the VNIR channels of the AVHRR/3 instruments [12] to improve aerosol detection for long-term ocean aerosol retrievals [46–48]. The albedo range from 0% to 25% is quantized from 0 to 500 counts while 25%–100% surface reflectance is quantized from 500 to 1023 digital numbers [12]. On the AVHRR/2 sensors, the counts uniformly represent the 0%–100% albedo range. The Kaufman et al. (1997) dark target approach (The Kaufman et al. approach uses the fact that the very dark pixels with spatial resolution (≥250 m) contain mostly radiance backscattered by aerosols—the darker the surface the higher the accuracy of the retrieved aerosol optical thickness [44]) was used to derive optical thickness values over dark targets where surface contribution in channel 1 is low [47,49]. However, the AVHRR ocean aerosol product [46,47,49] has been a reminder of how challenging it is to retrieve aerosol properties from space [50]. The uncertainty in AVHRR calibration has been the major limiting factor of ocean aerosol retrievals with this instrument [50]. Thus, the overwhelming majority of satellite-based aerosol retrievals use the new sensors data, e.g., MISR, MODIS, or SeaWiFS, combined with those of the international ground-based remote sensing aerosol networks, the AErosol RObotic NETwork AERONET [41,42]. Moreover, the dual-gain quantizing feature coupled with differences between the AVHRR/2 and AVHRR/3 VNIR spectral response function (SRF) [11,51] have complicated among-instrument AVHRR inter-calibration of VNIR channels [52] and derived products like the AVHRR NDVI (See Appendix A for details). Considering the uses of AVHRR data, the AVHRR NDVI is used orders of magnitude more often than AVHRR aerosol retrievals. The introduced design changes on the AVHRR/3 critically jeopardize the use of AVHRR NDVI data in long-term time series trend analysis.

Current efforts seek consistency on the AVHRR NDVI data record. Some of these efforts, like the NOAA Global Vegetation Index (GVI) [53], assume a stationary NDVI dynamics to establish consistency on the long-term data set at the expense of not being able to detect trends. In the GVI the pre-flight AVHRR channel one and two calibration coefficients are applied, and by assuming a “stable global maximum” NDVI it normalizes averages every time period for every pixel to adjust anomalous trends [53], even those due to non-stationary natural variability. Several other calibration efforts are focused on inter-calibration with the most advanced sensors, with on-board calibration, to estimate the calibration parameters. These studies include, inter-calibration with SPOT-4 for the NASA-GIMMS NDVIg dataset [54], inter-calibration with Meteosat-8 for AVHRR/3 [52], inter-calibration with MODIS based on synchronized nadir overpass (SNO) [55] for assessing consistency of AVHRR on NOAA-16 and NOAA-17 [56], or for providing calibration coefficients to every AVHRR instrument flown on the morning and afternoon NOAA or EUMESAT satellites and derive the Pathfinder Atmospheres Extended (PATMOS-x) reflectance dataset [57]. Others studies are focused on combining previous AVHRR processing with atmospheric corrections used in MODIS as in the Land Long Term Data Record (LTDR-V3) [58] or focused on techniques for correction of systematic errors based on synchronized nadir overpass (SNO) of TIROS-N observations using sources of reference calibration targets as processed in the Canada Center for Remote Sensing (CCRS) dataset [59]. However, integration of data sets to produce long-term records has been problematic because of differences between sensor characteristics of AVHRR-2 and AVHRR-3 themselves (see appendix A) and the more advanced sensors. For example, the NDVI vegetation index produced with the broad VNIR spectral bands on the AVHRR is different than the NDVI produced with the new sensors that have avoided the water absorption effects in the near infrared channels by narrowing its band pass [13–15]. The approaches using MODIS or SNO to produce a long-term dataset would have insufficiently reliable data for the estimation of the inter-calibration parameters of the NOAA-14 AVHRR/2 sensor since, during their overlapping periods, the NOAA-14 platform has a later overpass due to its drift (Table 1). It is possible as a result that cross-sensor differences or incompatibilities would still remain between AVHRR/2 and AVHRR/3. Incompatibilities are also expected in the LTDR-V3 time series that have replaced the AVHRR/3 component with the best available MODIS data [58].

The aforementioned inter-calibration approaches all follow a traditional (frequentist) approach to find optimal parameters—that is, parameters are considered to be unknown, but fixed; hence they are deterministic and they are estimated by finding the best set of parameters C* among all parameters C, i.e., those values that best match the actual measurements. Of course, there are different competing ways to define “best parameters”, but any approach that only produces a single best value C*, cannot explain the fact that measurements contain noise. In other words, deterministic inversion methods do not explain the uncertainty in parameter estimates [60]. In this paper, we consider an alternative, statistical approach to parameter estimation in inter-calibration problems—the Bayesian method—that takes a different viewpoint. Rather than trying to find a single best parameter value C*, parameters are considered to have a distribution P(C) that can be updated to reflect new information. We use SeaWiFs data from 1998 to 2008 to characterize the NDVI probability density function and inter-calibrate the NDVI probability density estimated from NOAA AVHRR/2 and AVHRR/3. This study grew from the Global Inventory Modeling and Mapping Studies (GIMMS) early calibration research that results in the first generation AVHRR/2 GIMMS NDVI dataset [32] and the second generation GIMMS NDVIg that inter-calibrates AVHRR/2 and AVHRR/3 with SPOT-4 Vegetation data to produce a bi-monthly time series from 1981 to 2006 [54]. Studies using the NDVIg time series reported the stability of the dataset [61–64] that fares well when compared to other data sets [36–38]. The inter-calibrated AVHRR/2 component of the NDVIg, from July 1981 to September 2000, was also recommended for time series analysis as being a consistent non-stationary dataset [38]. However, some inconsistencies were found at northern high latitudes in its AVHRR/3 record [65,66]. Investigating them, we found that recalibration was not possible using SPOT-4 Vegetation NDVI data at very high northern latitudes due to the truncation of SPOT-4 data above 72° N latitude. Substituting SPOT-4 NDVI (NDVISP4) with SeaWiFS NDVI (NDVISW) data in the Bayesian inter-calibration process, we compensated for the northern latitude inconsistencies, and obtained robustness that resulted in an improved consistent non-stationary NDVI3g dataset. The goal of our work is to produce a consistent non-stationary NDVI data set to quantify climate-driven seasonal and inter-annual variability in photosynthetic capacity.

In this paper, we show how to build a consistent non-stationary NDVI dataset derived from AVHRR/2 and AVHRR/3 sensors based on Bayesian methods and the SeaWiFS NDVI dataset. We characterized the NDVI probability density function through SeaWiFS data and corrected the inconsistencies (Due to sensor design differences between the AVHRR/2 and AVHRR/3 instruments (see Appendix A)) of the AVHRR probability density functions, known as “priors” in Bayes theory. To this end, in Section 2.1, we review the processing of our data sets, NDVIg and NDVI3g, to ensure that the results are traceable and consistent. We follow in Sections 2.2–2.4 with a brief introduction of Bayesian analysis in the context of sensor inter-calibration. We present a first set of results in Section 3.1 and extend them to discuss parameter and data uncertainties. In Section 3.2, we discuss data stewardship and the additional steps taken to ensure the integrity, accessibility and maintenance of our research NDVI3g dataset. Finally, we draw data quality conclusions in Section 4.

2. Methods

In this section, we review the inter-calibration processing chain developed for the NDVIg and current NDVI3g dataset versions to minimize AVHRR/2 and AVHRR/3 NDVI incompatibilities.

2.1. Bayesian Description of Inverse Problem

To infer parameters from indirect measurements, as on these inter-calibration efforts, is an inverse problem in the field of parameter estimation, since we used to convert the observed measurements into information about the parameters of a physical system [60]. Our goal is to describe Bayes’ learning rule that updates prior knowledge in light of measurement evidence data. In its most common form, the Bayes’ rule p(A|B) = p(B|A) p(A)/p(B), describes learning about proposition A, based on the evidence data B, where p(A) is our initial degree of belief or prior probability distribution, and p(A|B) is our degree of belief or posterior probability distribution after accounting for the evidence data. Several terms that enter the Bayes’ formula need to be defined [67]:

  • The prior probability p(A), in the Bayesian interpretation, encodes prior knowledge about the parameters A, such as the degree of correspondence between our two AVHRR/2 and AVHRR/3 NDVI prior distributions (NDVIpd).

  • The probability p(B) describes our knowledge about evidence data B, such as the SeaWiFS NDVI data (NDVISW).

  • The likelihood p(B/A) encodes our ability to predict how the system would behave as a function of A with a fixed value B.

  • The ratio p(B|A)/p(B) is a way to quantify how much support evidence B provides for proposition A.

  • The Learning p(A|B), in a Bayesian model, is the shifting of distribution in a proposition before and after accounting for evidence using Bayes’ rule.

The Bayesian perspective is natural for uncertainty quantification since it provides densities that can be propagated through models [68]. First, in the Bayesian framework, probabilities are treated as possibly subjective and they can be updated to reflect new information; second, they are considered to be a distribution rather than a single frequency value; and third, parameters are considered to be random variables with associated densities and the solution of the inverse problem is the posterior probability density.

2.2. Input Data—NDVIpd

Our AVHRR NDVI3g data set was formed exclusively from AVHRR/2 and AVHRR/3 instruments onboard NOAA-7 through NOAA-19 satellites (Table 1). The processing system of the current NDVI3g data set inherits many of the steps of its predecessor NDVIg. In particular, the resulting AVHRR/2 and AVHRR/3 NDVI data from steps 1–4 (below) are the same input NDVI prior data (NDVIpd) to the Bayesian inter-calibration analysis for the NDVIg and NDVI3g datasets.

The AVHRR NDVI data is processed using the following algorithms aimed at reducing the aforementioned effects on the NDVI signal:

(1)

Updated orbital models were used for better prediction of satellite position, thus minimizing navigation errors that result in less accurate co-registration [33,69];

(2)

Time-varying channel 1 and channel 2 vicarious calibrations were applied to AVHRR using

(a)

Atmospheric Rayleigh scattering over oceans approach of Vermote and Kaufman [27], followed by calibration of the NDVI itself using the desert calibration of Los [23] for the AVHRR/2 sensors and,

(b)

Operational NOAA-NESDIS (desert) vicarious calibration coefficients [56,70] for the AVHRR/3 data acquired from NOAA-16 to NOAA-19;

(3)

NDVI composites were assembled via maximum value compositing (Maximum value NDVI composites were formed globally with a bimonthly time step, from the 1st day of the month through the 15th and from day 16 to the end of each month [54]. It should be noted that maximum NDVI compositing does not completely remove atmospheric effects. The broad bands of the AVHRR/2 and AVHRR/3 channel 1 and 2 bands, coupled with varying on-orbit channel spectral response function changes of these channels, also makes it difficult to deterministically remove atmosphere effects in the AVHRR NDVI even if correction fields existed in the earlier part of the AVHRR record) to minimize effects of atmospheric water vapor, non-volcanic aerosols, and cloud-cover [71];

(4)

NDVI composites from AVHRR/2 were processed with

(c)

A radiative-transfer volcanic aerosol correction for the El Chichon and Mt. Pinatubo stratospheric aerosol periods [72];

(d)

An adaptive empirical mode decomposition/reconstruction procedure to reduce latitude varying solar zenith angles effects in the AVHRR/2 record due to orbital drift to later equatorial crossing times in the NOAA-7, NOAA-9, NOAA-11, and NOAA-14 platforms [73]. It should be noted that the NDVI, as a ratio, implicitly contains a directional correction since the effects in the two channels are similar [74].

The resulting NDVI data from steps 1–4 is input to the Bayesian approach as prior knowledge information and it is called NDVIpd hereafter. Although steps 1–4 produce a consistent non-stationary AVHRR/2 NDVIpd data set for the period 1981–2000, the dual-gain quantizing feature coupled with differences between the AVHRR/2 and AVHRR/3 VNIR spectral response function (SRF) has resulted in bias discontinuities in the complete NDVIpd that are NDVI dependent (Figure 1). Thus, an inter-calibration step is necessary to achieve a non-stationary consistent NDVI data set:

(5)

A Bayesian analysis was applied to update and minimize discrepancies that still remained from steps 1–4 between the AVHRR/2 and AVHRR/3 components of the NDVIpd.

2.3. Bayesian Inter-Calibration Analysis

The NDVIpd dynamic range depends on surface conditions and, as Figure 1 shows, on AVHRR instrument type. The NDVIpd tends to have values between −0.1 and 0.6, a shorter range than the NDVI from more recent and advanced sensors that tend to vary from −0.1 to 0.9 [54]. A continuous probability density function of global NDVI, e.g., a function p that has only non-negative values and integrates to 1, would describe the relative frequencies of the values from each sensor. As in many real-world situations, there is not a closed form expression p(NDVI) for this probability distribution function and we need to perform an extensive exploration of the data and model space. Instead, we have well-designed pseudo-random explorations that allow us to approximate this probability distribution function accurately on a dense grid of points spanning the range of global NDVI values. These random methods were called Monte Carlo techniques [75]. Monte Carlo methods provide us with a powerful tool for simulating NDVI distributions and creating a model of these data [67,75]. A large number of narrow NDVI intervals, e.g., Δ(NDVI) = 0.005, were used to approximate the area under the probability distribution function in each interval for the NDVIpd and the SeaWiFS NDVI data (NDVISW) (Figure 2). In Figure 2a, differences in the NDVI dynamic range from both the AVHRR/2 and AVHRR/3 instruments are apparent. The dual/single gain and SRF differences between the AVHRR/2 and AVHRR/3 instrument show the unintended consequence of expanding the NDVI dynamic range of the AVHRR/3 toward much more negative values. Using a Bayesian method, we aim to compensate for this unintended bias and produce a consistent AVHRR NDVI over the entire AVHRR/2 and AVHRR/3 combined records.

2.4. Prior and Posterior Distributions

To convey the idea of shifting or adjusting probability distribution functions to the AVHRR single/dual gain problem, we express Bayes’ rule slightly differently from its most common form as in Equation (1):

p ( pd | SW ) = p ( SW | pd ) × p ( pd ) ∑ pd p ( SW | pd ) = p ( SW | pd ) × p ( pd ) ( SW )

We use only NDVI subscripts to represent sensors, i.e., SW and pd for NDVISW and NDVIpd respectively. Equation (1) provides the means to correct the AVHRR data from bias using NDVISW as evidence. For example, the AVHRR/3 dual gain shifts NDVI values to more negative values than the regular AVHRR/2 single gain situation (Figure 2). This is unintended bias. NDVISW confirms that the shift in (A) does not represent changes on the ground. Furthermore, NDVISW provides the probability distribution function to transform the biased NDVIpd into a consistent and unbiased AVHRR NDVI (NDVI3g) over the 1981 to 2012 time period among the various AVHRR instruments. The Bayes’ rule (Equation (1)) is the means to shift from an NDVIpd biased prior probability distribution function to an unbiased posterior probability distribution function, p(NDVI3g). Figure 3 summarizes the Bayes’ rule process when it is applied four times, one for each overlapping period between corresponding NDVISW and NDVIpd values during 1998–1999 (NOAA-14, N14), 2002–2003 (NOAA-16, N16), 2004–2005 (NOAA-17, N17), and 2007–2008 (NOAA-18, N18) to derive corresponding recalibration parameters.

While the recalibration parameters found for NOAA-14 are applied to the consistent AVHRR/2 calibrated component of the NDVIpd data (NOAA-7 through NOAA-14, 1981 to 2000 (Table 1)), NOAA-16 through NOAA-18 have their own recalibration AVHRR/3 parameters. The recalibration parameters of NOAA-18 are applied to all new NDVI data that are derived from its AVHRR/3 instrument. NDVI data derived from AVHRR/3 instruments on board satellites that overlap the orbiting NOAA-18 period can apply a similar process using the corresponding recalibrated NDVI3g data as reference to recalibrate the new sensor and integrate the resulting NDVI into the multi-instrument AVHRR NDVI continuum. Again, a Monte Carlo method, applied on a dense grid for approximation, provides an estimation of priors, likelihoods, and posteriors with high accuracy.

It is intrinsic to any inferential statistical method to explore and describe data from observations [67]. This is also referred to as moving from passive to active learning. A passive perspective assumes that a learner is a passive observer with no indication of which of the observations are more or less certain than the others. On the other hand, a learner, in most of the real learning situations, has the opportunity to explore, compare and extract information that, if done properly, will be useful to improve data under consideration. In our AVHRR problem, Bayes rule not only allows us to correct the NDVIpd dual gain quantizing bias, but it also enables the AVHRR NDVI values to be transformed to the dynamic range of NDVISW values.

2.5. Correcting Bias

Figure 3 shows the dual-gain quantizing and SRF bias of the AVHRR/3 NDVI, not only on the low end of the NDVI dynamical range, but also elsewhere in the NDVI probability distribution function. The central tendency of these likelihoods prompts the definition of their corresponding biases as the values BSW-pd that minimizes the expected distance between it and all other normalized Xbias = NDVIpd/σpd − NDVIsw/σSW values. We use the common squared difference (X − B)2 to represent distance between X and B. This tractable algebraic feature enables a closed form for the bias adjustment as in Equation (2):

min ( ∑ X bias ( X bias − B SW − pd ) 2 ) ∑ X bias ( X bias − B SW − pd ) = 0 B SW − pd = ∑ X bias X bias N = ∑ X bias NDVI pd N σ pd − ∑ X bias NDVI SW N σ SW B SW − pd = E [ NDVI pd ] σ pd − E [ NDVI SW ] σ SW

The value BSW-pd that minimizes the squared distance is the difference between the expected values of the normalized E[NDVIpd]/σpd and E[NDVIsw]/σSW (If the distance between X and B is defined as |X − B|, then the value that minimizes the expected distance is the median. Similarly, the mode is the value if a distance is defined as zero for any exact match and one for mismatches [67]). A bias correction is obtained by a rearrangement of terms. We want an NDVI3g that eliminates the bias term from the NDVIpd and that matches NDVIsw dynamical range provided by σSW, as in Equation (3):

NDVI 3 g σ SW = NDVI pd σ pd − B SW − pd NDVI 3 g = σ SW ( NDVI pd − E [ NDVI pd ] ) σ pd + E [ NDVI SW ]

This posterior mean provides some information on where the bias is centered and information about the scatter around the posterior mean is given by the posterior standard deviation. However, the posterior density, p(NDVI3g), contains more information than just the posterior mean and standard deviations that help avoid common interpretation pitfalls, for example if the posterior is multimodal, i.e., there is more than one local maximum, the posterior mean may lie in a region where parameters are altogether unlikely [67].

Our purpose in creating a consistent non-stationary NDVI3g time series is to enable trend analysis for climate or other long-term studies with a consistent NDVI data set from multiple instruments with the same spectral band passes and the same spatial sampling of the surface. While NDVIpd fares badly in Figure 1, the NDVI3g appears to pass a first qualitative test, that the AVHRR/2 to AVHRR/3 NDVI bias has been attenuated and the resulting combined AVHRR NDVI dynamic ranges match those in NDVISW (Figure 4).

2.6. High Density Interval (HDI)

We now focus on the uncertainty associated with our Bayesian NDVI adjustment process. The standard deviation σx, since it measures how far the distribution of X is dispersed, is a measure of uncertainty and can be expressed by confidence intervals. If it is small, then we have more confidence in values near the mean. If it is large, we are less certain about the reliability of X. In Bayesian analysis, values that are close to the mean are more strongly preferred. Thus, they provide the highest density interval, an alternative to summarize uncertainty, variability, and confidence in the resulting probability distribution [67].

The highest density interval summarizes the distribution by specifying an interval that spans most of the distribution, usually 95% of it, such that every point inside the interval has higher believability or confidence than any point outside the interval [67]. Figure 5 illustrates the highest density interval concept using NDVI3g data. We plot three individual probability density functions, p(δxy | NDVI), on top of the parent NDVI probability density function. The average length of the highest density interval is 0.0036 resulting an uncertainty of about ±0.002 NDVI units. The way of displaying all individual p(δxy | NDVI) on top of the parent NDVI probability density function is equivalent to the way chosen to display likelihoods in the middle panel of the Bayes’ rule diagram in Figure 3.

3. Results and Discussion

The quality of the NDVI3g in terms of highest density intervals for different NDVI components, e.g., the spatial and temporal intrinsic coherence, the climate-related seasonal and inter-annual variability, provides intrinsic dynamic characteristics of this non-stationary NDVI data set. To assess this, we evaluate the stability of the Bayesian transformation (Btr) at reducing the dual-gain quantification and SRF bias. For each NDVI value within the effective NDVI3g dynamic range, the resulting distributions were grid-approximated using Monte Carlo techniques—one of the advantages of grid-based estimation. We do not need to rely on formal analysis to derive a specification of any distribution because we have spatially continuous bimonthly data for three decades. Another advantage of grid-based estimation of a distribution is that its highest density intervals can also be approximated. As in many practical situations, specifying a variable’s distribution and finding its corresponding highest density intervals by formal analysis can be challenging, but estimating them through Monte Carlo methods in a fine grid approximation is straightforward.

We computed these NDVI components for our evaluation at 0.005 NDVI intervals:

a)

Spatial coherence (δxy): for each pixel, δxy is the average of the differences between that element’s NDVI and the one from the surrounding eight pixels inside of a three by three pixel array;

b)

Temporal coherence (δt): for each pixel, δt is the average of the absolute NDVI values between consecutive composites for the same time interval within the entire 30+ years NDVI time series.

c)

Climate seasonal variability (Svc): for each pixel, is represented the average NDVI value for each bimonthly composite over the entire 30+ years NDVI time series.

d)

Climate inter-annual variability (IAvc): for each pixel, IAvc is the NDVI time series minus its Svc component and averaged for each year.

Similarly, the stability of the Bayesian transformation is given by highest density intervals of the distribution of the transformed values for each NDVI within the effective NDVI3g dynamical range.

3.1. Distributions Specified at a Fine Grid

Figure 6 shows the estimated distributions at each NDVI value within the effective NDVI3g dynamical range represented graphically by the vertical segments for deviations from the mean of (A) the combined spatial and temporal coherent components (δxy + δt); (B) the Bayesian transformation (Btr); (C) the climate-related seasonal (Svc); and (D) inter-annual (IAvc) variability components. The distribution for (δxy + δt) at any NDVI value concentrates values around zero implying high spatial and temporal homogeneity within small neighborhoods, which is compatible with the high spatial and temporal coherence found on NDVI images [76]. Small uncertainties are expected, are infrequent and unavoidable, and result from unusual episodes of biomass burning, volcanic eruptions, hurricanes, deforestation, droughts, etc.

Our Bayesian transformation concentrates its mass around zero for low and high NDVI values. In the interval from 0.1 to 0.6, the distribution is more dispersed as expected from the likelihood p(SW|pd) (central panel in Figure 3) which shows higher discrepancies between the sensors. At the low and high ends, an apparent functionality can be derived. The SeaWiFS instrument has much better spectral resolution with narrower bands in the visible and near infrared spectrum, has much better radiometric calibration and characterization, resulting in better NDVI discriminating features than the same for the AVHRR instruments [54]. This is the reason we use coincident SeaWiFS NDVI data to adjust the AVHRR NDVI through our Bayesian analysis.

The climate-related seasonal Svc component dominates our NDVI variability reflecting variable vegetation phenology in NDVI within the interval 0.3 to 0.7 for those areas that experience seasonality from wet to dry seasons and/or from warm to cold temperatures. Note that the inter-annual variation increases proportionally to NDVI values, as the vertical distribution is more dispersed at larger NDVI values. This feature has been key for identifying droughts and their real magnitude in many regions and would be near zero for a stationary NDVI data set [77]. In contrast, the non-surface uncertainty remaining in other AVHRR NDVI data has been questioned in previous papers [78,79]. Papers in this issue and elsewhere compare our data set to geophysical variables to independently establish the utility of our data set for monitoring non-stationary or climate phenomena at northern high latitude regions [80–84]. However, the preparation of the NDVI3g data for northern high latitude monitoring offers new challenges that we will revise in a future release of the data. Bhatt et al. [84] conclude that the NDVI3g data should be viewed as the best possible version at this time that will be improved in the future, as more high quality data are accumulated to guide improvements. We conform to Bayes rule, where new data present new opportunities for new information, depending upon their Bayesian comparison.

3.2. High Density Intervals

The distributions in Figure 6 have an equivalent high-density interval representation as we show in Figure 5. A visualization of the high-density interval allows us to explicitly define uncertainty. Figure 7 shows the correspondent high-density interval probability distributions for (A) IUδxy or spatial coherence and IUδt or temporal coherence plotted together; (B) Btr or the Bayesian transformation probability distribution; (C) Svc or the seasonal variability; and (D) IAvc or the inter-annual variability.

The high-density interval regions, shown in Figure 7, help to define uncertainties in the NDVI3g time series. Small contributions to the overall NDVI3g uncertainty come from spatial and temporal coherence variability: combined they are ±0.002 NDVI units and this low uncertainly enables application of our data to study seasonal and inter-annual non-stationary phenomena. Seasonal variability comprises most of the non-stationary uncertainty, as it should, and is greater than the inter-annual variability that it is also expected.

3.3. Data Stewardship

As digital technologies expand the power and reach of research, they also raise complex issues affecting research data with respect to ensuring its integrity, accessibility, and stewardship [85,86]. At the same time these advances in knowledge depend on the open flow of information from other researchers to check the quality of the data, verify analyses and conclusions. With this spirit in mind, we needed a platform that provides the information technology and management for meaningful access and reuse of our research data. Our prime goal is to support users’ science-driven demands while taking advantage of existing data system components. We found such a platform—the NASA Earth Exchange (NEX), a platform for scientific collaboration, knowledge sharing and research for the Earth science community, has welcomed our research data at: https://nex.nasa.gov/nex/projects/1349/wiki/general_data_description_and_access/.

The data described here are available in the NEX data-pool for NEX users who obtained their credentials for supercomputing access. It also provides direct access to non-NEX users at: http://ecocast.arc.nasa.gov/data/pub/gimms/3g/.

Future updates are expected expanding the time series at least 36 years and potentially 40+ years by integrating EUMESAT MetOp data—work towards this goal has been initiated.

4. Conclusions

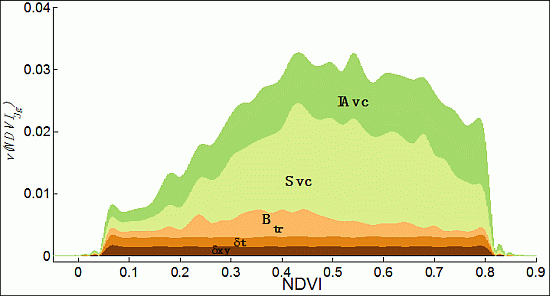
We describe our July 1981 to December 2012 AVHRR NDVI3g global data set and the various steps included in producing it. Figure 8 provides a graphical summary of our non-stationary NDVI3g data set: there is minor error with respect to spatial and temporal coherence, on the order of ±0.001 for both; the error or uncertainty resulting from our Bayesian transmission ɛ(tr) varies from ±0.001 to ±0.004 depending upon NDVI3g value; the seasonal NDVI3g variation is 0.01 to 0.015 for NDVI3g values between 0.25 and 0.75, reflecting that our data set captures seasonal variation where phenology is variable; and the among year variation is on the order of ±0.008, all units in NDVI3g units. Thus, our NDVI3g data set has a conservative measurement uncertainty on the order of ±0.005. This low measurement uncertainty suggests detection of non-stationary seasonal and inter-annual climate forcing using the NDVI3g data are possible. Specific comparisons between NDVI3g and independently measured appropriate climate phenomena are needed to improve our understanding of uncertainty and to substantiate these findings. In addition, we hope to continue adding to our AVHRR NDVI3g continuum while AVHRR/3 instruments continue operation on the MetOp satellites.

This work was partially supported by NASA Applied Science grant NNH08CD31C from 2009 to 2012. We thank the financial support by George Collatz, Torry Johnson, and Molly Brown during the last year. We thank Edwin Pak for processing the AVHRR/3 input data to NDVI3g. Creating a consistent NDVI3g time series has been 8 years in the making and many insightful works using the data set on their analysis have contributed to its improvement. We thank supportive feedback from George Collatz, Ranga Myneni, Uma Bhatt, Martha Raynolds, Howard Epstein and Skip Walker and thank them for their comments on various parts of this article. We also thank the anonymous reviewers for their valuable remarks and suggestions. Lastly, two more important acknowledgments: first, since digital data are ephemeral and access to data involves infrastructure and economic support, we are in debt with Ramakrishna Nemani and his group at NASA Earth Exchange (NEX) for providing the infrastructure that supports data stewardship and makes it viable. Second, we have been fortunate to interact with the group at the SeaWiFS project. They not only provided us with high quality SeaWiFS data, but also shared valuable information related to calibration, data processing, and handling that is generally not included in scientific journal articles.

Author Contributions

Jorge Pinzon and Compton J. Tucker conceptualized the study, Jorge Pinzon analyzed the data, and both authors contributed to the writing of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cracknell, A.P. The exciting and totally unanticipated success of the AVHRR in applications for which it was never intended. Adv. Space Res 2001, 28, 233–240. [Google Scholar]
  2. Townshend, J.R.G. Global data sets for land applications from the advanced very high resolution radiometer: An introduction. Int. J. Remote Sens 1994, 15, 3319–3332. [Google Scholar]
  3. Tucker, C.J.; Townshend, J.R.G.; Goff, T.E. African land cover classification using satellite data. Science 1985, 227, 369–375. [Google Scholar]
  4. Defries, R.S.; Belward, A.S. Global and regional land cover characterization from satellite data. Int. J. Remote Sens 2000, 21, 1083–1092. [Google Scholar]
  5. Tucker, C.J.; Nicholson, S.E. Variations in the size of the Sahara Desert from 1980 to 1997. Ambio 1999, 28, 587–591. [Google Scholar]
  6. Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A; Randall, D.A. A global 1° by 1° NDVI data set for climate studies. Part 2: The generation of global fields of terrestrial biophysical parameters from the NDVI. Int. J. Remote Sens 1994, 15, 3519–3545. [Google Scholar]
  7. Nemani, K.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982–1999. Science 2003, 300, 1560–1562. [Google Scholar]
  8. Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar]
  9. Cracknell, A.P. The Advanced Very High Resolution Radiometer; Taylor and Francis: London, UK, 1997; p. 534. [Google Scholar]
  10. Kidwell, K.B. NOAA Polar orbiter data user’s guide 1998. Available online: http://www.ncdc.noaa.gov/oa/pod-guide/ncdc/docs/podug/cover.htm (accessed on 23 September 2013).
  11. Wu, X. NOAA AVHRR spectral response functions 2009. Available online: http://www.star.nesdis.noaa.gov/smcd/spb/fwu/homepage/AVHRR/spec_resp_func/index.html (accessed on 23 September 2013).
  12. Robel, J.; Kidwell, K.B. NOAA KLM User’s Guide Section 7.1 Calibration Information for AVHRR/3 2009. Available online: http://www.ncdc.noaa.gov/oa/pod-guide/ncdc/docs/klm/html/c7/sec7-1.htm (accessed on 23 September 2013).
  13. Hooker, S.B.; Esaias, W.E.; Feldman, G.C.; Gregg, W.W.; McClain, C.R. An Overview of SeaWiFS and Ocean Color; NASA Tech. Memo 104566:. : Greenbelt, MD, USA, 1986; p. 24. [Google Scholar]
  14. Saint, G. SPOT-4 vegetation system—Association with high-resolution data for multiscale studies. Adv. Space Res 1995, 17, 107–110. [Google Scholar]
  15. Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ 2002, 83, 3–15. [Google Scholar]
  16. Gleason, J; Suomi, NPP. (National Polar-orbiting Partnership) Visible Infrared Imaging radiometer Suite (VIIRS) 2013. Available online: http://npp.gsfc.nasa.gov/viirs.html (accessed on 23 September 2013).
  17. Tucker, C.J.; Miller, L.D.; Pearson, R.L. Shortgrass praire spectral measurements. Photogramm. Eng. Remote Sens 1975, 41, 1157–1162. [Google Scholar]
  18. Tucker, C.J.; Maxwell, E.L. Sensor design for monitoring vegetation canopies. Photogramm. Eng. Remote Sens 1976, 42, 1399–1410. [Google Scholar]
  19. Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
  20. Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens 1995, 33, 481–486. [Google Scholar]
  21. Rao, C.R.N.; Chen, J. Inter-satellite calibration linkages for the visible and near-infrared channels of the Advanced Very High Resolution Radiometer on the NOAA-7, -9, and -11 spacecraft. Int. J. Remote Sens 1995, 16, 1931–1942. [Google Scholar]
  22. Rao, C.R.N.; Chen, J. Post-launch calibration of the visible and near-infrared channels of the Advanced Very High Resolution Radiometer (AVHRR) on the NOAA-14 spacecraft. Int. J. Remote Sens 1996, 17, 2743–2747. [Google Scholar]
  23. Los, S.O. Estimation of the ratio of sensor degradation between NOAA AVHRR channels 1 and 2 from monthly NDVI composites. IEEE Trans. Geosci. Remote Sens 1998, 36, 206–213. [Google Scholar]
  24. Vermote, E.F.; Saleus, N.Z. Calibration of NOAA16 AVHRR over a desert site using MODIS data. Remote Sens. Environ 2006, 105, 214–220. [Google Scholar]
  25. Kaufman, Y.J.; Holben, B.N. Calibration of the AVHRR visible and near-IR bands by atmospheric scattering, ocean glint and desert reflection. Int. J. Remote Sens 1993, 14, 21–52. [Google Scholar]
  26. Teillet, P.M.; Holben, B.N. Towards operational radiometric calibration of NOAA AVHRR imagery in the visible and near-infrared channels. Can. J. Remote Sens 1994, 20, 1–10. [Google Scholar]
  27. Vermote, E.F.; Kaufman, Y.J. Absolute calibration of AVHRR visible and near-infrared channels using ocean and cloud views. Int. J. Remote Sens 1995, 16, 2317–2340. [Google Scholar]
  28. Loeb, N.G. In-flight calibration of NOAA AVHRR visible and near-IR bands over Greenland and Antarctica. Int. J. Remote Sens 1997, 18, 447–490. [Google Scholar]
  29. James, M.E.; Kalluri, S.N. The Pathfinder AVHRR land data set: An improved coarse-resolution data set for terrestrial monitoring. Int. J. Remote Sens 1994, 15, 3347–3363. [Google Scholar]
  30. Eidenshink, J.C.; Faundeen, J.L. The 1-km AVHRR global land data set: First stages in implementation. Int. J. Remote Sens 1994, 15, 3443–3462. [Google Scholar]
  31. Los, S.O.; Justice, C.O.; Tucker, C.J. A global 1° × 1° NDVI data set for climate studies derived from the GIMMS continental NDVI data set. Int. J. Remote Sens 1994, 15, 3493–3518. [Google Scholar]
  32. Tucker, C.J.; Newcomb, W.W.; Dregne, H.E. AVHRR datasets for the determination of desert spatial extent. Int. J. Remote Sens 1994, 15, 3547–3566. [Google Scholar]
  33. Saleous, N.Z.; Vermote, E.F.; Justice, C.O.; Townshend, J.R.G.; Tucker, C.J.; Goward, S.N. Improvements in the global biospheric record from the advanced very high resolution radiometer. Int. J. Remote Sens 2000, 21, 1251–1277. [Google Scholar]
  34. Latifovic, R.; Thrischenko, A.P.; Chen, J.; Park, W.B.; Khlopenkov, K.; Fernandes, R.; Pouliot, D.; Ungureanu, C.; Luo, Y.; Wang, S.; et al. Generating historical AVHRR 1 km baseline satellite data records over Canada suitable for climate change studies. Can. J. Remote Sens 2005, 31, 324–346. [Google Scholar]
  35. Slayback, D.A.; Pinzon, J.E.; Los, S.O.; Tucker, C. Northern hemisphere photosynthetic trends 1982–99. Glob. Chang. Biol 2003, 9, 1–15. [Google Scholar]
  36. Fensholt, R.; Nielsen, T.T.; Stisen, S. Evaluation of AVHRR PAL and GIMMS 10-day composite NDVI time series products using SPOT-4 vegetation data for the African continent. Int. J. Remote Sens 2006, 27, 2719–2733. [Google Scholar]
  37. Hall, F.; Masek, J.G.; Collatz, G.J. Evaluation of ISLSCP initiative II FASIR and GIMMS NDVI products and implications for carbon cycle science. J. Geophys. Res 2006, 111, D22S08. [Google Scholar]
  38. Beck, H.E.; McVicar, T.R.; Dijk, A.I.J.M.; Schellekens, J.; Jeu, R.A.M.; Bruijnzeel, L.A. Global evaluation of four AVHRR-NDVI data sets: Inter-comparison against Landsat imagery. Remote Sens. Environ 2011, 115, 2547–2563. [Google Scholar]
  39. Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of inter-calibration of satellite instruments. IEEE Trans. Geosci. Remote Sens 2013, 51, 1056–1080. [Google Scholar]
  40. Justice, C.O.; Townshend, J.G.R. Date sets for global remote sensing: Lessons learnt. Int. J. Remote Sens 1994, 15, 3621–3639. [Google Scholar]
  41. Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; kaufman, Y.J.; Nakajima, T.; et al. AERONET-A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ 1998, 66, 1–16. [Google Scholar]
  42. Martonchik, V.; Diner, D.J.; Kahn, R.; Gaitley, B. Comparison of MISR and AERONET aerosol optical depths over desert sites. Geophys. Res. Lett 2004, 31, 1–4. [Google Scholar]
  43. Kaufman, Y.J.; Tanré, D.; Remer, L.A.; Vermote, E.F.; Chu, A.; Holben, B.N. The operational remote sensing of tropospheric aerosol over land from EOS moderate resolution imaging spectroradiometer. J. Geophys. Res 1997, 102, 17051–17067. [Google Scholar]
  44. Kaufman, Y.J.; Tanré, D.; Gordon, H.R.; Nakajima, T.; Lenoble, J.; Frouin, R.; Grassl, H.; Herman, B.M.; King, M.D.; Teillet, P.M. Passive remote sensing of tropospheric aerosol and atmospheric correction for the aerosol effect. J. Geophys. Res 1997, 102, 16815–16830. [Google Scholar]
  45. Kaufman, Y.J.; Tanré, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar]
  46. Rao, C.R.N.; Stowe, L.L.; McClain, P. Remote sensing of aerosols over oceans using AVHRR data: Theory, practice and applications. Int. J. Remote Sens 1989, 10, 743–749. [Google Scholar]
  47. Stowe, L.L.; Ignatov, A.M.; Singh, R.R. Development, validation and potential enhancements to the second-generation operational aerosol product at NOAA/DESDIS. J. Geophys. Res 1997, 102, 16923–16934. [Google Scholar]
  48. Stowe, L.L.; Jacobowitz, H.; Ohring, G.; Knapp, K.R.; Nalli, N.R. The Advanced Very High Resolution Radiometer (AVHRR) Pathfinder atmosphere (PATMOS) climate dataset: Initial analyses and evaluations. J. Clim 2002, 15, 1243–1260. [Google Scholar]
  49. Ignatov, A.M.; Sapper, J.; Cox, S.; Laszlo, I.; Nalli, N.R.; Kidwell, K.B. Operational aerosol observations (AEROBS) from AVHRR/3 on board NOAA-KLM satellites. J. Atmos. Ocean. Technol 2004, 21, 3–26. [Google Scholar]
  50. Mishchenko, M.I.; Geogdzhayev, I.V.; Cairns, B.; Carlson, B.E.; Chowdharry, J.; Lacis, A.A.; Liu, L.; Rossow, W.B.; Travis, L.D. Past, present, and future of global aerosol climatologies derived from satellite observations: A perspective. J. Quant. Spectrosc. Radiat. Transf 2007, 106, 325–347. [Google Scholar]
  51. Trishchenko, A.P. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors: Extension to AVHRR NOAA-17, 18 and METOP-A. Remote Sens. Environ 2009, 113, 335–341. [Google Scholar]
  52. Doelling, D.R.; Garber, D.P.; Avey, L.A.; Nguyen, L.; Minnis, P. The calibration of AVHRR visible dual gain using Meteosat-8 for NOAA-16 to 18. Proc. SPIE 2007, 6684. [Google Scholar] [CrossRef]
  53. Jiang, L.; Tarpley, J.D.; Mitchell, K.E.; Zhou, S.; Kogan, F.N.; Guo, W. Adjusting for long-term anomalous trends in NOAA’s Global Vegetation Index data sets. IEEE Trans. Geosci. Remote Sens 2008, 46, 409–422. [Google Scholar]
  54. Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N. An extended AVHRR-8km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
  55. Cao, C.; Weinreb, M.; Sullivan, J. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the inter-satellite calibration of radiometers. J. Atmos. Ocean. Technol 2004, 21, 537–542. [Google Scholar]
  56. Cao, C.; Xiong, X.; Wu, A.; Wu, X. Assessing the consistency of AVHRR and MODIS L1B reflectance for generating fundamental climate data records. J. Geophys. Res 2008, 113. [Google Scholar] [CrossRef]
  57. Heidinger, A.K.; Straka, W.C.; Molling, C.C.; Sullivan, J.T. Deriving an inter-sensor consistent calibration for the AVHRR solar reflectance data record. Int. J. Remote Sens 2010, 31, 6493–6517. [Google Scholar]
  58. Masuoka, E. Land long term data record—V3 LTDR continuation from MODIS records 2012. Available online: http://ltdr.nascom.nasa.gov/cgi-bin/ltdr/ltdrPage.cgi?fileName=MODIS2LTDR (accessed on 23 September 2013).
  59. Latifovic, R.; Pouliot, D.; Dillabaugh, C. Identification and correction of systematic error in NOAA AVHRR long-term data record. Remote Sens. Environ 2012, 127, 84–97. [Google Scholar]
  60. Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005; p. 342. [Google Scholar]
  61. Angert, A.; Biraud, S.; Bonfils, C.; Henning, C.C.; Buermann, W.; Pinzon, J.E.; Tucker, C.J.; Fung, I. Drier summers cancel out CO2 uptake enhancement induced by warmer springs. Proc. Natl. Acad. Sci. USA 2005, 102, 10823–10827. [Google Scholar]
  62. Lotsch, A.; Friedl, M.A.; Anderson, B.T.; Tucker, C.J. Coupled vegetation–precipitation variability observed from satellite and climate records. Geophys. Res. Lett 2003, 30, 125–132. [Google Scholar]
  63. Buermann, W.; Lintner, B.R.; Koven, C.D.; Angert, A.; Pinzon, J.E.; Tucker, C.J.; Fung, I. The changing carbon cycle at Mauna Loa Observatory. Proc. Natl. Acad. Sci. USA 2007, 104, 4249–4254. [Google Scholar]
  64. Poveda, G.; Salazar, L.F. Annual and interannual (ENSO) variability of spatial scaling properties of a vegetation index (NDVI) in Amazonia. Remote Sens. Environ 2005, 93, 391–401. [Google Scholar]
  65. Jia, G.J.; Epstein, H.E.; Walker, D.A. Greening of arctic Alaska. Geophys. Res. Lett 2003, 30, 1029–1033. [Google Scholar]
  66. Walker, D.A. Second Yamal Land-Cover Land-Use Change Workshop 2010. Arctic Centre, Rovaniemi, Finland. March 2010. Available online: http://www.geobotany.uaf.edu/yamal/rovMtg/ (accessed on 23 September 2013). [Google Scholar]
  67. Kruschke, J.K. Doing Bayesian Data Analysis; Academic Press: Oxford, UK, 2011; p. 653. [Google Scholar]
  68. Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM Computational Science & Engineering Series: Philadelphia, PA, USA, 2014; p. 382. [Google Scholar]
  69. Baldwin, D.; Emery, W.J. Spacecraft attitude variations of NOAA-11 inferred from AVHRR imagery. Int. J. Remote Sens 1995, 16, 531–548. [Google Scholar]
  70. Wu, X.; Sullivan, J.T.; Heidinger, A.K. Operational calibration of the Advanced High Resolution Resolution radiometer (AVHRR) visible and near-infrared channels. Can. J. Remote Sens 2010, 36, 602–616. [Google Scholar]
  71. Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens 1986, 7, 1417–1434. [Google Scholar]
  72. Vermote, E.F.; Saleus, N.E.; Kaufman, Y.J.; Dutton, E. Data preprocessing stratospheric aerosol perturbing effect on the remote sensing of vegetation: Correction method for the composite NDVI after the Pinatubo eruption. Remote Sens. Rev 1997, 15, 7–21. [Google Scholar]
  73. Pinzon, J.E.; Brown, M.E.; Tucker, C.J. Empirical mode decomposition correction of orbital drift artifacts in satellite data stream. In Hilbert-Huang Transform and Applications; Huang, N.E., Shen, S.S.P., Eds.; World Scientific: Hackensack, NJ, USA.
  74. Vermote, E.; Justice, C.O.; Breon, F.M. Generalized approach for correction of BRDF effect in MODIS directional reflectances. IEEE Trans. Geosci. Remote Sens 2009, 47, 898–908. [Google Scholar]
  75. Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc 1949, 44, 335–341. [Google Scholar]
  76. Pinzon, J.E.; Pierce, J.F.; Tucker, C.J.; Brown, M.E. Evaluating coherence of natural images by smoothness membership in Besov spaces. IEEE Trans. Geosci. Remote Sens 2001, 39, 1879–1889. [Google Scholar]
  77. Anyamba, A.; Tucker, C.J. Analysis of Sahelian vegetation dynamics using NOAA-AVHRR NDVI data from 1981–2003. J. Arid Environ 2005, 63, 596–614. [Google Scholar]
  78. Cihlar, J.; Chen, J.M.; Li, Z.; Huang, F.; Latifovic, R.; Dixon, R. Can interannual land surface signal be discerned in composite AVHRR data? J. Geophys. Res 1998, 103, 23163–23172. [Google Scholar]
  79. Gutman, G.G. On the use of long-term global data of land reflectances and vegetation indices derived from the advanced very high resolution radiometer. J. Geophys. Res 1999, 104, 6241–6255. [Google Scholar]
  80. Bhatt, U.S.; Walker, D.A.; Raynolds, M.K.; Comiso, J.C.; Epstein, H.E.; Jia, G.; Gens, R.; Pinzon, J.E.; Tucker, C.J.; Tweedie, C.E.; et al. Circumpolar Arctic tundra vegetation change is linked to sea ice decline. Earth Interact 2010, 14, 1–20. [Google Scholar]
  81. Epstein, H.E.; Raynolds, M.K.; Walker, D.A.; Bhatt, U.S.; Tucker, C.J.; Pinzon, J.E. Dynamics of aboveground phytomass of the circumpolar Arctic tundra during the past three decades. Environ. Res. Lett 2012, 7. [Google Scholar] [CrossRef]
  82. Walker, D.A.; Bhatt, U.S.; Epstein, H.E.; Bieniek, P.; Comiso, J.; Frost, G.V.; Pinzon, J.; Raynolds, M.K.; Tucker, C.J. Changing Arctic tundra vegetation biomass and Greenness. Bull. Am. Meteorol. Soc 2012, 93, S138–S139. [Google Scholar]
  83. Xu, L.; Myneni, R.B.; Chapin, F.S., III; Callaghan, T.V.; Pinzon, J.E.; Tucker, C.J.; Zhu, Z.; Bi, J.; Ciais, P.; Tommervik, H.; et al. Temperature and vegetation seasonality diminishment over northern lands. Nat. Clim. Chang 2013, 3, 1–6. [Google Scholar]
  84. Bhatt, U.S.; Walker, D.A.; Raynolds, M.K.; Bieniek, P.A.; Epstein, H.E.; Comiso, J.C.; Pinzon, J.E.; Tucker, C.J.; Polyakov, I.V. Recent declines in warming and vegetation greening trends over Pan-Arctic tundra. Remote Sens 2013, 5, 4229–4254. [Google Scholar]
  85. Kleppner, D.; Sharp, P.A. Ensuring the Integrity, Accessibility, and Stewardship of Research Data in the Digital Age; National Academies Press: Washington, DC, USA, 2009; p. 162. [Google Scholar]
  86. Berman, F.; Cerf, V. Who will pay for public access to research data? Policy Forum. Science 2013, 341, 616–617. [Google Scholar]
  87. Wilkinson, J.H. Rounding Errors in Algebraic Processes.
  88. Higham, N.J. Accuracy and Stability of Numerical Algorithms; SIAM: Philadelphia, PA, USA.

Appendix A. AVHRR Single/Double Gain and Spectral Response Function

It has been more than 50 years since the publication of the first thorough analysis of the effects of rounding errors in numerical algorithms, Wilkinson’s book “Rounding errors in algebraic processes” [87], and almost 20 years of the first edition of Higham’s book “Accuracy and stability of numerical algorithms” that provided an up-to-date treatment in finite precision arithmetic [88]. Both books remind us that uncertainty in data may arise in several ways, from accuracy errors of measuring physical quantities, or from errors in storing the data (rounding errors), or from precision errors processing the data even if the data are themselves a solution to another problem. The terms accuracy and precision should not be confused or use interchangeably. While accuracy refers to the absolute or relative error of an approximate quantity, precision is the accuracy with which the basic arithmetic operations (+, −, *, /) are performed. For many cases, these errors depend on design parameters whose values are a compromise between obtaining small error and a fast computation or small error and limited storing capacity [88]. The design changes in the AVHRR VNIR channels from single to double gains coupled with differences between the AVHRR/2 and AVHRR/3 VNIR spectral response function (SRF) [11,51], are examples of these compromises. The value for the radiance measured for each of the AVHRR bands is calculated directly from the radiometric calibration equations that the manufacturer characterized before launch from laboratory measurements. These equations are identical in form for each of the AVHRR/2 and AVHRR/3 bands.

Figure A1 shows the differences in spectral response functions between the AVHRR/2 and AVHRR/3 instruments that are reported by Wu [11] and Thrishchenko [51]. On orbit, however, there will be no mechanism for monitoring changes of individual components within the radiometers. Among other things, there will be no means of determining spectral shifts in the instruments after launch or changes in their sensitivity or absolute accuracy of the measured radiances. But, on orbit, it is possible to monitor relative changes in the output of the radiometer’s bands through the calibration equation parameters. Measurements on orbit give only the changes in the instrument’s sensitivity relative to that at launch. For practical considerations, we will assess the contribution to the NDVI discontinuities from the parameter values (single/double gains and offsets) determined by the manufacturer. Again, these values are determined solely through measurements by the manufacturer and cannot be checked after launch.

A.1. AVHRR Single and Double Gains

It is tempting to assume that calculations were free from errors and therefore, they must be accurate and stable, especially since they involve only a small number of simple operations, e.g., doubling sensitivity of the VNIR channels in the low albedo range (0%–25%) and reducing it 2/3 for high albedo (greater than 25%) in an instrument that responds nearly linearly to spectral radiance. Ideally, the instrument requires four input signals for calibration, two on each of its linear segments as the bilinear gain is implemented in SeaWiFS [13], but since the instrument only has one sensor for each channel, the dual gain is generated in the electronic subsystem that is identical for both low and high gain modes [70]. For calibration, it is assumed that instrument degradation is identical for both low and high gain modes [70]. With this assumption, one can express a single-gain count Cs in terms of dual-gain counts (Cd) in the low and high counts regions:

C s = { D sg + 1 2 ( C d − D dg ) for ) C d ≤ T dg B sg + 3 2 ( C d − T dg ) for ) C d ≤ T dg
where the dual-gain switch and interception are Tdg ≈ 500, Bsg = Dsg + ½ (Tdg − Ddg) ≈ 250, and the single-, dual-count dark thresholds, Dsg and Ddg respectively, are approximately 40. In the ideal case, the dual-gain implementation does not introduce any more sensitivity to perturbation than is inherent in the underlying problem. In assessing the effectiveness of the dual-gain implementation, we model the output radiances derived from the single-gain pre-launch calibration coefficients of NOAA-14 AVHRR/2 for channel-1 and channel-2 and compared with radiances derived from the double-gain coefficients of NOAA-18 (Figure A2). The high gain line does not intercept with the single-gain line, thus noticeable discrepancies are expected in channel-2.

Remotesensing 06 06929fa1 1024
Figure A1. The spectral response functions (SRF) of the VNIR channels for the (A) NOAA-7/9/11/14 AVHRR/2 and (B) NOAA-16/17/18/19 AVHRR/3 instruments are consistent among themselves but are slightly different from each other. In particular, the integrated spectral response function for the visible channel in the AVHRR/2 is about 0.11 μm compared to the AVHRR/3 integrated spectral response function of 0.08 μm bandwidth. The integrated spectral response functions for channel 2 for AVHRR/2 and AVHRR/3 are very similar.

Click here to enlarge figure

Figure A1. The spectral response functions (SRF) of the VNIR channels for the (A) NOAA-7/9/11/14 AVHRR/2 and (B) NOAA-16/17/18/19 AVHRR/3 instruments are consistent among themselves but are slightly different from each other. In particular, the integrated spectral response function for the visible channel in the AVHRR/2 is about 0.11 μm compared to the AVHRR/3 integrated spectral response function of 0.08 μm bandwidth. The integrated spectral response functions for channel 2 for AVHRR/2 and AVHRR/3 are very similar.
Remotesensing 06 06929fa1 1024
Remotesensing 06 06929fa2 1024
Figure A2. This figure shows the AVHRR/2 radiances derived from a single-gain count using NOAA-14 pre-flight coefficients and AVHRR/3 radiances using both low and high gain counts NOAA-18 pre-flight coefficients for (A) channel-1 and (B) channel-2.

Click here to enlarge figure

Figure A2. This figure shows the AVHRR/2 radiances derived from a single-gain count using NOAA-14 pre-flight coefficients and AVHRR/3 radiances using both low and high gain counts NOAA-18 pre-flight coefficients for (A) channel-1 and (B) channel-2.
Remotesensing 06 06929fa2 1024

When the single-gain count substitutes the correspondent double gain count as in equation A1, we can compute the absolute difference between radiances from single-gain NOAA-14 AVHRR/2 counts and radiances from NOAA-18 single-equivalent AVHRR/3 counts. Ideally, the lower and upper bounds of the difference are −0.05% and 0.05% respectively (Figure A3). The difference between the simulated NOAA-14 and NOAA-18 single-gain counts are 4 times higher than ideal in channel-1 and 40 times higher in channel-2 (Figure A3). Notice the change of slope from the low to the high gain counts in the differences between single- and double-gain in channel-1. This indicates difficulties on calibration since the low and high gain modes would have different degradation rates.

Remotesensing 06 06929fa3 1024
Figure A3. We show, (left) the lower and higher bounds for the differences between ideal dual- and single-gain implementation in both channels and, (right) the differences between the simulated NOAA-14 and NOAA-18 single-gain counts. In the ideal case, the lower and higher bounds of the difference are −0.05% and 0.05% respectively (left). The difference between the simulated NOAA-14 and NOAA-18 single-gain counts are 4 times higher than ideal in channel-1 and 40 times higher in channel-2. Notice the change of slope from the low to the high gain counts in the differences between single- and double-gain in channel-1 signaling difficulties on calibration when identical instrument degradation for both low and high gain modes is assumed.

Click here to enlarge figure

Figure A3. We show, (left) the lower and higher bounds for the differences between ideal dual- and single-gain implementation in both channels and, (right) the differences between the simulated NOAA-14 and NOAA-18 single-gain counts. In the ideal case, the lower and higher bounds of the difference are −0.05% and 0.05% respectively (left). The difference between the simulated NOAA-14 and NOAA-18 single-gain counts are 4 times higher than ideal in channel-1 and 40 times higher in channel-2. Notice the change of slope from the low to the high gain counts in the differences between single- and double-gain in channel-1 signaling difficulties on calibration when identical instrument degradation for both low and high gain modes is assumed.
Remotesensing 06 06929fa3 1024

Simulating NOAA-14 radiances from the actual count measurements of NOAA-18 AVHRR/3 and computing their associated NDVI to assess the effects on the differences on NDVI (Figure A4), we find a negative bias in the error budget that is compatible to the negative shift observed in Figure 1. Figure A4 also shows for comparison the error budget from NOAA-16 NDVI when their low- and high-gain are computed using the actual counts from NOAA-18.

Remotesensing 06 06929fa4 1024
Figure A4. Simulations of NOAA-14 NDVI from the actual count measurements of NOAA-18 AVHRR/3. A negative bias in the error budget is observed (red X points) that is compatible to the negative shift reported in Figure 1. The Figure also shows, for comparison, the error budget from NOAA-16 NDVI (blue circles) and the ideal error budget (green crosses) when their low- and high-gain are computed using the actual counts from NOAA-18. The NOAA-14 error is 3 times higher than the NOAA-16 and about 55% of the NDVI uncertainty (Figure 8).

Click here to enlarge figure

Figure A4. Simulations of NOAA-14 NDVI from the actual count measurements of NOAA-18 AVHRR/3. A negative bias in the error budget is observed (red X points) that is compatible to the negative shift reported in Figure 1. The Figure also shows, for comparison, the error budget from NOAA-16 NDVI (blue circles) and the ideal error budget (green crosses) when their low- and high-gain are computed using the actual counts from NOAA-18. The NOAA-14 error is 3 times higher than the NOAA-16 and about 55% of the NDVI uncertainty (Figure 8).
Remotesensing 06 06929fa4 1024

As we have done in Figure 6, we can disaggregate the NDVI error budget as a function of NDVI (Figure A5). The higher errors in these NOAA-14 simulations might well explain the NDVIpd discontinuities due to design changes reported in the main document. However, it is not possible to separate this contribution from changes on orbit in the instrument sensitivity. All that can be derived and corrected with the Bayesian approach is the combined effects on NDVI due to changes in the design and in the instrument sensitivity when on orbit.

Remotesensing 06 06929fa5 1024
Figure A5. NDVI error budget is disaggregated by NDVI values for simulated NOAA-14 (left) and NOAA-16 (right). The error budget ranges from −0.025 in the low NDVI values (high-gain mode in channel-2) to −0.01 in the high NDVI values. The channel-2 slope discrepancy in Figure A2 might account for this tendency.

Click here to enlarge figure

Figure A5. NDVI error budget is disaggregated by NDVI values for simulated NOAA-14 (left) and NOAA-16 (right). The error budget ranges from −0.025 in the low NDVI values (high-gain mode in channel-2) to −0.01 in the high NDVI values. The channel-2 slope discrepancy in Figure A2 might account for this tendency.
Remotesensing 06 06929fa5 1024

Appendix B. Readme File

GIMMS AVHRR Global NDVI 1/12-degree Geographic Lat/Lon

host: http://ecocast.arc.nasa.gov/data/pub/gimms/3g/

README 2014 June 2014

________________________________________________________________________________

  • Description

  • File Naming Convention

  • Grid Parameters

  • Data Format VI3g

  • Flags

________________________________________________________________________________

1. Description

  • This dataset is an inverse cartographic transformation and mosaicing of the

  • GIMMS AVHRR 8-km Albers Conical Equal Area continentals AF, AZ, EA, NA, and

  • SA to a global 1/12-degree Lat/Lon grid.

    • Continent demarcation and pixel selection is predetermined with an ancillary

    • NDVI-3G based land-water mask.

2. File Naming Convention

  • geo[year][month][period].n[sat][-[VI][version]g

    • where

    • year 2-int 2 digit year

    • month 3-char abbr. lower case month name

    • period 3-char alphanum period: bimonthly 15[ab]

    • sat 2-int satellite number

    • version n-int version number (3)

  • For example,

  • geo09jan15a.n17-VI3g

3. Grid Parameters

  • grid-name: Geographic Lat/Lon

  • pixel-size: 1/12=0.0833 degrees

  • size-x: 4320

  • size-y: 2160

    • upper-left-lat : 90.0 (center of pixel 90.0 − 1/24)

    • upper-left-lon : −180.0 (center of pixel −180.0 + 1/24)

    • lower-right-lat : −90.0 (center of pixel − 90.0 + 1/24)

    • lower-right-lon: 180.0 (center of pixel 180.0 − 1/24)*

  • *coordinates located at center of pixel

4. Data Format-VI3g *

  • datatype: 16-bit signed integer

  • byte-order: big endian

    • scale-factor: 10000

    • min-valid: −10000

    • max-valid: 10000 or 10004

    • mask-water: −10000

    • mask-nodata: −5000

  • *values include embedded flags (see full NDVI-3G documentation - in preparation)

5. Flag Values

  • Each NDVI data set (ndvi3g) is an INT16 file saved with ieee-big_endian

  • it ranges from −10000 to 10000 or 10004

  • with the flagW file added to the ndvi values as follows:

  •    ndvi3g = round(ndvi × 10000) + flagW − 1;

  •    flagW ranges from 1 to 7;

  • to retrieve the original ndvi and flagW values

  •    flagW = ndvi3g – floor(ndvi3g/10) × 10 + 1;

  •    ndvi = floor(ndvi3g/10)/1000

  • The meaning of the FLAG:

  •    FLAG = 7 (missing data)

  •    FLAG = 6 (NDVI retrieved from average seasonal profile, possibly snow)

  •    FLAG = 5 (NDVI retrieved from average seasonal profile)

  •    FLAG = 4 (NDVI retrieved from spline interpolation, possibly snow)

  •    FLAG = 3 (NDVI retrieved from spline interpolation)

  •    FLAG = 2 (Good value)

  •    FLAG = 1 (Good value)

  • END

Remotesensing 06 06929f1 1024
Figure 1. This figure displays the temporal dynamics for seven representative regions within Africa (A–G) of the input AVHRR NDVIpd data before any compensation for AVHRR channels one and two dual-gain quantizing. The seven time series are NDVI averages of a 3 × 3 element array for the coordinate location noted and indicated in the map at the bottom. Areas were selected to represent different vegetation densities and types.

Click here to enlarge figure

Figure 1. This figure displays the temporal dynamics for seven representative regions within Africa (A–G) of the input AVHRR NDVIpd data before any compensation for AVHRR channels one and two dual-gain quantizing. The seven time series are NDVI averages of a 3 × 3 element array for the coordinate location noted and indicated in the map at the bottom. Areas were selected to represent different vegetation densities and types.
Remotesensing 06 06929f1 1024
Remotesensing 06 06929f2 1024
Figure 2. We use a fine-grid δ(NDVI) of 0.005 to represent the NDVI probability density function from −0.2 to 1 using (A) NDVI derived from AVHRR in steps 1–4 (NDVIpd) and (B) NDVI from SeaWiFS (NDVISW) at two different periods, 1998–1999 and 2004–2005. The shifting in the probability distribution functions illustrates the discontinuities shown in Figure 1. The NDVISW does not show a shift from 1998 to 1999 and 2004–2005. Thus AVHRR NDVI shift in (A) is an indication of a spurious bias and the differences in the dynamic ranges from both sensors. The slight difference between the SeaWiFS NDVISW at two different periods in (is the global difference in surface conditions between these two time intervals.

Click here to enlarge figure

Figure 2. We use a fine-grid δ(NDVI) of 0.005 to represent the NDVI probability density function from −0.2 to 1 using (A) NDVI derived from AVHRR in steps 1–4 (NDVIpd) and (B) NDVI from SeaWiFS (NDVISW) at two different periods, 1998–1999 and 2004–2005. The shifting in the probability distribution functions illustrates the discontinuities shown in Figure 1. The NDVISW does not show a shift from 1998 to 1999 and 2004–2005. Thus AVHRR NDVI shift in (A) is an indication of a spurious bias and the differences in the dynamic ranges from both sensors. The slight difference between the SeaWiFS NDVISW at two different periods in (is the global difference in surface conditions between these two time intervals.
Remotesensing 06 06929f2 1024
Remotesensing 06 06929f3 1024
Figure 3. This diagram summarizes the Bayes’ rule process and the four different probability distribution functions when it is applied for each overlapping period between corresponding NDVISW and NDVIpd values during 1998–1999 (NOAA-14), 2002–2003 (NOAA-16), 2004–2005 (NOAA-17), and 2007–2008 (NOAA-18). The middle panel shows the likelihoods or the actual probability distribution functions P(SW/pd) corresponding to each overlapping period. The shifting observed in the prior NDVI data (plots at bottom panel) are corrected in the computed posterior (plots at right panel). Notice the small population of anomalous values in the N14 panels with an NDVIpd value of zero that corresponds to NDVISW values between the range of 0.5 and 0.7. These values indicate that there are points in the AVHRR/2 record that were flagged as missing data. Users should note flag values to avoid mis-interpretations in their analysis (see Appendix B or README file provided with the data). Also notice the comparable dynamic range and degree of probability distribution functions between the evidence NDVIsw (plots at left panel) and the posterior AVHRR NDVI data. Concurrently mapped SeaWiFS NDVI data enabled these corrections to be made at the same time intervals and same spatial resolution.

Click here to enlarge figure

Figure 3. This diagram summarizes the Bayes’ rule process and the four different probability distribution functions when it is applied for each overlapping period between corresponding NDVISW and NDVIpd values during 1998–1999 (NOAA-14), 2002–2003 (NOAA-16), 2004–2005 (NOAA-17), and 2007–2008 (NOAA-18). The middle panel shows the likelihoods or the actual probability distribution functions P(SW/pd) corresponding to each overlapping period. The shifting observed in the prior NDVI data (plots at bottom panel) are corrected in the computed posterior (plots at right panel). Notice the small population of anomalous values in the N14 panels with an NDVIpd value of zero that corresponds to NDVISW values between the range of 0.5 and 0.7. These values indicate that there are points in the AVHRR/2 record that were flagged as missing data. Users should note flag values to avoid mis-interpretations in their analysis (see Appendix B or README file provided with the data). Also notice the comparable dynamic range and degree of probability distribution functions between the evidence NDVIsw (plots at left panel) and the posterior AVHRR NDVI data. Concurrently mapped SeaWiFS NDVI data enabled these corrections to be made at the same time intervals and same spatial resolution.
Remotesensing 06 06929f3 1024
Remotesensing 06 06929f4 1024
Figure 4. This figure displays the temporal dynamics for the same seven representative regions within Africa (A–G) of the corrected AVHRR/2 and AVHRR/3 NDVI3g data after Bayesian adjustment for the AVHRR/3 instrument dual-gain quantizing for channels one and two. The seven time series are NDVI averages of a 3 × 3 element 8-km pixel array for the coordinate location noted and indicated in the map at the bottom. Areas were selected to represent different vegetation densities and types. Refer to Figure 1 for the NDVIs from the same areas without Bayesian compensation (NDVIpd). The differences are especially striking for the Sahel (A), the Sahara (D), and Kenya (E) while being significant for all seven areas in this figure.

Click here to enlarge figure

Figure 4. This figure displays the temporal dynamics for the same seven representative regions within Africa (A–G) of the corrected AVHRR/2 and AVHRR/3 NDVI3g data after Bayesian adjustment for the AVHRR/3 instrument dual-gain quantizing for channels one and two. The seven time series are NDVI averages of a 3 × 3 element 8-km pixel array for the coordinate location noted and indicated in the map at the bottom. Areas were selected to represent different vegetation densities and types. Refer to Figure 1 for the NDVIs from the same areas without Bayesian compensation (NDVIpd). The differences are especially striking for the Sahel (A), the Sahara (D), and Kenya (E) while being significant for all seven areas in this figure.
Remotesensing 06 06929f4 1024
Remotesensing 06 06929f5 1024
Figure 5. The top panel (A) shows an example of a 95% highest density interval (HDI) found from a fine grid approximating the probability density function, p(δxy | NDVI), using (B) NDVI3g data from the bottom panel’s NDVI value of 0.5. All the NDVI values inside the highest density interval region, the red line in the top panel, have higher density than any other value outside the distribution envelope. The area under the curve through the highest density interval line comprises 95% of all the data. Every NDVI value within the effective NDVI3g dynamical range would have its corresponding p(δxy | NDVI) distribution. In the bottom panel (B), NDVI values are centered at 0.3, 0.5 and 0.7 of the NDVI probability distribution function, in green, and their respective highest density intervals are represented by the smaller dotted curves. The top panel (A) is an expansion of the 2nd distribution p(δxy | NDVI = 0.5) and its respective highest density interval (−0.003, 0.002). The average width of all highest density intervals is 0.0036 giving an average uncertainty of ∼ ±0.002 NDVI units.

Click here to enlarge figure

Figure 5. The top panel (A) shows an example of a 95% highest density interval (HDI) found from a fine grid approximating the probability density function, p(δxy | NDVI), using (B) NDVI3g data from the bottom panel’s NDVI value of 0.5. All the NDVI values inside the highest density interval region, the red line in the top panel, have higher density than any other value outside the distribution envelope. The area under the curve through the highest density interval line comprises 95% of all the data. Every NDVI value within the effective NDVI3g dynamical range would have its corresponding p(δxy | NDVI) distribution. In the bottom panel (B), NDVI values are centered at 0.3, 0.5 and 0.7 of the NDVI probability distribution function, in green, and their respective highest density intervals are represented by the smaller dotted curves. The top panel (A) is an expansion of the 2nd distribution p(δxy | NDVI = 0.5) and its respective highest density interval (−0.003, 0.002). The average width of all highest density intervals is 0.0036 giving an average uncertainty of ∼ ±0.002 NDVI units.
Remotesensing 06 06929f5 1024
Remotesensing 06 06929f6 1024
Figure 6. All panels show, at each NDVI value within the effective NDVI3g dynamical range, the distribution (vertical segments) for deviations from the mean of (A) the combined spatial and temporal coherent components (δxy + δt); (B) the Bayesian transformation (Btr); (C) the climate seasonal (Svc); and (D) inter-annual (IAvc) variability components. The color bar represents the mass or variable density concentration along the vertical lines. This figure confirms that the temporal and spatial NDVI coherence of our data are high, shows that the aggregate error of our Bayesian transformation is ±0.002 NDVI units, and demonstrates that seasonal variation is higher and inter-annual variation is lower.

Click here to enlarge figure

Figure 6. All panels show, at each NDVI value within the effective NDVI3g dynamical range, the distribution (vertical segments) for deviations from the mean of (A) the combined spatial and temporal coherent components (δxy + δt); (B) the Bayesian transformation (Btr); (C) the climate seasonal (Svc); and (D) inter-annual (IAvc) variability components. The color bar represents the mass or variable density concentration along the vertical lines. This figure confirms that the temporal and spatial NDVI coherence of our data are high, shows that the aggregate error of our Bayesian transformation is ±0.002 NDVI units, and demonstrates that seasonal variation is higher and inter-annual variation is lower.
Remotesensing 06 06929f6 1024
Remotesensing 06 06929f7 1024
Figure 7. The top panel shows an example 95% highest density interval (HDI) found from the fine grid approximated probability density functions: (A) δxy or spatial coherence and δt or temporal coherence plotted together; (B) Btr or the Bayesian transformation probability distribution; (C) Svc or the seasonal variability; and (D) IAvc or the inter-annual variability, all as presented differently in Figure 6. All the x values inside the density interval regions, the red horizontal lines, have much higher density (95%) than any other x value outside (5%). Every NDVI value within the effective NDVI3g dynamical range would have its corresponding p(x | NDVI) distribution. In the bottom panels, centered at 0.1, 0.3, 0.5 and 0.7 NDVI units, are the correspondent four probability density functions represented by the smaller dotted horizontal curves on top of the parent NDVI3g’s probability distribution function, in green. The top panels in each subfigure are the labeled expansions in the vertical of the respective distributions at 0.5 NDVI units for the four probability distribution functions. Note the very high spatial and temporal coherence, the large seasonal variation, and the lower inter-annual variation that have resulted from the Bayesian adjustment of the AVHRR NDVI data using SeaWiFS NDVI.

Click here to enlarge figure

Figure 7. The top panel shows an example 95% highest density interval (HDI) found from the fine grid approximated probability density functions: (A) δxy or spatial coherence and δt or temporal coherence plotted together; (B) Btr or the Bayesian transformation probability distribution; (C) Svc or the seasonal variability; and (D) IAvc or the inter-annual variability, all as presented differently in Figure 6. All the x values inside the density interval regions, the red horizontal lines, have much higher density (95%) than any other x value outside (5%). Every NDVI value within the effective NDVI3g dynamical range would have its corresponding p(x | NDVI) distribution. In the bottom panels, centered at 0.1, 0.3, 0.5 and 0.7 NDVI units, are the correspondent four probability density functions represented by the smaller dotted horizontal curves on top of the parent NDVI3g’s probability distribution function, in green. The top panels in each subfigure are the labeled expansions in the vertical of the respective distributions at 0.5 NDVI units for the four probability distribution functions. Note the very high spatial and temporal coherence, the large seasonal variation, and the lower inter-annual variation that have resulted from the Bayesian adjustment of the AVHRR NDVI data using SeaWiFS NDVI.
Remotesensing 06 06929f7 1024
Remotesensing 06 06929f8 1024
Figure 8. This figure shows the accumulated spatial coherence, temporal coherence, Bayesian, seasonal, and interannual uncertainties sum to an average 0.023 NDVI units (δxy + δt + Btr + Svc + IAvc, respectively). The inter-annual variation increases proportionally to NDVI values but still it is lower than ±0.012 NDVI units. The major contributions to the uncertainty from seasonal variation occur within the NDVI interval from 0.3 to 0.7 where effects of vegetation phenology are greatest.

Click here to enlarge figure

Figure 8. This figure shows the accumulated spatial coherence, temporal coherence, Bayesian, seasonal, and interannual uncertainties sum to an average 0.023 NDVI units (δxy + δt + Btr + Svc + IAvc, respectively). The inter-annual variation increases proportionally to NDVI values but still it is lower than ±0.012 NDVI units. The major contributions to the uncertainty from seasonal variation occur within the NDVI interval from 0.3 to 0.7 where effects of vegetation phenology are greatest.
Remotesensing 06 06929f8 1024
Table Table 1. General characteristics of the global coarse-resolution satellite spectral vegetation index instruments, their host satellite, and period of operation. As the satellite orbits the Earth, data are both broadcast continually and recorded on board for subsequent download at the operating Command and Data Acquisition (CDA) ground stations—two in the case of NOAA CDA ground stations in Wallops, VA, and Fairbanks, AK—for relay to the national data centers that are responsible for data processing and the generation of environmental products on a timely basis (Collecting the data from Earth observing missions, deriving information from them, preserving and providing the data and information to all users are very important activities that are supported by the ground stations. People began thinking about satellite environmental data and information services not long after the widespread use of punched cards had become obsolete, i.e., the World Wide Web as we know it today was yet to be created. Although specific numbers are trivial today, the design principles and architecture considerations, e.g., modularity, scalability, adaptive flexibility, evolvement, are still essential to ensure continued improvements in the data and information systems, e.g., the NOAA National Environmental Data, and Information Service (NESDIS) or the twelve Distributed Active Archive Centers (DAAC)s of NASA’s Earth Science Data and Information System (ESDIS)). The spatial resolution (at nadir in km), number of spectral bands, global data volume (GB/day) and equally important the associated ground system corresponding to each satellite are provided in that order in parenthesis. One of the unique features of the MODIS and VIIRS instruments is their direct broadcast (DB) capability in addition to storing data for later download. The Terra MODIS instrument was one of the first satellites to constantly broadcast data for anyone with the right equipment and software to download data. The SeaWiFS project includes 3 ground support systems and 135 additional NASA approved HRTP stations (in parenthesis). To achieve science-quality data, every satellite record has been reprocessed several times. The only exception to this is VIIRS that has no reprocessing capability at this time, a major limitation of the current VIIRS system.

Click here to display table

Table 1. General characteristics of the global coarse-resolution satellite spectral vegetation index instruments, their host satellite, and period of operation. As the satellite orbits the Earth, data are both broadcast continually and recorded on board for subsequent download at the operating Command and Data Acquisition (CDA) ground stations—two in the case of NOAA CDA ground stations in Wallops, VA, and Fairbanks, AK—for relay to the national data centers that are responsible for data processing and the generation of environmental products on a timely basis (Collecting the data from Earth observing missions, deriving information from them, preserving and providing the data and information to all users are very important activities that are supported by the ground stations. People began thinking about satellite environmental data and information services not long after the widespread use of punched cards had become obsolete, i.e., the World Wide Web as we know it today was yet to be created. Although specific numbers are trivial today, the design principles and architecture considerations, e.g., modularity, scalability, adaptive flexibility, evolvement, are still essential to ensure continued improvements in the data and information systems, e.g., the NOAA National Environmental Data, and Information Service (NESDIS) or the twelve Distributed Active Archive Centers (DAAC)s of NASA’s Earth Science Data and Information System (ESDIS)). The spatial resolution (at nadir in km), number of spectral bands, global data volume (GB/day) and equally important the associated ground system corresponding to each satellite are provided in that order in parenthesis. One of the unique features of the MODIS and VIIRS instruments is their direct broadcast (DB) capability in addition to storing data for later download. The Terra MODIS instrument was one of the first satellites to constantly broadcast data for anyone with the right equipment and software to download data. The SeaWiFS project includes 3 ground support systems and 135 additional NASA approved HRTP stations (in parenthesis). To achieve science-quality data, every satellite record has been reprocessed several times. The only exception to this is VIIRS that has no reprocessing capability at this time, a major limitation of the current VIIRS system.
Instrument (km, n, GB/day, Ground System)Dates of OperationReferences, Comments
NOAA AVHRR/2 (4, 5, 0.6, 2)[9–11]
NOAA-7 (C)July 1981–February 1985Deactivated June 1986
NOAA-9 (F)February 1985–September 1988Deactivated February 1998
NOAA-11 (H)September 1988–September 1994No data after September 1994
NOAA-9 (F)-dSeptember 1994–January 1995Descending node, 9 am
NOAA-14 (J)January 1995–November 2000Late overpass after January 2001
NOAA AVHRR/3 (4, 5, 0.6, 3)[11,12]
NOAA-16 (L)November 2000–December 2003Data failures after January 2004
NOAA-17 (M)December 2003–January 2009No data after April 2010
NOAA-18 (N)08/2005–presentData used after December 2007
NOAA-19 (N’)06/2009–presentData used after December 2011
MetOp-A10/2006–present
MetOp-BSeptember 2012–present
MetOp-C2018 launch
SeaWiFS (4, 8, 0.4, 3 (135))September 1997–December 2010[13] No data after January 2011
SPOT-4 & -5 Vegetation (1, 4, 1, 4)May 1998–July 2013[14] No data after July 2013
PROBA Vegetation (0.33, 4, 15, 2)May 2013–present[14] Follow-on to Vegetation
MODIS (0.25-1, 32, 194, 12 (DB))[15]
TerraFebruary 2000–present
AquaJuly 2002–present
Suomi-NPP VIIRS (0.75, 21, 93, 12 (DB))October 2012–present[16]

Share and Cite

MDPI and ACS Style

Pinzon, J.E.; Tucker, C.J. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929-6960. https://doi.org/10.3390/rs6086929

AMA Style

Pinzon JE, Tucker CJ. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sensing. 2014; 6(8):6929-6960. https://doi.org/10.3390/rs6086929

Chicago/Turabian Style

Pinzon, Jorge E., and Compton J. Tucker. 2014. "A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series" Remote Sensing 6, no. 8: 6929-6960. https://doi.org/10.3390/rs6086929

APA Style

Pinzon, J. E., & Tucker, C. J. (2014). A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sensing, 6(8), 6929-6960. https://doi.org/10.3390/rs6086929

Article Metrics

Back to TopTop