Can I Trust My One-Class Classification?
Abstract
: Contrary to binary and multi-class classifiers, the purpose of a one-class classifier for remote sensing applications is to map only one specific land use/land cover class of interest. Training these classifiers exclusively requires reference data for the class of interest, while training data for other classes is not required. Thus, the acquisition of reference data can be significantly reduced. However, one-class classification is fraught with uncertainty and full automatization is difficult, due to the limited reference information that is available for classifier training. Thus, a user-oriented one-class classification strategy is proposed, which is based among others on the visualization and interpretation of the one-class classifier outcomes during the data processing. Careful interpretation of the diagnostic plots fosters the understanding of the classification outcome, e.g., the class separability and suitability of a particular threshold. In the absence of complete and representative validation data, which is the fact in the context of a real one-class classification application, such information is valuable for evaluation and improving the classification. The potential of the proposed strategy is demonstrated by classifying different crop types with hyperspectral data from Hyperion.1. Introduction
In the last decades, remote sensing sensor technology and data quality (in terms of radiometric, spectral, geometric, and/or temporal resolutions) improved vigorously [1]. The availability of such high quality data will probably increase further due to new data policies [2]. For example, with the recent and planned Landsat 8 [3], EnMAP [4], and Sentinel [5] missions the future availability of high-quality data is secured. Moreover, the availability of powerful and free/low cost image processing software for the analysis of remote sensing data, such as R [6], the EnMAP-Box [7], and the Orfeo Toolbox [8,9], fosters the operational use of earth observation (EO) data. In context of decision-making and surveying compliance of environmental treaties, land use land cover (LULC) classifications of remote sensing data are the most commonly used EO products. However, continuously increasing performance requirements demand for the development of adequate classification techniques. It is likely that future development in LULC classification of remote sensing images will be driven among others by: (i) the demand for more detailed as well as accurate LULC classifications; (ii) the interest in the distribution of only one or very few classes, e.g., invasive species; and (iii) limited financial resources and time constraints.
Regarding (ii)–(iii), supervised binary or multi-class classifiers such as the maximum likelihood classifier or support vector machine (SVM) are not necessarily appropriate approaches. These classifiers assign each pixel to one of the known classes defined in the training set. Thus, an accurate supervised classifier requires an exhaustive and mutually exclusive training set [10]. This means that ideally all the classes in the area of interest have to be defined in the training set. If this condition is not fulfilled, i.e., if the training set is incomplete, significant classification errors can occur because all pixels of the unknown classes will be mapped to one of the known classes. Thus, the larger the area of the unknown classes the higher the commission errors. Obviously but notably, these errors do not even appear in an accuracy assessment if the test set does not include the unknown classes [11].
Several LULC classification approaches were introduced which can handle incomplete training sets. In the scientific literature these approaches can be found under the terms “classification with reject option” [12–14], “partially supervised classification” [15], and “one-class classification” (OCC) [16,17]. While a common supervised classifier maps each pixel to one of the known classes, these classifiers reject the classification of a pixel if it does not sufficiently match one of the known classes. With such algorithms the cost for map production can be significantly reduced, particularly, if the cost for reference data acquisition is high and the user is interested in only one or few classes.
Although the lack of need for training samples from the classes of no interest can be a great facilitation in the training data acquisition step, it turns out to be a burden during the classification. Independent from the approach, an accurate classification requires adequate training data and parameter settings. When using supervised methods, estimation of accuracy measures from complete validation data or the training data itself by cross-validation is commonly used for the selection of an adequate classifier and parameter setting [18]. In contrast, in the case of OCC the full confusion matrix cannot be derived from the reference data available during the training stage because labeled samples are only available for the class of interest, i.e., the positive class, but not for the other classes, i.e., the negative class (Table 1). This is a serious problem for the user, because for an accurate classification the user’s and producer’s accuracies (UA and PA) need to be high.
Existing one-class classifiers can be separated into several categories, e.g., depending on the type of the training data and the classifier function. Two main categories, P-classifiers and PU-classifiers, are distinguished based on whether the training data set includes positive samples only (P-classifiers) or positive and unlabeled samples (PU-classifiers). PU-classifiers are computationally much more expensive, due to the fact that additional information is extracted extracted from an often very large number of unlabeled samples. However, PU-classifiers can be much more accurate, particularly in the case of significant spectral ambiguities between the positive and the negative class. In such cases a P-classifier cannot perform as accurate as a PU-classifier [15,19]. P-classifiers usually consist of two elements [17]: The first element is a similarity measure such as the distance between the positive training samples and the pixel to be classified. The second element is a threshold that is applied on the similarity measure to determine the final class membership. Different approaches to this problem are treated comprehensively in [17].
In the remote sensing community, the one-class SVM (OCSVM) [20–23] and the Support Vector Data Description (SVDD) [11,17,24–26] are state-of-the-art P-classifier. As in the case of a supervised SVM two parameters have to be determined, a kernel parameter and a regularization parameter. In practice, the regularization parameter is defined via the omission/false negative rate on (positive only) validation data. This means that the user has to specify the percentage of the positive training data to be rejected by the model. This parameter has to be chosen carefully in order to ensure a good classification result. While values such as 1% or 5% can be suitable when the positive class is well separable [21], these parameter settings will result in a high commission/false positive rate when a significant class overlap exists.
The SVDD has been applied in a one-class classifier ensemble where the single classifiers differed in the input features [27]. It has been shown that the ensemble outperformed feature fusion approach, i.e., the classification with the stacked features, which can possibly attributed to the higher dimensionality. It is worth noting that classifier ensembles have also been applied successfully in the field of species distribution modeling [28,29]. Furthermore they are a focus of intense research in pattern recognition and machine learning [30,31]. These are important developments because multiple classifier systems have been shown to be successful supervised classification of remote sensing data [32–34] and should be further investigated for one-class classification.
The aforementioned approaches can lead to optimal classification results if (i) there is insignificant class overlap or (ii) if the negative class is uniformly distributed in the part of the feature space where the positive class lives. In the case of significant classes overlap, the second condition is usually not true and any P-classifier will lead to relatively poor results. It is important to note that one-class classifier ensembles based on P-classifiers are also not suitable for such classification problems.
PU-classifiers try to overcome the problems by exploiting unlabeled data. Usually, it is not feasible to use all the unlabeled pixels of an image and a random selected subset is used. This should be as small as possible (such that the algorithm is computational efficient) but large enough to contain the relevant information. The adequate number of samples depends on the classification problem, particularly, the complexity of the optimal decision boundary and the occurrence probabilities of the positive and the overlapping negative classes. There are also support vector machine approaches which allow the exploitation of unlabeled samples such as the semi-supervised OCSVM (S2OCSVM) [22] and the biased SVM (BSVM, see also Section 3.1)[22,35].
Another possibility, which is also addressed in this paper, is the usage of Bayes’ rule for the one-class classification with positive and unlabeled data [16]:
There are different ways of solving the OCC problem based on Bayes’ rule. A probabilistic discriminative approach can be implemented to solve the classification problem [36,37]. Also different generative approaches have been proposed. They differ in the way that the probability density functions, p(xi|y+) and p(xi), and the a priori probability are estimated [38–43]. The Maxent approach [44–46], developed in the field of species distribution modeling, also estimates the density ratio . In contrast to the aforementioned approaches, Maxent has been used more frequently for one-class land cover classification in applied studies [19,47–50].
It is important to note that the probabilistic discriminative and the generative approaches return a posteriori probabilities which offers the user an intuitive possibility to solve the thresholding problem. Thresholding these probabilities at 0.5 corresponds to the maximum a posteriori rule and leads to an optimal classification result in terms of the minimum error rate. This requires accurate estimates of the terms of Bayes’ rule (see Equation (1)). In [19,47–50] P (y+) has not been available neither has it been estimated from the data. Thus, the derived continuous output is not an a posteriori probability with an intuitive meaning. Instead, the user has to find a different way to solve the threshold problem, i.e., the conversion of the continuous Maxent output, often called suitabilities, to a binary classification output. In [50] the value of 0.5 is applied on the logistic Maxent output, even though the authors are aware of the fact that they are not dealing with “true” probabilities. In [19] the 5 % omission rate estimated on a (positive only) validation set is used. A detailed theoretical and empirical comparison of threshold approaches used in the field of species distribution modeling is provided in [51]. However, it is important to underline that all these techniques do not generally provide the optimal classification result. The usefulness of such thresholds in terms of the minimum error rate depends on the specific classification problem. Therefore, the result must be evaluated by the user based on the limited reference data.
Besides the threshold selection, the solution by Bayes’ rule seems further interesting. The derived posteriori probabilities can be used as input in advanced spatial smoothing techniques [52,53] or for combining OCC outputs of several classes in one map [24,54]. With a posteriori probabilities it is also straightforward to consider different mis-classification costs for false positive and false negative classifications [55]. Finally, error probabilities (both the probability of omission and commission, i.e., false negative and false positive) can be estimated by integrating over the probability densities [16]. Unfortunately, it is very challenging to accurately estimate the required quantities p(xi|y+), p(xi), and P (y+), particularly, if the positive labeled training data is scarse and the dimensionality of the image is large. This is well known under the terms Hughes phenomena or course of dimensionality [56,57].
In this paper we propose a user-oriented strategy to support the user in handling one-class classifiers for a particular classification problem. Thus, the complicated handling of one-class classifiers can be overcome, the application of a state-of-the-art methodology is advanced and the increased requirements for effective analysis of remote sensing imagery may be easier fulfilled. In a nutshell, the user first performs any OCC, e.g., the BSVM as in this study. To evaluate the classification result, the continuous output of the one-class classifier is further analyzed, e.g., the distance to the separating hyperplane in case of the BSVM. The distributions of the classifier output and the positive and unlabeled training data are visualized. If interpreted carefully, this diagnostic plot is very informative and helps to understand (i) the discriminative power, or separability, of the classifier; and (ii) the suitability of a given threshold applied to convert the continuous output to class estimates. In addition, a posteriori probabilities are estimated by solving Bayes rule in the one-dimensional classifier output space. Therefore, the thresholding problem is objectively solved.
It is important to note that no new one-class classification algorithm is introduced. However, to the best of our knowledge the combination of a modern or state-of-the-art one-class classifiers, e.g., the BSVM, with subsequent analysis of the one-dimensional one-class classifier output space with Bayes’ rule has not been proposed before. Note, that one of the most important advantage of this strategy is the ease of visualization in one-dimensional feature space. In the absence of representative validation data, as in the case of OCC applications, this is useful to evaluate the quality of particular model outcomes, e.g., the continuous output, threshold, or a posteriori probabilitites. The presented strategy should support the user in better understanding a particular one-class classification outcome in the absence of complete reference data. This is an important component for successfully apply one-class classification in real-world applications and has not been addressed in previous studies. These studies propose particular solutions for the problems of model and threshold selection and prove the functioning of the selected approach by means of representative test sets. Testing new solutions by means of a representative test set is an essential element in a scientific research papers. However, it does not guaranteed that they perform well when applied on different data sets in new real-world applications. This is the case in general but particularly critical in one-class classification where reference data is extremely limited. We want to stress that the results of this strategy do not necessarily provide improved accuracies compared to other well working approaches. However, they provide the user with easy to interpret information in order to assess the quality of a selected threshold (see the synthetic example in Section 2), estimated a posteriori probabilities (see the example in Section 5.1), and/or the selected one-class classification model (parameterization) (see the experiment in Section 5.2). Therefore, poor solutions might be detected even without a representative reference set which we believe to be of utmost value in real world applications.
This paper is structured as follows: In the the next section we present the proposed strategy and illustrate it with a two-dimensional synthetic data set. The specific methods for the implementation of the strategy are described in Section 3. The data and experiments conducted to demonstrate the strategy are presented in Section 4. The results are presented and discussed in Section 5. The conclusions close the paper in Section 6.
2. A User-Oriented Strategy for One-Class Classification
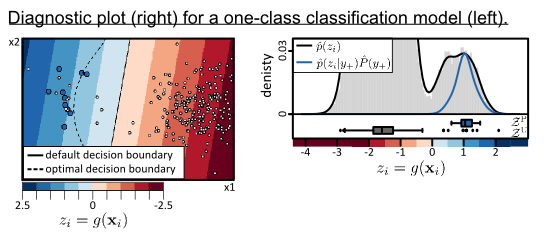
In this section the strategy is illustrated by means of a two dimensional synthetic data set. In two dimensions we can visualization the data and BSVM model (see Figure 1a.1,a.2) and should facilitate the understanding of this section and the strategy. In practice, visualization of the original input feature space is usually not possible because high-dimensional data sets are used for classification. Therefore, we recommend the analysis of the classification problem in the one-dimensional output space of a given one-class classifier, which can be visualized in practice (see Figure 1b.2).
The synthetic example is generated from three normal distributions (Figure 1a.1). Two of the normal distributions belong to negative class, one with an a priori probability of 0.96 and the other one with 0.02. The third normal distribution is assumed to generate the data of the positive class with an a priori probability of 0.02. The positive class overlaps with the “small negative distribution” but is well separable from the “large negative distribution” (see Figure 1a.1). Additionally a test set te consisting of 100,000 samples is generated from the three normal distributions according to their a priori probabilities. First, a one-class classifier g(·) is trained with the training data xi ∈ tr,PU with i ∈ {1,...,I}, consisting of 10 positive and 250 unlabeled samples (Figure 1a.1). In this paper the BSVM is used to implement g(·) (see also Section 3.1). The example training set, the mixture of normal distributions p(xi), the output of the trained classifier zi = g(xi), and the default and optimal decision boundaries are shown in Figure 1a.1, a.2. The default decision boundary of the BSVM, i.e., the separating hyperplane or z = 0, and the optimal decision boundary are also shown in Figure 1a.2). The latter is derived by applying the maximum a posteriori rule on the a posteriori probabilities derived by the known data generating distributions and a priori probabilites. For explanation and visualisation purposes the synthetic dataset is chosen to be two-dimensional and the optimal decision boundary is known because we defined the data generating processes. However, for the proposed user-oriented strategy for handling OCC, higher dimensional data can be used and the optimal trained classifier model need not to be known.
Second, the continuous classifier outputs are predicted using the trained classifier with 𝒵 = g(). Figure 1b.2 shows the so-called diagnostic plot. It comprises the density histogram of the predictions 𝒵 shown in gray and the distributions of the training data 𝒵PU = 𝒵P ∪ 𝒵U, where 𝒵P (shown as blue boxplot) and 𝒵U (shown as grey boxplot) are the cross-validated predictions of the training set tr,P and tr,U. In order to ensure that the predictions 𝒵PU are not biased, the held-out predictions of a ten-fold cross validation are used.
Third, a posteriori probabilities for the training sample set p(y+|zi) (see Figure 1b.1) are derived with Bayes’ rule
The diagnostic plot provides evidence on the plausibility of the Bayes’ analysis, i.e., the estimated quantities p̂(zi|y+), P̂(y+), p̂(zi), p̂(y+|zi), and of given binarization threshold, such θMAP derived from p̂(y+|zi) or the default threshold θ0 of the BSVM. It may thus reveal if inadequate models are used for estimating these quantities and/or if critical assumptions are violated. For example, a certain degree of class separability is usually assumed for estimating P (y+) (see Section 3.3). The visualized quantities in the diagnostic plot constitutes an informative source for interpretation and evaluation of the classification result, which is especially valuable if no complete and representative test set is available. Therefore, if implausible estimates are diagnosed, the user can go back to one of the previous steps in order to improve the results.
Let us first evaluate the two thresholds θ0 and θMAP based on the diagnostic plot (Figure 1b.2). It can be observed that θ0 and θMAP differ significantly. Apriori, we should not prefer one of the two thresholds because if any of the estimates p̂(zi|y+), P̂(y+), p̂(zi) are not plausible θMAP can lead to poorer binary classification result than θ0. Therefore, careful interpretation is required in order to decide which threshold is more plausible. The histogram of 𝒵 shows two main clusters of data which are separated by a low density region at zi ≈ 0 (Figure 1b.2). The default threshold of the BSVM θ0 is located in this low density region. It is tempting to believe that the data right of θ0 belong to the positive class and left to the θ0 to the negative class. However, the distribution of the positive data 𝒵P (the blue boxplot in Figure 1b.2) does not support such believes. It rather provides evidence that only a part of the data right to the low density area belongs to the positive class. Under the assumptions that (i) the positive training data tr,P contains representative samples of the positive class; and (ii) the cross-validated values 𝒵P of tr,P are not strongly biased, θMAP can be approved to be more suitable. More precisely, if the Bayes’ analysis is valid, we have to expect that the threshold θ0 leads to a very high producer’s accuracy (i.e., true positive rate) but also a very low user’s accuracy (i.e., a high false positive rate). Instead, with θMAP we can expect that the producer’s and user’s accuracies for the positive class are rather balanced. It is proved by the threshold dependent accuracies in Figure 1b.3 that this interpretation is correct. Please note that if we would belief that (i) θ0 =0 is a suitable threshold and (ii) over-predictions of the hold-out predictions 𝒵P are unlikely, than this implies that the positive training set is not representative and does not cover an important part of the positive class exhibiting differing spectral characteristics. In order to draw the right conclusion, the user should recall all knowledge, expectations and believes to judge the derived estimations.
This example also shows that the diagnostic plot is useful for understanding if the size of unlabeled training data |tr,U| is suitable. Remember 𝒵U are the cross-validated predictions of the unlabeled training data tr,U and are visulized by the grey boxplot in the diagnostic plot (Figure 1b.2). Here, the large part of the samples are located at very low z-values and only seven samples, i.e., 3 % of the unlabeled samples, exhibit z ≥ 0. This means that the most relevant region of the feature space, i.e., where the optimal decision boundary should be located, is not sampled very well (see Figure 1a.2). This also explains why the default BSVM threshold θ0 is very low. Therefore, in a practical application we would rather re-train the BSVM with a more suitable, e.g., larger, set of unlabeled training samples. Eventually, this could improve the discriminative power of the model.
Let us now evaluate the a posteriori probabilities. Figure 1b.1 shows that the a posteriori probabilities derived from the training and test sets are similar over a large part of the output range. However, at high z-values p̂(y+|zi) is obviously implausible. We reasonably assume that the a posteriori probability is monotonically increasing in z, which is not the case in Figure 1b.1. Here, the drop of the a posteriori probabilities are not plausible but rather an artifact of the non-matching densities in Figure 1b.2. Thanks to the simple structure of the one-dimensional feature space it is easy to correct for such implausible effects as is shown in Figure 1b.4,b.5 (see Section 3.4).
It has already been argued in Section 1 that there is no OCC approach which is likely to perform optimally in all classification problem. The same is true for the density and a priori estimation approaches. Thus, it is not the objective of this paper to promote any particular approach for g(·) or to derive p̂(zi|y+), P̂(y+), p̂(zi). Instead, it is recommended to start with simple approaches for all the steps, analyze the outcome and improve or change the approximations where necessary.
3. Implementation of the Framework
In this section we shortly describe the methods used for the (i) one-class classification; (ii) density estimation; (iii) estimation of the prior probability; and (iv) optimization of the density estimation, i.e., g(·), p(zi|y+), p(zi), and P (y+). To keep the paper concise only one method is considered for each of the estimation problems. However, the user can chose among different methods to find an optimal solution.
3.1. Biased Support Vector Machine
For the experiments in this paper the biased SVM (BSVM) [35] is used to implement the one-class classifier g(·). The BSVM is a special formulation of the binary SVM which is adapted to solve the OCC problem with a positive and unlabeled training set tr,PU.
Two mis-classification cost terms C+ and C0 are used for the positive and unlabeled training samples. If the unlabeled training set is large enough it contains a significant amount of positive samples. On the other hand, the positive training set is labeled and therefore no or only few negative samples are contained in it. Thus, it is reasonable to penalize the mis-classifications on the unlabeled training samples less strong. As in the case of the binary SVM the kernel trick can be applied to create a non-linear classifier by fitting the separating hyperplane in a transformed feature space. The Gaussian radial basis function is maybe the most commonly applied kernel and is also used here. Thus, the inverse kernel width σ needs to be tuned additionally to C+ and C0.
Tuning these three parameters is done by performing a grid search over the combinations of pre-specified parameter values. To select the optimal parameter combination a performance criteria is required which is estimated from the positive and unlabeled training data. Given the nature of the data, a reasonable goal is to correctly classify most of the positive labeled samples while minimizing the number of unlabeled samples to be classified as positives. This goal can be achieved by the performance criteria PCPU [59]
The BSVM has been implemented in R [6] via the package kernlab [60].
3.2. Density Estimation
For the estimation of p(zi|y+) an univariate kernel density estimation with adaptive kernel bandwidth is used as implemented in the package pdfCluster [61]. An adaptive kernel density estimation has been selected due to the fact that the size of 𝒵P is relatively small. In contrast, p(zi) can be estimated from the large data set 𝒵 and thus, it is estimated by a univariate kernel density estimation with fixed bandwidth. This is computationally feasible even with a large data set such as 𝒵. Here the implementation of the R base environment [6] is used.
3.3. Estimation of the a Priori Probability
The a priori probability P (y+) is estimated following the approach in [58], which is straightforward once the estimates p̂(zi|y+) and p̂(zi) are available. Accurate estimation of p(zi|y+) and p(zi) are thus a prerequisite for an accurate estimation of P (y+). The approach assumes that the positive and the negative class distributions do not overlap at the point z̃, i.e., p(z̃|y−) = 0. If this is true P (y+) can be derived with the following equation
In the experiments, the median of the cross-validated positive training samples 𝒵P (the blue boxplots in the diagnostic plot) is used to determine z̃. The visualization of the estimations p̂(zi) and p̂(zi|y+) P̂(y+) allows to examine their plausibility and gives evidence if the separability assumption is reasonable.
3.4. Optimizing the Density Estimation
If p(zi|y+) and p(zi) are estimated independently, p̂(zi|y+) can be adjusted to match with p̂(zi) at high z-values. For this region it is usually justifiable to assume that p(zi|y−) equals zero, or equivalently, to assume that only the positive class contributes to p(zi). Based on this assumption, p̂(zi|y+) can be adjusted by applying the following rule:
4. Data and Experiments
4.1. Data
In the experiments of this paper, a Hyperion spaceborne imaging spectroscopy dataset (Figure 2) is used to demonstrate the strategy. The data was acquired at 24 May 2012 over an agricultural landscape located in Saxony Anhalt, Germany (image center latitude/longitude: 51°23′01.62″N/11°44′39.12″E). The Level 1 Terrain Corrected (L1T) product of the image has been used. In order to further increase the geometric accuracy the image was shifted with a linear transformation according to eight ground control points selected uniformly over the image. The nominal size of a pixel at ground is 30 m.
From the 242 spectral bands 87 bands with low signal to noise ratio have been removed. The remaining 155 bands are located in the spectral ranges 426 nm–1336 nm (88 bands), 1477 nm–1790 nm (32 bands), and 1982 nm–2355 nm (35 bands). The pixel values of each spectral band were independently linearly scaled between 0 and 1.
The reference data used in this study was provided by the Ministry of Agriculture and Environment, Saxony Anhalt, Germany. The information was gathered in the framework of the Integrated Administration and Control System of the European Union. In order to receive financial support from the European Union the farmers need to declare the outlines of the agricultural parcels and the land use/land cover. It is assumed that all parcels of the classes of interest analyzed in this study (rapeseed and barley) have been declared and that irregularities can be neglected.
To evaluate the proposed strategy, the specific objective in our study is the classification of rapeseed (Example A, Section 5.1) and barley (Example B, Section 5.2). While we expect that the classification of rapeseed is relatively simple, the classification of barley is more challenging due to parcel size and spectral ambiguities between different cereal crop types.
For each class of interest, the following steps are a carried out to create the training and test sets. First, a fully labeled reference image corresponding to the Hyperion image data was created. The pixels within a parcel of the positive class were labeled positive and all other pixels were labeled negative (Figure 2). Additionally to we created a reference set INT without pixels at class borders, such that INT ∈ , in order to prevent dealing with mixed pixels (Table 2). This was done by excluding the pixels with positive and negative class occurrences in the spatial 3 × 3 neighborhood.
In order to generate the training set we randomly selected 50 parcels. The total number of parcels available for the class rapeseed was 626 and for the class barley 315. The positive training pixels tr,P were randomly selected among the non-border pixels of these parcels to minimize the probability of outliers in the set. For the rapeseed experiment we selected 30 and for the barley experiment 75 positive training samples. In both experiments 5000 pixels were selected randomly from the whole image and used as unlabeled training samples for g(·).
It is important to note that for a one-class classification the required number of positive labeled training data might be higher than in the case of supervised classification in order to yield good classification results. This is particularly true for approaches which estimate a posteriori probabilities in high-dimensional feature space. The number of labeled training samples used in many of these experiments are moderately to very large, i.e., between 100 and 3000 [15,22,37,41,43].
4.2. Experimental Setup
The two experiments presented in this paper are based on the data described in Section 4.1 and the methods described in Section 3. They have been selected in order to demonstrate the usefulness of the diagnostic plots in the context of model selection, derivation of a posteriori probabilities, and threshold selection.
We first selected suitable model parameters for the BSVM based on PCPU (Equation (3)) by ten-fold cross-validation using the training set tr,PU. The cross-validation is also used to generate the sets 𝒵P and 𝒵U used for constructing the diagnostic plots. The final model is trained with the selected parameters and the complete training data and used to derive the predicted image, i.e., 𝒵.
Next, we estimate p(zi|y+) with 𝒵P and p(zi) with 𝒵 (see Section 3.2). With derived density models and z̃ derived from 𝒵P we estimate P (y+) with Equation (4). Now the a posteriori probability p(y+|zi) can be calculated by applying Bayes’ rule (Equation (2)) which also gives the θMAP. Finally, Equation (5) is used for correcting p(zi|y+) and p(y+|zi) at high z-values.
Based on these estimates we construct the diagnostic plots.
With the test set te we perform an accuracy assessment for the binary classification results over the whole range of possible thresholds. Additionally to the confusion matrix we derive the overall accuracy (OA), Cohen’s kappa coefficient (κ), the producer’s accuracy (PA), and the user’s accuracy (UA) for the whole range of possible thresholds. Three thresholds are of particular interest: the “default” threshold θ0, i.e., 0 and corresponds to the hyperplane of the BSVM, the maximum a posteriori threshold θMAP, i.e., the the z-value where p(y+|zi) first exceeds 0.5, and the optimal threshold θOPT, i.e., the threshold which maximizes κ. It is worth to underline that θOPT cannot be derived in context of a real application, due to the incomplete reference data. However, it is used to analyze the experimental results.
The a posteriori probabilities are evaluated by estimating p(zi), p(zi|y+), P (y+) and p(y+|zi) with the test sets te and te,INT. Whereas, te,INT better represents the population from which the positive samples tr,P have been sampled.
For the class barley different diagnostic plots are generated to assess the potential of the plots in context of model selection. This experiment shows that the diagnostic plot can be helpful for manual model selection when the automatic selection process, here based on PCPU, selects an unconvincing model.
The statistical significance of the difference in accuracy has been evaluated a two-sided test based on the kappa coefficient [62] for all compared binary classification results. The widely used 5 percent level of significance has been used for determining if there is a difference. Note, that due to the high amount of test samples also relatively small differences in accuracy are significantly different.
5. Results and Discussion
5.1. Experiment 1: Rapeseed
The class rapeseed can be classified with very high accuracy. Table 3 show the confusion matrices and additional accuracy measures given the three thresholds θ0 (at z = 0), θ̂MAP (at z = −0.17), and θOPT (at z = −0.42). The overall accuracy and kappa coefficients exceed 97 % and 0.85 respectively given any of the three thresholds. Although the three thresholds provide comparable kappa coefficients are statistically significant at a 5 % percent level of significance [62].
These findings are clearly reflected in the diagnostic plot (Figure 3b). The predictive values of the positive class 𝒵P (shown as blue boxplot) correspond well with a distinctive cluster of predicted unlabeled data with high z-values. The wide low density range separating the two clusters corresponds to the wide range of thresholds leading to high classification accuracies. In this experiment, we can be confident to derive a good binary classification result with any threshold in the low density range.
The visual assessment of the classification and error maps underlines this findings (Figure 4). It is well known, that spectral properties of boundary pixels might be a mixture between both classes (e.g., two different crop types). Consequently these mixed pixels do not represent either of the two land cover classes and consequently a mis-classification is more likely to occur.
Deriving accurate a posteriori probabilities is more challenging, particularly with few positive training samples, as in the case here. Under the assumption that the data of the right cluster in Figure 3b belongs to the positive class, the distributions p̂(zi|y+) P̂(y+) and p̂(zi) should coincide in this range. However, p̂(zi|y+) P̂(y+) is less skewed towards high z-values than p̂(zi).
We assume the reason for the discrepancy to be the size of positive training data. It is possible that the small size, i.e., 30, is not sufficient to accurately capture the real distribution of the positive class. Moreover, one may argue that the redundancy is relatively low in a small training data set. When performing cross-validation with such a small set the hold out predictions are more likely to exhibit significantly lower values compared to the predictive values of similar data points predicted with the final model trained with all samples. Furthermore, if p̂(zi|y+) cannot be trusted it is unlikely that Equation (4) provides an accurate estimate of P̂(y+).
The visualization of the estimated densities (Figure 3b) and a posteriori probabilities (Figure 3a) supports the identification of implausible estimations and helps to find more suitable solutions. To improve the a posteriori probabilities, P̂(y+) has been re-calculated by the fraction of pixels with z ≥ −0.25, i.e., in the middle of the low density area. Regarding the visual interpretation of the diagnostic plot and the clear high separability of the classes, it seems adequate to re-calculate P̂(y+) by this approach. Remember that P̂(y+) is calculated by , where z̃ is the median of 𝒵P (see Section 3.3). Due to the fact that (i) p̂(zi|y+) and p̂(zi) do not match very well at z̃ and (ii) the separability is very high it is likely that the alternative way of estimating P (y+) is more accurate.
Then the adjusted p̂COR(zi|y+) P̂(y+) (Equation (5)) has been used to estimate the a posteriori probability. Figure 3d,e show that these solutions substantially improved p̂(y+|zi), which remains at a constant value of one for high z-values. Over the complete range of z it is now very close to pte,INT(y+|zi), i.e., the a posteriori probabilities derived with the test set without boundary pixels (Figure 3d,e). As expected, a stronger discrepancy exists between p̂(y+|zi) and pte(y+|zi) due to the influence of mixed pixels and geometric inaccuracies.
5.2. Experiment 2: Barley
As already underlined, in a practical OCC application no complete and representative validation set is available. Therefore, the OA or other accuracy measures based on complete validation sets cannot be estimated and cannot be used for the task of model selection. Instead, alternative performance measures, such as PCPU(Equation (3)), are used which can be derived from PU-data. However, as is the case in this experiment, these measures do not consequently lead to the optimal models in terms of the classification accuracy. In this experiment a positive but noisy relationship exists between PCPU and the OA (see Figure 5a). The noisiness is typical for PU-performance measures is a problem, as in this experiment, when the highest PCPU value points to a model with relatively low overall accuracy. Assuming the optimal threshold can be found, the selected model (model b in Figure 5) leads to an overall accuracy of 97.0% (κ = 0.57) while the optimal model (model g in Figure 5) to an overall accuracy of 97.9% (κ = 0.73).
It is shown in Figure 5 that comparing the diagnostic plots of different models can support the selection of a more suitable model when the automatic approach fails. In order to select a more accurate model the user can sequentially analyze the diagnostic plot of other models, e.g., in decreasing order of the optimization criteria PCPU. Between different diagnostic plots we would select the one where (i) the positive data 𝒵P is most concentrated at high z-values and (ii) where these samples correspond to a distinctive cluster of unlabeled data. Following these rules we would select the model shown in Figure 5e out of the seven options shown in Figure 5b–h. Table 4 shows the accuracies, given θOPT, of (i) the model with maximum PCPU(model b, see also Figure 5b); (ii) the model selected manually following the argumentation above (model e, see also Figure 5e); and (iii) the model with the highest overall accuracy (model g, see also Figure 5g). The overall accuracy/kappa coefficient of the manually selected model (97.7%/0.68) is 0.7%/0.11 higher than the ones of the model with maximum PCPU (97.0%/0.57) and only 0.02%/0.04 smaller than the model with highest overall accuracy. Thus, in this experiment the diagnostic plot helps to select a model with significantly higher discriminative power compared to the model selected by maximizing PCPU (see Figure 4). The findings are confirmed by a significance test returning statistically significant differences of the kappa coefficients at a 5% percent level of significance [62].
Based on the diagnostic plot of the manually selected model (Figure 6) a substantial amount of mis-classifications has to be expected. Contrary to the rapeseed example (Figure 3) there is no low density region separating the positive and negative class regions. Thus, the distributions of the two classes overlap and lead to significant mis-classifications for any given threshold (Table 5). As in the rapeseed example, the three thresholds provide comparable accuracies but due to the high amount of test samples the differences between the kappa coefficients are statistically significant at a 5% percent level of significance [62].
Also, the classifier performance, which is limited in comparison to the accuracies provided for rapeseed, can be assessed by the diagnostic plot. The analysis of the diagnostic plot (Figure 6b) underlines among others the threshold dependent trade-off between false positive and false negative classifications. Starting from θ0 = 0 and moving the threshold to the left apparently increases the false negative classification stronger than it reduces the false negative classifications. This can be concluded by the steep slope of p̂(zi) in this region.
The higher class overlap in the feature space is also underlined by the visual interpretation of the classification map (Figure 7). As in the rapeseed example, several boudary pixels are missclassified. The errors at the class border are mainly false negatives, which is in contrast to the rapeseed example where false positives and false negatives occurred in similar amounts. However, the significant amount of false negatives was to be expected, regarding the visual interpretation of the diagnostic plots. As in other studies, these mis-classifications firstly occur at pixels which lie along the boundaries of two objects, e.g., two field plots. Moreover, some complete mis-classified fields are obvious in the north of the study site. However, it is well known that the classification of agricultural areas can be affected by site-internal variations. Therefore we assume the reason for the mis-classifications to be crop growing conditions, which are different in the affected part of the study area.
At this point it is also worth noting that the diagnostic plot extends the interpretability of the classification map alone (Figure 7). Usually, noisier classification results (i.e., maps with a strong “salt and pepper” effect), such as the map in Figure 7, are assumed to contain more errors. Although this assumption might be fulfilled in specific case studies (e.g., [34]), it is not generally recommendable to base decisions related to model or threshold selection on the appearance of the classification map alone. For example, a lower threshold could lead to a less noisy classification map because the additional false positives possibly occur in clumps, e.g., in the fields of the most similar land cover class. As discussed before, careful analysis of the distributions of 𝒵P and 𝒵 reveal such over-predictions.
The example also shows that the derivation of accurate a posteriori probabilities is challenging in the case of strongly overlapping classes (Figure 6). Here, p̂(y+|zi) deviates significantly from both pte(y+|zi) and pte,INT(y+|zi). Nevertheless, this seems expectable following the interpretation of the diagnostic plot and the proposed strategy. Remember that the estimation of P̂(y+) is based on the assumption that P̂(y−) is zero at the median of 𝒵P (Equation (4)). But in this example it is unlikely that the assumption holds because p̂(zi) rises steeply just to the left of this point. Therefore, it has to be assumed that there is still a significant negative density at z̃ = 0.36, resulting in a smaller P̂(y+), lower p̂(zi|y+) P̂(y+), and a shift of the p̂(y+|zi)-curve towards higher z-values.
6. Conclusions
In the presented study, a novel strategy for solving the problem of one-class classification was proposed, tested in experiments, and discussed in the context of classifying hyperspectral data. Although various approaches have been introduced, the generation of accurate maps by one-class classifiers is challenging, due to the incomplete and unrepresentative reference data. As a matter of fact the model and threshold selection, cannot be solved based on traditional accuracy metrics, such as the overall accuracy or the kappa coefficient. Thus, the classification does not necessarily lead to optimal results.
The novelty and potential of the presented strategy lies in the analysis of the one-dimensional output of any one-class classifier. Based on our experiments, it can be assessed that the proposed framework for analyzing and interpreting the classifier outputs can reveal poor model and/or threshold selection results. A proposed diagnostic plot for one-class classification results supports the user in understanding the quality of a given one-class classification result and enables the user to manually select more accurate solutions, whether an automatic procedures failed. Furthermore, it has been shown that reliable a posteriori probabilities with small positive training sets can be derive in the one-dimensional output space of any one-class classifier. Overall, due to the proposed strategy, the use of state-of-the-art OCC can be advanced and the increased requirements for effective remote sensing image analysis of recent data may be easier fulfilled.
Future work should extend the strategy to the more general partially supervised classification problem, i.e., when more than one classes have to be mapped.
The implementations described in this paper have been implemented in the R software and are partially available in the package oneClass. The package is available via github [63] and can be installed directly from within R.
Acknowledgments
The study is realized in the framework of the EnMAP-BMP project funded by German Aeropspace Center (DLR) and Federal Ministry of Economics and Technology (BMWi) (DLR/BMWi: FKZ 50EE 1011). Reference data was made available by the Ministry of Agriculture and Environment, Saxony Anhalt, Germany. We acknowledge support by Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of Karlsruhe Institute of Technology.
Author Contributions
Benjamin Mack developed and implemented the presented strategy, carried out the data analyses, and mainly wrote the manuscript. Björn Waske and Ribana Roscher contributed significantly by suggestions and guidelines during the development of the strategy and writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richards, J. Analysis of remotely sensed data: The formative decades and the future. IEEE Trans. Geosci. Remote Sens 2005, 43, 422–432. [Google Scholar]
- European Union. Commission Delegated Regulation (EU) No 1159/2013 of 12 July 2013; European Union: Brussels, Belgium, 2013. [Google Scholar]
- Roy, D.; Wulder, M.; Loveland, T.; Woodcock, C.E.; Allen, R.; Anderson, M.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ 2014, 145, 154–172. [Google Scholar]
- Stuffler, T.; Förster, K.; Hofer, S.; Leipold, M.; Sang, B.; Kaufmann, H.; Penné, B.; Mueller, A.; Chlebek, C. Hyperspectral imaging—An advanced instrument concept for the EnMAP mission (Environmental Mapping and Analysis Programme). Acta Astronaut 2009, 65, 1107–1112. [Google Scholar]
- Malenovský, Z.; Rott, H.; Cihlar, J.; Schaepman, M.E.; García-Santos, G.; Fernandes, R.; Berger, M. Sentinels for science: Potential of Sentinel-1, -2, and -3 missions for scientific observations of ocean, cryosphere, and land. Remote Sens. Environ 2012, 120, 91–101. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2013. [Google Scholar]
- Rabe, A.; Jakimow, B.; Held, M.; van der Linden, S.; Hostert, P. EnMAP-Box Version 2.0: Software. Available online: http://www.enmap.org/?q=enmapbox (accessed on 16 September 2014).
- Inglada, J.; Christophe, E. The Orfeo Toolbox remote sensing image processing software. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. IV-733–IV-736.
- Christophe, E.; Inglada, J. Open source remote sensing: Increasing the usability of cutting-edge algorithms. IEEE Geosci. Remote Sens. Newsl 2009, 150, 9–15. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
- Foody, G.M.; Mathur, A.; Sanchez-Hernandez, C.; Boyd, D.S. Training set size requirements for the classification of a specific class. Remote Sens. Environ 2006, 104, 1–14. [Google Scholar]
- Dubuisson, B.; Masson, M. A statistical decision rule with incomplete knowledge about classes. Pattern Recognit 1993, 26, 155–165. [Google Scholar]
- Muzzolini, R.; Yang, Y.H.; Pierson, R. Classifier design with incomplete knowledge. Pattern Recognit 1998, 31, 345–369. [Google Scholar]
- Fumera, G.; Roli, F.; Giacinto, G. Multiple reject thresholds for improving classification reliability. In Advances in Pattern Recognition; Ferri, F.J., Iñesta, J.M., Amin, A., Pudil, P., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2000; Volume 1876, pp. 863–871. [Google Scholar]
- Byeungwoo, J.; Landgrebe, D. Partially supervised classification using weighted unsupervised clustering. IEEE Trans. Geosci. Remote Sens 1999, 37, 1073–1079. [Google Scholar]
- Minter, T.A. Single-class classification. In Proceedings of Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, 3–5 June 1975; pp. 2A-12–2A-15.
- Tax, D.M.J. One-Class Classification: Concept Learning in the Absence of Counter-Examples. Ph.D Thesis, Technische Universiteit Delft, Delft, The Netherlands. 2001. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer New York: New York, NY, USA, 2009. [Google Scholar]
- Li, W.; Guo, Q. A maximum entropy approach to one-class classification of remote sensing imagery. Int. J. Remote Sens 2010, 31, 2227–2235. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput 2001, 13, 1443–1471. [Google Scholar]
- Li, P.; Xu, H. Land-cover change detection using one-class support vector machine. Photogramm. Eng. Remote Sens 2010, 76, 255–263. [Google Scholar]
- Munoz-Mari, J.; Bovolo, F.; Gomez-Chova, L.; Bruzzone, L.; Camp-Valls, G. Semisupervised one-class support vector machines for classification of Remote Sensing Data. IEEE Trans. Geosci. Remote Sens 2010, 48, 3188–3197. [Google Scholar]
- Sánchez-Azofeifa, A.; Rivard, B.; Wright, J.; Feng, J.L.; Li, P.; Chong, M.M.; Bohlman, S.A. Estimation of the distribution of Tabebuia guayacan (Bignoniaceae) using high-resolution remote sensing imagery. Sensors 2011, 11, 3831–3851. [Google Scholar]
- Munoz-Mari, J.; Bruzzone, L.; Camps-Valls, G. A support vector domain description approach to supervised classification of remote sensing images. IEEE Trans. Geosci. Remote Sens 2007, 45, 2683–2692. [Google Scholar]
- Sanchez-Hernandez, C.; Boyd, D.S.; Foody, G.M. One-class classification for mapping a specific land-cover class: SVDD classification of fenland. IEEE Trans. Geosci. Remote Sens 2007, 45, 1061–1073. [Google Scholar]
- Bovolo, F.; Camps-Valls, G.; Bruzzone, L. A support vector domain method for change detection in multitemporal images. Pattern Recognit. Lett 2010, 31, 1148–1154. [Google Scholar]
- Munoz-Mari, J.; Camps-Valls, G.; Gomez-Chova, L.; Calpe-Maravilla, J. Combination of one-class remote sensing image classifiers. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1509–1512.
- Drake, J.M. Ensemble algorithms for ecological niche modeling from presence-background and presence-only data. Ecosphere 2014, 5, art76. [Google Scholar]
- Stohlgren, T.J.; Ma, P.; Kumar, S.; Rocca, M.; Morisette, J.T.; Jarnevich, C.S.; Benson, N. Ensemble habitat mapping of invasive plant species. Risk Anal 2010, 30, 224–235. [Google Scholar]
- Désir, C.; Bernard, S.; Petitjean, C.; Heutte, L. One class random forests. Pattern Recognit 2013, 46, 3490–3506. [Google Scholar]
- Krawczyk, B.; Woźniak, M.; Cyganek, B. Clustering-based ensembles for one-class classification. Inf. Sci 2014, 264, 182–195. [Google Scholar]
- Briem, G.; Benediktsson, J.; Sveinsson, J. Multiple classifiers applied to multisource remote sensing data. IEEE Trans. Geosci. Remote Sens 2002, 40, 2291–2299. [Google Scholar]
- Du, P.; Xia, J.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple classifier system for remote sensing image classification: A review. Sensors 2012, 12, 4764–4792. [Google Scholar]
- Waske, B.; Braun, M. Classifier ensembles for land cover mapping using multitemporal SAR imagery. ISPRS J. Photogramm. Remote Sens 2009, 64, 450–457. [Google Scholar]
- Liu, B.; Dai, Y.; Li, X.; Lee, W.S.; Yu, P.S. Building text classifiers using positive and unlabeled examples. In Proceedings of the Third IEEE International Conference on Data Mining, Melbourne, FL, USA, 19–22 November 2003; pp. 179–188.
- Elkan, C.; Noto, K. Learning classifiers from only positive and unlabeled data. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 213–220.
- Li, W.; Guo, Q.; Elkan, C. A positive and unlabeled learning algorithm for one-class classification of remote-sensing data. IEEE Trans. Geosci. Remote Sens 2011, 49, 717–725. [Google Scholar]
- Lin, G.C.; Minter, T.C. Bayes estimation on parameters of the single-class classifier. In Proceedings of Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, 29 June–1 July 1976; pp. 3A-22–3A-27.
- Byeungwoo, J.; Landgrebe, D.A. A new supervised absolute classifier. In Proceedings of the 10th Annual International Symposium on Geoscience and Remote Sensing, Washington, DC, USA, 20–24 May 1990; pp. 2363–2366.
- Fernández-Prieto, D. An iterative approach to partially supervised classification problems. Int. J. Remote Sens 2002, 23, 3887–3892. [Google Scholar]
- Mantero, P.; Moser, G.; Serpico, S. Partially supervised classification of remote sensing images through SVM-based probability density estimation. IEEE Trans. Geosci. Remote Sens 2005, 43, 559–570. [Google Scholar]
- Fernandez-Prieto, D.; Marconcini, M. A novel partially supervised approach to targeted change detection. IEEE Trans. Geosci. Remote Sens 2011, 49, 5016–5038. [Google Scholar]
- Marconcini, M.; Fernandez-Prieto, D.; Buchholz, T. Targeted land-cover classification. IEEE Trans. Geosci. Remote Sens 2014, 52, 4173–4193. [Google Scholar]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudík, M.; Chee, Y.E.; Yates, C.J. A statistical explanation of MaxEnt for ecologists. Divers. Distrib 2011, 17, 43–57. [Google Scholar]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model 2006, 190, 231–259. [Google Scholar]
- Phillips, S.J.; Dudík, M. Modeling of species distributions with Maxent: New extensions and a comprehensive evaluation. Ecography 2008, 31, 161–175. [Google Scholar]
- Amici, V. Dealing with vagueness in complex forest landscapes: A soft classification approach through a niche-based distribution model. Ecol. Inform 2011, 6, 371–383. [Google Scholar]
- Evangelista, P.H.; Stohlgren, T.J.; Morisette, J.T.; Kumar, S. Mapping invasive tamarisk (Tamarix): A comparison of single-scene and time-series analyses of remotely sensed data. Remote Sens 2009, 1, 519–533. [Google Scholar]
- Morán-Ordóñez, A.; Suárez-Seoane, S.; Elith, J.; Calvo, L.; Luis, E.D. Satellite surface reflectance improves habitat distribution mapping: A case study on heath and shrub formations in the Cantabrian Mountains (NW Spain). Divers. Distrib 2012, 18, 588–602. [Google Scholar]
- Ortiz, S.; Breidenbach, J.; Kändler, G. Early detection of bark beetle green attack using TerraSAR-X and RapidEye data. Remote Sens 2013, 5, 1912–1931. [Google Scholar]
- Liu, C.; White, M.; Newell, G.; Pearson, R. Selecting thresholds for the prediction of species occurrence with presence-only data. J. Biogeogr 2013, 40, 778–789. [Google Scholar]
- Roscher, R.; Waske, B.; Forstner, W. Incremental import vector machines for classifying hyperspectral data. IEEE Trans. Geosci. Remote Sens 2012, 50, 3463–3473. [Google Scholar]
- Moser, G.; Serpico, S.B. Combining support vector machines and markov random fields in an integrated framework for contextual image classification. IEEE Trans. Geosci. Remote Sens 2013, 51, 2734–2752. [Google Scholar]
- Guo, Q.; Li, W.; Liu, D.; Chen, J. A framework for supervised image classification with incomplete training samples. Photogramm. Eng. Remote Sens 2012, 78, 595–604. [Google Scholar]
- Bruzzone, L. An approach to feature selection and classification of remote sensing images based on the Bayes rule for minimum cost. IEEE Trans. Geosci. Remote Sens 2000, 38, 429–438. [Google Scholar]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar]
- Shahshahani, B.M.; Landgrebe, D.A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the Hughes phenomenon. IEEE Trans. Geosci. Remote Sens 1994, 32, 1087–1095. [Google Scholar]
- Guerrero-Curieses, A.; Biasiotto, A.; Serpico, S.; Moser, G. Supervised classification of remote sensing images with unknown classes. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 3486–3488.
- Li, X.L.; Liu, B. Learning to classify text using positive and unlabeled data. In Proceedings of the 19th International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 587–594.
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. Kernlab—An S4 package for kernel methods in R. J. Stat. Softw 2004, 11, 1–20. [Google Scholar]
- Azzalini, A.; Menardi, G. R. Package pdfCluster: Cluster analysis via nonparametric density estimation. J. Stat. Softw 2014, 11, 1–26. [Google Scholar]
- Foody, G. Thematic map comparison: Evaluating the statistical significance of differences in classification accuracy. Photogramm. Eng. Remote Sens 2004, 70, 627–633. [Google Scholar]
- Mack, B. oneClass: One-Class Classification in the Absence of Test Data, Version 0.1-1: Software. Available online: https://github.com/benmack/oneClass (accessed on 16 September 2014).







| y+ | y− | UA | |
|---|---|---|---|
| ŷ+ | ✓ | ✗ | ✗ |
| ŷ− | ✓ | ✗ | ✗ |
| PA | ✓ | ✗ | ✗ |
| Class | tr,PU | te | te,INT | |||||
|---|---|---|---|---|---|---|---|---|
| Positives | Unlabeled | Positives | Negatives | P (y+) | Positives | Unlabeled | P (y+) | |
| Rapeseed | 30 | 5000 | 96,787 | 775,317 | 0.11 | 63,924 | 732,540 | 0.08 |
| Barley | 75 | 5000 | 38,638 | 836,456 | 0.04 | 24,507 | 809,008 | 0.03 |
| θ0 | (+) | (−) | UA | θ̂MAP | (+) | (−) | UA | θOPT | (+) | (−) | UA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (+) | 80,941 | 4838 | 94.4% | (+) | 83,119 | 5906 | 93.37% | (+) | 85,899 | 8057 | 91.4% |
| (−) | 15,846 | 770,479 | 97.98% | (−) | 13,668 | 769,411 | 98.25% | (−) | 10,888 | 767,260 | 98.6% |
| PA | 83.6% | 99.4% | PA | 85.9% | 99.2% | PA | 88.8% | 99% | |||
| OA/κ | 97.6%/0.87 | OA/κ | 97.8%/0.88 | OA/κ | |||||||
| θOPT, b | (+) | (−) | UA | θOPT, e | (+) | (−) | UA | θOPT, g | (+) | (−) | UA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (+) | 18,530 | 6022 | 75.5% | (+) | 23,158 | 5039 | 82.1% | (+) | 24,904 | 4821 | 83.7% |
| (−) | 20,108 | 830,434 | 97.6% | (−) | 15,480 | 831,417 | 98.2% | (−) | 13,734 | 831,635 | 98.4% |
| PA | 48.0% | 99.3% | PA | 60.0% | 99.4% | PA | 64.5% | 99.4% | |||
| OA/κ | 97.0%/0.57 | OA/κ | 97.7%/0.68 | OA/κ | 97.9%/0.72 | ||||||
| θ0 | (+) | (−) | UA | θ̂MAP | (+) | (−) | UA | θOPT | (+) | (−) | UA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (+) | 24,016 | 5890 | 80.3% | (+) | 26,364 | 9939 | 72.6% | (+) | 23,158 | 5039 | 82.1% |
| (−) | 14,622 | 830,566 | 98.27% | (−) | 12,274 | 826,517 | 98.54% | (−) | 15,480 | 831,417 | 98.2% |
| PA | 62.2% | 99.3% | PA | 68.2% | 98.8% | PA | 59.9% | 99.4% | |||
| OA/κ | 97.7%/0.69 | OA/κ | 97.5%/0.69 | OA/κ | 97.7%/0.68 | ||||||
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mack, B.; Roscher, R.; Waske, B. Can I Trust My One-Class Classification? Remote Sens. 2014, 6, 8779-8802. https://doi.org/10.3390/rs6098779
Mack B, Roscher R, Waske B. Can I Trust My One-Class Classification? Remote Sensing. 2014; 6(9):8779-8802. https://doi.org/10.3390/rs6098779
Chicago/Turabian StyleMack, Benjamin, Ribana Roscher, and Björn Waske. 2014. "Can I Trust My One-Class Classification?" Remote Sensing 6, no. 9: 8779-8802. https://doi.org/10.3390/rs6098779
APA StyleMack, B., Roscher, R., & Waske, B. (2014). Can I Trust My One-Class Classification? Remote Sensing, 6(9), 8779-8802. https://doi.org/10.3390/rs6098779