A Global Grassland Drought Index (GDI) Product: Algorithm and Validation
Abstract
:1. Introduction
2. Data
2.1. Meteorological Station Data
2.2. Remote Sensing Data
2.2.1. MODIS Data
2.2.2. AMSR-E and GLDAS Soil Moisture
2.2.3. TRMM and CRU Precipitation
2.2.4. SPEI Data
2.3. Ancillary Data
2.3.1. Ground-Measured Data
2.3.2. USDM Maps
3. Methodology
3.1. The Basic Theory for Constructing the GDI
3.2. Retrieving CWC Information
3.3. The Estimation of SM
3.4. The Normalization and Integration of Precipitation, SM and CWC to Construct GDI
| Drought Indices | Formula |
|---|---|
| GDI-1 | 2/5 × PREscaled + 2/5 × SMscaled + 1/5 × CWCscaled |
| GDI-2 | 1/2 × PREscaled + 1/4 × SMscaled + 1/4 × CWCscaled |
| GDI-3 | 1/3 × PREscaled + 1/3 × SMscaled + 1/3 × CWCscaled |

3.5. Validation Schemes at the Regional Scale
3.5.1. Validation of the CWC Retrieval Method in Ruoergai Prairie

3.5.2. Quantitatively Validating GDI using in Situ SPI for the Grassland Regions of China

3.5.3. Qualitatively Validating GDI Using USDM Maps in the Contiguous US

3.6. Producing Schemes of the Global GDI Product
4. Results and Discussion
4.1. Validation Results of the CWC Retrieval Method

4.2. Results of Validating GDI Using SPI
4.2.1. Downscaling AMSR-E Soil Moisture

| Years | Correlation Coefficient (R) | RMSE (g/cm3) |
|---|---|---|
| 2002 | 0.8224 | 0.01614 |
| 2003 | 0.7832 | 0.01958 |
| 2004 | 0.7765 | 0.01959 |
| 2005 | 0.7807 | 0.0199 |
| 2006 | 0.7481 | 0.01986 |
| 2007 | 0.7416 | 0.02242 |
| 2008 | 0.7312 | 0.02101 |
| 2009 | 0.7625 | 0.02158 |
| 2010 | 0.7550 | 0.01952 |
4.2.2. Validation Results
| Parameters | SPI-1 Mon | SPI-3 Mon | SPI-6 Mon | SPI-9 Mon |
|---|---|---|---|---|
| scaled CWC | 0.12 | 0.12 | 0.15 | 0.14 |
| scaled SM | 0.15 | 0.17 | 0.10 | 0.11 |
| scaled NDVI | 0.14 | 0.20 | 0.20 | 0.20 |
| scaled LST | 0.31 | 0.24 | 0.23 | 0.24 |
| scaled TRMM-1 | 0.73 | 0.46 | 0.41 | 0.41 |
| scaled TRMM-3 | 0.43 | 0.70 | 0.63 | 0.62 |
| scaled TRMM-6 | 0.39 | 0.62 | 0.70 | 0.69 |
| Drought Indices | SPI-1 Mon (TRMM-1) | SPI-3 Mon (TRMM-3) | SPI-6 Mon (TRMM-6) | SPI-9 Mon (TRMM-6) |
|---|---|---|---|---|
| GDI-1 | 0.54 | 0.53 | 0.51 | 0.51 |
| GDI-2 | 0.62 | 0.60 | 0.59 | 0.59 |
| GDI-3 | 0.49 | 0.49 | 0.48 | 0.47 |
| SDCI | 0.64 | 0.61 | 0.61 | 0.61 |
| VHI | 0.29 | 0.28 | 0.27 | 0.28 |
4.3. Results of Validating the GDI Using USDM maps
4.3.1. Downscaling AMSR-E Soil Moisture

| Years | Correlation Coefficient (R) | RMSE (g/cm3) |
|---|---|---|
| 2002 | 0.6885 | 0.01598 |
| 2003 | 0.5775 | 0.01658 |
| 2004 | 0.3999 | 0.02103 |
| 2005 | 0.5213 | 0.02146 |
| 2006 | 0.5394 | 0.02172 |
| 2007 | 0.4803 | 0.02298 |
| 2008 | 0.4905 | 0.02008 |
| 2009 | 0.5140 | 0.01996 |
| 2010 | 0.5477 | 0.02024 |
4.3.2. Validation Results

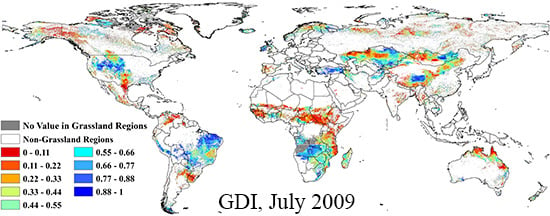
4.4. Generating and Evaluating the Global GDI Product






5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. Drought Glob. Assess. 2000, 1, 3–18. [Google Scholar]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar]
- Conner, R.; Siedl, A.; Tassell, L. USA Grasslands and Related Resources: An Economic and Biological Trends Assessment. Available online: http://irnr.tamu.edu/publications/research-reports/2001/united-states-grasslands-and-related-resources-an-economic-and-biological-trends-assessment/ (accessed on 24 September 2015).
- Caccamo, G.; Chisholm, L.; Bradstock, R.A.; Puotinen, M. Assessing the sensitivity of MODIS to monitor drought in high biomass ecosystems. Remote Sens. Environ. 2011, 115, 2626–2639. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring agricultural drought for arid and humid regions using multi-sensor remote sensing data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar] [CrossRef]
- Heim, R.R., Jr. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar]
- Tucker, C.J.; Choudhury, B.J. Satellite remote sensing of drought conditions. Remote Sens. Environ. 1987, 23, 243–251. [Google Scholar] [CrossRef]
- Bayarjargal, Y.; Karnieli, A.; Bayasgalan, M.; Khudulmur, S.; Gandush, C.; Tucker, C. A comparative study of NOAA-AVHRR derived drought indices using change vector analysis. Remote Sens. Environ. 2006, 105, 9–22. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Assessing vegetation response to drought in the Northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2003, 87, 85–98. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.; Teixeira, J.; Anderson, M.; Wardlow, B.; Hain, C. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Wood, A.W. The University of Washington Surface Water Monitor: An Experimental Platform for National Hydrologic Assessment and Prediction. In Proceedings of American Meteorology Society annual meeting, 22nd conference on hydrology, New Orleans, LA, USA, 20–24 January 2008.
- Wood, A.W.; Lettenmaier, D.P. A test bed for new seasonal hydrologic forecasting approaches in the western United States. Bull. Am. Meteorol. Soc. 2006, 87, 1699–1712. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A.; Nakhjiri, N.; Farahmand, A. Global integrated drought monitoring and prediction system. Sci. Data 2014, 1. [Google Scholar] [CrossRef] [PubMed]
- Lyon, B.; Bell, M.A.; Tippett, M.K.; Kumar, A.; Hoerling, M.P.; Quan, X.-W.; Wang, H. Baseline probabilities for the seasonal prediction of meteorological drought. J. Appl. Meteorol. Climatol. 2012, 51, 1222–1237. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Cabello, D.; Tomás-Burguera, M.; Martín-Hernández, N.; Beguería, S.; Azorin-Molina, C.; El Kenawy, A. Drought variability and land degradation in semiarid regions: Assessment using remote sensing data and drought indices (1982–2011). Remote Sens. 2015, 7, 4391–4423. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Department of Commerce, Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A.; Vanyarkho, O.V. Monitoring the 1996 drought using the standardized precipitation index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef]
- Heddinghaus, T.R.; Sabol, P. A review of the palmer drought severity index and where do we go from here. In Proceedings of the Seventh Conference on Applied Climatology, Boston, MA, USA, 10–13 September 1991.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993; pp. 179–183.
- Guttman, N.B. Accepting the Standardized Precipitation Index: A Calculation Algorithm. J. Am. Water Res. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.; Liu, H.; Batchily, K.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of changes in leaf water content using near-and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar]
- Claudio, H.C.; Cheng, Y.; Fuentes, D.A.; Gamon, J.A.; Luo, H.; Oechel, W.; Qiu, H.-L.; Rahman, A.F.; Sims, D.A. Monitoring drought effects on vegetation water content and fluxes in chaparral with the 970 nm water band index. Remote Sens. Environ. 2006, 103, 304–311. [Google Scholar] [CrossRef]
- Farrar, T.; Nicholson, S.; Lare, A. The influence of soil type on the relationships between NDVI, rainfall, and soil moisture in semiarid Botswana. II. NDVI response to soil moisture. Remote Sens. Environ. 1994, 50, 121–133. [Google Scholar] [CrossRef]
- Wang, J.; Price, K.; Rich, P. Spatial patterns of NDVI in response to precipitation and temperature in the central Great Plains. Int. J. Remote Sens. 2001, 22, 3827–3844. [Google Scholar] [CrossRef]
- Brown, J.F.; Wardlow, B.D.; Tadesse, T.; Hayes, M.J.; Reed, B.C. The vegetation drought response index (VegDRI): A new integrated approach for monitoring drought stress in vegetation. GISci. Remote Sens. 2008, 45, 16–46. [Google Scholar] [CrossRef]
- Park, S.; Feddema, J.J.; Egbert, S.L. Impacts of hydrologic soil properties on drought detection with MODIS thermal data. Remote Sens. Environ. 2004, 89, 53–62. [Google Scholar] [CrossRef]
- Kogan, F. Application of vegetation index and brightness temperature for drought detection. Adv. Sp. Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- McVicar, T.; Bierwirth, P. Rapidly assessing the 1997 drought in Papua New Guinea using composite AVHRR imagery. Int. J. Remote Sens. 2001, 22, 2109–2128. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of soil moisture deficit index (SMDI) and evapotranspiration deficit index (ETDI) for agricultural drought monitoring. Agr. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Gao, Z.; Gao, W.; Chang, N.-B. Integrating temperature vegetation dryness index (TVDI) and regional water stress index (RWSI) for drought assessment with the aid of Landsat TM/ETM+ images. Int. J. Appl. Earth Obs. Geoinform. 2011, 13, 495–503. [Google Scholar] [CrossRef]
- Kogan, F. World droughts in the new millennium from AVHRR-based vegetation health indices. Eos Trans. Am. Geophys. Union 2002, 83, 557–563. [Google Scholar] [CrossRef]
- Kogan, F.; Gitelson, A.; Zakarin, E.; Spivak, L.; Lebed, L. AVHRR-based spectral vegetation index for quantitative assessment of vegetation state and productivity. Photogramm. Eng. Remote Sens. 2003, 69, 899–906. [Google Scholar] [CrossRef]
- Liu, W.; Kogan, F. Monitoring brazilian soybean production using NOAA/AVHRR based vegetation condition indices. Int. J. Remote Sens. 2002, 23, 1161–1179. [Google Scholar] [CrossRef]
- Abbas, S.; Nichol, J.E.; Qamer, F.M.; Xu, J. Characterization of drought development through remote sensing: A case study in central Yunnan, China. Remote Sens. 2014, 6, 4998–5018. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Clim. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q. An evaluation of the standardized precipitation index, the China-z index and the statistical z-score. Int. J. Clim. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- China Meteorological Data Sharing Service System. Available online: http://cdc.nmic.cn/home.do (accessed on 2 March 2015).
- Level 1 and Atmosphere Archive and Distribution System. Available online: http://ladsweb.nascom.nasa.gov/ (accessed on 3 April 2015).
- National Snow and Ice Data Center. Available online: http://nsidc.org/ (accessed on 8 April 2015).
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geos. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Njoku, E.G. AMSR-E/Aqua Daily L3 Surface Soil Moisture, Interpretive Parameters, and QC EASE-Grids V002; National Snow and Ice Data Center: Boulder, CO, USA, 2008. [Google Scholar]
- Rodell, M.; Beaudoing, H.K. GLDAS Noah Land Surface Model l4 Monthly 0.25 × 0.25 Degree Version 2.0; Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2013. [Google Scholar]
- Hualan Rui, H.B. Readme Document for Global Land Data Assimilation System, 2nd. Available online: http://disc.sci.gsfc.nasa.gov/services/grads-gds/gldas (accessed on 23 September 2015).
- Goddard Earth Sciences Data and Information Services Center. Available online: http://disc.sci.gsfc.nasa.gov/ (accessed on 14 July 2015).
- Climate Research Unit. Available online: http://www.cru.uea.ac.uk/ (accessed on 1 January 2015).
- SPEI Global Drought Monitor. Available online: http://sac.csic.es/spei/index.html (accessed on 11 June 2015).
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.; Angulo, M.; El Kenawy, A. A new global 0.5 gridded dataset (1901–2006) of a multiscalar drought index: Comparison with current drought index datasets based on the palmer drought severity index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 66, 55–94. [Google Scholar] [CrossRef]
- US Drought Monitor. Available online: http://droughtmonitor.unl.edu/ (accessed on 29 April 2015).
- Bonan, G.B. Ecological Climatology: Concepts and Applications; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Quan, X.; He, B.; Li, X.; Tang, Z. Estimation of grassland live fuel moisture content from ratio of canopy water content and foliage dry biomass. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1903–1907. [Google Scholar] [CrossRef]
- Quan, X.; He, B.; Li, X. A Bayesian network-based method to alleviate the ill-posed inverse problem: A case study on leaf area index and canopy water content retrieval. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6507–6517. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The sail model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect+ sail models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Jacquemoud, S. Inversion of the prospect+ sail canopy reflectance model from AVIRIS equivalent spectra: Theoretical study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Institute de Physique du Globe de Paris. Available online: http://teledetection.ipgp.jussieu.fr/prosail/ (accessed on 29 April 2015).
- Jurdao, S.; Yebra, M.; Guerschman, J.P.; Chuvieco, E. Regional estimation of woodland moisture content by inverting radiative transfer models. Remote Sens. Environ. 2013, 132, 59–70. [Google Scholar] [CrossRef]
- Sow, M.; Mbow, C.; Hély, C.; Fensholt, R.; Sambou, B. Estimation of herbaceous fuel moisture content using vegetation indices and land surface temperature from MODIS data. Remote Sens. 2013, 5, 2617–2638. [Google Scholar] [CrossRef]
- Quan, X.; He, B.; Li, X.; Yin, C.; Liao, Z.; Xing, M. Retrieval of canopy water content using multiple priori inromation. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Québec, QC, Canada, 13–18 July 2014; pp. 1863–1866.
- Carlson, T.N.; Gillies, R.R.; Perry, E.M. A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover. Remote Sens. Rev. 1994, 9, 161–173. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M.; Cosh, M.H. Landslide susceptibility mapping using downscaled AMSR-E soil moisture: A case study from Cleveland Corral, California, US. Remote Sens. Environ. 2010, 114, 2624–2636. [Google Scholar] [CrossRef]
- Chauhan, N.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Panciera, R.; Rudiger, C.; Kerr, Y.H.; Walker, J. Downscaling SMOS-derived soil moisture using MODIS visible/infrared data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Zhang, Y.; Guindon, B.; Cihlar, J. An image transform to characterize and compensate for spatial variations in thin cloud contamination of Landsat images. Remote Sens. Environ. 2002, 82, 173–187. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar] [CrossRef]
- Earth Resources Observation and Science Center. Available online: http://glovis.usgs.gov/ (accessed on 12 September 2014).
- Li, X.; He, B.; Quan, X.; Liao, Z.; Bai, X. Use of the standardized precipitation evapotranspiration index (SPEI) to characterize the drying trend in southwest China from 1982–2012. Remote Sens. 2015, 7, 10917–10937. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Liao, Z.; Quan, X.; Li, X.; Hu, J. A Global Grassland Drought Index (GDI) Product: Algorithm and Validation. Remote Sens. 2015, 7, 12704-12736. https://doi.org/10.3390/rs71012704
He B, Liao Z, Quan X, Li X, Hu J. A Global Grassland Drought Index (GDI) Product: Algorithm and Validation. Remote Sensing. 2015; 7(10):12704-12736. https://doi.org/10.3390/rs71012704
Chicago/Turabian StyleHe, Binbin, Zhanmang Liao, Xingwen Quan, Xing Li, and Junjie Hu. 2015. "A Global Grassland Drought Index (GDI) Product: Algorithm and Validation" Remote Sensing 7, no. 10: 12704-12736. https://doi.org/10.3390/rs71012704
APA StyleHe, B., Liao, Z., Quan, X., Li, X., & Hu, J. (2015). A Global Grassland Drought Index (GDI) Product: Algorithm and Validation. Remote Sensing, 7(10), 12704-12736. https://doi.org/10.3390/rs71012704