Classification of Several Optically Complex Waters in China Using in Situ Remote Sensing Reflectance
Abstract
:1. Introduction

2. Materials and Methods
2.1. Data Acquisition and Processing

2.2. Classification of Rrs (λ) Spectra
2.3. Factor Analysis of Environmental Parameters
2.4. Characteristic Wavelength Extraction
3. Results and Discussion
3.1. Clustering and Determination of Centroid Sets



3.2. Links Between Rrs (λ) Spectra and Environment Characteristics
- (1)
- Environment Characteristics of Each Group
| Parameter | All Classes | Class 1 | Class 2 | Class 3 | Class 4 |
|---|---|---|---|---|---|
| chl-a (mg·m−3) | 44.2 (113.7) | 41.8 (35.8) | 7.8 (7.4) | 15.1 (28.2) | 429.0 (290.8) |
| (0.0251–942.6) | (5.98–165.8) | (0.025–18.9) | (0.0391–152.5) | (149.8–942.6) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| TSS (g·m−3) | 95.6 (66.1) | 48.9 (17.4) | 12.3 (6.5) | 150.6 (44.1) | 105.0 (61.1) |
| (3.75–244.9) | (21.5–91.1) | (3.75–26.6) | (55.2–244.9) | (32.6–213.9) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| PIM (g·m−3) | 78.1 (63.8) | 34.8 (20.7) | 8.29 (6.0) | 133.7 (45.1) | 24.3 (7.58) |
| (0–222.5) | (4.1–81.5) | (0–22.0) | (7.9–222.5) | (13.0–35.7) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| POM (g·m−3) | 17.5 (20.9) | 14.1 (9.8) | 4.0 (1.8) | 16.9 (6.4) | 80.7 (57.7) |
| (1.19–185) | (5.2–52.1) | (1.19–7.72) | (11.3–51.5) | (19.6–185.4) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| DOC (g·m−3) | 7.28 (2.03) | 7.24 (1.20) | 7.78 (2.28) | 7.15 (2.49) | 8.02 (0.65) |
| (4.31–14.2) | (4.73–10.1) | (4.31–10.45) | (4.6–14.2) | (7.03–8.96) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| aCDOM(440) (m−1) | 0.87 (0.426) | 0.98 (0.47) | 0.96 (0.70) | 0.76 (0.33) | 0.95 (0.24) |
| (0.290–2.40) | (0.35–2.40) | (0.29–2.36) | (0.33–2.14) | (0.68–1.42) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| chl-a/TSS (10−3) | 0.733 (1.14) | 0.99 (0.847) | 0.88 (1.21) | 0.165 (0.46) | 4.00 (0.77) |
| (0.00089–5.01) | (0.098–3.60) | (0.00114–4.53) | (0.00089–2.30) | (2.96–5.01) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| PIM/TSS | 0.738 (0.239) | 0.67 (0.234) | 0.606 (0.246) | 0.868 (0.13) | 0.287 (0.123) |
| (0–0.927) | (0.151–0.914) | (0–0.896) | (0.143–0.927) | (0.130–0.453) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| POM/TSS | 0.262 (0.239) | 0.326 (0.234) | 0.394 (0.246) | 0.132 (0.131) | 0.713 (0.123) |
| (0.073–1.00) | (0.0857–0.849) | (0.104–1) | (0.073–0.857) | (0.547–0.870) | |
| N = 135 | N = 44 | N = 19 | N = 65 | N = 7 | |
| bp (m−1) | 46.4 (29.0) | 24.1 (8.11) | 7.78 (2.34) | 74.0 (12.7) | 40.1 (32.5) |
| (4.81–104.3) | (11.3–49.5) | (4.81–11.7) | (52.3–103.4) | (11.9–104.3) | |
| N = 85 | N = 33 | N = 7 | N = 38 | N = 7 | |
| cpg(m−1) | 49.5 (30.7) | 25.9 (8.35) | 8.87 (2.19) | 77.5 (13.2) | 48.9 (41.7) |
| (6.18–133.7) | (12.4–52.0) | (6.18–12.2) | (55.1–108.3) | (14.0–133.7) | |
| N = 85 | N = 33 | N = 7 | N = 38 | N = 7 | |
| aCDOM/(ap+ aCDOM) | 0.157 (0.114) | 0.194 (0.0642) | 0.447 (0.065) | 0.0848 (0.0319) | 0.0850 (0.0819) |
| (0.0110–0.540) | (0.0606–0.343) | (0.358–0.540) | (0.0225–0.163) | (0.0110–0.254) | |
| N = 85 | N = 33 | N = 7 | N = 38 | N = 7 | |
| ad/(ap+ aCDOM) | 0.680 (0.235) | 0.594 (0.157) | 0.445 (0.0636) | 0.883 (0.0408) | 0.221 (0.124) |
| (0.0943–0.960) | (0.201–0.874) | (0.394–0.556) | (0.7809–0.960) | (0.0943–0.380) | |
| N = 85 | N = 33 | N = 7 | N = 38 | N = 7 | |
| aph/ap | 0.193 (0.239) | 0.255 (0.206) | 0.193 (0.0818) | 0.0358 (0.0178) | 0.748 (0.160) |
| (0.0118–0.902) | (0.0495–0.778) | (0.114–0.314) | (0.0118–0.0752) | (0.519–0.902) | |
| N = 85 | N = 33 | N = 7 | N = 38 | N = 7 |
| Class | Lake Chaohu | Three Gorges Reservoir | Lake Dianchi | Yellow River Estuary | Lake Taihu (Spring) | Lake Taihu (Summer) | Lake Taihu (Autumn) | Lake Taihu (Winter) | Total |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 21 | 2 | 24 | 4 | 67 | 39 | 31 | 44 | 232 |
| 2 | 0 | 4 | 1 | 43 | 7 | 3 | 6 | 5 | 69 |
| 3 | 8 | 16 | 6 | 7 | 51 | 1 | 3 | 47 | 139 |
| 4 | 0 | 0 | 0 | 0 | 6 | 1 | 0 | 0 | 7 |
| Total | 29 | 22 | 31 | 54 | 131 | 44 | 40 | 96 | 447 |

- (2)
- Characteristics of Rrs (λ) Spectra and correspondence with environmental parameters

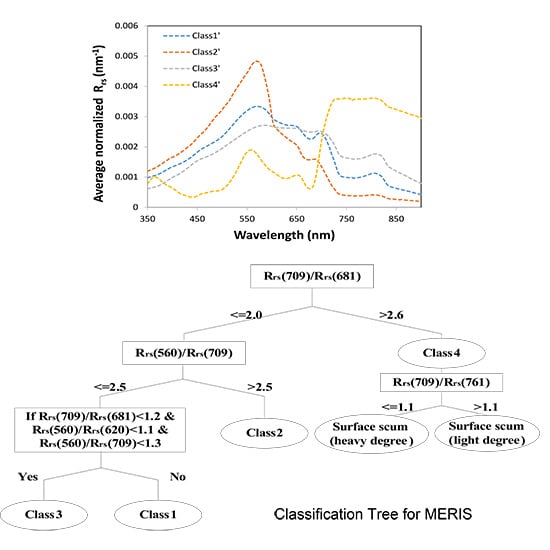
3.3. Classification Tree


3.4. Reflectance Discrimination Using Ocean Color Satellite Sensors




4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moore, T.S.; Dowell, M.D.; Bradt, S.; Ruiz Verdu, A. An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 2014, 143, 97–111. [Google Scholar] [CrossRef] [PubMed]
- Vantrepotte, V.; Loisel, H.; Dessailly, D.; Mériaux, X. Optical classification of contrasted coastal waters. Remote Sens. Environ. 2012, 123, 306–323. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Mélin, F. How optically diverse is the coastal ocean? Remote Sens. Environ. 2015, 160, 235–251. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, L.; Li, J.; Luo, L.; Yin, Y.; Liu, M.; Li, Y. Seasonal–spatial variation and remote sensing of phytoplankton absorption in Lake Taihu, a large eutrophic and shallow lake in China. J. Plankton. Res. 2010, 32, 1023–1037. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, Y.-X.; Li, D.-J.; Zhu, W.-J.; Suhyb Salama, M. Medium resolution imaging spectrometer (MERIS) estimation of chlorophyll-a concentration in the turbid sediment-laden waters of the Changjiang (Yangtze) Estuary. Int. J. Remote. Sens. 2010, 31, 4635–4650. [Google Scholar] [CrossRef]
- Ma, R.; Tang, J.; Dai, J.; Zhang, Y.; Song, Q. Absorption and scattering properties of water body in Taihu Lake, China: Absorption. Int. J. Remote. Sens. 2006, 27, 4277–4304. [Google Scholar] [CrossRef]
- Chen, J.; Cui, T.; Qiu, Z.; Lin, C. A three-band semi-analytical model for deriving total suspended sediment concentration from HJ-1A/CCD data in turbid coastal waters. ISPRS J. Photogramm. 2014, 93, 1–13. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Hu, C. Evaluation of remote sensing algorithms for cyanobacterial pigment retrievals during spring bloom formation in several lakes of East China. Remote Sens. Environ. 2012, 126, 126–135. [Google Scholar] [CrossRef]
- Wu, G.; Cui, L.; Duan, H.; Fei, T.; Liu, Y. An approach for developing Landsat-5 TM-based retrieval models of suspended particulate matter concentration with the assistance of MODIS. ISPRS J. Photogramm. 2013, 85, 84–92. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Li, L.; Lu, H.; Song, K.; Liu, Z.; Xu, Y.; Li, Z. Remote chlorophyll-a estimates for inland waters based on a cluster-based classification. Sci. Total. Environ. 2013, 444, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Loisel, H.; Morel, A. Light scattering and chlorophyll concentration in case 1 waters: A reexamination. Limnol. Oceanogr. 1998, 43, 847–858. [Google Scholar] [CrossRef]
- Jerlov, N.G. Marine optics, 2nd ed.; Elsevier Science Publishing Company: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Cannizzaro, J.P.; Carder, K.L. Estimating chlorophyll a concentrations from remote-sensing reflectance in optically shallow waters. Remote Sens. Environ. 2006, 101, 13–24. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Optics. 1998, 37, 6329–6338. [Google Scholar] [CrossRef]
- Sasmal, S. Optical classification of waters in the eastern Arabian Sea. J. Indian Soc. Remote Sens. 1997, 25, 73–78. [Google Scholar] [CrossRef]
- Koenings, J.; Edmundson, J. Secchi disk and photometer estimates of light regimes in Alaskan lakes: Effects of yellow color and turbidity. Limnol. Oceanogr. 1991, 36, 91–105. [Google Scholar] [CrossRef]
- Koponen, S.; Pulliainen, J.; Kallio, K.; Hallikainen, M. Lake water quality classification with airborne hyperspectral spectrometer and simulated MERIS data. Remote Sens. Environ. 2002, 79, 51–59. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Baker, K.S.; Smith, R.C. Bio-optical classification and model of natural waters. 2. Limnol. Oceanogr. 1982, 27, 500–509. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Wang, Q.; Le, C.; Lv, H.; Huang, C.; Gong, S. Specific inherent optical quantities of complex turbid inland waters, from the perspective of water classification. Photochem. Photobiol. 2012, 11, 1299–1312. [Google Scholar] [CrossRef] [PubMed]
- Reinart, A.; Herlevi, A.; Arst, H.; Sipelgas, L. Preliminary optical classification of lakes and coastal waters in Estonia and south Finland. J. Sea. Res. 2003, 49, 357–366. [Google Scholar] [CrossRef]
- de Lucia Lobo, F.; Novo, E.M.L.d.M.; Barbosa, C.C.F.; Galvão, L.S. Reference spectra to classify Amazon water types. Int. J. Remote. Sens. 2011, 33, 3422–3442. [Google Scholar] [CrossRef]
- Lubac, B.; Loisel, H. Variability and classification of remote sensing reflectance spectra in the eastern English Channel and southern North Sea. Remote Sens. Environ. 2007, 110, 45–58. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Zhang, H. Remote estimation of chlorophyll a in optically complex waters based on optical classification. Remote Sens. Environ. 2011, 115, 725–737. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Dowell, M.D. A class-based approach to characterizing and mapping the uncertainty of the MODIS ocean chlorophyll product. Remote Sens. Environ. 2009, 113, 2424–2430. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q.; Wu, C.; Zhao, S.; Xu, X.; Wang, Y.; Huang, C. Estimation of chlorophyll a concentration using NIR/RED bands of MERIS and classification procedure in inland turbid water. IEEE. Trans. Geosci. Remote Sens. 2012, 50, 988–997. [Google Scholar] [CrossRef]
- Liu, J.; Sun, D.; Zhang, Y.; Li, Y. Pre-classification improves relationships between water clarity, light attenuation, and suspended particulates in turbid inland waters. Hydrobiologia 2013, 711, 71–86. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.S.; Liu, Z.; Yin, K.; Li, Z.; Wai, O.W.; King, B. Integration of multi-source data for water quality classification in the Pearl River estuary and its adjacent coastal waters of Hong Kong. Cont. Shelf. Res. 2004, 24, 1827–1843. [Google Scholar] [CrossRef]
- Reinart, A.; Kutser, T. Comparison of different satellite sensors in detecting cyanobacterial bloom events in the Baltic Sea. Remote Sens. Environ. 2006, 102, 74–85. [Google Scholar] [CrossRef]
- Feng, H.; Campbell, J.W.; Dowell, M.D.; Moore, T.S. Modeling spectral reflectance of optically complex waters using bio-optical measurements from Tokyo Bay. Remote Sens. Environ. 2005, 99, 232–243. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Feng, H. A fuzzy logic classification scheme for selecting and blending satellite ocean color algorithms. IEEE. Trans. Geosci. Remote Sens. 2001, 39, 1764–1776. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA; 1967. [Google Scholar]
- Ainsworth, E.J.; Jones, I.S. Radiance spectra classification from the ocean color and temperature scanner on ADEOS. IEEE. Trans. Geosci. Remote Sens. 1999, 37, 1645–1656. [Google Scholar] [CrossRef]
- Martin Traykovski, L.V.; Sosik, H.M. Feature-based classification of optical water types in the northwest Atlantic based on satellite ocean color data. J. Geophys. Res. 2003, 108, C5. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Wang, Q.; Gao, J.; Le, C.; Huang, C.; Shaoqi, G. Hyperspectral remote sensing of the pigment c-phycocyanin in turbid inland waters, based on optical classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3871–3884. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, B.; Wang, X.; Li, J.; Feng, S.; Zhao, Q.; Liu, M.; Qin, B. A study of absorption characteristics of chromophoric dissolved organic matter and particles in Lake Taihu, China. Hydrobiologia 2007, 592, 105–120. [Google Scholar] [CrossRef]
- Zhang, B.; Li, J.; Shen, Q.; Chen, D. A bio-optical model based method of estimating total suspended matter of Lake Taihu from near-infrared remote sensing reflectance. Environ. Monit. Assess. 2008, 145, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Li, Y.; Wang, Q.; Le, C.; Huang, C.; Shi, K. Development of optical criteria to discriminate various types of highly turbid lake waters. Hydrobiologia 2011, 669, 83–104. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, Q.; Cui, T.; Xue, C.; Zhang, S. Suspended sediment monitoring and assessment for Yellow River estuary from Landsat TM and ETM+ imagery. Remote Sens. Environ. 2014, 146, 136–147. [Google Scholar] [CrossRef]
- Mueller, J.L.; Fargion, G.S.; McClain, C.R.; Mueller, J.; Brown, S.; Clark, D.; Johnson, B.; Yoon, H.; Lykke, K.; Flora, S. Special topics in ocean optics protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, 5th ed.NASA: Greenbelt, MD, USA, 2003; pp. 1–36. [Google Scholar]
- Lorenzen, C.J. Determination of chlorophyll and pheo-pigments: Spectrophotometric equations. Limnol. Oceanogr. 1967, 12, 343–346. [Google Scholar] [CrossRef]
- Simis, S.G.; Peters, S.W.; Gons, H.J. Remote sensing of the cyanobacterial pigment phycocyanin in turbid inland water. Limnol. Oceanogr. 2005, 50, 237–245. [Google Scholar] [CrossRef]
- Mitchell, B.G. Algorithms for determining the absorption coefficient for aquatic particulates using the quantitative filter technique. Proc. SPIE 1990, 1302, 137–148. [Google Scholar]
- Matlab. Fuzzy Logic Toolbox. Available online: http://www.mathworks.cn/cn/help/fuzzy/data-clustering.html (accessed on 8 June 2015).
- Zhao, Q.P.; Hautamaki, V.; Franti, P. Knee point detection in BIC for detecting the number of clusters. In Proceedings of Advanced Concepts for Intelligent Vision Systems, Juan-les-Pins, France, 20–24 October 2008; BlancTalon, J., Bourennane, S., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer-Verlag Berlin: Berlin, Germany, 2008; Volume 5259, pp. 664–673. [Google Scholar]
- Dunn, J.C. A fuzzy relative of the ISO data process and its use in detecting compact well-separated clusters. Cybernet. Syst. 1973, 3, 32–57. [Google Scholar]
- Bezdek, J.C. A physical interpretation of fuzzy ISODATA. IEEE Trans. Syst. Man Cybern. 1976, 6, 387–390. [Google Scholar] [CrossRef]
- Su, H.J.; Du, P.J.; Du, Q. Semi-supervised dimensionality reduction using orthogonal projection divergence-based clustering for hyperspectral imagery. Opt. Eng. 2012, 51, 111715-1. [Google Scholar] [CrossRef]
- Swain, P.H.; Davis, S.M. Remote Sensing: The Quantitative Approach; McGraw-Hill International Book Co.: New York, NY, USA, 1978; p. 396. [Google Scholar]
- Cureton, E.E.; D’Agostino, R.B. Factor Analysis: An Applied Approach; Lawrence Erlbaum Associates Inc.: Hillsdale, NJ, USA, 1983; p. 389. [Google Scholar]
- NIST/SEMATECH e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/eda/section3/eda357.htm (accessed on 31 July 2015.).
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.; Arnone, R.; He, M. Determination of primary spectral bands for remote sensing of aquatic environments. Sensors 2007, 7, 3428–3441. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, B.; Li, J.-S.; Wu, Y.-F.; Wu, D.; Song, Y.; Zhang, F.-F.; Wang, G.-L. Characteristic wavelengths analysis for remote sensing reflectance on water surface in Taihu Lake. Spectrosc. Spect. Anal. 2011, 31, 1892–1897. [Google Scholar]
- Ruffin, C.; King, R. The analysis of hyperspectral data using Savitzky-Golay filtering-theoretical basis. In Proceedings of Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; pp. 756–758.
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Congalton, R. The Use of Discrete Multivariate Analysis for the Assessment of Landsat Classification Accuracy. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, September 1981. [Google Scholar]
- IOCCG Report No. 3: Remote Sensing of Ocean Colour in Coastal, and other Optically-Complex, Waters; IOCCG Project Office: Dartmouth, UK, 2000; p. 8.
- Pulliainen, J.; Kallio, K.; Eloheimo, K.; Koponen, S.; Servomaa, H.; Hannonen, T.; Tauriainen, S.; Hallikainen, M. A semi-operative approach to lake water quality retrieval from remote sensing data. Sci. Total. Environ. 2001, 268, 79–93. [Google Scholar] [CrossRef]
- Gons, H.J. Optical teledetection of chlorophyll a in turbid inland waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Thiemann, S.; Kaufmann, H. Determination of chlorophyll content and trophic state of lakes using field spectrometer and IRS-1C satellite data in the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2000, 73, 227–235. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—Return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- Ruiz-Verdu, A.; Simis, S.G.H.; de Hoyos, C.; Gons, H.J.; Pena-Martinez, R. An evaluation of algorithms for the remote sensing of cyanobacterial biomass. Remote Sens. Environ. 2008, 112, 3996–4008. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Q.; Li, J.; Zhang, F.; Sun, X.; Li, J.; Li, W.; Zhang, B. Classification of Several Optically Complex Waters in China Using in Situ Remote Sensing Reflectance. Remote Sens. 2015, 7, 14731-14756. https://doi.org/10.3390/rs71114731
Shen Q, Li J, Zhang F, Sun X, Li J, Li W, Zhang B. Classification of Several Optically Complex Waters in China Using in Situ Remote Sensing Reflectance. Remote Sensing. 2015; 7(11):14731-14756. https://doi.org/10.3390/rs71114731
Chicago/Turabian StyleShen, Qian, Junsheng Li, Fangfang Zhang, Xu Sun, Jun Li, Wei Li, and Bing Zhang. 2015. "Classification of Several Optically Complex Waters in China Using in Situ Remote Sensing Reflectance" Remote Sensing 7, no. 11: 14731-14756. https://doi.org/10.3390/rs71114731
APA StyleShen, Q., Li, J., Zhang, F., Sun, X., Li, J., Li, W., & Zhang, B. (2015). Classification of Several Optically Complex Waters in China Using in Situ Remote Sensing Reflectance. Remote Sensing, 7(11), 14731-14756. https://doi.org/10.3390/rs71114731