A Generic Algorithm to Estimate LAI, FAPAR and FCOVER Variables from SPOT4_HRVIR and Landsat Sensors: Evaluation of the Consistency and Comparison with Ground Measurements

Abstract

The leaf area index (LAI) and the fraction of photosynthetically active radiation absorbed by green vegetation (FAPAR) are essential climatic variables in surface process models. FCOVER is also important to separate vegetation and soil for energy balance processes. Currently, several LAI, FAPAR and FCOVER satellite products are derived moderate to coarse spatial resolution. The launch of Sentinel-2 in 2015 will provide data at decametric resolution with a high revisit frequency to allow quantifying the canopy functioning at the local to regional scales. The aim of this study is thus to evaluate the performances of a neural network based algorithm to derive LAI, FAPAR and FCOVER products at decametric spatial resolution and high temporal sampling. The algorithm is generic, i.e., it is applied without any knowledge of the landcover. A time series of high spatial resolution SPOT4_HRVIR (16 scenes) and Landsat 8 (18 scenes) images acquired in 2013 over the France southwestern site were used to generate the LAI, FAPAR and FCOVER products. For each sensor and each biophysical variable, a neural network was first trained over PROSPECT+SAIL radiative transfer model simulations of top of canopy reflectance data for green, red, near-infra red and short wave infra-red bands. Our results show a good spatial and temporal consistency between the variables derived from both sensors: almost half the pixels show an absolute difference between SPOT and LANDSAT estimates of lower that 0.5 unit for LAI, and 0.05 unit for FAPAR and FCOVER. Finally, downward-looking digital hemispherical cameras were completed over the main land cover types to validate the accuracy of the products. Results show that the derived products are strongly correlated with the field measurements (R² > 0.79), corresponding to a RMSE = 0.49 for LAI, RMSE = 0.10 (RMSE = 0.12) for black-sky (white sky) FAPAR and RMSE = 0.15 for FCOVER. It is concluded that the proposed generic algorithm provides a good basis to monitor the seasonal variation of the vegetation biophysical variables for important crops at decametric resolution.

1. Introduction

Leaf area index (LAI) is defined as half the total developed area of green elements per unit horizontal ground area [1]. The fraction of photosynthetically absorbed radiation (FAPAR) is defined as the faction of the photosynthetically radiation (PAR) absorbed by the green leaves. It is a weighted sum of the direct FAPAR and diffuse FAPAR, depending on the source of the incoming radiation [2]. LAI and FAPAR have been recognized as Essential Climate Variables (ECV) by GCOS [3], for their key roles in energy, mass and momentum exchanges between the land surface and the atmosphere. FAPAR is also used as one of the main inputs in light use efficiency models [4]. Besides LAI and FAPAR variables, FCOVER, the fraction of the green vegetation in the nadir direction, is used to separate vegetation and soil in energy balance processes, including temperature and evapotranspiration. Over the last decade, several global LAI, FAPAR and FCOVER products have been generated from SPOT-VGT, SEAWIFS, MERIS, MODIS and AVHRR sensors at a spatial resolution close to 1km and a temporal sampling of 8 to 16 days [5,6,7,8,9,10]. However, this kilometric resolution is generally much larger than the typical length scales of most landscapes, limiting therefore the applications to the regional and local scales [11]. The development of LAI, FAPAR and FCOVER biophysical products from decametric spatial resolution sensors will be better suited for addressing these applications closely related to agriculture, ecosystem and environmental management. However, the monitoring capacity and actual use of such sensors is still limited by the revisit frequency or the cost of the images. The European Sentinel-2 Mission [12] (https://earth.esa.int/web/guest/missions/esa-future-missions/sentinel-2) will fulfill most of the requirements by providing global images with decametric resolution (10–20 m) every five days with two satellites, under constant viewing angles at each location.

A SPOT4 (Take5) experiment was started in 2013 by the French Agency Centre National d’Etudes Spatiales (CNES), aiming at providing time series of images with similar revisit frequency and resolution as Sentinel-2 data (http://www.cesbio.ups-tlse.fr/multitemp/) to prepare for the use of the data of this satellite that has just been launched in June 2015. However, the experiment lasted only few months, which is not enough to cover a full vegetation cycle. The series was therefore completed with Landsat 8 images at a 30m spatial resolution and 16 days revisit period, taking advantage of the overlap between satellite tracks allowing to double the revisit frequency.

Several studies demonstrated the capacity to derive biophysical products with a reasonable accuracy from decametric surface reflectance data. Among several authors, Ganguly et al. [13] generated 30-m LAI from LANDSAT-5 surface reflectance data based on the canopy spectral invariants theory and look-up table method. Panferov [14] generated LAI from LANDSAT ETM+ data over forests and Verger et al. [15,16] estimated FAPAR, FCOVER and LAI over crops using LANDSAT-5 data. Li and Fang [17] generated the FAPAR data over six FLUXNET sites from the lookup table method using the LANDSAT-5 images. However, these studies focus on single sensors, limiting the length and continuity of the time series that could be derived.

The objective of this study is to evaluate the performances of a generic algorithm to generate consistent time series of LAI, FAPAR and FCOVER products from the combination of SPOT4_HRVIR and Landsat 8 surface reflectance data acquired during a growth season, without any prior knowledge of the landcover. The study area and data sets will first be presented. Then, the algorithm developed to derive the products will be described. Finally, the performances of the products will be analyzed, with emphasis on the spatial and temporal consistency between products and the comparison with field measurements.

2. Study Area and Data Description

2.1. The Experimental Site: Southwest France

The site is a 13.2 × 14.4 km² area located near Toulouse, southwest France (43.54°N, 1.13°E, Figure 1). The region experiences a typical temperate continental climate with hot and dry summer and cold and humid winter [18]. More than 65% of the study area is covered by crops, including barley, rapeseed, wheat, maize and sunflower. Barley, rapeseed and wheat are winter crops sown from October to November and harvested in the beginning of July. Corn and sunflower are summer crops sown from mid-April to beginning of June and harvested until September to October. Most fields were located on flat soil with relatively uniform soil properties and cultural practices and are therefore relatively homogeneous. Grassland is distributed in the center and south west of the region, while broadleaf and needleleaf forests are mainly observed in the northwestern parts (Figure 1).

2.2. SPOT4_HRVIR and Landsat 8 Data

The SPOT4_HRVIR satellite was launched in March, 1998. In 2013, CNES lowered the altitude of SPOT4 by 2 km to increase the repeat cycle. On its nominal orbit, SPOT4 did 14.17 orbits per day, but reducing the altitude by two kilometers enabled it to reach 14.2 orbits per day, which results in exactly 71 orbits every five days. Therefore, on this sun-synchronous orbit inclined at 96.7°, it provided observations every five days over 45 sites distributed on the globe with an equatorial crossing time of 10:30. The images are acquired with varying viewing angles at a spatial resolution of 20m. Four spectral bands are available, including green, red, near-infra red (NIR) and short wave infra-red (SWIR, Figure 2). The raw images were firstly ortho-rectified based on the SIGMA tool developed by CNES [19,20]. Then the ortho-rectified top of atmosphere reflectance data were processed by the Multi-Sensor Atmospheric Correction Software (MACCS) [21,22] to generate top of canopy reflectance data, along with a cloud/cloud shadows/water/snow masks. The method uses multi-temporal criteria to build various masks and to quantify the aerosol optical thickness [23]. Sixteen SPOT4_HRVIR scenes were used in this study.

Figure 1. The location and land cover types of the study area (Landsat 8, 17 April 2013). The location of the ground measurements correspond to the red circles.

Figure 1. The location and land cover types of the study area (Landsat 8, 17 April 2013). The location of the ground measurements correspond to the red circles.

Landsat 8 launched on 11 February 2013, is the latest in a series of Landsat spacecrafts going back 40 years. Landsat 8 observes the world at a 705 km altitude orbit, with an inclination angle of 98.2°, a revisit frequency of 16 days and an equatorial crossing time of 10:00. The OLI sensor aboard Landsat 8 includes nine spectral bands with a spatial resolution of 30m for Bands 1 to 7 and 9 while band 8 has 15m spatial resolution. Only four bands (green (Band 3), red (band 4), NIR (Band 5) and SWIR-1 (Band 6)) will be used in this study (Figure 2) to keep the band setting consistent with that of SPOT4_HRVIR. The Level 1T Landsat 8 data were first ortho-rectified by USGS, using a global data base of ground control points. Radiometric calibration was performed using the coefficients provided with the Level 1T products. The data were further processed using the same MACCS algorithm as that used for SPOT4_HRVIR [21,22]. Note that because of the overlap between 2 Landsat 8 tracks over the site considered, the revisit frequency was doubled. 18 Landsat 8 scenes were used in this study.

Figure 2. The relative spectral responses of SPOT4_HRVIR (solid lines) and Landsat 8 (dashed lines) bands used in this study.

Figure 2. The relative spectral responses of SPOT4_HRVIR (solid lines) and Landsat 8 (dashed lines) bands used in this study.

A total of 16 SPOT4_HRVIR and 18 Landsat 8 top of canopy reflectance images, combined with a cloud/cloud shadow mask were downloaded through the THEIA land data center website (http://spirit.cnes.fr/take5/). The pixels contaminated by the clouds/cloud shadow or flagged as snow were not used in this study. The SPOT4_HRVIR data was resampled to 30m to be consistent with the Landsat 8 data.

2.3. Landcover Data

Although the proposed generic algorithm should apply to any landcover, its performances will be analyzed for the main landcover classes observed over the study site. The land cover types were produced based on the random forest classification method [24]. The random forest was trained using all the spectral information of 34 SPOT4_HRVIR Take 5 images and Landsat 8 images acquired from February 2013 to December 2013 [25]. Based on the knowledge of land cover and crop type distribution in the study area, 5 crop types (barley, wheat, rapeseed, sunflower and corn), needleleaf and broadleaf forests, grassland, urban areas and water bodies were identified as the final classes. The resulting map yielded an overall accuracy of 87% (Figure 1). Winter crops (Wheat, barley, rapeseed) are dominant (39.8%) followed (25.7%) by summer crops (Maize, sunflower) (Table 1). Forests and water bodies are marginally represented.

Table 1. The proportion of the each land cover type in the study area.

Type	Barley	Rapeseed	Wheat	Maize	Sunflower	Grassland	BroadleafForests	NeedleleafForests	Urban	Water
Proportion (%)	1.7	5.86	32.26	11.29	14.41	13.84	6.65	1.19	12.28	0.52

Table 1. The proportion of the each land cover type in the study area.

Type	Barley	Rapeseed	Wheat	Maize	Sunflower	Grassland	BroadleafForests	NeedleleafForests	Urban	Water
Proportion (%)	1.7	5.86	32.26	11.29	14.41	13.84	6.65	1.19	12.28	0.52

2.4. Ground Data

Ground measurements data over wheat, maize, and sunflower were collected from 17 April to 23 October 2013 using digital hemispherical photographs (DHPs). For each landcover class, the measurements were conducted within a 20 × 20 m² Elementary sampling unit (ESU) around every 10 days. The location of each ESU was recorded by a GPS instrument within an accuracy of few meters (Figure 1). Each ESU was sampled with 12–20 DHPs according to the VALERI spatial sampling protocol (http://w3.avignon.inra.fr/valeri). The DHPs were taken using a Nikon CoolPix 8400 camera equipped with a FC-E8 fisheye lens. The downward-looking camera was fixed at the top of a pole. The height of the pole changes throughout the measurements to keep a constant distance (~1.5 m) between the lens and top of the canopy [26]. All valid photos within an ESU were processed simultaneously using the CAN-EYE software (http://www4.paca.inra.fr/can-eye) to extract the LAI, FAPAR and FCOVER variables [27]. Effective LAI was derived by inverting the turbid medium transmittance model [28,29].

For green canopy, FAPAR is approximated as the fraction of intercepted PAR (FIPAR) calculated from the gap fraction [27]. This assumption is valid in the growing season due to the strong absorption capacity of the photosynthetic pigments [30] and the fact that the green leaves are mainly located at the top of the canopy. In this study, FIPAR is used for the validation since all field data were collected during the growing season. Both instantaneous black-sky (FIPAR_b) at 10:00 local solar time and white-sky FIPAR (FIPAR_w) were computed as follows:

$$FIPA{R}_b=GF({\theta }_{10:00})$$

(1)

$$FIPA{R}_w=2{\displaystyle \underset{0}{\overset{\pi /2}{\int }}(GF(\theta ))\cos \theta \sin \theta d\theta }$$

(2)

where GF is the measured green fraction on each viewing zenith angle $\theta$ and ${\theta }_{10:00}$ is the sun zenith angle at 10:00 local solar time. Note that the instantaneous black sky FIPAR at 10:00 local solar time is a close approximation of the daily integrated black sky FIPAR [5].

As it is impossible to get a green fraction in the exact nadir direction from the hemispherical photos, FCOVER in CAN-EYE is approximated from the green fraction ranging from nadir direction to ±10°.

$$FCOVER=GF({\theta }_{0-10})$$

(3)

where $GF({\theta }_{0-10})$ represents the integrated green fraction from nadir to ±10°.

3. Methods

The principle of this generic algorithm is to derive LAI, FAPAR and FCOVER using a neural network trained over a database generated by a radiative transfer model simulation. Many inversion algorithms have been proposed to estimate LAI, FAPAR and FCOVER. Among the several possible retrieval methods available [31], we selected a machine learning approach based on neural network technique because (i) they can describe any linear and nonlinear relationship between input and output variables if enough neurons and layers are used [32]; (ii) they are computationally efficient after the training process; (iii) they are able to provide good estimation results as the optimization operates directly over the target variables and they have efficient interpolation capacity [31]. Such machine learning inversion algorithm has been applied with success in many studies [5,16,33,34,35]. The outline of the algorithm is summarized in Figure 3. A training data set is first populated by simulating top of canopy reflectance corresponding to a large number of possible cases using a radiative transfer model. This training data set will be also used to build the definition domain, i.e., the convex hull of input reflectances in the space of the 4 bands used. Then, the architecture and the coefficients of the neurons are adjusted to provide the best match between the variables in the training database and those estimated by the neural network. More details are given in the following.

Figure 3. The outline of the algorithm. V_in represents the input variables for the radiative transfer model (RTM). R_e and R_m represent the estimated and measured top of canopy reflectance, respectively. NN is the neural network. V_out donates the output variables and U_out is the output uncertainties.

Figure 3. The outline of the algorithm. V_in represents the input variables for the radiative transfer model (RTM). R_e and R_m represent the estimated and measured top of canopy reflectance, respectively. NN is the neural network. V_out donates the output variables and U_out is the output uncertainties.

3.1. Reflectance Models

The widely used PROSAIL radiative transfer model [36] was selected in this study. The model couples the SAIL canopy reflectance model [37] and the PROSPECT leaf optical model [38]. The SAIL model assumes the canopy as a turbid medium within which the leaves are randomly located. This model has been already used with success in a number of studies to estimate the considered biophysical variables. Canopy structure is characterized by LAI, the average leaf angle (ALA) assuming an ellipsoidal distribution [39], and a hot spot parameter (HOT) [40]. The PROSPECT model is widely used to simulate leaf optical properties through several structural and chemistry characteristics. In this study, the PROSPECT model with the updated absorption coefficients proposed by [41] was used. The soil reflectance data was simulated using five typical soil reflectance spectra multiplied by a brightness coefficient allowing to accurately represent a large soil dataset where soil types, roughness, moisture and observational geometry vary [42].

3.2. Generate the Learning Database

To generate a learning database that could best represent the possible types and states of actual canopies, the distribution law of the variable should be well considered [5]. Table 2 lists the range and distribution law for all variables of PROSAIL model. Some constraints on the co-distributions between variables were also introduced to restrict the space of canopy realization while keeping high degree of realism. More detailed justifications of the range and distribution of values used to build the training database can be found in the Sentinel-2 algorithm report [43]. The variables distribution laws in this study are very similar as the ones used to generate the Sentinel-2 algorithm prototype, except for ALA and N with narrower distribution for this study due to the limited number of land cover types. Because of the generic nature of the proposed algorithm, the same training dataset, therefore the same neural network, will be applied to all land cover types.

Table 2. List of variables required to run PROSAIL model. The distribution law was described by using mode and standard deviation. Nb_Class represents the number of classes for each variable.

	Variable	Minimum	Maximum	Mode	Std	Nb_Class	Law
Canopy	LAI	0.0	15.0	2.0	2.0	6	Gauss
	ALA (°)	15	80	40	20	4	Gauss
	HOT	0.1	0.5	0.2	0.5	1	Gauss
Leaf	N	1.20	1.80	1.50	0.30	3	Gauss
	Cab (µg.m−2)	20	90	45	30	4	Gauss
	Cdm (g.m−2)	0.003	0.011	0.005	0.005	4	Gauss
	Cw_Rel	0.60	0.85	0.75	0.08	4	Uniform
	Cbp	0.00	2.00	0.00	0.30	3	Gauss
Soil	Bs	0.50	3.50	1.20	2.00	4	Gauss

Table 2. List of variables required to run PROSAIL model. The distribution law was described by using mode and standard deviation. Nb_Class represents the number of classes for each variable.

	Variable	Minimum	Maximum	Mode	Std	Nb_Class	Law
Canopy	LAI	0.0	15.0	2.0	2.0	6	Gauss
	ALA (°)	15	80	40	20	4	Gauss
	HOT	0.1	0.5	0.2	0.5	1	Gauss
Leaf	N	1.20	1.80	1.50	0.30	3	Gauss
	Cab (µg.m−2)	20	90	45	30	4	Gauss
	Cdm (g.m−2)	0.003	0.011	0.005	0.005	4	Gauss
	Cw_Rel	0.60	0.85	0.75	0.08	4	Uniform
	Cbp	0.00	2.00	0.00	0.30	3	Gauss
Soil	Bs	0.50	3.50	1.20	2.00	4	Gauss

A full orthogonal experimental plan was adopted to randomly sample the variables according to the number of classes, variation range and distribution law defined above [44]. This sampling scheme could account for all the interactions between variables and generate a learning data base evenly but quasi-randomly populated. For each combination of variables in the learning data base, the top of canopy reflectance on each wavelength was simulated by running the PROSAIL model in a forward mode. Then the reflectance was spectrally integrated to represent actual SPOT4_HRVIR and Landsat 8 bands according to the spectral response function of the sensor (Figure 2). Instantaneous black-sky FAPAR, at the satellite pass-by time (10:00 am for Landsat 8, 10:30 am for SPOT4_HRVIR), white-sky FAPAR and FCOVER were simulated by running the PROSAIL model in the forward mode using the same input variables.

The radiative transfer model introduces uncertainties associated with the simulated reflectance due to its adequacy to represent the actual canopy architecture. This mainly results in structured errors. The accuracy of actual measured top of canopy reflectance is also influenced by several possible factors, including the instrumental noise, radiometric calibration, atmospheric correction and cloud or cloud shadow contamination. These factors will lead to multiplicative or additive uncertainties to the measured reflectance [16]. To get a more realistic canopy reflectance simulated value, an uncertainty model was used to describe the additive and multiplicative uncertainties based on a white Gaussian noise:

R*(λ) = R(λ) (1+(MD(λ)+MI)/100)+AD(λ)+AI

(4)

where R(λ) is the raw simulated reflectance, R*(λ) is the reflectance contaminated with noise, MD is the multiplicative wavelength dependent noise, MI is the multiplicative wavelength independent noise, AD is the additive wavelength independent noise, and AI is the additive wavelength independent noise. In this study, the MD, MI, AD and AI were fixed to 0.02, 0.02, 0.01, and 0.01 for all bands of each sensor.

A total of 55,296 cases were simulated for each sensor with input canopy variables and output reflectance, FAPAR and FCOVER.

A definition domain was generated by the co-distribution of the simulated reflectance on each band. Figure 4 shows the definition domain for the four Landsat 8 bands used in this study (a similar definition domain was generated for SPOT4_HRVIR bands but was not shown for the sake of brevity). Pixels with reflectance values outside of the definition domain will be reported as “input out of range”. The solar zenith angle for each image was also calculated. Only the images with solar zenith angle smaller than 65° will be used in further analysis: atmospheric and directional effects are considered as too important for zenith angles larger than 65°.

Figure 4. The definition domain (colorful region) of the simulated TOC reflectance on four Landsat 8 bands (3, 4, 5, 6). (a) Band 4 and Band 3; (b) Band 5 and Band 3; (c) Band 6 and Band 3; (d) Band 5 and Band 4 (e) Band 6 and Band 4; (f) Band 6 and Band 5.

Figure 4. The definition domain (colorful region) of the simulated TOC reflectance on four Landsat 8 bands (3, 4, 5, 6). (a) Band 4 and Band 3; (b) Band 5 and Band 3; (c) Band 6 and Band 3; (d) Band 5 and Band 4 (e) Band 6 and Band 4; (f) Band 6 and Band 5.

3.3. Train the Neural Network

Two distinct databases were generated for LANDSAT8 and for SPOT4_HRVIR. Each database was divided into two parts: two thirds of the simulations were randomly selected to train the neural network, and the remaining simulations were used for the hyper-specialization control and the evaluation of the theoretical performances. For both sensors, a back-propagation artificial neural network [45] made of one input layer composed of the normalized input data, one hidden layer composed of 5 neurons with tangent sigmoid transfer functions and one output layer with a linear transfer function was selected. The input layer of the network corresponds to the surface reflectance for each band and the geometrical configurations: the cosine of the view zenith angle, the cosine of the sun zenith angle and the cosine of the relative azimuth angle between sun and view directions; the outputs are LAI, instantaneous black-sky FAPAR, white-sky FAPAR and FCOVER. The normalization applied to the input and output variables is expected to increase the performances of the Levenberg-Marquardt minimization algorithm [46] used in the training process. For each output variable and each sensor, five networks were trained with different initial solutions. The best one is then selected based on the smallest RMSE between the outputs (estimated variable) and the corresponding “reference” biophysical variables in the test data set. Results show that the theoretical performances of the 5 neural networks were very close. The best neural network achieved very good theoretical performances as observed in Figure 5 for Landsat 8. Table 3 shows that the theoretical performances are very close for SPOT4_HRVIR and Landsat 8.

Figure 5. The theoretical performances of the neural network for (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR, and (d) FCOVER. This neural network was trained for Landsat 8.

Figure 5. The theoretical performances of the neural network for (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR, and (d) FCOVER. This neural network was trained for Landsat 8.

Table 3. Comparison of the theoretical performances (R² and RMSE in bracket) between SPOT4_HRVIR and Landsat 8.

	LAI	Black-Sky FAPAR	White-Sky FAPAR	FCOVER
SPOT4_HRVIR	0.77 (0.84)	0.94 (0.06)	0.88 (0.08)	0.96 (0.05)
Landsat 8	0.8 (0.71)	0.94 (0.06)	0.9 (0.07)	0.96 (0.05)

Table 3. Comparison of the theoretical performances (R² and RMSE in bracket) between SPOT4_HRVIR and Landsat 8.

	LAI	Black-Sky FAPAR	White-Sky FAPAR	FCOVER
SPOT4_HRVIR	0.77 (0.84)	0.94 (0.06)	0.88 (0.08)	0.96 (0.05)
Landsat 8	0.8 (0.71)	0.94 (0.06)	0.9 (0.07)	0.96 (0.05)

Finally, the uncertainty of each variable is estimated. Based on the training dataset and validation dataset, the theoretical performances of algorithm can be calculated from the RMSE between the estimated and validation biophysical values (Figure 5 and Table 3). A specific neural network was then trained for each product to relate the theoretical performances of the neural network to the input reflectance and observation geometry values. More details can be found in [43].

3.4. Inversion

Once trained, the neural network can be applied over each pixel for a given sensor. However, the input reflectance in the four bands is first checked to verify if it belongs to the definition domain to ensure consistency with the training database. If the observation is outside the definition domain, a flag “inputs out of range” is raised. In addition, the output estimated variables should be also within a predefined range determined by the training dataset and extended by a small tolerance interval (Table 4, Equations (5) and (6)). Otherwise, an “output out of range” flag will be raised for the pixel. Only the data without the input or output “out of range” flag were used in the following analysis

if X_min − Tol ≤ X ≤ X_min, then X = X_min

(5)

if X_max ≤ X ≤ X_max + Tol, then X = X_max

(6)

where X is the output variable value, Xmin, Xmax and Tol are the minimum, maximum and tolerance values of the variable, respectively.

For each pixel, variable and the considered sensor, the corresponding uncertainties were finally computed.

Table 4. The minimum, maximum range and tolerance for each output product.

	Minimum	Maximum	Tolerance
LAI	0	7	0.2
Black-sky FAPAR	0	0.94	0.05
White-sky FAPAR	0	0.94	0.05
FCOVER	0	1	0.05

Table 4. The minimum, maximum range and tolerance for each output product.

	Minimum	Maximum	Tolerance
LAI	0	7	0.2
Black-sky FAPAR	0	0.94	0.05
White-sky FAPAR	0	0.94	0.05
FCOVER	0	1	0.05

4. Results

4.1. Spatial Consistency

The spatial consistency of the satellite products was assessed over cloud-free images acquired within few days for SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013). Results show that for LAI products, 62.8% of the total pixels are within the absolute difference 0.5 unit, and less than 2.5% of the pixels showing differences larger than 2 (Table 5). For the black-sky FAPAR products, 42.8% of the total pixels have an absolute difference lower than 0.05 units (Figure 6) while results degrade slightly for white sky FAPAR and FCOVER with respectively 32.5% and 28.5% pixels with absolute difference lower than 0.05 (Table 5).

The statistical relationship between the products derived from the two sensors shows that SPOT4_HRVIR and Landsat 8 LAI products are very consistent with, however, systematically higher values for SPOT4_HRVIR (Figure 7a) in agreement with the previous observations (Figure 6). The SPOT4_HRVIR black-sky FAPAR is very consistent with the Landsat 8 (Figure 7b). The white-sky FAPAR and FCOVER products are also very consistent with however a small bias of 0.07 (Figure 7c,d). The higher values of the SPOT4_HRVIR products may be partly resulted from the rapid development of the vegetation in April (Figure 7e). For all land cover types, similar consistency trends can be observed between SPOT4_HRVIR and Landsat 8 products (Table 6).

Table 5. The percentage of pixels from the difference map of the SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013) estimated products. The difference units for LAI are ±0.5, ±1 and ±2. Values in the bracket represent the difference units for black-sky FAPAR, white-sky FAPAR and FCOVER products.

	±0.5 (±0.05)	±1 (±0.1)	±2 (±0.2)
LAI	62.8%	86.2%	97.5%
Black-sky FAPAR	42.8%	68.5%	89.7%
White-sky FAPAR	32.5%	61.0%	88.6%
FCOVER	28.5%	53.0%	82.2%

Table 5. The percentage of pixels from the difference map of the SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013) estimated products. The difference units for LAI are ±0.5, ±1 and ±2. Values in the bracket represent the difference units for black-sky FAPAR, white-sky FAPAR and FCOVER products.

	±0.5 (±0.05)	±1 (±0.1)	±2 (±0.2)
LAI	62.8%	86.2%	97.5%
Black-sky FAPAR	42.8%	68.5%	89.7%
White-sky FAPAR	32.5%	61.0%	88.6%
FCOVER	28.5%	53.0%	82.2%

Figure 6. Spatial distribution of the differences between SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013) estimated products, (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR and (d) FCOVER. The black areas denote pixels where differences are not evaluated due to cloud or cloud shadow contamination, input or output out of range from both sensors.

Figure 6. Spatial distribution of the differences between SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013) estimated products, (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR and (d) FCOVER. The black areas denote pixels where differences are not evaluated due to cloud or cloud shadow contamination, input or output out of range from both sensors.

Figure 7. Regression between SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013) estimated products, (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR and (d) FCOVER. Subplot (e) shows the regression between the NDVI values of two images as reference.

Figure 7. Regression between SPOT4_HRVIR (17 April 2013) and Landsat 8 (14 April 2013) estimated products, (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR and (d) FCOVER. Subplot (e) shows the regression between the NDVI values of two images as reference.

Table 6. R square and bias (in bracket) values between SPOT4_HRVIR (Take5) (17 April 2013) and Landsat 8 (14 April 2013) estimated products over each land cover type.

	Barley	Rapeseed	Wheat	Corn	Sunflower	Grassland	Broadleaf	Needleleaf
LAI	0.763(0.270)	0.770(0.312)	0.772(0.325)	0.773(0.325)	0.765(0.321)	0.762(0.327)	0.776(0.326)	0.769(0.318)
Black-sky FAPAR	0.783(0.050)	0.798(0.060)	0.799(0.060)	0.798(0.060)	0.791(0.060)	0.787(0.060)	0.804(0.060)	0.798(0.060)
White-sky FAPAR	0.782(0.047)	0.799(0.059)	0.799(0.059)	0.798(0.059)	0.791(0.059)	0.786(0.060)	0.805(0.060)	0.799(0.057)
FCOVER	0.773(0.057)	0.788(0.067)	0.790(0.069)	0.790(0.069)	0.782(0.068)	0.778(0.069)	0.795(0.069)	0.785(0.066)

Table 6. R square and bias (in bracket) values between SPOT4_HRVIR (Take5) (17 April 2013) and Landsat 8 (14 April 2013) estimated products over each land cover type.

	Barley	Rapeseed	Wheat	Corn	Sunflower	Grassland	Broadleaf	Needleleaf
LAI	0.763(0.270)	0.770(0.312)	0.772(0.325)	0.773(0.325)	0.765(0.321)	0.762(0.327)	0.776(0.326)	0.769(0.318)
Black-sky FAPAR	0.783(0.050)	0.798(0.060)	0.799(0.060)	0.798(0.060)	0.791(0.060)	0.787(0.060)	0.804(0.060)	0.798(0.060)
White-sky FAPAR	0.782(0.047)	0.799(0.059)	0.799(0.059)	0.798(0.059)	0.791(0.059)	0.786(0.060)	0.805(0.060)	0.799(0.057)
FCOVER	0.773(0.057)	0.788(0.067)	0.790(0.069)	0.790(0.069)	0.782(0.068)	0.778(0.069)	0.795(0.069)	0.785(0.066)

4.2. Temporal Consistency

The temporal consistency of SPOT4_HRVIR and Landsat 8 products was evaluated by averaging the products for each landcover class for each date of image acquisition. The fraction of valid pixels on each image was calculated for each landcover class. Dates with the fractions smaller than 50% of valid pixels were not considered for a given landcover class.

Results show that the profile captures well the expected seasonal variation of each landcover class (Figure 8). The barley LAI increases around the beginning of March, reaches a maximum in April and May, and then decreases around the end of May (Figure 8a). The next growth cycle starts around September with the early sowing. For the other two winter crops that are rapeseed and wheat (Figure 8b,c), similar seasonal variation of the LAI can be observed. For the summer crops (Figure 8d), the LAI of corn increases from the beginning of June to a peak value of 2.5 in July, and then decreases slowly in September. The sunflower LAI shows a slight seasonal variation throughout the year (Figure 8e), ranging around 1. For the grassland (Figure 8f), the seasonal profile starts in the beginning of March, reaches the highest value of nearly 3 in May, and then decreases from June to remain nearly constant from August to the end of the year because of the lack of available water. The broadleaf and needleleaf forests follow a similar seasonal profile, although the needleleaf LAI is slightly higher than the broadleaf LAI in the beginning of the season as expected (Figure 8g,h). LAI values higher than 3 can be obtained for both forests in July.

Figure 8. Seasonal variation of LAI products estimated from SPOT4_HRVIR (Take5) and Landsat 8 sensors for eight biomes ((a) Barley, (b) Rapeseed, (c) Wheat, (d) Corn, (e) Sunflower, (f) Grassland, (g) Broadleaf and (h) Needleleaf) over the study area. Vertical bars represent the standard deviation of values from all pixels belonging to same landcover type.

Figure 8. Seasonal variation of LAI products estimated from SPOT4_HRVIR (Take5) and Landsat 8 sensors for eight biomes ((a) Barley, (b) Rapeseed, (c) Wheat, (d) Corn, (e) Sunflower, (f) Grassland, (g) Broadleaf and (h) Needleleaf) over the study area. Vertical bars represent the standard deviation of values from all pixels belonging to same landcover type.

Black-sky FAPAR and white-sky FAPAR (Figure 9) follow seasonal profiles similar to those of LAI. The white-sky FAPAR is higher than the black-sky FAPAR in the growing season. However, it is close or even lower than the black-sky FAPAR in the beginning and the end of growing season: when the sun zenith angle increases, the direct illumination has long penetration path in the canopy, leading to a higher absorption than that of the diffuse illumination. This has been demonstrated in the model simulation from Li and Fang [17]. The seasonal profiles for FCOVER are also similar to those of LAI and black-sky FAPAR (Figure 10).

Figure 9. Seasonal variation of black-sky FAPAR (black symbols) and white-sky FAPAR (gray symbols) products estimated from SPOT4_HRVIR (Take5) and Landsat 8 sensors for eight biomes ((a) Barley, (b) Rapeseed, (c) Wheat, (d) Corn, (e) Sunflower, (f) Grassland, (g) Broadleaf and (h) Needleleaf) over the study area. Vertical bars represent the standard deviation of values from all pixels belonging to same landcover type.

Figure 9. Seasonal variation of black-sky FAPAR (black symbols) and white-sky FAPAR (gray symbols) products estimated from SPOT4_HRVIR (Take5) and Landsat 8 sensors for eight biomes ((a) Barley, (b) Rapeseed, (c) Wheat, (d) Corn, (e) Sunflower, (f) Grassland, (g) Broadleaf and (h) Needleleaf) over the study area. Vertical bars represent the standard deviation of values from all pixels belonging to same landcover type.

The average profiles per landcover class shows a smooth behavior, demonstrating that high temporal consistency of the algorithm. Further, only marginal differences could be observed between SPOT4_HRVIR and Landsat 8 profiles, proving that a single algorithm adapted to two different sensors provides consistent estimates, confirming the previous observations on the spatial consistency. However, the averaging process per landcover class masks possible variability within a class due to environmental or cultural practices differences. Nevertheless, inspection of profiles of individual fields (data not shown for the sake of brevity) confirms the high temporal consistency (temporal smoothness) as well as the good match between SPOT4_HRVIR and Landsat 8 derived products.

Figure 10. Seasonal variation of FCOVER products estimated from SPOT4_HRVIR (Take5) and Landsat 8 sensors for eight biomes ((a) Barley, (b) Rapeseed, (c) Wheat, (d) Corn, (e) Sunflower, (f) Grassland, (g) Broadleef and (h) Needleleaf) over the study area. Vertical bars represent the standard deviation of values from all pixels belonging to same landcover type.

Figure 10. Seasonal variation of FCOVER products estimated from SPOT4_HRVIR (Take5) and Landsat 8 sensors for eight biomes ((a) Barley, (b) Rapeseed, (c) Wheat, (d) Corn, (e) Sunflower, (f) Grassland, (g) Broadleef and (h) Needleleaf) over the study area. Vertical bars represent the standard deviation of values from all pixels belonging to same landcover type.

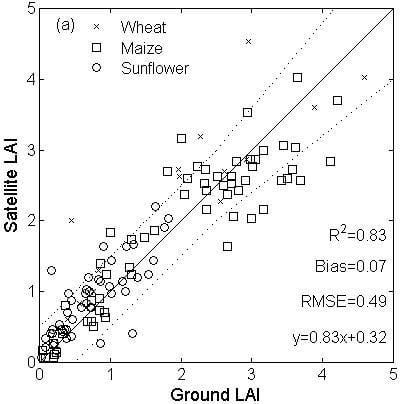
4.3. Direct Validation

The retrieved biophysical products were compared to the corresponding field measurements over three landcover classes. Single date field measurements were linearly interpolated to match the date of the satellite observation on the same location. The satellite estimated LAI corresponds well to the field measurements over all landcover classes (R² = 0.83, bias = 0.07) (Figure 11a). However, the satellite estimated LAI slightly overestimates the field LAI over the wheat and sunflower, while a small negative bias is observed for maize (Bias = −0.09) (Table 7). The underestimations over maize is mainly observed for the larger LAI values (LAI > 2.5). The satellite black-sky FAPAR estimates are strongly related to the field measured values, although showing a positive offset corresponding to an overestimation of the satellite black-sky and white sky FAPAR mainly for the lowest FAPAR values. (Figure 11b,c). The best relationship and lowest bias were observed on maize (R² = 0.91, bias = 0.01), while the largest bias of 0.11 was found on wheat. The FCOVER product is closely related to the field measured data, however some overestimations are observed over all the crops (0.05–0.13) (Figure 11d, Table 7). Table 8 shows the proportion of validation pixels that could meet the GCOS requirements for LAI, FAPAR and FCOVER products. LAI products have the best performance, with 77% of validation pixels within the GCOS boundaries (max(0.5, 20%)). However, more sunflower and maize validation pixels meet the GCOS requirement as compared to wheat. For FAPAR, 50% of the black-sky FAPAR and 52% of white-sky FAPAR meet the GCOS requirements (max(0.05, 10%)). For FCOVER, using the same requirements as for FAPAR, only 32% of validation pixels are within the GCOS range. Note that these percentage values are only calculated from the validation pixels, not the whole image.

Figure 11. Direct validation of (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR and (d) FCOVER products derived from the SPOT4_HRVIR (Take5) and Landsat 8 sensors with the ground measurements over three biomes. The dark line is the 1:1 line. Dashed lines represent the GCOS (2011) requirements boundaries.

Figure 11. Direct validation of (a) LAI, (b) black-sky FAPAR, (c) white-sky FAPAR and (d) FCOVER products derived from the SPOT4_HRVIR (Take5) and Landsat 8 sensors with the ground measurements over three biomes. The dark line is the 1:1 line. Dashed lines represent the GCOS (2011) requirements boundaries.

Table 7. Statistics of the direct validation results for satellite derived LAI, black-sky FAPAR, white-sky FAPAR and FCOVER with the ground measurements over wheat, maize and sunflowers.

	Wheat			Maize			Sunflower
	R2	Bias	RMSE	R2	Bias	RMSE	R2	Bias	RMSE
LAI	0.76	0.4	0.74	0.82	-0.09	0.5	0.65	0.16	0.36
Black-sky FAPAR	0.81	0.04	0.1	0.91	0.01	0.08	0.65	0.02	0.12
White-sky FAPAR	0.76	0.11	0.17	0.91	0.03	0.08	0.67	0.06	0.14
FCOVER	0.56	0.13	0.19	0.83	0.11	0.15	0.69	0.05	0.12

Table 7. Statistics of the direct validation results for satellite derived LAI, black-sky FAPAR, white-sky FAPAR and FCOVER with the ground measurements over wheat, maize and sunflowers.

	Wheat			Maize			Sunflower
	R2	Bias	RMSE	R2	Bias	RMSE	R2	Bias	RMSE
LAI	0.76	0.4	0.74	0.82	-0.09	0.5	0.65	0.16	0.36
Black-sky FAPAR	0.81	0.04	0.1	0.91	0.01	0.08	0.65	0.02	0.12
White-sky FAPAR	0.76	0.11	0.17	0.91	0.03	0.08	0.67	0.06	0.14
FCOVER	0.56	0.13	0.19	0.83	0.11	0.15	0.69	0.05	0.12

Table 8. Percentage of the validation pixels that meet the GCOS requirements.

	Wheat (%)	Maize (%)	Sunflower (%)	All (%)
LAI	64.29	72.88	85.11	76.67
Black-sky FAPAR	57.14	55.93	40.43	50
White-sky FAPAR	38.46	67.24	36.17	51.69
FCOVER	21.43	33.90	31.95	31.67

Table 8. Percentage of the validation pixels that meet the GCOS requirements.

	Wheat (%)	Maize (%)	Sunflower (%)	All (%)
LAI	64.29	72.88	85.11	76.67
Black-sky FAPAR	57.14	55.93	40.43	50
White-sky FAPAR	38.46	67.24	36.17	51.69
FCOVER	21.43	33.90	31.95	31.67

5. Discussions

A neural network based algorithm was developed in this study to retrieve LAI, FAPAR and FCOVER products from either SPOT4_HRVIR or Landsat 8 surface reflectance data. The neural networks were trained over a simulated learning data base by taking into account the distribution and co-distribution laws of the input variables. As the algorithm is not land cover dependent, we used a truncated Gaussian distribution law to be most representative of a wide range of landcover types and thus, mimic the actual distribution of the radiative transfer model input variables [16]. Furthermore, by considering the co-distribution law of variables with LAI, the realism of the learning data base is expected to be improved. However, the information related to the distribution and co-distribution laws of variables is actually limited. More studies should be conducted on this topic to improve the learning database generation.

The products derived from SPOT4_HRVIR and Landsat 8 data show very good spatial and temporal consistency (Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10). For very close acquisition dates, SPOT4_HRVIR and Landsat 8 products are very similar and most of the differences are within a limited range. The results demonstrate the robustness of the proposed algorithm and its suitability to be applied to several satellites. The temporal profiles show that two sensors complement themselves to describe the seasonal variation of vegetation: the combination of sensors may overcome the typical low revisit frequency of decametric sensors, allowing to build virtual constellations.

The comparisons with the field measurements demonstrate the good quality of the derived products (Figure 11, Table 7 and Table 8). Seventy-seven percent of the satellite LAI meets the GCOS requirement although it shows a slight underestimation over the maize crops when LAI is larger than 2. The assumptions made on canopy structure in the SAIL model may partly explain these artifacts. Further, the satellite derived LAI product corresponds to the green LAI, while the field measured LAI from the upward looking DHPs includes all components of the canopy (green and non-green elements). Both black-sky and white-sky FAPAR products show good relationships with the field measurements. More than half of FAPAR validation pixels meet the GCOS requirements. The RMSE value for FAPAR is in the same range as those reported by several studies [16,47,48]. For FCOVER, only 32% of FCOVER validation pixels are within the max (0.05, 10%) accuracy range, showing a small overestimation compared with the ground FCOVER value. The overestimation may result from the higher sensitivity of FCOVER to the contribution of soil reflectance, the clumping effect which is maximum in the vertical direction, as well as uncertainties related to the field measurements of FCOVER. Nevertheless, the RMSE value for FCOVER (RMSE = 0.15) is close to the values reported in other studies [16,49] .

6. Conclusions

This study shows the interest of this generic algorithm to derive LAI, FAPAR and FCOVER consistent products from SPOT4_HRVIR and Landsat 8 over the study area. These principles will be applied to the recently launched Sentinel-2 mission with a high revisit frequency and a decametric spatial resolution that will contribute to a large range of applications. To further improve the accuracy of the algorithm to apply for Sentinel-2, efforts should devoted towards three complementary directions: (i) first, more sites with field measurements need to be considered to better describe the limits of the algorithm; (ii) second, this algorithm is by construction “generic”: it applies potentially to all landcover types. Major improvements are expected from the development of more specific algorithms, i.e., when the training is achieved over a limited set of cases defined for each landcover type. This will imply that one could achieve a near real time estimation of the landcover class associated to each pixel. The temporal profiles generated from the output of the generic algorithm would help identifying the landcover class associated to each pixel. Then the “specific” biophysical algorithm will be run to fine tune the solution by exploiting the knowledge of the landcover class. (iii) Finally, the expected smoothness of the temporal profiles of these biophysical variables and their typical shape for each landcover type should be exploited to smooth out possible residual artifacts and help filling gaps due to cloud or snow cover.