Reducing the Influence of Soil Moisture on the Estimation of Clay from Hyperspectral Data: A Case Study Using Simulated PRISMA Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Soil Spectral Datasets
| Spectral dataset | ||
|---|---|---|
| SOLREFLIU | MAC | |
| N° samples | 89 | 72 |
| Type | Topsoil | Topsoil |
| Sampling area | France and China | Italy |
| Spectral measurement | Directional | Directional |
| Spectral range | 350–2500 | 350–2500 |
| Spectral resolution | 1 nm | 1 nm |
2.2. Narrow Band Soil Moisture Indices—SMIR
2.3. Reducing the Effect of Soil Moisture from Laboratory Soil Spectra
- (a)
- application of different prediction models according to the different soil moisture contents;
- (b)
- use of prediction models with synthetically dried soil spectra derived from wet soil spectra.
2.3.1. Use of Different Prediction Models according to Soil Moisture Content

2.3.2. Use of Prediction Models Calibrated with Synthetically Dried Soil Spectra
2.4. PRISMA Simulated Data
3. Results and Discussion
3.1. Soil Moisture Estimation
3.1.1. Laboratory Dataset


| Soil Moisture Index | Formula | r | a | b | c | RMSE (%) | RPIQ |
|---|---|---|---|---|---|---|---|
| SMIR_A | (R1770 − R2100)/(R1770 + R2100) | 0.89 | 0.03 | 1.63 | −1.89 | 0.05 | 4.25 |
| SMIR_B | R1506/R1770 | −0.88 | 0.48 | 0.24 | −0.75 | 0.05 | 4.25 |
| NSMI | (R1800 − R2119)/(R1800 + R2119) | 0.88 | 0.50 | −1.67 | 1.46 | 0.05 | 4.25 |
3.1.2. Simulated PRISMA Data
| Atmosphere | Statistics | SMIR_A | SMIR_B | NSMI |
|---|---|---|---|---|
| Summer | r | 0.89 | −0.81 | 0.88 |
| R2 | 0.8 | 0.67 | 0.78 | |
| RMSE (%) | 0.05 | 0.06 | 0.05 | |
| RPIQ | 4.25 | 3.54 | 4.25 | |
| Autumn | r | 0.89 | −0.86 | 0.88 |
| R2 | 0.8 | 0.74 | 0.78 | |
| RMSE (%) | 0.05 | 0.05 | 0.05 | |
| RPIQ | 4.25 | 4.25 | 4.25 | |
| Winter | r | 0.89 | −0.86 | 0.88 |
| R2 | 0.8 | 0.75 | 0.78 | |
| RMSE (%) | 0.05 | 0.06 | 0.05 | |
| RPIQ | 4.25 | 3.54 | 4.25 |
3.2. Clay Content Estimation Considering Soil Moisture
3.2.1. Clay Estimation from Full Spectra

| SM class | Clay index | r |
|---|---|---|
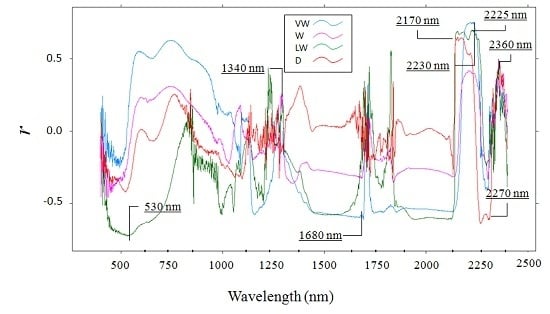
| VW | (BD2230 − BD1680)/(BD2230 + BD1680) | 0.70 |
| W | (BD1340 − BD2360)/(BD1340 + BD2360) | −0.73 |
| LW | BD530/BD2225 | 0.65 |
| D | (BD2170 − BD2270)/(BD2170 + BD2270) | 0.75 |
| Dataset | SM Reduction Method | SM Class | Clay Estimation Method | |||
|---|---|---|---|---|---|---|
| Spectral Indices | PLSR | |||||
| RMSE (%) | RPIQ | RMSE (%) | RPIQ | |||
| MAC | Different spectral indices according to SM level (a) | VW | 5.7 | 2.96 | 4.7 | 3.59 |
| W | 7.4 | 2.28 | 6.4 | 2.64 | ||
| LW | 7.8 | 2.16 | 5.0 | 3.37 | ||
| D | 6.0 | 2.81 | 3.9 | 4.33 | ||
| Mean | 6.7 | 2.52 | 5.0 | 3.37 | ||
| D model to all (mean value) | 9.3 | 1.81 | 15.7 | 1.07 | ||
| MAC synthetically dried using MAC (b) | Synthetically dried spectra (c) | VW | 7.9 | 2.13 | 7.6 | 2.22 |
| W | 6.5 | 2.58 | 7.9 | 2.14 | ||
| LW | 6.2 | 2.73 | 6.2 | 2.72 | ||
| D | 6.0 | 2.79 | 3.9 | 4.33 | ||
| Mean | 6.7 | 2.52 | 6.4 | 2.64 | ||
| MAC synthetically dried using SOLREFLIU (d) | Synthetically dried spectra | VW | 9.0 | 1.87 | 8.0 | 2.11 |
| W | 8.2 | 2.07 | 7.9 | 2.14 | ||
| LW | 6.6 | 2.58 | 6.5 | 2.60 | ||
| D | 6.0 | 2.79 | 4.7 | 3.59 | ||
| Mean | 7.4 | 2.27 | 6.8 | 2.49 | ||


3.2.2. Clay Estimation from Simulated PRISMA Data


| SM reduction method | SM class | Clay estimation method | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spectral indices | PLSR | |||||||||||||||||
| Summer | Autumn | Winter | Summer | Autumn | Winter | |||||||||||||
| RMSE (%) | RPIQ | RMSE (%) | RPIQ | RMSE (%) | RPIQ | RMSE (%) | RPIQ | RMSE (%) | RPIQ | RMSE (%) | RPIQ | |||||||
| Different spectral indices according to SM level(a) | VW | 6.6 | 2.6 | 6.3 | 2.7 | 6.3 | 2.7 | 7.1 | 2.4 | 6.7 | 2.5 | 7.4 | 2.3 | |||||
| W | 8.2 | 2.1 | 8.5 | 2 | 10.6 | 1.6 | 6.3 | 2.7 | 6.8 | 2.5 | 9.2 | 1.8 | ||||||
| LW | 8.5 | 2 | 8.2 | 2.1 | 7.8 | 2.2 | 9.5 | 1.8 | 9.1 | 1.9 | 9.5 | 1.8 | ||||||
| D | 5.9 | 2.9 | 6 | 2.8 | 5.9 | 2.9 | 4.7 | 3.6 | 5.8 | 2.9 | 7.3 | 2.3 | ||||||
| Mean | 7.3 | 2.3 | 7.3 | 2.3 | 7.7 | 2.2 | 6.9 | 2.6 | 7.1 | 2.4 | 8.4 | 2.3 | ||||||
| D to all (mean) | 13.2 | 1.3 | 13.3 | 1.3 | 11.9 | 1.4 | 15.8 | 1.1 | 15.6 | 1.1 | 10.4 | 1.6 | ||||||
| Synthetically dried spectra(b) | VW | 9.8 | 1.7 | 9.8 | 1.7 | 9.8 | 1.7 | 7.6 | 2.2 | 7.8 | 2.2 | 8.6 | 2 | |||||
| W | 9.2 | 1.8 | 9.2 | 1.8 | 9.2 | 1.8 | 7.4 | 2.3 | 7.2 | 2.3 | 8.5 | 2 | ||||||
| LW | 7.7 | 2.2 | 7.7 | 2.2 | 7.7 | 2.2 | 7.1 | 2.4 | 7.2 | 2.3 | 7.7 | 2.2 | ||||||
| D | 5.9 | 2.9 | 6 | 2.8 | 5.9 | 2.9 | 4.7 | 3.6 | 5.8 | 2.9 | 7.3 | 2.3 | ||||||
| Mean | 8.2 | 2.1 | 8.2 | 2.1 | 8.2 | 2.1 | 6.7 | 2.6 | 7 | 2.4 | 8 | 2.1 | ||||||
4. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Chabrillat, S.; Dematte, J.A.M.; Taylor, G.R.; Hill, J.; Whiting, M.L.; Sommer, S. Using imaging spectroscopy to study soil properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Richter, K.; Hank, T.; Atzberger, C.; Locherer, M.; Mauser, W. Regularization strategies for agricultural monitoring: The EnMAP vegetation analyzer (AVA). In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 6613–6616.
- Tanii, J.; Iwasaki, A.; Kawashima, T.; Inada, H. Results of evaluation model of Hyperspectral Imager Suite (HISUI). In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 131–134.
- Pignatti, S.; Acito, N.; Amato, U.; Casa, R.; de Bonis, R.; Diani, M.; Laneve, G.; Matteoli, S.; Palombo, A.; Pascucci, S.; et al. Development of algorithms and products for supporting the Italian hyperspectral PRISMA mission: The SAP4PRISMA project. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 127–130.
- Houborg, R.; Anderson, M.; Gao, F.; Schull, M.; Cammalleri, C. Monitoring water and carbon fluxes at fine spatial scales using HyspIRI-like measurements. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 7302–7305.
- Lobell, D.B.; Asner, G.P. Moisture effects on soil reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Morgan, C.L.S.; Waiser, T.H.; Brown, D.J.; Hallmark, C.T. Simulated in situ characterization of soil organic and inorganic carbon with visible near-infrared diffuse reflectance spectroscopy. Geoderma 2009, 151, 249–256. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; Noon, C.; van Wesemael, B. Prediction of soil organic carbon for different levels of soil moisture using Vis-NIR spectroscopy. Geoderma 2013, 199, 37–42. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Jacobson, A.R.; Laba, M.; Baveye, P.C. Alleviating Moisture Content Effects on the Visible Near-Infrared Diffuse-Reflectance Sensing of Soils. Soil Sci. 2009, 174, 456–465. [Google Scholar] [CrossRef]
- Waiser, T.H.; Morgan, C.L.S.; Brown, D.J.; Hallmark, C.T. In Situ Characterization of Soil Clay Content with Visible Near-Infrared Diffuse Reflectance Spectroscopy. Soil Sci. Soc. Am. J. 2007, 71, 389–396. [Google Scholar] [CrossRef]
- Ge, Y.; Morgan, C.L.S.; Ackerson, J.P. VisNIR spectra of dried ground soils predict properties of soils scanned moist and intact. Geoderma 2014, 221–222, 61–69. [Google Scholar] [CrossRef]
- Ackerson, J.P.; Demattê, J.A.M.; Morgan, C.L.S. Predicting clay content on field-moist intact tropical soils using a dried, ground VisNIR library with external parameter orthogonalization. Geoderma 2015, 259–260, 196–204. [Google Scholar] [CrossRef]
- Rienzi, E.A.; Mijatovic, B.; Mueller, T.G.; Matocha, C.J.; Sikora, F.J.; Castrignanò, A. Prediction of soil organic carbon under varying moisture levels using reflectance spectroscopy. Soil Sci. Soc. Am. J. 2014, 78, 958–967. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B.; Bellon-Maurel, V.; Roger, J.-M.; Gobrecht, A.; Ferrand, L.; Joalland, S. Removing the effect of soil moisture from NIR diffuse reflectance spectra for the prediction of soil organic carbon. Geoderma 2011, 167–168, 118–124. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Effect of spiking strategy and ratio on calibration of on-line visible and near infrared soil sensor for measurement in European farms. Soil Tillage Res. 2013, 128, 125–136. [Google Scholar] [CrossRef] [Green Version]
- Ji, W.; Viscarra Rossel, R.A.; Shi, Z. Accounting for the effects of water and the environment on proximally sensed vis-NIR soil spectra and their calibrations. Eur. J. Soil Sci. 2015, 66, 555–565. [Google Scholar] [CrossRef]
- Haubrock, S.‐N.; Chabrillat, S.; Lemmnitz, C.; Kaufmann, H. Surface soil moisture quantification models from reflectance data under field conditions. Int. J. Remote Sens. 2008, 29, 3–29. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus PLSR method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar] [CrossRef]
- Casa, R.; Castaldi, F.; Pascucci, S.; Basso, B.; Pignatti, S. Geophysical and hyperspectral data fusion techniques for in-field estimation of soil properties. Vadose Zone J. 2013. [Google Scholar] [CrossRef]
- Pascucci, S.; Casa, R.; Belviso, C.; Palombo, A.; Pignatti, S.; Castaldi, F. Estimation of soil organic carbon from airborne hyperspectral thermal infrared data: A case study. Eur. J. Soil Sci. 2014, 65, 865–875. [Google Scholar] [CrossRef]
- Li, D.; Chen, X.; Peng, Z.; Chen, S.; Chen, W.; Han, L.; Li, Y. Prediction of soil organic matter content in a litchi orchard of South China using spectral indices. Soil Tillage Res. 2012, 123, 78–86. [Google Scholar] [CrossRef]
- Casa, R.; Castaldi, F.; Pascucci, S.; Palombo, A.; Pignatti, S. A comparison of sensor resolution and calibration strategies for soil texture estimation from hyperspectral remote sensing. Geoderma 2013, 197–198, 17–26. [Google Scholar] [CrossRef]
- FAO-ISRIC-ISSS. World Reference Base for Soil Resources; World Soil Resources Report 84; Food and Agriculture Organisation: Rome, Italy, 1998. [Google Scholar]
- Soil Survey Staff. Keys to Soil Taxonomym, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014. [Google Scholar]
- Beuselinck, L.; Govers, G.; Poesen, J.; Degraer, G.; Froyen, L. Grain-size analysis by laser diffractometry: Comparison with the sieve-pipette method. Catena 1998, 32, 193–208. [Google Scholar] [CrossRef]
- Liu, W.; Baret, F.; Gu, X.; Zhang, B.; Tong, Q.; Zheng, L. Evaluation of methods for soil surface moisture estimation from reflectance data. Int. J. Remote Sens. 2003, 24, 2069–2083. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011. [Google Scholar]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN Cloud and Multiple Scattering Upgrades with Application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Clark, R.N. Chapter 1: Spectroscopy of rocks and minerals, and principles of spectroscopy. In Manual of Remote Sensing, Remote Sensing for the Earth Sciences; Rencz, A.N., Ed.; John Wiley and Sons: New York, NY, USA, 1999; Volume 3, pp. 3–58. [Google Scholar]
- Tóth, G.; Jones, A.; Montanarella, L. The LUCAS topsoil database and derived information on the regional variability of cropland topsoil properties in the European Union. Environ. Monit. Assess. 2013, 185, 7409–7425. [Google Scholar] [CrossRef] [PubMed]
- Summers, D.; Lewis, M.; Ostendorf, B.; Chittleborough, D. Visible near-infrared reflectance spectroscopy as a predictive indicator of soil properties. Ecol. Indic. 2011, 11, 123–131. [Google Scholar] [CrossRef]
- Bilgili, A.V.; Akbas, F.; van Es, H.M. Combined use of hyperspectral VNIR reflectance spectroscopy and kriging to predict soil variables spatially. Precis. Agric. 2010, 12, 395–420. [Google Scholar] [CrossRef]
- Lagacherie, P.; Baret, F.; Feret, J.-B.; Madeira Netto, J.; Robbez-Masson, J.M. Estimation of soil clay and calcium carbonate using laboratory, field and airborne hyperspectral measurements. Remote Sens. Environ. 2008, 112, 825–835. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis–NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Ackerson, C.; Morgan, L.S.; Ge, Y.; McBratney, A.; Minasny, B. A tale of two projections: Removing the effects of water content and intactness from in situ VisNIR spectra using external parameter orthagonalization and direct standardization. In Proceedings of the Pedometrics 2015, Cordoba, Spain, 14–17 September 2015; p. 70.
- Folkman, M.A.; Pearlman, J.; Liao, L.B.; Jarecke, P.J. EO-1/Hyperion hyperspectral imager design, development, characterization, and calibration. Proc. SPIE 2001. [Google Scholar] [CrossRef]
- Castaldi, F.; Casa, R.; Castrignanò, A.; Pascucci, S.; Palombo, A.; Pignatti, S. Estimation of soil properties at the field scale from satellite data: A comparison between spatial and non-spatial techniques. Eur. J. Soil Sci. 2014, 65, 842–851. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castaldi, F.; Palombo, A.; Pascucci, S.; Pignatti, S.; Santini, F.; Casa, R. Reducing the Influence of Soil Moisture on the Estimation of Clay from Hyperspectral Data: A Case Study Using Simulated PRISMA Data. Remote Sens. 2015, 7, 15561-15582. https://doi.org/10.3390/rs71115561
Castaldi F, Palombo A, Pascucci S, Pignatti S, Santini F, Casa R. Reducing the Influence of Soil Moisture on the Estimation of Clay from Hyperspectral Data: A Case Study Using Simulated PRISMA Data. Remote Sensing. 2015; 7(11):15561-15582. https://doi.org/10.3390/rs71115561
Chicago/Turabian StyleCastaldi, Fabio, Angelo Palombo, Simone Pascucci, Stefano Pignatti, Federico Santini, and Raffaele Casa. 2015. "Reducing the Influence of Soil Moisture on the Estimation of Clay from Hyperspectral Data: A Case Study Using Simulated PRISMA Data" Remote Sensing 7, no. 11: 15561-15582. https://doi.org/10.3390/rs71115561
APA StyleCastaldi, F., Palombo, A., Pascucci, S., Pignatti, S., Santini, F., & Casa, R. (2015). Reducing the Influence of Soil Moisture on the Estimation of Clay from Hyperspectral Data: A Case Study Using Simulated PRISMA Data. Remote Sensing, 7(11), 15561-15582. https://doi.org/10.3390/rs71115561