Spatial Accuracy Assessment and Integration of Global Land Cover Datasets
Abstract
:1. Introduction
2. Data
2.1. Global Land Cover Maps
| GLC Map | Globcover | LC-CCI | MODIS | Globeland30 |
|---|---|---|---|---|
| Spatial resolution at the Equator | 300 m | 300 m | 500 m | 250 m |
| Input data | MERIS: Bi-monthly from 10-day composites | MERIS global SR composite, SPOT-VGT time series (for updating) | MODIS: Monthly EVI, LST and 7 bands from 8-day composites | Landsat TM, ETM+ and HJ-1 multispectral images |
| Time of data collection | 2009 | 2008–2012 | 2010 | 2010 ± 1 year |
| Classification method | (Un)supervised spatio-temporal clustering; expert-based labeling | Unsupervised spatio-temporal clustering; machine learning classification | Supervised decision tree boosting | Integration of pixel and object based classification and Knowledge based interactive verification |
| Classification scheme | LCCS based:22 classes | LCCS based: 22 classes | 5 different legends including the IGBP (17 classes) | 10 classes |
| Reference | [26] | [27] | [28] | [3] |
| Code | Land Cover Class | Globcover | LC-CCI | IGBP (MODIS, STEP and VIIRS) | GLC2000 | Geo-Wiki | GLCNMO |
|---|---|---|---|---|---|---|---|
| 1 | Forest | 40–110, 160, 170 | 50–100, 160, 170 | 1–5, 8, 9 | 1–10 | 1 | 1–5 |
| 2 | Shrubland | 130 | 120 | 6, 7 | 11, 12 | 2 | 7 |
| 3 | Grassland | 120, 140 | 110, 130, 140 | 10 | 13 | 3 | 8, 9 |
| 4 | Cropland (incl. mixtures) | 11–30 | 10–40 | 12, 14 | 16–18 | 4 | 11, 12, 13 |
| 5 | Wetland vegetation | 180 | 180 | 11 | 15 | 6 | 15 |
| 6 | Urban/built up | 190 | 190 | 13 | 22 | 7 | - |
| 7 | Bare/sparse vegetation | 150, 200 | 150, 200 | 16 | 14, 19 | 9 | 10, 16, 17 |
| 8 | Water and Snow/Ice | 210, 220 | 210, 220 | 15, 17 | 20, 21 | 8, 10 | - |

2.2. Reference Datasets

3. Method
3.1. Spatial Correspondence Assessment

3.2. GLC Dataset Integration

3.2.1. Voting
3.2.2. Spatial Correspondence (SC)
3.2.3. Weighted Voting (WeVo)
3.2.4. Regression Kriging (RK)

3.2.5. Indicator Kriging (IK)

3.2.6. Cross-Validation
4. Results and Discussions
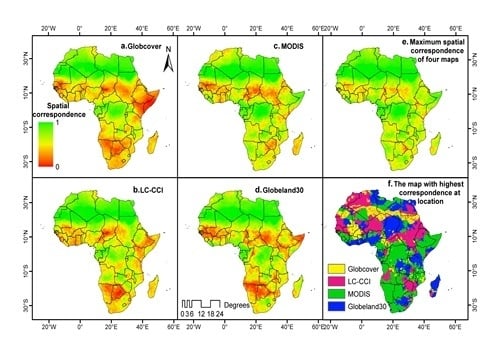
4.1. Spatial Correspondence of GLC Maps in Africa

4.2. GLC Dataset Integration Methods

4.3. Integrated LC and LC Probability Maps of Africa

| Globcover | LC-CCI | MODIS | Globeland30 | RK | |
|---|---|---|---|---|---|
| Forest | 71.1 | 67.3 | 90.2 | 63.7 | 84.9 |
| Shrubland | 11.9 | 21.3 | 26.9 | 17.3 | 70.8 |
| Grassland | 18.4 | 18.9 | 27.1 | 70.4 | 41.1 |
| Cropland | 57.7 | 79.2 | 66.7 | 76.0 | 75.0 |
| Wetland | 25.0 | 31.5 | 59.8 | 52.2 | 67.0 |
| Built-up | 74.5 | 91.5 | 78.7 | 91.5 | 89.4 |
| Bare/sparse vegetation | 76.0 | 78.5 | 75.0 | 72.0 | 87.6 |
| Water and snow/ice | 80.0 | 80.0 | 70.0 | 78.0 | 86.7 |
| Total | 50.7 | 55.4 | 62.8 | 57.1 | 76.3 |


4.4. On the Use of Available Reference Datasets for Integration
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Verburg, P.H.; Neumann, K.; Nol, L. Challenges in using land use and land cover data for global change studies. Glob. Chang. Biol. 2011, 17, 974–989. [Google Scholar] [CrossRef]
- Mora, B.; Tsendbazar, N.-E.; Herold, M.; Arino, O. Global land cover mapping: Current status and future trends. In Land Use and Land Cover Mapping in Europe; Springer: Dordrecht, The Netherlands, 2014; pp. 11–30. [Google Scholar]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Herold, M.; Mayaux, P.; Woodcock, C.E.; Baccini, A.; Schmullius, C. Some challenges in global land cover mapping: An assessment of agreement and accuracy in existing 1 km datasets. Remote Sens. Environ. 2008, 112, 2538–2556. [Google Scholar] [CrossRef]
- Fritz, S.; See, L.; McCallum, I.; Schill, C.; Obersteiner, M.; van der Velde, M.; Boettcher, H.; Havlík, P.; Achard, F. Highlighting continued uncertainty in global land cover maps for the user community. Environ. Res. Lett. 2011, 6, 044005. [Google Scholar] [CrossRef]
- Tsendbazar, N.E.; de Bruin, S.; Mora, B.; Schouten, L.; Herold, M. Comparative assessment of thematic accuracy of GLC maps for specific applications using existing reference data. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 124–135. [Google Scholar] [CrossRef]
- Kooistra, L.; Groenestijn, A.; Kalogirou, V.; Arino, O.; Herold, M. User requirements from the climate modelling community for next generation global products from land cover cci project. In Proceedings of the ESA-iLEAPS-EGU Joint Conference 2010, Frascati, Italy, 3–5 November 2010.
- Jung, M.; Henkel, K.; Herold, M.; Churkina, G. Exploiting synergies of global land cover products for carbon cycle modeling. Remote Sens. Environ. 2006, 101, 534–553. [Google Scholar] [CrossRef]
- See, L.; Schepaschenko, D.; Lesiv, M.; McCallum, I.; Fritz, S.; Comber, A.; Perger, C.; Schill, C.; Zhao, Y.; Maus, V.; et al. Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS J. Photogramm. Remote Sens. 2015, 103, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Iwao, K.; Nasahara, K.N.; Kinoshita, T.; Yamagata, Y.; Patton, D.; Tsuchida, S. Creation of new global land cover map with map integration. J. Geogr. Inf. Syst. 2011, 3, 160–165. [Google Scholar] [CrossRef]
- Tuanmu, M.-N.; Jetz, W. A global 1-km consensus land-cover product for biodiversity and ecosystem modelling. Glob. Ecol. Biogeogr. 2014, 23, 1031–1045. [Google Scholar] [CrossRef]
- Ge, Y.; Avitabile, V.; Heuvelink, G.B.; Wang, J.; Herold, M. Fusion of pan-tropical biomass maps using weighted averaging and regional calibration data. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 13–24. [Google Scholar] [CrossRef]
- Fritz, S.; See, L.; McCallum, I.; You, L.; Bun, A.; Moltchanova, E.; Duerauer, M.; Albrecht, F.; Schill, C.; Perger, C.; et al. Mapping global cropland and field size. Glob. Chang. Biol. 2015, 21, 1980–1992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avitabile, V.; Herold, M.; Heuvelink, G.; Lewis, S.; Phillips, O.; Asner, G.; Armston, J.; Asthon, P.; Banin, L.; Bayol, N. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, T.; Iwao, K.; Yamagata, Y. Creation of a global land cover and a probability map through a new map integration method. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 70–77. [Google Scholar] [CrossRef]
- Comber, A.; See, L.; Fritz, S.; van der Velde, M.; Perger, C.; Foody, G. Using control data to determine the reliability of volunteered geographic information about land cover. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 37–48. [Google Scholar] [CrossRef]
- Schepaschenko, D.; See, L.; Lesiv, M.; McCallum, I.; Fritz, S.; Salk, C.; Moltchanova, E.; Perger, C.; Shchepashchenko, M.; Shvidenko, A.; et al. Development of a global hybrid forest mask through the synergy of remote sensing, crowdsourcing and FAO statistics. Remote Sens. Environ. 2015, 162, 208–220. [Google Scholar] [CrossRef]
- GOFC-GOLD. GOFC-GOLD Reference Data Portal. Available online: http://www.gofcgold.wur.nl/sites/gofcgold_refdataportal.php (accessed on 22 October 2015).
- Fritz, S.; McCallum, I.; Schill, C.; Perger, C.; See, L.; Schepaschenko, D.; van der Velde, M.; Kraxner, F.; Obersteiner, M. Geo-wiki: An online platform for improving global land cover. Environ. Model. Softw. 2011, 31, 110–123. [Google Scholar] [CrossRef]
- Carneiro, J.D.; Pereira, M.J. Geostatistical stochastic simulation for spatial accuracy assessment of land cover maps derived from remotely sensed data. In Proceedings of the Ninth International Geostatistics Congress, Oslo, Norway, 11–15 June 2012.
- Kyriakidis, P.C.; Dungan, J.L. A geostatistical approach for mapping thematic classification accuracy and evaluating the impact of inaccurate spatial data on ecological model predictions. Environ. Ecol. Stat. 2001, 8, 311–330. [Google Scholar] [CrossRef]
- De Bruin, S. Predicting the areal extent of land-cover types using classified imagery and geostatistics. Remote Sens. Environ. 2000, 74, 387–396. [Google Scholar] [CrossRef]
- Huttich, C.; Herold, M.; Wegmann, M.; Cord, A.; Strohbach, B.; Schmullius, C.; Dech, S. Assessing effects of temporal compositing and varying observation periods for large-area land-cover mapping in semi-arid ecosystems: Implications for global monitoring. Remote Sens. Environ. 2011, 115, 2445–2459. [Google Scholar] [CrossRef]
- Kaptué Tchuenté, A.T.; Roujean, J.L.; de Jong, S.M. Comparison and relative quality assessment of the GLC2000, Globcover, MODIS and ECOCLIMAP land cover data sets at the African continental scale. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 207–219. [Google Scholar] [CrossRef]
- Defourny, P.; Bontemps, S.; Schouten, L.; Bartalev, S.; Cacetta, P.; de Wit, A.; di Bella, C.; Gérard, B.; Giri, C.; Gond, V.; et al. Globcover 2005 and Globcover 2009 Validation: Learnt Lessons; GOFC-GOLD Global Land Cover & Change Validation Workshop: Laxenburg, Austria, 2011. [Google Scholar]
- Bontemps, S.; Defourny, P.; van Bogaert, E.; Kalogirou, V.; Arino, O. Globcover 2009: Products Description and Validation Report; UCLouvain and ESA: Toulouse, France, 2009; p. 53. [Google Scholar]
- CCI-LC. CCI-LC Product User Guide; UCL-Geomatics: Louvain-la-Neuve, Belgium, 2014. [Google Scholar]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X.M. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Mayaux, P.; Eva, H.; Gallego, J.; Strahler, A.H.; Herold, M.; Agrawal, S.; Naumov, S.; de Miranda, E.E.; di Bella, C.M.; Ordoyne, C.; et al. Validation of the global land cover 2000 map. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1728–1739. [Google Scholar] [CrossRef]
- Schultz, M.; Tsendbazar, N.; Herold, M.; Jung, M.; Mayaux, P.; Goehmann, H. Utilizing the global land cover 2000 reference dataset for a comparative accuracy assessment of global 1 km land cover maps. Int. Arch. Photogramm, Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 503–510. [Google Scholar] [CrossRef]
- Tateishi, R.; Uriyangqai, B.; Al-Bilbisi, H.; Ghar, M.A.; Tsend-Ayush, J.; Kobayashi, T.; Kasimu, A.; Hoan, N.T.; Shalaby, A.; Alsaaideh, B.; et al. Production of global land cover data—GLCNMO. Int. J. Digit. Earth 2011, 4, 22–49. [Google Scholar] [CrossRef]
- Olofsson, P.; Stehman, S.V.; Woodcock, C.E.; Sulla-Menashe, D.; Sibley, A.M.; Newell, J.D.; Friedl, M.A.; Herold, M. A global land-cover validation data set, part I: Fundamental design principles. Int. J. Remote Sens. 2012, 33, 5768–5788. [Google Scholar] [CrossRef]
- Fritz, S.; McCallum, I.; Schill, C.; Perger, C.; Grillmayer, R.; Achard, F.; Kraxner, F.; Obersteiner, M. Geo-wiki. Org: The use of crowdsourcing to improve global land cover. Remote Sens. 2009, 1, 345–354. [Google Scholar] [CrossRef]
- Bicheron, P.; Defourny, P.; Brockmann, C.; Schouten, L.; Vancutsem, C.; Huc, M.; Bontemps, S.; Leroy, M.; Achard, F.; Herold, M.; et al. Globcover: Products Description and Validation Report; MEDIAS-France: Toulouse, France, 2008. [Google Scholar]
- Tsendbazar, N.; de Bruin, S.; Herold, M. Assessing global land cover reference datasets for different user communities. ISPRS J. Photogramm. Remote Sens. 2015, 103, 93–114. [Google Scholar] [CrossRef]
- Pebesma, E.J.; Wesseling, C.G. Gstat: A program for geostatistical modelling, prediction and simulation. Comput. Geosci. 1998, 24, 17–31. [Google Scholar] [CrossRef]
- Bierkens, M.; Burrough, P. The indicator approach to categorical soil data. J. Soil Sci. 1993, 44, 361–368. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Kempen, B.; Brus, D.J.; Heuvelink, G.B.; Stoorvogel, J.J. Updating the 1: 50,000 Dutch soil map using legacy soil data: A multinomial logistic regression approach. Geoderma 2009, 151, 311–326. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Goovaerts, P. Combining areal and point data in geostatistical interpolation: Applications to soil science and medical geography. Math. Geosci. 2010, 42, 535–554. [Google Scholar] [CrossRef] [PubMed]
- Kyriakidis, P.C.; Yoo, E.H. Geostatistical prediction and simulation of point values from areal data. Geogr. Anal. 2005, 37, 124–151. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area and map accuracy for stratified random sampling when the strata are different from the map classes. Int. J. Remote Sens. 2014, 35, 4923–4939. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsendbazar, N.-E.; De Bruin, S.; Fritz, S.; Herold, M. Spatial Accuracy Assessment and Integration of Global Land Cover Datasets. Remote Sens. 2015, 7, 15804-15821. https://doi.org/10.3390/rs71215804
Tsendbazar N-E, De Bruin S, Fritz S, Herold M. Spatial Accuracy Assessment and Integration of Global Land Cover Datasets. Remote Sensing. 2015; 7(12):15804-15821. https://doi.org/10.3390/rs71215804
Chicago/Turabian StyleTsendbazar, Nandin-Erdene, Sytze De Bruin, Steffen Fritz, and Martin Herold. 2015. "Spatial Accuracy Assessment and Integration of Global Land Cover Datasets" Remote Sensing 7, no. 12: 15804-15821. https://doi.org/10.3390/rs71215804
APA StyleTsendbazar, N. -E., De Bruin, S., Fritz, S., & Herold, M. (2015). Spatial Accuracy Assessment and Integration of Global Land Cover Datasets. Remote Sensing, 7(12), 15804-15821. https://doi.org/10.3390/rs71215804