Mapping Spatial Distribution of Larch Plantations from Multi-Seasonal Landsat-8 OLI Imagery and Multi-Scale Textures Using Random Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Data Acquisition and Preprocessing
| ID | Forest Type | Total Samples |
|---|---|---|
| 1 | LP | 5831 |
| 2 | BF | 2912 |
| 3 | MP | 949 |
| 4 | AP | 102 |
| 5 | HDF | 86 |
| 6 | PP | 29 |
| Total | 9909 |
2.3. Textural Analysis
2.3.1. Geostatistical Texture
2.3.2. GLCM Texture
2.4. Random Forests Classification and Feature Selection
2.4.1. Random Forests Classifier

2.4.2. Feature Selection
3. Results
3.1. Performance of Random Forests Classifier
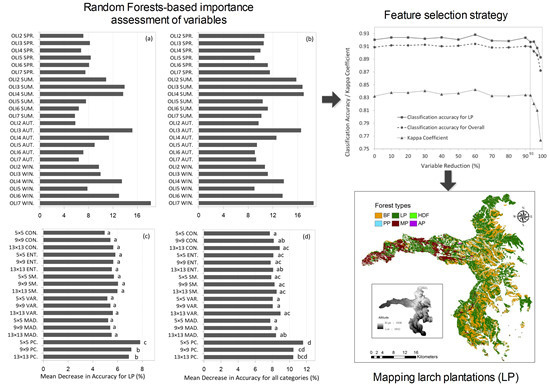
3.2. Importance Measure of Variables




3.3. Mapping LP by Feature Selection of Random Forests

| Reference Data | Classify as | |||||||
|---|---|---|---|---|---|---|---|---|
| BF | HDF | LP | MP | PP | AP | Total | Prod. Acc. | |
| BF | 781 | 0 | 94 | 5 | 0 | 0 | 880 | 0.888 |
| HDF | 23 | 0 | 2 | 0 | 0 | 0 | 25 | 0 |
| LP | 80 | 0 | 1671 | 11 | 0 | 0 | 1762 | 0.948 |
| MP | 1 | 0 | 27 | 233 | 0 | 0 | 261 | 0.893 |
| PP | 0 | 0 | 2 | 2 | 4 | 0 | 8 | 0.500 |
| AP | 1 | 0 | 22 | 5 | 0 | 7 | 35 | 0.200 |
| total | 886 | 0 | 1818 | 256 | 4 | 7 | 2971 | |
| User’s acc. | 0.881 | 0 | 0.919 | 0.910 | 1 | 1 | 0.907 | |

4. Discussion
4.1. Importance of Input Variables
4.2. Feature Selection of the most Important Variables
4.3. The Accuracy and Uncertainty of Random Forests Classification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mason, W.L.; Zhu, J.J. Silviculture of planted forests managed for multi-functional objectives: Lessons from Chinese and British experiences. In Challenges and Opportunities for the World’s Forests in the 21st Century; Fenning, T., Ed.; Springer: Berlin, Germany, 2014; pp. 39–50. [Google Scholar]
- Chinese Ministry of Forestry. Forest Resource Statistics of China; Department of Forest Resource and Management, Chinese Ministry of Forestry: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Wang, C.; Ouyang, H.; Shao, B.; Tian, Y.; Zhao, J.; Xu, H. Soil carbon changes following afforestation with Olga Bay Larch (Larix olgensis Henry) in Northeastern China. J. Integr. Plant Biol. 2006, 48, 503–512. [Google Scholar] [CrossRef]
- Zhu, J.J.; Yang, K.; Yan, Q.; Liu, Z.; Yu, L.; Wang, H. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch-broadleaved mixed forests. J. For. Res. 2010, 15, 71–80. [Google Scholar] [CrossRef]
- Yan, Q.; Zhu, J.J.; Gang, Q. Comparison of spatial patterns of soil seed banks between larch plantations and adjacent secondary forests in Northeast China: Implication for spatial distribution of larch plantations. Trees 2013, 27, 1747–1754. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, J.J.; Zhang, M.; Yan, Q.; Sun, O.J. Soil microbial biomass carbon and nitrogen in forest ecosystems of Northeast China: A comparison between natural secondary forest and larch plantation. J. Plant Ecol. 2010, 3, 175–182. [Google Scholar] [CrossRef]
- Yang, K.; Shi, W.; Zhu, J.J. The impact of secondary forests conversion into larch plantations on soil chemical and microbiological properties. Plant Soil 2013, 368, 535–546. [Google Scholar] [CrossRef]
- Engler, R.; Waser, L.T.; Zimmermann, N.E.; Schaub, M.; Berdos, S.; Ginzler, C.; Psomas, A. Combining ensemble modeling and remote sensing for mapping individual tree species at high spatial resolution. For. Ecol. Manag. 2013, 310, 64–73. [Google Scholar] [CrossRef]
- Alkemade, R.; Burkhard, B.; Crossman, N.D.; Nedkov, S.; Petz, K. Quantifying ecosystem services and indicators for science, policy and practice. Ecol. Indic. A 2014, 37, 161–162. [Google Scholar] [CrossRef]
- Bijalwan, A.; Swamy, S.L.; Sharma, C.; Sharma, N.; Tiwari, A.K. Land-use, biomass and carbon estimation in dry tropical forest of Chhattisgarh region in India using satellite remote sensing and GIS. J. For. Res. 2010, 21, 161–170. [Google Scholar] [CrossRef]
- Gao, T.; Xu, B.; Yang, X.; Jin, Y.; Ma, H.; Li, J.; Yu, H. Using MODIS time series data to estimate aboveground biomass and its spatio-temporal variation in Inner Mongolia’s grassland between 2001 and 2011. Int. J. Remote Sens. 2013, 34, 7796–7810. [Google Scholar] [CrossRef]
- Li, J.; Yang, X.; Jin, Y.; Yang, Z.; Huang, W.; Zhao, L.; Gao, T.; Yu, H.; Ma, H.; Qin, Z.; et al. Monitoring and analysis of grassland desertification dynamics using Landsat images in Ningxia, China. Remote Sens. Environ. 2013, 138, 19–26. [Google Scholar] [CrossRef]
- Folega, F.; Zhang, C.; Zhao, X.; Wala, K.; Batawila, K.; Huang, H.; Dourma, M.; Akpagana, K. Satellite monitoring of land-use and land-cover changes in northern Togo protected areas. J. For. Res. 2014, 25, 385–392. [Google Scholar] [CrossRef]
- Zeng, Y.; Schaepman, M.E.; Wu, B.; Clevers, J.G.P.W.; Bregt, A.K. Scaling-based forest structural change detection using an inverted geometric-optical model in the Three Gorges region of China. Remote Sens. Environ. 2008, 112, 4261–4271. [Google Scholar] [CrossRef]
- Grinand, C.; Rakotomalala, F.; Gond, V.; Vaudry, R.; Bernoux, M.; Vieilledent, G. Estimating deforestation in tropical humid and dry forests in Madagascar from 2000 to 2010 using multi-date Landsat satellite images and the random forests classifier. Remote Sens. Environ. 2013, 139, 68–80. [Google Scholar] [CrossRef]
- Corcoran, J.; Knight, J.; Gallant, A. Influence of multi-source and multi-temporal remotely sensed and ancillary data on the accuracy of random forest classification of wetlands in Northern Minnesota. Remote Sens. 2013, 5, 3212–3238. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random Forest classification of Mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2012, 34, 2607–2654. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Chica-Olmo, M. Land cover change analysis of a Mediterranean area in Spain using different sources of data: Multi-seasonal Landsat images, land surface temperature, digital terrain models and texture. Appl. Geogr. 2012, 35, 208–218. [Google Scholar] [CrossRef]
- Gasparri, N.I.; Parmuchi, M.G.; Bono, J.; Karszenbaum, H.; Montenegro, C.L. Assessing multi-temporal Landsat 7 ETM+ images for estimating above-ground biomass in subtropical dry forests of Argentina. J. Arid Environ. 2010, 74, 1262–1270. [Google Scholar] [CrossRef]
- Rakwatin, P.; Longépé, N.; Isoguchi, O.; Shimada, M.; Uryu, Y.; Takeuchi, W. Using multiscale texture information from ALOS PALSAR to map tropical forest. Int. J. Remote Sens. 2012, 33, 7727–7746. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Berberoğlu, S.; Akin, A.; Atkinson, P.M.; Curran, P.J. Utilizing image texture to detect land-cover change in Mediterranean coastal wetlands. Int. J. Remote Sens. 2010, 31, 2793–2815. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming, 2nd ed.; Dover Publications: Mineola, NY, USA, 2003. [Google Scholar]
- Mellor, A.; Haywood, A.; Stone, C.; Jones, S. The performance of random forests in an operational setting for large area sclerophyll forest classification. Remote Sens. 2013, 5, 2838–2856. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Watts, J.D.; Lawrence, R.L.; Miller, P.R.; Montagne, C. Monitoring of cropland practices for carbon sequestration purposes in north central Montana by Landsat remote sensing. Remote Sens. Environ. 2009, 113, 1843–1852. [Google Scholar] [CrossRef]
- Gleason, C.J.; Jungho, I. Forest biomass estimation from airborne LiDAR data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Wood, S.D.; Sheley, R.L. Mapping invasive plants using hyperspectral imagery and Breiman Cutler classifications (random Forest). Remote Sens. Environ. 2006, 100, 356–362. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Fan, H. Land-cover mapping in the Nujiang Grand Canyon: Integrating spectral, textural, and topographic data in a random forest classifier. Int. J. Remote Sens. 2013, 34, 7545–7567. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Dye, M.; Mutanga, O.; Ismail, R. Detecting the severity of woodwasp, Sirex noctilio, infestation in a pine plantation in KwaZulu-Natal, South Africa, using texture measures calculated from high spatial resolution imagery. Afr. Entomol. 2008, 16, 263–275. [Google Scholar] [CrossRef]
- Chica-Olmo, M.; Abarca-Hernández, F. Computing geostatistical image texture for remotely sensed data classification. Comput. Geosci. 2000, 26, 373–383. [Google Scholar] [CrossRef]
- Li, P.; Cheng, T.; Guo, J. Multivariate image texture by multivariate variogram for multispectral image classification. Photogramm. Eng. Remote Sens. 2009, 75, 147–157. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Lewis, P. Geostatistical classification for remote sensing: An introduction. Comput. Geosci. 2000, 26, 361–371. [Google Scholar] [CrossRef]
- Coburn, C.A.; Roberts, A.C.B. A multiscale texture analysis procedure for improved forest stand classification. Int. J. Remote Sens. 2004, 25, 4287–4308. [Google Scholar] [CrossRef]
- Pino-Mejías, R.; Cubiles-De-La-Vega, M.D.; Anaya-Romero, M.; Pascual-Acosta, A.; Jordán-López, A.; Bellinfante-Crocci, N. Predicting the potential habitat of oaks with data mining models and the R system. Environ. Model. Softw. 2010, 25, 826–836. [Google Scholar] [CrossRef]
- Chan, J.C.; Paelinckx, D. Evaluation of random forest and adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with random forest using very high spatial resolution 8-band worldview-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Hunt, E.R., Jr.; Li, L.; Yilmaz, M.T.; Jackson, T.J. Comparison of vegetation water contents derived from shortwave-infrared and passive-microwave sensors over central Iowa. Remote Sens. Environ. 2011, 115, 2376–2383. [Google Scholar] [CrossRef]
- Plummer, S.E. Exploring the relationships between leaf nitrogen content, biomass and the near-infrared/red reflectance ratio. Int. J. Remote Sens. 1988, 9, 177–183. [Google Scholar] [CrossRef]
- Ghioca-Robrecht, D.; Johnston, C.; Tulbure, M. Assessing the use of multiseason QuickBird imagery for mapping invasive species in a Lake Erie coastal Marsh. Wetlands 2008, 28, 1028–1039. [Google Scholar] [CrossRef]
- Helmer, E.H.; Ruzycki, T.S.; Benner, J.; Voggesser, S.M.; Scobie, B.P.; Park, C.; Fanning, D.W.; Ramnarine, S. Detailed maps of tropical forest types are within reach: Forest tree communities for Trinidad and Tobago mapped with multiseason Landsat and multiseason fine-resolution imagery. For. Ecol. Manag. 2012, 279, 147–166. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Hu, L.; Yu, L.; Clinton, N.; Huang, H.; Yang, J.; Gong, P. A circa 2010 thirty meter resolution forest map for China. Remote Sens. 2014, 6, 5325–5343. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, T.; Zhu, J.; Zheng, X.; Shang, G.; Huang, L.; Wu, S. Mapping Spatial Distribution of Larch Plantations from Multi-Seasonal Landsat-8 OLI Imagery and Multi-Scale Textures Using Random Forests. Remote Sens. 2015, 7, 1702-1720. https://doi.org/10.3390/rs70201702
Gao T, Zhu J, Zheng X, Shang G, Huang L, Wu S. Mapping Spatial Distribution of Larch Plantations from Multi-Seasonal Landsat-8 OLI Imagery and Multi-Scale Textures Using Random Forests. Remote Sensing. 2015; 7(2):1702-1720. https://doi.org/10.3390/rs70201702
Chicago/Turabian StyleGao, Tian, Jiaojun Zhu, Xiao Zheng, Guiduo Shang, Liyan Huang, and Shangrong Wu. 2015. "Mapping Spatial Distribution of Larch Plantations from Multi-Seasonal Landsat-8 OLI Imagery and Multi-Scale Textures Using Random Forests" Remote Sensing 7, no. 2: 1702-1720. https://doi.org/10.3390/rs70201702
APA StyleGao, T., Zhu, J., Zheng, X., Shang, G., Huang, L., & Wu, S. (2015). Mapping Spatial Distribution of Larch Plantations from Multi-Seasonal Landsat-8 OLI Imagery and Multi-Scale Textures Using Random Forests. Remote Sensing, 7(2), 1702-1720. https://doi.org/10.3390/rs70201702