A Robust Photogrammetric Processing Method of Low-Altitude UAV Images
Abstract
:1. Introduction
2. Related Research
3. General Strategy and Data Acquisition
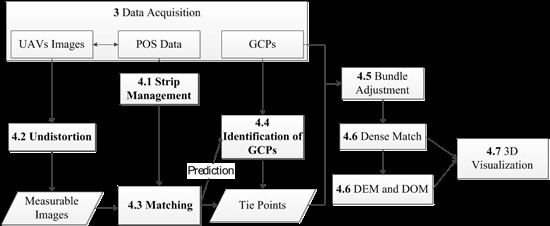
3.1. Strategy

3.2. Experimental Dataset 1: Yangqiaodian
3.3. Experimental Dataset 2: PDS



4. Photogrammetric Processing of UAV Images
4.1. Strip Management



4.2. Geometric Correction
| Method | First Image (s) | Remaining Images (s) | All (s) |
|---|---|---|---|
| Direct distortion correction | 10.4 | 10.4 | 314.0 |
| Lookup table-based distortion correction algorithm | 10.4 | 6.0 | 182.7 |
| Parallel lookup table-based interior orientation method | 5.8 | 3.4 | 104.4 |
4.3. Image Matching Strategy

- (1)
- Configure the default parameters of the SIFT feature-extraction algorithm or obtain the parameters from the users, including the number of blocks in the images, which is generally the number of cell rows and columns in one image. In our experiment, the images were divided into five rows and three columns with a total 15 cells shown in the top right corner of Figure 8, and an image block was 800 × 800 pixels in the center of the image cell; as such, there are 15 blocks in one image; This division is based on demand of the von Gruber locations in the traditional aerial photogrammetry;
- (2)
- Calculate the sizes of the blocks and their positions in the image according to the image size and parameters;
- (3)
- Extract SIFT features from the blocks; calculate the weighted average of the numbers of features in the blocks as T with the Equation (3):where n is the number of blocks in one image; Nib is the number of features in block ib; Hib is the image information entropy of block ib, calculated by the second formula; Pi is the probability of gray level i(i = 0,1,…,255) in the block ib; L equals 256 in our experiment;
- (4)
- If the number of features in one block is less than T, then go to step (5), otherwise extraction of this block is finished, go to step (7);
- (5)
- Modify the parameters of the SIFT feature-extraction algorithm in accordance with the current number of points, then go to step (6).
- (6)
- Redo the extraction on the image block with the new parameters, and continue to step (7) whether the number of features is less than T or not;
- (7)
- Finish extracting for the image.

4.4. Ground Control Point Prediction

4.5. Bundle Adjustment
4.6. Dense Matching and Generation of Digital Surface Models (DSM) and Digital Orthophoto Maps (DOM)

4.7. Three-Dimensional Visualization
5. Results and Discussion
5.1. Image Matching
5.1.1. Efficiency and Distribution of Features
| BlockSize | SIFT | BAoSIFT | BAoSIFT MT | ||
|---|---|---|---|---|---|
| Time (ms) | Number of Features | Time (ms) | Number of Features | Time (ms) | |
| 64 × 64 | 5007 | 9925 | 8018 | 12,749 | 2340 |
| 128 × 128 | 5054 | 12,203 | 8053 | 15,037 | 2424 |
| 256 × 256 | 5504 | 13,594 | 8081 | 16,606 | 2605 |
| 512 × 512 | 5679 | 14,209 | 8346 | 16,951 | 2659 |
| 1024 × 1024 | 5959 | 14,628 | 8736 | 17,635 | 2715 |

5.1.2. Feature Matching


| Method | a | b | c | d |
|---|---|---|---|---|
| Number of Correspondences | 631 | 1381 | 3845 | 3371 |
| Time(ms) | 2558 | 8074 | 72,649 | 73,415 |


5.2. Bundle Adjustment
5.2.1. Yangqiaodian
| Method | Control Points (m) | Check Points (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Evaluation | Max (ΔX) | Max (ΔY) | Max (ΔZ) | RMS (X) | RMS (Y) | RMS (Z) | Max (ΔX) | Max (ΔY) | Max (ΔZ) | RMS (X) | RMS (Y) | RMS (Z) |
| SIFT (a) | 1.51 | 0.61 | 0.97 | 0.32 | 0.24 | 0.54 | 0.57 | 0.37 | 0.83 | 0.23 | 0.22 | 0.51 |
| BAoSIFT (b) | 0.42 | 0.38 | 0.74 | 0.17 | 0.17 | 0.38 | 0.32 | 0.26 | 0.55 | 0.16 | 0.17 | 0.36 |
| VisualSFM | 1.21 | 0.98 | 1.33 | 0.65 | 0.56 | 0.82 | 1.42 | 1.01 | 1.46 | 0.78 | 0.68 | 0.91 |



5.2.2. PDS
| Method | Control Points (m) | Check Points (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | Std | Max | Std | |||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |
| SIFT | 0.140 | 0.114 | 0.657 | 0.035 | 0.032 | 0.189 | 0.142 | 0.052 | 0.437 | 0.048 | 0.025 | 0.167 |
| BAoSIFT | 0.135 | 0.070 | 0.192 | 0.021 | 0.019 | 0.042 | 0.132 | 0.046 | 0.231 | 0.039 | 0.019 | 0.070 |
| VisualSFM | 0.530 | 0.640 | 0.810 | 0.180 | 0.240 | 0.430 | 0.470 | 0.610 | 0.980 | 0.160 | 0.190 | 0.520 |
| VisualSFM-PATB | 0.149 | 0.056 | 0.842 | 0.025 | 0.024 | 0.140 | 0.139 | 0.055 | 0.589 | 0.038 | 0.027 | 0.159 |


5.3. 3D Visualization of Digital Elevation Model (DEM) and Digital Orthophoto Maps (DOM)

6. Conclusions

Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, Y.; Xiong, J.; Hao, L. Photogrammetric processing of low-altitude images acquired by unpiloted aerial vehicles. Photogramm. Rec. 2011, 26, 190–211. [Google Scholar] [CrossRef]
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV photogrammetry for mapping and 3d modeling–current status and future perspectives. In Proceedings of the International Conference on Unmanned Aerial Vehicle in Geomatics (UAV-g), Zurich, Switzerland, 14–16 September 2011.
- Büyüksali̇h, G.; Li, Z. Practical experiences with automatic aerial triangulation using different software packages. Photogramm. Rec. 2003, 18, 131–155. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Herrick, J.E.; Rango, A.; Winters, C. Acquisition, orthorectification, and object-based classification of unmanned aerial vehicle (UAV) imagery for rangeland monitoring. Photogramm. Eng. Remote Sens. 2010, 76, 661–672. [Google Scholar] [CrossRef]
- Pierrot-Deseilligny, M.; Luca, L.D.; Remondino, F. Automated image-based procedures for accurate artifacts 3d modeling and orthoimage generation. In Proceedings of the 23th International CIPA Symposium, Prague, Czech Republic, 12–16 September 2011.
- Visualsfm: A Visual Structure from Motion System. Available online: http://ccwu.me/vsfm/ (accessed on 17 February 2015).
- Deseilligny, M.P.; Clery, I. Apero, an open source bundle adjusment software for automatic calibration and orientation of a set of images. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Trento, Italy, 2–4 March 2011; Volume 38.
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from internet photo collections. Int. J. Comput. Vis. 2007, 80, 189–210. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3d mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Barazzetti, L.; Scaioni, M.; Remondino, F. Orientation and 3D modelling from markerless terrestrial images: Combining accuracy with automation. Photogram. Rec. 2010, 25, 356–381. [Google Scholar] [CrossRef]
- Barazzetti, L.; Remondino, F.; Scaioni, M.; Brumana, R. Fully automatic UAV image-based sensor orientation. In Proceedings of the ISPRS Commission I Mid-Term Symposium “Image Data Acquisition-Sensors & Platforms”, Calgary, AB, Canada, 15–18 June 2010.
- Haala, N.; Cramer, M.; Weimer, F.; Trittler, M. Performance test on UAV-based photogrammetric data collection. In Proceedings of the International Conference on Unmanned Aerial Vehicle in Geomatics (UAV-g), Zurich, Switzerland, 14–16 September 2011; Volume XXXVIII-1/C22.
- Pollefeys, M.; Gool, L.V. From images to 3d models. In Communications of the ACM-How the Virtual Inspires the Real; ACM: New York, NY, USA, 2002; pp. 50–55. [Google Scholar]
- Hao, X.; Mayer, H. Orientation and auto-calibration of image triplets and sequences. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, 34, 73–78. [Google Scholar]
- Nister, D. Automatic passive recovery of 3d from images and video. In Proceedings of the 2nd International Symposium on 3D Data Processing, Visualization and Transmission, Thessaloniki, Greece, 6–9 September 2004; pp. 438–445.
- Vergauwen, M.; Gool, L.V. Web-based 3d reconstruction service. Mach. Vis. Appl. 2006, 17, 411–426. [Google Scholar] [CrossRef]
- Barazzetti, L.; Remondino, F.; Scaioni, M. Automation in 3d reconstruction: Results on different kinds of close-range blocks. In Proceedings of the ISPRS Commission V Mid-Term Symposium “Close Range Image Measurement Techniques”, Newcastle upon Tyne, UK, 21–24 June 2010.
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the International Conference on Computer Vision, Corfu, Greece; 1999; pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Gr. Image Process. 1981, 24, 381–395. [Google Scholar]
- Förstner, W. A feature based correspondence algorithm for image matching. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 1986, 26, 150–166. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK; 1988; pp. 147–151. [Google Scholar]
- Laliberte, A.S.; Winters, C. A procedure for orthorectification of sub-decimeter resolution imagery obtained with an unmanned aerial vehicle (UAV). In Proceedings of the ASPRS 2008 Annual Conference, Portland, OR, USA, 28 April–2 May 2008.
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the 9th European conference on Computer Vision(ECCV’06), 7–13 May 2006; pp. 430–443.
- k2-photogrammetry. Patb. Available online: http://www.k2-photogrammetry.de/products/patb.html (accessed on 17 February 2015).
- SWDC Digital Aerial Camera. Available online: http://www.jx4.com/en/home/home/tjcp/SWDC_Digital/2014/0326/422.html (accessed on 17 February 2015).
- National Administration of Surveying, Mapping and Geoinformation of China (NASMG). Specifications for Field Work of Low-Altitude Digital Aerophotogrammetry; NASMG: Beijing, China, 2010; CH/Z 3004-2010. [Google Scholar]
- OpenMP.org. Openmp. Available online: http://openmp.org/wp/ (accessed on 17 February 2015).
- McGlone, C. Manual of Photogrammetry, 6th ed.; ASPRS: Bethesda, MD, USA, 2013. [Google Scholar]
- Huo, C.; Pan, C.; Huo, L.; Zhou, Z. Multilevel SIFT matching for large-size VHR image registration. IEEE Geosci. Remote Sens. Lett. 2012, 9, 171–175. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Bell, D.G.; Kuehnel, F.; Maxwell, C.; Kim, R.; Kasraie, K.; Gaskins, T.; Hogan, P.; Coughlan, J. NASA world wind: Opensource gis for mission operations. In Proceedings of the Aerospace Conference, Big Sky, MT, UAS, 3–10 March 2007; pp. 1–9.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, M.; Hu, Q.; Li, J.; Wang, M.; Yuan, H.; Wang, S. A Robust Photogrammetric Processing Method of Low-Altitude UAV Images. Remote Sens. 2015, 7, 2302-2333. https://doi.org/10.3390/rs70302302
Ai M, Hu Q, Li J, Wang M, Yuan H, Wang S. A Robust Photogrammetric Processing Method of Low-Altitude UAV Images. Remote Sensing. 2015; 7(3):2302-2333. https://doi.org/10.3390/rs70302302
Chicago/Turabian StyleAi, Mingyao, Qingwu Hu, Jiayuan Li, Ming Wang, Hui Yuan, and Shaohua Wang. 2015. "A Robust Photogrammetric Processing Method of Low-Altitude UAV Images" Remote Sensing 7, no. 3: 2302-2333. https://doi.org/10.3390/rs70302302
APA StyleAi, M., Hu, Q., Li, J., Wang, M., Yuan, H., & Wang, S. (2015). A Robust Photogrammetric Processing Method of Low-Altitude UAV Images. Remote Sensing, 7(3), 2302-2333. https://doi.org/10.3390/rs70302302