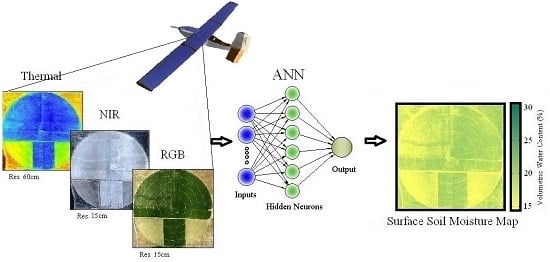
Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Artificial Neural Networks (ANNs)
2.2. Selection of Possible Input Variables
2.3. Study Area, Instrumentation, Techniques and Data
2.3.1. Study Area

2.3.2. Instrumentation: AggieAir Minion (Remote Sensing Platform)

2.3.3. Ground-Based Data Collection

2.3.4. Soil Texture Analysis

2.3.5. Relevant Vegetation Indices (VIs) from AggieAir Imagery
2.3.6. Model Validation
2.3.7. Wrapper Selection
2.3.8. Division Set Up in ANN Model Architecture
3. Results and Discussion
3.1. Input Data
3.1.1. Soil Moisture Data Calculation Results
| Crop Type/Date | NDVI(Mean) | |||
|---|---|---|---|---|
| 5/17/2013 | 6/1/2013 | 6/9/2013 | 6/17/2013 | |
| Three way, Oat, Barley , Wheat | 0.09 | 0.34 | 0.43 | 0.53 |
| Planting | continued growth | continued growth | full growth | |
| Alfalfa | 0.42 | 0.47 | 0.53/0.08 | 0.59/0.13 |
| continued growth | continued growth | full growth/ after cut | full growth/ after cut | |
| Oat, Alfalfa | 0.43 | 0.48 | 0.53 | 0.57 |
| germination | continued growth | full growth | full growth | |
3.1.2. Spatial Information of Vegetation Indices
3.2. Wrapper Selection Outcome

| ANN Inputs | Division Set up | # of Neurons | RMSE | MAE | r | e | R2 | |
|---|---|---|---|---|---|---|---|---|
| One Input | Thermal | 80/10/10 | 4 | 3.0 | 2.4 | 0.64 | 0.4 | 0.41 |
| Two Inputs | Thermal, Field capacity | 75/15/10 | 5 | 2.5 | 1.8 | 0.78 | 0.60 | 0.61 |
| Three Inputs | Red, Blue, Thermal | 70/15/15 | 7 | 2.7 | 2.1 | 0.74 | 0.54 | 0.55 |
| Four Inputs | Red, NDVI, VCI, VHI | 70/15/15 | 7 | 2.5 | 1.8 | 0.77 | 0.59 | 0.60 |
| Five Inputs | Green, Thermal, VCI, EVI, Field Capacity | 80/10/10 | 9 | 2.1 | 1.6 | 0.84 | 0.71 | 0.71 |
| Six Inputs | NIR, Thermal, NDVI, EVI, VHI, Field Capacity | 80/10/10 | 11 | 2.1 | 1.5 | 0.84 | 0.70 | 0.71 |
| Seven Inputs | Red, Blue, NIR, Thermal, NDVI, VCI, Field Capacity | 80/10/10 | 12 | 2.1 | 1.6 | 0.86 | 0.73 | 0.73 |
| Eight inputs | Red, Blue, NIR, Thermal, NDVI, EVI, VCI, Field Capacity | 80/10/10 | 17 | 2.0 | 1.3 | 0.85 | 0.75 | 0.77 |
| Nine Inputs | Red, Green, Blue, Thermal, NDVI, EVI, VCI, VHI, Field Capacity | 80/10/10 | 17 | 2.0 | 1.4 | 0.87 | 0.75 | 0.75 |
| Ten Inputs | Red, Green, Blue, NIR, Thermal, NDVI, EVI, VCI, VHI, Field Capacity | 80/10/10 | 19 | 2.0 | 1.3 | 0.85 | 0.73 | 0.73 |
3.3. Results Extracted from Artificial Neural Networks (ANNs)



| Crop Type/Date | Soil Moisture (Volumetric Water Content (%)) (Zonal Mean) | |||||||
|---|---|---|---|---|---|---|---|---|
| 5/17/2013 | 6/1/2013 | 6/9/2013 | 6/17/2013 | |||||
| Measured | Estimated | Measured | Estimated | Measured | Estimated | Measured | Estimated | |
| Three way, Oat, Barley , Wheat | 18.9 | 20.1 | 21.5 | 19.0 | 14.9 | 15.7 | 19.3 | 17.6 |
| Alfalfa | 27.6 | 25.9 | 25.0 | 23.5 | 18.4 | 18.9 | 21.2 | 20.4 |
| Oat, Alfalfa | 18.0 | 18.3 | 20.5 | 18.1 | 15.7 | 15.8 | 22.5 | 18.9 |
4. Conclusions
5. Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grayson, R.B.; Western, A.W. Towards areal estimation of soil water content from point measurements: Time and space stability of mean response. J. Hydrol. 1998, 207, 68–82. [Google Scholar] [CrossRef]
- Gill, K.; Kemblowski, M.; McKee, M. Soil moisture data assimilation using support vector machines and ensemble Kalman filter. JAWRA J. Am. Water Resour. Assoc. 2007, 43, 1004–1015. [Google Scholar] [CrossRef]
- Zaman, B.; McKee, M.; Neale, C.M.U. Fusion of remotely sensed data for soil moisture estimation using relevance vector and support vector machines. Int. J. Remote Sens. 2012, 33, 6516–6552. [Google Scholar] [CrossRef]
- Liu, W.; Baret, F.; Gu, X.; Zhang, B.; Tong, Q.; Zheng, L. Evaluation of methods for soil surface moisture estimation from reflectance data. Int. J. Remote Sens. 2003, 24, 2069–2083. [Google Scholar] [CrossRef]
- Idso, S.; Jackson, R.; Reginato, R. Estimating evaporation: A technique adaptable to remote sensing. Science 1975, 189, 991–992. [Google Scholar] [CrossRef] [PubMed]
- Idso, S.; Jackson, R.; Reginato, R. Compensating for environmental variability in the thermal inertia approach to remote sensing of soil moisture. J. Appl. Meteorol. 1976, 15, 811–817. [Google Scholar] [CrossRef]
- Reginato, R.; Idso, S.; Jackson, R.; Vedder, J.; Blanchard, M.; Goettelman, R. Soil water content and evaporation determined by thermal parameters obtained from ground-based and remote measurements. J. Geophys. Res. 1976, 81, 1617–1620. [Google Scholar] [CrossRef]
- Reginato, R.; Jackson, R.; Pinter, P. Evapotranspiration calculated from remote multispectral and ground station meteorological data. Remote Sens. Environ. 1985, 18, 75–89. [Google Scholar] [CrossRef]
- Jackson, T. Soil water modeling and remote sensing. IEEE Trans. Geosci. Remote Sens. 1986, 24, 37–46. [Google Scholar] [CrossRef]
- Quattrochi, D.; Luvall, J. Thermal infrared remote sensing for analysis of landscape ecological processes: Methods and applications. Landsc. Ecol. 1999, 14, 577–598. [Google Scholar] [CrossRef]
- Kaleita, A.; Tian, L.; Hirschi, M. Relationship between soil moisture content and soil surface reflectance. Trans. ASAE 2005, 48, 1979–1986. [Google Scholar] [CrossRef]
- Humes, K.; Kustas, W.; Jackson, T.; Schmugge, T.; Moran, M. Combined use of optical and microwave remotely sensed data for the estimation of surface energy balance components over a semi-arid watershed. In Proceedings of the IEEE Topical Symposium on Combined Optical-Microwave Earth and Atmosphere Sensing, Albuquerque, NM, USA, 22–25 March 1993; pp. 86–89.
- Njoku, E.G.; Jackson, T.J.; Lakshimi, V.; Chan, T.K.; Ngheim, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Aritola, J.F.; Pepper, I.L.; Brusseau, M.L. Environmental Monitoring and Characterization; Elsevier Academic Press: San Diego, CA, USA, 2004. [Google Scholar]
- Das, N.N.; Mohanty, B.P. Root zone soil moisture assessment using remote sensing and vadose zone modeling. Vadose Zone J. 2006, 5, 296–307. [Google Scholar] [CrossRef]
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global survey and statistics of radio-frequency interference in AMSR-E land observations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 938–947. [Google Scholar] [CrossRef]
- Crosson, W.L.; Limaye, A.S.; Laymon, C.A. Parameter sensitivity of soil moisture retrievals from airborn C- and X-band radiomter measurements in SMEX02. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2842–2853. [Google Scholar] [CrossRef]
- Crow, W.T.; Chan, T.K.; Entekhabi, D.; Houser, P.R.; Hsu, A.Y.; Jackson, T.J.; Njoku, E.G.; O’Neill, P.E.; Shi, J.; Zhan, X. An observing system simulation experiment for hydros radiomter-only soil moisture products. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1289–1303. [Google Scholar] [CrossRef]
- Fernandez-Galvez, J. Errors in soil moisture content estimates induced by uncertainties in the effective soil dielectric constant. Int. J. Remote Sens. 2008, 29, 3317–3323. [Google Scholar] [CrossRef]
- Cai, G.; Xue, Y.; Hu, Y.; Wang, Y.; Guo, J.; Luo, Y.; Wu, C.; Zhong, S.; Qi, S. Soil moisture retrieval from MODIS data in northern China plain using thermal inertia model. Int. J. Remote Sens. 2007, 28, 3567–3581. [Google Scholar] [CrossRef]
- Lu, S.; Ju, Z.; Ren, T.; Horton, R. A general approach to estimate soil water content from thermal inertia. Agric. For. Meteorol. 2009, 149, 1693–1698. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; van der Sande, C.J.; Grootaers, I.; Feyen, J. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests. Remote Sens. Environ. 2006, 101, 299–314. [Google Scholar] [CrossRef]
- Gill, M.; Asefa, T.; Kemblowski, M.; McKee, M. Soil moisture prediction using support vector machines. J. Am. Water Resour. Assoc. 2006, 42, 1033–1046. [Google Scholar] [CrossRef]
- Jiang, H.; Cotton, W. Soil moisture estimation using an artificial neural network: A feasibility study. Can. J. Remote Sens. 2004, 30, 827–839. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L; Torres-Rua, A.; Jensen, A.; McKee, M. Topsoil moisture estimation for precision agriculture using unmmaned aerial vehicle multispectral imagery. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3263–3266.
- Elshorbagy, A.; Parasuraman, K. On the relevance of using artificial neural networks for estimating soil moisture content. J. Hydrol. 2008, 362, 1–18. [Google Scholar] [CrossRef]
- Khalil, A.; Gill, M.K.; McKee, M. New applications for information fusion and soil moisture forecasting. In Proceedings of the 8th International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005; pp. 1622–1628.
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; MacMillan: New York, NY, USA, 1999. [Google Scholar]
- Khan, M.; Coulibaly, P. Streamflow forecasting with uncertainty estimate using Bayesian learning For ANN. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 5, pp. 2680–2685.
- Tokar, S.A.; Johnson, P.A. Rainfall-runoff modeling using artificial neural networks. J. Hydrol. Eng. 1999, 4, 232–239. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L.; PDP Research Group. Parallel Distributed Processing. Volume 1: Foundations; The MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Hecht-Nielsen, R. Neurocomputing; Addison-Wesley Publishing Company: Reading, MA, USA, 1990. [Google Scholar]
- Wasserman, P.D. Neural Computing Theory and Practice; Van Nostrand Reinhold: New York, NY, USA, 1989. [Google Scholar]
- Gillies, R.R.; Carlson, T.N. Thermal remote sensing of surface soil water content with partial vegetation cover for incorporation into climate models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- Wetzel, P.J.; Woodward, R.H. Soil moisture estimation using GOES-VISSR infrared data: A case study with a simple statistical method. J. Clim. Appl. Meteorol. 1987, 26, 107–117. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar-orbiting satellite data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Patel, N.K. Estimating volumetric surface moisture content for cropped soils using a soil wetness index based on surface temperature and NDVI. Agric. For. Meteorol. 2009, 149, 1327–1342. [Google Scholar] [CrossRef]
- Liang, S.; Rui, S.; Xiaowen, Li.; Shunlin,, L.; Renhua, Z. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information. Agric. For. Meteorol. 2012, 166, 175–187. [Google Scholar]
- Bhuiyan, C.; Singha, R.P.; Koganc, F.N. Monitoring drought dynamics in the Aravalli region (India) using different indices based on ground and remote sensing data. Int. J. Appl. Earth Observ. Geoinf. 2006, 8, 289–302. [Google Scholar] [CrossRef]
- Jensen, A.M. A Geospatial Real-Time Aerial Image Display for a Low-Cost Autonomous Multispectral Remote Sensing. Master’s Thesis, Utah State University, Logan, UT, USA, 2009. [Google Scholar]
- MosaicMill EnsoMOSAIC. Available online: http://www.ensomosaic.com (accessed on 6 May 2012).
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Decagon Devices, Inc. Available online: http://www.decagon.com/ (accessed on 20 November 2014).
- Israelson, O.W.; West, F.L. Water holding capacity of irrigated soils. Utah State Agric. Exp. Station Bull 1922, 183, 1–24. [Google Scholar]
- Costa, A.; Albuquerque, J.A.; Costa, A.; Pértile, P.; Silva, F.R. Water retention and availability in soils of the State of Santa Catarina-Brazil: Effect of textural classes, soil classes and lithology. Braz. Soil Sci. Soc. 2013, 37, 1535–1548. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Volume 12, pp. 1137–1143.
- Geisser, S. Predictive Inference; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Guyon, I. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 12, 273–324. [Google Scholar] [CrossRef]
- Glover, D.M.; Jenkins, W.J.; Doney, S.C. Least Squares and Regression Techniques, Goodness of Fit and Tests, Non-Linear Least Squares Techniques; Woods Hole Oceanographic Institute: Woods Hole, MA, USA, 2008. [Google Scholar]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Optimal division of data for neural network models in water resources applications. Water Resour. Res. 2002. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 2. Case study: Forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar] [CrossRef]
- Anctil, F.; Lauzon, N. Generalisation for neural networks through data sampling and training procedures, with applications to stream flow predictions. Hydrol. Earth Syst. Sci. 2004, 8, 940–958. [Google Scholar] [CrossRef]
- Jia, Y.; Culver, T.B. Bootstrapped artificial neural networks for synthetic flow generation with a small data sample. J. Hydrol. 2006, 331, 580–590. [Google Scholar] [CrossRef]
- Lauzon, N.; Anctil, F.; Petrinovic, J. Characterization of soil moisture conditions at temporal scales from a few days to annual. Hydrol. Process. 2004, 18, 3235–3254. [Google Scholar] [CrossRef]
- Whalley, W.R.; Leeds-Harrison, P.B.; Bowman, G.E. Estimation of soil moisture status using near infrared reflectance. Hydrol. Process. 1991, 5, 321–327. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L.; Torres-Rua, A.; McKee, M. Assessment of optimal irrigation water allocation for pressurized irrigation system using water balance approach, learning machines, and remotely sensed data. Agric. Water Manage. 2015, 153, 42–50. [Google Scholar] [CrossRef]
- Yin, Z.; Lei, T.; Yan, Q.; Chen, Z.; Dong, Y. A near-infrared reflectance sensor for soil surface moisture measurement. Comput. Electron. Agric. 2013, 99, 101–107. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sens. 2015, 7, 2627-2646. https://doi.org/10.3390/rs70302627
Hassan-Esfahani L, Torres-Rua A, Jensen A, McKee M. Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sensing. 2015; 7(3):2627-2646. https://doi.org/10.3390/rs70302627
Chicago/Turabian StyleHassan-Esfahani, Leila, Alfonso Torres-Rua, Austin Jensen, and Mac McKee. 2015. "Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks" Remote Sensing 7, no. 3: 2627-2646. https://doi.org/10.3390/rs70302627
APA StyleHassan-Esfahani, L., Torres-Rua, A., Jensen, A., & McKee, M. (2015). Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sensing, 7(3), 2627-2646. https://doi.org/10.3390/rs70302627