Next Article in Journal
Adjusting Lidar-Derived Digital Terrain Models in Coastal Marshes Based on Estimated Aboveground Biomass Density
Previous Article in Journal
Rice Fields Mapping in Fragmented Area Using Multi-Temporal HJ-1A/B CCD Images
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 7
Issue 4
10.3390/rs70403489
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Downscaling 250-m MODIS Growing Season NDVI Based on Multiple-Date Landsat Images and Data Mining Approaches

by
Yingxin Gu
1,* and
Bruce K. Wylie
2
1
ASRC InuTeq, Contractor to U.S. Geological Survey (USGS) Earth Resources Observation and Science (EROS) Center, 47914 252nd Street, Sioux Falls, SD 57198, USA
2
USGS EROS, 47914 252nd Street, Sioux Falls, SD 57198, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2015, 7(4), 3489-3506; https://doi.org/10.3390/rs70403489
Submission received: 22 January 2015 / Accepted: 17 March 2015 / Published: 24 March 2015
Browse Figures
Versions Notes

Abstract

:
The satellite-derived growing season time-integrated Normalized Difference Vegetation Index (GSN) has been used as a proxy for vegetation biomass productivity. The 250-m GSN data estimated from the Moderate Resolution Imaging Spectroradiometer (MODIS) sensors have been used for terrestrial ecosystem modeling and monitoring. High temporal resolution with a wide range of wavelengths make the MODIS land surface products robust and reliable. The long-term 30-m Landsat data provide spatial detailed information for characterizing human-scale processes and have been used for land cover and land change studies. The main goal of this study is to combine 250-m MODIS GSN and 30-m Landsat observations to generate a quality-improved high spatial resolution (30-m) GSN database. A rule-based piecewise regression GSN model based on MODIS and Landsat data was developed. Results show a strong correlation between predicted GSN and actual GSN (r = 0.97, average error = 0.026). The most important Landsat variables in the GSN model are Normalized Difference Vegetation Indices (NDVIs) in May and August. The derived MODIS-Landsat-based 30-m GSN map provides biophysical information for moderate-scale ecological features. This multiple sensor study retains the detailed seasonal dynamic information captured by MODIS and leverages the high-resolution information from Landsat, which will be useful for regional ecosystem studies.

Graphical Abstract

1. Introduction

Satellite remote sensing has become an essential tool for measuring and monitoring the dynamics of terrestrial ecosystems over large areas because of its wide coverage, high spatial and temporal resolutions, and consistency [1,2,3,4,5,6,7,8]. The satellite-derived Normalized Difference Vegetation Index (NDVI) is the normalized reflectance difference between the near-infrared (NIR) band and the visible red band [9,10]. NDVI represents the photosynthetic potential (or greenness) of a vegetation canopy. Higher NDVI values usually reflect greater vigor and greenness of the vegetation [10,11,12]. The growing season averaged (or integrated) NDVI (GSN) has been used as a proxy for vegetation biomass productivity, because GSN captures the seasonal dynamics related to ecological disturbances or weather variations through the growing season [13,14,15,16,17,18,19,20]. One limitation of using GSN to estimate vegetation productivity is that NDVI can reach saturation in dense vegetation canopies (i.e., NDVI becomes insensitive at high values of leaf area index) [14,21,22,23,24,25], which may lead to an underestimation of vegetation productivity in high (dense) biomass regions. Gu et al. developed an approach that adjusted NDVI (and GSN) pixel values that were near saturation to better characterize the cropland productivity in the Greater Platte River Basin, USA [26]. Generating a regional to global long-term time series GSN database with multiple spatial resolutions (e.g., 30-m and 250-m) can help better understand the biophysical character of a region, the dynamics of local to global ecosystems (e.g., changes and trends), and climate change impacts on ecosystem services. This long-term multi-scale GSN database can also be used as an input for biogeochemical, ecological, and climate change models [27].
The Moderate Resolution Imaging Spectroradiometer (MODIS), a key instrument aboard the Terra and Aqua satellites, has been widely used for monitoring and studying global dynamics and processes on the land, in the oceans, and in the lower atmosphere [28]. MODIS provides radiometrically sensitive (12-bit) data for 36 spectral bands (wavelengths range from 0.4 µm to 14.4 µm) for the entire Earth’s surface every one to two days. The spatial resolutions for MODIS data are 250 m for red and NIR bands, and 500 m and 1000 m for the other bands. High temporal resolution with a wide range of wavelengths make the MODIS land surface products (atmospherically corrected for cloud, cloud shadows, and aerosols) robust and reliable [29]. The long-term time series of 250-m MODIS GSN data derived from the MODIS red and NIR bands has been successfully used for terrestrial ecosystem modeling and monitoring [17,19,30,31,32,33]. However, these 250-m MODIS GSN maps can only provide the approximate ecological conditions and spatial patterns of a region and cannot capture the more detailed site-specific information at a regional scale. Therefore, developing a high spatial resolution (e.g., 30-m) GSN map for better understanding the site-specific biophysical and ecological dynamics of a region is needed.
The Landsat data series provides the longest (>40 years) continuous global record of space-based Earth surface observations and improves our understanding of Earth systems [34,35]. The advantage of the 30-m spatial resolution Landsat imagery available since 1981 is that it is global in coverage, and the resolution is detailed enough for characterizing human-scale processes (e.g., urban growth and deforestation) [36]. The long-term Landsat data have successfully been used for land cover and land change studies, ecological characterizations, and other Earth science applications [36,37,38,39,40,41,42,43,44,45,46,47,48]. Despite the advantage of the historical high spatial resolution Landsat data, using Landsat data for terrestrial ecosystem monitoring compared to MODIS land surface products has some limitations. For example, the 16-day Landsat revisit time (or possible 8-day revisit capabilities through two Landsat satellites) [49] lowers the capability of detecting rapid ecosystem changes (e.g., ecological disturbances such as wildfire) [50] and decreases the availability of cloud-free surface observation data [51,52] relative to the 1~2 day revisit time of MODIS. The wide wavelength ranges in the Landsat NIR and shortwave infrared bands may decrease the spectral sensitivity to vegetation canopy and may induce more atmospheric contamination in the raw data [50,53]. The weak cloud and aerosol detection compared to the MODIS sensors may cause more uncertainty in the Landsat land surface products [51,54,55,56,57]. In addition, the sparse Landsat temporal observations limit the use of temporal smoothing techniques to correct the NDVI values for cloudy pixels.
The main goal of this study is to develop an approach that combines both 250-m MODIS atmospherically corrected GSN data and 30-m Landsat observations to generate a quality-improved, atmospherically corrected, high spatial resolution (30-m) GSN product. A data mining technique is applied to develop the rule-based piecewise regression GSN models based on the MODIS GSN (dependent variable) and the degraded (250-m) Landsat data. The resulting 30-m GSN map provides biophysical and ecological information at a detailed level and will be useful for local, regional, and global ecosystem dynamic monitoring and modelling.

2. Data and Method

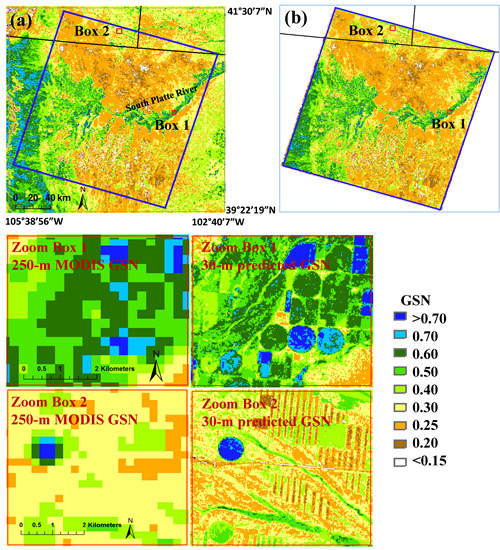
2.1. Study Area

Our pilot study area covers one Landsat scene and is mainly located in northeastern Colorado, plus a small portion of Wyoming and Nebraska.
Remotesensing 07 03489 g001 1024
Figure 1. Location of the study area (inside the blue outline) and the land cover types as identified in the National Land Cover Database (NLCD) 2001.
Figure 1. Location of the study area (inside the blue outline) and the land cover types as identified in the National Land Cover Database (NLCD) 2001.
Remotesensing 07 03489 g001
The study area represents varying levels of vegetation productivity, ranging from the low productivity semiarid grasslands to the highly productive irrigated croplands. The main vegetation cover types in the study area include cultivated crops (>33%) and grassland and herbaceous (~51%). Other vegetation cover types are forest, pasture and hay, and shrubland [37]. Multiple vegetation cover types with a wide range of productivities in the study area provide a wide range of GSN and help insure a robust, unbiased, and reliable model. The land cover types, state names and boundaries, and study area (within the blue outline) are shown in Figure 1.

2.2. Data

2.2.1. Landsat Data

Six Landsat 7 (8-bit) scenes with low cloud cover were selected for the 2002 growing season using browse images [58]. These six Landsat 7 scenes represent each month from April to September of 2002. The 30-m land surface reflectance data for Landsat visible and infrared bands (bands 1–5), Landsat NDVI product, and cloud mask data (“CFmask” data for cloud and cloud shadow) for the six Landsat scenes were obtained through the U.S. Geological Survey (USGS) Landsat Surface Reflectance Climate Data Record (CDR) [59]. The CDR approach is based on the National Aeronautics and Space Administration (NASA)-funded Landsat Ecosystem Disturbance Adaptive Processing System (LEDAPS) program [60].
The 30-m Landsat surface reflectance and NDVI data for the six scenes were upscaled to 250 m using the “spatial averaging” method. The percentage of 30-m cloudy/cloud shadow pixels within each 250-m MODIS pixel was calculated based on the 30-m CFmask data. The 250-m cloud mask maps for the six scenes were developed based on the percentage of cloud or shadow for each 250-m pixel (>85% cloudy pixel, <15% clear pixel). The 30-m averaged NDVI based on the six Landsat scenes was calculated and was used to evaluate the predicted 30-m GSN.

2.2.2. MODIS GSN Data

The 7-day maximum value composites of 250-m MODIS NDVI data were obtained from the USGS expedited MODIS (eMODIS) data archive [61]. The NDVI data were stacked by year and were saturation-corrected using an NDVI saturation correction approach [26]. The time series NDVI were then smoothed using a weighted least-squares approach to reduce additional atmospheric noise [62]. Finally, the growing season averaged NDVI for 2002 was calculated using weekly time series NDVI data with the start of season time as early April (~Julian date 100) and the end of season time as late October (~Julian date 300) [63].

2.3. Approach for Developing a 30-m GSN Map Based on MODIS and Landsat Data

2.3.1. Building Rule-based Piecewise Regression GSN Models

A data mining technique using Cubist software (version 2.05, [64]) was applied to develop the rule-based piecewise regression GSN models at 250-m resolution. Cubist models have been successfully used for ecosystem monitoring and modeling [5,6,7,65,66,67,68,69]. Cubist develops generalized rule sets (or piecewise regressions) from regression trees resulting in optimal multiple regression models that are constrained by data ranges of variables [64]. Data used for training the rule-based piecewise regression GSN models included (1) 250-m MODIS GSN data (dependent variables) and (2) 250-m multi-date (six scenes) Landsat 7 surface reflectance data for bands 1–5, NDVI data, and cloud masks (independent variables). More than 7200 samples were randomly extracted from the cloud-free regions and the cloudy regions across the six Landsat scenes and were used to build the GSN model.

2.3.2. Improving the GSN Model for Developing a 30-m MODIS-Landsat GSN Map

The 250-m estimated GSN map was generated based on the GSN models and the 250-m multiple-date Landsat scene data. The estimated GSN error (absolute difference between the predicted GSN and the actual MODIS GSN) map was also produced to assess the performance of the GSN regression tree model. Several high absolute error regions were identified in areas of extreme high or low GSN values (e.g., cultivated crops or open water areas). To make the GSN model more robust and less prone to prediction bias, additional training points (~650 pixels) were manually selected from the high GSN error regions. These new points were added to the original training dataset to develop the final updated GSN regression tree model. Finally, a 30-m MODIS-Landsat GSN map was generated by applying the final updated GSN model to the original multiple-date 30-m Landsat data. Developing a model at a coarse resolution and then subsequently applying it to a higher resolution was successfully accomplished by Rover et al. [69]. Figure 2 summarizes our approach for developing the 30-m MODIS-Landsat GSN map.
Remotesensing 07 03489 g002 1024
Figure 2. Flowchart for developing the 30-m MODIS-Landsat based GSN map.
Figure 2. Flowchart for developing the 30-m MODIS-Landsat based GSN map.
Remotesensing 07 03489 g002

2.3.3. Evaluating the 30-m MODIS-Landsat GSN Map

Statistical results derived from the Cubist software for assessing the performance of the GSN regression tree model including the important Landsat variables that contributed more in the GSN model, as well as the less important (or unused) Landsat variables. The final 30-m MODIS-Landsat GSN map was evaluated by comparing it with the 250-m MODIS GSN map, the original 30-m Landsat RGB images, and the average NDVI map based on the six Landsat scenes. The zoomed GSN maps for both cloud-free (clear) regions and cloudy regions are illustrated and discussed in the “Results and Discussion” Section.

2.4. Testing and Identifying the Optimal Landsat Date Combinations for the GSN Model

One goal of this study is to apply our downscaled MODIS-Landsat GSN approach to the historical Landsat data over a large area or globally. A computer with a high-speed processer and large disk space is needed for successfully implementing this approach globally. Therefore, reducing Landsat dates to decrease the computational time and disk space is advantageous. In this study, we tested and assessed the GSN regression tree models using six, five, and three Landsat date combinations. The best and the worst five- and three-date combinations for the GSN models were identified and compared with the six-date GSN results. The possibility of using three Landsat scenes (by selecting the optimal combination) to predict 30-m GSN based on MODIS and Landsat is also discussed in the paper.

3. Results and Discussion

3.1. GSN Regression Tree Model for the Cloud-Free Pixels

In order to investigate the relationship between MODIS GSN and Landsat data directly without any cloud impacts, we first tested and built the MODIS-Landsat GSN regression tree models (250-m scale) for the cloud-free regions in the six scenes. Results show a strong correlation between the actual MODIS GSN and the predicted GSN (r = 0.98, absolute average error = 0.015 for the 249 test samples), indicating that using Landsat products can successfully predict the MODIS GSN (Figure 3a). The most important Landsat variables that contribute more in the rule-based piecewise regression modeling for predicting GSN are Landsat NDVI in late spring (May) and in the late summer (August and September). This finding suggests that spring and late summer Landsat NDVI values play essential roles in the GSN prediction. None of the Landsat cloud mask data for the six scenes was used in the GSN model because this model only investigated cloud-free regions.
Remotesensing 07 03489 g003 1024
Figure 3. Scatterplots for the actual MODIS GSN and the predicted GSN. (a) Clear pixels only; (b) Clear and cloudy pixels.
Figure 3. Scatterplots for the actual MODIS GSN and the predicted GSN. (a) Clear pixels only; (b) Clear and cloudy pixels.
Remotesensing 07 03489 g003
The correlation coefficients (r) and the average errors between the actual MODIS GSN and the Landsat-based predicted GSN for the six, five, and three Landsat date combinations are shown in Table 1. Results indicate that the three-scene combination could have the same strong correlation and similar absolute error between the actual MODIS GSN and the Landsat-based predicted GSN (r = 0.98, absolute average error = 0.015, Table 1) as the six- or five-scene combination did. The best three-date Landsat combinations for the optimal GSN regression tree model are May-July-September or June-August-September (r = 0.98, absolute average error = 0.015) and the worst three-date combination for the GSN regression tree model is April-May-June (r = 0.93, absolute average error = 0.026). These results suggest that the three-date Landsat combinations, which include early, middle, and late (or middle and late) portions of the growing season, would generate the best GSN model. On the other hand, the three-date Landsat combination that was only selected from the early portion of the entire growing season, where late season effects would not be represented, would lead to a weaker GSN model. Figure 4 is the error (i.e., the difference between the predicted GSN and the actual MODIS GSN) histograms for the “6-scene” (blue) and the “worst 3-scene combination, April-May-June” (green) listed in Table 1. The “3-scene” based predicted GSN has more pixels with large errors (i.e., error < −0.05 or error > 0.05) than the “6-scene” based predicted GSN (Figure 4). The possibility of using optimal three-date Landsat scene combinations to develop the MODIS Landsat-based GSN model is discussed in the “Discussion” section.
Table
Table 1. The highest and the lowest correlation coefficients (r) and the absolute average errors between the actual MODIS GSN and the predicted GSN for the six, five, and three Landsat date combinations (for clear pixels only).
Table 1. The highest and the lowest correlation coefficients (r) and the absolute average errors between the actual MODIS GSN and the predicted GSN for the six, five, and three Landsat date combinations (for clear pixels only).
6-SceneHighest r for the 5-Scene CombinationLowest r for the 5-Scene CombinationHighest r for the 3-Scene CombinationLowest r for the 3-Scene Combination
Month4–94,5,6,8,94,6,7,8,95,7,9 (or 6,8,9)4,5,6
r0.980.980.970.980.93
Average error0.0150.0140.0150.0150.026
Remotesensing 07 03489 g004 1024
Figure 4. Error (difference between the predicted GSN and the actual MODIS GSN) histograms (% of total) for the “6-scene” (blue) and the “3-scene, April-May-June” (green). Histogram with “orange” color represents the differences between the upscaled LANDSAT NDVI and the 250-m MODIS NDVI for a single scene. Discussion on the “Orange” histogram can be found in the “Discussions” section.
Figure 4. Error (difference between the predicted GSN and the actual MODIS GSN) histograms (% of total) for the “6-scene” (blue) and the “3-scene, April-May-June” (green). Histogram with “orange” color represents the differences between the upscaled LANDSAT NDVI and the 250-m MODIS NDVI for a single scene. Discussion on the “Orange” histogram can be found in the “Discussions” section.
Remotesensing 07 03489 g004

3.2. GSN Regression Tree Model for the “Clear and Cloudy” Pixels

The final MODIS-Landsat GSN regression tree model, which included cloudy examples, was developed using a set of five successive piecewise regression models, with each successive model improving on the errors of the previous model (“Five-committee member model”) [70]. The first committee model includes 47 rules and associated pricewise regression equations with different combinations of independent variables and stratification criteria. The GSN model has 232 piecewise regression equations for all five committee models. The final prediction for each pixel is the averaged values of all the committee predictions.
Strong correlation between the actual MODIS GSN and the predicted GSN (r = 0.97, absolute average error = 0.026, Figure 3b) suggests that this MODIS-Landsat GSN approach can also be successfully applied to the minor amounts of cloudy coverage in the Landsat scenes. The most important Landsat variables that contribute more in the GSN rule-based piecewise regression modeling for “clear and cloudy” regions are NDVI in May and August (Table 2). The input Landsat variables that are not important and rarely used in the GSN regression tree models are Fmask data (only one Fmask data in June was used by the GSN model, Table 2). This implies that the Landsat reflectance data have already accounted for the cloud information. Theoretically, only spectral information from specific locations or data conditions, which helps explain significant variations in MODIS GSN, will be used by the regression tree model in prediction. Therefore, Landsat cloud masks may not be necessary for developing the GSN regression tree model if cloud coverage is low. Exclusion of the cloud mask should improve computational efficiencies and minimize disk space requirements and running time. The contributions of Landsat variables in the GSN regression tree model for the “clear and cloudy” areas (Table 2) are in good agreement with the cloud-free results (Table 1), with spring and late summer Landsat NDVIs having essential roles in the GSN prediction and demonstrating the reliability of our method and model.
Table
Table 2. Attribute usage in the rule-based piecewise regression GSN model. Name explanation: (1) the first character of the name represents the month (e.g., 4 represents April) and (2) B1–5 represents reflectance of the Landsat bands 1–5 (e.g., 4B5 means Landsat surface reflectance for April derived from band 5; 8NDVI means NDVI for August).
Table 2. Attribute usage in the rule-based piecewise regression GSN model. Name explanation: (1) the first character of the name represents the month (e.g., 4 represents April) and (2) B1–5 represents reflectance of the Landsat bands 1–5 (e.g., 4B5 means Landsat surface reflectance for April derived from band 5; 8NDVI means NDVI for August).
NameUsage in Rule StratificationUsage in Regression Model Average Usage
8NDVI74%81%78%
5NDVI55%81%68%
4B532%58%45%
4NDVI29%61%45%
9NDVI14%74%44%
6NDVI32%53%43%
9B419%65%42%
7NDVI11%73%42%
5B316%67%42%
8B116%65%41%
5B18%66%37%
8B26%68%37%
9B33%70%37%
8B47%63%35%
9B16%64%35%
8B370%-35%
9B270%-35%
4B22%64%33%
5B48%58%33%
5B23%62%33%
5B526%35%31%
4B46%54%30%
7B31%59%30%
4B159%-30%
7B22%53%28%
6B32%53%28%
7B59%45%27%
7B41%53%27%
4B353%-27%
9B52%44%23%
6B45%40%23%
6B21%44%23%
8B542%-21%
6B12%38%20%
6B59%30%20%
7B12%33%18%
6Fmask7%-4%
Table
Table 3. Correlation coefficients (r) and the absolute average errors between the actual MODIS GSN and the predicted GSN for the three Landsat date combinations for the “clear and cloudy” regions.
Table 3. Correlation coefficients (r) and the absolute average errors between the actual MODIS GSN and the predicted GSN for the three Landsat date combinations for the “clear and cloudy” regions.
Month456457458459467468469478479489
Correlation coefficient (r)0.950.950.950.930.930.940.940.940.940.93
Absolute average error (×100)3.93.33.13.83.73.33.63.63.53.6
Month567568569578579589678679689789
Correlation coefficient (r)0.960.960.960.950.950.960.940.930.950.91
Absolute average error (×100)3.32.93.33.13.13.23.63.63.34.2
We also tested and assessed the GSN regression tree models by using all possible combinations of six, five, and three Landsat dates for “clear and cloudy” areas to demonstrate the application of this approach to years with high cloud frequencies and low occurrences of cloud-free scenes. The correlation coefficients (r) and the average errors between the actual MODIS GSN and the Landsat-based predicted GSN for the three Landsat date combinations are presented in Table 3. The best three-date Landsat combination for the GSN regression tree model is May-June-August (r = 0.96, absolute average error = 0.029), and the worst three-date combination for the GSN regression tree model is July-August-September (r = 0.91, absolute average error = 0.042, Table 3). Results from Table 3 indicate that most of the three-date Landsat combinations (including “clear and cloudy” areas) can build a good quality GSN regression tree model (r > 0.93, absolute average error < 0.036, Table 3). The three-date combinations that only contained the early or latter part of the growing season (e.g., April-May-June and July-August-September) do not represent the entire growing season and resulted in relatively weak GSN regression tree models. Therefore, using a three-date Landsat combination that includes Landsat acquisitions across the growing season is recommended to optimize the MODIS-Landsat GSN regression tree prediction.

3.3. MODIS-Landsat GSN Map

3.3.1. Comparing the Predicted 30-m GSN with the 250-m MODIS GSN

The 30-m MODIS-Landsat GSN estimation map was generated based on the 30-m Landsat data and the final 250-m GSN regression tree model developed in the previous section. Figures 5a,b is the 250-m MODIS GSN (actual GSN) and the 30-m MODIS-Landsat GSN (predicted GSN) maps, showing agreement in the general spatial patterns between the actual and the predicted GSN maps. For example, both maps show the highly productive croplands along the South Platte River as well as the relatively low productive dryland rangeland located in the northern and southern parts of the study area (Figure 5a). The GSN regression tree model appears to have produced a high quality GSN map. Differences between the actual MODIS GSN and the predicted Landsat-based GSN are caused by the different spatial resolutions. To provide a more detailed view of the two GSN maps, we zoomed in on two small sample boxes located along the Platte River and southeastern Wyoming (red squares in Figures 5a,b) for the two GSN maps.
Remotesensing 07 03489 g005 1024
Figure 5. GSN maps for the study area. (a) 250-m MODIS GSN; (b) 30-m MODIS Landsat-based predicted GSN. Locations of the two zoomed boxes are shown in Figures 5a,b (red squares). The main vegetation cover types are irrigated croplands and grasslands for Box 1 and row crops and rangeland for Box 2.
Figure 5. GSN maps for the study area. (a) 250-m MODIS GSN; (b) 30-m MODIS Landsat-based predicted GSN. Locations of the two zoomed boxes are shown in Figures 5a,b (red squares). The main vegetation cover types are irrigated croplands and grasslands for Box 1 and row crops and rangeland for Box 2.
Remotesensing 07 03489 g005
In the “Zoom Box 1” maps, highly productive irrigated croplands (dominated by center pivot irrigations) are clearly shown as circular features in the 30-m predicted GSN map, but they are not distinguishable in the 250-m MODIS GSN map. The 250-m MODIS GSN map only provides a more smoothed pattern of NDVI for the zoomed region, which is largely attributable to the coarse spatial resolution. Similarly, in the “Zoom Box 2” maps, the spatial patterns for the center pivot irrigated crop, strip cropping (crop rotations), and dryland rangelands are clearly illustrated in the 30-m predicted GSN map; however, these detailed ecological features are blurred in the 250-m GSN map.
Remotesensing 07 03489 g006 1024
Figure 6. Illustration maps for a selected cloudy area. (a) Location of the selected cloudy area (red box); (b) Zoomed in Landsat scene for 2002 day of year (DOY) 167; (c) Zoomed in Landsat scene for 2002 DOY 199; (d) Zoomed in 250-m MODIS GSN; (e) Zoomed in 30-m predicted GSN; (f) Zoomed in 30-m original Landsat GSN.
Figure 6. Illustration maps for a selected cloudy area. (a) Location of the selected cloudy area (red box); (b) Zoomed in Landsat scene for 2002 day of year (DOY) 167; (c) Zoomed in Landsat scene for 2002 DOY 199; (d) Zoomed in 250-m MODIS GSN; (e) Zoomed in 30-m predicted GSN; (f) Zoomed in 30-m original Landsat GSN.
Remotesensing 07 03489 g006

3.3.2. Assessing the Impacts of Clouds

Since our data-driven GSN regression tree model was based on all the cloud condition scenarios (i.e., cloud free, mixture, and cloudy), the final 30-m MODIS-Landsat GSN estimation map indicated that the GSN model handled the cloud condition very well. Figure 6 is an example showing how the 30-m GSN map looked under cloudy conditions. A heavily cloudy region (red box in Figure 6a) in Landsat 2002167 scene (Julian date 167, 2002) was selected and zoomed in (Figure 6b). To illustrate the actual ecological and biophysical condition of the selected box, a cloud-free Landsat scene (Julian date 199, 2002) map for the selected box is shown in Figure 6c. The 250-m MODIS GSN, the predicted 30-m GSN map, and the original 30-m Landsat growing season averaged NDVI map for the same region were also illustrated in Figure 6d–f. Results from these zoomed in regions indicate that the predicted 30-m GSN map has similar spatial patterns to the Landsat cloud-free map (e.g., center pivot irrigation and strip cropping), better agreement with the 250-m MODIS GSN than the original 30-m Landsat GSN, and provides more detailed regional ecological information than the 250-m MODIS GSN (Figures 6c–e). These results demonstrate the robustness of the MODIS-Landsat GSN model. The original 30-m Landsat GSN values (Figure 6f) are much lower than the 250-m MODIS GSN (Figure 6d) in some regions, probably because of the cloud impact (lower NDVI values) (Figure 6b). In addition, the wider range of wavelength in Landsat NIR band (compared with MODIS NIR band) may also contribute to the lower Landsat-derived GSN values.

3.4. Discussion

Although it might be simple to calculate the growing season averaged NDVI based on the original Landsat 30-m NDVI data, the derived GSN may be much lower than the actual GSN for the heavily cloudy regions. To demonstrate the improvement of the derived 30-m MODIS-Landsat GSN map, we upscaled the original 30-m Landsat NDVI to 250-m for one single scene (i.e., Julian date 167, 2002) and compared it with the 250-m MODIS NDVI acquired from the similar date (i.e., dates 165–171 for the 7-day MODIS composite in 2002). The correlation coefficient (r) between the upscaled Landsat NDVI and the MODIS NDVI (for Julian date 167) is 0.77, which is much lower than the correlation coefficients between the predicted GSN and the MODIS GSN shown in Table 1 and Table 3 (r > 0.91). The absolute average error for the upscaled Landsat NDVI is 0.128, which is much higher than the absolute average error of the predicted GSN shown in Table 1 and Table 3 (<0.042). The error histogram indicates that more than 67% of the total pixels had large negative NDVI differences (<−0.05) for the upscaled Landsat NDVI (Orange color in Figure 4). These results imply that using the original Landsat NDVI data to calculate the GSN may cause large errors, our proposed GSN model can improve the correlation from the original Landsat scene.
Furthermore, applying temporal smoothing to the original Landsat NDVI data may reduce cloudy effects [62]. However, temporal smoothing may affect the NDVI peak values and miscalculate the shoulder season NDVI, which will lead to a poor GSN result. Therefore, further investigations on correcting the original Landsat NDVI values for cloudy pixels are needed before averaging the original Landsat NDVI data to estimate the 30-m GSN.
Using three-Landsat scene data to develop a MODIS-Landsat GSN regression tree model can reduce computer disk space and running time; however, the model may not be robust for areas where all three Landsat scenes could be covered by clouds. Therefore, additional Landsat scenes are needed and recommended for developing a more reliable GSN model. It appears that the GSN can be predicted at a reasonable degree of reliability by data from middle to late summer. The mid-late season data contain more vegetation growth information than the early season data, so the mid-late season data have some capability for estimating the total growing season productivity. The final GSN model indicates that the cloud mask data are not important and are rarely used in the regression tree models, we suggest excluding Landsat cloud mask data from the model training dataset for the future study (e.g., for a larger study area and a different geographic location).
Since all the training data used for developing the GSN model was done at 250-m resolution to match the MODIS data, some extreme GSN values (e.g., extreme high or low values) in the 30-m Landsat data may be smoothed out by 250-m model development. Therefore, the 250-m GSN model may not capture the extreme cases and may need to apply an “extrapolation” approach [56] when estimating the 30-m GSN. An “extrapolation” approach is to set a relatively high extrapolation allowance in the GSN model, which will allow a wide range of the predicted GSN values (i.e., beyond the model development data range). Moreover, even though the NDVI plays an important role in the GSN model, results indicate that including all the variables (i.e., surface reflectance and NDVI for all bands and dates) to develop the GSN model will increase the accuracy of the model (higher r value and lower average error). The Landsat surface reflectance derived from the different bands explains more of the MODIS GSN variation than Landsat NDVI alone does. Therefore, using NDVI and surface reflectance from different bands to develop the GSN model is recommended for the future study.
Previous investigations on downscaling MODIS products (e.g., land channels, fraction of absorbed photosynthetically active radiation, land surface temperature, and vegetation indices) using Landsat observations and regression or Area-to-point prediction (ATPP) methods were conducted [71,72,73,74,75,76,77]. However, these studies were mostly focused on single data comparisons, we are not aware of similar studies that related to downscaling MODIS seasonal integrated NDVI (i.e., GSN) data. Zhu et al. [78] developed an algorithm for Continuous Change Detection and Classification (CCDC) of land cover using all available Landsat data. However, the CCDC algorithm did not include the atmospheric corrected MODIS products. Gao et al. [50] developed a spatial and temporal adaptive reflectance fusion model (STARFM) algorithm that blended Landsat and MODIS surface reflectance to produce a synthetic “daily” surface reflectance product at 30-m resolution. The STARFM approach used MODIS and Landsat observations to predict 30-m Landsat reflectance, which was different from the approach presented in this study. Our approach is using Landsat data and rule-based piecewise regression tree model to predict 30-m MODIS GSN. This study provides another method for downscaling MODIS GSN data. The advantage of this approach is that it requires relatively less computational costs, which will be an important advantage when the global data records need to be processed. This approach can also be applied to the other high spatial resolution data from multiple satellite data sources, such as Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), China-Brazil Earth Resources Satellite (CBERS), or other commercial satellites.

4. Conclusions

This study develops an approach that integrates 250-m MODIS growing season NDVI and 30-m Landsat multiple-date observations to develop a GSN model based on MODIS and Landsat. Results show that there is a strong correlation between the predicted GSN and the actual GSN (r = 0.97, average absolute error = 0.026) for the “cloudy and clear” regions. The most important Landsat variables that contribute more in the GSN regression model are NDVI in May and August. On the other hand, Landsat cloud mask data were rarely used in the GSN regression tree models and were not important for predicting the MODIS GSN. Results also indicate that the GSN model handled cloud conditions very well and supported the hypothesized robustness of the MODIS-Landsat GSN model. The MODIS-Landsat 30-m GSN estimation map provides detailed biophysical and ecological feature-based information of a site and can be used for regional dynamic ecosystem monitoring, modeling, and land management.

Acknowledgments

This work was performed under USGS contract G13PC00028 and funded by the USGS Land Change Science Program in support of Renewable Energy-Biofuels. The authors thank Thomas R. Loveland, Thomas Adamson, and three anonymous reviewers for their valuable suggestions and comments. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Author Contributions

Yingxin Gu processed the data, analyzed the results, and wrote the manuscript. Bruce K. Wylie designed the study, interpreted the results, and co-authored the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; U.S. Geological Survey: Reston, VA, USA, 1976; p. 28. [Google Scholar]
  2. Reed, B.C.; Brown, J.F.; Vanderzee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
  3. Peters, A.J.; Walter-Shea, E.A.; Ji, L.; Viña, A.; Hayes, M.; Svoboda, M.D. Drought monitoring with NDVI-based standardized vegetation index. Photogramm. Eng. Remote Sens. 2002, 68, 71–75. [Google Scholar]
  4. Gu, Y.; Brown, J.F.; Verdin, J.P.; Wardlow, B. A five-year analysis of MODIS NDVI and NDWI for grassland drought assessment over the central great plains of the United States. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
  5. Gu, Y.; Wylie, B.K. Detecting ecosystem performance anomalies for land management in the upper Colorado river basin using satellite observations, climate data, and ecosystem models. Remote Sens. 2010, 2, 1880–1891. [Google Scholar] [CrossRef]
  6. Wylie, B.K.; Zhang, L.; Bliss, N.B.; Ji, L.; Tieszen, L.L.; Jolly, W.M. Integrating modelling and remote sensing to identify ecosystem performance anomalies in the boreal forest, Yukon river basin, Alaska. Int. J. Digit. Earth 2008, 1, 196–220. [Google Scholar] [CrossRef]
  7. Gu, Y.; Boyte, S.P.; Wylie, B.K.; Tieszen, L.L. Identifying grasslands suitable for cellulosic feedstock crops in the greater Platte river basin: Dynamic modeling of ecosystem performance with 250 m eMODIS. GCB Bioenergy 2012, 4, 96–106. [Google Scholar] [CrossRef]
  8. Kimball, J.S.; Zhao, M.; McDonald, K.C.; Running, S.W. Satellite remote sensing of terrestrial net primary production for the pan-Arctic basin and Alaska. Mitig. Adapt. Strateg. Glob. Chang. 2006, 11, 783–804. [Google Scholar] [CrossRef]
  9. Rouse, J.W., Jr.; Haas, H.R.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; Texas A and M University: Greenbelt, MD, USA, 1974. [Google Scholar]
  10. Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
  11. Chen, D.; Brutsaert, W. Satellite-sensed distribution and spatial patterns of vegetation parameters over a tallgrass prairie. J. Atmos. Sci. 1998, 55, 1225–1238. [Google Scholar] [CrossRef]
  12. Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef] [PubMed]
  13. Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; van Ittersum, G. Satellite remote sensing of total herbaceous biomass production in the Senegalese Sahel: 1980–1984. Remote Sens. Environ. 1985, 17, 233–249. [Google Scholar] [CrossRef]
  14. Hobbs, T.J. The use of NOAA-AVHRR NDVI data to assess herbage production in the arid rangelands of Central Australia. Int. J. Remote Sens. 1995, 16, 1289–1302. [Google Scholar] [CrossRef]
  15. Tieszen, L.L.; Reed, B.C.; Bliss, N.B.; Wylie, B.K.; DeJong, D.D. NDVI, C3 and C4 production, and distributions in Great Plains grassland land cover classes. Ecol. Appl. 1997, 7, 59–78. [Google Scholar]
  16. Gitelson, A.A.; Viña, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
  17. Funk, C.; Budde, M.E. Phenologically-tuned MODIS NDVI-based production anomaly estimates for Zimbabwe. Remote Sens. Environ. 2009, 113, 115–125. [Google Scholar] [CrossRef]
  18. Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
  19. Gu, Y.; Wylie, B.K.; Bliss, N.B. Mapping grassland productivity with 250-m eMODIS NDVI and SSURGO database over the greater Platte river basin, USA. Ecol. Indic. 2013, 24, 31–36. [Google Scholar] [CrossRef]
  20. Wylie, B.K.; Denda, I.; Pieper, R.D.; Harrington, J.A.; Reed, B.C.; Southward, G.M. Satellite-based herbaceous biomass estimates in the pastoral zone of Niger. J. Range Manag. 1995, 48, 159–164. [Google Scholar] [CrossRef]
  21. Hatfield, J.L.; Kanemasu, E.T.; Asrar, G.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Idso, S.B. Leaf-area estimates from spectral measurements over various planting dates of wheat. Int. J. Remote Sens. 1985, 6, 167–175. [Google Scholar] [CrossRef]
  22. Asrar, G.; Fuchs, M.; Kanemasu, E.T.; Hatfield, J.L. Estimating absorbed photosynthetic radiation and leaf area index from spectral reflectance in wheat. Agron. J. 1984, 76, 300–306. [Google Scholar] [CrossRef]
  23. Chen, P.-Y.; Fedosejevs, G.; Tiscareño-López, M.; Arnold, J.G. Assessment of MODIS-EVI, MODIS-NDVI and vegetation-NDVI composite data using agricultural measurements: An example at corn fields in Western Mexico. Environ. Monit. Assess. 2006, 119, 69–82. [Google Scholar] [CrossRef] [PubMed]
  24. Asner, G.P.; Scurlock, J.M.O.; Hicke, J.A. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar] [CrossRef]
  25. Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
  26. Gu, Y.; Wylie, B.K.; Howard, D.M.; Phuyal, K.P.; Ji, L. NDVI saturation adjustment: A new approach for improving cropland performance estimates in the greater Platte river basin, USA. Ecol. Indic. 2013, 30, 1–6. [Google Scholar] [CrossRef]
  27. Potter, C.; Klooster, S.; Huete, A.; Genovese, V. Terrestrial carbon sinks for the United States predicted from MODIS satellite data and ecosystem modeling. Earth Interact. 2007, 11, 1–21. [Google Scholar] [CrossRef]
  28. NASA MODIS Web. Available online: http://modis.gsfc.nasa.gov/ (accessed on 22 January 2015).
  29. Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov/products/modis_products_table/modis_overview (accessed on March 20 2015).
  30. Wylie, B.K.; Boyte, S.P.; Major, D.J. Ecosystem performance monitoring of rangelands by integrating modeling and remote sensing. Rangel. Ecol. Manag. 2012, 65, 241–252. [Google Scholar] [CrossRef]
  31. Rigge, M.; Smart, A.; Wylie, B.; Gilmanov, T.; Johnson, P. Linking phenology and biomass productivity in South Dakota mixed-grass prairie. Rangel. Ecol. Manag. 2013, 66, 579–587. [Google Scholar] [CrossRef]
  32. Tan, Z.; Liu, S.; Wylie, B.K.; Jenkerson, C.B.; Oeding, J.; Rover, J.; Young, C. MODIS-informed greenness responses to daytime land surface temperature fluctuations and wildfire disturbances in the Alaskan Yukon river basin. Int. J. Remote Sens. 2012, 34, 2187–2199. [Google Scholar] [CrossRef]
  33. Spruce, J.P.; Sader, S.; Ryan, R.E.; Smoot, J.; Kuper, P.; Ross, K.; Prados, D.; Russell, J.; Gasser, G.; McKellip, R.; et al. Assessment of MODIS NDVI time series data products for detecting forest defoliation by gypsy moth outbreaks. Remote Sens. Environ. 2011, 115, 427–437. [Google Scholar] [CrossRef]
  34. NASA Landsat Science. Available online: http://landsat.gsfc.nasa.gov/ (accessed on 22 January 2015).
  35. Williams, D.L.; Goward, S.; Arvldson, T. Landsat: Yesterday, today, and tomorrow. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar] [CrossRef]
  36. Goward, S.N.; Masek, J.G.; Williams, D.L.; Irons, J.R.; Thompson, R.J. The Landsat 7 mission—Terrestrial research and applications for the 21st century. Remote Sens. Environ. 2001, 78, 3–12. [Google Scholar] [CrossRef]
  37. Homer, C.; Huang, C.; Yang, L.; Wylie, B.; Coan, M. Development of a 2001 national land-cover database for the United States. Photogramm. Eng. Remote Sens. 2004, 70, 829–840. [Google Scholar] [CrossRef]
  38. Wulder, M.A.; White, J.C.; Goward, S.N.; Masek, J.G.; Irons, J.R.; Herold, M.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Landsat continuity: Issues and opportunities for land cover monitoring. Remote Sens. Environ. 2008, 112, 955–969. [Google Scholar] [CrossRef]
  39. Goward, S.N.; Williams, D.L. Landsat and earth systems science: Development of terrestrial monitoring. Photogramm. Eng. Remote Sens. 1997, 63, 887–900. [Google Scholar]
  40. Huang, C.; Goward, S.; Masek, J.; Thomas, N.; Zhu, Z.; Vogelmann, J. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ. 2010, 114, 183–198. [Google Scholar] [CrossRef]
  41. Huang, C.; Kim, S.; Song, K.; Townshend, J.R.G.; Davis, P.; Altstatt, A.; Rodas, O.; Yanosky, A.; Clay, R.; Tucker, C.J.; et al. Assessment of Paraguay’s forest cover change using Landsat observations. Glob. Planet. Change 2009, 67, 1–12. [Google Scholar] [CrossRef]
  42. Vogelmann, J.E.; Xian, G.; Homer, C.; Tolk, B. Monitoring gradual ecosystem change using Landsat time series analyses: Case studies in selected forest and rangeland ecosystems. Remote Sens. Environ. 2012, 122, 92–105. [Google Scholar] [CrossRef]
  43. Gasparri, N.I.; Parmuchi, M.G.; Bono, J.; Karszenbaum, H.; Montenegro, C.L. Assessing multi-temporal Landsat 7 ETM+ images for estimating above-ground biomass in subtropical dry forests of Argentina. J. Arid Environ. 2010, 74, 1262–1270. [Google Scholar] [CrossRef]
  44. Röder, A.; Udelhoven, T.; Hill, J.; del Barrio, G.; Tsiourlis, G. Trend analysis of Landsat-TM and -ETM+ imagery to monitor grazing impact in a rangeland ecosystem in Northern Greece. Remote Sens. Environ. 2008, 112, 2863–2875. [Google Scholar] [CrossRef]
  45. Xian, G.; Crane, M. An analysis of urban thermal characteristics and associated land cover in Tampa bay and Las Vegas using Landsat satellite data. Remote Sens. Environ. 2006, 104, 147–156. [Google Scholar] [CrossRef]
  46. Herold, N.D.; Haack, B.N. Comparison and integration of radar and optical data for land use/cover mapping. Geocarto Int. 2006, 21, 9–19. [Google Scholar] [CrossRef]
  47. Spruce, J.P.; Smoot, J.C.; Ellis, J.T.; Hilbert, K.; Swann, R. Geospatial method for computing supplemental multi-decadal us coastal land use and land cover classification products, using Landsat data and C-CAP products. Geocarto Int. 2014, 29, 470–485. [Google Scholar] [CrossRef]
  48. Spruce, J.P.; Smoot, J.; Graham, W. Developing new coastal forest restoration products based on Landsat, Aster, and MODIS data. In Proceedings of the MTS/IEEE Biloxi—Marine Technology for Our Future: Global and Local Challenges, OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009.
  49. USGS Landsat Missions. Available online: http://landsat.usgs.gov/ (accessed on 22 January 2015).
  50. Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
  51. Irish, R.R.; Barker, J.L.; Goward, S.N.; Arvidson, T. Characterization of the landsat-7 ETM+ automated cloud-cover assessment (ACCA) algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 1179–1188. [Google Scholar] [CrossRef]
  52. Ju, J.; Roy, D.P. The availability of cloud-free Landsat ETM+ data over the conterminous United States and globally. Remote Sens. Environ. 2008, 112, 1196–1211. [Google Scholar] [CrossRef]
  53. Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
  54. Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Atmos. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
  55. Platnick, S.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Baum, B.A.; Riédi, J.C.; Frey, R.A. The MODIS cloud products: Algorithms and examples from terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–472. [Google Scholar] [CrossRef]
  56. Helmer, E.H.; Ruefenacht, B. Cloud-free satellite image mosaics with regression trees and histogram matching. Photogramm. Eng. Remote Sens. 2005, 71, 1079–1089. [Google Scholar] [CrossRef]
  57. Kaufman, Y.J.; Wald, A.E.; Remer, L.A.; Gao, B.-C.; Li, R.-R.; Flynn, L. MODIS 2.1-μm channel—Correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
  58. USGS Global Visualization Viewer. Available online: http://glovis.usgs.gov/ (accessed on 22 January 2015).
  59. USGS CDR Data. Available online: http://landsat.usgs.gov/CDR_LSR.php (accessed on 22 January 2015).
  60. NASA LEDAPS. Available online: http://ledapsweb.nascom.nasa.gov/ (accessed on 22 January 2015).
  61. Jenkerson, C.B.; Maiersperger, T.K.; Schmidt, G.L. eMODIS—A User-Friendly Data Source. Available online: http://pubs.usgs.gov/of/2010/1055/ (accessed on 22 January 2015).
  62. Swets, D.L.; Reed, B.C.; Rowland, J.R.; Marko, S.E. A weighted least-squares approach to temporal smoothing of NDVI. In Proceedings of the ASPRS Annual Conference, from Image to Information, Portland, OR, USA, 17–21 May1999.
  63. USGS Remote Sensing Phenology. Available online: http://phenology.cr.usgs.gov/ (accessed on 22 January 2015).
  64. RuleQuest Research. Available online: http://www.rulequest.com/ (accessed on March 20 2015).
  65. Gu, Y.; Howard, D.; Wylie, B.; Zhang, L. Mapping carbon flux uncertainty and selecting optimal locations for future flux towers in the Great Plains. Landsc. Ecol. 2012, 27, 319–326. [Google Scholar] [CrossRef]
  66. Zhang, L.; Wylie, B.K.; Ji, L.; Gilmanov, T.G.; Tieszen, L.L. Climate-driven interannual variability in net ecosystem exchange in the Northern Great Plains grasslands. Rangel. Ecol. Manag. 2010, 63, 40–50. [Google Scholar] [CrossRef]
  67. Boyte, S.P.; Wylie, B.K.; Major, D.J.; Brown, J.F. The integration of geophysical and enhanced moderate resolution imaging spectroradiometer normalized difference vegetation index data into a rule-based, piecewise regression-tree model to estimate cheatgrass beginning of spring growth. Int. J. Digit. Earth 2013, 8, 1–15. [Google Scholar]
  68. Ji, L.; Wylie, B.K.; Nossov, D.R.; Peterson, B.E.; Waldrop, M.P.; McFarland, J.W.; Rover, J.A.; Hollingsworth, T.N. Estimating aboveground biomass in interior Alaska with Landsat data and field measurements. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 451–461. [Google Scholar] [CrossRef]
  69. Rover, J.; Wylie, B.K.; Ji, L. A self-trained classification technique for producing 30 m percent-water maps from Landsat data. Int. J. Remote Sens. 2010, 31, 2197–2203. [Google Scholar] [CrossRef]
  70. Quinlan, J.R. Boosting first-order learning. In Algorithmic Learning Theory; Arikawa, S., Sharma, A., Eds.; Springer Berlin Heidelberg: Berlin, Germany, 1996; Volume 1160, pp. 143–155. [Google Scholar]
  71. Trishchenko, A.P.; Luo, Y.; Khlopenkov, K.V. A method for downscaling MODIS land channels to 250-m spatial resolution using adaptive regression and normalization. Proc. SPIE 2006, 6366. [Google Scholar] [CrossRef]
  72. Hwang, T.; Song, C.; Bolstad, P.V.; Band, L.E. Downscaling real-time vegetation dynamics by fusing multi-temporal MODIS and Landsat NDVI in topographically complex terrain. Remote Sens. Environ. 2011, 115, 2499–2512. [Google Scholar] [CrossRef]
  73. Bindhu, V.M.; Narasimhan, B.; Sudheer, K.P. Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration. Remote Sens. Environ. 2013, 135, 118–129. [Google Scholar] [CrossRef]
  74. Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
  75. Hansen, M.C.; Roy, D.P.; Lindquist, E.; Adusei, B.; Justice, C.O.; Altstatt, A. A method for integrating MODIS and Landsat data for systematic monitoring of forest cover and change in the Congo basin. Remote Sens. Environ. 2008, 112, 2495–2513. [Google Scholar] [CrossRef]
  76. Hong, S.-H.; Hendrickx, J.M.H.; Borchers, B. Down-scaling of SEBAL derived evapotranspiration maps from MODIS (250 m) to Landsat (30 m) scales. Int. J. Remote Sens. 2011, 32, 6457–6477. [Google Scholar] [CrossRef]
  77. Kim, J.; Hogue, T.S. Evaluation and sensitivity testing of a coupled Landsat-MODIS downscaling method for land surface temperature and vegetation indices in semi-arid regions. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
  78. Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Gu, Y.; Wylie, B.K. Downscaling 250-m MODIS Growing Season NDVI Based on Multiple-Date Landsat Images and Data Mining Approaches. Remote Sens. 2015, 7, 3489-3506. https://doi.org/10.3390/rs70403489

AMA Style

Gu Y, Wylie BK. Downscaling 250-m MODIS Growing Season NDVI Based on Multiple-Date Landsat Images and Data Mining Approaches. Remote Sensing. 2015; 7(4):3489-3506. https://doi.org/10.3390/rs70403489

Chicago/Turabian Style

Gu, Yingxin, and Bruce K. Wylie. 2015. "Downscaling 250-m MODIS Growing Season NDVI Based on Multiple-Date Landsat Images and Data Mining Approaches" Remote Sensing 7, no. 4: 3489-3506. https://doi.org/10.3390/rs70403489

APA Style

Gu, Y., & Wylie, B. K. (2015). Downscaling 250-m MODIS Growing Season NDVI Based on Multiple-Date Landsat Images and Data Mining Approaches. Remote Sensing, 7(4), 3489-3506. https://doi.org/10.3390/rs70403489

Article Metrics

Back to TopTop