Exploring the Vertical Distribution of Structural Parameters and Light Radiation in Rice Canopies by the Coupling Model and Remote Sensing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiments
| Experiment | Year | Site Location | Cultivar | Nitrogen Rate (kg∙ha−2) | Planting Density | Sampling Date | Planting Data |
|---|---|---|---|---|---|---|---|
| 1 | 2012 | Rugao 120°19ʹE 32°14ʹN | Wuxiangjing14 (WXJ14, V1) Shanyou63 (SY63, V2) | 150 (N1) 250 (N2) 350 (N4) | 22.2 plants/m2 (D1) 13.3 plants/m2 (D2) | 7/22, 8/6, 8/19 8/30, 9/15, 9/24 | 6/18 |
| 2 | 2013 | Rugao 120°19ʹE 32°14ʹN | Wuxiangjing14 (WXJ14, V1) Shanyou63 (SY63, V2) | 150 (N1) 300 (N3) | 22.2 plants/m2 (D1) 13.3 plants/m2 (D2) | 7/9, 7/19, 7/30 8/8, 8/18, 8/30 9/10, 9/17 | 6/21 |
2.2. Spectral Measurements of Canopy Leaves

2.3. Irradiance Measurements
2.4. Determination of Agronomic Parameters
2.5. Meteorological Data
2.6. Calculation
2.6.1. Growing Degree Day Calculation
2.6.2. Spectral Index Calculation
2.6.3. Leaf Area Index Vertical Distribution Model
2.6.4. Leaf Angle Distribution Simulation Model
2.6.5. Rice Canopy Radiation Vertical Distribution Model
3. Results
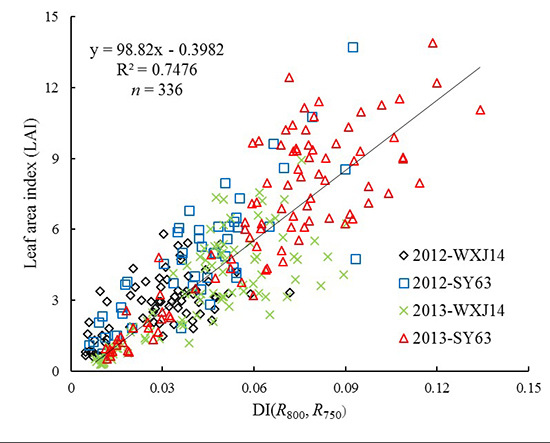
3.1. Determination Partial Model Parameters Using RS and GDD



3.2. Radiation Transfer of Different Light Qualities (Wavelengths)

3.3. Validation of LAI Vertical Distribution Model


3.4. Simulation Analysis of Leaf Angle Distribution


3.5. Validation of Rice Canopy Light Radiation Vertical Distribution Model



4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hirose, T. Development of the monsi-saeki theory on canopy structure and function. Ann. Bot. 2005, 95, 483–494. [Google Scholar]
- Yu, Q.; Wang, T.D.; Liu, J.D.; Sun, F. A mathematical study on crop architecture and canopy photosynthesis I. Model. Sci. Agric. Sin. 1998, 24, 7–15. [Google Scholar]
- Sassenrath-Cole, G.F. Dependence of canopy light distribution on leaf and canopy structure for two cotton (gossypium) species. Agric. For. Meteorol. 1995, 77, 55–72. [Google Scholar] [CrossRef]
- Stewart, D.W.; Costa, C.; Dwyer, L.M.; Smithc, D.L.; Hamiltona, R.I.; Ma, B.L. Canopy structure, light interception, and photosynthesis in maize. Agron. J. 2003, 95, 1465–1474. [Google Scholar] [CrossRef]
- Tappeiner, U.; Cernusca, A. Model simulation if spatial distribution of photosynthesis in structurally differing plant communities in the central Caucasus. Ecol. Model. 1998, 24, 272–279. [Google Scholar]
- Wang, W.M.; Li, Z.L.; Su, H.B. Comparison of leaf angle distribution functions: Effects on extinction coefficient and fraction of sunlit foliage. Agric. For. Meteorol. 2007, 143, 106–122. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. Uber den lichtfaktor in den pflanzengesellschaften und seine bedeutung fur die stoffproduktion. Jpn. J. Bot. 1953, 14, 22–52. [Google Scholar]
- Li, Y.D.; Tang, L.; Zhang, Y.P.; Liu, L.L.; Cao, W.X.; Zhu, Y. Spatiotemporal distribution of photosynthetically active radiation in rice canopy. Chin. J. Appl. Ecol. 2010, 21, 952–958. [Google Scholar]
- Liu, R.Y.; Huang, W.J.; Ren, H.Z.; Yang, G.J.; Xie, D.H.; Wang, J. Photosynthetically active radiation vertical distribution model in maize canopy. Trans. Chin. Soc. Agric. Eng. 2011, 27, 115–121. [Google Scholar]
- Tang, L.; Li, Y.D.; Zhang, Y.P.; Zhu, X.C.; Liu, X.J.; Cao, W.X.; Zhu, Y. Simulation of canopy light distribution and application in rice. Rice Sci. 2011, 4, 427–434. [Google Scholar]
- Wang, F.M.; Huang, J.F.; Tang, Y.L.; Wang, X.Z. New vegetation index and its application in estimating leaf area index of rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Campbell, G.S. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agric. For. Meteorol. 1986, 36, 317–321. [Google Scholar] [CrossRef]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. For. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Springer Science & Business Media: Boston, MA, USA, 1981. [Google Scholar]
- Campbell, G.S. Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol. 1990, 49, 173–176. [Google Scholar] [CrossRef]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canopies. Ph.D. Thesis, Wageningen Agricultural University, Wageningen, The Netherlands, 1998. [Google Scholar]
- Wang, X.Y.; Guo, Y.; Li, B.G. Evaluating a three dimensional model of diffuse radiation in maize canopies. Int. J. Biometeorol. 2006, 50, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.Y.; Shi, L.J.; Ma, Y.T. Comparison of architecture among different cultivars of hybrid rice using a spatial light model based on 3d digitizing. Funct. Plant Biol. 2008, 35, 900–910. [Google Scholar] [CrossRef]
- Tian, Y.C.; Yang, J.; Yao, X.; Zhu, Y.; Cao, W.X. Quantitative relationships between hyperspectral vegetation indices and leaf area index of rice. Chin. J. Appl. Ecol. 2009, 20, 1685–1690. [Google Scholar]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Gallo, K.P.; Daughtry, C.S.T. Techniques for measuring intercepted and absorbed photosynthetically active radiation in corn canopies. Agron. J. 1986, 78, 752–756. [Google Scholar] [CrossRef]
- McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- Wallach, D.; David, M.; Jones, J.W. Working with Dynamic Crop Models; Elsevier BV: Boston, MA, USA, 2006. [Google Scholar]
- Tian, Y.C.; Yao, X.; Yang, J.; Cao, W.X.; Hannaway, D.B.; Zhu, Y. Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground- and space-based hyperspectral reflectance. Field Crops Res. 2011, 120, 299–310. [Google Scholar] [CrossRef]
- Li, Y.D.; Tang, L.; Zhang, Y.P.; Zhu, X.C.; Cao, W.X.; Zhu, Y. Relationship of par interception of canopy to leaf area and yield in rice. Sci. Agric. Sin. 2010, 43, 3296–3305. [Google Scholar]
- Ruimy, A.; Kergoat, L.; Bondeau, A. Comparing global models of terrestrial net primary productivity (NPP): Analysis of differences in light absorption and light-use efficiency. Glob. Chang. Biol. 1999, 5, 56–64. [Google Scholar] [CrossRef]
- Hu, N.; Yao, K.M.; Zhang, X.C.; Lv, C.G. Effect and simulation of plant type on canopy structure and radiation transmission in rice. Rice Sci. 2011, 25, 535–543. [Google Scholar]
- Zhou, Y.H.; Xiang, Y.Q.; Lin, Z.H. Radiation interception by erectophile maize colony. Chin. J. Appl. Ecol. 1997, 8, 21–25. [Google Scholar]
- Liu, Q.; Liang, S.; Xiao, Z.; Fang, H. Retrieval of leaf area index using temporal, spectral, and angular information from multiple satellite data. Remote Sens. Environ. 2014, 145, 25–37. [Google Scholar] [CrossRef]
- Wang, X.P.; Guo, Y.; Wang, X.Y. Estimating photosynthetically active radiation distribution in maize canopies by a three-dimensional incident radiation model. Funct. Plant Biol. 2008, 35, 867–876. [Google Scholar] [CrossRef]
- Evers, J.B.; Vos, J.; Yin, X.; Romero, P.; van der Putten, P.E.; Struik, P.C. Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation. J. Exp. Bot. 2010, 61, 2203–2216. [Google Scholar] [CrossRef] [PubMed]
- Sarlikioti, V.; de Visser, P.H.; Marcelis, L.F. Exploring the spatial distribution of light interception and photosynthesis of canopies by means of a functional-structural plant model. Ann. Bot. 2011, 107, 875–883. [Google Scholar] [CrossRef] [PubMed]
- Ross, J.K.; Marshak, A.L. Calculation of canopy bidirectional reflectance using the Monte Carlo method. Remote Sens. Environ. 1988, 24, 213–225. [Google Scholar] [CrossRef]
- Chelle, M.; Andrieu, B. The nested radiosity model for the distribution of light within plant canopies. Ecol. Model. 1998, 111, 75–91. [Google Scholar] [CrossRef]
- Awad, M.A.; Wsgenmakers, P.S.; de Jager, A. Effect of light on flavonoid and chlorugenic acid levels in the skin of “jonagold” apples. Sci. Hortic. 2001, 88, 289–298. [Google Scholar] [CrossRef]
- Yang, C.M.; Yang, L.Z.; Wei, C.L.; Ding, C.C. Canopy spectral characteristics of different rice varieties. Chin. J. Appl. Ecol. 2002, 13, 689–692. [Google Scholar]
- Fang, H.; Li, W.; Wei, S.; Jiang, C. Seasonal variation of leaf area index (LAI) over paddy rice fields in NE China: Intercomparison of destructive sampling, LAI-2200, digital hemispherical photography (DHP), and AccuPAR methods. Agric. For. Meteorol. 2014, 198–199, 126–141. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Zhang, L.; Qin, Y.; Zhu, Y.; Cao, W.; Tian, Y. Exploring the Vertical Distribution of Structural Parameters and Light Radiation in Rice Canopies by the Coupling Model and Remote Sensing. Remote Sens. 2015, 7, 5203-5221. https://doi.org/10.3390/rs70505203
Guo Y, Zhang L, Qin Y, Zhu Y, Cao W, Tian Y. Exploring the Vertical Distribution of Structural Parameters and Light Radiation in Rice Canopies by the Coupling Model and Remote Sensing. Remote Sensing. 2015; 7(5):5203-5221. https://doi.org/10.3390/rs70505203
Chicago/Turabian StyleGuo, Yongjiu, Ling Zhang, Yehui Qin, Yan Zhu, Weixing Cao, and Yongchao Tian. 2015. "Exploring the Vertical Distribution of Structural Parameters and Light Radiation in Rice Canopies by the Coupling Model and Remote Sensing" Remote Sensing 7, no. 5: 5203-5221. https://doi.org/10.3390/rs70505203
APA StyleGuo, Y., Zhang, L., Qin, Y., Zhu, Y., Cao, W., & Tian, Y. (2015). Exploring the Vertical Distribution of Structural Parameters and Light Radiation in Rice Canopies by the Coupling Model and Remote Sensing. Remote Sensing, 7(5), 5203-5221. https://doi.org/10.3390/rs70505203