Towards Detection of Cutting in Hay Meadows by Using of NDVI and EVI Time Series

Abstract

The main requirement for preserving European hay meadows in good condition is through prerequisite cut management. However, monitoring these practices on a larger scale is very difficult. Our study analyses the use of MODIS vegetation indices products, namely EVI and NDVI, to discriminate cut and uncut meadows in Slovakia. We tested the added value of simple transformations of raw data series (seasonal statistics, first difference series), compared EVI and NDVI, and analyzed optimal periods, the number of scenes and the effect of smoothing on classification performance. The first difference series transformation saw substantial improvement in classification results. The best case NDVI series classification yielded overall accuracy of 85% with balanced rates of producer’s and user’s accuracies for both classes. EVI yielded slightly lower values, though not significantly different, although user accuracy of cut meadows achieved only 67%. Optimal periods for discriminating cut and uncut meadows lay between 16 May and 4 August, meaning only seven consecutive images are enough to accurately detect cutting in hay meadows. More importantly, the 16-day compositing period seemed to be enough for detection of cutting, which would be the time span that might be hopefully achieved by upcoming on-board HR sensors (e.g., Sentinel-2).

1. Introduction

Hay meadows in Europe provide important services for humans mainly by providing fodder for animals. Furthermore, extensively used hay meadows bear high biodiversity values, they represent high nature value farmlands [1] and when traditional practices were applied in rural landscapes, they provide great aesthetic values. All these services are critically dependent on specific agricultural management and particularly on regular cutting at a specific time of the season [2]. This implies that hay meadows are very sensitive and of a dynamic nature because when proper management is neglected they decline from a good status quite fast [3]. In Central Europe, a good historical example was the intensification of extensive hay meadows (both due to intensive cutting and grazing) during the Communist era [4] and when collective farming collapsed, agriculture was abandoned followed by overgrowing and shrub encroachment [5]. However, the traditional agricultural management of hay meadows is not very profitable and today subsides are needed from the EU’s Common Agricultural Policy (CAP) in order to sustain the good condition of hay meadows and the services they provide [6]. In this respect, proper tools are needed in order to monitor hay meadow management in large areas with the aim of assessing the success of specific CAP-implemented measures. It is obvious that comprehensive, timely monitoring (e.g., on an annual basis) through field research is not feasible on a broader scale (e.g., national wide), when bearing in mind the costs and variability of cutting practices across such a large area. Therefore, remote sensing (RS) approaches need to be analyzed and tested in order to deliver consistent spatial information on proper hay meadow management practices in larger areas [7].

Remote sensing (RS) approaches have been widely used mainly for mapping and classifying grasslands and for estimating the biomass they provide. However, grassland studies have seen variable success and depend mainly on site specific conditions, grassland types and the landscape’s spatial composition. In general, the more homogenous grassland landscape is, the better the classification success, which can be documented, for example, by relatively good grassland classification accuracy in the Netherlands [8], as opposed to complicated detection of grasslands in the Carpathians [9]. Use of multi-temporal classification approaches was found to be of essential help mainly when grasslands were found in complex agricultural areas [10]. Furthermore, with the increased availability of vegetation indices (VI) time series (e.g., derived from AVHRR, MERIS, MODIS or Landsat archive), many studies demonstrated these products could be utilized for grassland studies, such as for mapping of specific grassland types [11], characterizing their vegetation state [12] or classifying their management practices [13]. In the context of grassland management, these studies were mainly motivated by the identification of degraded grasslands due to overgrazing, for example in Southern Europe [14], where grazing seems to be the main driver of good condition of grasslands. In Central Europe on the other hand, proper cut management of grasslands is an important driver specifically for hay meadows [7]. However, with the use of RS approaches, cutting practices were identified mainly indirectly within the complex classification studies and they were inherently included in different categories, for instance in distinguishing managed and unmanaged agriculture classes [15,16], improved and unimproved grasslands [17,18], and conservation as opposed to moderately productive grasslands [19]. To our knowledge, only three published studies were found by us that exactly analyzed RS approaches for detecting cut practices in European grasslands. Franke et al. [7] used indicators of proper cutting practices through Rapid Eye data time series in order to detect extensively used hay meadows in Germany. Schuster et al. [20] and Voormansik et al. [21] analyzed radar time series to detect local scale cutting in grasslands, resulting in completely opposite results. All the authors have suggested that high spatial resolution data are needed to detect grassland management as it is highly fragmented in Europe. However, Nitze et al. [17] used MODIS VI time series to distinguish improved and semi-improved grasslands in Ireland, and Alcantara et al. [16] used the coarser resolution MODIS data to differentiate active agriculture (including regularly cut grasslands) and abandoned agriculture (including unmanaged grasslands) in Central Europe, with both studies providing promising results. They documented that, besides specific classification algorithm, pre-processing of input data, use of a specific period and number of scenes and differences between EVI and NDVI vegetation indices should be considered when using multi-temporal classification for grassland studies.

Our study aims to analyze the potential of MODIS VI time series to detect cutting in hay meadows. We are aware of the spatial limitation in MODIS products for grassland studies in Central Europe, therefore we based our analysis on homogenous samples in order to minimize mixed pixel and MODIS gridding artifact effects. The main objective here is to set up a conceptual framework for analyzing annual VI time series, motivated by its potential utilization after MODIS-like data products become available with a higher spatial resolution (e.g., by combining of Sentinel2 and Landsat VI products). Therefore, we focused in addition to simple classification, on comparing specific VIs (NDVI vs. EVI), analyzing the optimal time period and number of scenes needed, the effect of smoothing and the added value of simple transformations (first difference series, seasonal statistics) for classification performance in order to suggest the proper way for using MODIS data to monitor cutting practices in hay meadows.

2. Study Area and Methods

The study area covers all of Slovakia, with quite a diverse landscape that reflects mainly heterogeneous geological formations, soils, elevations and terrain [22]. The climate is also quite diverse, exemplified by the area covering four climate zones and nine European-based climatic strata [23] with the continental zone having the biggest coverage. Grasslands in Slovakia are formed mainly as small scattered patches with a diverse spatial arrangement (Figure 1).

Based on national agricultural statistics, the total coverage of grasslands (excluding natural alpine grasslands) is estimated to be approx. 15% of Slovakia and 30% of its agricultural landscape. Grassland vegetation types vary broadly based on nutrition, geological substrate, soils, hydrology and elevation. Land use is an important driver of grasslands, including cutting on meadows, grazing at different intensities on pastures or both (spring cutting and autumn grazing). A substantial proportion of grasslands were abandoned and became overgrown after socioeconomic changes in the early 1990s. Recently, agro-environmental subsidies have introduced special management in the most valuable semi-natural grasslands in Slovakia [24]. This study focuses on “semi-natural” or extensively used grasslands with traditional grassland management practices and high biodiversity values. Of these, the great majority, evenly distributed in Slovakia, are mesophilous hay meadows, classified as Habitat 6510 (lowland hay meadows) under the EU Habitat Directive [25]. A first cut (mainly in late June or early July) is the prerequisite for proper management in order to sustain the hay meadows in good condition. Optionally, either a second cut or soft grazing is undertaken in these grassland types [26]. When these hay meadows are not cut, however, grassland values can be threatened and farmers are unable to obtain financial support from agro-environmental programmes. Because of CAP subsides, these grassland habitats were intensively mapped in Slovakia and registered in agricultural map portal (www.podnemapy.sk). However, there is no information about the cutting management of the grasslands in Slovakia so we needed to gather ground truth data as follows. Firstly, we took 150 random locations within the grassland land cover class (Corine class 231) across Slovakia. These locations were visually inspected on Google Earth and agricultural map portal to obtain a homogenous uncut Natura 6510 habitat site that was closest to the randomly selected point in order to minimize mixed-pixel problems and gridding artifacts in the MODIS data [27]. The absent cutting on these sites was preliminarily detected by visual interpretation of Landsat images series of 2012 (Figure 2). Secondly, we took another 150 random locations and repeat the process for selection of 6510 habitat sites, where cutting was preliminarily detected (Figure 2).

Sample sites varied in size and shape but only one MODIS pixel (approx. 250 × 240 m in native projection) was selected for each site (Figure 3).

Figure 1. Study area and sampled hay meadows (red dots) that were used for the analyses. Green areas represent all grasslands in Slovakia (Corine Land Cover class 231 [28]).

Figure 1. Study area and sampled hay meadows (red dots) that were used for the analyses. Green areas represent all grasslands in Slovakia (Corine Land Cover class 231 [28]).

Figure 2. Preliminary detection of cutting on selected sites. A. Cutting before 11.7.2012. B. and C. cutting between 11.7, and 27.7. 2012. D. No cutting in these periods.

Figure 2. Preliminary detection of cutting on selected sites. A. Cutting before 11.7.2012. B. and C. cutting between 11.7, and 27.7. 2012. D. No cutting in these periods.

Figure 3. Selection of MODIS homogenous pixels for analyses.

Figure 3. Selection of MODIS homogenous pixels for analyses.

These 300 sites were randomly split into training set (200) and validation set (100) and monitored for other years (2013–2014) based on regular field visits and visual inspection of Landsat images in order to confirm the preliminarily estimated cutting per site. The field visit during this period included also consultation with local farmers about the cut management. Visual interpretation of Landsat images series helped in confirmation of permanent absence of cut management on site. Those sites where we were not sure about the cutting performed were masked for the analyses. Finally, the cutting treatment information from 2012 was used in analyses with final distribution of samples as it is listed in Table 1.

Table 1. Final proportion of treatments in training and validation data sets.

	Training Set	Validation Set
Cut (2012)	84	46
Uncut (2012)	102	54

Table 1. Final proportion of treatments in training and validation data sets.

	Training Set	Validation Set
Cut (2012)	84	46
Uncut (2012)	102	54

Annual series of EVI and NDVI vegetation indices for the period from 2012–2014 were extracted from MOD13Q1 and MYD13Q1 products (16 days, 250 meters) along with quality assurance information from the Land Processes Distributed Active Archived Center (LPDAAC, https://lpdaac.usgs.gov/) for the area covered by the h19v04 MODIS grid tile. Data were downloaded using EarthExplorer (http://earthexplorer.usgs.gov/) and re-projected to the native coordination system (Krovak projection, JTSK EastNorth coordination system). Only good quality pixels (VI usefulness index good and higher) were selected for analysis in order to minimize the negative effects of clouds, cloud shadows, aerosols, sun-sensor geometries and snow. There were a total of 46 VI images per year, and the data therefrom were lumped together using MOD13Q1 product as reference (e.g., MYD13Q1 product was used only when MOD13Q1 VI usefulness index was less than good) to obtain 23 images per year, which was thought to reflect vegetation development over a 16-day time span and increase availability of good quality data. No missing data interpolation was done for the period from Day of the Year (DOY) 97 to Julian Day 257. Temporal median substitution (for three years) of bad quality data followed by linear interpolation of three consecutive images was done for the winter and late autumn periods (DOY 1–97; DOY 273–365). The final analyses involved annual series from 2012 because that period had the highest good quality data available. Because of the analysis of the optimal period and number of images needed for classification performance, the series was split into sets with different temporal extents centered on the main harvesting period (3 July, DOY 184), resulting in 11 raw data NDVI series (RD NDVI) and 11 raw data EVI series (RD EVI). Later, we used simple transformations of the raw data series. The first transformation involved basic seasonal statistics such as the mean (MN), maximum (MAX), minimum (MIN), range (RG) and standard deviation (SD). These seasonal statistics were computed for entire seasons (23 images) and for different time spans centered on the main harvesting period (3 July, DOY 184), producing 11 NDVI seasonal statistics series (SS NDVI) and 11 EVI seasonal statistics series (SS EVI). The second transformation involved the so-called first difference series [29], namely substituting the image value (in this case VI value) from the first consecutive image in the time series. Similarly, these transformation series were split into a set of the series with a different temporal extents centered on the main harvesting period (3 July, DOY 184), resulting in 11 first difference NDVI series (FD NDVI) and 11 first difference EVI series (FD EVI). The way how the different input variables were used and aggregated for respective periods is illustrated in Figure 4.

Figure 4. First difference transformation, notation and selection of input variables for the respective classification run. Solid line—raw data (RD), dotted line—first difference transformed data (FD).

Figure 4. First difference transformation, notation and selection of input variables for the respective classification run. Solid line—raw data (RD), dotted line—first difference transformed data (FD).

Smoothing techniques based on Fourier adjustment [30] was done using different levels of Fourier terms (2,3,4,5) in order to test the impact of smoothing on classification algorithms (Figure 5).

Figure 5. The effect of Fourier adjustments by using different levels of Fourier terms on temporal profile of VI.

Figure 5. The effect of Fourier adjustments by using different levels of Fourier terms on temporal profile of VI.

Simple classification tree (CART) [31] algorithm was used to classify cut and uncut meadows because of its simplicity and easy interpretation of classification logic, what allows production of simple set of rules (or production rules), which should be meaningful and could later serve as an input to knowledge based classification as it was suggested by [32]. Specifically, we used C4.5 algorithm[33], gini measure of purity as splitting rule [34] and direct stopping rule for pruning the trees (not less than 5% proportion in node). Totally, we performed 90 classification runs with different periods and input variables as they are listed in Table 2.

Table 2. List of all classification runs with different data series. The best case series for different types of the data sets are marked in bold. RD—raw data, SS—seasonal statistics, FD—first difference, FA—Fourier adjustment.

Classification Run	VI	Type/Transformation	Period	Number of Input Variables
CT01	NDVI	RD	8 January–26 December 2012	23
CT02	NDVI	RD	21 January–10 December 2012	21
CT03	NDVI	RD	9 February–24 November 2012	19
CT04	NDVI	RD	25 February–8 November 2012	17
CT05	NDVI	RD	13 March–23 October 2012	15
CT06	NDVI	RD	29 March–7 October 2012	13
CT07	NDVI	RD	14 April–21 September 2012	11
CT08	NDVI	RD	30 April–5 September 2012	9
CT09	NDVI	RD	16 May–20 August 2012	7
CT10	NDVI	RD	1 June–4 August 2012	5
CT11	NDVI	RD	17 June–19 July 2012	3
CT12	NDVI	SS	8 January–26 December 2012	5
CT13	NDVI	SS	21 January–10 December 2012	5
CT14	NDVI	SS	9 February–24 November 2012	5
CT15	NDVI	SS	February25–8 November 2012	5
CT16	NDVI	SS	13 March13–23 October 2012	5
CT17	NDVI	SS	29 March29–7 October 2012	5
CT18	NDVI	SS	14 April–21 September 2012	5
CT19	NDVI	SS	30 April–5 September 2012	5
CT20	NDVI	SS	16 May–20 August 2012	5
CT21	NDVI	SS	1 June–4 August 2012	5
CT22	NDVI	SS	17 June–19 July 2012	5
CT23	NDVI	FD	21 January–26 December 2012	22
CT24	NDVI	FD	9 February–10 December 2012	20
CT25	NDVI	FD	25 February–24 November 2012	18
CT26	NDVI	FD	13 March–8 November 2012	16
CT27	NDVI	FD	29 March–23 October 2012	14
CT28	NDVI	FD	14 April–7 October 2012	12
CT29	NDVI	FD	30 April–21 September 2012	10
CT30	NDVI	FD	16 May–5 September 2012	8
CT31	NDVI	FD	1 June–20 August 2012	6
CT32	NDVI	FD	17 June–4 August 2012	4
CT33	NDVI	FD	3 July–19 July 2012	2
CT34	NDVI	FA(2 harmonics) of the RD	30 April–5 September 2012	9
CT35	NDVI	FA(3 harmonics) of the RD	30 April–5 September 2012	9
CT36	NDVI	FA(4 harmonics) of the RD	30 April–5 September 2012	9
CT37	NDVI	FA(5 harmonics) of the RD	30 April–5 September 2012	9
CT38	NDVI	SS using FA(2 harmonics) instead of RD	16 May–20 August 2012	5
CT39	NDVI	SS using FA(3 harmonics) instead of RD	16 May–20 August 2012	5
CT40	NDVI	SS using FA(4 harmonics) instead of RD	16 May–20 August 2012	5
CT41	NDVI	SS using FA(5 harmonics) instead of RD	16 May–20 August 2012	5
CT42	NDVI	FD using FA(2 harmonics) instead of RD	1 June–20 August 2012	6
CT43	NDVI	FD using FA(3 harmonics) instead of RD	1 June–20 August 2012	6
CT44	NDVI	FD using FA(4 harmonics) instead of RD	1 June–20 August 2012	6
CT45	NDVI	FD using FA(5 harmonics) instead of RD	1 June–20 August 2012	6
CT46	EVI	RD	8 January–26 December 2012	23
CT47	EVI	RD	21 January–10 December 2012	21
CT48	EVI	RD	9 February–24 November 2012	19
CT49	EVI	RD	25 February–8 November 2012	17
CT50	EVI	RD	13 March–23 October 2012	15
CT51	EVI	RD	29 March–7 October 2012	13
CT52	EVI	RD	14 April–21 September 2012	11
CT53	EVI	RD	30 April–5 September 2012	9
CT54	EVI	RD	16 May–20 August 2012	7
CT55	EVI	RD	1 June–4 August 2012	5
CT56	EVI	RD	17 June–19 July 2012	3
CT57	EVI	SS	8 January–26 December 2012	5
CT58	EVI	SS	21 January–10 December 2012	5
CT59	EVI	SS	9 February–24 November 2012	5
CT60	EVI	SS	25 February–8 November 2012	5
CT61	EVI	SS	13 March–23 October 2012	5
CT62	EVI	SS	29 March–7 October 2012	5
CT63	EVI	SS	14 April–21 September 2012	5
CT64	EVI	SS	30 April–5 September 2012	5
CT65	EVI	SS	16 May– 20 August 2012	5
CT66	EVI	SS	1 June–4 August 2012	5
CT67	EVI	SS	17 June–19 July 2012	5
CT68	EVI	FD	21 January–26 December 2012	22
CT69	EVI	FD	9 February–10 December 2012	20
CT70	EVI	FD	25 February–24 November 2012	18
CT71	EVI	FD	13 March–8 November 2012	16
CT72	EVI	FD	29 March–23 October 2012	14
CT73	EVI	FD	14 April–7 October 2012	12
CT74	EVI	FD	30 April–21 September 2012	10
CT75	EVI	FD	16 May–5 September 2012	8
CT76	EVI	FD	1 June–20 August 2012	6
CT77	EVI	FD	17 June–4 August 2012	4
CT78	EVI	FD	3 July–19 July 2012	2
CT79	EVI	FA(2 harmonics) of the RD	14 April–21 September 2012	11
CT80	EVI	FA(3 harmonics) of the RD	14 April–21 September 2012	11
CT81	EVI	FA(4 harmonics) of the RD	14 April–21 September 2012	11
CT82	EVI	FA(5 harmonics) of the RD	14 April–21 September 2012	11
CT83	EVI	SS using FA(2 harmonics) instead of RD	1 June–4 August 2012	5
CT84	EVI	SS using FA(3 harmonics) instead of RD	1 June–4 August 2012	5
CT85	EVI	SS using FA(4 harmonics) instead of RD	1 June– 4 August 2012	5
CT86	EVI	SS using FA(5 harmonics) instead of RD	1 June– 4 August 2012	5
CT87	EVI	FD using FA(2 harmonics) instead of RD	16 May–5 September 2012	8
CT88	EVI	FD using FA(3 harmonics) instead of RD	16 May–5 September 2012	8
CT89	EVI	FD using FA(4 harmonics) instead of RD	16 May–5 September 2012	8
CT90	EVI	FD using FA(5 harmonics) instead of RD	16 May–5 September 2012	8

Table 2. List of all classification runs with different data series. The best case series for different types of the data sets are marked in bold. RD—raw data, SS—seasonal statistics, FD—first difference, FA—Fourier adjustment.

Classification Run	VI	Type/Transformation	Period	Number of Input Variables
CT01	NDVI	RD	8 January–26 December 2012	23
CT02	NDVI	RD	21 January–10 December 2012	21
CT03	NDVI	RD	9 February–24 November 2012	19
CT04	NDVI	RD	25 February–8 November 2012	17
CT05	NDVI	RD	13 March–23 October 2012	15
CT06	NDVI	RD	29 March–7 October 2012	13
CT07	NDVI	RD	14 April–21 September 2012	11
CT08	NDVI	RD	30 April–5 September 2012	9
CT09	NDVI	RD	16 May–20 August 2012	7
CT10	NDVI	RD	1 June–4 August 2012	5
CT11	NDVI	RD	17 June–19 July 2012	3
CT12	NDVI	SS	8 January–26 December 2012	5
CT13	NDVI	SS	21 January–10 December 2012	5
CT14	NDVI	SS	9 February–24 November 2012	5
CT15	NDVI	SS	February25–8 November 2012	5
CT16	NDVI	SS	13 March13–23 October 2012	5
CT17	NDVI	SS	29 March29–7 October 2012	5
CT18	NDVI	SS	14 April–21 September 2012	5
CT19	NDVI	SS	30 April–5 September 2012	5
CT20	NDVI	SS	16 May–20 August 2012	5
CT21	NDVI	SS	1 June–4 August 2012	5
CT22	NDVI	SS	17 June–19 July 2012	5
CT23	NDVI	FD	21 January–26 December 2012	22
CT24	NDVI	FD	9 February–10 December 2012	20
CT25	NDVI	FD	25 February–24 November 2012	18
CT26	NDVI	FD	13 March–8 November 2012	16
CT27	NDVI	FD	29 March–23 October 2012	14
CT28	NDVI	FD	14 April–7 October 2012	12
CT29	NDVI	FD	30 April–21 September 2012	10
CT30	NDVI	FD	16 May–5 September 2012	8
CT31	NDVI	FD	1 June–20 August 2012	6
CT32	NDVI	FD	17 June–4 August 2012	4
CT33	NDVI	FD	3 July–19 July 2012	2
CT34	NDVI	FA(2 harmonics) of the RD	30 April–5 September 2012	9
CT35	NDVI	FA(3 harmonics) of the RD	30 April–5 September 2012	9
CT36	NDVI	FA(4 harmonics) of the RD	30 April–5 September 2012	9
CT37	NDVI	FA(5 harmonics) of the RD	30 April–5 September 2012	9
CT38	NDVI	SS using FA(2 harmonics) instead of RD	16 May–20 August 2012	5
CT39	NDVI	SS using FA(3 harmonics) instead of RD	16 May–20 August 2012	5
CT40	NDVI	SS using FA(4 harmonics) instead of RD	16 May–20 August 2012	5
CT41	NDVI	SS using FA(5 harmonics) instead of RD	16 May–20 August 2012	5
CT42	NDVI	FD using FA(2 harmonics) instead of RD	1 June–20 August 2012	6
CT43	NDVI	FD using FA(3 harmonics) instead of RD	1 June–20 August 2012	6
CT44	NDVI	FD using FA(4 harmonics) instead of RD	1 June–20 August 2012	6
CT45	NDVI	FD using FA(5 harmonics) instead of RD	1 June–20 August 2012	6
CT46	EVI	RD	8 January–26 December 2012	23
CT47	EVI	RD	21 January–10 December 2012	21
CT48	EVI	RD	9 February–24 November 2012	19
CT49	EVI	RD	25 February–8 November 2012	17
CT50	EVI	RD	13 March–23 October 2012	15
CT51	EVI	RD	29 March–7 October 2012	13
CT52	EVI	RD	14 April–21 September 2012	11
CT53	EVI	RD	30 April–5 September 2012	9
CT54	EVI	RD	16 May–20 August 2012	7
CT55	EVI	RD	1 June–4 August 2012	5
CT56	EVI	RD	17 June–19 July 2012	3
CT57	EVI	SS	8 January–26 December 2012	5
CT58	EVI	SS	21 January–10 December 2012	5
CT59	EVI	SS	9 February–24 November 2012	5
CT60	EVI	SS	25 February–8 November 2012	5
CT61	EVI	SS	13 March–23 October 2012	5
CT62	EVI	SS	29 March–7 October 2012	5
CT63	EVI	SS	14 April–21 September 2012	5
CT64	EVI	SS	30 April–5 September 2012	5
CT65	EVI	SS	16 May– 20 August 2012	5
CT66	EVI	SS	1 June–4 August 2012	5
CT67	EVI	SS	17 June–19 July 2012	5
CT68	EVI	FD	21 January–26 December 2012	22
CT69	EVI	FD	9 February–10 December 2012	20
CT70	EVI	FD	25 February–24 November 2012	18
CT71	EVI	FD	13 March–8 November 2012	16
CT72	EVI	FD	29 March–23 October 2012	14
CT73	EVI	FD	14 April–7 October 2012	12
CT74	EVI	FD	30 April–21 September 2012	10
CT75	EVI	FD	16 May–5 September 2012	8
CT76	EVI	FD	1 June–20 August 2012	6
CT77	EVI	FD	17 June–4 August 2012	4
CT78	EVI	FD	3 July–19 July 2012	2
CT79	EVI	FA(2 harmonics) of the RD	14 April–21 September 2012	11
CT80	EVI	FA(3 harmonics) of the RD	14 April–21 September 2012	11
CT81	EVI	FA(4 harmonics) of the RD	14 April–21 September 2012	11
CT82	EVI	FA(5 harmonics) of the RD	14 April–21 September 2012	11
CT83	EVI	SS using FA(2 harmonics) instead of RD	1 June–4 August 2012	5
CT84	EVI	SS using FA(3 harmonics) instead of RD	1 June–4 August 2012	5
CT85	EVI	SS using FA(4 harmonics) instead of RD	1 June– 4 August 2012	5
CT86	EVI	SS using FA(5 harmonics) instead of RD	1 June– 4 August 2012	5
CT87	EVI	FD using FA(2 harmonics) instead of RD	16 May–5 September 2012	8
CT88	EVI	FD using FA(3 harmonics) instead of RD	16 May–5 September 2012	8
CT89	EVI	FD using FA(4 harmonics) instead of RD	16 May–5 September 2012	8
CT90	EVI	FD using FA(5 harmonics) instead of RD	16 May–5 September 2012	8

Variable importance ranking was estimated based on summing the drop (delta) in node impurity for all predictors over all nodes in the trees and expressing these sums relative to the largest sum found over all predictors, as implemented in Statistica v. 9 software (StatSoft, Inc., Tulsa, OK, USA). The main criteria for classification performance were accuracy measures such as overall accuracy (OA), producer’s accuracy (PA), user’s accuracy (UA) and Cohen’s kappa [35]. Significant differences between the classifications were subjected to McNemar tests, as suggested and described by Foody [36].

3. Results

The seasonal profile of VI in grasslands exhibits a typical shape, which reflects green biomass development during the season, with a sharp increase in spring reaching the maximum in early summer and a smooth decrease thereafter until the end of the vegetation season (Figure 6).

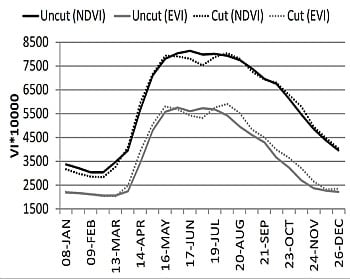
The small decrease visible after the period when the seasonal maximum is reached may be a response to summer drought and hay harvesting. The effect of grass cutting is more influential, which is apparent when cut and uncut meadows are plotted separately (Figure 7). After the hay harvesting period, vegetation re-growth is evident, reaching the second VI peak in late summer. Variation of this profile is the highest during the spring vegetation increase, followed by the autumn and the harvesting period, which is the lowest during both vegetation peaks in late spring and late summer. Here, variation in late autumn and winter is not considered as this is largely affected by low data quality due to clouds or snow. The temporal EVI and NDVI patterns are similar. EVI bears constantly lower values and higher spatial variability throughout the season.

However, when the cut and uncut meadows are analyzed separately, the bigger difference appears. EVI bears higher values in cut meadows compared to uncut meadows over the entire season except for a short period after harvesting (Figure 7). In contrast, NDVI is almost the same in cut and uncut meadows during the whole season except for more apparent difference occurring between the two vegetation peaks (16 May and 4 August).

Figure 6. Temporal profile of NDVI and EVI (bars represent standard deviation) in all sampled hay meadows (286 sites).

Figure 6. Temporal profile of NDVI and EVI (bars represent standard deviation) in all sampled hay meadows (286 sites).

Figure 7. Temporal profile of NDVI and EVI in cut (dot line) and uncut (solid line) hay meadows.

Figure 7. Temporal profile of NDVI and EVI in cut (dot line) and uncut (solid line) hay meadows.

The best case classifications from all the raw and transformed data sets are visible in Figure 8 and accuracy measures for the best case classifications are reported in Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8. In general, the best classification results yield first difference series followed by seasonal statistics series and raw data series. However, differences in the best case classifications were statistically significant only in NDVI at the 0.05 (FD NDVI vs. SS NDVI) and 0.01 (FD NDVI vs. RD NDVI) level, respectively. Moreover, the FD series classification trees were quite simple (5 rules/splits) compared to very complex trees composed of raw data series (9 splits) and seasonal statistics series (7–9 splits), making them difficult to interpret (Table 7). When shorter periods centered on the harvesting date were used, better results were achieved (Figure 4). This was consistent across all classifications, where the best results in the FD series were seen using the period between 16 May and 5 September (EVI) and between 1 June and 20 August (NDVI). The best classification in all types was compared to their smoothing counterparts using different numbers of harmonics in temporal Fourier analysis. By using smoothing series for all the best case classifications (RD, SS, FD), significantly lower accuracies were obtained, although this was not the case when five harmonics were used. Using raw VI and seasonal statistics, EVI series yield better classification accuracies than NDVI series, yet these were not statistically significant.

On the other hand, though not statistically significant, NDVI yielded consistently better accuracies than EVI in FD series classifications, where the best was for the period between 1 June and 20 August using two images less than the best FD EVI classification. User’s and producer’s accuracies were well balanced in the NDVI series (Table 7) and cut detection using NDVI outperformed the EVI series, reaching producer’s accuracies of 85% in comparison to just 67% using the EVI series.

Table 3. Confusion matrix and accuracies of raw NDVI data set (30 April to 5 September).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	31	14	45	68.89
Uncut	15	40	55	72.73
Total	46	54	100
Producer’s Accur. %	67.39	74.07
Overall Accur. %	71
Cohen’s Kappa	0.42

Table 3. Confusion matrix and accuracies of raw NDVI data set (30 April to 5 September).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	31	14	45	68.89
Uncut	15	40	55	72.73
Total	46	54	100
Producer’s Accur. %	67.39	74.07
Overall Accur. %	71
Cohen’s Kappa	0.42

Table 4. Confusion matrix and accuracies of raw EVI data set (14 April to 21 September).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	29	9	38	76.32
Uncut	17	45	62	72.58
Total	46	54	100
Producer’s Accur. %	63.04	83.33
Overall Accur. %	74
Cohen’s Kappa	0.46

Table 4. Confusion matrix and accuracies of raw EVI data set (14 April to 21 September).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	29	9	38	76.32
Uncut	17	45	62	72.58
Total	46	54	100
Producer’s Accur. %	63.04	83.33
Overall Accur. %	74
Cohen’s Kappa	0.46

Figure 8. Classification performance of the all tested data series with different periods used. (a) raw data series RD, (b) seasonal statistics series SS, (c) first difference series FD. NDVI—solid line, EVI—dot line. The best case series for each NDVI and EVI are marked with the value of Cohen`s kappa. Bold line indicated significant difference in comparison to the best case of relevant series. Filled boxes indicated significant difference between EVI vs. NDVI using the same data set.

Figure 8. Classification performance of the all tested data series with different periods used. (a) raw data series RD, (b) seasonal statistics series SS, (c) first difference series FD. NDVI—solid line, EVI—dot line. The best case series for each NDVI and EVI are marked with the value of Cohen`s kappa. Bold line indicated significant difference in comparison to the best case of relevant series. Filled boxes indicated significant difference between EVI vs. NDVI using the same data set.

Table 5. Confusion matrix and accuracies of NDVI seasonal statistics data set (16 May to 20 August).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	33	12	45	73.33
Uncut	13	42	55	76.36
Total	46	54	100
Producer’s Accur. %	71.74	77.78
Overall Accur. %	75
Cohen’s Kappa	0.50

Table 5. Confusion matrix and accuracies of NDVI seasonal statistics data set (16 May to 20 August).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	33	12	45	73.33
Uncut	13	42	55	76.36
Total	46	54	100
Producer’s Accur. %	71.74	77.78
Overall Accur. %	75
Cohen’s Kappa	0.50

Table 6. Confusion matrix and accuracies of EVI seasonal statistics data set (1 June to 4 August).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	29	5	34	85.29
Uncut	17	49	66	74.24
Total	46	54	100
Producer’s Accur. %	63.04	90.74
Overall Accur. %	78
Cohen’s Kappa	0.54

Table 6. Confusion matrix and accuracies of EVI seasonal statistics data set (1 June to 4 August).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	29	5	34	85.29
Uncut	17	49	66	74.24
Total	46	54	100
Producer’s Accur. %	63.04	90.74
Overall Accur. %	78
Cohen’s Kappa	0.54

Table 7. Confusion matrix and accuracies of first difference NDVI data set (1 June to 20 August).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	39	8	47	82.98
Uncut	7	46	53	86.79
Total	46	54	100
Producer’s Accur. %	84.78	85.19
Overall Accur. %	85
Cohen’s Kappa	0.70

Table 7. Confusion matrix and accuracies of first difference NDVI data set (1 June to 20 August).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	39	8	47	82.98
Uncut	7	46	53	86.79
Total	46	54	100
Producer’s Accur. %	84.78	85.19
Overall Accur. %	85
Cohen’s Kappa	0.70

Table 8. Confusion matrix and accuracies of first difference EVI data set (16 May to 5 September).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	31	3	34	91.18
Uncut	15	51	66	77.27
Total	46	54	100
Producer’s Accur. %	67.39	94.44
Overall Accur. %	82
Cohen’s Kappa	0.63

Table 8. Confusion matrix and accuracies of first difference EVI data set (16 May to 5 September).

	Cut	Uncut	Total	User’s Accur. (%)
Cut	31	3	34	91.18
Uncut	15	51	66	77.27
Total	46	54	100
Producer’s Accur. %	67.39	94.44
Overall Accur. %	82
Cohen’s Kappa	0.63

The logic behind the classifications could be partly explained by the analysis of variability importance. In the raw data EVI series, the most influential images for differentiation of cut and uncut meadows lay in late summer (with 20 August being the highest), followed by an image ranked far lower in importance after the harvest (3 July) and with the lowest importance for the images during the harvesting periods (Figure 9).

When the NDVI series is used, despite the similar importance of late summer images, the high influence of images from the harvesting period (17 June and 1 June) for differentiating cut and uncut meadows is apparent. This reflects well the dissimilar pattern of the VI seasonal profile from EVI and NDVI in cut and uncut meadow values in these periods (Figure 7). The importance of SS for classifying cut and uncut meadows is similar in NDVI and EVI, where range, minimum and standard deviation (Figure 10) rank highest in importance.

Figure 9. Variable importance for the best case classification of the raw data series (RD).

Figure 9. Variable importance for the best case classification of the raw data series (RD).

Figure 10. Variable importance for the best case classification of the seasonal statistics series (SS).

Figure 10. Variable importance for the best case classification of the seasonal statistics series (SS).

In the FD EVI series (Figure 11), several periods are comparably important for classification, namely late summer (20 August), which can reflect the higher increase (vegetation re-growth) in cut meadows compared to uncut meadows; after the harvest period (3 July), reflecting the removal of biomass after the harvest and before the harvest period (1 June), which may respond to dissimilarities in cut and uncut meadows at the vegetation biomass peak (Figure 7). Contrarily, the FD NDVI series saw only a decrease after the harvest in different periods ranging from 3 July until 4 August, which is of comparably high importance for classification. The final classification trees for the best case FD series for EVI and NDVI are presented in Figure 12. In both series, cutting is classified by 5 leaf paths (production rules) and uncut meadows only by one leaf path what reflects higher variability of cut meadows and cutting practices. Seventy-five percent (63 sites) of cut and 80% (82 sites) of uncut training sites in NDVI series and 62% (52 sites) of cut and 84% (86 sites) of uncut training sites in EVI series were used in the final pruned tree. Cutting was classified mainly by decision rules that reflect decrease in NDVI between consecutive 16 days periods (e.g., in 19 July, 17 June) and increase of EVI (e.g., 4 August, 20 August). Again, this could reflect the dissimilar pattern of VI seasonal profile of EVI and NDVI in cut and uncut meadows, which may lead to different ways of discriminating cut and uncut meadows using the EVI and NDVI FD series.

Figure 11. Variable importance for the best case classification of the first difference series (FD).

Figure 11. Variable importance for the best case classification of the first difference series (FD).

Figure 12. Classification tree and splitting rules of the best case first difference series for EVI (a) and NDVI (b). Values are in VI × 10000. Percentages in parentheses represent the proportion of the classified sites of the respective leaf to the total amount of sites in that specific class. Thus, sum of these percentages represents proportion of sites from the respective class, which were used in the final pruned tree.

Figure 12. Classification tree and splitting rules of the best case first difference series for EVI (a) and NDVI (b). Values are in VI × 10000. Percentages in parentheses represent the proportion of the classified sites of the respective leaf to the total amount of sites in that specific class. Thus, sum of these percentages represents proportion of sites from the respective class, which were used in the final pruned tree.

4. Discussion

4.1. Temporal Profile of VIs

The VI grassland seasonal pattern can vary substantially, reflecting not only differences in vegetation type and dominant species phenology [37] but also land use such as for pasture or meadows [38], farming practices like the timing and cutting regime [7], local climate variability and site hydrology [39], or abandonment rate [16]. The shape of the VI temporal curve of hay meadows in our study is comparable to other grassland studies in Europe [10,40], although differences in the timing and magnitude of peaks can vary because of climate variability and regionally specific grassland management. The spatial variability of VI is constantly lower throughout the season in non-managed meadows (Figure 6), which means that management practices have affected seasonal development of VI more than differences in local climate or dominant species phenology. The small decrease after the period when the seasonal maximum was achieved mainly reflects hay harvesting. Similarly, Nitze et al. [17] used a land-cover classification study from grass dominated landscape in Ireland to describe these small scale fluctuations during the summer and linked them with typical management practices such as cutting and grazing, stating they were more apparent in improved than in unimproved grasslands. Peterson et al. [41] described another distinctive feature of managed as opposed to unmanaged grasslands reflected in the VI temporal profile, namely the lower speed and later green-up in unmanaged grasslands because of a thick litter layer not cut in previous season. However, this phenomenon was not apparent in our VI profiles.

4.2. Classification Performance

It is quite difficult to compare accuracy measures of our results with other studies because of the different classification schemes used in the related studies, as mentioned in the introductory section. For example, Prischepov et al. [15] aimed in their agricultural land abandonment study to distinguish managed (e.g., harvested) grasslands and abandoned (unmanaged) grasslands. They used Landsat multi-temporal classifications resulting in substantially higher classification accuracies of managed (UA = 95.7%; PA = 82.7%) as opposed to unmanaged grasslands (UA = 50%; PA = 78.1%). The authors reported that abandoned (unmanaged) grasslands were frequently misclassified as managed grasslands, concluding that unless a satellite image was available for the period just after the cut, it would become very difficult to detect whether grassland management had taken place in a given year. Similarly, Alcantara et al. [16] distinguished an active agriculture class (with inclusion of managed grasslands) and an abandoned agriculture class defined as areas covered by secondary succession such as grasses that were neither mown nor grazed. They used MODIS time series combining NDVI and derived phenometrics. Though they reported quite promising results for a complex classification task (OA of 65%), slightly lower accuracies levels of 41% (UA) and 56% (PA) were obtained for the specific abandoned agriculture class. It was mainly for misclassification of active agricultural classes that they discussed as the possible effect of spatial proximity; the fact that many abandoned agriculture areas were intermixed with still active agriculture and MODIS gridding artifacts that cause changes in the spectral information reported for a given MODIS pixel over time as it is reported in Tan et al. [27]. Our study obtained slightly better results (in respect to accuracies), which could be caused by more exact class definition, homogenous samples used and a smaller study area with lower variability of grasslands and their management practices. As for the ecological and economic importance of grasslands in Ireland’s grass dominated landscape, Nitze et al. [17] used 16-day MODIS VI time series for multi-temporal classification of improved and semi-improved grasslands. The authors analyzed all VI value combinations for each year over a ten-year period (2000–2010) in order to identify the optimal number of images for classification. Obviously, increasing the number of images using NDVI improved classification accuracies. With only three images, average accuracy reaches 82.6%, only 3.4% less than the maximum of 86% reached with the 17 different input images. EVI data yielded even better results by up to 5%. They also reported the results varying widely between years, ranging from 80% to 95%, while obtaining slightly better accuracies than in our example, which can imply that using similar approaches produces better differentiation of improved as opposed to unimproved grasslands than unimproved (in our case considered as cut meadows) and unmanaged grasslands. Using the VHR Rapid Eye for multi-temporal classification of grasslands in Germany, Franke et al. [7] achieved overall accuracies ranging from 74.8% with kappa coefficient of 0.45, when using three scenes per vegetation season, up to 82.5% and kappa of 0.60 when using five scenes. In addition to semi-natural grasslands and extensive grasslands (which can be compared to our classes of uncut and cut meadows, respectively), they classified other types of grasslands as intensive and tilled, reporting mean class accuracy of 82.6%. The authors stated that three scenes are sufficient to reliably classify grassland management types with respect to tilled and intensively used grasslands, although additional scenes are needed if classification of semi-natural and extensively used grasslands is required, which they concluded based on frequent misclassification between semi-natural and extensively used grasslands. It is in any case obvious that VHR also matches the spatial pattern of grassland use intensities, the objective, which is not possible with just MODIS data in Central Europe. The combination of VHR and multi-temporal approaches based on MODIS data seem to be promising, as was documented, for example, by Aragon et al. [39] and Esch et al. [10]. Except the spatial pattern of grassland management types, similar accuracies as the above studies have been yielded by us, which may serve as a proper approach for later multisource classification approaches of grasslands. The best case classification in our study (Table 7) reached 85% overall accuracy with balanced rate of user’s and producer’s accuracies which is exactly the commonly recommended minimum target of 85% [35]. Grasslands as such are classified with difficulties in complex land cover classification studies, especially in heterogeneous landscape like in Slovakia. For example, Corine land cover product from 2006 reached only 39% of producers and 75.5% of users accuracies of grassland land cover class 231 based on the homogenous sample similar to that of our study [42]. In this respect, we think that the classification results reached an acceptable level of accuracy. However, we performed only a binary classification of single land cover class and we assume that if the same approach was used within complex land cover classification, the accuracy levels would decrease a bit because of possible misclassification of uncut meadows with shrubs and cut meadows with some annual crops. Regarding the management needs described in the introductory section, we think that this approach with the analyzed data sets should be used with caution for the full coverage mapping of cutting (e.g., for the subsidies control system) because of spatial limitation of MODIS VI data. However, when the proper full coverage land cover data set is available (or high resolution layers of grasslands) the cut detection described by our study could serve as a promising tool for monitoring of selected sites of special interest (e.g., NATURA 2000 sites) or for describing the spatial trends or substantial regional differences (e.g., for the regional managers).

Besides accuracy, robustness and simplicity are common goals when specific classification algorithms are developed with the general objective of the algorithm’s transferability in space and time. In this respect, the great advantage of tree based classifiers is their easy interpretation and thus, can be changed to the simple rule-based classifier based on a set of the simple meaningful rules [18]. In this respect, we tried to minimize dimensions of the raw data by simple transformations of the raw series. Such transformation usually helps in achieving better classification results. Seasonal statistics of Vis [43] or variety of phenometrics [16] are often used for this purpose. In our case, we demonstrated that FD transformed series outperformed the raw series, resulting in a substantially simpler decision tree that allows simple interpretations (Table 9). The final classification tree, based on the NDVI data, looks like a set of simple decision rules reflecting the sudden decrease of NDVI values after cutting, varying only in the specific time of harvesting (Figure 12). These set of quantitative rules could be considered as thresholds to be later recalibrated and upgraded by expert knowledge and transferred to another spatial or temporal domain. Similarly, Franke et al. [7] based their multi-temporal classification on assuming that removal of plant material for fodder or litter through mowing the grasslands causes spectral changes and so can be an indicator for the intensity of utilization and thus specific land management practice. They transferred the knowledge about temporal aspects of different grassland management types into a set of rules which they derived from quantitative thresholds called MASD (mean absolute spectral dynamic). They documented such an approach outperforming CART based machine learning algorithm on test sites by up to 19%. The main advantage of their context-based rule set was a decrease in the number of rules (from 10 to 4) and the number of variables from 8 to 4.

Table 9. Structure of the best case classification trees from the different data sets used.

		Period	Input Variables	Used Variables	Number of Rules (Splits)
NDVI	Raw data	30 April–5 September	9	30 April;17 June; 3 July; 20 August; 19 July	9
	Seasonal statistics	16 May–20 August	5	Max; Min; Mean; Sd; Range	9
	First difference	1 June–20 August	6	3 July; 1 June; 17 June; 19 July; 4 August	5
EVI	Raw data	14 April–21 September	9	20 August; 4 August; 1 June; 3 July; 30 April	9
	Seasonal statistics	1 June–4 August	5	Max; Min; Mean; Sd; Range	7
	First difference	16 May–5 September	8	19 July; 1 June; 4 August; 20 August	5

Table 9. Structure of the best case classification trees from the different data sets used.

		Period	Input Variables	Used Variables	Number of Rules (Splits)
NDVI	Raw data	30 April–5 September	9	30 April;17 June; 3 July; 20 August; 19 July	9
	Seasonal statistics	16 May–20 August	5	Max; Min; Mean; Sd; Range	9
	First difference	1 June–20 August	6	3 July; 1 June; 17 June; 19 July; 4 August	5
EVI	Raw data	14 April–21 September	9	20 August; 4 August; 1 June; 3 July; 30 April	9
	Seasonal statistics	1 June–4 August	5	Max; Min; Mean; Sd; Range	7
	First difference	16 May–5 September	8	19 July; 1 June; 4 August; 20 August	5

4.3. Optimal Period

The optimal period for classification is important and can largely influence classification performance. Furthermore, this information is critical for data availability reasons. From this perspective, the shorter the required period, the better because of the lower data demands. Our analysis revealed that the 16-day time span in a relatively short seasonal period (e.g., using seven or eight compositing periods from May to August) is sufficient for accurately detecting cut meadows. Nitze et al. [17] documented that the optimal number of images required for achieving good classification accuracies is between six to ten (out of 23 images/per year), after which the value gained from additional images becomes marginal. Wen et al. [44] also reported that using a shorter vegetation growth period was better than the whole annual cycle for classifying different Tibetan grassland types. In fact, analysis of the entire annual series may be negatively influenced by the winter period due to noise in data which may lead to higher misclassification rates [8]. Based on the series of multi-temporal classifications of German semi natural grasslands using 24 Rapid Eye annual series, Schmidt et al. [37] showed that a three-scene composite reaches more than 0.8 overall accuracy and the best trade-off amount between the number of acquisition dates and classification accuracy is achieved by using a seven-scene NDVI composite. Furthermore, the most important season for differentiating semi-natural grasslands was early summer (defined as the period from 4 June to 17 June), followed by late spring, late summer and mid-summer. On the other hand, Prishchepov [15] reported through a less dense Landsat series that the factor which influenced the accurate detection of abandoned as opposed to managed grasslands was the number of multi-seasonal images dates (the more the better) rather than their exact dates. Our case study found the best case FD NDVI series classification was the period from 1 June to 20 August, which resulted in an OA of 85%. The narrower series of four images (17 June to 4 August) and two images (3 July to 19 July) resulted in significantly lower accuracies (Figure 4c). This can reflect the variability of the timing for cutting because of the quite large study region. However, we think that the number of scenes needed could be decreased even further in regional dependent applications. The more important fact is that the 16-day compositing period seems to be enough to detect cutting management, which is the time span that might be hopefully achieved by upcoming on-board HR sensors (Sentinel2) with the high temporal resolution followed by a combination with the existing platforms (e.g., Landsat).

4.4. Smoothing Effect

Smoothing series for all the best classifications (RD, SS, FD) obtained lower accuracies, although they were not significantly different when five harmonics were used. Lower Fourier terms (e.g., 2,3,4) caused significantly lower accuracy values. This agrees with Geerken et al. [45], who stated that at least 5 harmonics should be used in order to properly classify rangeland vegetation when shaped-based classification is applied from Fourier filtered cycle similarity. Only two or three harmonics are commonly used to remove the noise in VI time series. In fact, the reflection from grass cutting in the VI temporal profile could be considered as noise in such cases, which could lead to problematic detection of grasslands in complex classification tasks, for instance in crop type mapping [46]. On the other hand, interpolation techniques followed by smoothing could essentially improve the amount of useful input data, leading to more representative coverage of study areas. Therefore, proper analysis of missing data effects and the utilization of proper interpolation and smoothing techniques should be done in future grassland classification studies.

4.5. EVI vs. NDVI

Higher EVI variability during peak biomass periods is obvious because EVI was designed to have higher dynamic range to solve the well-known deficit of NDVI being saturated at high biomass levels, e.g., more than 0.8 [47,48]. On the other hand, slightly higher NDVI sensitivity to relatively low biomass levels during the early spring was evident, something in line with what other authors have found [17,48]. Nitze et al. [17] documented similar EVI and NDVI behaviors when comparing temporal profiles in improved and unimproved grasslands. They stated that EVI time series exhibit better distinction of these classes, where improved grasslands are characterized by constantly higher values than unimproved grasslands. Furthermore, they also documented that NDVI exhibits higher sensitivity to less intense vegetation, in their case—peatlands. Higher dynamic range and atmospheric and background corrections are the reasons why EVI is more frequently used in classification tasks [48]. In our case, when using RD or SS data, EVI outperforms NDVI in detecting cut meadows. However, the logic behind these classifications is not as apparent in the quite complex final decision trees and rules. When we decrease the dimension of the data by transforming them to FD series, an abrupt biomass decrease (as the reaction to cutting) was constantly evident in NDVI classification rules, resulting in a quite simple and readable decision tree. However, this was not the case in the EVI series, which we think is due to EVI’s higher sensitivity, reflected in the complex dissimilarity of cut, as opposed to uncut meadows, across the whole season. In any case, NDVI and EVI responded in complementary way, thus, their combine usage is advised. Furthermore, though NDVI and EVI are among the most popular VIs, other VIs and especially those, which are sensitive to plant water content should be considered for detection of cutting.

5. Conclusions

We reported here the possible usage of VI time series for detection of cut management in hay meadows. Transformation of raw series clearly helps, mainly FD, which decreases the complexity of the resulting classification trees. Specifically, FD series classification trees resulted in simple tree with 5 rules/splits compared to very complex trees composed of raw data series (9 splits) and seasonal statistics series (7–9 splits). We think that such simple rule-based algorithms should be better transferable than complex trees. However, this needs to be tested in different regions, grassland types and years. We do slightly consider regional differences here as the relatively large study area includes different bioregions, but we do not consider other grassland types and more importantly we do not consider climate variability between years. This needs to be tested in longer term case studies that may include anomaly years as well. NDVI slightly outperformed EVI in the best case FD classification. Specifically, the best case NDVI FD series classification yielded overall accuracy of 85%, EVI FD series yielded slightly lower values (82%), though not significantly different. Moreover, user’s and producer’s accuracies were well balanced in the NDVI series and cut detection using NDVI outperformed the EVI series, reaching producer’s accuracies of 85% in comparison to just 67% using the EVI series. This might be caused mainly by the higher variability of EVI and different VI response to cutting in the temporal profile, leading to different ways of discriminating cut and uncut meadows. All other differences were masked in the NDVI profile except the apparent biomass decrease after the harvest in different time periods. Contrary, EVI saw constantly higher values in cut meadows over a longer period and their higher variability may have caused the higher misclassification rates and omission errors of cut meadows. By using smoothing series for all the best case classifications (RD, SS, FD), significantly lower accuracies were obtained, although this was not the case when five harmonics were used. On the other hand, interpolation techniques followed by smoothing is a method commonly used and they could essentially improve the amount of useful input data, leading to more representative coverage of study areas and full coverage products. Therefore, proper analysis of the missing data effect and utilization of proper interpolation and smoothing techniques should be done in future grassland classification studies. There is no need to have the whole annual series in order to sufficiently detect cutting. In fact, the optimal period for detection lay between 1 June and 20 August. More importantly, the 16-day compositing period seemed to be enough for detection of cutting, which would be the time span that might be hopefully achieved by upcoming on-board HR sensors (e.g., Sentinel2), followed by combining them with existing platforms (e.g., Landsat). This looks promising when the possible usage of similar concepts at finer scales is borne in mind.