Development of a High Resolution BRDF/Albedo Product by Fusing Airborne CASI Reflectance with MODIS Daily Reflectance in the Oasis Area of the Heihe River Basin, China
Abstract
:1. Introduction
2. A Compact Airborne Spectrographic Imager (CASI)-Based Airborne Experiment in the Heihe Watershed Allied Telemetry Experimental Research (HiWATER)

3. Deriving the CASI and MODIS (Moderate Resolution Imaging Spectroradiometer) BRDF/Albedo (Bidirectional Reflectance Distribution Function) Algorithm
3.1. Archetypal BRDF
3.2. Land-Type-Based Linear BRDF Unmixing (LLBU) Model Construction
3.3. LLBU Inversion

3.4. Albedo Calculation
4. Results
4.1. Investigation of BRF Fitting Ability at Different Scales


| RSE | LLBU CASI | LLBU MODIS | AMBRALS MODIS |
|---|---|---|---|
| Band1 | 0.0007 | 0.0103 | 0.0098 |
| Band2 | 0.0011 | 0.0242 | 0.0239 |
| Band3 | 0.0004 | 0.0059 | 0.0084 |
| Band4 | 0.0003 | 0.0074 | 0.0078 |
4.2. The BRDF Analysis and Assessments
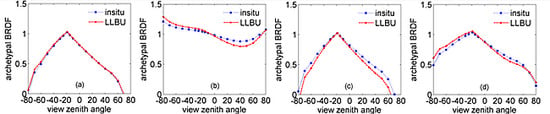
4.2.1. The CASI Land-Type-Specific Archetypal BRDF and Its Comparison with in situ BRDF



4.2.2. The Archetypal BRDF at MODIS Scale and Its Comparison with MCD43A1 Results



| Best Agreement | Good Agreement | Poor Agreement | |
|---|---|---|---|
| Band1 | 26% | 37% | 37% |
| Band2 | 100% | 0% | 0% |
| Band3 | 21% | 35% | 44% |
| Band4 | 54% | 22% | 24% |


4.3. Visual Assessments of Normalizing the Angular Effects on the CASI Scale

4.4. Albedo Validation and Comparison
4.4.1. CASI Albedo Validation


4.4.2. MODIS Albedo Comparison


| Cropland | Manmade Features | Bare Soil | Bushes | |
|---|---|---|---|---|
| Band 1 | 1.50 | 0.45 | 0.95 | 1.42 |
| Band 2 | 1.12 | 1.16 | 1.25 | 1.04 |
| Band 3 | 1.46 | 0.36 | 0.70 | 1.45 |
| Band 4 | 1.23 | 0.57 | 0.94 | 1.18 |
5. Discussions
6. Conclusions
Acknowledgments
Author Contributions
Appendix
A. Nomenclature
| Θ | view geometry |
| s | illumination direction |
| v | viewing direction |
| zenith angle | |
| azimuth angle | |
| λ | wavelength or waveband |
| F | archetypal BRDF |
| kvol | volumetric scattering kernel |
| kgeo | geometric-optical kernel |
| fiso, fvol, fgeo | coefficients of isotropic, volumetric, and geometric-optical scattering |
| BRF of MOIDS | |
| geographical location | |
| i | land type index |
| n | number of land types |
| Ai | area of land type i in a MODIS pixel |
| A | area of a MODIS pixel |
| ξ | error item |
| ρ | BRF of CASI |
| αi, βi | the slope and intercept item of correctors for land type i |
| similarity indicator of BRDF shapes | |
| p | iteration index |
| broad-band blue-sky albedo | |
| broad-band back-sky albedo | |
| broad-band white-sky albedo | |
| d | diffuse sky light fraction of the total illumination |
| anisotropic factor | |
| simulated reflectance of the BRDF model |
B. Abbreviations
| AMBRALS | the Algorithm for Modeling (MODIS) Bidirectional Reflectance Anisotropies of the Land Surface |
| BRDF | Bidirectional reflectance distribution function |
| BRF | bidirectional function factor |
| CASI | Compact Airborne Spectrographic Imager |
| CAR | Cloud Absorption Radiometer |
| CCD | Charge-Coupled Device |
| DOY | Day of Year |
| FEA | Foci Experimental Area |
| HiWATER | Heihe Watershed Allied Telemetry Experimental Research |
| HJ | HuanJing satellite |
| LAI | index/leaf area index |
| LB | land-type-based |
| LLBU | Land-cover-based linear BRDF unmixing |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MISR | Multi-angle Imaging Spectroradiometer |
| NDVI | Normalized Difference Vegetation Index |
| PB | Pixel-Based |
| POLDER | Polarization and Directionality of Earth Reflectance |
| RSP | Research Scanning Polarimeter |
| RVI | Ratio Vegetation Index |
| SZA | Sun Zenith Angle |
| TM | Thematic Mapper |
| VZA | View Zenith Angle |
Conflicts of Interest
References
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Croft, H.; Anderson, K.; Kuhn, N. Reflectance anisotropy for measuring soil surface roughness of multiple soil types. Catena 2012, 93, 87–96. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G.; Miller, J.R.; Freemantle, J.; Loechel, S.E.; Walthall, C.L.; Innanen, K.A.; White, H.P. Compact Airborne Spectrographic Imager (CASI) used for mapping biophysical parameters of boreal forests. J. Geophys. Res.: Atmos. 1999, 104, 27945–27958. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Glofbal clumping index map derived from the MODIS brdf product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H.; Woodcock, C.E. A hybrid geometric optical-radiative transfer approach for modeling albedo and directional reflectance of discontinuous canopies. IEEE Trans. Geosci. Remote Sens. 1995, 33, 466–480. [Google Scholar]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P. First operational BRDF, albedo NADIR reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Vermote, E. Correction of modis surface reflectance time series for BRDF effects. Remote Sens. Environ. 2012, 125, 1–9. [Google Scholar] [CrossRef]
- Weyermann, J.; Damm, A.; Kneubuhler, M.; Schaepman, M.E. Correction of reflectance anisotropy effects of vegetation on airborne spectroscopy data and derived products. IEEE Trans. Geosci. Remote Sens. 2014, 52, 616–627. [Google Scholar] [CrossRef]
- Liang, S.; Stroeve, J.; Box, J.E. Mapping daily snow/ice shortwave broadband albedo from Moderate Resolution Imaging Spectroradiometer (MODIS): The improved direct retrieval algorithm and validation with greenland in situ measurement. J. Geophys. Res.: Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Martonchik, J.; Diner, D.; Kahn, R.; Ackerman, T.; Verstraete, M.; Pinty, B.; Gordon, H. Techniques for the retrieval of aerosol properties over land and ocean using multiangle imaging. IEEE Trans. Geosci. Remote Sens. 2002, 36, 1212–1227. [Google Scholar] [CrossRef]
- Martonchik, J.; Diner, D.; Pinty, B.; Verstraete, M.; Myneni, R.; Knyazikhin, Y.; Gordon, H. Determination of land and ocean reflective, radiative, and biophysical properties using multiangle imaging. IEEE Trans. Geosci. Remote Sens. 2002, 36, 1266–1281. [Google Scholar] [CrossRef]
- Martonchik, J.; Pinty, B.; Verstraete, M. Note on an improved model of surface BRDF-atmospheric coupled radiation. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1637–1639. [Google Scholar] [CrossRef]
- Bacour, C.; Bréon, F.-M. Variability of biome reflectance directional signatures as seen by polder. Remote Sens. Environ. 2005, 98, 80–95. [Google Scholar] [CrossRef]
- Hautecœur, O.; Leroy, M.M. Surface bidirectional reflectance distribution function observed at global scale by POLDER/ADEOS. Geophys. Res. Lett. 1998, 25, 4197–4200. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Román, M.O.; Gatebe, C.K.; Schaaf, C.B.; Poudyal, R.; Wang, Z.; King, M.D. Variability in surface brdf at different spatial scales (30 m–500 m) over a mixed agricultural landscape as retrieved from airborne and satellite spectral measurements. Remote Sens. Environ. 2011, 115, 2184–2203. [Google Scholar] [CrossRef]
- Gatebe, C.K.; King, M.D.; Platnick, S.; Arnold, G.T.; Vermote, E.F.; Schmid, B. Airborne spectral measurements of surface-atmosphere anisotropy for several surfaces and ecosystems over southern Africa. J. Geophys. Res.: Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Román, M.O.; Gatebe, C.K.; Shuai, Y.; Wang, Z.; Gao, F.; Masek, J.G.; He, T.; Liang, S.; Schaaf, C.B. Use of in situ and airborne multiangle data to assess MODIS-and Landsat-based estimates of directional reflectance and albedo. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1393–1404. [Google Scholar] [CrossRef]
- Knobelspiesse, K.D.; Cairns, B.; Schmid, B.; Roman, M.O.; Schaaf, C.B. Surface brdf estimation from an aircraft compared to MODIS and ground estimates at the southern great plains site. J. Geophys. Res. Atmos. (1984–2012) 2008, 113. [Google Scholar] [CrossRef]
- Feingersh, T.; Ben-Dor, E.; Filin, S. Correction of reflectance anisotropy: A multi-sensor approach. Int. J. Remote Sens. 2010, 31, 49–74. [Google Scholar] [CrossRef]
- Colgan, M.S.; Baldeck, C.A.; Féret, J.-B.; Asner, G.P. Mapping savanna tree species at ecosystem scales using support vector machine classification and brdf correction on airborne hyperspectral and lidar data. Remote Sens. 2012, 4, 3462–3480. [Google Scholar] [CrossRef]
- Sandmeier, S.; Müller, C.; Hosgood, B.; Andreoli, G. Physical mechanisms in hyperspectral brdf data of grass and watercress. Remote Sens. Environ. 1998, 66, 222–233. [Google Scholar] [CrossRef]
- Luo, Y.; Trishchenko, A.P.; Latifovic, R.; Li, Z. Surface bidirectional reflectance and albedo properties derived using a land cover-based approach with moderate resolution imaging spectroradiometer observations. J. Geophys. Res.: Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Li, F.; Jupp, D.L.; Reddy, S.; Lymburner, L.; Mueller, N.; Tan, P.; Islam, A. An evaluation of the use of atmospheric and brdf correction to standardize landsat data. IEEE J. Sel. Top. Appl. Earth Observ. 2010, 3, 257–270. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (hiwater): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.-L.; Herman, M.; Morcette, J.-J. Second simulation of the satellite signal in the solar spectrum, 6s: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L. Assessment of coarse-resolution land cover products using CASI hyperspectral data in an arid zone in northwestern China. Remote Sens. 2014, 6, 2864–2883. [Google Scholar] [CrossRef]
- Khlopenkov, K.; Trishchenko, A.; Luo, Y. Analysis of brdf and albedo properties of pure and mixed surface types from terra misr using landsat high-resolution land cover and angular unmixing. In Proceedings of the Fourteenth ARM Science Team Meeting, Albuquerque, New Mexico, 22–26 March 2004.
- Li, F.; Jupp, D.; Lymburnera, L.; Tana, P.; McIntyrea, A.; Thankappana, M.; Lewisa, A.; Held, A. Characteristics of MODIS BRDF shape and its relationship with land cover classes in Australia. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013.
- Wanner, W.; Li, X.; Strahler, A. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res.: Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Strahler, A.H.; Muller, J.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Li, X.; Lewis, P.; Barnsley, M.J. MODIS BRDF/Albedo Product: Algorithm Theoretical basis Document Version 5.0. MODIS Doc.. 1999. Available online: http://modis-sr.ltdri.org/publications/MODIS_BRDF.pdf (accessed on 26 May 2015).
- Wu, A.; Li, Z.; Cihlar, J. Effects of land cover type and greenness on advanced very high resolution radiometer bidirectional reflectances: Analysis and removal. J. Geophys. Res.: Atmos. 1995, 100, 9179–9192. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Sailor, D.J.; Resh, K.; Segura, D. Field measurement of albedo for limited extent test surfaces. Sol. Energy 2006, 80, 589–599. [Google Scholar] [CrossRef]
- Barker, J.; Burelhach, J. MODIS image simulation from landsat TM imagery. Glob. Chang. Educ. ASPRSACSMRT 1992, 92, 156–165. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, D.; Wen, J.; Xiao, Q.; Liu, Q.; Liu, Q.; Tang, Y.; Dou, B.; Peng, J. Development of a High Resolution BRDF/Albedo Product by Fusing Airborne CASI Reflectance with MODIS Daily Reflectance in the Oasis Area of the Heihe River Basin, China. Remote Sens. 2015, 7, 6784-6807. https://doi.org/10.3390/rs70606784
You D, Wen J, Xiao Q, Liu Q, Liu Q, Tang Y, Dou B, Peng J. Development of a High Resolution BRDF/Albedo Product by Fusing Airborne CASI Reflectance with MODIS Daily Reflectance in the Oasis Area of the Heihe River Basin, China. Remote Sensing. 2015; 7(6):6784-6807. https://doi.org/10.3390/rs70606784
Chicago/Turabian StyleYou, Dongqin, Jianguang Wen, Qing Xiao, Qiang Liu, Qinhuo Liu, Yong Tang, Baocheng Dou, and Jingjing Peng. 2015. "Development of a High Resolution BRDF/Albedo Product by Fusing Airborne CASI Reflectance with MODIS Daily Reflectance in the Oasis Area of the Heihe River Basin, China" Remote Sensing 7, no. 6: 6784-6807. https://doi.org/10.3390/rs70606784
APA StyleYou, D., Wen, J., Xiao, Q., Liu, Q., Liu, Q., Tang, Y., Dou, B., & Peng, J. (2015). Development of a High Resolution BRDF/Albedo Product by Fusing Airborne CASI Reflectance with MODIS Daily Reflectance in the Oasis Area of the Heihe River Basin, China. Remote Sensing, 7(6), 6784-6807. https://doi.org/10.3390/rs70606784