Research on the Contribution of Urban Land Surface Moisture to the Alleviation Effect of Urban Land Surface Heat Based on Landsat 8 Data

Abstract

This paper presents a new assessment method for alleviating urban heat island (UHI) effects by using an urban land surface moisture (ULSM) index. With the aid of Landsat 8 OLI/TIRS data, the land surface temperature (LST) was retrieved by a mono-window algorithm, and ULSM was extracted by tasselled cap transformation. Polynomial regression and buffer analysis were used to analyze the effects of ULSM on the LST, and the alleviation effect of ULSM was compared with three vegetation indices, GVI, SAVI, and FVC, by using the methods of grey relational analysis and Taylor skill calculation. The results indicate that when the ULSM value is greater than the value of an extreme point, the LST declines with the increasing ULSM value. Areas with a high ULSM value have an obvious reducing effect on the temperature of their surrounding areas within 150 m. Grey relational degrees and Taylor skill scores between ULSM and the LST are 0.8765 and 0.9378, respectively, which are higher than the results for the three vegetation indices GVI, SAVI, and FVC. The reducing effect of the ULSM index on environmental temperatures is significant, and ULSM can be considered to be a new and more effective index to estimate UHI alleviation effects for urban areas.

1. Introduction

Rapid urban expansion due to large scale land use/cover change [1] and the conversion of water bodies, vegetation and low-lying areas to urban land have caused extensive and varied environmental degradation [2]. Urban development has always been accompanied by the process of replacing natural vegetation with non-transpiring and non-evaporating impervious surfaces [3]. Significant differences in mean surface temperatures were found between land cover types [4]. Impervious surfaces in urban areas will not only absorb and accumulate more solar radiation and heat but also impede long-wave sky radiation loss [5,6], which will cause the phenomenon defined as the urban heat island (UHI) effect, where atmospheric and land surface temperatures (LST) in urban areas are higher than in surrounding rural areas [6,7,8]. Traditionally, meteorological station networks and mobile measurements of the urban canopy layer have been the most commonly used methods to monitor UHI [9]. Recently, with the development of remote sensing (RS) technology, remote sensing data, such as surface radiative temperatures derived from remote imagery thermal bands, are increasingly used to analyze the quantity, time and space distribution of UHI [10].

Because the urban heat island effect has a large negative influence on climate, ecology and human living environments in urban and surrounding areas, research that focuses on the alleviation effects of UHI have great significance. The relationship between LST and biophysical parameters indicates that the persistent loss of green space favors an increase in the detectable heat exchange, which is a driver of the UHI effect [11]. Much research has found that vegetation transpiration can relieve the UHI effect [9]. The relationship between NDVI (Normalized Difference Vegetation Index) [12,13,14,15,16] and LST indicates that vegetation is important in urban heat reduction [9]. FVC (Fractional Vegetation Coverage) is also a key parameter in thermal remote-sensing analysis from which surface emissivity can be estimated [17,18,19], and it is an indicator of the LST, with which it has a negative linear relationship [19,20]. In addition, SAVI (Soil Adjusted Vegetation Index) [21] and GVI (Green Vegetation Index) [22] have also been shown to have a negative relationship with LST. In addition to vegetation, water bodies are also important factors in reducing the UHI effect. Generally, the presence of water bodies is not the dominant factor for reducing the UHI effect in urban areas; however, it is the most direct and effective factor for reducing environmental temperatures [23].

Water content is one of the main factors that impact photosynthesis and vegetation biomass. The water content can reach 40-80% in a vegetation canopy [24]. Therefore, the land surface water content, or land surface moisture, can be used as an important parameter for extracting land surface vegetation information. Studies have found that indices, such as SRWI (Simple Ratio Water Index) [25], WI (Wetness Index) [26], and NDWI (Normalized Difference Water Index) [27], can be used to extract the vegetation water content. For the Landsat 8 satellite, shortwave infrared bands 6 and 7 are the most sensitive to soil and vegetation moisture [28]. The third component (Wetness) of tasseled cap transformation can also be used to extract the water content of soil and vegetation; however, little research has focused on this index. In urban areas, a higher moisture content is a common feature of vegetation and water bodies, and land surface moisture can be considered to be a common index to extract areas that make a contribution to cooling the environment. The research purposes of this paper were mainly focused on validating the alleviation effect of ULSM on UHI and exploring the contribution level of ULSM in comparison with common vegetation indices.

2. Materials and Methods

2.1. Study Area

Xu Zhou is in the northwest of China’s Jiangsu province and is located between 116°22′ and 118°40′ east longitude and 33°43′ and 34°58′ north latitude. It is located at the junction of the Jiangsu, Shandong, Henan and Anhui provinces and is a very important water and land traffic hub in China, which has been called the “crossroads” of the economic ties between north and south China [29]. Xuzhou is the second largest city in Jiangsu province, as well as the node city with the strongest agglomeration and radiation force in the north of the Yangtze River delta, and it is an important growth pole. Xuzhou is in the warm semi-humid climate zone. Because it is narrow from west to east and is influenced by the ocean differently, east Xuzhou has a warm humid monsoon climate, while the west has a warm semi-humid climate that is strongly influenced by the southeast monsoon. Its annual sunshine duration is 2284 to 2495 hours, sunshine rate is 52% to 57%, annual average temperature is 14 °C, annual average frost free period is 200 to 220 days, and annual average precipitation is 800 to 930 millimeters, with precipitation in the rainy season accounting for 56% of the annual total participation. The climate of this area provides a very good environment for crops.

To explore the effects of land surface moisture on the land surface temperature in the inner city, the built up area of Xuzhou city was chosen as the research area; the geographical position and borders of the research area are shown in Figure 1.

2.2. Data Source

In 13 February 2013, NASA successfully launched the Landsat 8 satellite. There are two main payloads in Landsat 8, the OLI (Operational Land Imager) and the TIRS (Thermal Infrared Sensor) [30]. The OLI includes nine bands, from band 1 to band 9; TIRS band 10 and band 11 provide the atmospheric rectification for the thermal infrared data [31,32]. The spatial resolution of the first nine bands is 30 m, except for band 8, which has a resolution of 15 m; the spatial resolution of band 10 and band 11 is 100 m. For this research, four Landsat 8 OLI/TIRS images of the Xuzhou area in summer from 2013 to 2014 were selected as the research data. The acquisition date and location information of the four images are shown in Table 1.

Figure 1. Location of Jiangsu in China, location of the Xuzhou urban area in Jiangsu, and location of the border of the Xuzhou urban area.

Figure 1. Location of Jiangsu in China, location of the Xuzhou urban area in Jiangsu, and location of the border of the Xuzhou urban area.

The acquisition season of each image was spring or summer; the vegetation coverage was richer and the temperature was higher in these two seasons, which is advantageous for extracting land surface information and calculating the land surface temperature. Meanwhile, the definition and weather conditions for the four images are clear, sunny and cloudless. Because the atmospheric condition has little influence on the accuracy of the land surface temperature inversion, the four images are suitable as research data.

Table 1. Acquisition date and location information of four Landsat 8 images of study area.

Scene	Landsat Scene ID	Acquisition Date	Path/Row
1	LC81220362013141LGN01	21 May 2013	122/36
2	LC81210362013246LGN00	3 September 2013	121/36
3	LC81210362014121LGN00	1 May 2014	121/36
4	LC81210362014265LGN00	22 September 2014	121/36

Table 1. Acquisition date and location information of four Landsat 8 images of study area.

Scene	Landsat Scene ID	Acquisition Date	Path/Row
1	LC81220362013141LGN01	21 May 2013	122/36
2	LC81210362013246LGN00	3 September 2013	121/36
3	LC81210362014121LGN00	1 May 2014	121/36
4	LC81210362014265LGN00	22 September 2014	121/36

2.3. Data Pre-Processing

All of the OLI bands were first resampled to a resolution of 30 m. Because atmospheric scattering effects should be removed prior to analysis to extract land cover information efficiently from Landsat 8 data, the method of DOS (Dark-Object Subtraction) atmospheric correction was used to correct the Landsat 8 OLI bands [33]. The Mono-window algorithm [34] was used for LST inversion; the influence of the atmosphere was considered in the process of calculation, so there was no need for atmospheric correction for the TIRS bands [35]. Fifty pixels were chosen from vegetation and water bodies to calculate the average value of the spectral reflectance of each wavelength. Figure 2 shows the effect of DOS atmospheric correction. Geometric calibration of OLI and TIRS was then performed for the bands on scene 2, scene 3 and scene 4 by using scene 1 as a benchmark to ensure that the overall error would be controlled within 0.5 pixels. Then, the vector boundary of Xuzhou area was overlaid on the four images to mask the initial study area. Finally, to prepare for land surface temperature inversion retrieval, the land surface of the initial study area was classified as construction land, vegetation, or a water body.

Figure 2. Comparison between spectral lines with and without atmospheric correction on 21 May 2013. (a) Spectral lines of vegetation. The standard spectral line (Vegetation) was obtained from the ASTER Spectral Library; (b) Spectral lines of water. The standard Spectral Line (Water) was obtained from Yao [36].

Figure 2. Comparison between spectral lines with and without atmospheric correction on 21 May 2013. (a) Spectral lines of vegetation. The standard spectral line (Vegetation) was obtained from the ASTER Spectral Library; (b) Spectral lines of water. The standard Spectral Line (Water) was obtained from Yao [36].

2.4. Land Surface Temperature Inversion

The methods for the retrieval of LSTs from satellite TIR data can be broadly classified into three categories: single-channel methods, multi-channel methods (split-window algorithm, SWA), and multi-angle methods [30,37]. Recently, three different SWAs for LST retrieval from Landsat-8 TIR data have been proposed [38,39], and single-channel algorithms for LST retrieval have been adapted to Landsat 8 TIRS data [40]. Wang et al. [41] also proposed an improved mono-window algorithm [34,41] from Landsat 8 data. In comparison with other methods, the mono-window algorithm is simpler and only two atmospheric parameters were needed; therefore, the mono-window algorithm was used to calculate the land surface temperature (LST) for the Landsat 8 images The mono-window algorithm’s calculation formula is as follows [41].

$$T_s=\left\{a\left(1-C-D\right)+\left[b\left(1-C-D\right)+C+D\right]T_{10}-D{T}_a\right\}/C$$

(1)

In the formula, T_s refers to the true land surface temperature; a and b are regression coefficients (within the temperature range of 0~70 °C, a = −70.1775, b = 0.4581); T₁₀ refers to the brightness temperature (K) observed by the thermal infrared sensor (band 10) at the height of the satellite; T_a refers to the average atmospheric operative temperature; C and D are the intermediate variables. The following formulas are used to calculate C and D, respectively.

$$C=\text{ετ}$$

(2)

$$D=\left(1-\text{τ}\right)\left[1+\left(1-\text{ε}\right)\text{τ}\right]$$

(3)

In this formula, ε refers to the land surface emissivity and τ refers to the atmospheric transmittance. Therefore, the true land surface temperature could be computed as long as T₁₀ (the brightness temperature observed by the thermal infrared sensor), T_a (the average atmospheric operative temperature), ε (land surface emissivity), and τ (atmospheric transmittance) had been determined.

2.4.1. Brightness Temperature (T₁₀) Inversion

According to the mono-window algorithm, the original DN value of the thermal infrared band (band 10) should be converted to a radiation brightness value that could be used to retrieve the brightness temperature T₁₀. The radiation brightness value formula of Landsat 8 is as follows.

$$L_{\text{λ}}=L_{min}+\left(\frac{L_{max}-L_{min}}{QCA{L}_{max}-QCA{L}_{min}}\right)\left(QCAL-QCA{L}_{min}\right)$$

(4)

In the formula, L_λ refers to the radiation brightness value; L_max and L_min refer to the maximum and minimum radiation brightness value observed by the thermal infrared sensor of Landsat 8; QCAL refers to the original DN value; QCAL_max and QCAL_min refer to the maximum and minimum original DN values. For band 10 of a Landsat 8 image, L_max = 22.00180 mWcm⁻²sr⁻¹μm⁻¹, L_min = 0.10033 mWcm⁻²sr⁻¹μm⁻¹, QCAL_max = 65,535, and QCAL_min = 1; these four values can be obtained from the image header files.

After L_λ has been calculated, the brightness temperature T₁₀ can be retrieved by using the following formula.

$$T_{10}=K_2/\text{ln}\left(1+K_1/L_{\text{λ}}\right)$$

(5)

In the formula, K₁ and K₂ are preset constants; for band 10 of a Landsat 8 image K₁ = 774.89, K₂ = 1321.08.

2.4.2. Average Atmospheric Temperature (T_a) Calculation

Because the Xuzhou region is located in the mid-latitudes and the acquisition season for the four remote sensing images was spring or summer, according to the research of Qin [34], T_a can be calculated by using an average atmospheric temperature empirical formula in summer for a mid-latitude area. The empirical formula is as follows.

$$T_a=16.0110+0.92621T_0$$

(6)

In the formula, T₀ refers to the air temperature at the ground. According to the Xuzhou climate log data set from the China Meteorological Data Sharing Service System, the air temperatures of the ground when these four images were taken are shown in Table 2.

Table 2. Atmospheric information of Xuzhou area.

Satellite Transit Time	Air Temperature of Ground T0 (K)	Average Ground Vapor Pressure e (hpa)	Atmospheric Transmittance e (τ)
21 May 2013	299.25	17.7	0.6153
03 September 2013	297.25	17.3	0.6242
01 May 2014	296.05	17.8	0.6131
22 September 2014	295.65	15.5	0.6645

Table 2. Atmospheric information of Xuzhou area.

Satellite Transit Time	Air Temperature of Ground T0 (K)	Average Ground Vapor Pressure e (hpa)	Atmospheric Transmittance e (τ)
21 May 2013	299.25	17.7	0.6153
03 September 2013	297.25	17.3	0.6242
01 May 2014	296.05	17.8	0.6131
22 September 2014	295.65	15.5	0.6645

2.4.3. Land Surface Emissivity (ε) Calculation

Land surface emissivity can be calculated by using different approaches than NDVI values [42,43]. NDVI^THM [44] is an index that uses certain NDVI values (thresholds) to distinguish between pixels with soil cover (NDVI < NDVI_s) and pixels with full vegetation cover (NDVI > NDVI_v) [45]; for mixed pixels (NDVI_s ≤ NDVI ≤ NDVI_v), the three types of land cover type can be calculated by using the following three formulas [45,46], respectively.

$${\text{ε}}_{vegetation}=P_v{R}_v{\text{ε}}_v+\left(1-P_v\right)R_s{\text{ε}}_s+d_{\text{ε}}$$

(7)

$${\text{ε}}_{construction}=P_v{R}_v{\text{ε}}_v+\left(1-P_v\right)R_m{\text{ε}}_m+d_{\text{ε}}$$

(8)

$${\text{ε}}_{water}=0.995$$

(9)

In these formulas, ε_vegetation, ε_construction, and ε_water refer to the land surface emissivity of vegetation, construction land and water bodies, respectively; P_v refers to the proportion of vegetation in mixed pixels; R_v, R_s, and R_m, respectively, represent the temperature ratio of vegetation, bare soil land, and construction land; and d_ε refers to the impact value of land surface emissivity, which is due to the interaction between vegetation and bare soil. For land surface coverage in which vegetation or bare soil area accounts for 100%, ε_v = 0.986 and ε_s = 0.972. For construction land, ε_m = 0.970.

The proportion of vegetation in mixed pixels can be calculated by the following formula [45].

$$P_v={\left[\left(NDVI-NDV{I}_s\right)/\left(NDV{I}_v-NDV{I}_s\right)\right]}^2$$

(10)

In these formulas, NDVI refers to the normalized difference vegetation index because there is no detailed regional vegetation and soil spectrum. According to the research of Jimenez-Munoz et al. [47], NDVI_v = 0.50 and NDVI_s = 0.15 can be used to estimate the NDVI value of vegetation and bare soil areas.

R_v, R_s, and R_m can be calculated by the following formulas.

$$R_v=0.9332+0.0585P_v$$

(11)

$$R_s=0.9902+0.1068P_v$$

(12)

$$R_m=0.9886+0.1278P_v$$

(13)

d_ε can be estimated by P_v, with formulas as follows.

$$P_v\le 0.5, d_{\text{ε}}=0.0038P_v$$

(14)

$$P_v>0.5, d_{\text{ε}}=0.0038(1-P_v)$$

(15)

According to Formulas (7) to (15), the calculation of land surface emissivity can be simplified as follows:

$$P_v\le 0.5, {\text{ε}}_{vegetation}=-0.0461{P_v}^2+0.0652P_v+0.9625$$

(16)

$${\text{ε}}_{construction}=-0.0663{P_v}^2+0.0854P_v+0.9589$$

(17)

$$P_v>0.5, {\text{ε}}_{vegetation}=-0.0461{P_v}^2+0.0576P_v+0.9663$$

(18)

$${\text{ε}}_{construction}=-0.0663{P_v}^2+0.0778P_v+0.9627$$

(19)

2.4.4. Atmospheric Transmittance (τ) Calculation

According to atmospheric transmittance estimating equations [41], under the precondition of a high temperature in summer, the relations between the atmospheric transmittance (τ) and atmospheric moisture content (ω) are as follows.

$$0.2<\text{ω}\le 1.6, \text{τ}=0.9184-0.0725\text{ω}$$

(20)

$$1.6<\text{ω}\le 4.4, \text{τ}=1.0163-0.1330\text{ω}$$

(21)

Because this is a good linear relationship between atmospheric moisture content (ω) and ground vapor pressure (e) [48], the following empirical formula is used to calculate atmospheric moisture content.

$$W=a_0+a_{1}e$$

(22)

For the Xuzhou area, a₀ = 0.0397 and a₁ = 0.1681. According to the Xuzhou climate year data set from the China Meteorological Data Sharing Service System, the average ground vapor pressure of 2013 and 2014 are shown in Table 2.

Land surface temperature images from four periods from 2013 to 2014 were calculated using the mono-window algorithm. According to the results of the land use classification, the boundary of the urban area mainly covered by construction land was extracted. The boundary has already been shown in Figure 1. The vector boundary of the urban area was used to mask LST images; then, the temperature and geographic coordinate data for each pixel were exported. Finally, the land surface temperature data were obtained. The land surface temperature distribution is shown in Figure 3.

Figure 3. (a) Land surface temperature distribution on 21 May 2013; (b) 03 September 2013; (c) 01 May 2014; (d) 22 September 2014.

Figure 3. (a) Land surface temperature distribution on 21 May 2013; (b) 03 September 2013; (c) 01 May 2014; (d) 22 September 2014.

2.5. Urban Land Surface Moisture Inversion

Tasseled cap transformation (TCT) was first put forward by Kauth and Thomas in 1976 [49], it is a useful tool for compressing spectral data into a few bands associated with physical scene characteristics with minimal information loss [50]. The first study on calculating TCT for TM data was conducted by Crist and Cicone [51], who also derived the Landsat TM TCT index. After Landsat 8 had been successfully launched, there was little research on a TCT index for Landsat 8 OLI data until Baig [50] derived new TCT coefficients that were more representative of vegetation and other land cover types. In this research, the moisture component of TCT was needed to extract the index of urban land surface moisture. The moisture coefficients of TCT for Landsat 8 OLI data are shown in Table 3.

Table 3. Moisture coefficients of TCT for Landsat 8 OLI data [50].

Component	Band 2	Band 3	Band 4	Band 5	Band 6	Band 7
Wetness(Moisture)	0.1511	0.1973	0.3283	0.3407	−0.7117	−0.4559
Greenness	−0.2941	−0.243	−0.5424	0.7276	0.0713	−0.1608

Table 3. Moisture coefficients of TCT for Landsat 8 OLI data [50].

Component	Band 2	Band 3	Band 4	Band 5	Band 6	Band 7
Wetness(Moisture)	0.1511	0.1973	0.3283	0.3407	−0.7117	−0.4559
Greenness	−0.2941	−0.243	−0.5424	0.7276	0.0713	−0.1608

For Landsat 8 images, the original DN value range of each band was from 1 to 65355. Because this would lead to the band math results being too high to be analyzed conveniently, the following formula was used to simplify the DN value range before tasseled cap transformation was performed.

$$D{N}_{new}=\left(\frac{QCAL}{QCA{L}_{max}-QCA{L}_{min}}\right)\times 255$$

(23)

After tasseled cap transformation was completed, the images of the moisture component were obtained and then masked with the vector boundary of the urban area, which was extracted in Chapter 2.3.5, to produce moisture images of the urban area. After the moisture and geographic coordinate data of each pixel were exported, the urban land surface moisture (ULSM) data were finally obtained.

3. Results

3.1. The Trend of the Influence of Urban Land Surface Moisture on the Land Surface Temperature

To investigate the influence of urban land surface moisture on the land surface temperature, a 2D scatter diagram of the LST vs. ULSM was made for each period to reflect the relationship between the two indicators. Because water bodies have obvious effects on the LST, water bodies in LST and ULSM images were masked before a 2D scatter diagram was made. The results are shown in Figure 4.

Figure 4. (a) 2D scatterplot of the LST vs. ULSM on 21 May 2013; (b) 03 September 2013; (c) 01 May 2014; (d) 22 September 2014. The blue curve is the fitting curve of polynomial fitting of degree 4.

Figure 4. (a) 2D scatterplot of the LST vs. ULSM on 21 May 2013; (b) 03 September 2013; (c) 01 May 2014; (d) 22 September 2014. The blue curve is the fitting curve of polynomial fitting of degree 4.

The scatter diagrams show that when ULSM reaches a particular value, the land surface temperature increases with the increase of ULSM; the areas in which the ULSM value is greater than this particular value can be called the “Effective Moisture Area”. The definition of the “Effective Moisture Area” is that it is a region with a high ULSM value that can have an alleviation effect on its own land surface temperature. To extract the “Effective Moisture Area”, polynomial fitting was performed on scatterplots by using Matlab 2013b. Polynomial fitting of degree 4 was chosen as the best fit. The results of polynomial fitting are shown in Table 4, and the fitting curves are drawn in Figure 4.

Table 4. The coefficient of polynomial fitting.

	Coefficient	a4(x4)	a3(x3)	a2(x2)	a1(x)	a0	R2
	Date
21 May 2013		−9.460 × 10−5	−0.008275	−0.2269	−2.0720	309.1	0.5129
03 September 2013		−7.8330 × 10−7	−0.007263	−0.2017	−1.618	309.0	0.5006
01 May 2014		−1.8850 × 10−4	−0.0002262	−0.1283	−1.519	303.1	0.5043
22 September 2014		−7.5600 × 10−4	0.01293	−0.0685	−1.459	302.1	0.3599

Table 4. The coefficient of polynomial fitting.

	Coefficient	a4(x4)	a3(x3)	a2(x2)	a1(x)	a0	R2
	Date
21 May 2013		−9.460 × 10−5	−0.008275	−0.2269	−2.0720	309.1	0.5129
03 September 2013		−7.8330 × 10−7	−0.007263	−0.2017	−1.618	309.0	0.5006
01 May 2014		−1.8850 × 10−4	−0.0002262	−0.1283	−1.519	303.1	0.5043
22 September 2014		−7.5600 × 10−4	0.01293	−0.0685	−1.459	302.1	0.3599

It can be seen from Figure 4 that all of the fitting curves in (a) to (d) begin to decline after a particular extreme value point has been reached. This extreme value point can be obtained by calculating the roots of the first derivative of the fitting curve function. Setting the first derivative function equal to 0 and solving for its roots, the x values of the extreme points of the fitting curves were derived and are shown in Table 5.

Table 5. The x value of extreme value point.

Date	x Value of Extreme Point
21 May 2013	−6.8903
3 September 2013	−5.5328
1 May 2014	−6.3189
22 September 2014	−5.6224

Table 5. The x value of extreme value point.

Date	x Value of Extreme Point
21 May 2013	−6.8903
3 September 2013	−5.5328
1 May 2014	−6.3189
22 September 2014	−5.6224

The areas in which pixel values were greater than the x value of the extreme point in the ULSM images, the “Effective Moisture Areas”, were extracted. This demonstrates that urban land surface moisture has a negative influence on land surface temperature within a certain range.

3.2. The Effect of ULSM on the LST of Surrounding Areas

3.2.1. “High Efficiency Moisture Areas” Extraction

Because it was demonstrated that ULSM has a negative influence on the LST in the “Effective Moisture Area”, the effect of the influence of “Effective Moisture Area” on the land surface temperature of its surrounding areas was studied further. Because not all “Effective Moisture Areas” had significant effects on the land surface temperature in the surrounding areas, the average value of ULSM in the “Effective Moisture Areas” was calculated; then; the areas in which their ULSM value reached the average level were extracted (Table 6). These areas were defined as “High Efficiency Moisture Areas”.

Table 6. The average value of ULSM in “Effective Moisture Areas”.

Date	The Average Value of ULSM
21 May 2013	−0.7009
03 September 2013	0.0628
01 May 2014	−0.3129
22 September 2014	−0.6986

Table 6. The average value of ULSM in “Effective Moisture Areas”.

Date	The Average Value of ULSM
21 May 2013	−0.7009
03 September 2013	0.0628
01 May 2014	−0.3129
22 September 2014	−0.6986

A “High Efficiency Moisture Area” is a region in which the ULSM value is high enough to have obvious effects on the land surface temperatures of its surrounding areas within a certain radius. The difference between a “High Efficiency Moisture Area” and an “Effective Moisture Area” is that the former’s ULSM value is higher, which not only can reduce its own temperature but also has an alleviating effect on the temperature of the surrounding areas within a certain radius. To demonstrate the differences of land cover types between “High Efficiency Moisture Areas” and other areas, some typical areas were chosen on Google Earth. Figure 5 shows that the land cover types for “High Efficiency Moisture Areas” were mostly vegetation and water bodies, and the other areas were mostly construction land.

Figure 5. Typical areas of “High Efficiency Moisture Areas” and other areas. The pictures were extracted from Google Earth, and the pictures were taken on 14 December 2014.

Figure 5. Typical areas of “High Efficiency Moisture Areas” and other areas. The pictures were extracted from Google Earth, and the pictures were taken on 14 December 2014.

To analyze the effects of the influence of “High Efficiency Moisture Areas” on the land surface temperatures of the surrounding areas, “High Efficiency Moisture Areas” were set as core areas and then 5 buffer zones were established outward every 30 m using ArcGIS. The buffer zones of “High Efficiency Moisture Areas” are shown in Figure 6.

Figure 6. (a) Buffer zones of “High Efficiency Moisture Areas” on 21 May 2013; (b) 3 September 2013; (c) 1 May 2014; (d) 22 September 2014.

Figure 6. (a) Buffer zones of “High Efficiency Moisture Areas” on 21 May 2013; (b) 3 September 2013; (c) 1 May 2014; (d) 22 September 2014.

3.2.2. The Regression Analysis between the Changes of LST and ULSM in “High Efficiency Moisture Areas” and Their Surrounding Areas

To explore the changing situation of LST and ULSM in core areas and buffer zones, the vector data of the core areas and buffer zones were overlaid onto LST images and ULSM images; then, statistical analyses of average values of LST and ULSM were performed in the core areas and for each layer of the buffer zones. The results are shown in Figure 7.

Two types of trends can be seen in Figure 7: (1) The ULSM average value of the core areas has the highest value, and the average value declines with increasing distance from the core region; (2) the LST average value of the core area has the lowest value, and the average value increases with increasing distance from the core region. It can be seen that the LST average value increases, whereas the ULSM average value declines.

To determine if ULSM value has a negative effect on the LST of the surrounding environment, the outer buffer layer’s ULSM average value was subtracted from the inner buffer layer’s ULSM average value from the core areas to the last layer of the buffer zones. The ULSM Declining value (ULSMD) of each of two adjacent layers was thus obtained. Then, the LST increasing (LSTI) value of each of two adjacent layers was calculated by using the same method. Finally, a 2D scatterplot of ULSMD and LSTI was made and linear fitting was performed, with the result shown in Figure 8.

Figure 7. Average value of the land surface temperature and urban land surface moisture in core areas and in each layer of the buffer zones. The zero point on the x axis refers to a core area.

Figure 7. Average value of the land surface temperature and urban land surface moisture in core areas and in each layer of the buffer zones. The zero point on the x axis refers to a core area.

Figure 8. Fitting curve of the LST increasing value vs. the ULSM declining value.

Figure 8. Fitting curve of the LST increasing value vs. the ULSM declining value.

In Figure 8, the result of the linear fit between the LST increasing value and the ULSM declining value is that there is a significant positive correlation between the values of these two indices. Areas with higher ULSM values have a larger cooling effect on the surrounding areas. In addition, within a certain radius, the greater the difference of ULSM value between neighboring areas, the more obvious the LST change.

3.3. The LST Alleviation Effect Comparison with Several Commonly Used Indices

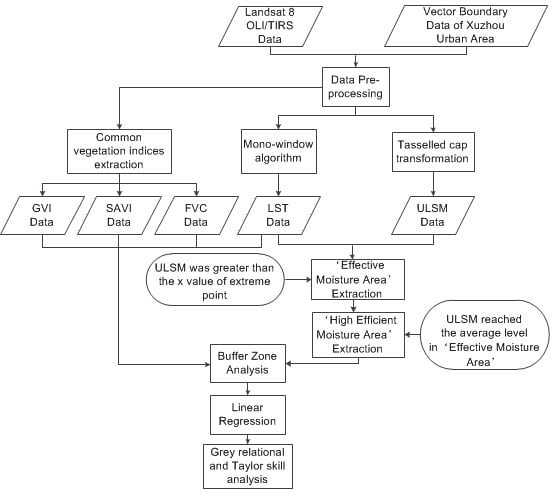
3.3.1. Comparative Indicators Selection

Previous studies have shown that vegetation has a very important effect on land surface temperatures in urban areas [12,14,20]. Latent heat exchange is higher in areas of urban regions with concentrated vegetation [52]. Studies have shown that the fractional vegetation cover (FVC) index [53], soil adjusted vegetation index (SAVI) [54] and Greenness vegetation index (GVI) [51] have a negative correlation relationship with the land surface temperature [21,22,55]. Therefore, the effect of the influence of ULSM, FVC, SAVI and GVI on the land surface temperature is a question that needs to be further studied. The equation for FVC is shown as formula 10 (P_V), the equation for GVI is shown in Table 3 (Greenness), and the algorithm for SAVI [21] is as follows.

$$SAVI=\frac{{\text{ρ}}_{nir}-{\text{ρ}}_{red}}{{\text{ρ}}_{nir}+{\text{ρ}}_{red}+L}\left(1+L\right)$$

(24)

where ρ_nir is near red band reflectance (band 5), ρ_red is red band reflectance (band 4) and L is an adjustment factor, set to minimum background effects (L = 0.5).

Figure 9 shows that on the whole, GVI, SAVI and FVC decrease as the distance increases from the core areas. The value changes of GVI, SAVI and FVC compared with the changes of the land surface temperature in each layer of the buffer zones were basically the opposite.

Figure 9. (a) GVI average value in the core areas and each layer of the buffer zones; (b) SAVI average value in the core areas and each layer of the buffer zones; (c) FVC average value in the core areas and each layer of the buffer zones. The zero points on the x axis refers to core areas.

Figure 9. (a) GVI average value in the core areas and each layer of the buffer zones; (b) SAVI average value in the core areas and each layer of the buffer zones; (c) FVC average value in the core areas and each layer of the buffer zones. The zero points on the x axis refers to core areas.

3.3.2. Indices Normalized and Univariate Linear Regression Analysis

After the GVI, SAVI and FVC average values of the core areas and each layer of the buffer zones were extracted, the declining value of these three indices in each layer were calculated using the inner average value minus the outer average value in turn from the core areas to the last layer of the buffer zones. To compare the influence of the four indices on the land surface temperatures of the surrounding areas, normalized processing was used to eliminate the influence of the magnitude order. For instance, normalized processing of the SAVI declining value was as follows.

$$SAVI{D}_N=\frac{SAVID-SAVI{D}_{min}}{SAVI{D}_{max}-SAVI{D}_{min}}$$

(25)

SAVID is the declining value of SAVI, SAVID_N is the normalized processing value of SAVID, SAVID_MIN is the minimum value of SAVID and SAVID_MAX is the minimum value of SAVID. The normalized processing declining value of ULSM, GVI, SAVI, and FVC and the increasing value of LST are shown in Table 7.

Table 7. The normalized processing value of ULSMD, GVID, SAVID, FVCD and LSTI. C refers to core area, L_i (i = 1,2,3,4,5) refer to each layer of buffer zones.

Index	21 May 2013					03 September 2013
	C-L1	L1-L2	L2-L3	L3-L4	L4-L5	C-L1	L1-L2	L2-L3	L3-L4	L4-L5
ULSMDN	0.9274	0.4549	0.1303	0.0121	0.0473	0.8956	0.4340	0.1253	0.0582	0.0019
GVIDN	0.7923	0.7452	0.2729	0.0975	0.1350	0.7319	1.0000	0.3620	0.1822	0.0000
SAVIDN	0.9207	0.7970	0.2640	0.0990	0.1237	0.5966	1.0000	0.3456	0.1718	0.0000
FVCDN	1.0000	0.4240	0.1257	0.0645	0.0680	0.9605	0.6231	0.1853	0.0960	0.0000
LSTIN	1.0000	0.3048	0.1382	0.0075	0.0485	0.7290	0.3086	0.1564	0.0814	0.0000
Index	01 May 2014					22 September 2014
	C-L1	L1-L2	L2-L3	L3-L4	L4-L5	C-L1	L1-L2	L2-L3	L3-L4	L4-L5
ULSMDN	1.0000	0.4129	0.0971	0.0463	0.0000	0.7473	0.3324	0.1091	0.0618	0.0286
GVIDN	0.7463	0.7175	0.2576	0.1445	0.0431	0.1951	0.2691	0.1907	0.1578	0.0869
SAVIDN	0.5781	0.7439	0.2583	0.1439	0.0392	0.3146	0.0920	0.1058	0.1224	0.0734
FVCDN	0.8599	0.3868	0.1235	0.0772	0.0288	0.1631	0.1381	0.0696	0.0664	0.0490
LSTIN	0.8840	0.2858	0.1342	0.0681	0.0007	0.6386	0.1961	0.1004	0.0592	0.0182

Table 7. The normalized processing value of ULSMD, GVID, SAVID, FVCD and LSTI. C refers to core area, L_i (i = 1,2,3,4,5) refer to each layer of buffer zones.

Index	21 May 2013					03 September 2013
	C-L1	L1-L2	L2-L3	L3-L4	L4-L5	C-L1	L1-L2	L2-L3	L3-L4	L4-L5
ULSMDN	0.9274	0.4549	0.1303	0.0121	0.0473	0.8956	0.4340	0.1253	0.0582	0.0019
GVIDN	0.7923	0.7452	0.2729	0.0975	0.1350	0.7319	1.0000	0.3620	0.1822	0.0000
SAVIDN	0.9207	0.7970	0.2640	0.0990	0.1237	0.5966	1.0000	0.3456	0.1718	0.0000
FVCDN	1.0000	0.4240	0.1257	0.0645	0.0680	0.9605	0.6231	0.1853	0.0960	0.0000
LSTIN	1.0000	0.3048	0.1382	0.0075	0.0485	0.7290	0.3086	0.1564	0.0814	0.0000
Index	01 May 2014					22 September 2014
	C-L1	L1-L2	L2-L3	L3-L4	L4-L5	C-L1	L1-L2	L2-L3	L3-L4	L4-L5
ULSMDN	1.0000	0.4129	0.0971	0.0463	0.0000	0.7473	0.3324	0.1091	0.0618	0.0286
GVIDN	0.7463	0.7175	0.2576	0.1445	0.0431	0.1951	0.2691	0.1907	0.1578	0.0869
SAVIDN	0.5781	0.7439	0.2583	0.1439	0.0392	0.3146	0.0920	0.1058	0.1224	0.0734
FVCDN	0.8599	0.3868	0.1235	0.0772	0.0288	0.1631	0.1381	0.0696	0.0664	0.0490
LSTIN	0.8840	0.2858	0.1342	0.0681	0.0007	0.6386	0.1961	0.1004	0.0592	0.0182

Univariate linear regression analysis was used between LSTI_N and ULSM_N, GVI_N, SAVI_N, and FVCD_N. The results of the regression analysis are shown in Figure 10 and Table 8.

Figure 10. (a) Linear regression between LSTI_N and ULSMD_N; (b) Linear regression between LSTI_N and GVID_N; (c) Linear regression between LSTI_N and SAVID_N; (d) Linear regression between LSTI_N and FVCD_N.

Figure 10. (a) Linear regression between LSTI_N and ULSMD_N; (b) Linear regression between LSTI_N and GVID_N; (c) Linear regression between LSTI_N and SAVID_N; (d) Linear regression between LSTI_N and FVCD_N.

Table 8. Result of regression analysis between LSTI_N and ULSMD_N, GVID_N, SAVID_N, FVCD_N.

Index	Correlation Coefficient	Regression Equation	RMSE	P-Value
LSTIN vs. ULSMDN	0.9790	y1 = 0.8804 x1 − 0.0027	0.0642	6.99 × 10−14 < 0.05
LSTIN vs. GVIDN	0.7031	y2 = 0.7035 x2 + 0.0073	0.2240	5.44 × 10−4 < 0.05
LSTIN vs. SAVIDN	0.6921	y3 = 0.6725 x3 + 0.0297	0.2274	7.21 × 10−4 < 0.05
LSTIN vs. FVCDN	0.8939	y4 = 0.8430 x4 + 0.0256	0.1412	1.09 × 10−7 < 0.05

Table 8. Result of regression analysis between LSTI_N and ULSMD_N, GVID_N, SAVID_N, FVCD_N.

Index	Correlation Coefficient	Regression Equation	RMSE	P-Value
LSTIN vs. ULSMDN	0.9790	y1 = 0.8804 x1 − 0.0027	0.0642	6.99 × 10−14 < 0.05
LSTIN vs. GVIDN	0.7031	y2 = 0.7035 x2 + 0.0073	0.2240	5.44 × 10−4 < 0.05
LSTIN vs. SAVIDN	0.6921	y3 = 0.6725 x3 + 0.0297	0.2274	7.21 × 10−4 < 0.05
LSTIN vs. FVCDN	0.8939	y4 = 0.8430 x4 + 0.0256	0.1412	1.09 × 10−7 < 0.05

It can be seen from Figure 10 and Table 8 that these four indices all have significant linear positive correlation with LSTI_N within the confidence interval of 95%. In addition, LSTI_N and ULSMD_N have the best fitting effect with the highest correlation coefficient value of 0.9790 and the lowest RMSE value of 0.0642. On the other hand, LSTI_N and SAVID_N have a poor fitting effect, with a lowest correlation coefficient value of 0.6921 and a highest RMSE value of 0.2274 compared with the other three indices. The univariate regression analysis reveals that the change of ULSM has a high correlation with the change of the land surface temperature in the surrounding areas.

3.3.3. Grey Relational and Taylor Skill Analysis

The fact that the declining value of ULSM had a higher correlation with the increasing value of the land surface temperature cannot statistically prove that the ULSM is more important than other indices of GVI, SAVI and FVC. Therefore, grey relational analysis was chosen for multi-factor correlation analysis.

Grey relational analysis was first put forward by Julong Deng [56]. It is applied to measure the correlation degree between different factors based on similarity in the developing trends of these factors. Because the increasing value of the LST and the declining value of ULSM, GVI, SAVI and FVC have linear positive relationships, grey relational analysis was thought to be very suitable for calculating the various influence degrees of ULSM, GVI, SAVI, and FVC on land surface temperature changes. According to the regression equation in Table 6, the LSTI_N predicted values (y₁, y₂, y₃, y₄) were calculated through ULSMD_N (x₁), GVID_N (x₂), SAVID_N (x₃) and FVCD_N (x₄), and then, 20 predicted data points for each index were exported in the order of time and buffer hierarchy (Figure 11).

The variation trend of the ULSMD_N predicted value was closest to the variation trend of the LSTI normalized index compared to the predicted value of the other three indices. In the theory of grey relational analysis, the correlation degree is in essence the difference of the geometric shape between different curves. Thus, the difference between different curves can be used to measure the relation degree. For instance, in Figure 11, for x = 1, when the values of y₀(1), y₁(1), y₂(1), y₃(1), and y₄(1) are obtained, the difference between y₀(1) and y_i(1) (i = 1,2,3,4) can be described as the difference between curve 0 and curve i at x = 1. For a standard data array y₀ with several comparison data arrays y₁, y₂, …, y_n, the association coefficient ξ (y_i) between the standard data array and each comparison data array in each moment (that is, each calibration on the x axis) can be calculated by the following formula.

$$\text{ξ}\left(k\right)=\frac{{}^{min}{}_{i k }{}^{ min}|y_0\left(k\right)-y_i\left(k\right)|+{\text{ρ}}^{max} {}_{i k }{}^{max}|y_0\left(k\right)-y_i\left(k\right)|}{|y_0\left(k\right)-y_i\left(k\right)|+{\text{ρ}}^{max} {}_{i k }{}^{max}|y_0\left(k\right)-y_i\left(k\right)|}$$

(26)

Figure 11. Change trends of the LSTI_N predicted value and the LSTI_N observation value.

Figure 11. Change trends of the LSTI_N predicted value and the LSTI_N observation value.

This formula gives the association coefficient of y_i for y₀ in k moment. y₀(k) refers to LSTI_N; y_i(k) (i = 1,2,3,4) refers to the predicted value of LSTI_N calculated by ULSMD_N, GVID_N, SAVID_N and FVCD_N; k refers to each point in the curve (k = 1,2,3,…,20); and ρ refers to the resolution coefficient, generally chosen as ρ = 0.5. The association coefficient of each data array in each moment has been shown in Table 9.

Table 9. The association coefficient of each data array.

k	ξ1(k)	ξ2(k)	ξ3(k)	ξ4(k)
1	0.5711	0.3626	0.4136	0.6541
2	0.7277	0.5223	0.4872	0.7605
3	0.9057	0.8032	0.7830	0.9763
4	0.9999	0.7846	0.7369	0.7741
5	0.9641	0.8229	0.7948	0.8788
6	0.8144	0.5453	0.4539	0.7000
7	0.7786	0.3812	0.3863	0.5055
8	0.8366	0.7019	0.7016	0.9079
9	0.8841	0.8219	0.7961	0.9087
10	0.9975	0.9730	0.8942	0.9071
11	0.9766	0.4133	0.3472	0.6505
12	0.7684	0.5228	0.5038	0.7903
13	0.8289	0.8213	0.7827	0.9843
14	0.8929	0.8597	0.8105	0.9175
15	0.9882	0.8715	0.8184	0.8348
16	0.9386	0.3339	0.3840	0.3426
17	0.7260	0.9998	0.7038	0.8221
18	0.9738	0.8592	1.0000	0.9409
19	0.9721	0.8085	0.8254	0.9180
20	0.9846	0.8326	0.8036	0.8362
Average	0.8765	0.7021	0.6714	0.8005

Table 9. The association coefficient of each data array.

k	ξ1(k)	ξ2(k)	ξ3(k)	ξ4(k)
1	0.5711	0.3626	0.4136	0.6541
2	0.7277	0.5223	0.4872	0.7605
3	0.9057	0.8032	0.7830	0.9763
4	0.9999	0.7846	0.7369	0.7741
5	0.9641	0.8229	0.7948	0.8788
6	0.8144	0.5453	0.4539	0.7000
7	0.7786	0.3812	0.3863	0.5055
8	0.8366	0.7019	0.7016	0.9079
9	0.8841	0.8219	0.7961	0.9087
10	0.9975	0.9730	0.8942	0.9071
11	0.9766	0.4133	0.3472	0.6505
12	0.7684	0.5228	0.5038	0.7903
13	0.8289	0.8213	0.7827	0.9843
14	0.8929	0.8597	0.8105	0.9175
15	0.9882	0.8715	0.8184	0.8348
16	0.9386	0.3339	0.3840	0.3426
17	0.7260	0.9998	0.7038	0.8221
18	0.9738	0.8592	1.0000	0.9409
19	0.9721	0.8085	0.8254	0.9180
20	0.9846	0.8326	0.8036	0.8362
Average	0.8765	0.7021	0.6714	0.8005

Finally, the relation degrees were derived by calculating the average value of the association coefficients of each data array. The performance of four types of predicted results are presented in an adjusted Taylor diagram (Figure 12).

Figure 12. Performance of the predicted values calculated by four indices (the statistics in the Taylor diagram); an ideal model would have a standard deviation ratio (σ_norm) of 1.0 and a correlation coefficient of 1.0 (REF is the reference point).

Figure 12. Performance of the predicted values calculated by four indices (the statistics in the Taylor diagram); an ideal model would have a standard deviation ratio (σ_norm) of 1.0 and a correlation coefficient of 1.0 (REF is the reference point).

In this research, the Taylor diagram was adjusted by changing the correlation coefficient axis into a grey relation degree axis. A single point indicates the grey relation degree (R_d = ξ) and the ratio of the standard deviations (σ) between the prediction (σ_p) and the observation (σ_o) (σ_norm = σ_p/σ_o). An ideal model would have a standard deviation ratio of 1.0 and a grey relation degree of 1.0, i.e., the reference point (REF) on the x axis [57]. Taylor skill (S) is a single value summary of a Taylor diagram where unity indicates perfect agreement with observations. Traditionally, skill scores have been defined to vary from 0 (least skillful) to 1 (most skillful), each point for any arbitrary data group [58,59] can be scored as follows:

$$S=\frac{2\left(1+R_d\right)}{{\left({\sigma }_{norm}+1/{\sigma }_{norm}\right)}^2}$$

(27)

The calculation results of ξ, σ_norm, and S are shown in Table 10.

Table 10. The association coefficient of each data array.

Indicator	y1	y2	y3	y4
σnorm (σp/σo)	0.9790	0.7031	0.6921	0.8939
Rd (ξ)	0.8765	0.7021	0.6714	0.8005
Taylor skill (S)	0.9378	0.7536	0.7320	0.8890

Table 10. The association coefficient of each data array.

Indicator	y1	y2	y3	y4
σnorm (σp/σo)	0.9790	0.7031	0.6921	0.8939
Rd (ξ)	0.8765	0.7021	0.6714	0.8005
Taylor skill (S)	0.9378	0.7536	0.7320	0.8890

4. Discussion

In polynomial regressions, before the ULSM values reached the inflection value, the LST showed no obvious relationship with ULSM. This phenomenon is due to the urban land cover type of an impervious surface area (ISA) [3,60]. In comparison with vegetation, soil and water, the ULSM value of ISA is lowest because there is scarcely any water content in ISA, and ISA has a positive effect on the LST [61]; therefore, the ULSM index that was extracted from ISA pixels has no effect on the LST.

For the linear regression between four indices change values and LST change values, the change value of the common vegetation indices GVI, SAVI and FVC showed a good fit with the LST increasing value (LSTI), especially the declining value of FVC. This is consistent with Gao [21], Ma [22], and Xu’s research conclusions [55]. However, the ULSM declining value (ULSMD) showed the best simulating effect with LSTI, with the highest correlation coefficient of 0.9790 and the lowest root-mean-square error of 0.0642. The order of the grey relation degrees was ξ₁ > ξ₄ > ξ₂ > ξ₃, which means that the predicted value of LSTI calculated from the value of ULSMD has the highest relation degree with the observations of LSTI. The order of Taylor skill was also S₁ > S₄ > S₂ > S₃. In comparison with the other three vegetation prediction models, the ULSM prediction model is most skillful.

Whether from the results of the regression analysis with the land surface temperature or from the prediction results of the land surface temperature change values, the simulation effect of ULSM was better in comparison with the other three vegetation indices. Therefore, ULSM might be a better index for reflecting land surface temperature changes in urban areas.

There was another notable result, that of the three vegetation indices, FVC showed a better performance in the land surface temperature simulation. The correlation coefficient, the grey relation degree and Taylor skill values between the FVC declining value and LST increasing value were 0.8939, 0.8005, and 0.8890. Those values were significantly higher than the results of GVI and SAVI, so FVC is also an effective index for indicating land surface temperature change.

Finally, it can be concluded that the areas (vegetation or water bodies) that have the power to reduce UHI effects can be comprehensively extracted by using the ULSM index, and the reduction can also be expressed by the value of ULSM. In addition, the simulation result for urban land surface temperature regulation effects obtained by using the ULSM index is better than that achieved by using common vegetation indices.

5. Conclusions

As a new index for indicating the alleviation effects of urban heat islands, the urban land surface moisture (ULSM) index extracted from Landsat 8 images has shown good correlation with land surface temperatures. Comparisons with GVI, SAVI and FVC have been carried out based on regression analysis and buffer analysis, showing the following characteristics of ULSM. (1) In a particular urban area, ULSM has no obvious effect on the land surface temperature unless its value has reached an inflection point; when the ULSM value is above the value of an inflection point, it will have a significant regulating effect on the land surface temperature; (2) When a region’s ULSM value reaches the average level above the inflection point, ULSM can also have an obvious temperature lowering effect on the region’s surrounding areas within a particular radius. Therefore, the change of the ULSM value can be an indicator of the land surface temperature change; (3) Comparing the temperature lowering effects of ULSM with the other three common vegetation indices, FVC, SAVI, and GVI, the grey correlation degrees and Taylor skill scores demonstrate that the lowering effect of ULSM on the environmental temperature is most obvious and that the contribution of ULSM to the alleviation effects of urban heat islands is more significant.

This study of urban land surface moisture suggests that ULSM can be an effective index for exploring alleviation mechanisms for urban heat islands. One future research direction is studying the cooling effect of ULSM over a longer time scale and a broader regional scale. Other worthwhile future research should to develop a more accurate algorithm for extracting land surface moisture information in different urban areas.