The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses
Abstract
:1. Introduction
2. Study Area and Data Source


| Sensor | ALS60 |
|---|---|
| Data capture date | 9/12/2012 |
| Total number of points | 5,875,674 |
| Minimum height (m) | 162.140 |
| Maximum height (m) | 208.990 |
| Median height (m) | 179.264 |
| Average point density (pts/m2) | 35.480 |
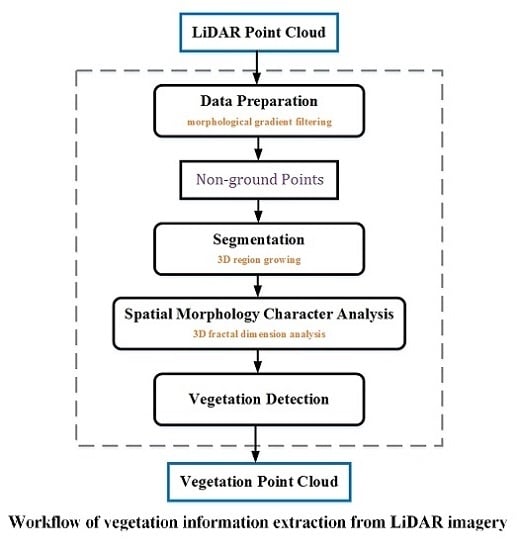
3. Methods

3.1. LiDAR Data Preparation

3.2. Three-Dimensional Fractal Dimension

3.3. Region Segmentation and 3D Fractal Dimension Analysis

| High Density | Medium Density | Low Density | |
|---|---|---|---|
| Point density (pts/m2) | ≥20 | 5–20 | ≤5 |


4. Results and Discussion
4.1. Vegetation Extraction Results



4.2. Accuracy Assessment
| Classification Results | |||
|---|---|---|---|
| Tall Trees | Non-Tall Trees | ||
| Reference data | Tall trees | A | B |
| Non-tall trees | C | D | |
| Classification Results | |||
|---|---|---|---|
| Tall Trees | Non-Tall Trees | ||
| Reference data | Tall trees | 3093606 | 137046 |
| Non-tall trees | 252747 | 994201 | |
| Completeness | 95.57% | Results | 91.83% |
| Index Kappa | 0.8006 | ||
4.3. Error Analysis and Discussion

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bienert, A.; Scheller, S.; Keane, E.; Mohan, F.; Nugent, C. Tree detection and diameter estimations by analysis of forest terrestrial laserscanner point clouds. In Proceedings of the ISPRS Workshop on Laser Scanning, Espoo, Finland, 12–14 September 2007; pp. 50–55.
- Elseberg, J.; Borrmann, D.; Nuchter, A. Full wave analysis in 3D laser scans for vegetation detection in urban environments. In Proceedings of the Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 27–29 October 2011; pp. 1–7.
- Hilker, T.; Coops, N.C.; Coggins, S.B.; Wulder, M.A.; Brown, M.; Black, T.A.; Nesic, Z.; Lessard, D. Detection of foliage conditions and disturbance from multi-angular high spectral resolution remote sensing. Remote Sens. Environ. 2009, 113, 421–434. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, G.A.; Castro, K.; Wright, S.J.; Gamon, J.; Kalacska, M.; Rivard, B.; Schnitzer, S.A.; Feng, J.L. Differences in leaf traits, leaf internal structure, and spectral reflectance between two communities of lianas and trees: Implications for remote sensing in tropical environments. Remote Sens. Environ. 2009, 113, 2076–2088. [Google Scholar] [CrossRef]
- Wilson, B.A.; Brocklehurst, P.S.; Clark, M.J.; Dickinson, K. Vegetation survey of the Northern Territory, Australia; Technical Report for Explanatory Notes and 1:1,000,000 Map Sheets; Conservation Commission of the Northern Territory Australia: Palmerston, Australia, 1990. [Google Scholar]
- Wood, E.M.; Pidgeon, A.M.; Radeloff, V.C.; Keuler, N.S. Image texture as a remotely sensed measure of vegetation structure. Remote Sens. Environ. 2012, 121, 516–526. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Combining object-based texture measures with a neural network for vegetation mapping in the Everglades from hyperspectral imagery. Remote Sens. Environ. 2012, 124, 310–320. [Google Scholar] [CrossRef]
- Han, W.; Zhao, S.; Feng, X.; Chen, L. Extraction of multilayer vegetation coverage using airborne LiDAR discrete points with intensity information in urban areas: A case study in Nanjing, China. Int. J. Appl. Earth Obs. Geoinform. 2014, 30, 56–64. [Google Scholar] [CrossRef]
- Hyyppa, J. Feasibility for estimation of single tree characteristics using laser scanner. In Proceedings of Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; pp. 981–983.
- Wagner, W.; Hollaus, M.; Briese, C.; Ducic, V. 3D vegetation mapping using small-footprint full-waveform airborne laser scanners. Int. J. Remote Sens. 2008, 29, 1433–1452. [Google Scholar] [CrossRef]
- Ackermann, F. Airborne laser scanning—Present status and future expectations. ISPRS J. Photogramm. Remote Sens. 1999, 54, 64–67. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Li, W.; Dai, H. A multiresolution hierarchical classification algorithm for filtering airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 1–9. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Zhang, L.; Wu, J. An object-based two-stage method for a detailed classification of urban landscape components by integrating airborne LiDAR and color infrared image data: A case study of downtown Houston. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009; pp. 1–8.
- Sánchez-Lopera, J.; Lerma, J.L. Classification of LiDAR bare-earth points, buildings, vegetation, and small objects based on region growing and angular classifier. Int. J. Remote Sens. 2014, 35, 6955–6972. [Google Scholar] [CrossRef]
- Lafarge, F.; Mallet, C. Modeling Urban Landscapes from Point Clouds: A Generic Approach; Technical Report for Vision, Perception and Multimedia; HAL: Nice, France, 1–5 May 2011. [Google Scholar]
- Rutzinger, M.; Höfle, B.; Geist, T.; Stötter, J. Object based building detection based on airborne laser scanning data within GRASS GIS environment. In Proceedings of the UDMS 2006: Urban Data Management Symposium, Aalborg, Denmark, 15–17 May 2006; pp. 37–48.
- Rutzinger, M.; Höfle, B.; Hollaus, M.; Pfeifer, N. Object-based point cloud analysis of full-waveform airborne laser scanning data for urban vegetation classification. Sensors 2008, 8, 4505–4528. [Google Scholar] [CrossRef]
- Kim, H.B.; Sohn, G. Random forests-based multiple classifier system for power-line scene classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII-5/W12, 253–259. [Google Scholar] [CrossRef]
- Xu, G.S.; Vosselman, S.; Elberink, O. Multiple-entity based classification of airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 88, 1–15. [Google Scholar] [CrossRef]
- Geerling, G.W.; Labrador Garcia, M.; Clevers, J.G.P.W.; Ragas, A.M.J.; Smits, A.J.M. Classification of floodplain vegetation by data fusion of spectral (CASI) and LiDAR data. Int. J. Remote Sens. 2007, 28, 4263–4284. [Google Scholar] [CrossRef]
- Secord, J.; Zakhor, A. Tree detection in urban regions using aerial LiDAR and image data. IEEE Geosci. Remote Sens. Lett. 2007, 4, 196–200. [Google Scholar] [CrossRef]
- Ramdani, F. Urban vegetation mapping from fused hyperspectral image and LiDAR data with application to monitor urban tree heights. J. Geo. Inf. St. 2013, 5, 404–408. [Google Scholar] [CrossRef]
- Reese, H.; Nordkvist, K.; Nyström, M.; Bohlin, J.; Olsson, H. Combining point clouds from image matching with SPOT 5 multispectral data for mountain vegetation classification. Int. J. Remote Sens. 2015, 36, 403–416. [Google Scholar] [CrossRef]
- Chen, X.; Vierling, L.; Rowell, E.; DeFelice, T. Using LiDAR and effective LAI data to evaluate IKONOS and Landsat 7 ETM+ vegetation cover estimates in a ponderosa pine forest. Remote Sens. Environ. 2004, 91, 14–26. [Google Scholar] [CrossRef]
- Heinzel, J.; Koch, B. Exploring full-waveform LiDAR parameters for tree species classification. Int. J. Appl. Earth Obs. Geoinform. 2011, 13, 152–160. [Google Scholar] [CrossRef]
- Antonarakis, A.S.; Richards, K.S.; Brasington, J. Object-based land cover classification using airborne LiDAR. Remote Sens. Environ. 2008, 112, 2988–2998. [Google Scholar] [CrossRef]
- Höfle, B.; Hollaus, M.; Hagenauer, J. Urban vegetation detection using radiometrically calibrated small-footprint full-waveform airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2012, 67, 134–147. [Google Scholar] [CrossRef]
- Hug, C.; Ullrich, A.; Grimm, A. Litemapper-5600—A waveform-digitizing LiDAR terrain and vegetation mapping system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 24–29. [Google Scholar]
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform LiDAR data for the classification of deciduous and coniferous trees. Int. J. Remote Sens. 2008, 29, 1407–1431. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Forlani, G. Adaptive filtering of aerial laser scanning data. Int. Archiv. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 130–135. [Google Scholar]
- Sohn, G.I.D. Terrain surface reconstruction by the use of tetrahedron model with the MDL criterion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 336–344. [Google Scholar]
- Roggero, M. Object segmentation with region growing and principal component analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 289–294. [Google Scholar]
- Zhang, K.; Chen, S.C.; Whitman, D. A progressive morphological filter for removing nonground measurements from airborne LiDAR data. IEEE Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Yong, L.; Wu, H. DEM extraction from LiDAR data by morphological gradient. In Proceedings of the IEEE Fifth International Joint Conference INC, IMS and IDC, Seoul, Korea, 10 December 2009; pp. 1301–1306.
- Sithole, G.; Vosselman, G. The Full Report: ISPRS Comparison of Existing Automatic Filters. Availbale online: http://www.itc.nl/isprswgIII-3/filtertest/ (accessed on 19 August 2015).
- Mandelbrot, B.D. Fractals: Form, Chance and Dimension, 1st ed.; W.H. Freeman and Company: San Francisco, SF, USA, 1977. [Google Scholar]
- Falconer, K.J. The Geometry of Fractal Sets; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Bisoi, A.K.; Mishra, J. On calculation of fractal dimension of images. Pattern Recog. Lett. 2001, 22, 631–637. [Google Scholar] [CrossRef]
- Fan, J.; Yau, D.Y.; Elmagarmid, A.K.; Aref, W.G. Automatic image segmentation by integrating color-edge extraction and seeded region growing. IEEE Trans. Image Process. 2001, 10, 1454–1466. [Google Scholar] [PubMed]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Chen, W.; Qian, T.; Shen, D.; Wang, J. The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses. Remote Sens. 2015, 7, 10815-10831. https://doi.org/10.3390/rs70810815
Yang H, Chen W, Qian T, Shen D, Wang J. The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses. Remote Sensing. 2015; 7(8):10815-10831. https://doi.org/10.3390/rs70810815
Chicago/Turabian StyleYang, Haiquan, Wenlong Chen, Tianlu Qian, Dingtao Shen, and Jiechen Wang. 2015. "The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses" Remote Sensing 7, no. 8: 10815-10831. https://doi.org/10.3390/rs70810815
APA StyleYang, H., Chen, W., Qian, T., Shen, D., & Wang, J. (2015). The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses. Remote Sensing, 7(8), 10815-10831. https://doi.org/10.3390/rs70810815