Lake Level Estimation Based on CryoSat-2 SAR Altimetry and Multi-Looked Waveform Classification

Abstract

In this study, reliable water levels for four lakes are estimated based on an innovative processing strategy using a semi-automatic CryoSat-2 Synthetic Aperture Radar (SAR) multi-looked waveform classification. The selection of valid water returns is an essential step in inland altimetry applications. In order to identify reliable observations allowing for an accurate retracking, an unsupervised classification method for CryoSat-2 SAR multi-looked waveforms has been developed based on the k-mean algorithm. With this approach, changes in the water surface extent or surrounding inundation areas can be taken into account. In addition, a modified version of the Improved Threshold Retracker is developed in order to obtain optimal results for the lake heights. The used method is based on the identification of the optimal sub-waveform by employing height thresholds. The validation of the derived CryoSat-2 SAR time series with in-situ gauging data yields root mean square (RMS) differences between 3 and 90 cm for the different lakes. Compared to modeled CryoSat-2 water heights derived according to the approach used in the AltWater database our water level time series are slightly improved in terms of RMS accuracy but they contain more gaps due to the lack of reliable observations. In comparison with classical radar altimeter missions such as Envisat or Jason-2, the SAR-based time series show smaller RMS differences for the small lakes but larger RMS differences for the large lakes covered by multiple repeat missions. The presented innovative processing strategy can be easily adopted to other satellite altimetry SAR data such as from the new Sentinel-3 mission.

1. Introduction

Monitoring water levels from lakes, reservoirs and rivers is important for several reasons. The change of terrestrial water balance has an impact on human life since water is used for drinking, irrigation for agriculture, industrial products, etc. Additionally, it holds the risk of flooding of residential areas and plays an essential role in the description of the global water cycle.

In-situ gauging stations allow to observe water levels with high accuracy. Unfortunately, they are expensive and complicated to maintain, especially in remote areas. As a consequence, the number of operational gauges has been decreasing continuously since the 1970s [1]. Alternatively, satellite altimetry is used increasingly to monitor water levels of inland waters from space. The advantages are that no high additional costs arise and that even remote areas can be monitored. The disadvantages are that up to now (1) water level time series derived from satellite alitmetry are not as accurate as gauge data; (2) the temporal resolution is more sparse; (3) small inland water bodies are not always covered by satellites’ observations; and (4) satellite tracks do not cover 100% of the Earth surface.

Formore than 20 years classical radar altimetry has been used to estimate inland water levels, especially lakes (e.g., [2,3,4,5]). The estimation of inland water level variations with radar altimetry is a challenging task, because numerous altimeter waveforms are contaminated by land reflections due to the large altimeter footprint size of up to 15 km in mountainous area. The smaller the footprint size of the satellite altimeter, the less the altimeter waveforms are corrupted by land signals. Thus, even small inland water bodies can be observed reliably. With the launch of the ESA CryoSat-2 satellite in April 2010 a new era in radar altimetry began. It carries for the first time a Synthetic Aperture Interferometric Radar Altimeter (SIRAL) on-board which allows to measure in three different modes: Low Resolution (LR), Synthetic Aperture Radar (SAR) and SAR Interferometer (SARIn). While the LR mode conforms to the classical pulse-limited satellite radar altimeter with a footprint size up to 15 km in mountainous area, the SAR and SARIn mode allow to exploit the full Doppler bandwidth with the Delay-Doppler/SAR altimeter that has a remarkable smaller along-track footprint size of about 0.3 km. Over the oceans and the ice sheet interiors CryoSat-2 operates in LR mode, whereas over sea ice and very few inland lakes and rivers CryoSat-2 operates in SAR mode. Ice sheet margins and mountain glaciers are observed with the SARIn mode. In contrast to most classical altimetry missions, CryoSat-2 uses a long-repeat orbit of 369 days with a sub-cycle of about 30 days. This ensures a dense ground track pattern of about 8 km track distance at the equator. Thus, more lakes are covered by observations. However, the temporal resolution of water levels of small lakes might be sparse.

Several studies exist related to the estimation of lake levels based on classical radar altimetry whereas only very few studies exist concerning the performance of CryoSat-2 SAR data over lakes [6,7]. This study is focused on the estimation of lake levels by using CryoSat-2 SAR measurements. An innovative processing strategy is developed based on an unsupervised classification of altimetry waveforms. The selection of usable observations over inland waters is a challenging task. Usually, constant water masks—provided for instance by the World Wildlife Fund (WWF) website (https://www.worldwildlife.org/pages/global-lakes-and-wetlands-database) or extracted from remote sensing images—are applied ([6,7]). However, these external information does not consider changes in the water surface extent or surrounding inundation areas. Alternatively, waveform classification approaches can be used to identify valid water returns from altimetry waveforms itself (e.g., [8,9,10]). These waveform classification approaches are all based on certain threshold levels of special waveform parameters depending on the applied altimeter mission and the study area. Unlike these approaches, in this study, we present an unsupervised classification method based on the k-mean algorithm for CryoSat-2 SAR multi-looked waveforms in order to identify valid lake return echoes. Beside the identification of inland waters the retracking of the waveforms is a challenging task, because the waveforms at the land-water transition are contaminated by land signals. In our approach, we apply a modified version of the Improved Threshold Retracker [11] in order to obtain optimal results for lake water levels.

The objective of our novel and robust processing strategy is the estimation of accurate water level time series for lakes by using precise CryoSat-2 SAR mode observations. We validate our CryoSat-2 SAR results by matching with in-situ gauging data. Moreover, the results are compared to water level time series derived from classical radar altimeter missions such as Envisat, Jason-2, and SARAL/AltiKa in order to investigate the performance improvements due to the SAR approach. Last but not least, the estimated water level time series are compared to modeled water heights derived from CryoSat-2 SAR data according to the approach described in Nielsen et al. [6].

2. Study Area

Since CryoSat-2 operates in three different modes and the SAR mode is only available in selected areas depending on a geographical mode mask (https://earth.esa.int/web/guest/-/geographical-mode-mask-7107), not many lakes exist to apply our processing strategy. In order to allow for representative results and meaningful validation, lakes with different characteristics concerning their size, form and surroundings are necessary and the existence of reliable in-situ gauging stations must be ensured. Furthermore, the lakes in the study should be observable by the classical radar altimeter satellite missions such as Envisat, Jason-2 and SARAL/AltiKa in order to allow for a comparison between classical and SAR altimetry results.

This study focuses on four different lakes: Tonle Sap (Cambodia), Vättern (Sweden), Okeechobee (FL, USA), and Lough Neagh (North Ireland). They show different surface extents, surrounding landscape and water level variations. In the following, the characteristics of the investigated lakes are briefly described:

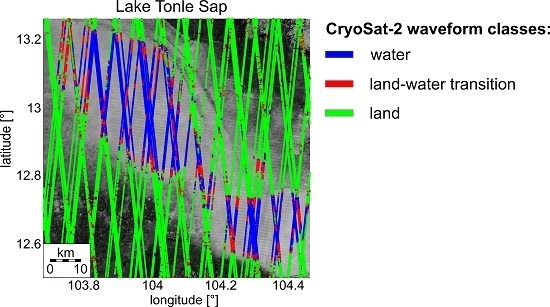
• Tonle Sap is the largest lake in Southeast Asia with a surface area of about 2600 km${}^2$ during the dry season and 10,400 km${}^2$ during the flood season. Accordingly, the water level of the lake shows a strong annual signal which varies between 2.3 m and 12.4 m. The surrounding landscape of the lake is flat and contains a great deal of rivers and wetland areas especially during the flood season.
• Vättern is the second largest lake in Sweden with a surface area of about 1912 km${}^2$. It does not show a significant annual signal and the water level of the lake shows only variations of about 1 m. The landscape around the lake is flat with three small lakes around the lake Vättern.
• Okeechobee is the largest lake in Florida with a surface area of about 1900 km${}^2$. The water level of the lake varies between 2.6 m and 5.4 m with no significant annual signal. The lake is located in a flat territory and it is mainly surrounded by wetlands.
• Lough Neagh is the largest lake of the island Ireland with a surface area of about 392 km${}^2$. The water level of the lake shows an annual signal and varies between 12.2 m and 13.3 m. The lake is situated in lowland with a few smaller lakes around Lough Neagh.

3. Data Sources

This section describes the data used in the study. The main observations are the multi-looked waveforms of CryoSat-2 SAR, the other data sets are necessary for the pre-processing and the validation of the computed time series.

3.1. CryoSat-2 L1b Product: SAR Mode

CryoSat-2 is the first altimeter (partly) using the Delay-Doppler measurement principle [12]. For selected areas, the altimeter provides so-called SAR data sets. In contrast to the classical pulse-limited altimeter the full Doppler bandwidth is exploited here. By averaging all reflected echoes from the same along-track surface location of interest seen from different look angles so-called multi-looked waveforms are obtained. These SAR waveforms correspond to classical waveforms of pulse-limited altimetry but their shape is much peakier. ESA provides these waveforms in the Level 1b SAR products with a temporal resolution of 20 Hz (ftp://science-pds.cryosat.esa.int). In this study, we present the results obtained with the new Baseline C products.

The data are selected for rectangular areas including the lakes based on latitude and longitude information. The waveforms are provided as scaled products. However, we need unscaled information for our waveform classification (Section 4.1). Thus, in a first pre-processing step, the unscaled averaged power of the multi-looked waveforms $P_i$ are derived with [13]

$$P_i\left(t\right)=P_i^{scaled}\left(t\right)\times (scalefactor\left(t\right)\times {10}^{-9})\times 2^{scalepower\left(t\right)}$$

(1)

from the scaled averaged waveform power $P_i^{scaled}$ and their echo scale factors and powers. These SAR waveforms are used for classification and retracking. Section 4.2 describes the determination of the retracking correction. By adding the retracker correction to the uncorrected range derived from the window delay and applying the geophysical corrections the corrected range is obtained:

$$range=0.5\times c\times windowdelay+retrackingcorrection+geophysicalcorrections.$$

(2)

where c is the speed of light in vacuum. We apply the following geophysical corrections: ionosphere, wet and dry troposphere, solid Earth and pole tide which are described in

Table 1. Geophysical corrections applied within this study.

Correction	Source/Model	Reference
Ionosphere	Jet Propulsion Laboratory-Global Ionosphere Maps (JPL-GIM), International Reference Ionosphere (IRI) scaled	[15]
Wet troposphere	ECMWF ($2.5^{\circ }\times 2.0^{\circ }$) for Vienna Mapping Functions 1 (VMF1)	[16]
Dry troposphere	ECMWF ($2.5^{\circ }\times 2.0^{\circ }$) for Vienna Mapping Functions 1 (VMF1)	[16]
Solid Earth tide	CryoSat-2 Level 1b	[13]
Pole tide	CryoSat-2 Level 1b	[13]

. To determine the surface elevations H with respect to the EGM 2008 geoid model [14] the range and the geoid height N have to be subtracted from the height of the CryoSat-2 satellite $h_{Sat}$ above the reference ellipsoid:

$$H=h_{Sat}-range-N.$$

(3)

3.2. In-Situ Gauging Data

In order to evaluate the SAR-based water level time series and to get information on their accuracies, we use daily in-situ observations from different gauging stations for comparison. For each of the four lakes a different national institution provides different data sets.

• The Mekong River Commission (http://ffw.mrcmekong.org/) maintains the gauging station Prek Kdam which is not located directly at the Lake Tonle Sap but next to the Lake Tonle Sap at the Prek Kdam Bridge crossing the Tonle Sap River. Therefore, these gauging data represent the water level of the Lake Tonle Sap quite well. Unfortunately, since 2009 the water level time series are only provided during the flood season from June to October but not for the dry season from November to May. The water level time series are referred to the zero gauge which is 0.08 m above the mean sea level.
• The Swedish Meteorological and Hydrological Institute (http://vattenwebb.smhi.se/station/) offers gauging data for the Lake Vättern with respect to the Swedish height system “Rikets höjdsystem 1900” (RH 00). The gauging station for the Lake Vättern is located in the city Motala along the river Motala ström.
• The National Water Information System (http://waterdata.usgs.gov/nwis/sw) provides gauging data for the Lake Okeechobee regarding to the National Geodetic Vertical Datum of 1929 (NGVD 29). The daily water levels are averages of the measurements of the 14 gauging stations located at the Lake Okeechobee.
• The Rivers Agency, Department of Agriculture and Rural Development (https://www.dardni.gov.uk/rivers-agency) holds gauging data for the Lake Lough Neagh with respect to the height system metres ordance datum Belfast (mOD Belfast). While for the time span 2002–2008 the data of two gauging stations on the Lake Lough Neagh are averaged, for the time span 2008–2016 the data of four gauging stations on the Lake Lough Neagh are averaged.

As one can see all in-situ gauging data are referred to different height systems. For the validation, all these water level time series are shifted to refer to the same datum as the DAHITI water levels (see Section 3.3). Thus, for each time series a constant offset with respect to the DAHITI time series is computed and subtracted from the in-situ data as well as from the CryoSat SAR time series. In this way all time series in this paper are given relative to the EIGEN-6c3stat geoid model and the validation is based on water level variations only.

3.3. DAHITI: Water Level Time Series from Multi-Mission Satellite Altimetry

In order to compare the SAR altimetry lake levels with standard altimeter products, we use DAHITI water level time series. The Database for Hydrological Time Series over Inland Waters (DAHITI, http://dahiti.dgfi.tum.de/en/) is an open web service provided by the Deutsches Geodätisches Forschungsinstitut der Technischen Universität München (DGFI-TUM). It offers water level time series not only of lakes and reservoirs but also of rivers and wetlands derived from classical radar altimeter satellite missions such as Envisat, Jason-2, SARAL/AltiKa, etc. The water level time series relative to the EIGEN-6c3stat geoid model [17] are used in order to validate the results of this study. The processing strategy of DAHITI is described in detail by Schwatke et al. [18]. It is a satellite altimetry multi-mission approach that is based on an extended outlier detection and a Kalman filtering.

The elimination of unusable observations is based on lake specific latitude and water height thresholds and an along-track outlier detection using support vector regression (SVR) [19]. In the standard approach no waveform classification is applied. The surface heights are computed using the Improved Threshold Retracker [11]. For larger lakes all available altimetry tracks (from one or more missions) are combined in a Kalman filter. In order to ensure a consistent combination range corrections computed by a global multi-mission crossover analysis [20] are applied to all measurements. Only the most precise water heights of each overflight are averaged taking their formal errors into account. If necessary, a final outlier rejection is performed for the water level time series based on SVR.

From the four lakes used in this study, only the Tonle Sap allows for a multi-mission approach. Data from two Envisat/SARAL tracks and one Jason-2 track are combined in the final time series. For the other three lakes, only one track of Envisat/SARAL is usable since these lakes are small and not covered by more than one mission.

3.4. AltWater: Modeled Water Level Time Series From CryoSat-2

Altimetry for inland water (AltWater, http://www.altwater.dtu.space/index.html) is an open service provided by the Technical University of Denmark (DTU) that currently offers water level time series for various lakes derived from CryoSat-2 observations in LR, SAR and SARIn mode. In this study, we use the modeled water level time series relative to the EGM2008 geoid model [14] for validating our results. The applied method is described in Nielsen et al. [6]. DTU uses constant water masks from WWF for the identification of all observations over the lakes. DTU developed a dynamic model, with random variables, that use the correlation between neighboring (close) times to improve the estimates at each time. In this way, the state-space model takes into account that successively observations are strongly correlated, which allows the model to figure out how the true water level is developing over time. Input data for this approach are the along-track lake levels derived from the multi-looked CryoSat-2 SAR Baseline B waveforms retracked with the Narrow Primary Peak Threshold Retracker (NPPTR) [21]. Here, we use water level time series of our study areas, which are not based on CryoSat-2 SAR Baseline B waveforms but on CryoSat-2 SAR Baseline C waveforms to compare them with our results. These modeled lake levels have been provided by DTU directly.

4. Method

Satellite altimetry yields optimal accuracies over large open water areas, e.g., oceans. If different reflectors (land, water, vegetation) are present in the altimeter footprint—as it is the case for most inland applications—the returned radar echo is complex and the derivation of a reliable height is challenging. This section describes a novel and robust processing strategy to estimate water level time series of lakes from CryoSat-2 SAR mode observations. The approach is separated into three steps: (1) classification of the multi-looked CryoSat-2 SAR waveforms in order to identify reliable and usable observations; (2) retracking of the selected waveforms for estimating along-track water heights; (3) rejection of remaining outliers and determination of the mean water level per overflight.

4.1. Waveform Classification

The most essential step in inland altimetry applications is the selection of usable observations. Only measurements taken directly over the lake should be analyzed. In principle, the identification can be done by applying constant water masks provided for instance by WWF or extractable from remote sensing images. However, these external information will not account for changes in lake surface extent or surrounding inundation areas. Moreover, observations near the water edges might also be contaminated by land and should be excluded from further processing. Our approach is solely based on the altimetry waveforms itself to identify valid water returns. An unsupervised classification method is used in order to group the waveforms in three classes: water, land-water transition, and land. As input for this clustering we use three characteristics to describe the waveforms. These parameters are defined by the Offset Center Of Gravity (OCOG) retracker [22]: amplitude A and width W of the waveform as well as the bin position of the waveform center of gravity (COG). The OCOG parameters are determined according to the following equations [11]:

$$A\left(t\right)=\sqrt{\frac{{\sum }_{i=1+n_1}^{N-n_2}{P}_i{\left(t\right)}^4}{{\sum }_{i=1+n1}^{N-n_2}{P}_i{\left(t\right)}^2}},W\left(t\right)=\frac{{\left({\sum }_{i=1+n_1}^{N-n_2}P{\left(t\right)}^2\right)}^2}{{\sum }_{i=1+n_1}^{N-n_2}{P}_i{\left(t\right)}^4},COG\left(t\right)=\frac{{\sum }_{i=1+n_1}^{N-n_2}i{P}_i{\left(t\right)}^2}{{\sum }_{i=1+n_1}^{N-n_2}{P}_i{\left(t\right)}^2},$$

(4)

where $P_i$ is the unscaled averaged waveform power (see Equation (1)), $N=256$ is the total number of bins of the waveform and $n_1=n_2=4$ are the bins at the beginning and end of the waveform, which are affected by aliasing. These parameters have been chosen for the classification because they are sensitive to the shape of the waveforms, as shown in Figure 1. The bin-position of COG strongly depends on the location of the maximum of the waveform, i.e., the range between satellite and lake surface. Since we need comparable COG for all waveforms, we shift the waveforms before the determination of the three OCOG parameters as follows: If the waveform power $P_i$ is smaller than $0.05\%$ of the sum of all $P_i$, the waveform power is set to zero. In the next step, all zero values are shifted to the end of the waveform. In Figure 1 shifted waveforms for the three surface classes are shown together with the originally provided waveforms.

While the land-like waveforms exhibit a strong single peak with high power ($A\approx 3\times {10}^{-11}$), the water-like waveforms conform to ocean-like waveforms with significantly smaller power ($A\approx 3\times {10}^{-14}$). The waveforms at the land-water transition contain multiple peaks with medium power ($A\approx 1\times {10}^{-13}$). The width of the waveforms over land is very small ($W\approx 2$), it gets larger for waveforms over water ($W\approx 25$) and waveforms at the land-water transition show the largest widths ($W\approx 37$). Furthermore, the COG of the shifted waveforms over land is significantly smaller ($COG\approx 13$) than the COG of the shifted waveforms over water ($COG\approx 26$) and the shifted waveforms at the land-water transition ($COG\approx 37$).

In order to assign the recorded waveforms to the three surface classes, we apply a widely used unsupervised method: the k-means algorithm [23]. It groups the CryoSat-2 SAR multi-looked waveforms acquired in the spherical rectangular area of the Lake Tonle Sap into 30 automatically defined clusters - purely based on the three OCOG parameters. The Lake Tonle Sap was chosen for the clustering because it is one of the biggest lakes observed by CryoSat-2 in the SAR mode and exhibits all features of the landscape: lake, rivers, wetlands and flat land except mountains. Thus, the derived classes should be applicable for most other regions, too. Figure 2 shows the three OCOG parameters for the model building area. The location of the lake is clearly visible in all three parameters.

As input for the clustering algorithm, we define the amplitude vector $\mathbf{A}=\left(A\right(t\left)\right)$, the width vector $\mathbf{W}=\left(W\right(t\left)\right)$ and the center of gravity vector $\mathbf{COG}=\left(COG\right(t\left)\right)$ containing the OCOG parameters of all unscaled shifted waveforms in the training area and we formulate the $m\times n$ data matrix $\mathbf{X}$ with $j=1,\dots ,m$ (total number of waveforms) and n = 3:

$$\mathbf{X}=[\mathbf{W}\mathbf{COG}\mathbf{A}\times {10}^{11}].$$

(5)

Due to the fact that the magnitude of the amplitude vector is significantly smaller than of the width and COG vector, the amplitude vector has to be scaled by ${10}^{11}$. Otherwise this selection criteria would not be equivalent considered by the clustering algorithm. The m observations ${\mathbf{X}}_m$ of the data matrix are partitioned into K centroid clusters – sensitivity analysis have shown that with $K=30$ the best results are obtained—in which each observation belongs to the cluster with the nearest mean. Therefore, the sum of the distance functions of each observation point in the cluster to the center of the cluster has to be minimized iteratively. In a first step, K n-dimensional cluster centers $C_i$ with $i=1,\dots ,K$ are chosen arbitrarily and the point-to-centroid distances between waveform j and cluster i are determined here according to the city block metric (a special case of the Minkowski metric) with [24]

$$Dist(X_j,C_i)=\sum _{p=1}^n|{\mathbf{X}}_{jp}-{\mathbf{C}}_{ip}|.$$

(6)

We use the city block metric instead of the Euclidean metric because it is more robust against outliers and less sensitive to parameter differences [25]. Afterwords, the observation points are assigned to the clusters with respect to their minimal distance to the cluster center. In the next step, the mean points of each cluster are calculated by averaging their parameters. These mean points are used to update the cluster centers $C_i$ and to assign the observation points to the new clusters. This processing step will be done iteratively until the clusters are stable.

At the end of the processing each waveform is assigned to one of the 30 clusters. This large number of clusters is necessary in order to allow the algorithm to perform a reliable clustering. There exist no efficient and universal methods for the selection of K [26]. If the number of clusters is too small outliers occur in the clusters. Sensitivity analysis have shown that for our approach the optimal results can be obtained with 30 clusters. However, in order to group the observations into the three surface types we defined earlier, a post-processing step is necessary. This is done manually based on visual inspection of the waveform shapes. In Figure 3, the shape of the shifted waveforms of the thirty cluster centers are shown, grouped into the three classes: water, land-water transition and land. As mentioned before the water-like waveforms conform to ocean-like waveforms, the waveforms at the land-water transition contain multiple peaks and the land-like waveforms exhibit one strong single peak. Figure 4a presents the classification result for the area of the Lake Tonle Sap. The lake and the land-water transition gets clearly visible. However, there are some points outside the lake which are classified as water or land-water transition. As can be seen in Figure 4a these points are located mainly in areas where the probability is higher that the area is sometimes covered by water (lighter gray). These points will be removed later by the applied waveform retracking algorithm and outlier rejection (see Section 4.2 and Section 4.3).

The clustering result of the Tonle Sap data set can be used to classify the waveforms of other lakes such as Vättern, Okeechobee, and Lough Neagh. Therefore, we set up the data matrix $\mathbf{X}$ (Equation (5)) for each lake and determined the city block distance to each cluster center of the model building area Tonle Sap (Equation (6)). In the next step, the observation points are assigned to the nearest cluster center. Figure 4 shows the classification results for all four lakes. Obviously, the clustering and the class centers are transferable to other lakes. In order to evaluate this apparent result we did the clustering for each lake, and compare the RMS accuracies of the derived water level time series with respect to the gauging data. The best results are yield with the Tonle-Sap-Clustering, probably due to the small amount of data for the other lakes. Thus, we found that this classification strategy can be used for all other lakes, too and that the clustering result, i.e., the cluster centers are transferable between different areas.

4.2. Waveform Retracking Algorithm

After the identification of the usable waveforms, these can be used for range estimation. We only retrack the unscaled and unshifted waveforms of the classes water and land-water transition. In order to extract reliable results, we use a modified version of the Improved Threshold Retracker (ITR) [11]. In a first step sub-waveforms are identified. If $(P_{i+2}-P_i)/2>{ϵ}_1$ the beginning of a sub-waveform is located and if $(P_{i+1}-P_i)<{ϵ}_2$ the end of the actual sub-waveform is found. However, compared to Gommenginger et al. [11], we use slightly different values for the bounds ${ϵ}_1$ and ${ϵ}_2$. Empirical tests have shown that with ${ϵ}_1=0.1\times S$ and ${ϵ}_2=0.08\times S_1$ the best results can be obtained, where S is the standard deviation of all power differences at the next but one bins, determinted via [11]:

$$S=\sqrt{\frac{(N-2){\sum }_{i=1}^{N-2}{((P_{i+2}-P_i)/2)}^2-{\left({\sum }_{i=1}^{N-2}((P_{i+2}-P_i)/2)\right)}^2}{(N-2)(N-3)}}$$

(7)

and $S_1$ is the standard deviation of all power differences at neighboring bins, determined via:

$$S_1=\sqrt{\frac{(N-1){\sum }_{i=1}^{N-1}{(P_{i+1}-P_i)}^2-{\left({\sum }_{i=1}^{N-1}(P_{i+1}-P_i)\right)}^2}{(N-1)(N-2)}}.$$

(8)

In the next step, the leading edge and the corresponding retracker correction are determined by applying the ITR with a threshold level of 50%. By using the Equations (2) and (3) the water level is computed for each sub-waveform. In the next step the median of the water heights of each track crossing the investigated lake are determined in order to identify the maximum and minimum water height thresholds of the lake water level time series. Due to the fact that all sub-waveforms are considered this water level time series contains some outliers. Therefore, in a next step in each case the “best” surface height and sub-waveform is selected by introducing the a priori water height thresholds. Furthermore empirical analysis have shown that the length of the “best” sub-waveform should be greater than 6 bins. Figure 5 shows examples of waveforms over water and at the land-water transition together with the identified sub-waveforms. Furthermore, the surface heights obtained from all sub-waveforms and obtained from the “best” sub-waveforms of a CryoSat-2 track passing over the Lake Tonle Sap are plotted. This shows, that our retracking method is able to provide reliable water levels, even when applied to multiple-peak waveforms originating from land-water transitions.

4.3. Outlier Rejection

Before the determination of the median of the water heights of each track crossing the investigated lake an outlier rejection has to be applied in order to eliminate remaining inaccurate water heights. These will occur mostly due to water returns from inundation areas in the surrounding of the lakes. Analysis have shown that only two outlier criteria have to be applied to obtain optimal results for all lakes. By using latitude and longitude thresholds a rectangular area around a lake is defined to reduce the influence of surrounding water bodies (such as rivers, other lakes, and wetlands) on the lake level estimation. This box was already necessary for data extraction (see Section 3.1). Furthermore, we determine the moving 5-point standard deviation $[i-2,\cdots ,i+2]$ for each water height estimated along the satellite track. If the standard deviation exceeds 10 cm the water height is rejected before the determination of the median along the satellite track. We have tested different moving box widths from 3 to 9 and different thresholds for the standard deviation from 2 cm to 20 cm for all lakes. These empirical analysis have shown that with a moving box width of 5 and a threshold level of 10 cm the optimal results for all lakes can be obtained. Figure 6 shows water heights determined for a track crossing Lake Okeechobee near the land-water transition. The closer the tracking point is located to the land, the higher the standard deviation of the estimated water height.

5. Results, Validation and Discussion

In this section, our water level time series for the lakes Tonle Sap, Vättern, Okeechobee and Lough Neagh derived from CryoSat-2 SAR Baseline C data via multi-looked waveform classification are presented and compared with in-situ gauging data. While Figure 7 shows the water level time series,

Table 2. Root mean square (RMS) differences (cm) and squared correlation coefficients ($R^2$) of the water level time series derived from satellite altimetry with respect to in-situ gauging data for the time span (8 April 2010–31 December 2015). Furthermore the size of the lakes (km${}^2$), the number of CryoSat-2 tracks crossing the lakes as well as the number of points in the water level time series (No.) are given (identical with the number of used data points for the comparison with in-situ data).

Lake	Size	Tracks	DGFI-TUM			DTU			DAHITI
			RMS	${\mathit{R}}^2$	No.	RMS	${\mathit{R}}^2$	No.	RMS	${\mathit{R}}^2$	No.
Tonle Sap	2600	107	90.1	0.90	107	96.1	0.87	137	72.4	0.93	233
Vättern	1912	76	3.9	0.79	71	4.6	0.75	71	4.0	0.73	29
Okeechobee	1900	54	3.8	0.99	52	7.3	0.98	73	4.9	0.97	33
Neagh	392	54	3.1	0.95	43	6.5	0.88	47	4.2	0.94	30

gives an overview of the root mean square (RMS) differences and squared correlation coefficients ($R^2$) with respect to the in-situ gauging data. The RMS of our water level time series for the lakes Vättern, Okeechobee and Lough Neagh range between 3.1 cm and 3.9 cm, whereas the RMS for the Lake Tonle Sap is significantly higher and yields 90.1 cm—although this is (by far) the largest lake in our study. This is related to the water level variations itself: the water level of Tonle Sap show much higher changes (up to 10.1 m) than the other lakes that exhibit only moderate variations between 0.5 m and 2.8 m. Furthermore, contrary to the other lakes, the gauging station of Tonle Sap is not located directly at the lake but about 90 km away at the Tonle Sap River. This might increase the RMS difference.

Table 2 also shows the number of tracks over each lakes as well as the used data points for validation. One can see that for the three largest lakes (>1500 km${}^2$) nearly all tracks crossing the lake can be processed. This holds not for Lake Neagh where only about 80% of the tracks are usable—even if waveforms classified as “land-water transition“ are exploited.

All results presented up to now are based on both water classes including land-water transition areas. We also investigate if the results improve when using only the waveforms classified as open water. Figure 8 shows the differences of these two solutions with respect to the in-situ gauging data. If the waveform class ”land-water transition“ is not considered, less tracks can be processed, especially for smaller lakes. However, the RMS differences change only slightly. For all lakes, except the Lake Okeechobee, the consideration of additional waveforms from the land-water transition increases the performance, especially for smaller lakes such as the Lake Lough Neagh. Therefore, we recommend to consider the waveform class ”land-water transition“ by the determination of lake levels.

To check the quality of the CryoSat-2 SAR lake water level time series with respect to results from classical satellite altimetry we compare DAHITI water level time series with in-situ gauging data (see Figure 7 and Table 2). The RMS values for the lakes Vättern, Okeechobee and Lough Neagh range between 4.0 cm and 4.9 cm, while the RMS for the Lake Tonle Sap amounts to 72.4 cm. These values are in the same order of magnitude with the SAR results. For the three smaller lakes, the RMS differences of the CryoSat-2 SAR water level time series estimated at the DGFI-TUM are up to 1 cm smaller than the RMS differences of the conventional altimeter results. This shows the capability of the SAR technology since for both results only one mission is usable (CryoSat-2 or Envisat/SARAL). In contrast, for the Lake Tonle Sap two Envisat/SARAL tracks and one Jason-2 track exists allowing to apply the multi-mission approach. This is also visible in the number of used data points for comparison with the validation data. Under these circumstances, the multi-mission DAHITI water level time series performs significantly better than the CryoSat-2 only solution.

Last but not least, we validate our CryoSat-2 water level time series with modeled CryoSat-2 water heights offered by DTU (see also Figure 7 and Table 2). For these DTU results, the RMS values with respect to the in-situ gauging data range between 4.6 cm and 7.3 cm for the lakes Vättern, Okeechobee and Lough Neagh, whereas the RMS value for the Lake Tonle Sap amounts to 96.1 cm. The number of points in the DTU water level time series are higher than the number of points in the DGFI-TUM water level time series since we have to remove epochs for which we are not able to estimate reliable water levels. For a more correct comparison we compare RMS values based only on times where both methods DGFI-TUM and DTU produce estimates, see

Table 3. RMS differences (cm) and squared correlation coefficients ($R^2$) of the DGFI-TUM and Technical University of Denmark (DTU) water level time series with respect to in-situ gauging data at times where both methods produce estimates.

	DGFI-TUM		DTU
	RMS	${\mathit{R}}^2$	RMS	${\mathit{R}}^2$
Tonle Sap	90.1	0.90	94.5	0.89
Vättern	3.9	0.80	4.1	0.78
Okeechobee	3.3	0.99	6.2	0.98
Neagh	3.0	0.95	5.7	0.82

. In this case the RMS values for the lakes Vättern, Okeechobee and Lough Neagh range between 4.1 cm and 6.2 cm and the RMS value for the Lake Tonle Sap amounts to 94.5 cm. For all four lakes, these numbers are not as good as the results computed with our approach, even if the comparison is performed only at epoches where both methods provide results. Thus, our new processing strategy outperforms the DTU method in terms of RMS accuracy.

6. Conclusions

In this study, we propose an innovative processing strategy for lake level estimation using CryoSat-2 SAR observations. The approach is based on a semi-automatic classification of all measurements in order to estimate reliable lake levels time series. The selection of usable observations is the most essential step in inland altimetry applications. Therefore, we developed an unsupervised classification method based on the k-mean algorithm for CryoSat-2 SAR multi-looked waveforms. In contrast to classical application of constant water masks, this approach allows for taking into account changes in the water surface extent or surrounding inundation areas. Beside the identification of reliable water returns, the retracking of CryoSat-2 SAR multi-looked waveforms is a challenging task, because the waveforms at the land-water transition are influenced by land reflections. In our approach, we applied a modified version of the Improved Threshold Retracker in order to obtain optimal results for lake water levels.

We apply our method to four globally distributed lakes of different size. The results show that the waveform classification approach work out very well for all of them. Comparison with in-situ data sets show RMS differences between 3 and 90 cm. The relative accuracy is better than 10% for all lakes. We found that it is important to consider the waveforms at the land-water transition in order to improve the water level time series and to minimize the data gaps due to the lack of observations. This is especially important for smaller lakes. Compared to modeled CryoSat-2 water heights as described in Nielsen et al. [6] our water level time series show slightly improved RMS accuracies but their temporal resolution is reduced. Thus, to further improve the water level time series for lakes a combination of both methods seems to be promising.

For lakes that are covered only by one track of a classical satellite altimetry mission our SAR processing strategy allow to estimate improved lake water level time series up to 1 cm (about 25%) with respect to lake water level time series derived from classical altimetry according to the DAHITI approach. For larger lakes, no improvement with respect to multi-mission time series are detectable. Due to these findings, we suggest to combine conventional satellite altimetry observations with CryoSat-2 SAR measurements in order to determine improved long-term water level time series for all kind of lakes.

Finally, it should be noted that this innovative processing strategy has been developed for CryoSat-2 SAR data, but it can easily adopted to other satellite altimetry SAR data such as from the new Sentinel-3 mission. Due to the fact that Sentinel-3 mission is continuously operating in SAR mode with a repeat orbit of 27 days more inland waters are observable. To further improve the precision of our semi-automatic classification approach we suggest to apply it to the original SAR stack data instead of the pre-processed multi-look waveforms. This might help to exclude more land-contaminated radar returns and to exploit the full information of the SAR technology.