Estimating and Up-Scaling Fuel Moisture and Leaf Dry Matter Content of a Temperate Humid Forest Using Multi Resolution Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. In Situ Leaf Moisture and Dry Matter Content Data Collection
2.3. Calculation of Leaf Moisture and Dry Matter Content
2.4. Remotely Sensed Data
2.5. Pre-Processing of Remote Sensing Data
2.6. Upscaling In Situ Leaf Moisture and Leaf Dry Matter Content Using Landsat ETM+ Data
2.6.1. Multiple Linear Regression (MLR)
2.6.2. Artificial Neural Network (ANN)
2.7. Upscaling Fuel Moisture and Leaf Dry Matter Content Derived from ETM+ to MODIS
2.7.1. Multiple Linear Regression (MLR)
2.7.2. Artificial Neural Network (ANN)
2.8. Validation of Empirical Models
3. Results
3.1. Leaf Moisture and Dry Matter Content (MCI)
3.2. Validation of Leaf Moisture and Dry Matter Content (MCI) Estimations Using Satellite Data
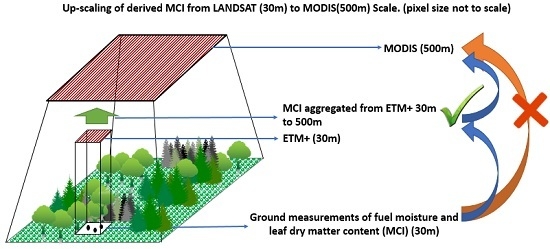
3.3. Scale Discrepancy between Plot and Satellite Data
3.4. Mapping Leaf Moisture and Dry Matter Content (MCI) Using ETM+ Data
3.5. Mapping Leaf Moisture and Dry Matter Content (MCI) Using MODIS Data
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Biophysical Indices and Atmospheric Variables | |
| * # | [91] |
| * # | [92] |
| * # | [93,94] |
| * # | [94] |
| * # | [95] |
| * # | [50] |
| * # | [96] |
| * # | [97] |
| Vegetation Indices | |
| * | [71] |
| * | [30] |
| * | [34] |
| * | [71] |
| * | [21] |
| * | [98] |
| * | [30] |
| * | [65] |
| * | [35] |
Abbreviations
| ARND | Accumulated Relative NDVI Decrement |
| ETM+ | Enhanced Thematic Mapper Plus |
| GVMI | Global Vegetation Moisture Index |
| IM | Inversion Models |
| IRS | Infra-Red Scanner (HJ-1B IRS) |
| IVDI | Improved VDI |
| LOPEX | Leaf Optical Properties Experiment |
| LR | Linear Regression |
| LST | Land Surface Temperature |
| MSI | Moisture Stress Index |
| MCI | Moisture Content Index |
| MODIS | MODerate-resolution Imaging Spectroradiometer |
| NDII | Normalized Difference Infrared Index |
| NDVI | Normalized Difference Vegetation Index |
| NDWI | Normalized Difference Water Index |
| RGRE | Relative Greenness |
| SIWSI | Shortwave Infrared Water Stress Index |
| SPOT | Satellites Pour l’Observation de la Terre or Earth-observing Satellites |
| SRWI | Simple Ratio Water Index |
| TM | Landsat Thematic Mapper |
| VARI | Visible Atmospheric Resistant Index |
| VDI | Vegetation Dryness Index |
References
- Papió, C.; Trabaud, L. Structural characteristics of fuel components of five meditarranean shrubs. For. Ecol. Manag. 1990, 35, 249–259. [Google Scholar] [CrossRef]
- Bisquert, M.; Sánchez, J.M.; Caselles, V. Modeling fire danger in Galicia and Asturias (Spain) from MODIS images. Remote Sens. 2014, 6, 540–554. [Google Scholar] [CrossRef]
- Silva, D.M.; Batalha, M.A.; Cianciaruso, M.V. Influence of fire history and soil properties on plant species richness and functional diversity in a neotropical savanna. Acta Bot. Bras. 2013, 27, 490–497. [Google Scholar] [CrossRef]
- Brady, M.A.; de Groot, W.J.; Goldammer, J.G.; Keenan, T.; Lynham, T.J.; Justice, C.O.; Csiszar, I.A.; O’Loughlin, K. Developing a global early warning system for wildland fire. In Managing Weather and Climate Risks in Agriculture; Sivakumar, M.V.K., Motha, R.P., Eds.; Springer: Berlin, Germany, 2007; pp. 355–366. [Google Scholar]
- Chowdhury, E.H.; Hassan, Q.K. Development of a new daily-scale forest fire danger forecasting system using remote sensing data. Remote Sens. 2015, 7, 2431–2448. [Google Scholar] [CrossRef]
- De Groot, W.J.; Goldammer, J.G.; Keenan, T.; Brady, M.A.; Lynham, T.J.; Justice, C.O.; Csiszar, I.A.; O’Loughlin, K. Developing a global early warning system for wildland fire. For. Ecol. Manag. 2006, 234, S10. [Google Scholar] [CrossRef]
- Grassein, F.; Till-Bottraud, I.; Lavorel, S. Plant resource-use strategies: The importance of phenotypic plasticity in response to a productivity gradient for two subalpine species. Ann. Bot. 2010, 106, 637–645. [Google Scholar] [CrossRef] [PubMed]
- Davies, G.; Legg, C. Fuel moisture thresholds in the flammability of calluna vulgaris. Fire Technol. 2011, 47, 421–436. [Google Scholar] [CrossRef]
- Viegas, D.X.; Piñol, J.; Viegas, M.T.; Ogaya, R. Estimating live fine fuels moisture content using meteorologically-based indices. Int. J. Wildland Fire 2001, 10, 223–240. [Google Scholar] [CrossRef]
- Pausas, J.G.; Paula, S. Fuel shapes the fire–climate relationship: Evidence from mediterranean ecosystems. Glob. Ecol. Biogeogr. 2012, 21, 1074–1082. [Google Scholar] [CrossRef]
- Saura-Mas, S.; Lloret, F. Leaf and shoot water content and leaf dry matter content of mediterranean woody species with different post-fire regenerative strategies. Ann. Bot. 2007, 99, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Cornelissen, J.H.C.; Lavorel, S.; Garnier, E.; Díaz, S.; Buchmann, D.N.; Gurvich, D.E.; Reich, P.B.; Steege, H.T.; Morgan, H.D.; van der Heijden, M.G.A.; et al. A handbook of protocols for standardised and easy measurement of plant functional traits worldwide. Aust. J. Bot. 2003, 51, 335–380. [Google Scholar] [CrossRef]
- Marino, E.; Dupuy, J.-L.; Pimont, F.; Guijarro, M.; Hernando, C.; Linn, R. Fuel bulk density and fuel moisture content effects on fire rate of spread: A comparison between firetec model predictions and experimental results in shrub fuels. J. Fire Sci. 2012, 30, 277–299. [Google Scholar] [CrossRef]
- Rachmilevitch, S.; DaCosta, M.; Huang, B. Physiological and biochemical indicators for stress tolerance. In Plant-Environment Interactions, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 321–355. [Google Scholar]
- Zhang, J.; Wu, J.; Zhou, L. Retrieval of fuel moisture content from hyperspectral data via partial least square. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010.
- Yool, S. Broad-scale monitoring of live fuel moisture. Geogr. Compass 2009, 3, 1703–1716. [Google Scholar] [CrossRef]
- Dimitrakopoulos, A.P.; Bemmerzouk, A.M.; Mitsopoulos, I.D. Evaluation of the canadian fire weather index system in an eastern mediterranean environment. Meteorol. Appl. 2011, 18, 83–93. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Teyip, T.; Li, Z.-L. Modified perpendicular drought index (MPDI): A real-time drought monitoring method. ISPRS J. Photogramm. Remote Sens. 2007, 62, 150–164. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Zhang, S.; Hao, X.; Dasgupta, S. Soil moisture estimation using MODIS and ground measurements in Eastern China. Int. J. Remote Sens. 2007, 28, 1413–1418. [Google Scholar] [CrossRef]
- Hassan, Q.; Bourque, C.; Meng, F.-R.; Cox, R. A wetness index using terrain-corrected surface temperature and normalized difference vegetation index derived from standard MODIS products: An evaluation of its use in a humid forest-dominated region of Eastern Canada. Sensors 2007, 7, 2028–2048. [Google Scholar] [CrossRef]
- Schneider, P.; Roberts, D.A.; Kyriakidis, P.C. A vari-based relative greenness from MODIS data for computing the fire potential index. Remote Sens. Environ. 2008, 112, 1151–1167. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Cocero, D.; Riaño, D. Design of an empirical index to estimate fuel moisture content from NOAA-AVHRR images in forest fire danger studies. Int. J. Remote Sens. 2003, 24, 1621–1637. [Google Scholar] [CrossRef]
- Hufkens, K.; Bogaert, J.; Dong, Q.; Lu, L.; Huang, C.; Ma, M.; Che, T.; Li, X.; Veroustraete, F.; Ceulemans, R. Impacts and uncertainties of upscaling of remote-sensing data validation for a semi-arid woodland. J. Arid Environ. 2008, 72, 1490–1505. [Google Scholar] [CrossRef]
- Lin, C.C. Modeling fine dead fuel moisture in Taiwan Red Pine Forests. Taiwan J. For. Sci. 2004, 19, 27–33. [Google Scholar]
- Weise, D.R.; Fujioka, F.M.; Nelson, R.M., Jr. A comparison of three models of 1-h time lag fuel moisture in Hawaii. Agric. For. Meteorol. 2005, 133, 28–39. [Google Scholar] [CrossRef]
- Aguado, I.; Chuvieco, E.; Borén, R.; Nieto, H. Estimation of dead fuel moisture content from meteorological data in mediterranean areas. Applications in fire danger assessment. Int. J. Wildland Fire 2007, 16, 390–397. [Google Scholar] [CrossRef]
- Sharples, J.J.; Matthews, S. Evaluation of some simplified models for predicting the moisture content of fine, dead fuels. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 2011; pp. 242–248.
- Danson, F.; Bowyer, P. Estimating live fuel moisture content from remotely sensed reflectance. Remote Sens. Environ. 2004, 92, 309–321. [Google Scholar] [CrossRef]
- Dennison, P.E.; Roberts, D.A.; Peterson, S.H.; Rechel, J. Use of normalized difference water index for monitoring live fuel moisture. Int. J. Remote Sens. 2005, 26, 1035–1042. [Google Scholar] [CrossRef]
- Verbesselt, J.; Somers, B.; Lhermitte, S.; Jonckheere, I.; van Aardt, J.; Coppin, P. Monitoring herbaceous fuel moisture content with spot vegetation time-series for fire risk prediction in savanna ecosystems. Remote Sens. Environ. 2007, 108, 357–368. [Google Scholar] [CrossRef]
- Dasgupta, S.; Qu, J.J.; Hao, X.; Bhoi, S. Evaluating remotely sensed live fuel moisture estimations for fire behavior predictions in Georgia, USA. Remote Sens. Environ. 2007, 108, 138–150. [Google Scholar] [CrossRef]
- Stow, D.; Niphadkar, M. Stability, normalization and accuracy of MODIS-derived estimates of live fuel moisture for Southern California chaparral. Int. J. Remote Sens. 2007, 28, 5175–5182. [Google Scholar] [CrossRef]
- Yunhao, C.; Jing, L.; Guangxiong, P. Forest fire risk assessment combining remote sensing and meteorological information. N. Z. J. Agric. Res. 2007, 50, 1037–1044. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E.; Riaño, D. Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agric. For. Meteorol. 2008, 148, 523–536. [Google Scholar] [CrossRef]
- Peterson, S.H.; Roberts, D.A.; Dennison, P.E. Mapping live fuel moisture with MODIS data: A multiple regression approach. Remote Sens. Environ. 2008, 112, 4272–4284. [Google Scholar] [CrossRef]
- Todone, F.; Bianchi, L.O; Defossé, G.E. First Field Sampling Results of Dead and Live Fuel Moisture Prediction in Patagonia; Internal Report IR3.157b of the Integrated Project “Fire Paradox”, Project No. FP6-18505; European Commission: Patagonia, Argentina, 2009. [Google Scholar]
- Qi, Y.; Dennison, P.; Spencer, J.; Riaño, D. Monitoring live fuel moisture using soil moisture and remote sensing proxies. Fire Ecol. 2012, 8, 71–87. [Google Scholar] [CrossRef]
- Sow, M.; Mbow, C.; Hély, C.; Fensholt, R.; Sambou, B. Estimation of herbaceous fuel moisture content using vegetation indices and land surface temperature from MODIS data. Remote Sens. 2013, 5, 2617–2638. [Google Scholar] [CrossRef]
- Li, L.; Ustin, S.L.; Riano, D. Retrieval of fresh leaf fuel moisture content using genetic algorithm partial least squares (GA-PLS) modeling. IEEE Geosci. Remote Sens. Lett. 2007, 4, 216–220. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.; Zhou, L. Deriving vegetation leaf water content from spectrophotometric data with orthogonal signal correction-partial least square regression. Int. J. Remote Sens. 2011, 32, 7557–7574. [Google Scholar] [CrossRef]
- Farzipour, B. Climate Change Impacts on Forest Fires in Iran; University of Toronto: Toronto, ON, Canada, 2011. [Google Scholar]
- Allard, G.B. The Fire Situation in Islamic Republic of Iran; FAO, Forestry Department: Rome, Italy, 2001. [Google Scholar]
- Adab, H.; Kanniah, K.D.; Solaimani, K.; Sallehuddin, R. Modelling static fire hazard in a semi-arid region using frequency analysis. Int. J. Wildland Fire 2015, 24, 763–777. [Google Scholar] [CrossRef]
- Sagheb-Talebi, K.; Sajedi, T.; Yazdian, F. Forests of Iran; Research Institute of Forests and Rangelands: Tehran, Iran, 2004. [Google Scholar]
- Desbois, N.; Deshayes, M.; Beudoin, A. Protocol for fuel moisture content measurements. In A Review of Remote Sensing Methods for the Study of Large Wildland Fires; Chuvieco, E., Ed.; Universidad de Alcalá: Alcalá de Henares, Spain, 1997; pp. 61–72. [Google Scholar]
- Garnier, E.; Shipley, B.; Roumet, C.; Laurent, G. A standardized protocol for the determination of specific leaf area and leaf dry matter content. Funct. Ecol. 2001, 15, 688–695. [Google Scholar] [CrossRef]
- Pinto, A.; Espinosa-Prieto, J.; Rossa, C.; Matthews, S.; Loureiro, C.; Fernandes, P.M. Modelling fine fuel moisture content and the likelihood of fire spread in blue gum (Eucalyptus globulus) litter. In VII International Conference on Forest Fire Research; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2014; pp. 353–359. [Google Scholar]
- Rego, F.; Moreira, F.; João Maia, M.; Catry e Conceição Colaço, F. Fire Paradox: An Innovative Approach of Integrated Wildland Fire Management Regulating the Wildfire Problem by the Wise Use of Fire: Solving the Fire Paradox; Instituto Superior De Agronomia: Lisboa, Portugal, 2010. [Google Scholar]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a web-based atmospheric correction tool for single thermal band instruments. Proc. SPIE 2005. [Google Scholar] [CrossRef]
- Sobrino, J.A.; El Kharraz, J.; Li, Z.L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Tonooka, H. Atmospheric correction of MODIS thermal infrared bands by water vapor scaling method. Proc. SPIE 2005. [Google Scholar] [CrossRef]
- Maxwell, S.K.; Schmidt, G.L.; Storey, J.C. A multi-scale segmentation approach to filling gaps in Landsat ETM+ SLC-off images. Int. J. Remote Sens. 2007, 28, 5339–5356. [Google Scholar] [CrossRef]
- Pringle, M.J.; Schmidt, M.; Muir, J.S. Geostatistical interpolation of SLC-off Landsat ETM+ images. ISPRS J. Photogramm. Remote Sens. 2009, 64, 654–664. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Travis, D. Gaps-fill of SLC-off Landsat ETM+ satellite image using a geostatistical approach. Int. J. Remote Sens. 2007, 28, 5103–5122. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Chen, C.; Chang, C.T.; Shih, L.M. Single-hidden-layer feed-forward quantum neural network based on grover learning. Neural Netw. 2013, 45, 144–150. [Google Scholar] [CrossRef] [PubMed]
- García, S.R.; Romo, M.P.; Mayoral, J.M. Estimation of peak ground accelerations for Mexican subduction zone earthquakes using neural networks. Geofís. Int. 2007, 46, 51–62. [Google Scholar]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2007, 29, 617–663. [Google Scholar] [CrossRef]
- Mofidi, A.; Soltanzadeh, I.; Yousefi, Y.; Zarrin, A.; Soltani, M.; Masoompour Samakosh, J.; Azizi, G.; Miller, S.T.K. Modeling the exceptional South Foehn Event (GARMIJ) over the alborz mountains during the extreme forest fire of December 2005. Nat. Hazard. 2014, 75, 2489–2518. [Google Scholar] [CrossRef]
- Özelkan, E.; Örmeci, C. Risk assessment of forest fires by using satellite data with remote sensing techniques. In Proceedings of the 28th Remote Sensing for a Changing Europe, Istanbul, Turkey, 2–5 June 2008.
- Jolly, W.M. Sensitivity of a surface fire spread model and associated fire behaviour fuel models to changes in live fuel moisture. Int. J. Wildland Fire 2007, 16, 503–509. [Google Scholar] [CrossRef]
- Chuvieco, E.; Cocero, D.; Riaño, D.; Martin, P.; Martínez-Vega, J.; de la Riva, J.; Pérez, F. Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sens. Environ. 2004, 92, 322–331. [Google Scholar] [CrossRef]
- Molavi-Arabshahi, M.; Arpe, K.; Leroy, S.A.G. Precipitation and temperature of the Southwest Caspian Sea region during the last 55 years: Their trends and teleconnections with large-scale atmospheric phenomena. Int. J. Climatol. 2016, 36, 2156–2172. [Google Scholar] [CrossRef]
- Lopes, S.; Viegas, D.X.; de Lemos, L.; Viegas, M.T. Rainfall effects on fine forest fuels moisture content. In Advances in Forest Fire Research; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2014; p. 427. [Google Scholar]
- Van Wagner, C.; Forest, P. Development and Structure of the Canadian Forest Fireweather Index System; Cannada Forest Service: Ottawa, ON, Canada, 1987.
- Tucker, C.J. Remote sensing of leaf water content in the near infrared. Remote Sens. Environ. 1980, 10, 23–32. [Google Scholar] [CrossRef]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral properties of plants. Appl. Opt. 1965, 4, 11–20. [Google Scholar] [CrossRef]
- Bowyer, P.; Danson, F.M. Sensitivity of spectral reflectance to variation in live fuel moisture content at leaf and canopy level. Remote Sens. Environ. 2004, 92, 297–308. [Google Scholar] [CrossRef]
- Leghari, S.K.; Zaidi, M.A.; Sarangzai, A.M. Seasonal variation in leaf relative water, dry matter and live fine fuel moisture contents in some common plant species of Quetta, Balochistan. FUUAST J. Biol. 2013, 3, 73–76. [Google Scholar]
- Tanentzap, F.M.; Stempel, A.; Ryser, P. Reliability of leaf relative water content (RWC) measurements after storage: Consequences for in situ measurements. Botany 2015, 93, 535–541. [Google Scholar] [CrossRef]
- Mataix-Solera, J.; Cerdà, A.; Arcenegui, V.; Jordán, A.; Zavala, L.M. Fire effects on soil aggregation: A review. Earth Sci. Rev. 2011, 109, 44–60. [Google Scholar] [CrossRef]
- Yang, X.; Guo, X.; Fitzsimmons, M. Assessing light to moderate grazing effects on grassland production using satellite imagery. Int. J. Remote Sens. 2012, 33, 5087–5104. [Google Scholar] [CrossRef]
- Keane, E.R. Fuel moisture. In Wildland Fuel Fundamentals and Applications; Springer International Publishing: Cham, Germany, 2015; pp. 71–82. [Google Scholar]
- Finney, M.A. Farsite: Fire Area Simulator: Model Development and Evaluation; US Department of Agriculture, Forest Service, Rocky Mountain Research Station Ogden: Fort Collins, CO, USA, 2004.
- Nolan, R.H.; Resco de Dios, V.; Boer, M.M.; Caccamo, G.; Goulden, M.L.; Bradstock, R.A. Predicting dead fine fuel moisture at regional scales using vapour pressure deficit from MODIS and gridded weather data. Remote Sens. Environ. 2016, 174, 100–108. [Google Scholar] [CrossRef]
- Hardwick, S.R.; Toumi, R.; Pfeifer, M.; Turner, E.C.; Nilus, R.; Ewers, R.M. The relationship between leaf area index and microclimate in tropical forest and oil palm plantation: Forest disturbance drives changes in microclimate. Agric. For. Meteorol. 2015, 201, 187–195. [Google Scholar] [CrossRef]
- Punalekar, S.; Verhoef, A.; Tatarenko, I.V.; van der Tol, C.; Macdonald, D.M.; Marchant, B.; Gerard, F.; White, K.; Gowing, D. Characterization of a highly biodiverse floodplain meadow using hyperspectral remote sensing within a plant functional trait framework. Remote Sens. 2016, 8, 112. [Google Scholar] [CrossRef]
- Ray, D.; Nepstad, D.; Brando, P. Predicting moisture dynamics of fine understory fuels in a moist tropical rainforest system: Results of a pilot study undertaken to identify proxy variables useful for rating fire danger. New Phytol. 2010, 187, 720–732. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Saunders, S.C.; Crow, T.R.; Naiman, R.J.; Brosofske, K.D.; Mroz, G.D.; Brookshire, B.L.; Franklin, J.F. Microclimate in forest ecosystem and landscape ecology: Variations in local climate can be used to monitor and compare the effects of different management regimes. BioScience 1999, 49, 288–297. [Google Scholar] [CrossRef]
- Merzouki, A.; Leblon, B. Mapping fuel moisture codes using MODIS images and the getis statistic over western canada grasslands. Int. J. Remote Sens. 2011, 32, 1619–1634. [Google Scholar] [CrossRef]
- Wang, L.; Hunt, E.R., Jr.; Qu, J.J.; Hao, X.; Daughtry, C.S.T. Remote sensing of fuel moisture content from ratios of narrow-band vegetation water and dry-matter indices. Remote Sens. Environ. 2013, 129, 103–110. [Google Scholar] [CrossRef]
- Trombetti, M.; Riaño, D.; Rubio, M.A.; Cheng, Y.B.; Ustin, S.L. Multi-temporal vegetation canopy water content retrieval and interpretation using artificial neural networks for the continental USA. Remote Sens. Environ. 2008, 112, 203–215. [Google Scholar] [CrossRef]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riaño, D.; Zylstra, P.; Hunt, E.R., Jr.; Danson, F.M.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Chuvieco, E.; Riano, D.; Aguado, I.; Cocero, D. Estimation of fuel moisture content from multitemporal analysis of landsat thematic mapper reflectance data: Applications in fire danger assessment. Int. J. Remote Sens. 2002, 23, 2145–2162. [Google Scholar] [CrossRef]
- Riano, D.; Vaughan, P.; Chuvieco, E.; Zarco-Tejada, P.J.; Ustin, S.L. Estimation of fuel moisture content by inversion of radiative transfer models to simulate equivalent water thickness and dry matter content: Analysis at leaf and canopy level. IEEE Trans. Geosci. Remote Sens. 2005, 43, 819–826. [Google Scholar] [CrossRef]
- Jurdao, S.; Yebra, M.; Guerschman, J.P.; Chuvieco, E. Regional estimation of woodland moisture content by inverting radiative transfer models. Remote Sens. Environ. 2013, 132, 59–70. [Google Scholar] [CrossRef]
- Mendiguren, G.; Pilar Martín, M.; Nieto, H.; Pacheco-Labrador, J.; Jurdao, S. Seasonal variation in grass water content estimated from proximal sensing and modis time series in a mediterranean fluxnet site. Biogeosciences 2015, 12, 5523–5535. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.H.; Jin, X.; Zhu, Q. Comparisons of radiative transfer models of vegetation canopies and laboratory measurements. Remote Sens. Environ. 1997, 61, 129–138. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; le Maire, G. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Hunt, E.R., Jr.; Jackson, T.J. Remote sensing of vegetation water content from equivalent water thickness using satellite imagery. Remote Sens. Environ. 2008, 112, 2514–2522. [Google Scholar] [CrossRef]
- Saito, K.; Ogawa, S.; Aihara, M.; Otowa, K. Estimates of Lai for forest management in Okutama. In Proceedings of the 22nd Asian Conference on Remote Sensing, Singapore, 5–9 November 2001.
- Su, B.; Wang, M.S.L. Help for Sebs 4 ILWIS, Water Resources (SEBS); 52° North ITC: Enschede, The Netherlands, 2010. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Liang, S.; Shuey, C.J.; Russ, A.L.; Fang, H.; Chen, M.; Walthall, C.L.; Daughtry, C.S.T.; Hunt, R., Jr. Narrowband to broadband conversions of land surface albedo: II. Validation. Remote Sens. Environ. 2003, 84, 25–41. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B. Revised Landsat-5 TM radiometric calibration procedures and postcalibration dynamic ranges. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2674–2677. [Google Scholar] [CrossRef]
- Tursilowati, L.; Djundjunan, J.D. Use of remote sensing and GIS to compute temperature humidity index as human comfort indicator relate with Land Use-Land Cover change (LULC) in Surabaya. In Proceedings of the 73rd International Symposium on Sustainable Humanosphere, Bandung, Indonesia, 22–25 July 2007; pp. 160–166.
- Adab, H.; Kanniah, K.; Solaimani, K.; Tan, K.P. Estimating atmospheric humidity using MODIS cloud-free data in a temperate humid region. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing, Melbourne, Australia, 21–26 July 2013.
- Yoder, B.J.; Waring, R.H. The normalized difference vegetation index of small douglas-fir canopies with varying chlorophyll concentrations. Remote Sens. Environ. 1994, 49, 81–91. [Google Scholar] [CrossRef]





| Type of Fuel | Parameters Used | Satellite Data | Vegetation Type (Study Area) | Method | Reference |
|---|---|---|---|---|---|
| Litter Dead fuel | Relative Humidity (RH), Air Temperature (AT), Wind Speed, Cloudiness | Not used | Red Pine forests-Taiwan | Linear Regression (LR) R = 0.7 | [24] |
| Litter Dead fuel | AT, RH, Precipitation, Incoming Solar Radiation; Moisture Content, Fuel Surface Temperature, wind speed and direction | Not used | Grasses and herbaceous vegetation-Hawaii | LR R = 0.01–0.85 | [25] |
| Litter, Grasslands Dead fuel | Temperature, Humidity | Not used | Grasslands, shrubs and deciduous-Spain | LR R = 0.11–0.52 | [26] |
| Litter Dead fuel | Maximum Daily Temperature, Minimum Daily RH | Not used | Jarrah and Karri forests-southwest Western Australia | LR R = 0.66 | [27] |
| Live leaves | NDVI ,LST, Relative Greenness Index (RGRE) | AVHRR | Herbaceous and shrubs-Spain | LR R = 0.68 | [22] |
| Live leaves | MSI, NDWI, Water Index (WI), TM5/TM7, Global Vegetation Moisture Index (GVMI) | LOPEX | Mediterranean Species-UK | LR R = 0.71 | [28] |
| Live leaves | NDVI, NDWI | MODIS | Shrubs-US | LR R = 0.6–0.8 | [29] |
| Live leaves | NDVI, NDWI, Vegetation Dryness Index (VDI), Improved VDI (IVDI), Accumulated Relative NDVI Decrement (ARND) | SPOT veg | Herbaceous-South Africa | LR R = 0.75 | [30] |
| Live leaves | NDWI, Normalized Difference Infrared Index (NDII) | MODIS | Cypress stands, shrubs-US | LR R = 0.51 | [31] |
| Live leaves | NDII, NDWI, Visible Atmospheric Resistant Index (VARI) | MODIS | Chaparral (shrubs)-US | LR R = 0.72 | [32] |
| Live leaves | Shortwave Infrared Water Stress Index (SIWSI) | MODIS | Tropical rainforests-Malaysia | LR R = 0.68 | [33] |
| Live leaves | NDVI, Soil Adjusted Vegetation Index (SAVI), Enhanced Vegetation Index (EVI), Global Environmental Monitoring Index (GEMI) ,VARI, NDII, NDWI, Global Vegetation Moisture Index (GVMI) | MODIS | Grasslands and shrub-lands-Spain | IM, LR R = 0.7−0.92 | [34] |
| Live leaves | VARI, NDVI | MODIS | Evergreen shrub, brush-US | LR R = 0.72 | [21] |
| Live leaves | NDVI, NDWI, NDII, Vegetation Index (VI green), VARI, Enhanced Vegetation Index (EVI) | MODIS | Chaparral, coastal sage scrub-US | LR R = 0.72–0.85 | [35] |
| Live leaves | NDVI, VARI, NDWI, NDII, MSI, SRWI, Spectral Reflectance | MODIS | Deciduous forest-Argentina | LR R = 0.72 | [36] |
| Live leaves | NDVI, NDWI, Canopy Water Content (CWC), Soil moisture (SM) | MODIS | Gambel oak and big sagebrush-US | LR R = 0.49 | [37] |
| Live leaves | NDWI, NDII, SRWI, MSI, GVMI | MODIS | Savanna-Senegal | LR R = 0.63 | [38] |
| Live leaves | Spectral Reflectance range 410–2500 nm | LOPEX | Area of the JRC, Ispra, Italy | GA-PLS regression R2 = 0.87–0.89 | [39] |
| Live leaves | Spectral Reflectance range 400–2500 nm | LOPEX | Area of the JRC, Ispra, Italy | PLS R2 = 0.74–0.92 | [40] |
| MCI | Caculated Equation |
|---|---|
| Live Fuel Moisture Content (LFMC) | |
| Dead Fuel Moisture Content (DFMC) | |
| Leaf Dry Matter Content (LDMC) | |
| Leaf Relative Water Content (RWC) |
| Estimated Indicators | Dataset | RMSE | MAE | MAPE | R² |
|---|---|---|---|---|---|
| LFMC (ETM+) | Training (ANN) | 14 | 11.3 | 7.6% | 0.94 |
| Validation (ANN) | 15.6 | 12.6 | 5.9% | ||
| Training (MLR) | 19.9 | 15.4 | 9.82% | 0.90 | |
| Validation (MLR) | 24.4 | 20.7 | 16.03% | ||
| LFMC (MODIS) | Training (ANN) | 43.4 | 31 | 26.63% | 0.70 |
| Validation (ANN) | 48 | 33 | 29.25% | ||
| Training (MLR) | 47.1 | 34.6 | 30.21% | 0.65 | |
| Validation (MLR) | 50.2 | 36.8 | 32.98% | ||
| RWC (ETM+) | Training (ANN) | 4.4 | 3.8 | 6% | 0.94 |
| Validation (ANN) | 5.8 | 3.6 | 6.1% | ||
| Training (MLR) | 3.5 | 2.9 | 4.59% | 0.90 | |
| Validation (MLR) | 6.4 | 5.1 | 7.77% | ||
| RWC (MODIS) | Training (ANN) | 7.3 | 4.5 | 7.84% | 0.75 |
| Validation (ANN) | 8 | 5 | 8.58% | ||
| Training (MLR) | 7.6 | 5 | 8.87% | 0.73 | |
| Validation (MLR) | 8.3 | 5.5 | 9.42% | ||
| LDMC (ETM+) | Training (ANN) | 2.5 | 1.9 | 8% | 0.76 |
| Validation (ANN) | 2.2 | 1.8 | 7.7% | ||
| Training (MLR) | 2.2 | 1.7 | 7.14% | 0.73 | |
| Validation (MLR) | 5.2 | 4.1 | 17.32% | ||
| LDMC (MODIS) | Training (ANN) | 4.8 | 2.9 | 11.19% | 0.78 |
| Validation (ANN) | 4.6 | 2.9 | 11% | ||
| Training (MLR) | 5.4 | 3.7 | 14.41% | 0.72 | |
| Validation (MLR) | 5.2 | 3.7 | 14.6% | ||
| DFMC (ETM+) | Training (ANN) | 1.7 | 2.5 | 12.67% | 0.79 |
| Validation (ANN) | 3 | 2.2 | 12.2% | ||
| Training (MLR) | 2.8 | 2.2 | 14.43% | 0.76 | |
| Validation (MLR) | 4.8 | 3.8 | 16.68% | ||
| DFMC (MODIS) | Training (ANN) | 2.17 | 1.4 | 9.6% | 0.71 |
| Validation (ANN) | 2.6 | 1.7 | 12.1% | ||
| Training (MLR) | 2.45 | 1.7 | 11.6% | 0.64 | |
| Validation (MLR) | 2.9 | 1.99 | 13.9% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adab, H.; Devi Kanniah, K.; Beringer, J. Estimating and Up-Scaling Fuel Moisture and Leaf Dry Matter Content of a Temperate Humid Forest Using Multi Resolution Remote Sensing Data. Remote Sens. 2016, 8, 961. https://doi.org/10.3390/rs8110961
Adab H, Devi Kanniah K, Beringer J. Estimating and Up-Scaling Fuel Moisture and Leaf Dry Matter Content of a Temperate Humid Forest Using Multi Resolution Remote Sensing Data. Remote Sensing. 2016; 8(11):961. https://doi.org/10.3390/rs8110961
Chicago/Turabian StyleAdab, Hamed, Kasturi Devi Kanniah, and Jason Beringer. 2016. "Estimating and Up-Scaling Fuel Moisture and Leaf Dry Matter Content of a Temperate Humid Forest Using Multi Resolution Remote Sensing Data" Remote Sensing 8, no. 11: 961. https://doi.org/10.3390/rs8110961
APA StyleAdab, H., Devi Kanniah, K., & Beringer, J. (2016). Estimating and Up-Scaling Fuel Moisture and Leaf Dry Matter Content of a Temperate Humid Forest Using Multi Resolution Remote Sensing Data. Remote Sensing, 8(11), 961. https://doi.org/10.3390/rs8110961