Building Change Detection Using Old Aerial Images and New LiDAR Data

Abstract

Building change detection is important for urban area monitoring, disaster assessment and updating geo-database. 3D information derived from image dense matching or airborne light detection and ranging (LiDAR) is very effective for building change detection. However, combining 3D data from different sources is challenging, and so far few studies have focused on building change detection using both images and LiDAR data. This study proposes an automatic method to detect building changes in urban areas using aerial images and LiDAR data. First, dense image matching is carried out to obtain dense point clouds and then co-registered LiDAR point clouds using the iterative closest point (ICP) algorithm. The registered point clouds are further resampled to a raster DSM (Digital Surface Models). In a second step, height difference and grey-scale similarity are calculated as change indicators and the graph cuts method is employed to determine changes considering the contexture information. Finally, the detected results are refined by removing the non-building changes, in which a novel method based on variance of normal direction of LiDAR points is proposed to remove vegetated areas for positive building changes (newly building or taller) and nEGI (normalized Excessive Green Index) is used for negative building changes (demolish building or lower). To evaluate the proposed method, a test area covering approximately 2.1 km² and consisting of many different types of buildings is used for the experiment. Results indicate 93% completeness with correctness of 90.2% for positive changes, while 94% completeness with correctness of 94.1% for negative changes, which demonstrate the promising performance of the proposed method.

1. Introduction

The rapid process of urbanization has expedited the dynamics of the cities: numerous buildings are constructed or demolished every year in developing countries such as China. Hence, updating the existing cadastral maps and three-dimensional (3D) models are becoming important. However, these tasks often need time-consuming and expensive manual work in the current practices. Therefore, an automatic or semi-automatic change detection that locates changed buildings can greatly facilitate the updating process, thus being a great interest in the field of photogrammetry and remote sensing.

Conventional change detection methods were mainly based on radiometric information analysis of multi-temporal remote sensed spectral or optical images. Applications include monitoring land use/land cover classes, disaster assessment [1,2,3,4,5]. Image co-registration is an important procedure which can easily be influenced by perspective distortion and imaging conditions [6]. However, change detection results using only 2D image information are often impacted by a significant amount of false alarms mainly caused by seasonal variations, different weather conditions, shadows and occlusions. Moreover, due to the similar spectral characteristics, it is difficult to distinguish buildings from other artificial constructions as bridges and roads [7]. These issues can be particularly problematic for pixel-based methods. Moreover, pixel-based strategies also lead to noisy outputs like isolated pixels, holes in the changed objects or jagged boundaries, since they mainly focus on the spectral values and mostly ignore the spatial context [8,9]. To alleviate these problems, Hopfield neural network [10,11] and deterministic simulated annealing approach [12] have been used to consider the spatial context information to determine image changes. Except from these methods, object-based methods were proposed to compare spectral values with pixel groups [13,14,15,16]. However, this kind of method largely relies on the performance of segmentation or classification, which however varies with image quality and scene complexity [9]. Moreover, 2D image information based methods cannot be easily used to determine the changes at an individual building level and explore the volumetric information changes [17]. Therefore, research on change detection remains an active topic and new techniques are demanded to effectively use available data from satellite, airborne, even low-altitude platforms.

With the increasing available Digital Surface Model (DSM) generated from images using advanced stereo image dense matching algorithm [18,19] and airborne laser scanning technology, 3D information was introduced to determine the change patterns. This is because the height information can be effectively used as an indicator of building changes. During the past decade, various methods using 3D information for change detection have been developed, they can be generally classified into two categories according to the used data: 3D change detection using a single source of multi-temporal data or multiple source of multi-temporal data.

In the first category, the same source of multi-temporal data including multi-temporal stereo images, multi-temporal LiDAR data or a hybrid use of both is employed to detect building changes. Jung [20] compared Digital Elevation Model (DEM) and Tian et al. [21] compared DSM at two different dates to obtain initial change candidate area, and then they used decision trees and box-fitting shape information to determine true building changes respectively. Nevertheless, since the height information comes from dense image matching, it can lead to noisy results if only the height information was used to determine the change area. Because there may be some matching failures caused by occlusions and poor image quality. To perform more robust change detection, Tian et al. [7] employed Dempster–Shafer fusion theory that combined a DSM height difference and a Kullback–Leibler divergence similarity measure of the images to improve the change detection accuracy using IKONOS and WorldView-2 stereo pairs. Nebiker et al. [22] extracted buildings via a rule based method integrating DSM and images from multi-temporal historical aerial photographs, then refine the building extraction result with a cadastral database to support subsequent object-based change detection. Guerin et al. [23] formed the change detection procedure as a labeling problem and solved it by a generalized dynamic programming algorithm with a spatial regularization constraint. However, this method could not handle changed buildings surrounded by vegetation.

Nowadays, LiDAR systems are widely used to acquire dense and accurate 3D information of urban areas [24], and change detection using LiDAR data has increasingly become a research hotspot. In the early days, multi-temporal LiDAR data were used to detect building changes by simply comparing interpolated DSMs [25]. To investigate how to determine the change-type information from multi-temporal LiDAR data, a histogram thresholding was applied in Vu et al. [26]. In another approach, Choi et al. [27] used the classification result to determine real changes after DSM substraction. Different from DSM-based methods, point-based change detection methods were proposed for LiDAR data [28,29,30,31]. Due to the huge data volume and irregular distribution of LiDAR point clouds, an octree was usually used to organize LiDAR data in these methods [31]. To obtain the semantic change information, some object-based methods were proposed to calculate the change map [32,33,34,35], in which LiDAR point clouds were segmented as planes to obtain finally building change map.

In the second category, different sources of multi-temporal data are employed to detect building changes. This category used the existing geographic database as the first-phase data and the aerial images, LiDAR data or a hybrid of these two as the second-phase data [36]. Vosselman et al. [37] and Awrangjeb et al. [38,39] used the geographic database as the first-phase data to compare with building extraction from the newly-available LiDAR data to detect building changes. In addition, Malpica and Alonso [40,41] used the building extraction results from combining images and LiDAR data. However, the detection accuracy of these researches depends on the building extraction results in the second phase data. Liu et al. [42] used the existing CAD data and the aerial images as the first and second phase data to detect building changes. In this method, displacements and occlusion between buildings from CAD data and edge extraction results from images had a significantly influence on the height-change detection. 3D models can also be used as the early date data. Chen and Lin [43] developed a double-threshold strategy to detect building changes to update the 3D building models by using old 3D building models and new LiDAR data. Qin [44] used LOD (Level of Detail) 2 building models with very high resolution space borne stereo imagery to detect building changes and update the 3D database. Inherent geometric consistency, height difference and texture similarity were employed to reduce false alarms of final change result.

In addition to existing of topographic and 3D model database, there are a large number of old aerial images archived that can be used for change detection. Aerial photographs have been systematically collected over decades for civilian map production purposes. Along with the development of airborne laser scanning technology, the frequency of LiDAR data acquisition is also increasing. Thus, it is meaningful to investigate using old aerial images and new LiDAR data to detect changes for applications such as urban growth monitoring or discovering illegal buildings. However, there is limited research focused on building change detection using old aerial images and new LiDAR data. Relevant research can be found in Stal et al. [45], who employed airborne photogrammetry and LiDAR to extract DSMs for detecting the 3D changes over an urban area. Their major focus was to compare the performance and feasibility of using airborne photogrammetry and LiDAR techniques for 3D surface modeling, and extracting 3D building changes information were only performed using DSM differencing. Therefore, a new method using old aerial images and new LiDAR data to detect building changes can enrich the methods for building change detection.

In this paper, we propose an automatic method using aerial images and LiDAR data to detect building changes in urban areas. Robust height difference which takes the minimum height difference over a window [7] and grey-scale information are combined as change indicators, meanwhile, the change detection is modeled as a multi-label Markov Random Field (MRF) and the graph cuts method is employed to determine the change map. A novel method based on variance of normal direction of LiDAR points and nEGI (normalized Excessive Green Index) [46] based on color information are used to alleviate false alarms of vegetation. The rest of the paper is organized as follows: Section 2 describes the case study material and the proposed methodology including three steps of detail. Section 3 presents the experimental results. The proposed methodology is further discussed in Section 4. Section 5 draws the conclusion.

2. Data and Methodology

2.1. Data

The studied area is around Wuhan University in central of Wuhan City in China covering approximately 2.1 km². Wuhan is an old and rapidly developing city, there are many shantytowns among skyscrapers, which are in the process of demolition, and a large amount of urban constructions are happening. Therefore, automatic building change detection in such area is important and challenging.

The test area and the data source are shown in Figure 1. The aerial images shown in Figure 1a were captured by Microsoft UltraCamXp camera in the year of 2010, with a resolution of 0.1m. The used LiDAR data shown in Figure 1b was obtained by Leica ALS 5.0 system in the year of 2014, with an average point density of 10 points/m². The aerial images cover about 4.1 km² while LiDAR data cover about 2.1 km². The LiDAR data is fully overlapped with images (approximately 2.1 km²). This region is mostly flat with the top right of this area including part of a hill. As shown from the mosaicked image from the four UltraCamXp images in Figure 1a, the test area contains dense buildings with complex shapes, and highly disparate building heights (from 3 meters to 130 meters) and sizes (from a few square meters to a few thousands). In addition, several buildings are surrounded by a large number of trees. These characteristics make the building change detection task difficult in this area. Details that represent four different types of buildings are shown in Figure 2.

2.2. Overview of the Proposed Method

Given multiple aerial images and new LiDAR data, the proposed method begins with a co-registration process, which includes three steps. The first step is to orient all available aerial images and obtain dense photogrammetric point clouds using Pix4D. The second step is to remove possible noise in LiDAR data to improve the quality of LiDAR point clouds based on statistical analysis filtering. The third step is to align the photogrammetric point clouds to LiDAR point clouds using a modified ICP (Iterative Closest Point) algorithm [47,48,49]. After that, robust height difference based on a vicinity window [7] will be calculated from the interpolated DSMs. Meanwhile, grey-scale similarity will be computed as another change indicator. Based on these two change indicators, the graph cuts algorithm will be adopted to determine the raw change map. Finally, two different post-processing methods are applied to refine the raw change map. For the positive changes, a novel method based on the variance of normal direction of LiDAR points is proposed to remove the vegetated areas. Meanwhile, nEGI based on color information is used for refining the negative changes. The framework of the method is illustrated in Figure 3.

2.3. Data Preprocessing

In this study, Pix4D is used to perform aerial triangulation for orienting all aerial images and producing dense point clouds (termed photogrammetric point clouds hereafter). The derived point clouds from Pix4D are produced with arbitrary coordinate system due to the lack of ground control points. Since LiDAR point clouds are in a world coordinate, measured with a high-precision on-board GNSS (global navigation satellite system), 3-D similarity transformation is used to these two kinds of point clouds for following co-registration.

During the LiDAR point clouds acquiring, some sparse outliers can be caused by flying birds or the measurement errors. These sparse outliers may lead to some errors in the interpolated DSM influencing the building change detection results. To alleviate these noisy effects in the LiDAR data, a statistical analysis based filtering method is applied [50]. Firstly, for each point $p_i$, the mean distance ${\mu }_i$ from it to all its $k$ nearest neighbor points is calculated. Afterward, global mean distance $\mu$ and standard distance deviation $\sigma$ are calculated and then the points whose mean distance ${\mu }_i$ is outside $\left[\mu -t\sigma ,\mu +t\sigma \right]$ can be considered as outliers. In our implementation, the neighborhood size $k$ is set to 30 and $t$ is empirically set to 5.

After that, a two-step method based on the ICP algorithm is used to complete co-registration. Firstly, three corresponding points are manually selected from both of the point clouds to estimate initial transformation parameters, and then a modified ICP algorithm is used to achieve a fine registration of multi-temporal point clouds. For detailed description of the ICP algorithm, the readers may refer to [47,48,49].

Due to the different quality and density of the photogrammetric and LiDAR point clouds, point-based comparison may lead to unfavorable results. Therefore, a DSM-based comparing method is adopted in our research. After co-registration of the two point clouds data, the Inverse Distance Weighted (IDW) interpolation method is used to generate DSM [51,52]. To facilitate comparison, both DSMs from both the photogrammetric (denoted as DSMold hereafter) and LiDAR point clouds (denoted as DSMnew hereafter) are resampled to 0.5 m.

2.4. Change Detection

2.4.1. Change Indicator

(1) Height Difference

If DSMold and DSMnew both have a good quality, a direct pixel-wise subtraction of DSMs can obtain a good change indicator. However, the quality of these two DSMs is quite different. Moreover, there may be a residual shift in three dimensions after the co-registration procedure. Therefore, such a direct pixel-wise subtraction of DSMs is generally not appropriate [7,53]. To alleviate such effects, a robust height difference method based on a vicinity window is employed [7]. For a pixel $(i,j)$ in DSM, the robust difference refers to the minimum difference between $X_2(i,j)$ in the DSMnew, and a certain vicinity of the pixel $X_1(i,j)$ in the DSMold. The robust positive difference $\Delta Z_P(i,j)$ and negative difference $\Delta Z_N(i,j)$ corresponding to the pixel $(i,j)$ are defined as Equation (1):

$$\{\begin{array}{l}\Delta Z_P(i,j)=min\left\{\begin{array}{cc}{Z}_2(i,j)-Z_1(p,q),& Z_2(i,j)-Z_1(p,q)>0\end{array}\right\}\\ \Delta Z_N(i,j)=max\left\{\begin{array}{cc}{Z}_2(i,j)-Z_1(p,q),& Z_2(i,j)-Z_1(p,q)<0\end{array}\right\}\end{array}$$

(1)

where $Z_1(p,q)$ and $Z_2(i,j)$ refer to the elevation value of pixel $X_1(p,q)$ and $X_2(i,j)$, $p\in \left\{i-w,i+w\right\}$, $q\in \left\{j-w,j+w\right\}$, and $w$ is the vicinity window size (empirically set to 3). Based on Equation (1), a height difference map can be calculated.

(2) Grey-scale Similarity

As the used photogrammetric point clouds are derived from image pairs, if we back-project a 3D photogrammetric point to the stereo image pair, it will appear as a correspondence in image space. After co-registering photogrammetric and LiDAR point clouds, the back-projected LiDAR points to the stereo image pair will also appear as a correspondence, if there is none height change. However, if there is a height change, it will no longer be a correct correspondence. As shown in Figure 4a, projecting the point $A_{old}(X_i,Y_j,Z_o)$ in DSMold to corresponding images will get a match ($x_1,x_2$) in image space. If we calculate the Normalized Cross-Correlation (NCC) in a neighborhood taking the match as center, this NCC value will tend to 1. If there is no height change for $A_{new}(X_i,Y_i,Z_n)$ in DSMnew, i.e., $Z_n$ equal to $Z_o$, we project $A_{new}(X_i,Y_i,Z_n)$ to both images will get the same match ($x_1,x_2$). As shown in Figure 4a, if there is height change for $A_{new}(X_i,Y_i,Z_n)$, the back-projection image points ($x_1^{\prime },x_2^{\prime }$) could no longer be a correct corresponding point because height change occurs in this position. In such case, as X and Y coordinate is same, difference in Z value will lead to a smaller NCC values calculated from the pixels around ($x_1^{\prime },x_2^{\prime }$). However, if $Z_n$ close to $Z_o$, NCC values will also be higher. As illustrated in Figure 4b, object $P_1$ has no height change so it gets correspondence in image space. On the contrary, object $P_2$ does not get correct correspondence due to height change. Thus, this observation is used as another indicator to infer changes [44]. We project each grid center of the DSMnew into all the old images to obtain NCC map. The NCC value is computed among each other images and the maximum value is adopted for each grid. Window size for computing NCC is set to 13 × 13. The calculated NCC map is shown in Figure 4c, where it can be seen that the changed building marked in the ellipse in Figure 4b has low NCC value.

2.4.2. Change Optimization Using Graph Cuts

As the height difference is sometimes unreliable especially on small buildings and areas lack of texture. When calculating the grey-scale similarity indicator, occlusions can lead to a lower similarity, which makes the grey-scale similarity unreliable too. Therefore, the height difference and grey-scale similarity should be combined suitably. In addition, the adjacent DSM cells which have similar height difference and grey-scale similarity are likely to have the same change status. Thus, we model the change detection task as a multi-label Markov Random Field considering the contexture constraints, and used the graph cuts algorithm to solve it [54,55].

The graph cuts algorithm has been widely used in the field of computer vision for labeling optimization [54,55]. The basic idea is to construct a weighted graph based on the pixels and their neighborhoods. Each edge is weighted according to the similarities between its connected two nodes, and this forms part of the cost in an energy function. The objective of graph cuts algorithm is to find a label $lp$ for each node of the graph by minimizing the energy function as defined as Equation (2).

$$E\left(l\right)={\displaystyle \sum _{p\in P}{D}_p(l_p)}+\beta {\displaystyle \sum _{p,q\in N}{V}_{p,q}(l_p,l_q)}$$

(2)

The first term ${\displaystyle \sum _{p\in P}{D}_p(l_p)}$ relates to the data cost. The second term ${\displaystyle \sum _{p,q\in N}{V}_{p,q}(l_p,l_q)}$ relates to the smooth cost imposing a spatial smoothness.

In this research, three types of change detection are defined: no change, positive change (corresponding to newly built buildings or stories), and negative change (corresponding to demolished buildings or stories). The purpose of the change detection is to assign a label from the three labels to each pixel in the DSM. This task as a multi-labeling problem can be solved by graph cuts. The data term for each pixel p is comprised of two terms as Equation (3): height difference term (HD) and grey-scale similarity (GS).

$$D_p(l_p)=(1-\lambda )\cdot HD+\lambda \cdot GS$$

(3)

where

$$HD=\{\begin{array}{ll}\frac{1}{1+{\mathrm{e}}^{-K(\left|\Delta Z\right|-T)}},& l_p=0(nochange)\\ 1-\frac{1}{1+{\mathrm{e}}^{-K(\Delta Z-T)}},& l_p=1(positivechange)\\ 1-\frac{1}{1+{\mathrm{e}}^{-K(-\Delta Z-T)}},& l_p=2(negativechange)\end{array}$$

(4)

$$GS=\{\begin{array}{ll}1-NCC,& l_p=0(nochange)\\ NCC,& l_p=1(positivechange)\\ NCC,& l_p=2(negativechange)\end{array}$$

(5)

$$NCC=\{\begin{array}{ll}NCC,& if(NCC\ge 0)\\ 0,& if(NCC<0)\end{array}$$

(6)

where $\Delta Z$ is obtained from height difference map, and NCC is obtained from NCC map. The parameter $\lambda$ defines the balance between height difference and grey-scale similarity in the data term. As the value of GS ranges from 0 to 1, while HD is out of this range, it should be normalized to the same range. In Equation (4), HD is normalized by a logistic function into a “S” shaped curve which controls the sensitivity of height difference. The parameter $T$ is the minimal height of building object and is empirically set to 3.0 m (about the height of a floor). $K$ controls the steepness of the curve. In our research, $K$ is set to 3.0 which gets the best balance between the detected results and false alarms.

The smooth term of the labels $l_p$ and $l_q$ on the adjacent pixels p and q is defined in Equation (7):

$${\delta }_{pq}=\{\begin{array}{ll}1& (if{l}_p-l_q=0)\\ 0& (if{l}_p-l_q\ne 0)\end{array}$$

(7)

As mentioned in Equation (2), $\beta$ controls the weight of smooth term and has certain impacts on the results. Higher $\beta$ will lead to the smoother results.

After defining the energy function, standard $\alpha$-expansion [55] is used to solve the multi-label optimization problem and the output gives a label for each DSM pixel.

2.5. Post-Processing

The results processed by graph cuts still contain noise, which mainly comes from vegetated areas, small clusters and linear-shaped outliers caused by uncertainty of the building boundary. Hence, post-processing is carried out to refine the raw detection results. Positive changes refer to new buildings appearing in new LiDAR data. Thus this type of change can be refined on new LiDAR data. Negative changes refer to buildings demolished and no longer present in the later LiDAR data set, so the refinement needs to be performed on the first time of data. Therefore, different procedures are proposed to refine the change detection results and distinguish the changed buildings from vegetated areas. The biggest difference between these two post-processing methods is the use of LiDAR geometric features and image color to exclude vegetated areas respectively. Moreover, an extra occlusion filter is applied to alleviate false alarms of negative change due to the dense image matching failure.

2.5.1. Positive Building Change Results Refinement

The workflow of positive building change refinement is shown in Figure 5, and the detailed procedure is described in the following paragraphs.

(a) Blunder filter

As some linear-shaped outliers near the building boundary due to the different resolution of the aerial image and LiDAR data and small clusters remaining in the raw detection results, a morphological opening operation is applied to filter these blunders [56]. The kernel is set to 8 $\times$ 8 pixels.

(b) Area threshold

Because the quality of the DSM from the stereo dense matching technique is not accurate enough, there will be several small fragments of false alarm in the detection result. As the areas of most buildings are usually larger than a certain value, the change map is segmented by connected component analysis, and then small segment regions smaller than 50 m² are removed.

(c) Vegetation filter

After performing the above filtering, there will be some false alarms in the positive changes caused by vegetation growth or new vegetation. Usually, the building roofs contain planar surfaces while the surface of the trees are irregular. Thus, the roughness index can be applied to differentiate false alarms caused by trees. In the work of Pang et al. [35] and Stal et al. [45], a plane filter and roughness index were employed to remove the vegetated areas, respectively. However, since building roofs may be more complex, especially for a skyscraper, it is almost impossible to fit planes or calculate the roughness as the index. Therefore, a flexible method based on normal statistics is proposed to remove the vegetated areas. This method assumes that the normals of the points within vegetated areas have many different directions while the normals of building contain only a few. Thus, a histogram based on the angle $\alpha V$ of the normal to vertical direction is calculated for each changing object, and then squared coefficient of variation (abbreviated as scv hereafter) of the histogram is used as an index to indicate the dispersion of normal direction frequency count around the mean frequency count. An example of a building and a vegetation area is shown in Figure 6. For each point, $\alpha V$ is calculated, then these $\alpha V$ are color-coded to display their distribution. From the result, we can see that much point display one principal color as shown in Figure 6a, while Figure 6b illustrates more uniform color distribution, which means the normal direction of the building aggregated to a principle direction.

To calculate the index for each object, the normal of each corresponding LiDAR point of the processed change object is calculated via its neighboring points. The histogram of $\alpha V$ in each object is then calculated. After that, scv is computed by Equation (8):

$$\begin{array}{l}scv=\frac{{\delta }^2}{u^2}\\ {\delta }^2=\frac{{\displaystyle \sum _{i=1}^{noi}{(ni-u)}^2}}{noi}\\ u=\frac{N}{noi}\end{array}$$

(8)

where $noi$ is the number of bins, $n_i(i=1,2,\dots ,noi)$ is the point number of each bin, and $N$ is number of all points of an object. A small scv indicates the object has no principal direction and can be determined as vegetation. From Figure 6c,d, we can see that the building area has a principal direction, thus scv is higher, while the scv for vegetation object is lower. In our research, the objects whose absolute height calculated by subtracting the height of the lowest point to height of the highest point is taller than 50 m are considered as buildings, and other objects will be filtered by the proposed method. In this method, the number of bins for histogram is set to 9 and the threshold $T_{scv}$ of scv is set to 1.1.

2.5.2. Negative Building Change Results Refinement

To refine the negative building change map, the processes of blunder filtering, and area threshold filtering are used in a similar way as mentioned Section 2.5.1. In addition, a different vegetation filter and an extra occlusion filter are proposed to alleviate false alarms. The workflow of negative building change refinement is shown in Figure 7, and the detailed procedures of occlusion filter and vegetation filter are described in the following paragraphs.

(a) Occlusion filter

Occlusions caused by buildings can easily result in matching failure or holes in the derived photogrammetric point clouds from dense matching. These holes in the subsequent DSMold will be filled with interpolated height values, and then DSMold in such area will get higher elevation values than its true value. Since this occlusion problem may not exist in LiDAR data, false negative changes will exist in these areas. Thus, to alleviate the disturbances caused by occlusion, the standard deviation ${\delta }_H$ of the neighborhood for each pixel of the DSMold which lacks original photogrammetric 3D points is calculated by Equation (9):

$${\delta }_H=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{(H_i-{\mu }_H)}^2}}$$

(9)

where $H_i$ is the height of neighborhood DSMold grid, and ${\mu }_H$ is the average height value. Pixel with ${\delta }_H>T_H$ ($T_H$ is empirically set to 0.5 m to get a balance between the occlusion areas and weak texture areas) is marked as an occlusion area. The window size for ${\delta }_H$ calculation is set to 11 × 11 pixels. After getting the occlusion-mask, the changed detection results within the occlusion-mask will be removed to eliminate the false alarms.

Figure 8 provides an example to illustrate the occlusion filtering processing. Figure 8a,b is a corresponding region in DSMold and DSMnew. It can be seen that the building area in DSMold is larger than the corresponding building in DSMnew. This is because that there are interpolated errors in the occlusion area below the sides of these buildings. This phenomenon does not exist in DSMnew. This situation will lead to the false detection, as shown in Figure 8c. After occlusion filtering, the occlusion areas can be mostly be removed as shown in Figure 8d, the linear-shape bundlers as shown in the red polygon area will be removed by a morphological opening operation.

(b) Vegetation filter

Building roofs can falsely appear uneven and discontinuous, as a result of inaccuracies in stereo matching. Accordingly, scv can be unreliable for the negative changes. However, the negative building change refinement can take full advantage of the color information from images. Thus, nEGI [46] is adopted in this paper to remove possible vegetated areas. nEGI is calculated for each change cluster as Equation (10):

$$nEGI=\frac{2\times G-R-B}{2\times G+R+B}$$

(10)

where $R,G$ and $B$ are the color value extracted from the back-projecting point on the nearest images of DSM pixel. Clusters whose average nEGI with all of the pixels is larger than a given threshold (set to 0.05) are removed.

3. Experimental Results

3.1. Data Preprocessing Results

The photogrammetric point clouds generated from the aerial images are shown in Figure 9a and there are several obvious holes in the point clouds especially around the tall buildings. After obtaining the photogrammetric point clouds, a pre-processing step is performed to co-register these two sets of point clouds. The RMSE (Root Mean Square Error) between two point clouds is about 0.2 m. After co-registration, a profile of point clouds in the cyan solid line of Figure 9b from these two sets of point clouds is selected to demonstrate registration accuracy. The profile is shown in Figure 9c and it indicates these two sets of point clouds are well aligned after the registration. To further evaluate the registration result, a part of the selected profile about a building roof is amplified and shown in Figure 9d. The maximal distance between these two profiles is about 0.28 m.

After data co-registration, DSMold and DSMnew are interpolated from photogrammetric points and LiDAR data, respectively, using IDW interpolation method. The interpolated DSM results are in shown as Figure 10.

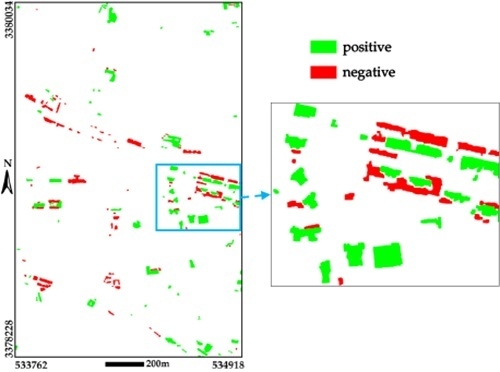
3.2. Building Change Detection Results

There are several parameters in the proposed method. Some of them have a minimal impact on the results and can be empirically set while others have a relatively significant impact. Three key parameters are set as in

Table 1. The key parameters of the proposed method.

Parameters	Description	Value	Set Mode
$T_{scv}$	Threshold for squared coefficient of variation of the histogram	1.1	Experimentally
$\lambda$	the weight of grey-scale similarity in the data term	0.6	Experimentally
$\beta$	the weight of smooth term in the energy function	0.75	Experimentally

and the influence of the parameter will be analyzed subsequently.

To quantitatively evaluate the proposed method, reference data are manually drawn with the assistance of point clouds and aerial images. Building changes are classified into two types: positive change (corresponding to newly buildings or taller buildings) and negative change (corresponding to demolished buildings or lower buildings). There are in total 89 positively changed buildings and 85 negatively changed buildings in the reference data. The details of the building change detection results and reference data are shown in Figure 11, where there are a large number of changed buildings in this area with different and complex shapes.

Since only changed buildings larger than 50 m² are kept in our results, we only compare it to the corresponding ground-truth changes. From Figure 11, it can be seen that most of the building changes are detected, and these contain even some small buildings. The results indicates that the proposed method can effectively detect building changes in an urban area using images and LiDAR data. Moreover, most vegetation changes are excluded by nEGI and the proposed variance of normal distribution. In order to make a quantitative analysis of the results, completeness and correctness defined as follows is used to evaluate the result:

$$\begin{array}{l}Completness=\frac{TDN}{RN}\times 100\%\\ Correctness=\frac{TDN}{DN}\times 100\%\end{array}$$

(11)

where TDN (true detected number) is the number of real changed buildings correctly detected as changed, RN (Reference Number) is the number of changed buildings in the reference data and DN (Detected Number) is the number of changed buildings in the detected results. For the object-based evaluation, as long as the detected object has an overlap with the reference data, the object is accepted as being detected correctly [35]. Building change detection results of the proposed method are listed in

Table 2. The building change detection results of the proposed method.

Type	Reference Number	Detected Number	True Detected Number	False Detected Number	Completeness	Correctness
Positive	89	92	83	9	93.3%	90.2%
Negative	85	85	80	5	94.1%	94.1%

.

As shown in Table 2, the completeness of positive and negative building change is 93.3% and 94.1%, respectively, while the correctness is 90.2% and 94.1%. Generally, most negative changes are low-rise buildings which can be easily influenced by the surrounding objects and difficult to detect, but in our results, the completeness of negative building change is more than 94%, which is a promising result. The six omissions for positive changes are mainly caused by two circumstances:

(1)

The buildings with complex structures of roofs or covered by vegetation are removed by the proposed method, which is the main cause of omissions (Figure 12).

(2)

The newly built low-rise buildings with a lower height.

The nine false alarms for positive change are mainly caused by the matching failure in the dense image matching step which leads to significant errors on the height of interpolated DSM.

The five omissions of negative changes mainly refer to change of low-rise buildings, especially in cases where a low-rise building changed into smooth vegetated area that leads to nearly none height change.

The five false alarms for negative changes are mainly caused by two circumstances:

(1)

Some vegetated areas have insignificant green color which is hard to be removed using the nEGI.

(2)

A newly built underground passage results in the subsidence of ground. As shown in Figure 13, there are almost 5 m changes in ground height.

4. Discussion

4.1. Prameter Selection and Sensitivity Analysis

A sensitivity analysis of the three key parameters listed in Table 1 is performed and the results are shown in Figure 14.

It should be noted that the parameter $T_{scv}$ only influences the result of positive building changes, therefore only the positive changes are counted in Figure 14a while for the parameter $\lambda$ and $\beta$, the positive and negative changes are both included.

In Figure 14a, when $T_{scv}$ increases, completeness decreases gradually, and correctness increases. This can be explained by part of the changed building object being mistakenly identified as vegetation and removed. According to the comprehensive comparison, $T_{scv}=1.1$ obtained the best balance between completeness and correctness. In this research, the number of bins is set to 9, and through our experiment, the bins number can be set 6 to 10 which are all appropriate.

From Figure 14b, it can be seen that the combined grey-scale similarity and height difference effectively increases completeness, since both indicators are compensating to each other. If only the height difference were employed as the change indicator, a number of changed building may be missed due to the uncertainties of the height difference, and these omissions may be detected when the grey-scale similarity are considered. However, it can also be seen that when the weight of grey-scale similarity is larger than 0.6 (i.e., the weight of height difference is less than 0.4), the completeness and correctness will both decrease significantly. This can be explained that there are several uncertainties among grey-scale similarity, and when the weight of grey-scale similarity is too large, there will be significant false alarms that lead to the decrease of correctness. In addition, height difference can determine the changes are positive or negative while the grey-scale similarity can indicates binary changes. Therefore, when the weight of height difference is too small, positively or negatively changed buildings are not determinable, which leads to the decrease of completeness. Thus, good leverage between height difference and grey-scale similarity in the data term of the energy function is important. According to our comprehensive test and evaluation, $\lambda =0.6$ leads to the best result in our experiment.

As shown in Figure 14c, the weight of smooth term may impact the results, especially on the completeness. When $\beta$ is between 0 to 0.75, completeness increases significantly, contributed by the consideration of neighborhood relationship by using graph cuts, but when the weight $\beta$ is too large, some buildings especially small buildings will be absorbed by the background. In our experiment, we obtained the best results with $\beta$ = 0.75.

It is worth mentioning that some of the parameters might be adjusted to adapt the different urban environment and the used data source for better change detection results. From Figure 14, it can be observed that $\lambda$ is relatively sensitive, thus, the balance between two change indicators, height difference and grey-scale similarity, is important, and should be tuned carefully.

4.2. Comparison

The main objective of the proposed method is to detect building changes using old aerial images and new LiDAR data. The relevant methods in the literatures used the same source of multi-temporal data [7,31,35] or using post remote sensing data to detect changes in the existing map or 3D model [38,43,44]. Thus, a direct and thoroughly comparison to these methods is difficult for different data source was employed. Therefore only the object-based calculated completeness and correctness reported in some typical studies are presented in

Table 3. Comparison results of Completeness and Correctness to relevant studies (× means no relevant result).

Methods	Data Source		Completeness (%)	Correctness (%)
	First Time	Second Time
Xu et al. [31]	LiDAR data	LiDAR data	94.81	×
Pang et al. [35]	LiDAR data	LiDAR data	97.8	91.2
Chen and Lin [43]	polyhedral building model	LiDAR data and aerial imagery	91.67	82.6
Qin [44]	3D model	stereo satellite imagery	82.6	×
Awrangjeb [38]	building database	LiDAR data	99.6	63.2
Tian et al. [7]	stereo satellite image	stereo satellite imagery	93.33	87.5
The proposed method	aerial imagery	LiDAR data	93.5	92.15

. Some of them are calculated via Equation (11) using the experimental results from the selected literature, such as [7,43,44]. For the results of [7], one of the better results is listed. For the result of [38] and the proposed method, average result is compared. From Table 3, we can see that our results compare well with these methods. The comparison results reveal that the proposed method can provide a good balance between Completeness and Correctness.

4.3. Limitations of the Proposed Building Change Detection

Due to the noise and uncertainties of dense photogrammetric point clouds, the boundary of changed buildings cannot be accurately determined by the proposed method. A further extension of our method to object-based analysis and post-processing without building outline detection may potentially solve this issue to a certain extent.

The vegetation filtering of the positive and negative detected object is based on the surface normal and nEGI, which demonstrated good performance in our experiment. However, since some vegetation appears to be in green, not to mention if the images are taken in the fall or winter, so false alarms may occur in these cases. For the variance of surface normal, buildings with complex roof or covered by vegetation may be removed, leading to omission errors. Therefore, the vegetation filtering method needs to be further investigated.

5. Conclusions

During recent decades, aerial imagery has frequently been acquired and archived. LiDAR nowadays is more widely employed to acquire accurate 3D information of urban areas. Thus, this paper investigated the use of aerial images and LiDAR data to determine the building changes. In our proposed method, graph cuts labeling is employed to determine changes, and the height difference is combined with the grey-scale similarity to form the data term of the energy function, and the efficiency of the combined methodology is validated in the experiment. To remove the vegetated areas, nEGI and a novel method based on the variance of the surface normal are employed. A test area covering approximately 2.1 km² and consisting of many different types of buildings is used in the experiment. The results show that the completeness of more than 93% for positive changes, 94% for negative changes, and correctness of 90.2% and 94.1%, respectively, which are promising results in a building change detection task. It can be compared to the building detection result with the same source of multi-temporal data. The proposed method can enrich the current change detection methods, especially when the same source multi-temporal data are not available for change analysis or the old cadastral database is not available for locating areas of buildings.

The key contributions of this study are as follows: First, it is a valuable attempt to detect building changes using images and LiDAR data from two dates, which have rarely been researched before. Second, height difference and grey-scale similarity are extracted as two change indicators and the graph cuts method is employed to determine the changes considering neighborhood relationships, and this approach can also be used for change detection with other data source. Third, a novel method based on the squared coefficient of variation of a histogram generated from surface normal directions is proposed to distinguish the vegetation from buildings of the LiDAR point clouds.

In future work, a robust dense image matching is planned to acquire accurate height information for aerial images. Object-based methods will be used to determine the more precise shape of changed buildings. For complex urban areas, more information should be taken into account to improve the change detection results, such as building shapes and texture features.