Quantitative Retrieval of Organic Soil Properties from Visible Near-Infrared Shortwave Infrared (Vis-NIR-SWIR) Spectroscopy Using Fractal-Based Feature Extraction
Abstract
:1. Introduction
2. Materials and Methods
2.1. The LUCAS Topsoil Database
2.2. Fractal Feature Extraction Method
2.2.1. Concept of Fractal Dimension
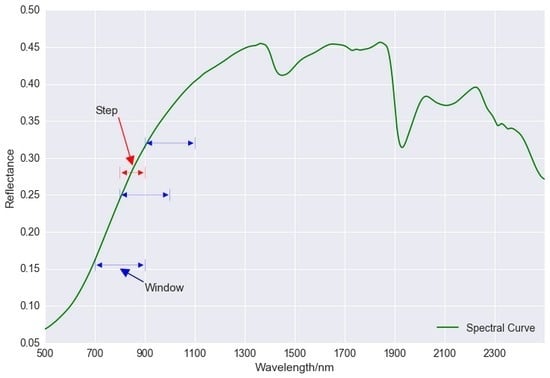
2.2.2. Variation Method for Fractal Dimension
2.2.3. Fractal Feature Generation
2.3. Gradient-Boosting Regression Model
2.4. Evaluation
3. Results
3.1. Fractal Features for Soil Spectroscopy
3.2. Effects of Different Step and Window Size on Extracted Fractal Features
3.3. Modelling Soil Properties with Fractal Features
3.4. Comparison with PLS Regression
4. Discussion
4.1. The Importance of Fractal Dimension for Soil Spectra
4.2. Modelling Soil Properties with Fractal Features
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of soil organic carbon at the European scale by visible and near infraRed reflectance spectroscopy. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Chabrillat, S.; Ben-Dor, E.; Viscarra Rossel, R.A.; Demattê, J.A.M. Quantitative soil spectroscopy. Appl. Environ. Soil Sci. 2013, 2013, 616578. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar]
- Nocita, M.; Stevens, A.; van Wesemael, B.; Aitkenhead, M.; Bachmann, M.; Barthès, B.; Ben-Dor, E.; Brown, D.J.; Clairotte, M.; Csorba, A.; et al. Soil spectroscopy: An alternative to wet chemistry for soil monitoring. Adv. Agron. 2015, 132, 139–159. [Google Scholar]
- Ben-Dor, E.; Taylor, R.G.; Hill, J.; Demattê, J.A.M.; Whiting, M.L.; Chabrillat, S.; Sommer, S. Imaging spectrometry for soil applications. Adv. Agron. 2008, 97, 321–392. [Google Scholar]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Behrens, T.; Schmidt, K.; Stevens, A.; Demattê, J.A.M.; Scholten, T. The spectrum-based learner: A new local approach for modeling soil Vis-NIR spectra of complex datasets. Geoderma 2013, 195, 268–279. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; MacDonald, L.M.; McLaughlin, M.J. The performance of visible, near-, and mid-infrared reflectance spectroscopy for prediction of soil physical, chemical, and biological properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- Epema, G.F.; Kooistra, L.; Wanders, J. Spectroscopy for the assessment of soil properties in reconstructed river floodplains. In Proceedings of the 3rd EARSeL Workshop on Imaging Spectroscopy, Herrsching, Germany, 13–16 May 2003; pp. 13–16.
- Udelhoven, T.; Emmerling, C.; Jarmer, T. Quantitative analysis of soil chemical properties with diffuse refectance spectrometry and partial least-square regression: A feasibility study. Plant Soil 2003, 251, 319–329. [Google Scholar] [CrossRef]
- McBratney, A.B.; Minasny, B.; Viscarra Rossel, R.A. Spectral soil analysis and inference systems: A powerful combination for solving the soil data crisis. Geoderma 2006, 136, 272–278. [Google Scholar] [CrossRef]
- Shepherd, K.D.; Walsh, M.G. Infrared spectroscopy—Enabling an evidence-based diagnostic surveillance approach to agricultural and environmental management in developing countries. J. Near Infrared Spectrosc. 2007, 15, 1–19. [Google Scholar] [CrossRef]
- Tóth, G.; Hermann, T.; Da Silva, M.R.; Montanarella, L. Heavy metals in agricultural soils of the European Union with implications for food safety. Environ. Int. 2016, 88, 299–309. [Google Scholar] [CrossRef] [PubMed]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Ji, W.; Li, S.; Chen, S.; Shi, Z.; Viscarra Rossel, R.A.; Mouazen, A.M. Prediction of soil attributes using the Chinese soil spectral library and standardized spectra recorded at field conditions. Soil Tillage Res. 2016, 155, 492–500. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Franceschini, M.H.D.; Demattê, J.A.M.; da Silva Terra, F.; Vicente, L.E.; Bartholomeus, H.; de Souza Filho, C.R. Prediction of soil properties using imaging spectroscopy: Considering fractional vegetation cover to improve accuracy. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 358–370. [Google Scholar] [CrossRef]
- Steinberg, A.; Chabrillat, S.; Stevens, A.; Segl, K.; Foerster, S. Prediction of common surface soil properties based on Vis-NIR airborne and simulated EnMAP imaging spectroscopy data: Prediction accuracy and influence of spatial resolution. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Tóth, G.; Jones, A.; Montanarella, L. LUCAS Topsoil Survey: Methodology, Data, and Results; Joint Research Centre, European Commission: Ispra, Italy, 2013. [Google Scholar]
- Vågen, T.G.; Shepherd, K.D.; Walsh, M.G.; Winowiecki, L.; Desta, L.T.; Tondoh, J.E. AfSIS Technical Specifications: Soil Health Surveillance; World Agroforestry Centre: Nairobi, Kenya, 2010. [Google Scholar]
- Mukherjee, K.; Ghosh, J.K.; Mittal, R.C. Dimensionality reduction of hyperspectral data using spectral fractal feature. Geocarto Int. 2012, 27, 515–531. [Google Scholar] [CrossRef]
- Huang, H.; Luo, F.; Liu, J.; Yang, Y. Dimensionality reduction of hyperspectral images based on sparse discriminant manifold embedding. ISPRS J. Photogramm. Remote Sens. 2015, 106, 42–54. [Google Scholar] [CrossRef]
- Qiao, T.; Ren, J.; Craigie, C.; Zabalza, J.; Maltin, C.; Marshall, S. Quantitative prediction of beef quality using visible and NIR spectroscopy with large data samples under industry conditions. J. Appl. Spectrosc. 2015, 82, 137–144. [Google Scholar] [CrossRef]
- Xing, C.; Ma, L.; Yang, X. Stacked denoise autoencoder based feature extraction and classification for hyperspectral images. J. Sensors 2015, 2016, 3632943. [Google Scholar] [CrossRef]
- Li, F.; Xu, L.; Wong, A.; Clausi, D.A. Feature extraction for hyperspectral imagery via ensemble localized manifold learning. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2486–2490. [Google Scholar]
- Bakir, C. Nonlinear feature extraction for hyperspectral images. Int. J. Appl. Math. Electron. Comput. 2015, 3, 244–248. [Google Scholar] [CrossRef]
- Lunga, D.; Prasad, S.; Crawford, M.M.; Ersoy, O. Manifold-learning-based feature extraction for classification of hyperspectral data: A review of advances in manifold learning. IEEE Signal Process. Mag. 2014, 31, 55–66. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Chen, C. Digitally mapping the information content of visible-near infrared spectra of surficial Australian soils. Remote Sens. Environ. 2011, 115, 1443–1455. [Google Scholar] [CrossRef]
- Zheng, L.; Li, M.; An, X.; Pan, L.; Sun, H. Spectral feature extraction and modeling of soil total nitrogen content based on NIR technology and wavelet packet analysis. SPIE Asia-Pac. Remote Sens. 2010, 7857. [Google Scholar] [CrossRef]
- Ramirez-lopez, L.; Behrens, T.; Schmidt, K.; Viscarra Rossel, R.A.; Demattê, J.A.M.; Scholten, T. Distance and similarity-search metrics for use with soil vis-NIR spectra. Geoderma 2013, 199, 43–53. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Roweis, S. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Kalousis, A.; Prados, J.; Rexhepaj, E.; Hilario, M. Feature extraction from mass spectra for classification of pathological states. In Proceedings of the 9th European Conference on Principles and Practice of Knowledge Discovery in Databases, Porto, Portugal, 3–7 October 2005.
- Ghosh, J.K.; Somvanshi, A. Fractal-based dimensionality reduction of hyperspectral images. J. Indian Soc. Remote Sens. 2008, 36, 235–241. [Google Scholar] [CrossRef]
- Junying, S.; Ning, S. A dimensionality reduction algorithm of hyper spectral image based on fract analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 297–302. [Google Scholar]
- Mukherjee, K.; Bhattacharya, A.; Ghosh, J.K.; Arora, M.K. Comparative performance of fractal based and conventional methods for dimensionality reduction of hyperspectral data. Opt. Lasers Eng. 2014, 55, 267–274. [Google Scholar] [CrossRef]
- Tóth, G.; Jones, A.; Montanarella, L. The LUCAS topsoil database and derived information on the regional variability of cropland topsoil properties in the European Union. Environ. Monit. Assess. 2013, 185, 7409–7425. [Google Scholar] [CrossRef] [PubMed]
- Ballabio, C.; Panagos, P.; Monatanarella, L. Mapping topsoil physical properties at European scale using the LUCAS database. Geoderma 2016, 261, 110–123. [Google Scholar] [CrossRef]
- Reljin, I.S.; Reljin, B.D.; Avramov-Ivić, M.L.; Jovanović, D.V.; Plavec, G.I.; Petrović, S.D.; Bogdanović, G.M. Multifractal analysis of the UV/VIS spectra of malignant ascites: Confirmation of the diagnostic validity of a clinically evaluated spectral analysis. Phys. A Stat. Mech. Its Appl. 2008, 387, 3563–3573. [Google Scholar] [CrossRef]
- Hall, P.; Wood, A. On the performance of box-counting estimators of fractal dimension. Biometrika 1993, 80, 246–251. [Google Scholar] [CrossRef]
- Constantine, A.G.; Hall, P. Characterizing surface smoothness via estimation of effective fractal dimension. J. R. Stat. Soc. Ser. B 1994, 56, 97–113. [Google Scholar]
- Chan, G.; Hall, P.; Poskitt, D. Periodogram-based estimators of fractal properties. Ann. Stat. 1995, 1684–1711. [Google Scholar] [CrossRef]
- Klinkenberg, B. A review of methods used to determine the fractal dimension of linear features. Math. Geol. 1994, 26, 23–46. [Google Scholar] [CrossRef]
- Gneiting, T.; Sevcikova, H.; Percival, D.B. Estimators of fractal dimension: Assessing the roughness of time series and spatial data. Stat. Sci. 2011, 27, 247–277. [Google Scholar] [CrossRef]
- Mukherjee, K.; Ghosh, J.K.; Mittal, R.C. Variogram fractal dimension based features for hyperspectral data dimensionality reduction. J. Indian Soc. Remote Sens. 2013, 41, 249–258. [Google Scholar] [CrossRef]
- Friedman, J.H.J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Song, R.; Chen, S.; Deng, B.; Li, L. eXtreme gradient boosting for dentifying individual users across different digital devices. In Proceedings of the 17th International Conference on Web-Age Information Management, Nanchang, China, 3–5 June 2016; pp. 43–54.
- Chen, T.; Guestrin, C. XGBoost: Reliable large-scale tree boosting system. In Proceedings of the 22nd SIGKDD Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794.
- Mustapha, I.B.; Saeed, F. Bioactive molecule prediction using extreme gradient boosting. Molecules 2016, 21. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV-Vis-NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Höskuldsson, A. PLS regression methods. J. Chemom. 1988, 2, 211–228. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; Toth, G.; Panagos, P.; van Wesemael, B.; Montanarella, L. Prediction of soil organic carbon content by diffuse reflectance spectroscopy using a local partial least square regression approach. Soil Biol. Biochem. 2014, 68, 337–347. [Google Scholar] [CrossRef]
- Kopačková, V. Using multiple spectral feature analysis for quantitative pH mapping in a mining environment. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 28–42. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, T.; Liu, J.; Lin, Z.; Li, S.; Wang, R.; Ge, Y. Soil pH value, organic matter and macronutrients contents prediction using optical diffuse reflectance spectroscopy. Comput. Electron. Agric. 2015, 111, 69–77. [Google Scholar] [CrossRef]
- Wijaya, A.; Marpu, P.R.; Gloaguen, R. Geostatistical texture classification of tropical rainforest in Indonesia. In Proceedings of the 5th International Symposium for Spatial Data Quality (ISSDQ), Enschede, The Netherlands, 13–15 June 2007.









| Rodogram | Madogram | Variogram | |
|---|---|---|---|
| SOC | −0.40 | −0.47 | −0.54 |
| N | −0.38 | −0.43 | −0.50 |
| pH | −0.12 | −0.13 | −0.12 |
| Method | Step Size/nm | Window Size/nm | Dimension | R2 | |
|---|---|---|---|---|---|
| SOC | PCA | - | - | 28 | 0.813 |
| Rodogram | 2.5 | 80 | 769 | 0.847 | |
| Madogram | 2.5 | 90 | 765 | 0.847 | |
| Variogram | 2.5 | 105 | 759 | 0.851 | |
| N | PCA | - | - | 34 | 0.735 |
| Rodogram | 2.5 | 50 | 781 | 0.756 | |
| Madogram | 2.5 | 90 | 765 | 0.767 | |
| Variogram | 2.5 | 65 | 775 | 0.776 | |
| pH | PCA | - | - | 34 | 0.814 |
| Rodogram | 5 | 55 | 390 | 0.806 | |
| Madogram | 2.5 | 100 | 761 | 0.818 | |
| Variogram | 7.5 | 45 | 261 | 0.821 |
| Features | Modelling | OC (R2) | N (R2) | pH (R2) | |
|---|---|---|---|---|---|
| Method A | PLS components | Linear regression | 0.834 | 0.743 | 0.87 |
| Method B | PLS components | Gradient-boosting regression | 0.846 | 0.759 | 0.823 |
| Method C | Fractal features | Gradient-boosting regression | 0.851 | 0.776 | 0.821 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ji, M.; Dong, Y.; Zhang, R.; Buchroithner, M. Quantitative Retrieval of Organic Soil Properties from Visible Near-Infrared Shortwave Infrared (Vis-NIR-SWIR) Spectroscopy Using Fractal-Based Feature Extraction. Remote Sens. 2016, 8, 1035. https://doi.org/10.3390/rs8121035
Liu L, Ji M, Dong Y, Zhang R, Buchroithner M. Quantitative Retrieval of Organic Soil Properties from Visible Near-Infrared Shortwave Infrared (Vis-NIR-SWIR) Spectroscopy Using Fractal-Based Feature Extraction. Remote Sensing. 2016; 8(12):1035. https://doi.org/10.3390/rs8121035
Chicago/Turabian StyleLiu, Lanfa, Min Ji, Yunyun Dong, Rongchung Zhang, and Manfred Buchroithner. 2016. "Quantitative Retrieval of Organic Soil Properties from Visible Near-Infrared Shortwave Infrared (Vis-NIR-SWIR) Spectroscopy Using Fractal-Based Feature Extraction" Remote Sensing 8, no. 12: 1035. https://doi.org/10.3390/rs8121035
APA StyleLiu, L., Ji, M., Dong, Y., Zhang, R., & Buchroithner, M. (2016). Quantitative Retrieval of Organic Soil Properties from Visible Near-Infrared Shortwave Infrared (Vis-NIR-SWIR) Spectroscopy Using Fractal-Based Feature Extraction. Remote Sensing, 8(12), 1035. https://doi.org/10.3390/rs8121035