The Added Value of Stratified Topographic Correction of Multispectral Images
Abstract
:1. Introduction
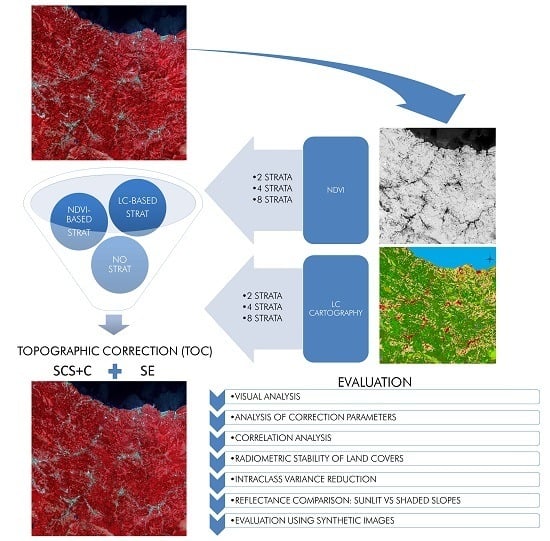
Stratified Topographic Correction
| TOC Method | Stratification Criteria | No. of Classes | Source | Ref. |
|---|---|---|---|---|
| EMIN | LULC/OTHER | 2 | Ground truth from aerial photographs | [6] |
| EMIN | VI/OTHER | 3/many | NDVI/sliding windows | [17] |
| SE, MIN, CC, others | LULC | 2 | Vegetation information derived from aerial photography | [23] |
| SE, MIN, CC, EKS | VI | 10 | NDVI | [28] |
| EMIN | OTHER | 3 | Interferometric coherence | [29] |
| EMIN | LULC | 3 | Visually homogeneous regions | [22] |
| EMIN | VI | 3 | NDVI | [21] |
| MIN, EMIN, CC, sCC | LULC | 13 + outliers | Unsupervised classification | [20] |
| MIN | LULC | 13 | Land cover map | [24] |
| SE, EMIN, CC, MM | VI | 2 | NDVI | [16] |
| CC, MIN, SCS+C | LULC | 3 | Ground data and aerial photograph | [25] |
| SE, CC, MIN, ICOS, VECA | VI+OTHER | 3 | NDVI + spectral decision rules | [19] |
| EMIN, SCS+C, CC, others | OTHER | 2 | Main land cover | [15] |
| CC | VI | 3 | NDVI | [27] |
| MM | VI | 2 | Vegetation index | [13] |
2. Material and Methods
2.1. Study Area

2.2. Data Acquisition and Processing
2.3. Ancillary Information
| LC | % | Min | Max | Mean | SD |
|---|---|---|---|---|---|
| Artificial surfaces | 3.70 | MASKED | |||
| Agricultural areas (pastures) | 15.48 | 0.014 | 1.000 | 0.783 | 0.123 |
| Broad-leaved forest | 18.52 | 0.002 | 1.000 | 0.676 | 0.192 |
| Coniferous forest | 26.66 | 0.002 | 1.000 | 0.723 | 0.178 |
| Mixed forest | 13.90 | 0.001 | 1.000 | 0.719 | 0.175 |
| Natural grasslands | 2.54 | 0.003 | 1.000 | 0.758 | 0.167 |
| Shrubs, moors and heathland | 4.58 | 0.005 | 1.000 | 0.744 | 0.174 |
| Fruit-trees, vineyards | 1.27 | 0.096 | 1.000 | 0.791 | 0.118 |
| Open spaces with little or no vegetation | 2.04 | 0.002 | 1.000 | 0.707 | 0.195 |
| Water bodies (+ wetlands) | 11.31 | MASKED | |||
2.4. Stratification Strategies
| Approach | Number of Strata | Land Cover | Code | Coverage (%) | Masked |
|---|---|---|---|---|---|
| NO-STRAT. | 1 | All land covers | ALL | 100.00 | - |
| LC-2 | 2 | Artificial surfaces | ARTIF | 3.70 | YES |
| Non forested areas | NOFOREST | 25.91 | NO | ||
| Forested areas | FOREST | 59.08 | NO | ||
| Water bodies | WATER | 11.31 | YES | ||
| LC-4 | 4 | Artificial surfaces | ARTIF | 3.70 | YES |
| Agricultural areas (pastures) | AGRIC-4C | 15.48 | NO | ||
| Forested areas | FOREST | 59.08 | NO | ||
| Shrubs, moors, heathlands | SHRUB | 4.58 | NO | ||
| Grasslands, bare soil and rocks | OTHER | 5.85 | NO | ||
| Water bodies (+ wetlands) | WATER | 11.31 | YES | ||
| LC-8 | 8 | Artificial surfaces | ARTIF | 3.70 | YES |
| Agricultural areas (pastures) | AGRIC-8C | 15.48 | NO | ||
| Broad-leaved forest | BROAD | 18.52 | NO | ||
| Coniferous forest | CONIF | 26.66 | NO | ||
| Mixed forest | MIXED | 13.90 | NO | ||
| Natural grasslands | GRASS | 2.54 | NO | ||
| Shrubs, moors and heathland | SHRUB | 4.58 | NO | ||
| Fruit-trees, vineyards | FRUIT | 1.27 | NO | ||
| Open spaces with little or no vegetation | NOVEGET | 2.04 | NO | ||
| Water bodies (+ wetlands) | WATER | 11.31 | YES | ||
| NDVI-2 | 2 | 0 < NDVI < 0.4 | NDVI 0-4 | 13.30 | NO |
| 0.4 < NDVI < 1 | NDVI 4-1 | 86.70 | NO | ||
| NDVI-4 | 4 | 0 < NDVI < 0.4 | NDVI 0-4 | 13.30 | NO |
| 0.4 < NDVI < 0.6 | NDVI 4-6 | 5.91 | NO | ||
| 0.6 < NDVI < 0.8 | NDVI 6-8 | 23.32 | NO | ||
| 0.8 < NDVI < 1 | NDVI 8-1 | 57.47 | NO | ||
| NDVI-8 | 8 | 0 < NDVI < 0.2 | NDVI 0-2 | 4.54 | NO |
| 0.2 < NDVI < 0.4 | NDVI 2-4 | 8.77 | NO | ||
| 0.4 < NDVI < 0.5 | NDVI 4-5 | 2.50 | NO | ||
| 0.5 < NDVI < 0.6 | NDVI 5-6 | 3.40 | NO | ||
| 0.6 < NDVI < 0.7 | NDVI 6-7 | 7.32 | NO | ||
| 0.7 < NDVI < 0.8 | NDVI 7-8 | 16.00 | NO | ||
| 0.8 < NDVI < 0.9 | NDVI 8-9 | 55.32 | NO | ||
| 0.9 < NDVI < 1 | NDVI 9-1 | 2.15 | NO |
2.5. Selected Topographic Correction Algorithms
2.6. Evaluation Strategies
2.6.1. Visual Analysis
2.6.2. Analysis of Correction Parameters
2.6.3. Correlation Analysis
2.6.4. Radiometric Stability of Land Covers
2.6.5. Intraclass Variance Reduction
2.6.6. Comparison of Reflectance between Sunlit and Shaded Slopes
2.6.7. Evaluation Using Synthetic Images
3. Results
3.1. Visual Analysis

3.2. Analysis of Correction Parameters



3.3. Correlation Analysis


3.4. Radiometric Stability of Land Covers

3.5. Intraclass Variance Reduction


3.6. Comparison of Reflectance between Sunlit and Shaded Slopes

3.7. Evaluation Using Synthetic Images
| TOC | SCS+C | SE | ||||||
|---|---|---|---|---|---|---|---|---|
| STRAT. | b1 | b2 | b3 | b4 | b1 | b2 | b3 | b4 |
| NO-CORR. | 0.801 | 0.794 | 0.720 | 0.612 | 0.801 | 0.794 | 0.720 | 0.612 |
| NO-STRAT. | 0.890 | 0.885 | 0.882 | 0.857 | 0.894 | 0.879 | 0.878 | 0.846 |
| LC-2 | 0.807 | 0.792 | 0.790 | 0.742 | 0.816 | 0.798 | 0.789 | 0.748 |
| LC-4 | 0.879 | 0.869 | 0.877 | 0.823 | 0.890 | 0.874 | 0.875 | 0.835 |
| LC-8 | 0.881 | 0.870 | 0.878 | 0.830 | 0.890 | 0.873 | 0.872 | 0.838 |
| NDVI-2 | 0.891 | 0.885 | 0.884 | 0.859 | 0.895 | 0.880 | 0.883 | 0.853 |
| NDVI-4 | 0.872 | 0.868 | 0.882 | 0.840 | 0.871 | 0.861 | 0.872 | 0.801 |
| NDVI-8 | 0.877 | 0.874 | 0.878 | 0.841 | 0.875 | 0.867 | 0.869 | 0.808 |
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| RS | Remote Sensing |
| DEM | Digital Elevation Model |
| LULC | Land Use/Land Cover |
| LC | Land cover |
| NDVI | Normalized Difference Vegetation Index |
| TOC | TOpographic Correction |
| STOC | Stratified Topographic Correction |
| SE | Statistical-Empirical method |
| SCS+C | Sun-Canopy-Sensor + C |
| CC | C-Correction method |
| COS | Cosine method |
| ICOS | Improved COSine method |
| VECA | Variable Empirical Coefficient Algorithm |
| MM | Modified Minnaert method |
| MIN | MINnaert method |
| EMIN | Enhanced MINmethod |
| EKS | EKStrand method |
| sCC | Smooth C-Correction method |
| 2SN | Two Stage Normalization method |
| SM | Slope Matching Technique |
| UTC | Coordinated Universal Time |
| DN | Digital Number |
| TOARD | Top Of Atmosphere RaDiance |
| IGN | Instituto Geográfico Nacional (Spain) |
| LIDAR | Light detection and ranging |
| PNOA | Plan Nacional de Ortofotografía Aérea (Spain) |
| IQR | Interquartile Range |
| SD | Standard Deviation |
| SH | Synthetic Horizontal image |
| SR | Synthetic Real image |
| MSSIM | Mean Structural SIMilarity Index |
References
- Leprieur, C.E.; Durand, J.M. Influence of topography on forest reflectance using landsat thematic mapper and digital terrain data. Photogramm. Eng. Remote Sens. 1988, 54, 491–496. [Google Scholar]
- Richter, R.; Kellenberger, T.; Kaufmann, H. Comparison of topographic correction methods. Remote Sens. 2009, 1, 184–196. [Google Scholar] [CrossRef] [Green Version]
- Riano, D.; Chuvieco, E.; Salas, J.; Aguado, I. Assessment of different topographic corrections in Landsat-TM data for mapping vegetation types. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1056–1061. [Google Scholar] [CrossRef]
- Sola, I.; González de Audícana, M.; Álvarez-Mozos, J.; Torres, J.L. Synthetic images for evaluating topographic correction algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1799–1810. [Google Scholar] [CrossRef]
- Lu, D.; Ge, H.; He, S.; Xu, A.; Zhou, G.; Du, H. Pixel-based minnaert correction method for reducing topographic effects on a Landsat 7 ETM+ image. Photogramm. Eng. Remote Sens. 2008, 74, 1343–1350. [Google Scholar]
- Tokola, T.; Sarkeala, J.; Van der Linden, M. Use of topographic correction in Landsat TM-based forest interpretation in Nepal. Int. J. Remote Sens. 2001, 22, 551–563. [Google Scholar] [CrossRef]
- Balthazar, V.; Vanacker, V.; Lambin, E.F. Evaluation and parameterization of ATCOR3 topographic correction method for forest cover mapping in mountain areas. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 436–450. [Google Scholar] [CrossRef]
- Couturier, S.; Gastellu-Etchegorry, J.P.; Martin, E.; Patiño, P. Building a forward-mode three-dimensional reflectance model for topographic normalization of high-resolution (1–5 m) imagery: Validation phase in a forested environment. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3910–3921. [Google Scholar] [CrossRef]
- Reese, H.; Olsson, H. C-correction of optical satellite data over alpine vegetation areas: A comparison of sampling strategies for determining the empirical c-parameter. Remote Sens. Environ. 2011, 115, 1387–1400. [Google Scholar] [CrossRef]
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the slope-aspect correction of multispectral scanner data. Can. J. Remote Sens. 1982, 8, 84–106. [Google Scholar] [CrossRef]
- Smith, J.A.; Lin, T.L.; Ranson, K.J. The lambertian assumption and landsat data. Photogramm. Eng. Remote Sens. 1980, 46, 1183–1189. [Google Scholar]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. Scs+c: A modified sun-canopy-sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Atmospheric/Topographic Correction for Satellite Imagery; Atcor-2/3 User Guide, Version 9.0.0; ReSe Applications Schläpfer: Wil, Switzerland, 2015; pp. 185–244. [Google Scholar]
- Goslee, S.C. Topographic corrections of satellite data for regional monitoring. Am. Soc. Photogramm. Remote Sens. 2012, 78, 973–981. [Google Scholar] [CrossRef]
- Moreira, E.P.; Valeriano, M.M. Application and evaluation of topographic correction methods to improve land cover mapping using object-based classification. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 208–217. [Google Scholar] [CrossRef]
- Hantson, S.; Chuvieco, E. Evaluation of different topographic correction methods for Landsat imagery. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 691–700. [Google Scholar] [CrossRef]
- Bishop, M.P.; Colby, J.D. Anisotropic reflectance correction of SPOT-3 HRV imagery. Int. J. Remote Sens. 2002, 23, 2125–2131. [Google Scholar] [CrossRef]
- Bishop, M.P.; Shroder, J.F., Jr.; Colby, J.D. Remote sensing and geomorphometry for studying relief production in high mountains. Geomorphology 2003, 55, 345–361. [Google Scholar] [CrossRef]
- Szantoi, Z.; Simonetti, D. Fast and robust topographic correction method for medium resolution satellite imagery using a stratified approach. Sel. Top. IEEE J. Appl. Earth Obs. Remote Sens. 2013, 6, 1921–1933. [Google Scholar] [CrossRef]
- Baraldi, A.; Gironda, M.; Simonetti, D. Operational two-stage stratified topographic correction of spaceborne multispectral imagery employing an automatic spectral-rule-based decision-tree preliminary classifier. IEEE Trans. Geosci. Remote Sens. 2010, 48, 112–146. [Google Scholar] [CrossRef]
- Twele, A.; Kappas, M.; Lauer, J.; Erasmi, S. The effect of stratified topographic correction on land cover classificacion in tropical mountainous regions. In Proceedings of ISPRS Commission VII Mid-term Symposium "Remote Sensing: From Pixels to Processes”, Enschede, The Netherlands, 8–11 May 2006.
- Blesius, L.; Weirich, F. The use of the minnaert correction for land-cover classification in mountainous terrain. Int. J. Remote Sens. 2005, 26, 3831–3851. [Google Scholar] [CrossRef]
- McDonald, E.R.; Wu, X.; Caccetta, P.; Campbell, N. Illumination correction of Landsat TM data in South East NSW. In Proceedings of 10th Australasian Remote Sensing and Photogrammetry Conference, Adelaide, Australia, 21–25 August 2000.
- Mariotto, I.; Gutschick, V.P. Non-lambertian corrected albedo and vegetation index for estimating land evapotranspiration in a heterogeneous semi-arid landscape. Remote Sens. 2010, 2, 926–938. [Google Scholar] [CrossRef]
- Ediriweera, S.; Pathirana, S.; Danaher, T.; Nichols, D.; Moffiet, T. Evaluation of different topographic corrections for Landsat TM data by prediction of foliage projective cover (FPC) in topographically complex landscapes. Remote Sens. 2013, 5, 6767–6789. [Google Scholar] [CrossRef]
- Kobayashi, S.; Sanga-Ngoie, K. A comparative study of radiometric correction methods for optical remote sensing imagery: The IRC vs. Other image-based c-correction methods. Int. J. Remote Sens. 2009, 30, 285–314. [Google Scholar] [CrossRef]
- Adhikari, H.; Heiskanen, J.; Maeda, E.; Pellikka, P. Does topographic normalization of landsat images improve fractional tree cover mapping in tropical mountains? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40-7/W3, 261–267. [Google Scholar] [CrossRef]
- Törmä, M.; Härmä, P. Topographic correction of Landsat ETM images in finnish Lapland. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS ‘03), Toulouse, France, 21–25 July 2003.
- Twele, A.; Erasmi, S. Evaluating topographic correction algorithms for improved land cover discrimination in mountainous areas of central Sulawesi. In Remote Sensing & GIS for Environmental Studies; Erasmi, S., Cyffka, B., Kappas, M., Eds.; Göttinger Geographische Abhandlungen: Göttingen, Germany, 2005; Volume 113, pp. 287–295. [Google Scholar]
- Gleriani, J.M.; Homem, M.A.; Soares, V.P.; Alvares, C.A. Land cover variation of Minnaert constant for topographic correction on Thematic Mapper. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012.
- Colby, J.D. Topographic normalization in rugged terrain. Photogramm. Eng. Remote Sens. 1991, 57, 531–537. [Google Scholar]
- Richter, R. Correction of satellite imagery over mountainous terrain. Appl. Opt. 1998, 37, 4004–4015. [Google Scholar] [CrossRef] [PubMed]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the enhanced vegetation index (EVI) and normalized difference vegetation index (NDVI) to topographic effects: A case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef]
- Köppen Climate Classification. Available online: http://en.wikipedia.org/wiki/K%C3%B6ppen_climate_ classification (accessed on 10 November 2015).
- Chavez, P.S. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Cartografía de Hábitats, Vegetación Actualy Usos del Suelo de la Comunidad Autónoma del País Vasco. Available online: http://www.geo.euskadi.eus/geograficos/habitats-vegetacion-actual-y-usos-del-suelo/s69-geodir/es/ (accessed on 15 April 2015).
- Ojeda, J.C.; Martínez, J. PNOA-LIDAR. Plan Nacional de Ortofotografía Aérea. Empleo del LIDAR en aplicaciones ambientales terrestres. In Proceedings of the XV Congreso Nacional Tecnologías de Información Geográfica, Madrid, Spain, 19–21 September 2012.
- Gu, D.; Gillespie, A. Topographic normalization of Landsat TM images of forest based on subpixel Sun-Canopy-Sensor geometry. Remote Sens. Environ. 1998, 64, 166–175. [Google Scholar] [CrossRef]
- Ghasemi, N.; Mohammadzadeh, A.; Reza Sahebi, M. Assessment of different topographic correction methods in ALOS AVNIR-2 data over a forest area. Int. J. Digit. Earth 2011, 6, 1–17. [Google Scholar] [CrossRef]
- Zhang, W.C.; Gao, Y.N. LULC classification and topographic correction of Landsat-7 ETM+ imagery in the Yangjia river watershed: The influence of DEM resolution. Sensors 2009, 9, 1980–1995. [Google Scholar]
- Vincini, M.; Frazzi, E. Multitemporal evaluation of topographic normalization methods on deciduous forest tm data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2586–2590. [Google Scholar] [CrossRef]
- Shepherd, J.D.; Dymond, J.R. Correcting satellite imagery for the variance of reflectance and illumination with topography. Int. J. Remote Sens. 2003, 24, 3503–3514. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Pérez-Cabello, F.; Lasanta, T. Assessment of radiometric correction techniques in analyzing vegetation variability and change using time series of landsat images. Remote Sens. Environ. 2008, 112, 3916–3934. [Google Scholar] [CrossRef]
- Sola, I.; González-Audícana, M.; Álvarez-Mozos, J. Validation of a simplified model to generate multispectral synthetic images. Remote Sens. 2015, 7, 2942–2951. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Koukal, T.; Weisberg, P.J. A sun–crown–sensor model and adapted C-correction logic for topographic correction of high resolution forest imagery. ISPRS J. Photogram. Remote Sens. 2014, 96, 94–105. [Google Scholar] [CrossRef]
- Pons, X.; Pesquer, L.; Cristóbal, J.; González-Guerrero, O. Automatic and improved radiometric correction of Landsat imagery using reference values from MODIS surface reflectance images. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 243–254. [Google Scholar] [CrossRef]
- Gao, Y.N.; Zhang, W.C. A simple empirical topographic correction method for ETM+ imagery. Int. J. Remote Sens. 2009, 30, 2259–2275. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sola, I.; González-Audícana, M.; Álvarez-Mozos, J. The Added Value of Stratified Topographic Correction of Multispectral Images. Remote Sens. 2016, 8, 131. https://doi.org/10.3390/rs8020131
Sola I, González-Audícana M, Álvarez-Mozos J. The Added Value of Stratified Topographic Correction of Multispectral Images. Remote Sensing. 2016; 8(2):131. https://doi.org/10.3390/rs8020131
Chicago/Turabian StyleSola, Ion, María González-Audícana, and Jesús Álvarez-Mozos. 2016. "The Added Value of Stratified Topographic Correction of Multispectral Images" Remote Sensing 8, no. 2: 131. https://doi.org/10.3390/rs8020131
APA StyleSola, I., González-Audícana, M., & Álvarez-Mozos, J. (2016). The Added Value of Stratified Topographic Correction of Multispectral Images. Remote Sensing, 8(2), 131. https://doi.org/10.3390/rs8020131