Next Article in Journal
The Potential of Autonomous Ship-Borne Hyperspectral Radiometers for the Validation of Ocean Color Radiometry Data
Next Article in Special Issue
Tree Species Abundance Predictions in a Tropical Agricultural Landscape with a Supervised Classification Model and Imbalanced Data
Previous Article in Journal
The Combined Use of Airborne Remote Sensing Techniques within a GIS Environment for the Seismic Vulnerability Assessment of Urban Areas: An Operational Application
Previous Article in Special Issue
Airborne Hyperspectral Data Predict Fine-Scale Plant Species Diversity in Grazed Dry Grasslands
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 2
10.3390/rs8020149
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Moving Towards Dynamic Ocean Management: How Well Do Modeled Ocean Products Predict Species Distributions?

by
Elizabeth A. Becker
1,2,*,
Karin A. Forney
1,
Paul C. Fiedler
3,
Jay Barlow
3,
Susan J. Chivers
3,
Christopher A. Edwards
4,
Andrew M. Moore
4 and
Jessica V. Redfern
3
1
NOAA, Southwest Fisheries Science Center, 110 Shaffer Rd, Santa Cruz, CA 95060, USA
2
ManTech International Corporation, 420 Stevens Ave, Solana Beach, CA 92075, USA
3
NOAA, Southwest Fisheries Science Center, 8901 La Jolla Shores Dr., La Jolla, CA 92037, USA
4
Ocean Sciences Department, University of California, Santa Cruz, CA 95064, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2016, 8(2), 149; https://doi.org/10.3390/rs8020149
Submission received: 12 November 2015 / Revised: 16 January 2016 / Accepted: 1 February 2016 / Published: 16 February 2016
(This article belongs to the Special Issue Remote Sensing of Biodiversity)
Browse Figures
Versions Notes

Abstract

:
Species distribution models are now widely used in conservation and management to predict suitable habitat for protected marine species. The primary sources of dynamic habitat data have been in situ and remotely sensed oceanic variables (both are considered “measured data”), but now ocean models can provide historical estimates and forecast predictions of relevant habitat variables such as temperature, salinity, and mixed layer depth. To assess the performance of modeled ocean data in species distribution models, we present a case study for cetaceans that compares models based on output from a data assimilative implementation of the Regional Ocean Modeling System (ROMS) to those based on measured data. Specifically, we used seven years of cetacean line-transect survey data collected between 1991 and 2009 to develop predictive habitat-based models of cetacean density for 11 species in the California Current Ecosystem. Two different generalized additive models were compared: one built with a full suite of ROMS output and another built with a full suite of measured data. Model performance was assessed using the percentage of explained deviance, root mean squared error (RMSE), observed to predicted density ratios, and visual inspection of predicted and observed distributions. Predicted distribution patterns were similar for models using ROMS output and measured data, and showed good concordance between observed sightings and model predictions. Quantitative measures of predictive ability were also similar between model types, and RMSE values were almost identical. The overall demonstrated success of the ROMS-based models opens new opportunities for dynamic species management and biodiversity monitoring because ROMS output is available in near real time and can be forecast.

Graphical Abstract

1. Introduction

Understanding spatial and temporal changes in species distributions is a key factor in establishing conservation and management strategies. Species distribution models are now widely used in conservation and management to predict suitable habitat for marine species such as seabirds, fish, sea turtles, and cetaceans, and to assess risks from human activities [1,2,3,4,5,6,7,8,9,10,11,12]. Dynamic habitat data for such models are generally derived from a combination of measured-data sources, including shipboard in situ sampling (e.g., conductivity-temperature-depth profiles, chlorophyll concentration) and remotely sensed oceanic variables (e.g., sea surface temperature [SST], sea surface height [SSH]). Given the time and expense of collecting and processing in situ oceanic data, models developed using these data can only describe past species distributions. Near-real-time (or “nowcast”) and forecast predictions [13], which are useful for management applications, are only feasible through the use of remotely-sensed data or modeled oceanic information. However, satellite data are often patchy due to cloud cover, especially in the coastal zone, and the spatial and temporal resolutions of habitat models are consequently limited by data availability. Ocean circulation models such as the Regional Ocean Modeling System (ROMS [14]), the CSIRO BLUElink model [15], the Hybrid Coordinate Ocean Model (HYCOM [16]), the Global Navy Coastal Ocean Model (NCOM [17]), the Simple Ocean Data Assimilation (SODA [18]), and others, overcome these limitations. Their accuracy and resolution has increased in recent years as the capability to assimilate historical measured data, including remotely sensed data, has advanced (e.g., [19]). Through data assimilation, controls of ocean model output, such as model initial conditions and/or forcing fields, are adjusted so that model-data misfit is reduced relative to an unconstrained model [20]. Ocean circulation models have the potential to enhance marine species distribution forecasting because they provide detailed physical characteristics describing features known to be important to marine predators [1,4,10,12,21,22,23,24,25].
Dynamic species management is an emerging approach that uses nowcast and forecast data to guide policies addressing the location of potentially harmful anthropogenic activities [26,27,28]. Dynamic management techniques are appealing for areas with substantial temporal and spatial variability in the distribution of marine species, such as seabirds, marine mammals, sea turtles, and certain highly migratory fish [29,30,31,32,33]. Habitat models based on ocean modeled variables present new opportunities for dynamic species management because ocean modeled output is available in near real time and can be forecast. However, successful implementation of dynamic management requires that model-based species distribution forecasts are sufficiently accurate, and none of these previous studies validated the performance of their models relative to those provided by actual measured data, such as in situ sampling or remotely sensed measurements. In a recent feasibility study, Becker et al. [13] demonstrated the nowcast and forecast capabilities of cetacean habitat models based on remotely sensed and ocean modeled SST data. The results provide a foundation for building more complex cetacean habitat models using ocean modeled predictor variables such as sea surface salinity, mixed layer depth [MLD], and SSH, all shown to be important habitat predictors for cetaceans [1,11,25,34,35,36].
In the present study, we build upon Becker et al. [13] by comparing the performance of cetacean density models built with a larger suite of predictors derived from ocean modeled output to those based on measured data. Models were developed based on shipboard line-transect surveys for 11 taxonomically diverse cetacean species in the California Current Ecosystem. The main objective of this study was to compare the performance of models built with ocean modeled predictors to those built with measured data. If ocean model-based habitat models are shown to perform as well or better than models built with measured data, they can be used to support dynamic species management. This capability is increasingly important for assessing current and future risks to marine species due to changes in their distribution patterns in response to seasonal and interannual environmental variability (e.g., ENSO and PDO), as well as potential long-term climate change effects [32,37,38,39,40].

2. Methods

We developed predictive habitat-based models of cetacean density based on seven shipboard cetacean surveys conducted during summer and fall between 1991 and 2009 in the California Current Ecosystem. Models were built for 11 taxonomically diverse species with a range of habitat associations, group sizes, and seasonal presence in the study area (i.e., year-round residents vs. seasonal visitors): striped dolphin (Stenella coeruleoalba), short-beaked common dolphin (Delphinus delphis), long-beaked common dolphin (D. capensis), common bottlenose dolphin (Tursiops truncatus), Risso’s dolphin (Grampus griseus), Pacific white-sided dolphin (Lagenorhynchus obliquidens), northern right whale dolphin (Lissodelphis borealis), Dall’s porpoise (Phocoenoides dalli), fin whale (Balaenoptera physalus), blue whale (B. musculus), and humpback whale (Megaptera novaeangliae).

2.1. Study Area and Field Methods

Cetacean sighting data used to build the habitat-based density models were collected in the California Current Ecosystem during the summer and fall (July through early December) of 1991, 1993, 1996, 2001, 2005, 2008, and 2009 using systematic line-transect methods [41]. The 1991–2008 surveys covered a broad area off the entire United States west coast (Figure 1; [42]), while the 2009 survey focused on waters off southern California (Figure 1; [43]). During all the surveys, a team of three experienced observers stationed on the flying bridge of the ship visually searched for and recorded cetacean sightings using standardized line-transect protocols [44]. Starboard and port observers searched for animals using pedestal-mounted 25 × 150 binoculars, and a third observer searched from a center observation and data recording station using unaided eye and 7 × 50 handheld binoculars. When cetaceans were detected, the ship would typically divert from the trackline to approach the animals to estimate group size and identify the species to the finest possible taxonomic level. All observers independently provided best, high, and low group size estimates and estimated percentages of each species for mixed group sightings [44]. To obtain a single group size estimate for each sighting, we averaged the best estimates for each species.
Remotesensing 08 00149 g001 1024
Figure 1. Completed transects for the Southwest Fisheries Science Center systematic ship surveys conducted between 1991 and 2009 in the California Current Ecosystem study area used for this study. The green lines show on-effort transect coverage in Beaufort sea states of 0-5 for (a) surveys conducted late July through early December in 1991, 1993, 1996, 2001, 2005, and 2008 off the US west coast; and (b) a smaller scale survey conducted September through December of 2009.
Figure 1. Completed transects for the Southwest Fisheries Science Center systematic ship surveys conducted between 1991 and 2009 in the California Current Ecosystem study area used for this study. The green lines show on-effort transect coverage in Beaufort sea states of 0-5 for (a) surveys conducted late July through early December in 1991, 1993, 1996, 2001, 2005, and 2008 off the US west coast; and (b) a smaller scale survey conducted September through December of 2009.
Remotesensing 08 00149 g001
During all surveys, a thermosalinograph continuously recorded SST and sea surface salinity at 0.5 to 2 min intervals. Surface chlorophyll a concentration and MLD (the depth at which temperature is 0.5 °C less than surface temperature [45]) were measured three to five times per day at a spacing of 30–55 km along-track. MLD estimates were obtained from expendable bathythermograph (XBT) drops and conductivity, temperature, and depth (CTD) casts. Surface chlorophyll was estimated from the surface bottle on the CTD or from bucket samples analyzed by standard techniques [46]. Detailed descriptions of the oceanographic sampling methods can be found in Philbrick et al. [47,48].

2.2. Analytical Methods

2.2.1. Habitat Variables

The full suite of measured dynamic predictors included remotely sensed SST derived using optimal interpolation methods [49], the standard deviation (SD) of SST (a proxy for fronts, calculated for a block of 9 pixels centered on the pixel containing the modeling segment midpoint), as well as salinity, log-transformed surface chlorophyll concentration, and MLD interpolated from data collected in situ during the 1991–2009 surveys to provide continuous spatial grids of these variables at a spatial resolution of 0.05 degrees [24]. Remotely sensed data served at 25 km2 spatial resolution were downloaded as NetCDF files from NOAA’s Environmental Research Division Data Access Program (ERDDAP) web site [50], and subsequently processed using custom code developed in R (v. 3.1.0) and the R package ncdf4 (v.1.12). The spatial resolution of the remotely sensed SST data was consistent with measured-data models developed in previous studies and found to produce results similar to models built with SST at approximate 10 km2 spatial resolution [13,51]. We used 8-day running average SST composites to represent average survey-day conditions [51].
Dynamic ocean modeled variables were derived from the ROMS California Current System 31-Year Historical Reanalysis data files downloaded from the UC Santa Cruz Ocean Modeling and Data Assimilation group (http://oceanmodeling.pmc.ucsc.edu) [19,52,53] and included SST, the SD of SST (calculated for a block of 9 pixels centered on the pixel containing the modeling segment midpoint using the approximate 10-km spatial resolution of the native dataset), salinity, MLD, potential energy anomaly (the work per unit volume required to redistribute the mass in a complete mixing to a depth of 300m, providing a robust measure of stratification), SSH (to reflect circulation and density structure) and the SD of SSH (to reflect the mesoscale variability of SSH). ROMS output is served in overlapping 8-day cycles; we used 8-day running average composites centered on the date of each survey segment to provide consistent representation of average survey-day conditions. The California Current System configuration of ROMS [54] extends from approximately 30° to 48°N and covers the coastal ocean to 134° west offshore, encompassing our entire study area. Model resolution is 0.1° in the horizontal (about 10 km) direction, with 42 vertical levels at variable depths. The accuracy of the ROMS output is improved by assimilating available remotely sensed data, including temperature, salinity, and SSH, as well as in situ oceanographic data from ships, buoys, gliders, and profiling floats. The 4-dimensional variational assimilation approach used for this output has been shown to nearly eliminate bias in multiple fields and reduce root mean squared error (RMSE) by approximately half [55]. The 31-year reanalysis has been assessed against independent data and shown to capture interannual variability in various physical fields [56]. Data collected in situ during the 1991–2009 surveys were not used in the ROMS assimilation and thus the measured data and ROMS output used in this analysis were independent.
The variables in common to both data sets included SST, the SD of SST, sea surface salinity, and MLD. Static predictors were offered to both model types and included water depth, bathymetric slope, and aspect (i.e., slope direction). Bathymetric variables were derived from ETOPO1 [57], a 1 arc-minute global-relief model. Slope and aspect were calculated using ArcGIS Spatial Analyst (Version 10.1, ESRI).

2.2.2. Modeling Framework

Samples for modeling were created by dividing the continuous survey effort into segments of approximately 5-km length as described by Becker et al. [51]. Species-specific sighting information (number of sightings, mean group size) was assigned to each segment, and habitat data were obtained based on the segment’s geographical midpoint. Sighting data were truncated at a distance of 5.5 km perpendicular to the track line for the delphinids and large whales, and at 3 km for Dall’s porpoise to eliminate the most distant groups [41] and maintain consistency with the species-specific effective-strip-width estimates derived by Barlow et al. [58] for the same survey data and used in this study to estimate animal densities. Generalized Additive Models [59] were developed in R (v. 3.1.1; R Core Team 2014) using the package “mgcv” (v. 1.8-3, [60]) which includes cross-validation as part of the model selection process. Parameter estimates were optimized using restricted maximum likelihood (REML). Correlations among the predictor variables in our study ranged from 0.024–0.73 (absolute values), but mgcv is robust to such effects (termed “concurvity”; [61]). Model selection was performed with automatic term selection [62] and guided by the approximate p-values of each predictor [60,63]. Models were initially built with all potential predictors. Non-significant predictors (α = 0.05) were then excluded and models were re-fit using an iterative process until all predictors were significant.
Two different species-specific modeling frameworks were used, depending on group size characteristics. For species with small group sizes (large whales and Dall’s porpoise), a single response model was fit where the number of individuals detected on each segment was modeled as the response variable, using a Tweedie error distribution to account for overdispersion [64]. For species with large, variable group sizes (all delphinids), separate encounter rate and group size models were developed. Encounter rate models were built using all transect segments, regardless of whether they included sightings, while group size models were built using only those segments that included sightings. The number of sightings per segment was modeled as the response variable in the encounter rate models using a Tweedie error distribution. Given observed geographical differences in group sizes for many delphinids [23,65,66], group size was modeled using a tensor product smooth of latitude and longitude [67], and the natural log of group size as the response variable with a Gaussian link function. The natural log of the effective area searched (described below) was included as an offset in both the single response and encounter rate models.
The habitat predictors included in both model types are proxies for unmeasured underlying ecological processes linking cetaceans to their prey. Some of these proxy relationships (e.g., with SST) are stable throughout the study area [13,24,35,51], while others may vary with latitude or longitude, as the study area spans temperate to sub-tropical and shallow to deep-water habitats with water masses of different origin [68,69]. In such cases, a bivariate predictor that includes latitude or longitude may provide a more robust proxy for the entire study area [70]. For this reason, interaction terms with latitude or longitude were considered on a species-by-species basis, depending on initial modeling results. A year covariate was also included as a potential predictor to capture trends for species whose abundance has substantially increased during the time period considered in our analyses (i.e., 1991–2009). These include fin whales and humpback whales [71,72].

2.2.3. Density Predictions

Density (number of animals per km2) was estimated by incorporating the model results into the standard line-transect equation [41]:
D i =   n i   ·   s i A i
where i is the segment, n is the number of sightings, s is the average group size, and A is the effective area searched:
A i = 2 · L i · E S W i   · g ( 0 ) i
where i is the segment, L is the length of the effort segment, ESW is the effective strip half-width, and g(0) is the probability of detection on the transect line. Species-specific and segment-specific estimates of both ESW and g(0) were incorporated into the models based on the recorded viewing conditions on that segment using coefficients estimated by Barlow et al. [58] for ESW and Barlow [66] for g(0). Previous modeling studies have used segment-specific ESW values [11,73], but this is the first habitat modeling study to also incorporate segment-specific g(0) values. Barlow [66] developed a method to estimate g(0) for 20 cetacean taxa using line-transect survey data collected in the eastern Pacific from 1986–2010 (including the 1991–2008 survey data used in this study), and found that g(0) has historically been underestimated, particularly for high sea states. The resulting g(0) estimates are specific to Beaufort sea state conditions [66], and weighted g(0) values based on each segment’s average Beaufort value were incorporated into the habitat models to improve their accuracy.
Density predictions for distinct 8-day composites covering the entire survey periods were averaged to produce spatial grids of average species density at 10-km2 resolution within the California Current study area, as well as spatially-explicit measures of uncertainty, estimated from the full set of 8-day prediction grids. The final prediction grids thus provide a “multi-year average” of predicted 8-day cetacean species densities, taking into account the varying oceanographic conditions during the 1991–2009 summer/fall SWFSC cetacean surveys. The prediction grid was clipped to the boundaries of the approximate 1,141,800-km2 study area. The greatest source of uncertainty in these models is the interannual variability in population density due to movement of animals within or outside of the study area [24,35], and we focused on this source of uncertainty to produce the log-normal 90% confidence intervals for the spatial density estimates.

2.2.4. Model Comparison

For this comparative study, we constructed GAMs with the full suites of either the selected ROMS output variables or the measured data. During preliminary analyses, we also compared models restricted only to those variables in common for both sources of oceanographic information; however, these models did not perform as well as those including the full suite of available variables (Supplementary Materials, Tables S1 and S2); since we wanted to compare the best possible models we could develop from the respective datasets, the restricted models were not considered further. Model performance was evaluated based on a variety of metrics (as previously described in Barlow et al. [35], Becker et al. [51,73,74], and Forney et al. [24]), including the percentage of explained deviance, RMSE, and ratios of observed to predicted density (calculated for each segment and summed to obtain study area density ratios). In addition, density predictions were plotted and visually compared to actual sightings made during the surveys. Previous studies using these survey data and similar methods have validated the measured-data models using cross validation [24,35,51,70], predictions on novel data sets [13,24,35,39], and expert opinion [24,35,74]. Density predictions from similar measured-data models for humpback and blue whales have also been found to correspond well to Biologically Important Areas identified using a completely different dataset [75]. The measured-data models thus provide an ideal comparison for the models built with ROMS output.
To examine potential bias in the habitat-based models, we compared the models’ study area abundance estimates to standard line-transect estimates derived from the same dataset used for modeling. The standard line-transect estimates were derived from the 1991–2009 survey data using Equations (1) and (2) above, but without the inclusion of habitat predictors. Model-based abundance estimates for each grid cell were calculated by multiplying the cell area (in km2) by the predicted species density, exclusive of any portions of the cells located outside the study area or on land. Area calculations were completed using the R packages geosphere and gpclib in R (version 2.15.0, The R Foundation for Statistical Computing 2012). The model-based abundance estimates for the entire study area were calculated as the sum of the individual grid cell abundances. These grid-based abundance estimates made at 8-day temporal and 10 km2 spatial resolution include finer-scale information on habitats and cetacean distribution patterns than previous studies in this region [24,35,51,74].

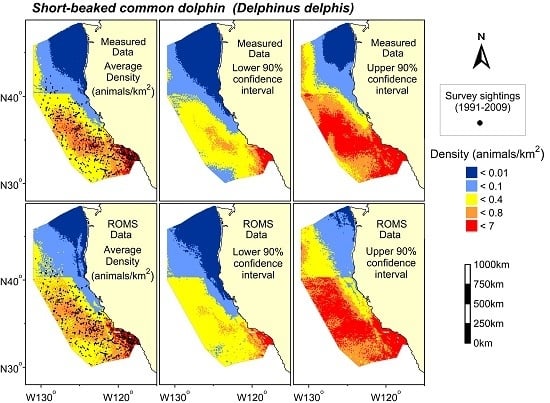
3. Results

The final ROMS and measured-data models for each species included different predictor variables with varying degrees of freedom and relative significance (Table 1 and Supplementary Materials, Figure S1). The models built with measured data showed habitat relationships similar to those in previous studies that used subsets of the same survey data [10,24,35,74]. The ROMS models showed similar habitat relationships to those of the measured-data models for those dynamic variables in common to both data sets (i.e., SST, the SD of SST, salinity, and MLD), as well as the static predictors. However, for the majority of species (9 of 11), the ROMS models also included the unique dynamic variables (i.e., potential energy anomaly, SSH, and the SD of SSH). Likewise, 7 of the 11 measured-data models included log chlorophyll, the single unique dynamic variable in this dataset (Table 1).
Table
Table 1. Summary of the final encounter rate (delphinids) or single response (Dall’s porpoise and large whales) Generalized Additive Models (GAMs) built with either measured data or Regional Ocean Modeling System (ROMS) output. Terms are represented as smoothing spline functions with associated effective degrees of freedom to indicate the level of smoothing (e.g., s(3.24)) or linear terms (“linear”). A tensor product smooth is represented as “te” with the bivariate terms and associated effective degrees of freedom (e.g., te(LON,LAT, 7.97)). Variable abbreviations are as follows: SST = sea surface temperature, MLD = mixed layer depth, lnCHL = ln(chlorophyll concentration), SAL = sea surface salinity, sdSST = standard deviation of SST, PEA = potential energy anomaly, SSH = sea surface height, sdSSH = standard deviation of SSH, DEPTH = bathymetric depth, SLOPE = bathymetric slope, ASPECT = slope direction, d200 = distance to the 200-m isobath, LON = longitude, and LAT = latitude. p-values are indicated with *** (<0.001), ** (<0.01), and * (<0.05). All models were corrected for effort with an offset for the effective area searched, and both fin whale models also included a year covariate that captured their increase in abundance during the 1991–2009 survey years (see text for details).
Table 1. Summary of the final encounter rate (delphinids) or single response (Dall’s porpoise and large whales) Generalized Additive Models (GAMs) built with either measured data or Regional Ocean Modeling System (ROMS) output. Terms are represented as smoothing spline functions with associated effective degrees of freedom to indicate the level of smoothing (e.g., s(3.24)) or linear terms (“linear”). A tensor product smooth is represented as “te” with the bivariate terms and associated effective degrees of freedom (e.g., te(LON,LAT, 7.97)). Variable abbreviations are as follows: SST = sea surface temperature, MLD = mixed layer depth, lnCHL = ln(chlorophyll concentration), SAL = sea surface salinity, sdSST = standard deviation of SST, PEA = potential energy anomaly, SSH = sea surface height, sdSSH = standard deviation of SSH, DEPTH = bathymetric depth, SLOPE = bathymetric slope, ASPECT = slope direction, d200 = distance to the 200-m isobath, LON = longitude, and LAT = latitude. p-values are indicated with *** (<0.001), ** (<0.01), and * (<0.05). All models were corrected for effort with an offset for the effective area searched, and both fin whale models also included a year covariate that captured their increase in abundance during the 1991–2009 survey years (see text for details).
SpeciesModel typeGeneralized Additive Model (GAM)
SSTMLDlnCHLSALsdSSTPEASSHsdSSHDEPTHSLOPEASPECTBivariate
Striped dolphinMeasured s(3.08)* linear***
ROMS s(4.533)* s(3.75)* s(3.53)***
Short-beaked common dolphinMeasureds(4.64)***s(1.44)***s(5.69)***s(3.83)*** s(5.47)*** s(3.85)***
ROMSs(6.76)*** s(5.80)*** s(3.95)*** s(6.72)*** s(3.70)***
Long-beaked common dolphinMeasuredlinear*** s(2.92)**linear** te(LON,LAT, 5.65)***
ROMSlinear* s(1.37)*te(LON,LAT, 7.97)***
Common bottlenose dolphinMeasureds(3.91)**s(2.85)* te(LAT,d200, 12.46)***
ROMSs(2.32)***s(3.41)** linear* linear** te(LAT,d200, 12.22)***
Risso’s dolphinMeasureds(4.46)* te(LAT,d200, 17.49)***
ROMSs(6.70)** s(1.59)*te(LAT,d200, 17.63)***
Pacific white-sided dolphinMeasured s(4.89)**s(3.44)*** s(4.11)***
ROMSlinear** s(3.63)*** s(3.71)***
Northern right whale dolphinMeasureds(4.27)***linear*** s(5.22)***
ROMSs(3.64)*** linear* s(5.45)** s(5.47)***
Dall’s porpoiseMeasureds(2.69)*** s(5.54)***s(4.75)***s(5.43)*** s(6.31)***linear**
ROMSs(3.34)*** s(5.32)*** s(3.86)**s(3.10)***linear*s(6.56)***linear***
Fin whaleMeasureds(4.68)***s(4.50)***s(6.96)***s(3.47)***s(2.65)*** s(5.81)**
ROMSs(4.24)*** s(6.59)*** s(4.75)**s(3.92)*** s(5.00)*** te(LAT,MLD, 12.60)***
Blue whaleMeasureds(5.85)***s(4.25)***s(7.02)***s(5.28)***s(4.96)**
ROMSs(5.32)*** s(3.56)*** s(4.11)** te(LAT,MLD, 13.73)***
Humpback whaleMeasureds(4.61)*** s(3.90)***s(6.97)*** s(1.64)***linear*s(5.91)**
ROMSs(6.41)*** s(4.35)** s(5.65)***s(4.97)***linear*s(2.04)***linear*s(6.76)***
A year covariate was included in the final fin whale models for both datasets, and successfully captured the documented increasing population trend for this species [71]. Given the general offshore distribution of striped dolphin, which was not well sampled during the 2009 survey, data from this year were not included in the models for this species.
Initial modeling results indicated that interaction terms were required for selected species to better capture their observed distribution patterns. The ROMS models for fin and blue whales included an interaction term between MLD and latitude (Table 1). MLD is an important predictor of foraging habitat for these species within the southern portion of the California Current Ecosystem, with highest whale densities found in areas of shallow MLD [10,76]; however, this relationship is not as pronounced at higher latitudes, and preliminary models without the interaction term overestimated whale abundance at higher latitudes where the mixed layer was relatively shallow, especially near the coast. An interaction between latitude and the 200-m isobath was included in both the final ROMS and measured-data models for common bottlenose dolphin and Risso’s dolphin (Table 1), which are commonly encountered on the continental shelf and far offshore in deep waters, but appear to have a lower-density region in between these two areas [42]. Finally, a spatial interaction term was included in the final ROMS and measured-data models for long-beaked common dolphin, consistent with their nearshore distribution in the southern portion of the study area [43,77,78].
Despite the different sources of predictor variables, the final ROMS and measured-data models exhibited similar performance based on a comparison of explained deviance, RMSE, and study area ratios of observed-to-predicted abundance (Table 2). The explained deviance of models built with measured data ranged from 2% (striped dolphin) to 52% (long-beaked common dolphin), and from 3% (short-beaked common dolphin) to 51% (long-beaked common dolphin) for models built with ROMS output (Table 2). Of the 11 species, explained deviance was higher for five of the measured-data models and six of the ROMS models. RMSE values were almost identical for both the ROMS and measured-data models, with slightly better performance exhibited by seven of the ROMS models and three of the measured-data models (RMSE values were identical for striped dolphin). Performance as indicated by study area density ratios showed minor differences among species, with slightly better performance exhibited by five of the ROMS models and five of the measured-data models (ratios were identical for blue whale). However, neither model type consistently performed better overall (Table 2).
For the majority of species, model-based grid abundance estimates for the entire study area were similar for both model types, although estimates from the ROMS-based models were consistently higher for all species except Risso’s dolphin (Table 3). The common bottlenose dolphin abundance estimate from the ROMS model was almost four times higher than that of the model built with measured data, and more than double the standard line-transect density estimate derived from the survey data (Table 3). The ROMS model abundance estimate for Pacific white-sided dolphin was also notably higher than both the measured-data model and standard line-transect estimate (Table 3). With the exception of common bottlenose and Pacific white-sided dolphins, study area density estimates for the remaining nine species were almost identical for both the ROMS and measured-data models (Table 3).
Table
Table 2. Percentage of explained deviance (Expl. Dev.) and root mean squared error (RMSE) for the final encounter rate (delphinids) or single response (Dall’s porpoise and large whales) GAMs built with either measured data or ROMS output. Percentage of explained deviance is also shown for the delphinid group size models (same spatial model used for both data types). The number of sightings (No. sites) reflects the total available for model development. Ratios of line-transect over model-predicted density estimates (Ratio) are for the total study area as calculated for each segment and summed. Values indicating better performance are shown in bold.
Table 2. Percentage of explained deviance (Expl. Dev.) and root mean squared error (RMSE) for the final encounter rate (delphinids) or single response (Dall’s porpoise and large whales) GAMs built with either measured data or ROMS output. Percentage of explained deviance is also shown for the delphinid group size models (same spatial model used for both data types). The number of sightings (No. sites) reflects the total available for model development. Ratios of line-transect over model-predicted density estimates (Ratio) are for the total study area as calculated for each segment and summed. Values indicating better performance are shown in bold.
SpeciesNo. Sites Data TypeGroup Size Model
MeasuredROMS
Striped dolphin103Expl.Dev.2.345.0119.7
RMSE0.0860.086
Ratio1.1001.023
Short-beaked common dolphin718Expl.Dev.5.502.798.4
RMSE0.2210.220
Ratio1.0041.049
Long-beaked common dolphin128Expl.Dev.51.950.510.0
RMSE0.0890.088
Ratio1.0201.029
Common bottlenose dolphin61Expl.Dev.31.934.515.3
RMSE0.0660.064
Ratio0.9921.000
Risso’s dolphin172Expl.Dev.13.314.54.2
RMSE0.1100.109
Ratio0.9760.977
Pacific white-sided dolphin137Expl.Dev.20.618.27.2
RMSE0.0970.099
Ratio0.9180.857
Northern right whale dolphin108Expl.Dev.14.317.08.7
RMSE0.0850.084
Ratio1.0000.989
Dall’s porpoise527Expl.Dev.37.036.0
RMSE1.0411.043NA
Ratio0.9390.944
Fin whale362Expl.Dev.12.015.0
RMSE0.5120.508NA
Ratio0.8760.898
Blue whale261Expl.Dev.16.317.3
RMSE0.2580.257NA
Ratio0.9530.953
Humpback whale275Expl.Dev.48.347.0
RMSE0.3220.337NA
Ratio0.980.974
Table
Table 3. Predicted abundance and density estimates for the California Current study area from GAMs built with either measured data or ROMS output. “Grid” abundance values were calculated as the sum of the individual model-predicted grid cell abundances throughout the study area. Segment-based line-transect abundance and density estimates were made using standard methods without the inclusion of habitat predictors. Uncertainty is not presented since all estimates were derived from the same dataset and included the same parameters, i.e., segment-specific estimates of ESW and g(0).
Table 3. Predicted abundance and density estimates for the California Current study area from GAMs built with either measured data or ROMS output. “Grid” abundance values were calculated as the sum of the individual model-predicted grid cell abundances throughout the study area. Segment-based line-transect abundance and density estimates were made using standard methods without the inclusion of habitat predictors. Uncertainty is not presented since all estimates were derived from the same dataset and included the same parameters, i.e., segment-specific estimates of ESW and g(0).
Model ModelModelLine-TransectLine-Transect
SpeciesData TypeGrid AbundanceGrid DensitySegment AbundanceSegment Density
Striped dolphinMeasured18,3100.01619,8870.017
ROMS18,3900.016
Short-beaked common dolphinMeasured346,6430.303490,9610.430
ROMS351,5230.308
Long-beaked common dolphinMeasured60,4760.053161,5890.142
ROMS63,4960.056
Common bottlenose dolphinMeasured3,2620.0035,8710.005
ROMS12,4550.011
Risso’s dolphinMeasured13,8400.01214,9350.013
ROMS12,2830.011
Pacific white-sided dolphinMeasured36,7740.03233,4460.029
ROMS49,6610.043
Northern right whale dolphinMeasured24,6710.02220,3020.018
ROMS25,6490.022
Dall’s porpoiseMeasured41,0020.03635,3550.031
ROMS42,8270.037
Fin whaleMeasured4,3370.0044,3220.004
ROMS4,6290.004
Blue whaleMeasured1,5350.0011,8730.002
ROMS1,8050.002
Humpback whaleMeasured1,1590.0011,4260.001
ROMS1,3190.001
Segment-based standard line-transect density estimates were substantially higher than the grid-based model estimates for short-beaked common dolphin, and an order of magnitude higher for long-beaked common dolphin (Table 3). Although the standard line-transect estimates are not necessarily unbiased, they are currently the standard measure used to estimate cetacean abundance and provide a separate measure for which to compare the model-based estimates. With the exception of the ROMS-based density estimates for common bottlenose dolphin and Pacific white-sided dolphin, for all other species the grid-based density estimates for both the ROMS and measured-data models were similar to the standard line-transect estimates, and no consistent bias was evident (Table 3).
The multi-year average density plots for the two model types (ROMS and measured data) were similar for the majority of species (i.e., short-beaked common dolphin, long-beaked common dolphin, Risso’s dolphin, northern right whale dolphin, Dall’s porpoise, blue whale, fin whale, and humpback whale; Figure 2), and almost indistinguishable for striped dolphin (Figure 2a). The density plots for common bottlenose dolphin and Pacific white-sided dolphin showed obvious dissimilarities, with the ROMS model predicting very high densities of common bottlenose dolphin in the southwest corner of the study area (Figure 2d), and high densities of Pacific white-side dolphin throughout the northwest portion of the study area (Figure 2f). There were very few sightings of these species in their respective predicted higher-density areas, despite relatively good survey coverage (Figure 1).
Remotesensing 08 00149 g002a 1024Remotesensing 08 00149 g002b 1024Remotesensing 08 00149 g002c 1024Remotesensing 08 00149 g002d 1024Remotesensing 08 00149 g002e 1024Remotesensing 08 00149 g002f 1024
Figure 2. Predicted densities and uncertainty measures from the habitat-based density models built with measured data (top panels) and ROMS output (bottom panels), for (a) striped dolphin, (b) short-beaked common dolphin, (c) long-beaked common dolphin, (d) common bottlenose dolphin, (e) Risso’s dolphin, (f) Pacific white-sided dolphin, (g) northern right whale dolphin, (h) Dall’s porpoise, (i) fin whale, (j) blue whale, and (k) humpback whale. Panels show the multi-year average (Avg) density, and 90% confidence limits (L90% and U90%). Predictions are shown for the study area (1,141,800 km2). Density ranges were selected to encompass all values within the confidence limits. Black dots show actual sighting locations from the ship surveys.
Figure 2. Predicted densities and uncertainty measures from the habitat-based density models built with measured data (top panels) and ROMS output (bottom panels), for (a) striped dolphin, (b) short-beaked common dolphin, (c) long-beaked common dolphin, (d) common bottlenose dolphin, (e) Risso’s dolphin, (f) Pacific white-sided dolphin, (g) northern right whale dolphin, (h) Dall’s porpoise, (i) fin whale, (j) blue whale, and (k) humpback whale. Panels show the multi-year average (Avg) density, and 90% confidence limits (L90% and U90%). Predictions are shown for the study area (1,141,800 km2). Density ranges were selected to encompass all values within the confidence limits. Black dots show actual sighting locations from the ship surveys.
Remotesensing 08 00149 g002aRemotesensing 08 00149 g002bRemotesensing 08 00149 g002cRemotesensing 08 00149 g002dRemotesensing 08 00149 g002eRemotesensing 08 00149 g002f
Consistent with the differences in each model’s average density plot, the lower- and upper-90% confidence interval (CI) plots for Pacific white-sided dolphin also showed major differences between model types. The upper-90% CI plot for the ROMS model showed very high Pacific white-sided dolphin density throughout the northwest portion of the study area, a pattern that was not supported by the sighting data (Figure 2f). Given the differences between the common bottlenose dolphin model’s average density plots, surprisingly, the lower- and upper-90% CI plots were fairly similar (Figure 2d). Despite the similarity of the multi-year average density plots, the uncertainty plots for the three large whale species showed obvious dissimilarities (Figure 2i–k). The upper-90% CI plots for fin whale showed very different patterns between model types in the northern portion of the study area. For example, the measured-data model showed very low density in the nearshore region off the Washington coast, while the ROMS model showed this as an occasionally mid- to high-density region. Further, the measured-data model showed very high density further offshore along the north-northwest border of the study area, encompassing an area of lower density; neither of these patterns matched those of the ROMS model, which were more consistent with the sighting data (Figure 2i). The upper-90% CI plots for blue whale also differed in this region, with the measured-data model showing mid- to high-density areas off the northern Washington coast and in the northwest portion of the study area that were not consistent with the ROMS model predictions or the sighting data (Figure 2j). Based on the ROMS upper-90% CI plot for humpback whale, mid-range density estimates extended well offshore, almost throughout the study area, and high densities also extended south along the coast to the southern extent of the United States EEZ (Figure 2k). These patterns were not consistent with the measured-data model’s upper-90% CI plot, where mid- to high-density estimates were confined mainly to the coast, consistent with this species largely nearshore distribution.
The apparent, abrupt discontinuity at 40°N that appears in many of the multi-year average density and uncertainty plots (i.e., Figure 2a,b,f–h) is a real bathymetric feature, the Mendocino Escarpment, and appears in the majority of the models that included depth or slope as a significant predictor.

4. Discussion

Dynamic species management is of growing interest for marine resource management, but requires nowcast and forecast predictions of species distributions that can only be obtained with real-time and modeled ocean data, respectively [26,27,28]. Dynamic management approaches that use real-time habitat predictions of species distributions have been used successfully to limit bycatch of southern bluefin tuna in the Eastern Australia longline fishery [29,79] and loggerhead sea turtles in the Central North Pacific Hawaii-based longline fishery [30,33]. Species-habitat models based on measured data have been used effectively to predict cetacean density and support conservation measures [5,6,7,8,9,10,11,80,81]. Previous cetacean habitat modeling studies have also used ocean modeled data to forecast species distributions [e.g., 37, 38, 40] but to date, the only study to directly evaluate the ability of these data to accurately forecast cetacean distribution patterns included sea surface temperature and static variables as predictors [13]. In this study, we used cetaceans as a case study to examine whether species distribution models built with a broad suite of predictors derived from modeled ocean state estimates could provide similar results as those based on measured data. We demonstrated that habitat-based density models built with ROMS output generally performed as well or better than models built with traditional measured-data sources at the relatively broad spatial scales used in these analyses (i.e., approximately 10 km2). The assimilation of in situ and remotely sensed data into ocean circulation models has enhanced model fidelity to a level that allowed us to use this information to develop robust species distribution models. This finding indicates that species distribution models can be created from modeled ocean data in support of marine species management for the temporal and spatial scales addressed herein (8-day predictions at 10 km2). This scale is too coarse to forecast finer-scale distribution patterns required for some dynamic management applications, e.g., ship-strike risk. Future studies should examine if finer scale distribution patterns can be captured by ocean modeled data as well as measured data and evaluate the ability of coarse-scale models to predict finer-scale density estimates. Neither of these analyses were possible in this study given the current resolution of the ROMS data and the lack of fine-scale systematic survey data in our study area.
Ocean model output overcomes many of the limitations of in situ oceanographic data, which require prolonged data collection and processing time, thus limiting their utility for dynamic management applications [26,27,28]. Satellite data provide broad spatial coverage in near real-time, but their availability can be limited due to cloud cover, they typically do not have consistent spatial and temporal resolution, and they are limited to surface fields. Habitat models based on ocean modeled output provide a powerful new tool for understanding marine species distributions and biodiversity. Further, they allow for nowcast or forecast predictions of species distributions at a ~10-km spatial resolution in the present study, with higher resolution model output in the future. This ability opens up new opportunities for forecasting changes in species distributions due to seasonal and interannual variability (e.g., ENSO and PDO), as well as exploring potential long-term effects of climate change [32,37,40]. Many of the other ocean circulation models are currently available at significantly lower spatial resolution (e.g., 0.25–1.0 degree) than the ROMS output used in this study. However, the approach used here could be applied to address broad scale distribution questions in other regions. Data assimilative ocean models may also be useful for evaluating historic changes in cetacean abundance and distribution (i.e., hindcasts) based on past surveys, which are otherwise not possible because of the lack of historic coverage for many oceanic variables of interest. For example, the current ROMS data assimilation analyses used in this study provide hindcasts to January 1980, and could thus provide insight into multi-decadal patterns of species distribution.
The functional forms were similar for the variables in common to both datasets, but in general both model types included variables unique to the respective datasets (Table 1 and Supplementary Materials, Figure S1). When variables differed between the two model types, they appeared to serve as different proxies for oceanic processes. For example, the measured-data model for Pacific white-sided dolphin included chlorophyll, MLD, and depth, while the ROMS model included SST, potential energy anomaly, and depth (Table 1). The functional forms of the depth variable were similar between the two model types (Supplementary Materials, Figure S1). In the measured-data model, the functional form showed more animals in waters with higher chlorophyll, and the ROMS model showed more animals in the coolest waters in the study area; both variables reflect the occurrence of Pacific white-sided dolphins in upwelling-modified waters of the study area, consistent with previous studies [24,35,39,51]. Similarly, MLD and potential energy anomaly provide different measures of stratification as reflected in the measured-data and ROMS models, respectively.
The common bottlenose dolphin model is for the offshore ecotype, since the transect coverage provided by the 1991–2009 surveys does not appropriately sample the range of the coastal ecotype, which is found within about 1 km from shore [82,83]. Fine-scale coastal oceanographic and physiographic data are required to build a robust habitat model for the coastal ecotype of bottlenose dolphin. Given their largely coastal distribution, habitat-based density models for long-beaked common dolphin would be much improved with finer resolution oceanographic sampling. Availability of higher resolution remotely sensed data and ocean model output could improve models for all species and ultimately increase our understanding of fine-scale distribution patterns. This is especially important for species with coastal habitats given their generally higher vulnerability to anthropogenic impacts (e.g., ship strikes [10,25]).
The habitat models for both common bottlenose and Risso’s dolphins show a disjunct longitudinal distribution that suggests we are modeling two separate populations with different habitat preferences. Both species are commonly encountered on the continental shelf and far offshore in deep waters, separated by a lower-density region in between these two areas [42]. Including an interaction term between latitude and the 200-m isobath resolved this spatial pattern in the final measured-data and ROMS models for both common bottlenose and Risso’s dolphins; however, additional genetic data are required to identify potential species’ population differences.
A few caveats deserve consideration when predicting density and distribution patterns from ROMS-based habitat models. Chlorophyll was an important predictor in the measured-data models, but a reliable ocean-modeled version of this variable was not included in the 31-year reanalysis used in this study. Data assimilative methods to produce reliable, data-constrained biological variables from ocean models are less mature than their physical counterparts, but in active development. Gregg [84] and Edwards et al. [20] provide reviews of oceanographic biological assimilation efforts and Song et al. [85,86,87] apply the present 4D-Variational assimilative methodology to biological variables in the California Current System. Experimental efforts to produce near real-time chlorophyll estimates are underway also. In the future, statistical models that use data assimilative estimates of biological fields may benefit from the complete spatial and temporal coverage provided (whereas satellite chlorophyll estimates suffer from frequent cloud-induced data loss), but increases in predictive model skill over the approach discussed in this paper will have to be demonstrated.
Sea surface chlorophyll was included as a significant (p = < 0.001) predictor in the final measured-data models for both fin and blue whales. MLD has also previously been shown to be an important predictor for fin and blue whales within the southern portion of our study area [10,76], but our initial ROMS models that included MLD as a univariate predictor overestimated abundance within the northern portion of the study area. This may be an indication of differences in the ecological effect of MLD on whale prey as latitude changes (e.g., because of changes in water temperature, daylight length, or cloud cover and their effects on productivity). For this reason, an interaction term between MLD and latitude was included as a proxy term to capture regional (north to south) differences in the effect of MLD on fin and blue whales in the final ROMS models. This interaction term allowed more accurate model predictions, but is specific to the California Current Ecosystem and may not be effective in other study areas. An interaction term was not needed for the measured-data models for either species most likely because chlorophyll was included and resolved the relevant spatial patterns. Since the inclusion of latitude or longitude may limit the forecasting ability of a habitat model, particularly for potential climate change scenarios, the need to include spatial terms to resolve observed patterns is a limitation of the ROMS models. Further, the use of spatial interaction terms requires a priori knowledge of species distribution patterns and local oceanography [70].
Bivariate predictors with latitude or longitude were included in many of the models to provide better proxies for oceanic processes that span the entire study area [70]. As noted above, the use of latitude and longitude does not allow for predicting outside of the study area, and may reduce our ability to identify trophic links between oceanic processes, prey, and cetaceans. Identifying such relationships requires dedicated studies of linkages and is currently only possible for cetacean species with very short links such as blue whales [88] and North Atlantic right whales [1]. Rather than attempting to describe ecological dynamics, our objective was to identify persistent relationships between species and habitat variables to allow predictions of species distribution within our study area, thus enabling this model comparison.
The percentage of explained deviance was very similar between model types for each species, but there was a substantial spread of explained deviance across species (Table 2). The difference in explained deviance may be attributed in part to the specific habitat requirements of the different species. For example, long-beaked common dolphins have a strong geographically affinity [43,77] and thus have tighter habitat associations and associated greater explained deviance (50.5–51.9; Table 2) as compared to the expansive range of short-beaked common dolphins in our study area [42], which thus have a broader species niche and associated lower explained deviance (2.79–5.50; Table 2).
No consistent bias was evident from the comparison of modeled grid-based and standard line-transect density estimates, and for most species, estimates were similar (Table 3). However, standard line-transect density estimates were nearly three times higher than the grid-based model density estimates for long-beaked common dolphin (Table 3). Previous annual abundance estimates for long-beaked common dolphin have varied substantially throughout the 1991–2009 survey period [42,43,89], and recent estimates that incorporated the ESW and g(0) values used in this study ranged from 9258 animals (CV = 1.23) in 2005 to 94,361 animals (CV = 0.76) in 2008 [90]. This extreme interannual variability in abundance estimates may in part be attributable to north-south shifts in the distribution of this species [43,77]. However, the relatively coarse, broad-scale transect coverage of the 1991–2008 surveys was not optimal for this neritic species, resulting in high sampling variation because each year had only a few sightings [42,90] and the observed average group sizes ranged from approximately 2 to 2150 animals. The finer scale 2009 survey was specifically designed to sample long-beaked common dolphin habitat but this survey only covered one of the seven survey years within our study and covered a small portion of the study area. The model-based abundance estimates, which include consideration of habitat, may be more precise than traditional California Current wide line-transect estimates because they include information from all survey years combined.
There were some discrepancies observed between the models based on ROMS output and measured-data for common bottlenose and Pacific white-sided dolphins. The common bottlenose dolphin study area density estimate from the ROMS model was about four times higher than both the measured-data model and standard line-transect estimates (Table 3). Inspection of the individual grid predictions from the ROMS common bottlenose dolphin model revealed extremely high predictions (e.g., >14 animals/km2) in the southwest corner of the study area, as evident from the density plot (Figure 2d). The Pacific white-sided dolphin study area abundance prediction from the ROMS model was 35% higher than that of the measured-data model, and 48% higher than the line-transect based estimate (Table 3). The range of Pacific white-sided dolphin density estimates predicted by the ROMS model were similar to those of previous studies [24,35,51,74], and inspection of the individual grid predictions did not reveal any outliers. Instead, the mid-to high density estimates covered a much greater area, extending west off the entire northwest coast (Figure 2f); this effect is particularly noticeable in the uncertainty plots. Given Pacific white-sided dolphin distribution patterns documented in past studies [24,74], and the lack of sightings in the predicted mid- to high density region, there is a potential mis-specification of the model built with ROMS output. Errors in ROMS output, even though it is data assimilative, are unavoidable, and particularly challenging to identify in places where no measured data exist. Currently available data are not sufficient to resolve the patterns identified in this study. Given these findings, it is critical to continue to validate predictions from habitat models, because unvalidated habitat models that over- or under-predict species abundance or are not consistent with documented distribution patterns can hamper conservation and management efforts. In this case, given the extensive validation the measured-data model has received in previous studies, the ROMS model results appear suspect and should be further validated using novel survey data. In a future study, we plan to conduct such additional model validation using a novel survey dataset collected in our study area in 2014 [90]. Given the particularly warm waters in the eastern North Pacific that year [91], the line-transect survey data presented in Barlow [90] offer an ideal opportunity for assessing the predictive performance of these models during an anomalously warm water period.
The areas of high density identified in this study for fin, blue, and humpback whales are similar to previous models developed from an overlapping data set [10,24,35,51], and the blue and humpback whale density predictions are also in good agreement with ‘Biologically Important Areas’ determined for these species from a separate data set [75]. However, measures of model uncertainty exhibited spatial variability that differed between model types, and deserve careful consideration for management applications. For example, if only the multi-year average predictions were used to guide management actions, the ROMS and measured-data models provide consistent input. However, if the spatially-explicit measures of uncertainty were also taken into account, different areas may receive different consideration depending on which model type was used. All three species are listed as endangered under the Endangered Species Act, and to assess and develop measures to minimize anthropogenic impacts requires an understanding of their fine-scale distribution patterns and how this varies through time. As noted previously, the spatial scale used in this study is too coarse to forecast finer-scale distribution patterns required for many dynamic management applications.
Given the importance of chlorophyll concentration as a predictor variable in the measured-data models (7 of the 11 species models included log-chlorophyll as a significant predictor; Table 1), the development of a valid ocean modeled chlorophyll product is a critical need for those using these data to improve model performance and support dynamic management decisions. In the future, habitat-based models of cetacean distribution may be improved if modeled ocean data can produce reliable estimates for additional biological variables (e.g., phytoplankton, zooplankton), which are more closely linked to cetacean prey [92,93].

5. Conclusions

The main purpose of this study was to assess the performance of modeled ocean data in species distribution models, which are useful for both management and monitoring regional species diversity. We used cetaceans as a case study given the extensive work on previous spatial distribution models, and selected a suite of species with diverse habitat associations, group size characteristics, and seasonal presence in the study area. Quantitative measures of predictive ability were similar between habitat models built with either a combination of in situ and remotely sensed oceanic variables or ROMS output, and root mean squared error values were almost identical. The majority of the models (9 of 11 species) built with ocean modeled data predicted cetacean distributions as well and in some cases better than models built with traditional data sources that have been extensively validated. Ocean modeled output overcomes many of the limitations of traditional measured-data sources; unlike in situ oceanographic data, ocean modeled data do not require prolonged data collection and processing time, and they are provided at a consistent spatial and temporal resolution, unlike most remotely sensed data. Further, ocean modeled data are not limited to surface fields. The overall demonstrated success of the data assimilative ROMS-based models provides a foundation for other habitat modeling efforts aimed at supporting dynamic management decisions because ocean modeled output is available in near real time and can be forecast. Each species and region will present challenges that require unique analyses given the type and amount of survey data, present knowledge of the species and ecosystem, and the scale and availability of ocean modeled data. The identified discrepancies for the common bottlenose dolphin and Pacific white-sided dolphin models require additional data to resolve, but the new ROMS models form a robust foundation for exploring climate variability and its effect on broad-scale species distribution. Ocean model output may help us to understand biodiversity in the marine realm at a variety of temporal scales – past, present, and future.

Supplementary Materials

The following are available online at www.mdpi.com/ 2072-4292/8/2/149, Tables S1 and S2, Figure S1.

Acknowledgments

This project was funded by the Navy, Commander, U.S. Pacific Fleet and by the National Oceanic and Atmospheric Administration (NOAA), National Marine Fisheries Service (NMFS), Southwest Fisheries Science Center (SWFSC). AMM and CAE gratefully acknowledge the support of NSF (OCE-1061434) which contributed to this manuscript. We thank Chip Johnson, Julie Rivers (U.S. Pacific Fleet, U.S. Navy) and Sean Hanser (Naval Facilities Engineering Command, Pacific, U.S. Navy) for providing us with the opportunity to update the California Current habitat-based density models. The marine mammal survey data and in situ oceanographic data used in this study were collected by a large dedicated team at SWFSC, and we thank the cruise leaders, marine mammal observers, oceanographers, survey coordinators, ship’s crew, and officers who have contributed to collecting these data. Chief Scientists for the ship surveys included Tim Gerrodette and three of the co-authors (JB, SJC, and KAF). We thank the NOAA Environmental Research Division ERDDAP team, especially Roy Mendelssohn for his assistance with the remotely sensed data acquisition. Our project benefited greatly from our close collaboration with Jason Roberts and Laura Mannocci at Duke University, and Dave Miller at the Centre for Research into Ecological and Environmental Modelling (CREEM). This manuscript was improved by the helpful reviews of Anita Gilles, Leigh Torres, and two anonymous reviewers. We dedicate this study to the memory of our friend and colleague Dave Foley, who taught us so much and from whom we wished we could learn so much more.

Author Contributions

Elizabeth Becker, Karin Forney, and Jessica Redfern conceived and designed the study. Elizabeth Becker, Karin Forney, and Paul Fiedler processed and analyzed cetacean and oceanographic data. Christopher Edwards and Andrew Moore developed the ROMS historical reanalysis and contributed the ROMS output. Jay Barlow, Susan Chivers, and Karin Forney designed, conducted and contributed the cetacean survey data. All authors participated in writing the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Baumgartner, M.F.; Cole, T.V.N.; Clapham, P.J.; Mate, B.R. North Atlantic right whale habitat in the lower Bay of Fundy and on the SW Scotian Shelf during 1999–2001. Mar. Ecol. Prog. Ser. 2003, 264, 137–154. [Google Scholar] [CrossRef]
  2. Leathwick, J.R.; Elith, J.; Francis, M.P.; Hastie, T.; Taylor, P. Variation in demersal fish species richness in the oceans surrounding New Zealand: An analysis using boosted regression trees. Mar. Ecol. Prog. Ser. 2006, 321, 267–281. [Google Scholar] [CrossRef]
  3. Louzao, M.; Hyrenbach, K.D.; Arcos, J.; Abello, P.; Gil De Sola, L.; Oro, D. Oceanographic habitat of an endangered Mediterranean procellariiform: Implications for marine protected areas. Ecol. Appl. 2006, 16, 1683–1695. [Google Scholar] [CrossRef]
  4. Benson, S.R.; Eguchi, T.; Foley, D.G.; Forney, K.A.; Bailey, H.; Hitipeuw, C.; Samber, B.P.; Tapilatu, R.F.; Rei, V.; Ramohia, P.; et al. Large-scale movements and high-use areas of western Pacific leatherback turtles, Dermochelys coriacea. Ecosphere 2011. [Google Scholar] [CrossRef]
  5. Gilles, A.; Adler, S.; Kaschner, K.; Scheidat, M.; Siebert, U. Modelling harbor porpoise seasonal density as a function of the German Bight environment: Implications for management. Endanger. Species Res. 2011, 14, 157–169. [Google Scholar] [CrossRef]
  6. Goetz, K.T.; Montgomery, R.A.; Ver Hoef, J.M.; Hobbs, R.C.; Johnson, D.S. Identifying essential summer habitat of the endangered beluga whale Delphinapterus leucas in Cook Inlet, Alaska. Endanger. Species Res. 2012, 16, 135–147. [Google Scholar] [CrossRef]
  7. Keller, C.A.; Garrison, L.; Baumstark, R.; Ward-Geiger, L.I.; Hines, E. Application of a habitat model to define calving habitat of the North Atlantic right whale in the southeastern United States. Endanger. Species Res. 2012, 18, 73–87. [Google Scholar] [CrossRef]
  8. Oppel, S.; Meirinho, A.; Ramírez, I.; Gardner, B.; O’Connell, A.F.; Miller, P.I.; Louzao, M. Comparison of five modelling techniques to predict the spatial distribution and abundance of seabirds. Biol. Conserv. 2012, 156, 94–104. [Google Scholar] [CrossRef]
  9. Hammond, P.S.; Mcleod, K.; Berggren, P.; Borchers, D.L.; Burt, L.; Canadas, A.; Desportes, G.; Donovan, G.P.; Gilles, A.; Gillespie, R.G.; et al. Cetacean abundance and distribution in European Atlantic shelf waters to inform conservation and management. Biol. Conserv. 2013, 164, 107–122. [Google Scholar] [CrossRef] [Green Version]
  10. Redfern, J.V.; McKenna, M.F.; Moore, T.J.; Calambokidis, J.; DeAngelis, M.L.; Becker, E.A.; Barlow, J.; Forney, K.A.; Fiedler, P.C.; Chivers, S.J. Assessing the risk of ships striking large whales in marine spatial planning. Conserv. Biol. 2013, 27, 292–302. [Google Scholar] [CrossRef] [PubMed]
  11. Forney, K.A.; Becker, E.A.; Foley, D.G.; Barlow, J.; Oleson, E.M. Habitat-based models of cetacean density and distribution in the central North Pacific. Endanger. Species Res. 2015, 27, 1–20. [Google Scholar] [CrossRef]
  12. Torres, L.G.; Sutton, P.J.H.; Thompson, D.R.; Delord, K.; Weimerskirch, H.; Sagar, P.M.; Sommer, E.; Dilley, B.J.; Ryan, P.G.; Phillips, R.A. Poor transferability of species distribution models for a pelagic predator, the grey petrel, indicates contrasting habitat preferences across ocean basins. PLoS ONE 2015, 10, e0120014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Becker, E.A.; Foley, D.G.; Forney, K.A.; Barlow, J.; Redfern, J.V.; Gentemann, C.L. Forecasting cetacean abundance patterns to enhance management decisions. Endanger. Species Res. 2012, 16, 97–112. [Google Scholar] [CrossRef]
  14. Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
  15. Oke, P.R.; Brassington, G.B.; Griffin, D.A.; Schiller, A. The BLUElink ocean data assimilation system (BODAS). Ocean Model. 2008, 21, 46–70. [Google Scholar] [CrossRef]
  16. Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (Hybrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
  17. Barron, C.N.; Kara, A.B.; Martin, P.J.; Rhodes, R.C.; Smedstad, L.F. Formulation, implementation and examination of vertical coordinate choices in the Global Navy Coastal Ocean Model (NCOM). Ocean Model. 2006, 11, 347–375. [Google Scholar] [CrossRef]
  18. Carton, J.A.; Giese, B.S. A Reanalysis of ocean climate using Simple Ocean Data Assimilation (SODA). Mon. Weather Rev. 2008, 136, 2999–3017. [Google Scholar] [CrossRef]
  19. Moore, A.M.; Arango, H.G.; Broquet, G.; Edwards, C.A.; Veneziani, M.; Powell, B.S.; Foley, D.; Doyle, J.D.; Costa, D.; Robinson, P. The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems. II: Performance and application to the California current system. Prog. Oceanogr. 2011, 91, 50–73. [Google Scholar] [CrossRef]
  20. Edwards, C.A.; Moore, A.M.; Hoteit, I.; Cornuelle, B.D. Regional ocean data assimilation. Annu. Rev. Mar. Sci. 2015, 7, 21–42. [Google Scholar] [CrossRef] [PubMed]
  21. Fiedler, P.C.; Reilly, S.B. Interannual variability of dolphin habitats in the eastern tropical Pacific. I: Research vessel surveys, 1986–1990. Fish. Bull. 1994, 92, 434–450. [Google Scholar]
  22. Ballance, L.T.; Pitman, R.L.; Fiedler, P.C. Oceanographic influences on seabirds and cetaceans of the eastern tropical Pacific: A review. Prog. Oceanogr. 2006, 69, 360–390. [Google Scholar] [CrossRef]
  23. Ferguson, M.C.; Barlow, J.; Fiedler, P.; Reilly, S.B.; Gerrodette, T. Spatial models of delphinid (family Delphinidae) encounter rate and group size in the eastern tropical Pacific Ocean. Ecol. Model. 2006, 193, 645–662. [Google Scholar] [CrossRef]
  24. Forney, K.A.; Ferguson, M.C.; Becker, E.A.; Fiedler, P.C.; Redfern, J.V.; Barlow, J.; Vilchis, I.L.; Gerrodette, T.; Balance, L.T. Habitat-based spatial models of cetacean density in the eastern Pacific Ocean. Endanger. Species Res. 2012, 16, 113–133. [Google Scholar] [CrossRef]
  25. Dransfield, A.; Hines, E.; McGowan, J.; Holzman, B.; Nur, N.; Elliott, M.; Howar, J.; Jahncke, J. Where the whales are: Using habitat modeling to support changes in shipping regulations within National Marine Sanctuaries in Central California. Endanger. Species Res. 2014, 26, 39–57. [Google Scholar] [CrossRef]
  26. Hobday, A.J.; Hartog, J.R. Dynamic Ocean Features for use in Ocean Management. Oceanography 2014, 27, 134–145. [Google Scholar] [CrossRef]
  27. Lewison, R.L.; Hobday, A.J.; Maxwell, S.M.; Hazen, E.L.; Hartog, J.R.; Dunn, D.C.; Briscoe, D.K.; Fossette, S.; O’Keefe, C.E.; Barnes, M.; et al. Dynamic Ocean Management: Identifying the Critical Ingredients of Dynamic Approaches to Ocean Resource Management. Bioscience 2015. [Google Scholar] [CrossRef]
  28. Maxwell, S.M.; Hazen, E.L.; Lewison, R.L.; Dunn, D.C.; Bailey, H.; Bograd, S.J.; Briscoe, D.K.; Fossette, S.; Hobday, A.J.; Bennett, M.; et al. Dynamic ocean management: Defining and conceptualizing real-time management of the ocean. Mar. Policy 2015, 58, 42–50. [Google Scholar] [CrossRef]
  29. Hobday, A.J.; Hartmann, K. Near real-time spatial management based on habitat predictions for a longline bycatch species. Fish. Manag. Ecol. 2006, 13, 365–380. [Google Scholar] [CrossRef]
  30. Howell, E.A.; Kobayashi, D.R.; Parker, D.M.; Balazs, G.H.; Polovina, J.J. TurtleWatch: A tool to aid in the bycatch reduction of loggerhead turtles Caretta caretta in the Hawaii-based pelagic longline fishery. Endanger. Species Res. 2008, 5, 267–278. [Google Scholar] [CrossRef]
  31. Hobday, A.J.; Hartog, J.R.; Timmis, T.; Fielding, J. Dynamic spatial zoning to manage southern bluefin tuna capture in a multi-species longline fishery. Fish. Oceanogr. 2010, 19, 243–253. [Google Scholar] [CrossRef]
  32. Hartog, J.; Hobday, A.J.; Matear, R.; Feng, M. Habitat overlap of southern bluefin tuna and yellowfin tuna in the east coast longline fishery-implications for present and future spatial management. Deep Sea Res. Part II 2011, 58, 746–752. [Google Scholar] [CrossRef]
  33. Howell, E.A.; Hoover, A.A.; Benson, S.R.; Bailey, H.; Polovina, J.J.; Seminoff, J.A.; Dutton, P.H. Enhancing the TurtleWatch product for leatherback sea turtles, a dynamic habitat model for ecosystem-based management. Fish. Oceanogr. 2015, 24, 57–68. [Google Scholar] [CrossRef]
  34. Redfern, J.V.; Barlow, J.; Balance, L.T.; Gerrodette, T.; Becker, E.A. Absence of scale dependence in cetacean-habitat models for the eastern tropical Pacific Ocean. Mar. Ecol. Prog. Ser. 2008, 363, 1–14. [Google Scholar] [CrossRef]
  35. Barlow, J.; Ferguson, M.C.; Becker, E.A.; Redfern, J.V.; Forney, K.A.; Vilchis, I.L.; Fiedler, P.C.; Gerrodette, T.; Balance, L.T. Predictive Modeling of Cetacean Densities in the Eastern Pacific Ocean; NOAA Technical Memorandum NMFS-SWFSC-444; NOAA: La Jolla, CA, USA, 2009.
  36. Mannocci, L.; Catalogna, M.; Dorémus, G.; Laran, S.; Lehodey, P.; Massart, W.; Monestiez, P.; Van Canneyt, O.; Watremez, P.; Ridoux, V. Predicting cetacean and seabird habitats across a productivity gradient in the South Pacific gyre. Prog. Oceanogr. 2014, 120, 383–398. [Google Scholar] [CrossRef]
  37. Hazen, E.L.; Jorgensen, S.J.; Rykaczewski, R.; Bograd, S.J.; Foley, D.G.; Jonsen, I.D.; Shaffer, S.A.; Dunne, J.; Costa, D.P.; Crowder, L.B.; et al. Predicted Habitat Shifts of Pacific Top Predators in a Changing Climate. Nature Climate Change 2013. [Google Scholar] [CrossRef]
  38. Torres, L.G.; Smith, T.D.; Sutton, P.; Macdiarmid, A.; Bannister, J.; Miyashita, T. From exploitation to conservation: Habitat models using whaling data predict distribution patterns and threat exposure of an endangered whale. Divers. Distrib. 2013, 19, 1138–1152. [Google Scholar] [CrossRef]
  39. Becker, E.A.; Forney, K.A.; Foley, D.G.; Smith, R.C.; Moore, T.J.; Barlow, J. Predicting seasonal density patterns of California cetaceans based on habitat models. Endanger. Species Res. 2014, 23, 1–22. [Google Scholar] [CrossRef]
  40. Dell, J.T.; Wilcox, C.; Matear, R.J.; Chamberlain, M.A.; Hobday, A.J. Potential impacts of climate change on the distribution of longline catches of yellowfin tuna (Thunnus albacares) in the Tasman Sea. Deep Sea Res. Part II 2015, 113, 235–245. [Google Scholar] [CrossRef]
  41. Buckland, S.T.; Anderson, D.R.; Burnham, K.P.; Laake, J.L.; Borchers, D.L.; Thomas, L. Introduction to Distance Sampling: Estimating Abundance of Biological Populations; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
  42. Barlow, J.; Forney, K.A. Abundance and density of cetaceans in the California Current ecosystem. Fish Bull. 2007, 105, 509–526. [Google Scholar]
  43. Carretta, J.V.; Chivers, S.J.; Perryman, W.L. Abundance of the long-beaked common dolphin (Delphinus capensis) in California and western Baja California waters estimated from a 2009 ship-based line-transect survey. Bull. South. Calif. Acad. Sci. 2011, 110, 152–164. [Google Scholar] [CrossRef]
  44. Kinzey, D.; Olson, P.; Gerrodette, T. Marine Mammal Data Collection Procedures on Research Ship Line-Transect Surveys by the Southwest Fisheries Science Center; Report No. LJ-00-08; Southwest Fisheries Science Center: La Jolla, CA, USA, 2000.
  45. Monterey, G.; Levitus, S. Seasonal Variability of Mixed Layer Depth for the World Ocean; NOAA Atlas NESDIS; NOAA: Silver Spring, MD, USA, 1997; Volume 14, p. 100.
  46. Holm-Hansen, O.; Lorenzen, C.J.; Holmes, R.W.; Strickland, J.D. Fluorometric determination of chlorophyll. J. Cons. Perm. Int. Explor. Mer. 1965, 30, 3–15. [Google Scholar] [CrossRef]
  47. Philbrick, V.A.; Fiedler, P.C.; Fluty, J.T.; Reilly, S.B. Report of Oceanographic Studies Conducted during the 2000 Eastern Tropical Pacific Ocean Survey on the Research Vessels David Starr Jordan and McArthur; NOAA Technical Memorandum NMFS-SWFSC-309; NOAA: La Jolla, CA, USA, 2001.
  48. Philbrick, V.A.; Fiedler, P.C.; Balance, L.T.; Demer, D.A. Report of Ecosystem Studies Conducted during the 2001 Oregon, California, and Washington (ORCAWALE) Marine Mammal Survey on the Research Vessels David Starr Jordan and McArthur; NOAA Technical Memorandum NMFS-SWFSC-349; NOAA: La Jolla, CA, USA, 2003.
  49. Reynolds, R.W.; Smith, T.M. Improved global sea surface temperature analyses using optimum interpolation. J. Clim. 1994, 7, 929–948. [Google Scholar] [CrossRef]
  50. Simons, R.A. ERDDAP. Available online: http://coastwatch.pfeg.noaa.gov/erddap (accessed on 26 February 2015).
  51. Becker, E.A.; Forney, K.A.; Ferguson, M.C.; Foley, D.G.; Smith, R.C.; Barlow, J.; Redfern, J.V. Comparing California Current cetacean-habitat models developed using in situ and remotely sensed sea surface temperature data. Mar. Ecol. Prog. Ser. 2010, 413, 163–183. [Google Scholar] [CrossRef]
  52. Crawford, W.; Moore, A.M.; Jacox, M.G.; Neveu, E.; Fiechter, J.; Edwards, C.A. An historical analysis of the California Current using ROMS 4D-Var. Part II: Climate variability. Ocean Model. in press.
  53. Neveu, E.; Moore, A.M.; Edwards, C.A.; Fiechter, J.; Drake, P.T.; Jacox, M.G.; Nuss, E. An historical analysis of the California Current using ROMS 4D-Var. Part I: System configuration and diagnostics. Ocean Model. in press. [CrossRef]
  54. Veneziani, M.; Edwards, C.A.; Doyle, J.D.; Foley, D.G. A central California coastal ocean modeling study: 1. Forward model and the influence of realistic versus climatological forcing. J. Geophys. Res. 2009, 114, C04015. [Google Scholar] [CrossRef]
  55. Broquet, G.; Edwards, C.A.; Moore, A.M.; Powell, B.S.; Veneziani, M.; Doyle, J.D. Application of 4D-Variational data assimilation to the California Current System. Dyn. Atmos. Oceans 2009. [Google Scholar] [CrossRef]
  56. Schroeder, I.D.; Santora, J.A.; Moore, A.M.; Edwards, C.A.; Fiechter, J.; Hazen, E.; Bograd, S.J.; Field, J.C.; Wells, B.K. Application of a data-assimilative regional ocean modeling system for assessing California Current System ocean conditions, krill, and juvenile rockfish interannual variability. Geophys. Res. Lett. 2014. [Google Scholar] [CrossRef]
  57. Amante, C.; Eakins, B.W. ETOPO1 1 arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center: Boulder, CO, USA, 2009.
  58. Barlow, J.; Balance, L.T.; Forney, K.A. Effective Strip Widths for Ship-Based Line-Transect Surveys of Cetaceans; NOAA Technical Memorandum NMFS-SWFSC-484; NOAA: La Jolla, CA, USA, 2011.
  59. Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman & Hall/CRC: Boca Raton, FL, USA, 1990; Volume 43. [Google Scholar]
  60. Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric Generalized Linear Models. J. R. Stat. Soc. Ser. B 2011, 73, 3–36. [Google Scholar] [CrossRef] [Green Version]
  61. Wood, S. Fast stable direct fitting and smoothness selection for generalized additive models. J. R. Statis. Soc. B 2008, 70, 495–518. [Google Scholar] [CrossRef] [Green Version]
  62. Marra, G.; Wood, S. Practical variable selection for generalized additive models. Comput. Stat. Data Anal. 2011, 55, 2372–2387. [Google Scholar] [CrossRef]
  63. Wood, S.N. Generalised Additive Models–An Introduction with R; Chapman and Hall/CRS: Boca Raton, FL, USA, 2006. [Google Scholar]
  64. Miller, D.L.; Burt, M.L.; Rexstad, E.A.; Thomas, L.; Gimenez, O. Spatial models for distance sampling data: Recent developments and future directions. Methods Ecol. Evol. 2013, 4, 1001–1010. [Google Scholar] [CrossRef]
  65. Cañadas, A.; Hammond, P.S. Abundance and habitat preferences of the short-beaked common dolphin Delphinus delphis in the southwestern Mediterranean: Implications for conservation. Endanger. Species Res. 2008, 4, 309–331. [Google Scholar] [CrossRef]
  66. Barlow, J. Inferring trackline detection probabilities, g(0), for cetaceans from apparent densities in different survey conditions. Mar. Mamm. Sci. 2015. [Google Scholar] [CrossRef]
  67. Wood, S.N. Thin plate regression splines. J. R. Stat. Soc. Ser. B 2003, 65, 95–114. [Google Scholar] [CrossRef]
  68. Reid, J.L., Jr.; Roden, G.I.; Wyllie, J.G. Studies of the California Current System. Calif. Ocean. Fish. Invest. Rep. 1958, 6, 28–56. [Google Scholar]
  69. McClatchie, S. Regional Fisheries Oceanography of the California Current System: The CalCOFI Program; Springer: New York, NY, USA, 2014. [Google Scholar]
  70. Forney, K.A. Environmental models of cetacean abundance: Reducing uncertainty in population trends. Conserv. Biol. 2000, 14, 1271–1286. [Google Scholar] [CrossRef]
  71. Moore, J.E.; Barlow, J. Bayesian state-space model of fin whale abundance trends from a 1991–2008 time series of line-transect surveys in the California Current. J. Appl. Ecol. 2011, 48, 1195–1205. [Google Scholar] [CrossRef]
  72. Barlow, J.; Calambokidis, J.; Falcone, E.A.; Baker, C.S.; Burdin, A.M.; Clapham, P.J.; Ford, J.K.B.; Gabriele, C.M.; LeDuc, R.; Mattila, D.K.; et al. Humpback whale abundance in the North Pacific estimated by photographic capture-recapture with bias correction from simulation studies. Mar. Mamm. Sci. 2011, 27, 793–818. [Google Scholar] [CrossRef]
  73. Becker, E.A.; Forney, K.A.; Foley, D.G.; Barlow, J. Density and Spatial Distribution Patterns of Cetaceans in the Central North Pacific Based on Habitat Models; NOAA Technical Memorandum NMFS-SWFSC-490; NOAA: La Jolla, CA, USA, 2012.
  74. Becker, E.A.; Forney, K.A.; Ferguson, M.C.; Barlow, J.; Redfern, J.V. Predictive Modeling of Cetacean Densities in the California Current Ecosystem Based on Summer/Fall Ship Surveys in 1991–2008; NOAA Technical Memorandum NMFS-SWFSC-499; NOAA: La Jolla, CA, USA, 2012.
  75. Calambokidis, J.; Steiger, G.H.; Curtice, C.; Harrison, J.; Ferguson, M.C.; Becker, E.A.; DeAngelis, M.; Van Parijs, S.M. Biologically important areas for selected cetaceans within U.S. waters-West Coast region. Aquat. Mamm. 2015, 41, 39–53. [Google Scholar] [CrossRef]
  76. Fiedler, P.C.; Reilly, S.B.; Hewitt, R.P.; Demer, D.; Philbrick, V.A.; Smith, S.; Armstrong, S.W.; Croll, D.A.; Tershy, B.R.; Mate, B.R. Blue whale habitat and prey in the California Channel Islands. Deep Sea Res. Part II Top. Stud. Oceanogr. 1998, 45, 1781–1801. [Google Scholar] [CrossRef]
  77. Heyning, J.E.; Perrin, W.F. Evidence for two species of common dolphin (genus Delphinus) from the eastern North Pacific. Contrib. Sci. Mus. Nat. Hist. Los Angel. 1994, 442, 1–35. [Google Scholar]
  78. Gerrodette, T.; Eguchi, T. Precautionary design of a marine protected area based on a habitat model. Endanger. Species Res. 2011, 15, 159–166. [Google Scholar] [CrossRef]
  79. Hobday, A.J.; Hartog, J.R.; Spillman, C.M.; Alves, O. Seasonal forecasting of tuna habitat for dynamic spatial management. Can. J. Fish. Aquat. Sci. 2011, 68, 898–911. [Google Scholar] [CrossRef]
  80. Hooker, S.K.; Whitehead, H.; Gowans, S. Marine protected area design and the spatial and temporal distribution of cetaceans in a submarine canyon. Conserv. Biol. 1999, 13, 592–602. [Google Scholar] [CrossRef]
  81. Cañadas, A.; Sagarminaga, R.; Urquiola, E.; Hammond, P.S. Habitat preference modelling as a conservation tool: Proposals for marine protected areas for cetaceans in southern Spanish waters. Aquat. Conserv. 2005, 15, 495–521. [Google Scholar] [CrossRef]
  82. Carretta, J.V.; Forney, K.A.; Laake, J.L. The abundance of southern California coastal bottlenose dolphins estimated from tandem aerial surveys. Mar. Mamm. Sci. 1998, 14, 655–675. [Google Scholar] [CrossRef]
  83. Defran, R.H.; Weller, D.W.; Kelly, D.L.; Espinosa, M.A. Range characteristics of Pacific coast bottlenose dolphins (Tursiops truncatus) in the Southern California Bight. Mar. Mamm. Sci. 1999, 15, 381–393. [Google Scholar] [CrossRef]
  84. Gregg, W.W. Assimilation of SeaWiFS ocean chlorophyll data into a three-dimensional global ocean model. J. Marine Syst. 2008, 69, 205–225. [Google Scholar] [CrossRef]
  85. Song, H.; Edwards, C.A.; Moore, A.M.; Fiechter, J. Data assimilation in a coupled physical-biogeochemical model of the California Current System using an incremental lognormal 4-dimensional variational approach: Part 1, Model formulation and biological data assimilation twin experiments. Ocean Model. submitted.
  86. Song, H.; Edwards, C.A.; Moore, A.M.; Fiechter, J. Data assimilation in a coupled physical-biogeochemical model of the California Current System using an incremental lognormal 4-dimensional variational approach: Part 2, Joint physical and biological data assimilation twin experiments. Ocean Model. in press.
  87. Song, H.; Edwards, C.A.; Moore, A.M.; Fiechter, J. Data assimilation in a coupled physical-biogeochemical model of the California Current System using an incremental lognormal 4-dimensional variational approach: Part 3, Assimilation in a realistic context using satellite and in situ observations. Ocean Model. in press.
  88. Croll, D.A.; Marinovic, B.B.; Benson, S.; Chavez, F.P.; Black, N.; Ternullo, R.; Tershy, B.R. From wind to whales: Trophic links in a coastal upwelling system. Mar. Ecol. Prog. Ser. 2005, 289, 117–130. [Google Scholar] [CrossRef]
  89. Barlow, J. Cetacean Abundance in the California Current Estimated from a 2008 Ship-Based Line-Transect Survey; NOAA Technical Memorandum NMFS-SWFSC-456; NOAA: La Jolla, CA, USA, 2010.
  90. Barlow, J. Cetacean Abundance in the California Current Estimated from Ship-Based Line-Transect Surveys in 1991–2014; NOAA Administrative Report; NMFS-SWFSC; NOAA: La Jolla, CA, USA, in press.
  91. Bond, N.A.; Cronin, M.F.; Freeland, H.; Mantua, N. Causes and impacts of the 2014 warm anomaly in the NE Pacific. Geophys. Res. Lett. 2015, 42, 3414–3420. [Google Scholar] [CrossRef]
  92. Hazen, E.L.; Nowacek, D.P.; St Laurent, L.; Halpin, P.N.; Moretti, D.J. The relationship among oceanography, prey fields, and beaked whale foraging habitat in the Tongue of the Ocean. PLoS ONE 2011, 6, e19269. [Google Scholar] [CrossRef] [PubMed]
  93. Lambert, C.; Mannocci, L.; Lehodey, P.; Ridoux, V. Predicting cetacean habitats from their energetic needs and the distribution of their prey in two contrasted tropical regions. PLoS ONE 2014, 9, e105958. [Google Scholar] [CrossRef] [PubMed]

Share and Cite

MDPI and ACS Style

Becker, E.A.; Forney, K.A.; Fiedler, P.C.; Barlow, J.; Chivers, S.J.; Edwards, C.A.; Moore, A.M.; Redfern, J.V. Moving Towards Dynamic Ocean Management: How Well Do Modeled Ocean Products Predict Species Distributions? Remote Sens. 2016, 8, 149. https://doi.org/10.3390/rs8020149

AMA Style

Becker EA, Forney KA, Fiedler PC, Barlow J, Chivers SJ, Edwards CA, Moore AM, Redfern JV. Moving Towards Dynamic Ocean Management: How Well Do Modeled Ocean Products Predict Species Distributions? Remote Sensing. 2016; 8(2):149. https://doi.org/10.3390/rs8020149

Chicago/Turabian Style

Becker, Elizabeth A., Karin A. Forney, Paul C. Fiedler, Jay Barlow, Susan J. Chivers, Christopher A. Edwards, Andrew M. Moore, and Jessica V. Redfern. 2016. "Moving Towards Dynamic Ocean Management: How Well Do Modeled Ocean Products Predict Species Distributions?" Remote Sensing 8, no. 2: 149. https://doi.org/10.3390/rs8020149

APA Style

Becker, E. A., Forney, K. A., Fiedler, P. C., Barlow, J., Chivers, S. J., Edwards, C. A., Moore, A. M., & Redfern, J. V. (2016). Moving Towards Dynamic Ocean Management: How Well Do Modeled Ocean Products Predict Species Distributions? Remote Sensing, 8(2), 149. https://doi.org/10.3390/rs8020149

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop