Stable Imaging and Accuracy Issues of Low-Altitude Unmanned Aerial Vehicle Photogrammetry Systems

Abstract

Stable imaging of an unmanned aerial vehicle (UAV) photogrammetry system is an important issue that affects the data processing and application of the system. Compared with traditional aerial images, the large rotation of roll, pitch, and yaw angles of UAV images decrease image quality and result in image deformation, thereby affecting the ground resolution, overlaps, and the consistency of the stereo models. These factors also cause difficulties in automatic tie point matching, image orientation, and accuracy of aerial triangulation (AT). The issues of large-angle photography of UAV photogrammetry system are discussed and analyzed quantitatively in this paper, and a simple and lightweight three-axis stabilization platform that works with a low-precision integrated inertial navigation system and a three-axis mechanical platform is used to reduce this problem. An experiment was carried out with an airship as the flight platform. Another experimental dataset, which was acquired by the same flight platform without a stabilization platform, was utilized for a comparative test. Experimental results show that the system can effectively isolate the swing of the flying platform. To ensure objective and reliable results, another group of experimental datasets, which were acquired using a fixed-wing UAV platform, was also analyzed. Statistical results of the experimental datasets confirm that stable imaging of a UAV platform can help improve the quality of aerial photography imagery and the accuracy of AT, and potentially improve the application of images acquired by a UAV.

1. Introduction

Unmanned aerial vehicles (UAV), as a flexible aerial photography platform, have been widely used in many applications, such as agriculture, water conservation, geophysical exploration, mapping, 3D reconstruction, and disaster relief [1,2,3,4,5,6,7,8]. The ability to obtain high-resolution images makes large-scale mapping possible. As a supplementary photogrammetry platform for satellite and traditional aerial photogrammetry systems, low-altitude UAV has several advantages, such as low altitude, low speed (for a low-altitude aerial photography system, high speed will result in a blurred image), low cost, flexible and simple operation, and high-resolution images [9]. However, UAV has problems that differ from those of the flight platform of traditional photography. Generally, the tilt angle of the images for a traditional aerial photogrammetry platform is not more than 3°, but for a low-altitude UAV platform, the typical unstable flight attitude may lead to a large rotation angle in photography. For example, a light and small UAV and an unmanned airship platform are not as reliable as the traditional aerial photography system, and are more likely to be affected by wind and other weather factors, the rotation angle may be increased to 10° or even more (for the airship platform) [1,2]. These issues seriously affect the data processing and application of the UAV photogrammetry system.

Automated data processing in traditional aerial photogrammetry is relatively developed. In recent years, more software packages have been designed and developed to fit UAV images (e.g., Pix4D, Photo Modeler, VirtuoZo v3.6 [10], and AgiSoft Photoscan [11,12]). Image matching is a key step in data processing of aerial photogrammetry images. Feature extraction methods, which were proposed by Förstner [13] and Harris [14], are widely used for traditional aerial images to obtain precision tie points. Least squares matching is employed to improve the precision of tie points (0.1 pixel) [15]. Certain factors, including large number, small frame, and large rotation angles of UAV images, cause difficulties in automatic tie point matching. The Scale Invariant Feature Transform (SIFT) [16,17,18,19,20,21] match algorithm is widely adopted for UAV image matching to generate a sufficient number of tie points. To improve the result of SIFT, Random Sample Consensus (RANSAC) [10,22] algorithm is used to remove erroneous matching points. Ai Mingyao proposed the BAoSIFT matching algorithm to improve the SIFT with block feature extraction to generate more even distribution of tie points [10].

The image quality and accuracy of aerial triangulation (AT) are the key points of applying the remote sensing images acquired by UAVs. In this paper, the stable imaging issues of low-altitude UAV photogrammetry systems mainly focused on are the large rotation angles of the images caused by the unstable flight attitude of the flying platform and the effects of the rotation angles on the data processing and accuracy of the results. A large rotation angle of photogrammetry will lead to poor image ground resolution, low precision of the matching result, poor precision of AT, and low accuracy of the stereo model. The complex relationship among rotation angles (roll, pitch, and yaw), image quality, ground resolution, overlaps, precision and distribution of tie points, accuracy of AT, and stereo model is discussed and analyzed in this paper. A low-cost three-axis stabilization platform for a low-altitude unmanned airship photogrammetry system, which works with a GNSS/IMU system and a simple mechanical structure, is used to improve the pose of images. Experiments confirm that the stabilization platform can help the isolation swing of the flight platform and improve the quality of images and the precision of AT.

The issues of large rotation angle of low altitude UAV images are discussed and analyzed in Section 2. The structure and workflow of the proposed three-axis stabilization platform, and the experimental datasets from different flying platforms with and without stabilization are introduced in Section 3. Section 4 describes the experimental results of the test flight of the proposed three-axis stabilization platform and the accuracy of different data. Conclusions and topics for further research are given in Section 5.

2. Stable Imaging Issues of Low-Altitude UAV Images

2.1. Optical Characteristics of Low-Altitude Aerial Photography

Most cameras for UAV photogrammetry systems include an image sensor, a fixed-focal lens, which works with several glass lenses, and a shutter system. According to the principle of photometry, the illuminance characteristics of the lens can be expressed as Equation (1) [15]:

$$E_{\theta }=E{\cos }^4\theta$$

(1)

where $E$ is the illuminance value of a pixel on the main optical axis, and $E_{\theta }$ is the illuminance value of a pixel with field angle $\theta$. The equation indicates that with an increasing field angle, the difference between $E_{\theta }$ and $E$ becomes more significant [15].

Table 1. Illuminance ratio of image points off and on axis with different field angles.

$\mathbf{\theta }$	0°	10°	20°	30°	40°	50°	60°
$\raisebox{1ex}{$E_{\theta }$}\!\left/ \!\raisebox{-1ex}{$E$}\right.$	1	0.941	0.780	0.563	0.344	0.171	0.063

presents the illuminance ratio of the image points off and on axis with different field angles $\theta$.

For the digital camera system, the equation can be expressed as Equation (2):

$$E_{\left(x,y\right)}=E*{\left(f/\sqrt{f^2+x^2+y^2}\right)}^4$$

(2)

where $f$ is the focal length (mm), and $x$ and $y$ are the image coordinates of the pixel (mm), $E_{\left(x,y\right)}$ is the illuminance value of the image point ($x$, $y$). Equation (2) shows that focal length is another factor that affects the illuminance ratio of image points. A shorter focal length denotes a poorer illuminance ratio. However, in most situations, small light-UAV photogrammetry systems take a camera with a short fixed focal lens for improving work efficiency and survey accuracy. Thus, this problem is more significant in images acquired by UAVs.

Another important factor that affects image optical characteristics is the photographic distance from the projection center to the object. In terms of such a photographic distance, low-altitude aerial photography has a definite advantage optically. According to the principle of photometry, the illuminance of an image is inversely proportional to the square of the distance. In vertical photography, this influence is mainly related to the field angle of the image point and the regular distribution in the image. If the rotation angle of the image is not zero, then the influence becomes more complex and serious; the rotation angle increases the distance of the objects at the edge of the image and results in a lower intensity of image illumination. The direct optical effect on the performance of digital cameras is noise, which results in a poorer image quality [15,23].

2.2. Image Deformation Issues

Generally, according to the central projection imaging equation, the projection error that is caused by terrain changes in a traditional vertical aerial photography image [7,24] can be expressed as Equation (3):

$$\mathsf{\delta }h=\frac{\Delta h}{H}*r$$

(3)

where $\mathsf{\delta }h$ is the projection error, $\Delta h$ is the terrain change of objects, as shown in Figure 1a (m), such as buildings and other objects; $H$ is the distance from the camera projection center to the ground (m); and $r$ is the radial distance to the principal point of the image (mm). On the basis of Equation (3), a lower altitude results in a larger projection error of a ground object. The projection error of an object on the edge of the image is higher than that of an object inside an image. The result would vary for images with a large rotation angle. The projection error can be calculated using Equation (4):

$$\mathsf{\delta }{h}_{\alpha }=\frac{\Delta h}{H}{r}_n(1-\frac{r_n}{2f}\sin \phi \sin 2\alpha )/(1-\frac{\Delta h}{2Hf}{r}_n\sin \phi \sin 2\alpha )$$

(4)

where $\mathsf{\delta }{h}_{\alpha }$ is the projection error, $r_n$ is the distance between the “n” and “a” points, as shown in the Figure 1b (mm); $f$ is the focal length (mm); and $\alpha$ and $\phi$ are defined in Figure 1b. Equation (4) shows that the rotation angle of the image affects the projection error. The projection error of the image feature is reflected in the image deformation, such as the tilt and occlusion of buildings. Thus, the deformation issues for low-altitude aerial photogrammetry images are more serious in cities and mountainous areas [7].

2.3. Image Ground Sample Distance Issues

The ground sample distance (GSD) of a traditional vertical aerial photography image is consistent for every pixel without considering the topography and can be expressed as $GS{D}_v$ using Equation (5) [25]:

$$GS{D}_v=\frac{H}{f}*d$$

(5)

where $f$ is the focal length (mm); $H$ is the distance from the camera projection center to the ground (m); and $d$ is the size of a pixel (mm), which is square for most digital cameras.

When the image rotation angle is not zero, the GSD varies from pixel to pixel. The relationship between rotation angles and pixels can be calculated and expressed in the following equations. First, the coordinate of every pixel in the image space aids the coordinate system $\left(X,Y\right)$ and can be calculated in geodetic coordinates by using a collinear equation. Here, the camera projection center is set as (0.0, 0.0, 0.0), as indicated in Equation (6):

$$\{\begin{array}{c}X=\frac{H\left(a_{1}x+a_{2}y-a_{3}f\right)}{c_{1}x+c_{2}y-c_{3}f}\\ Y=\frac{H\left(b_{1}x+b_{2}y-b_{3}f\right)}{c_{1}x+c_{2}y-c_{3}f}\end{array}$$

(6)

where $x$ and $y$ are the image coordinates of a pixel (mm), and $a_i$, $b_i$, $c_i$ ($i=1,2,3$) are the nine elements from the rotation matrix, which are calculated with the rotation angles ($\omega ,\phi ,\kappa$) of the image. $\kappa$ affects the direction of the image footprint only and does not contribute to the GSD of the image. $\kappa =0$ is set, and the elements of the rotation matrix are replaced with rotation angles $\omega$ and $\phi$. For a digital camera, the coordinates ($x,y$) can be defined as ($m*d,n*d$); where $m$ and $n$ are the image coordinates of a pixel, and the GSD of $X_{m,n}$ and $Y_{m,n}$ can be expressed as Equation (7):

$$\{\begin{array}{c}{X}_{m,n}=\frac{\partial X}{\partial m}=\frac{H\left(d\cos \phi \overline{Z}+\left(md\cos \phi -f\sin \phi \right)*\left(d\sin \phi \cos \omega \right)\right)}{{\overline{Z}}^2}\\ Y_{m,n}=\frac{\partial Y}{\partial n}=\frac{H\left(d\cos \omega \overline{Z}-\left(md\sin \phi \sin \omega +nd\cos \omega +f\cos \phi \sin \omega \right)*d\sin \omega \right)}{{\overline{Z}}^2}\end{array}$$

(7)

where

$$\overline{Z}=nd\sin \omega -md\sin \phi \cos \omega -f\cos \phi \cos \omega$$

(8)

$H=500$ (m), $f=35$ (mm) are set, and the image format is 6000 × 6000 pixels (each pixel is approximately 6.4 μm in the sensor). On the basis of Equation (5), the GSD is approximately 0.091 m when $\omega$ and $\phi$ are zero. Figure 2 and Figure 3 indicate the relationship between the rotation angle and GSD ($X_{m,n}$ is used in Figure 2, and $Y_{m,n}$ is shown in Figure 3) where the image color shows the ratio of the GSD from Equations (5) and (7) of every pixel. The values of $\omega$ and $\phi$ in Figure 2 and Figure 3 are 3°, 5°, 10°, and 15°.

On the basis of Figure 2 and Figure 3, we can determine that the decline of GSD of a pixel increases with $\omega$ and $\phi$, particularly the pixels on the edge of the image.

Table 2. Statistical information of the GSD distribution with the changing angle.

Angle	$GSD \left(X_{m,n}\right)/GS{D}_v$				$GSD \left(Y_{m,n}\right)/GS{D}_v$
	>1.1	>1.2	>1.3	Max	>1.1	>1.2	>1.3	Max
3°	0.0%	0.0%	0.0%	1.10	0.0%	0.0%	0.0%	1.10
5°	10.9%	0.0%	0.0%	1.18	14.2%	0.0%	0.0%	1.18
7°	23.9%	3.8%	0.0%	1.28	31.0%	5.0%	0.0%	1.28
10°	37.7%	17.0%	5.7%	1.47	48.2%	22.5%	7.5%	1.47
15°	51.4%	36.5%	24.1%	1.94	62.9%	47.2%	31.5%	1.95
20°	61.0%	50.0%	40.2%	2.83	71.7%	61.3%	50.9%	2.88

provides detailed statistical data.

Table 2 shows that the GSD of an image is changed with the value of $\omega$ and $\phi$, the influence is limited when the value of $\omega$ and $\phi$ angle is less than 3°. The GSD of every pixel is close to the GSD of vertical aerial photography. The pixels are not larger than 1.1 times the $GS{D}_v$. However, as the rotation angle increases, its influence on image GSD cannot be disregarded. When the angle increases to 5°, the GSD of more than 14.2% of the pixels are more than 1.1 times that of the vertical aerial photography. When the angle is 7°, the number increases to 31.0%. If the angle increases to 10°, then the GSD of nearly half of the pixels is more than 1.1 times that of vertical aerial photography. The proportion increased to 62.9% and 71.7%, whereas the angle increased to 15° and 20°. This result confirms that increasing the roll and pitch angle not only led to poorer image GSD, but also disrupted the consistent distribution of the GSD in an image (on the basis of Equation (6), we can determine that the GSD of every pixel is the same in vertical aerial photography).

In most situations, UAV aerial photogrammetry systems can take only a small commercial camera with a short fixed focal length. According to Equation (7), focal length does affect the GSD of every pixel if the roll and pitch angle values are not zero.

Table 3. Relationship between focal length and distribution of GSD.

Focal Length (mm)	$GSD \left(Y_{m,n}\right) /GS{D}_v$
	>1.1	>1.2	>1.3	Max
18	54.8%	41.8%	29.6%	2.23
24	52.6%	34.6%	20.2%	1.77
35	48.2%	22.5%	7.5%	1.47
50	41.9%	10.1%	0.1%	1.31
85	26.4%	0.0%	0.0%	1.20

shows the relationship between the focal length and the distribution of GSD, where the values of $\omega$ and $\phi$ angle are set to 10°.

Table 3 shows that the effect of the angles on GSD increases as the focal length shortens. However, most UAV photogrammetry systems fly at a low altitude with a short fixed focal length camera for improved work efficiency and survey accuracy. Thus, this problem is more serious in the UAV platform, and the ability to enhance the stability of imaging is more meaningful.

The statistical results in Table 2 and Table 3 indicate that a stable imaging system for the UAV is significant. The GSD of an image is one of the most important indicators of image quality. Uneven distribution of GSD will cause difficulties in data processing. More details will be introduced in the following sections.

2.4. Tie Point Matching and Aerial Triangulation Issues

As concluded in the previous sections, serious optical effects, increasing image deformation, and inconsistent distribution of GSD, which is caused by the swing of a low-altitude UAV system, also cause difficulties in auto tie point matching, and bundle adjustment (BA) of images.

Image deformation and reduction of GSD increase the difficulty of feature extraction, particularly for the edges of an image. The increase of roll and pitch angle seriously affects the deformation of features on the edge of the image, as well as the number and quality of image features [15]. The optical effects and inconsistent distribution of image GSD also result in inconsistent accuracy of tie points. The accuracies of every tie point in different areas of an image are different. A larger GSD leads to lower accuracy of tie points. The tie points should be evenly distributed for the bundle adjustment, but the decrease of image quality will inevitably affect the numbers and accuracy of tie points of image matching result, thereby leading to a weakly connected network and affecting the even distribution of tie points. Thus, the accuracy of AT is adversely affected [24].

Generally, highly precise and evenly distributed tie points are the keys for AT processing. Thus, this paper aims to determine how the larger rotation angles of images affect the number, distribution, and accuracy of tile points. The experimental sections will provide detailed statistical results.

2.5. Image Overlaps and Stereo Model Issues

Wang pointed out that the distribution of mapping accuracy in traditional aerial photogrammetry is not even [25], and a large rotation angle (roll, pitch, and yaw) complicates problems. In traditional aerial photogrammetry, the rotation angle for photogrammetry is limited, and the stereo model between images is regular [9]. However, for the UAV system, large rotation angles break the regular arrangement of images. Figure 4a–d show the layout of the stereo models and the overlaps between images with the roll, pitch, and yaw rotation angles. Regular overlaps between images are broken. The overlap increases for some areas and reduces for others. The reduction of the overlap between images may lead to low overlap problem. Generally, the BA needs tie points with three degrees of overlaps. Thus, most UAV systems fly with a large overlap (similar to that with more than 80% forward overlap and 50% side overlap). Stereo mapping is performed manually, and a reduction in the image ground resolution would lead to a decline in the accuracy of stereo mapping. In addition, the image rotation angle will increase the parallax of the features, thereby resulting in occlusion problems between features, particularly for urban areas. Thus, roads are often blocked by buildings.

3. Methodology and Data Acquisition

3.1. Methodology

In a traditional aerial photography system, the stabilization platform is widely used to isolate the swing of the aerial photography platform (springs are used to reduce the high-frequency vibration) [7]. However, many factors need to be considered in a UAV system, such as size, weight, installation requirements, power consumption, precision, payload, and cost. Thus, a simple three-axis stabilization platform (Figure 5a), which is controlled with a proportion integration and differentiation (PID) algorithm, is used in this study. The system includes an integrated GNSS/ inertial navigation system (INS) (Figure 5b) that works with a triaxial gyroscope and dual-GNSS device, which is a mechanical rotating platform that can rotate with three digital rudders; this platform is controlled by a microcomputer (Figure 5c) with the PID program.

In the inertial navigation system, which is a mature product, the two GNSS devices, which are installed in the flight direction at a distance of approximately 1.5 m, are used to improve the precision of the heading angle measured by the gyroscope. The precision of the heading angle is 0.2°, and the precision of roll and pitch angles are 0.5°. The GNSS device which is installed on the front is used as the main station, the precision of position is 2.0 m. The rudders are connected with the microcomputer by serial ports. The three rudders are numbered for independent control command, and the rotating accuracy of rudders is 0.3°. The working angle is −35° to 35° for roll, pitch, and yaw rudders. The weight of the entire system is 4 kg, and the system can carry a 10 kg payload and is powered with a 12 V 5000 mAH lithium battery. The system was designed and manufactured by the Chinese Academy of Surveying and Mapping and for installation on an unmanned airship aerial photogrammetry platform.

3.2. Experimental Test Area 1: Baoding

The UAV remote sensing platform used in the experiments of dataset 1 is a low-altitude unmanned airship, which is composed of a helium balloon, an image sensor, a power compartment with two gasoline aviation engines, a small commercial programmable flight management system, and a ground monitoring system. The flight speed of the platform is approximately 50 km/h, and the payload is roughly 25 kg. The camera system is mounted on the proposed three-axis stabilization platform. The inertial navigation system, which works with two GNSS systems, can record the position of each exposure. The imaging sensor, which is mounted on the platform, is a digital camera with a fixed focal length of 35.4621 mm and is calibrated by the provider. The image format is 6000 × 6000 pixels (each pixel is approximately 6.4 μm on the sensor).

In September 2014, 461 images were acquired by the system with a stabilization platform, covering an urban area of Baoding, Hebei Province in China, where the terrain is significantly flat such that the ground elevation varies from 10 to 25 m and the highest object on terrain is less than 20 m. As shown in Figure 6a, the images belong to eight strips in the north–south direction with a flight route of 6.5 km and a flight span of approximately 2 km. The area is approximately 13 km², and the images were taken at an average altitude of 250 m above ground level, which corresponds to a vertical photography GSD of 4.5 cm. The forward overlap of the images is approximately 70% and the side overlap is approximately 50%. The block contains 45 full natural GCPs. A total of 35 GCPs are used as control points for aerial triangulation processing, whereas the remaining 10 points are used as check points. All the points are surveyed by the GPS real-time kinematic (RTK) method, and the plane and elevation precision of the GCPs is 0.02 m.

3.3. Experimental Test Area 2: Yuyao

The flying platform used in the experiments of dataset 2 is the same low-altitude unmanned airship used in the experiments of dataset 1. The only difference between the flights of the two experiments is that the same camera system works without the three-axis stabilization platform and is fixed directly below the flight platform. The flight management system provided the approximate position and pose of each exposure.

In May 2014, 376 images were acquired by the system without a stabilization platform, covering an urban area of Yuyao, Zhejiang Province in China, where the terrain is significantly flat such that the ground elevation varies from approximately 3 to 15 m and the highest object on the terrain is less than 15 m. As shown in Figure 6b, the images belong to eight strips in the east-west direction with a flight route of 5.0 km and a flight span of roughly 2.5 km. The area is approximately 10.5 km², and the images are taken at an average altitude of 250 m above ground level, which corresponds to a vertical photography GSD of 4.5 cm. The forward overlap of the images is approximately 70% and the side overlap is approximately 50%. The block contains 44 full natural GCPs. 34 of these GCPs are used as control points, whereas the remaining 10 points are utilized as check points. All the points are surveyed by using the GPS RTK method, and the plane and elevation precision of the GCPs is 0.02 m.

3.4. Experimental Test Area 3: Zhang Jiakou Block1 and Block2

The image dataset was acquired by a fixed-wing UAV that works with a programmable flight- management system as shown in Figure 7b. The remote imaging sensor is a digital camera with a fixed focal length of 51.7568 mm, which is calibrated by the UAV system provider. The image format is 7168 × 5240 pixels (each pixel is approximately 6.4 μm in the sensor).

The images of block1 and block2 were acquired by the same fixed-wing UAV system with the same camera system in the two flights. As shown in Figure 8a,b, the dataset block1 covers a rectangular area of 12 km × 2.5 km, and the area is approximately 30 km². A total of 778 images from eight strips in the east-west direction were taken, which included 38 natural GCPs. Twenty eight of them are used as control points, and the remaining 10 are utilized as check points. The dataset block2 contains 764 images that belong to the other eight strips that are close to block1. The area is approximately 30 km². It contains 39 natural GCPs, and 29 of these GCPs are used as control points for data processing; the others are used as check points. The images of block1 and block2 are taken at an average altitude of 700 m above ground level in a hilly area of Zhang Jiakou, Hebei Province in China, where the ground elevation varies from 870 to 950 m and the highest object on the terrain is less than 10 m. The ground resolution is approximately 8.7 cm. The forward overlap of the images is approximately 70% and the side overlap is approximately 50%. The difference between the two blocks is the flight attitude of the UAV platform. In block1, the light fixed-wing UAV system is influenced by the wind; the max roll and pitch angle increase to 10° (the max roll and pitch angle for block2 is smaller than 4°). All the GCPs are surveyed by using the same GPS RTK method, and the plane and elevation precision of the GCPs is 0.02 m.

Table 4. Statistical information of the experimental datasets.

Dataset	Type UAV	Stable Platform	Type Area	GSD (cm)	Overlap	N. GCPs	N. CPs
Baoding	Airship	YES	Urban	4.5	70%/50%	35	10
Yuyao	Airship	NO	Urban	4.5	70%/50%	34	10
Zhang block1	Fixed wings	NO	Hilly	7.8	70%/50%	28	10
Zhang block2	Fixed wings	NO	Hilly	7.8	70%/50%	29	10

shows the basic parameters of the experimental datasets.

4. Results and Discussion

In the following sections, the experimental datasets are analyzed to document the importance of stable imaging for a UAV photogrammetry system. The Yuyao and Baoding datasets, which were acquired by the same flight platform with the same camera system, are employed to demonstrate the influence of rotation angle on image resolution, overlaps, distribution and accuracy of tie points, and precision of the AT and stereo model, and the results also indicate the feasibility and accuracy of the stabilization platform. To ensure objective and reliable results, the datasets from Zhang Jiakou, which were acquired by another fixed-wing UAV system with the same camera system, were also analyzed.

4.1. Image Quality and Overlaps with Rotation Angle

On the basis of the analysis in Section 2.2, we determined that the rotation angle not only seriously effects the deformation of images, but also breaks the even distribution of image GSD, thereby leading to reduced image quality. To verify the result, two groups of continuous images from the Yuyao and Baoding experimental datasets which were obtained with and without the stable platform were adopted to demonstrate the difference of image quality. 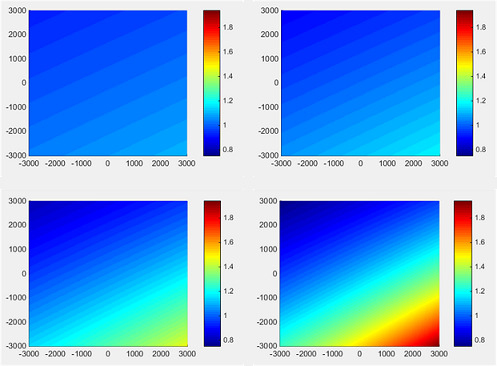Figure 9 shows the GSD distribution of four continuous images and tile images of the same objects from the Yuyao dataset. Figure 9a–d indicate the image GSD distribution of the four images, and Figure 9e–h show the pictures highlighted by the small rectangles in Figure 9a–d. The rotation angles for images “105” and “106” are close, and the difference in GSD is not highly significant. With increased rotation angles, the difference between GSD becomes more significant. The first most significant change in the images caused by the increasing of GSD is the size of the building; the sizes of the buildings in the image “108” are smaller than those of other images (all four images are shown in the same pixel scale, as the GSD is different, the size of the object is different). The deformation of the buildings are very clear and become more and more seriously deformed with the increasing of rotation angles and closing to the edge of images. Moreover, the texture quality of image “107” (as shown in the red circle) is not as good as those of images “105” and “106”. As the angle is increased to 7.4° ($\omega$) and 13.6° ($\phi$) in image “108,” the texture quality of the image decreased significantly as the increasing of image GSD and closing to the edge of the image, and its texture was not as clear as those of images “105” and “106”.

Figure 10 presents the continuous images from the Baoding experimental dataset, which were acquired with a stable imaging platform. The max rotation angles for the images are not worse than 3°, and the angle for most images is smaller than 2°. On the basis of the results of the analysis in Section 2.2 and a comparison of the four images in Figure 10, Figure 10a–d indicates that the difference in the image GSD distribution of the four images is very limited, and the resolution of the continuous images acquired from different viewing angles almost did not exhibit any change.

Image overlap is an important indicator of aerial photogrammetry. In traditional aerial photography, the overlap of aerial images can be estimated by using coverage width and the baseline length of two images without considering the image rotation angle. However, for a low-altitude UAV platform, the effect of the rotation angle on image overlap is so significant that it cannot be disregarded. Figure 11 indicates the footprint views of the experimental dataset Zhang Jiakou block1 and block2. The enlarged view of block1 is not as orderly as that of block2 because of varying and rotation angles.

In this research, the area of the image footprint is used to calculate the overlap between images. Figure 12 shows the statistical information of the image forward overlaps of Baoding and Yuyao.

Figure 12 indicates that the values of the horizontal axis are the indexes of the image pairs in the strip order. The values of the vertical axis are the overlaps of the image pairs. The designed forward overlap is approximately 70% for Yuyao and Baoding. However, the maximum forward overlap of the image acquired in Yuyao is 85%, whereas the minimum is 58%. In comparison, the forward overlap of the dataset from Baoding is only 65% to 72%. The curve fluctuation of Yuyao is more significant than that of Baoding, thereby indicating that image overlaps are influenced by the larger rotation angles of images.

4.2. Distribution and Accuracy of Tie Points

Generally, the precision of AT is affected by many factors, such as image quality and ground resolution, number and distribution of tie points, and overlaps between images. In this paper, the difference in the experimental datasets is the pose of images acquired by the UAV system. Large rotation angle photography results in different overlaps, numbers, and distribution of tie points.

Image measurements for AT of all experimental datasets are performed by Inpho MATCH-AT software with the same parameters. The a priori standard deviations for the auto tie point observations are set at 2 μm.

Table 5. Number and RMS statistics of the tie points.

Dataset	Tie Point Number of Image			RMS of Tie Points in Image Plane (μm)
	Min	Max	Mean	x	y	Sigma 0
Yuyao	63	275	156	3.4	3.3	3.9
Baoding	72	399	231	2.5	2.4	3.0
Zhang Jiakou block1	105	371	200	2.2	3.0	3.1
Zhang Jiakou block2	114	434	302	1.6	2.0	2.2

provides statistical information about the number, RMS, and sigma values of all the photogrammetric residuals after bundle adjustments for all experimental datasets.

Table 5 indicates that the number of tie points for each image is sufficient for exterior orientation processing. A comparison of the results of the datasets indicates that the results are highly consistent. The images with a smaller rotation angle generated more tie points. The statistical results of RMS and sigma 0 in Table 5 also demonstrate that decreasing the image rotation angles (roll, pitch, and yaw) can improve the precision of the tie points.

In this study, we added the numbers of tie points in all the images of one dataset to better analyze the distribution of tie points. We divided the image by using a small 100 × 100 pixel grid according to the image format size. Then, we counted the number of tie points of each grid. The tie point numbers of each small grid were normalized to (0–255) for visualization and to obtain an objective view of the different distributions of tie points because the image number of the datasets and the tie point density vary. The statistical results are presented in Figure 13, which shows the distribution of tie points in different colors.

A comparison between Figure 13a,b clearly indicates that the distribution of tie points in the Baoding dataset is more even than that in the Yuyao dataset. The MATCH-AT is a famous and popular software which performs well in the matching of tie points. As the software package uses LSM matching algorithm to improve the accuracy of the tie points, the image quality is recognized as a key factor that affects the number and accuracy of the matching result. However, as the analysis in the Section 2, the optical effects, image deformation, and uneven distribution of GSD seriously affect the image quality, especially for the edges of the image, thereby resulting in an uneven distribution of matching results in different areas of the image. In the statistical data from Yuyao, the tie points are distributed mainly in the central part of the image, closer to the center of the image the greater density of tie points, and only a small portion of tie points distributed at the edges and corners of the image. However, the statistical distribution of the tie points in Baoding shows that tie points are evenly distributed in each part of the image. The result in Figure 13c,d shows a similar view as that in Figure 13a,b, which indicates that the rotation angle of photography will affect the distribution of the tie points. The following sections provide more detailed statistical results of AT.

4.3. Accuracy of Aerial Triangulation

The accuracy of AT is one of the most important factors in the application of the images acquired by the UAV photogrammetry system. To further demonstrate the effects of a large image rotation angle, detailed statistical results of AT for the four study areas are provided. The root-mean-square (RMS) values of GCPs and check points are presented in

Table 6. Precision of AT in the experimental datasets.

Dataset	Control Points (m)						Check Points (m)
	Max			RMS			Max			RMS
	X	Y	Z	X	Y	Z	X	Y	Z	X	Y	Z
Yuyao	0.247	0.276	0.287	0.121	0.136	0.154	0.281	0.263	0.232	0.147	0.162	0.189
Baoding	0.208	0.170	0.220	0.070	0.069	0.085	0.210	0.137	0.187	0.085	0.088	0.095
Zhang block1	0.267	0.249	0.249	0.132	0.102	0.153	0.255	0.346	0.585	0.185	0.141	0.223
Zhang block2	0.233	0.202	0.222	0.106	0.105	0.128	0.211	0.229	0.323	0.157	0.127	0.213

. A comparison between Baoding and Yuyao, the statistical result demonstrates that the max error of GCPs and check points of Baoding is smaller than the result of Yuyao, the difference between the RMS values of GCPs and check points is even more significant. The RMS values of Yuyao are nearly twice as large as Baoding. The statistical results of Zhang Jiakou block2 is better than that of block1. However, the difference of rotation angle between Zhang Jiakou block1 and block2 is smaller than that between Yuyao and Baoding (difference of camera focal length is another factor), the difference of the max and RMS values of GCPs and check points between Zhang Jiakou block1 and block2 is not as significant as that between Baoding and Yuyao. Thus, the statistical result points out that the rotation angles of images have an effect on the precision of AT, and this effect becomes significant with the increasing of rotation angles of the images.

In this paper, the errors of control points and check points in different stereo models are calculated to demonstrate the effects of rotation angle on the precision of stereo models. We have classified all the images of dataset Yuyao to three classes in regards to their rotation angle ($\omega$ and $\phi$ < 3°, $\omega$ and $\phi$ > 8°, others), and calculated the errors of control points for all stereo models, and then calculate the RMS values of the errors in all stereo models for each rotation class. The statistical results are presented in

Table 7. Errors of control points in different stereo models for Yuyao.

Dataset	<3°			Others			>8°
	X	Y	Z	X	Y	Z	X	Y	Z
Yuyao	0.156	0.161	0.196	0.205	0.213	0.258	0.251	0.263	0.313

. The statistical result indicates that the accuracy of stereo models affected by the rotation angle of images and the errors in the stereo models with smaller rotation angle of images are better.

4.4. Effect of the Three-Axis Stabilization Platform

In the previous sections, the theoretical analysis in Section 2 was verified by the results of the experimental datasets. In this study, the simple, low-cost three-axis stabilization platform was used to reduce this problem. The experimental result of Baoding demonstrated that this platform can improve the quality and precision of the images and the result, respectively.

To analyze the effect of the three-axis stabilization platform, the statistical results of the rotation angle for the images in Yuyao and Baoding are utilized, as shown in Figure 12. The result of AT (three angle elements, $\omega ,\phi ,\kappa$) is adopted to analyze the image rotation angles. Here, the value of $\kappa$ is replaced by the difference between the route angle and $\kappa$. The datasets of Yuyao and Baoding are acquired by the same UAV platform with the same camera system, the difference is that the Baoding dataset is acquired with the three-axis stabilization platform. The statistical result of

Table 8. Statistical results of rotation angles for Yuyao and Baoding.

Angle Threshold	Yuyao			Baoding
	$\mathbf{\omega }$	$\mathbf{\phi }$	$\mathbf{\kappa }$	$\mathbf{\omega }$	$\mathbf{\phi }$	$\mathbf{\kappa }$
<16°	100%	100%	100%
<10°	88.2%	75.3%	88.6%
<5°	59.9%	33.6%	53.4%
<4°	52.5%	25.2%	40.5%
<3°	40.5%	16.8%	25.1%	100%	100%	100%
<2°	28.1%	10.0%	22.9%	96.7%	92.3%	92.2%
<1°	13.4%	3.8%	7.6%	77.9%	60.2%	83.9%
<0.5°	6.0%	1.4%	4.9%	45.4%	32.4%	65.0%

shows that the flight attitude of the unmanned airship platform is unstable (the camera system is mounted on the platform to work without a stabilization platform, and the camera swings with the flight platform). The average rotation angle reaches 8°, and the maximum rotation angle is larger than 15°. By contrast, the statistical result of the Baoding dataset is significantly better than that of the Yuyao dataset. The maximum rotation angle is less than 3°, and more than 90% of the rotation angles are less than 2°. Furthermore, a comparative analysis among the three rotation angles ($\omega ,\phi ,\kappa$) in the Baoding dataset indicates that the precisions of $\omega$ and $\phi$ are nearly the same. However, the precision of $\kappa$ is better. Nearly two-thirds of $\mathrm{the}\kappa$ value is smaller than 0.5°, whereas the percentage for $\omega$ and $\phi$ is only 45.4% and 32.4%. This result is consistent with the precision of the inertial navigation system that works with two GNSS systems (the precision for the yaw angle is 0.2° and 0.5° for the roll and pitch, respectively). The result also confirms that the simple three-axis stabilization platform can effectively isolate the swing of the flight platform and improve the attitude of images.

5. Summary and Conclusions

Theoretical analysis of the optical effects, image deformation, GSD, overlaps, and stereo models of the images acquired by a low-altitude UAV photogrammetry system with a short fixed-focal length camera is provided in detail. The effects of rotation angles on image overlaps, the precision and distribution of tie points, and accuracy of AT and stereo models are discussed and analyzed. A simple three-axis stabilization platform is used to address the poor attitude issues of a low-altitude UAV platform. Four datasets are evaluated in the empirical part of this paper. Two of the datasets were acquired by the same UAV with the same camera with and without a stabilization platform, and the two other datasets were obtained by another light fixed-wing UAV.

Experimental results demonstrate that stable imaging is potentially significant for a low-altitude UAV aerial photogrammetry system. The large rotation of images will decrease image quality and serious the image deformation; it also results in poorer and uneven distribution of image ground resolution, irregular overlap between images and inconsistency of stereo models. These factors also affect the precision and distribution of tie points, thus affecting the accuracy of AT and stereo models. The statistical results of the datasets indicate that stable imaging for low-altitude UAVs can help improve the quality of aerial photography imagery and the accuracy of AT. For this reason, improving the attitude of images acquired by the low-altitude UAV flight platform requires further research attention. A stabilization platform is one solution to this problem. The precision of a stabilization platform does not need to be as high as that of a traditional aerial photography stabilization platform. The systems, which can control the rotation angle to within less than 3°, are sufficiently useful. A two-axis stabilization platform (for roll and pitch) is useful for most small and light UAVs, and can also help improve image attitude. Enhancing the anti-wind performance and developing a powerful flight management system are other effective ways to improve the stability of UAVs.