Estimating Stand Volume and Above-Ground Biomass of Urban Forests Using LiDAR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Stand Delineation
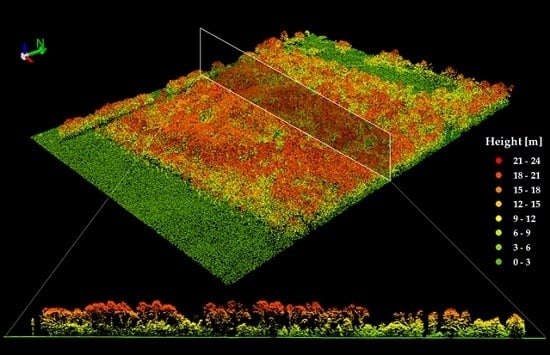
2.2. LiDAR Data
2.3. LiDAR-Derived Basal Area (BA)
2.4. LiDAR-Derived Mean Stand Height
2.5. Model Development
3. Results
3.1. Basal Area (BA)
3.2. Mean Stand Height
3.3. Model Selection and Validation
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AGB | Above-ground biomass |
| AIC | Akaike information criterion |
| BA | Basal area |
| DBH | Diameter at breast height |
| DTM | Digital Terrain Model |
| ESS | Ecosystem services |
| H | Mean stand height |
| LiDAR | Light detection and ranging |
| LOOCV | Leave-One-Out Cross-Validation |
| MSE | Mean square error |
| MSEn | Normalized mean square error |
| PNM | Parco Nord Milano |
| RMSE | Root mean square error |
| RMSEcv | Root mean square error from cross validation |
References
- Lafortezza, R.; Corry, R.C.; Sanesi, G.; Brown, R.D. Visual preference and ecological assessments for designed alternative brownfield rehabilitations. J. Environ. Manag. 2008, 89, 257–269. [Google Scholar] [CrossRef] [PubMed]
- Nowak, D.J. Assessing urban forest structure: Summary and conclusions. Aboricult. Urban For. 2008, 34, 391–392. [Google Scholar]
- Oldfield, E.E.; Felson, A.J.; Wood, S.A.; Hallett, R.A.; Strickland, M.S.; Bradford, M.A. Positive effects of afforestation efforts on the health of urban soils. For. Ecol. Manag. 2014, 313, 266–273. [Google Scholar] [CrossRef]
- Vesterdal, L.; Ritter, E.; Gundersen, P. Change in soil organic carbon following afforestation of former arable land. For. Ecol. Manag. 2002, 169, 137–147. [Google Scholar] [CrossRef]
- Bottalico, F.; Pesola, L.; Vizzarri, M.; Antonello, L.; Barbati, A.; Chirici, G.; Corona, P.; Cullotta, S.; Garfì, V.; Giannico, V.; et al. Modeling the influence of alternative forest management scenarios on wood production and carbon storage: A case study in the Mediterranean region. Environ. Res. 2016, 144, 72–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, D.J.; Crane, D.E.; Stevens, J.C. Air pollution removal by urban trees and shrubs in the United States. Urban For. Urban Green. 2006, 4, 115–123. [Google Scholar] [CrossRef]
- Picot, X. Thermal comfort in urban spaces: Impact of vegetation growth: Case study: Piazza della Scienza, Milan, Italy. Energy Build. 2004, 36, 329–334. [Google Scholar] [CrossRef]
- Yu, C.; Hien, W.N. Thermal benefits of city parks. Energy Build. 2006, 38, 105–120. [Google Scholar] [CrossRef]
- Sanesi, G.; Padoa Schioppa, E.; Lorusso, L.; Bottoni, L.; Lafortezza, R. Avian ecological diversity as an indicator of urban forest functionality. Results from two case studies in northern and southern Italy. Arboric. Urban For. 2009, 35, 80–86. [Google Scholar]
- Marziliano, P.A.; Lafortezza, R.; Colangelo, G.; Davies, C.; Sanesi, G. Structural diversity and height growth models in urban forest plantations: A case-study in northern Italy. Urban For. Urban Green. 2013, 12, 246–254. [Google Scholar] [CrossRef]
- Breuste, J.; Qureshi, S.; Li, J. Applied urban ecology for sustainable urban environment. Urban Ecosyst. 2013, 16, 675–680. [Google Scholar] [CrossRef]
- Sandström, U.G.; Angelstam, P.; Mikusiński, G. Ecological diversity of birds in relation to the structure of urban green space. Landsc. Urban Plan. 2006, 77, 39–53. [Google Scholar] [CrossRef]
- Means, S.A.A.J.E. Predicting forest stand characteristics with airborne scanning LiDAR. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K. A voxel-based LiDAR method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Corona, P. Airborne Laser Scanning to support forest resource management under alpine, temperate and Mediterranean environments in Italy. Eur. J. Remote Sens. 2012, 27–37. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. LiDAR remote sensing of the canopy structure and biophysical properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Parker, G.G.; Harmon, M.E.; Lefsky, M.A.; Chen, J.; Pelt, R.V.; Weis, S.B.; Thomas, S.C.; Winner, W.E.; Shaw, D.C.; Frankling, J.F. Three-dimensional structure of an old-growth pseudotsuga-tsuga canopy and its implications for radiation balance, microclimate, and gas exchange. Ecosystems 2004, 7, 440–453. [Google Scholar] [CrossRef]
- Chopping, M.; North, M.; Chen, J.; Schaaf, C.B.; Blair, J.; Martonchik, J.V.; Bull, M.A. Forest canopy cover and height from MISR in topographically complex southwestern US landscapes assessed with high quality reference data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 44–58. [Google Scholar] [CrossRef]
- Tanhuanpää, T.; Vastaranta, M.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Raisio, J. Mapping of urban roadside trees—A case study in the tree register update process in Helsinki City. Urban For. Urban Green. 2014, 13, 562–570. [Google Scholar] [CrossRef]
- Müller, J.; Brandl, R. Assessing biodiversity by remote sensing in mountainous terrain: The potential of LiDAR to predict forest beetle assemblages. J. Appl. Ecol. 2009, 46, 897–905. [Google Scholar] [CrossRef]
- Simonson, W.D.; Allen, H.D.; Coomes, D.A. Use of an Airborne LiDAR system to model plant species composition and diversity of mediterranean oak forests. Conserv. Biol. 2012, 26, 840–850. [Google Scholar] [CrossRef] [PubMed]
- Bässler, C.; Stadler, J.; Müller, J.; Förster, B.; Göttlein, A.; Brandl, R. LiDAR as a rapid tool to predict forest habitat types in Natura 2000 networks. Biodivers. Conserv. 2010, 20, 465–481. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and LiDAR data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Omasa, K.; Hosoi, F.; Uenishi, T.M.; Shimizu, Y.; Akiyama, Y. Three-dimensional modeling of an urban park and trees by combined airborne and portable on-ground scanning LiDAR remote sensing. Environ. Model. Assess. 2007, 13, 473–481. [Google Scholar] [CrossRef]
- Shrestha, R.; Wynne, R.H. Estimating biophysical parameters of individual trees in an urban environment using small footprint discrete-return imaging LiDAR. Remote Sens. 2012, 4, 484–508. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, B.; Zhou, J.; Hu, C.; Tan, W.; Hu, Z.; Wu, J. Toward automatic estimation of urban green volume using airborne LiDAR data and high resolution remote sensing images. Front. Earth Sci. 2012, 7, 43–54. [Google Scholar] [CrossRef]
- Sanesi, G.; Lafortezza, R.; Marziliano, P.A.; Ragazzi, A.; Mariani, L. Assessing the current status of urban forest resources in the context of Parco Nord, Milan, Italy. Landsc. Ecol. Eng. 2007, 3, 187–198. [Google Scholar] [CrossRef]
- Tabacchi, G.; Cosmo, L.D.; Gasparini, P. Aboveground tree volume and phytomass prediction equations for forest species in Italy. Eur. J. For. Res. 2011, 130, 911–934. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Bailey, R.L.; Dell, T.R. Quantifying Diameter Distributions with the Weibull Function. For. Sci. 1973, 19, 97–104. [Google Scholar]
- Maltamo, M.; Puumalainen, J.; Päivinen, R. Comparison of beta and weibull functions for modelling basal area diameter distribution in stands of pinus sylvestris and picea abies. Scand. J. For. Res. 1995, 10, 284–295. [Google Scholar] [CrossRef]
- Gorgoso, J.J.; Álvarez González, J.G.; Rojo, A.; Grandas Arias, J.A. Modelling diameter distributions of Betula alba L. stands in Northwest Spain with the two-parameter Weibull function. Investig. Agrar. Sist. Recur. For. Esp. 2007, 16, 113–123. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Statistics and Computing; Springer: New York, NY, USA, 2002. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Hollaus, M.; Wagner, W.; Maier, B.; Schadauer, K. Airborne laser scanning of forest stem volume in a mountainous environment. Sensors 2007, 7, 1559–1577. [Google Scholar] [CrossRef]
- Goldberger, A.S. The Interpretation and Estimation of Cobb-Douglas Functions. Econometrica 1968, 36, 464–472. [Google Scholar] [CrossRef]
- Maindonald, J.H.; Braun, W.J. DAAG: Data Analysis and Graphics Data and Functions. Available online: https://cran.r-project.org/web/packages/DAAG/index.html (accessed on 14 April 2016).
- Michaelsen, J. Cross-validation in statistical climate forecast models. J. Clim. Appl. Meteorol. 1987, 26, 1589–1600. [Google Scholar] [CrossRef]
- Andersen, H.-E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LiDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Nelson, B.W.; Mesquita, R.; Pereira, J.L.G.; Garcia Aquino de Souza, S.; Teixeira Batista, G.; Bovino Couto, L. Allometric regressions for improved estimate of secondary forest biomass in the central Amazon. For. Ecol. Manag. 1999, 117, 149–167. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: I. Aboveground biomass. Agric. Ecosyst. Environ. 2012, 158, 216–224. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface LiDAR remote sensing of basal area and biomass in deciduous forests of eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Scrivani, J.A. Fusion of small-footprint LiDAR and multispectral data to estimate plot-level volume and biomass in deciduous and pine forests in Virginia, USA. For. Sci. 2004, 50, 551–565. [Google Scholar]
- Ioki, K.; Imanishi, J.; Sasaki, T.; Morimoto, Y.; Kitada, K. Estimating stand volume in broad-leaved forest using discrete-return LiDAR: Plot-based approach. Landsc. Ecol. Eng. 2009, 6, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. (Tony) Estimating canopy structure of Douglas-fir forest stands from discrete-return LiDAR. Trees 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Van Breugel, M.; Ransijn, J.; Craven, D.; Bongers, F.; Hall, J.S. Estimating carbon stock in secondary forests: Decisions and uncertainties associated with allometric biomass models. For. Ecol. Manag. 2011, 262, 1648–1657. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; Kaasalainen, M. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Næsset, E. Practical large-scale forest stand inventory using a small-footprint airborne scanning laser. Scand. J. For. Res. 2004, 19, 164–179. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne LiDAR. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Lafortezza, R.; Chen, J. The provision of ecosystem services in response to global change: Evidences and applications. Environ. Res. 2016, 147, 576–579. [Google Scholar] [CrossRef] [PubMed]






| Characteristic | Specifications |
|---|---|
| Laser scanner | Riegl LMS-Q680i |
| Point density | ±10/m2 |
| Laser pulse rate | 290 kHz |
| Wavelength | Near infrared |
| Position accuracy | ±10 cm |
| Height accuracy | ±7 cm |
| Field of View | 60° |
| Number of returns | ≤7 |
| LiDAR Derived Variables | Forest Stand Measurements | |
|---|---|---|
| BA | DBH | |
| wbnofirst | 0.78 | 0.81 |
| Anofirst0_10 | 0.23 | −0.08 |
| Anofirst0_20 | 0.39 | 0.13 |
| Anofirst0_30 | 0.38 | 0.08 |
| Anofirst0_40 | 0.36 | 0.08 |
| Anofirst0_50 | 0.33 | 0.05 |
| Anofirst0_60 | 0.33 | 0.05 |
| Anofirst0_70 | 0.36 | 0.09 |
| H | ||
| Afirst80_90 | −0.36 | |
| Afirst80_95 | −0.47 | |
| Afirst80_99 | −0.51 | |
| Afirst90_95 | −0.57 | |
| Afirst90_99 | −0.68 | |
| Afirst95_99 | −0.62 | |
| Percfirst90 | 0.92 | |
| Percfirst95 | 0.91 | |
| Percfirst99 | 0.89 | |
| Response Variable | Model | R2 | AIC | RMSE | RMSEcv |
|---|---|---|---|---|---|
| ln VOL (m3·ha−1) | ln wbnofirst + ln Percfirst95 | 0.81 | 4.59 | 23.66 (23.3%) | 32.86 (32.3%) |
| ln Anofirst0_10 + ln Percfirst90 | 0.76 | 6.81 | 26.19 (25.7%) | 35.64 (35%) | |
| ln wbnofirst + ln Percfirst95 (i) | 0.81 | 6.58 | 23.67 (23.3%) | 34.1 (33.5%) | |
| ln Anofirst0_20 + ln Percfirst95 (i) | 0.84 | 4.71 | 20.18 (19.8%) | 33.9 (33.3%) | |
| ln AGB (Mg·ha−1) | ln wbnofirst + ln Percfirst95 | 0.77 | 4.8 | 19.59 (23.9%) | 26.89 (32.9%) |
| ln Anofirst0_10 + ln Percfirst90 | 0.72 | 6.81 | 21.52 (26.3%) | 28.76 (35.1%) | |
| ln wbnofirst + ln Percfirst95 (i) | 0.77 | 6.79 | 19.63 (24%) | 27.81 (34%) | |
| ln Anofirst0_20 + ln Percfirst95 (i) | 0.80 | 5.31 | 17.97 (22%) | 31.11 (38%) |
| Response Variable | Model | β0 | β1 | β2 |
|---|---|---|---|---|
| lnVOL | 0.38 | 1.49 | 0.37 | |
| lnAGB | 0.78 | 1.44 | 0.19 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannico, V.; Lafortezza, R.; John, R.; Sanesi, G.; Pesola, L.; Chen, J. Estimating Stand Volume and Above-Ground Biomass of Urban Forests Using LiDAR. Remote Sens. 2016, 8, 339. https://doi.org/10.3390/rs8040339
Giannico V, Lafortezza R, John R, Sanesi G, Pesola L, Chen J. Estimating Stand Volume and Above-Ground Biomass of Urban Forests Using LiDAR. Remote Sensing. 2016; 8(4):339. https://doi.org/10.3390/rs8040339
Chicago/Turabian StyleGiannico, Vincenzo, Raffaele Lafortezza, Ranjeet John, Giovanni Sanesi, Lucia Pesola, and Jiquan Chen. 2016. "Estimating Stand Volume and Above-Ground Biomass of Urban Forests Using LiDAR" Remote Sensing 8, no. 4: 339. https://doi.org/10.3390/rs8040339
APA StyleGiannico, V., Lafortezza, R., John, R., Sanesi, G., Pesola, L., & Chen, J. (2016). Estimating Stand Volume and Above-Ground Biomass of Urban Forests Using LiDAR. Remote Sensing, 8(4), 339. https://doi.org/10.3390/rs8040339