Next Article in Journal
Simulation of the Impact of a Sensor’s PSF on Mixed Pixel Decomposition: 1. Nonuniformity Effect
Previous Article in Journal
Study of the Effect of Temporal Sampling Frequency on DSCOVR Observations Using the GEOS-5 Nature Run Results (Part II): Cloud Coverage
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 5
10.3390/rs8050430
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform

by
Wentao Li
1,
Xihong Cui
1,*,
Li Guo
2,
Jin Chen
1,
Xuehong Chen
1 and
Xin Cao
1
1
State Key Laboratory of Earth Surface Processes and Resource Ecology, Beijing Normal University, Beijing 100875, China
2
Department of Ecosystem Science and Management, the Pennsylvania State University, University Park, PA 16802, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2016, 8(5), 430; https://doi.org/10.3390/rs8050430
Submission received: 27 January 2016 / Revised: 9 April 2016 / Accepted: 17 May 2016 / Published: 20 May 2016
Browse Figures
Versions Notes

Abstract

:
As a nondestructive geophysical tool, Ground penetrating radar (GPR) has been applied in tree root study in recent years. With increasing amounts of GPR data collected for roots, it is imperative to develop an efficient automatic recognition of roots in GPR images. However, few works have been completed on this topic because of the complexity in root recognition problem. Based on GPR datasets from both controlled and in situ experiments, the randomized Hough transform (RHT) algorithm was evaluated in root object recognition for different center frequencies (400 MHz, 900 MHz, and 2000 MHz) in this paper. Reasonable accuracy was obtained (both a high recognition rate and a low false alarm rate) in these datasets, which shows it is feasible to apply the RHT algorithm for root recognition. Furthermore, we evaluated the influence of root and soil factors on the recognition. We found that the performance of RHT algorithm is mainly affected by root interval length, root orientation, and clutter noise of soil. The recognition results by RHT could be applied for large scale root system distribution study in belowground ecology. Further studies should be conducted to reduce clutter noise and improve the recognition of the complex root reflections.

Graphical Abstract

1. Introduction

Ground penetrating radar (GPR), a nondestructive geophysical technique, has been widely used in detecting underground objects such as soil horizons, bedrocks, water tables, pipes, cables, and buried artifacts [1,2,3]. Since 1999, GPR has provided an important method for non-invasive study of plant root system, including coarse root mapping [4,5,6,7], root system architecture reconstruction [8,9], and root diameter or biomass estimation [10,11,12,13,14,15]. Unlike optical images, raw GPR radargrams provide insufficient geometrical information of buried targets and are always disturbed by soil clutter noise. Hence, locating and identifying root objects in GPR radargrams is a prerequisite step in GPR data processing. However, collected radargrams of roots are interpreted manually so far [5,6], which is time-consuming and the accuracy depends on the operator’s personal experience. The artificial interpretation method especially cannot meet the requirement of huge amounts of GPR data processing for large scale, whole-root system distribution of plant community in field conditions [9], which is significant in belowground ecology. Therefore, it is imperative to explore an effective and accurate automatic method for identifying root objects in GPR images.
Tree roots generally show hyperbolic patterns on GPR images, which are similar to other linear objects such as pipes and cables. Methods for automatic recognition of these linear objects in GPR images can be classified mainly into three types: machine learning based methods, clustering based methods, and Hough transform (HT) based methods [16]. Machine learning methods usually require a training process, and the accuracy of recognition results depends on the quality and quantity of the training data [17,18,19], which limits its application. Traditional clustering methods usually require prior knowledge on the number of the clusters, and are not able to detect noisy and interfering hyperbolas. Janning et al. [20,21] developed an algorithm named GamRec to handle these problems. However, it was only tested in synthetic radargrams, its application accuracy in practical radargrams is still unknown. The HT is a typical algorithm to detect hyperbolic patterns in GPR images. The HT algorithm was first proposed in 1962 by Hough for detecting imperfect curves with certain shapes [22,23]. It is based on the transformation from a variable-space to the parameter-space. The randomized Hough transform (RHT), as one of the popular variants of the Hough transform [24,25,26], applies random sampling and converging mapping strategy to overcome the drawbacks of Hough transform regarding computational cost, detection accuracy, and resistance to noise [25,26]. As a result, the RHT has been applied widely in actual automatic recognition of landmines and pipelines in GPR images [27,28,29,30].
Although the Hough transform class method has been applied successfully for the automatic recognition of objects such as buried pipes and cables in GPR images, few works have been done to evaluate this method in the identification of underground root systems [31]. Thus far, the influence of root system features on the pattern recognition on GPR images remains unclear. Although a single root and a single pipe share similar hyperbolic pattern on GPR image, root systems possess more complex characteristics than underground pipes or cables: (1) the size and depth of roots are uncertain; (2) the directions and angles of root stretching are variable; (3) the distribution range of root systems is not certain; and (4) the soil environment where roots grow is more complex. These factors render the automatic identification of root systems more difficult than pipes in GPR images.
As a part of a long-term research on root detection based on GPR, this paper presents a detailed study on automatic recognition of root objects in GPR images using RHT. Based on GPR datasets from controlled experiments and in situ fieldwork, the objectives of this study were to: (1) quantitatively evaluate the feasibility and accuracy of RHT algorithm in root recognition; (2) analyze the influencing factors in root recognition by RHT algorithm; and (3) discuss the suitable conditions of RHT in root recognition. Some future improvements of the automatic root recognition method are also put forward. Our study can greatly enhance the interpretation of GPR data in large scale, long-term mapping and monitoring of root system distribution under field conditions.

2. Materials and Methods

2.1. Data Collection

Root detection datasets by GPR were obtained from controlled and in situ experiments in order to test the RHT algorithm in root object recognition. A field-portable GPR system MF HI-MOD (Ingegneria Dei Sistemi Inc., Pisa, Italy) was used to detect root objects in these experiments. The center frequency of the pulse used by GPR (refer to “center frequency” hereafter) includes 900 MHz, 400 MHz and 2000 MHz, which were chosen by former experiments [11,12].
It should be noted that in our study region, the soil is relatively homogenous sand with few other objects like stones, which may cause hyperbolic reflections. Therefore, it is assumed that the hyperbolic signals in GPR images are mainly reflections of root objects. In other words, the recognition of hyperbolic signals is equivalent to the recognition of roots in this study.

2.1.1. Controlled Experiments

The controlled experiments were designed with consideration of three factors in GPR detection: (1) root diameter; (2) root depth; and (3) root stretching angle. These experiments were conducted in Xilingol League (43°54′52″N, 116°12′89″E), Inner Mongolia, China, during August 2013. The soil in the experiment region was dry sandy-clay (~80% sand and ~20% silt and clay) with gravimetric water content of ~5.04% (measured by oven drying), which is suitable for GPR detection. Root samples of a dominant shrub, Caragana microphylla (C. microphylla), were collected from this region. The selected root samples were relatively straight root branches, with diameters ranging from approximately 1 cm to 2 cm and a length of 0.5 m.
The controlled experiment included four trenches in total. Trench I–III were originally designed for the study of root orientation by Guo et al. [32], with 4 m length and 0.5 m depth. Figure 1a shows trench I as an example. Seven holes were drilled into the sidewall of each trench at horizontal intervals of 0.5 m. The root orientation includes two angles, the vertical inclination angle α and the azimuth angle θ, as shown in Figure 1d,e. The vertical inclination is defined as the angle of the projection of the root onto the x-z plane and x-axis. The azimuth angle is defined as the acute angle between the projection of the buried root onto the ground plane (x–y plane) and the direction of the scanning line of the GPR. The holes are drilled with vertical inclinations of 0°, 30° and 45° for Trenches I–III, respectively. Then, in each trench, six roots with different diameters were inserted into the holes, and one empty hole was left as a reference. Trench IV was designed for analyzing the factor of root depth, as shown in Figure 1b. Seven holes were drilled perpendicular to the profile of the trench at different depths from 0.1 m to 0.7 m, with 0.1 m vertical increment, and a horizontal interval of 0.3 m. Then, seven root samples with similar diameters were inserted into these holes.
After the trenches were prepared, the sand trench was filled and surface was flattened. GPR detection was performed with center frequency of 900 MHz. For Trenches I–III, a 6 m long survey line was first scanned along the long side of the trench to obtain a radargram perpendicular to all the roots in the trench. Then, three 1 m long survey lines were scanned with cross angles of 30°, 45°, and 60° with each root orientation. Thus, radargrams for the roots at three different vertical inclination angles (0°, 30°, and 45°) and four azimuth angles (90°, 60°, 45°, and 30°) were collected. For Trench IV, a 4 m long survey line was scanned along the long side of the trench and a radargram with roots at different depths was obtained.

2.1.2. In Situ Experiments

Four cases of in situ experiments for root system detection by GPR were applied to test the recognition algorithm in practice (listed in Table 1). The center frequencies in the first two cases were 400 MHz and 900 MHz. Case I was carried out in Xilingol League, China, in July 2012. The root system of a dominant shrub, C. microphylla, was selected for detection. The local soil was almost homogeneous sand with low moisture content, and gravimetric water content of ~4.94%. The radii of ten concentric circular survey lines were from 40 cm to 220 cm, with increments of 20 cm. Case II was carried out in Jingbian (37°31′19″N, 108°27′26″E), Shaanxi, China, in April 2014. The root system of a tree, Populus simonii, was selected. The soil in the experiment region was sandy-clay (~50% sand and ~50% silt and clay) with gravimetric water content of ~1.51%. Furthermore, the soil contained some layers caused by human behavior such as digging and filling, which cause difficulties in GPR detection. This root system was scanned by GPR along concentric circular lines from 50 cm to 400 cm from the tap root, with increments of 50 cm.
Case III and IV were conducted in Wushen Banner (38°16′51″N, 108°27′16″E) and Otog Front Banner (38°23′34″N, 107°43′27″E), Inner Mongolia, China, in July 2011, respectively. The root systems of a dominant shrub, Caragana korshinskii Kom., were selected in these two cases. The center frequencies of GPR used in these two cases were 900 MHz and 2000 MHz. The soil was also sandy-clay, with gravimetric water content of 6.41% and 2.86%, respectively. Grid survey lines (a total of twenty four) were set in a shrub-centered 5 meter × 6 meter rectangle at intervals of 50 cm.

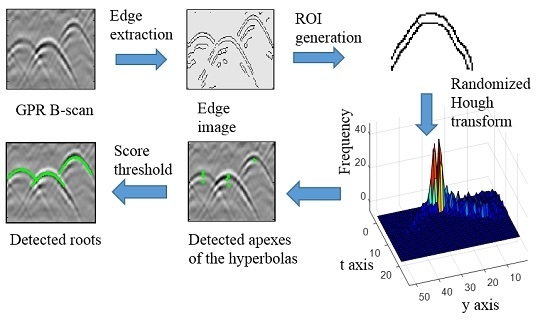
2.2. Automatic Root Signal Recognition Algorithm Based on RHT

Prior to recognition of root objects, several common preprocessing procedures were applied to raw GPR radargrams, including first break time correction, background removal, band pass filtering, and amplitude compensation. The signal amplitude was compensated according to the amplitude decay function fitted automatically. These GPR data processing steps were completed in MATGPR, software developed by Andreas Tzanis [33]. The process of automatic identification of root objects can be divided into three parts: (1) edge extraction and region of interest (ROI) generation; (2) recognition of hyperbolas using randomized Hough transform (RHT); and (3) target determination [27,34]. An example of a radargram processed using the algorithm is shown in Figure 2. A flowchart of the processing is shown in Figure 3. Details are described as follows.

2.2.1. Edge Extraction and Region of Interest (ROI) Generation

A gray-level radargram is firstly processed by performing edge extraction using the Sobel operator. To reduce computation time, the algorithm is applied to a region of interest (ROI), which contains usually one hyperbola curve (Figure 2b). Similar to the method used by Falorni et al. [30], the ROI is generated in the binary image by simply labeling the connected edges.

2.2.2. Recognition of Hyperbolas Using Randomized Hough Transform (RHT)

The RHT algorithm was applied to seek hyperbolic patterns within each ROI in the binary edge image. As the root diameter in this study is usually less than 2.5 cm, it is assumed that the diameters of roots can be ignored [29]. In this manner, the hyperbola function could be applied in Equation (1), according to the geometry relationship shown in Figure 4 [28],
Z 2 = ( V t i / 2 ) 2 − ( y i − Y ) 2
where Z is the depth of the root, Y is the horizontal location of the root, V is the velocity of electromagnetic wave in the medium, ti is the time of flight from the antenna to the root, and yi is the horizontal location of the antenna along the B-scan.
In each iteration for RHT, three points (yi, ti) are selected randomly at a time in the image-space to solve the three unknown parameters Z, Y, and V using Equation (1). Then, this set of solved parameters is recorded in the corresponding bin for the parameters in the accumulator. The sampling and accumulating process is repeated until the number of the iteration k reaches a certain value, kmax, defined by Equation (2), according to Xu et al. [26],
k max = c N 3 n 3 min
where N is the number of the points in the ROI, nmin is a constant value which represents the least number of points in a hyperbola curve, and c is a constant parameter around 10~100. The higher recognition accuracy can be obtained given a higher kmax value, but at the expense of computation time. In this study, an appropriate kmax value of 5000 was selected by testing until the recognition precision does not increase obviously.
After all the iterations, the parameters corresponding to the peaks in the accumulator are selected as the parameters for possible hyperbola curves. The accumulated frequency of these peaks is considered as “score”, an indicator to show the probability of whether the curve is a real hyperbola. The higher the score is, the higher the probability of the curve to be a real hyperbola.

2.2.3. Target Determination

After the RHT is performed, real hyperbolas could be determined using a score threshold (Figure 2d). Recognized curves with scores higher than the threshold are considered as real hyperbolas, and curves with scores lower than the threshold are considered as noise. The threshold should be selected carefully to make a compromise between two accuracy indicators, the recognition rate and the false alarm rate (refer to Section 2.2.4.). In practice, it is feasible to test a proper threshold value using a small number of radargrams, and then apply it to other radargrams in the same region.

2.2.4. Accuracy Evaluation

To get the number of correctly recognized roots and false alarms, the apexes of the automatically recognized hyperbolas (referred to as “recognized apex” hereafter) were compared with manually picked apexes (referred to as “real apex” hereafter). Specifically, for each real apex, a rectangular buffer is established. If a recognized apex exists inside the buffer, the root is considered to be recognized correctly; otherwise, the root is considered to be missed. Besides, recognized apexes existing outside the buffer of any real apex are considered as false alarms. The height of the buffer is determined by the time length of the multiple reflections from the roots. The width of the buffer is set as 0.2 m in the experiments, which is an empirical value to ensure the recognized results are next to the real root locations in GPR B-scan.
The recognition result is evaluated using two indicators, recognition rate and false alarm rate, which are typically used in pipe or mine detection based on GPR [27,35]. The recognition rate is the ratio of the number of correctly recognized roots to the number of all the roots. The false alarm rate is the number of false alarms per meter, which measures the rate of clutter noise that is mistakenly recognized as roots and can be larger than one.
The receiver operating characteristic (ROC) curve was also applied to show the two indicators graphically at different thresholds of the recognition algorithm (the RHT score or ANN output). The ROC curve shows that when the recognition rate increases, the false alarm rate also increases. Therefore, a proper threshold should be selected to compromise between a good recognition rate and a low false alarm rate. Moreover, the ROC curve can also be used to compare the accuracies of the recognition results. The result is more accurate if the ROC curve is closer to the top left corner of the graph, given a certain false alarm rate.

2.3. Comparison with ANN

To illustrate the quality of the recognition results of the RHT algorithm, we made a comparison between RHT and artificial neural network (ANN) method as a baseline, which is a simple and typical algorithm for pipe recognition [36]. Similar to Gamba’s method, the ANN used here is a standard feedforward network, which classifies the sub image of GPR profile within a moving window as hyperbola or clutter noise [36]. The network structure is three-level, including 300 input nodes (corresponding to a 15 × 20 window), a hidden level of 25 nodes and one output node (1 means target curve, 0 means clutter noise). The size of the window was determined by testing on real radargrams to contain the complete shape for most of the hyperbolas. The ANN was established and trained by gradient descent with momentum method in MATLAB neural network toolbox. From the radargrams collected in the same region as in Case III, we picked about 50 images including hyperbolas (positive samples) and nearly 150 images not including hyperbolas (negative samples) for both frequencies (2000 MHz and 900 MHz). The sample sets were adjusted until a good performance of the ANN was obtained. The training set was established by randomly selecting 90% samples from each of the positive and negative sample set and the testing set was the rest of the dataset. The trained network for 900 MHz reached a recognition rate of 87.8% for the training set and 82.7% for the testing set; and the network for 2000 MHz reached a recognition rate of 88.4% for the training set and 87.7% for the testing set, which showed that the design of the network and the training sample set were effective both for the training and the testing set.

3. Results

3.1. Controlled Experiment Results

3.1.1. Roots with Different Diameters and Depths

Figure 5a,b shows results of recognition by RHT for roots with different diameters and depths at an azimuth angle of 90° without vertical inclination of the roots. In general, most of the visible hyperbolas reflected by roots could be recognized correctly for either different diameters or depths. Only two roots with diameters less than 1 cm are missed (marked by red points in Figure 5a), because the diameters of these roots are too thin and the reflected hyperbolas became invisible. Figure 5b shows the results for roots at different depths. In this experiment, the diameters of all the roots were larger than 1 cm and all the reflected hyperbolas were obvious. Although the opening angle of the hyperbola increased with the increase of root depth, recognition results by RHT were good. Only two hyperbolas (marked by red point in Figure 5b) could not be recognized, because the hyperbolic reflections become incomplete due to the interference from the neighbors. These results indicate that root diameter and root depth have slight influence on the RHT method when the hyperbolic reflection is visible and complete.

3.1.2. Roots with Different Stretching Angles

Results of recognition by RHT for roots with different stretching angles are shown in Figure 5c,d. Figure 5c shows the results for a root with various azimuth angles and no vertical inclination. In Figure 5c, the reflected hyperbola shape became vague and the tails of the hyperbola faded away when the azimuth angle changed from 90° to 45°. When the azimuth angle was 30°, the signal became invisible. Similar results were observed for other roots with different diameters. When the signal was visible, it could be recognized by RHT.
Figure 5d shows the results for a root with various azimuth angles and a vertical inclination of 30°. With the decrease of azimuth angle, not only the amplitude of the reflection became weaker, but also the shape of the reflection became incomplete. Only half of the hyperbola existed when the azimuth angle was less than or equal to 45°. As a result, only the root with azimuth angle of 90° or 60° could be recognized by RHT. Results for other roots with different diameters were also similar in this case. Besides, the results for roots with vertical inclination angles of 45° in Trench III were not visible in the radargram and these roots could not be recognized (figure not shown). These results indicate that root stretching angle has significant impact on both the amplitude and the shape of reflections, so it is an important factor for recognition by RHT.

3.2. In Situ Experiment Results

Figure 6 shows examples of the results by RHT for the four cases of in situ experiments. Most of the hyperbolas could be recognized correctly (green points), but some roots were missed (red circles) because of weak signals (Figure 6a), interfered hyperbolas of clustered roots (Figure 6d), and incomplete hyperbolas (Figure 6e). It can be inferred that these missed signals may be caused by root growth factors as in our controlled experiments, such as root diameters, root angles and root interval length, which proves the importance of these factors in root recognition. Moreover, the incomplete and interfering reflections do exist in actual root system detection and they significantly impact the RHT recognition method. The problem of false alarms (red triangles) was mainly caused by soil clutter noise in the radargrams, particularly for Case II (Figure 6c), where the soil in the study site was significantly heterogeneous. This indicates that the RHT algorithm is also sensitive to soil background noise.
Figure 7 shows results of the quantitative evaluation of root recognition using the RHT and ANN method for the four in situ cases. The ROC curves for RHT were all higher than those for ANN, which shows that RHT is better than ANN for all of the four cases. In each case, the two ROC curves for the two center frequencies were very close for each method, which indicates that the center frequency has little effect on the performance of recognition by RHT.
Table 2 shows the recognition rate and false alarm rate at a proper threshold for each case. The threshold was chosen by the method described in Section 2.2.4. For RHT algorithm, the recognition rate and false alarm rate for Cases I and III were similar at approximately 80% recognition rate and false alarm rate of 1.5/m. For Case IV, a recognition rate of about 90% and a false alarm rate of 1.5/m was obtained, which was the best among the four cases, owing to the high signal-to-noise ratio in the radargram of Case IV (Figure 6g,h). For Case II, the recognition rate was approximately 70% and the false alarm rate was around 2/m, due to the clutter noise in GPR profiles (Figure 6c,d). In general, except for cases with serious soil clutter noise such as in Case II, the RHT method is feasible in recognizing root objects in GPR radargrams. Compared with RHT, the performance of ANN is worse. For Case I, III and IV, a recognition rate of 70% and a false alarm rate of approximately 2/m was obtained. For Case II, when the recognition rate was 60%, the false alarm rate was nearly 4/m, which indicates that the ANN is not suitable for radargrams with much clutter noise such as in Case II. In brief, the RHT algorithm outperforms the ANN algorithm in all of the four cases.

4. Discussion

4.1. Factors Influencing Root Recognition Using RHT Algorithm in GPR Images

With the improvement of studies on nondestructive detection of root systems by GPR, automatic identification of root objects in GPR images has become an urgent and important task [37]. However, successful works on this topic are still limited. Hence, it is crucial to clarify the limiting factors for root automatic recognition by GPR. Based on both controlled and in situ experiments for root detection using GPR, this study presents, to our knowledge, the first attempt on comprehensive analysis of factors for root object automatic recognition based on GPR. A two-level framework of the limiting factors has been applied, as shown in Figure 8, namely root growth level (root properties, root distribution and soil) and signal level (signal strength, signal incompleteness, signal interference and clutter noise). The root growth factors influence the GPR signal, which in turn affects the recognition of root by the RHT algorithm. Details of the influence of each factor are discussed as follows.

4.1.1. Root Property Factors

Root property factors refer to the physical properties of the root, such as root diameter and water content. Previous studies reported that when root diameter is less than 5 mm, the root could not be detected using GPR with frequencies ranging from 400 MHz to 1500 MHz [13,14]. The contrast of water content between roots and soil affects the contrast of permittivity, which also determines the amplitude of reflection signals [12]. As long as the signal is strong enough to be distinguished in radargram, the reflection of roots can be recognized. Therefore, root property factors are not important factors for the recognition by RHT.

4.1.2. Root Distribution Factors

Root distribution factors refer to the root stretching angle (azimuth angle and vertical inclination angle), root interval, and root depth. As a linear target, the reflection amplitude of root is influenced by the root direction relative to the antenna [38,39]. Tanikawa [40] and Guo [32] analyzed the impact of horizontal azimuth angle on root detection using GPR and pointed out that horizontal orientation significantly influences both the amplitude and the opening angle of reflected hyperbolic signals, which supports our results (Figure 5c). However, few studies have focused on the combined effects of both horizontal and vertical inclination of roots in GPR detection. In this study, the results are consistent with existing research on horizontal orientation of roots (Figure 5c). Furthermore, we found that when the root orientation involves both vertical and horizontal inclinations relative to the GPR survey line, the reflected hyperbolic signal becomes weaker and incomplete in radargrams (Figure 5d). The incomplete hyperbola is difficult to be distinguished from clutter noise, which impacts the performance of recognition by RHT seriously. Therefore, the root stretching angle is an important limiting factor for root recognition in GPR images.
As for root interval factor, Hirano reported that roots could be distinguished for visual interpretation using 900 MHz GPR when the interval length is greater than 20 cm [14]. Results in our study also show that the reflected hyperbolas of nearby roots are intersected with each other (Figure 6a,b,d), which leads to difficulties for ROI generation and the recognition by RHT algorithm. This implies that root interval is another important limiting factor. Besides, root depth is not an important limiting factor, since hyperbolas in different depths can be recognized by RHT when the signals are visible in radargram.
In other words, complex root distribution causes weak, incomplete, and interfering hyperbolic signals in radargrams, which complicates the automatic recognition of root object for the RHT method.

4.1.3. Soil Background Factors

Several studies have pointed out that in practice, field soil conditions have dramatic impact on root detection using GPR [10,13]. Dry sand soil with low water content is an ideal medium for GPR detection [10]. On the contrary, for heterogeneous soil environment caused by variation of water or clay content, the detection of roots by GPR would be difficult. As for the impact of soil factor on recognition, results show that the clutter noise caused by the heterogeneity of the soil background weakens and disturbs the hyperbolic reflections of roots (Figure 6c,d). Moreover, the clutter noise is difficult to be distinguished from hyperbolas by the RHT algorithm, which leads to false alarm errors. Consequently, the heterogeneity of the soil background is a non-negligible factor in the root automatic recognition in GPR images.
From the above discussion, it is clear that signal strength, incompleteness, interference, and soil clutter noise are the main factors affecting the signal level in the automatic recognition of root objects by RHT. Among these factors, root distribution and soil heterogeneity factors in the root growth level (Figure 8) are the crucial factors in root automatic recognition in GPR images by RHT, because these factors lead to interfering or incomplete reflections and clutter noise. Compared with these root distribution and soil heterogeneity factors, root properties have less impact on the recognition by RHT.

4.2. Feasibility of Applying RHT for Root Recognition in GPR Profiles

The existing studies applied Hough class method were mainly focused on recognition of metal object, such as pipes, cables and land mines. Carlotto used the Hough transform for buried mine detection and got better accuracy than the energy detector method [35]. Simi et al. applied the RHT algorithm in underground pipeline recognition, and obtained a recognition rate of more than 85% and a false alarm rate of less than 0.2/m [27]. Compared with Simi’s study, the performance of the RHT algorithm for root recognition in this work is slightly worse with a recognition rate of approximately 80% and a false alarm rate of less than 1.5/m (Table 2). The reason is that the condition for root recognition is more complex than for the pipe recognition. As a complex of woody cellular material, water and air [41], the reflection signal from roots is much weaker than the reflection of thick metal pipes, which impacts the performance of recognition. Moreover, as roots grow in a clustered pattern, the interval length of roots (usually less than 0.5 m) is usually less than that for pipes (such as 0.5–1 m in Simi’s study), which lead to more interference problems. Besides, unlike horizontally distributed pipes, roots grow with vertical inclination, which leads to incomplete reflections in GPR profiles as mentioned in Section 4.1. All these features of roots generate more complex reflections than pipes, which seriously impacts the recognition. However, although the accuracy for root recognition was lower than for pipe recognition, it is sufficient for ecology application in root study. For example, the accuracy of the recognition result by RHT is enough for research about the three-dimensional distribution or architecture of coarse root system [6,7,9].
The results of the in situ experiments proved that the RHT method is more suitable than the ANN method in recognizing the various hyperbolic reflections of roots. According to the hyperbola function in Equation (1), roots in different depths lead to hyperbolas with different eccentricities, which impact the performance of ANN. Moreover, as the complex root distribution and soil clutter noise cause incomplete and interfering reflections, the process of training ANN classifier for root recognition becomes difficult. It is infeasible to obtain enough training samples including all the various cases of reflections [42]. On the contrary, the RHT method makes use of the hyperbola function and is more suitable than the ANN method to recognize the various reflection of roots.
From the discussion of limiting factors for root recognition by RHT, we suggested that the RHT method is suitable in root recognition under such conditions: (1) most of the lateral roots grow without large vertical inclination; (2) the intervals between the nearby root branches are sufficiently wide to be distinguished in GPR profiles; and (3) the soil background is relatively homogeneous. Under these conditions, the impact of the limiting factors discussed above on the RHT algorithm would decrease and an acceptable recognition probability could be obtained. However, for other plant species or more complicated soil conditions, the practicability of the RHT-based algorithm needs to be further tested.

4.3. Further Improvement of the Automatic Recognition Algorithm for Root Signal in GPR Profiles

Since the influence of different factors discussed above on root recognition cannot be avoided, we propose certain potential improvements to the automatic root object recognition method in GPR images.

4.3.1. Development of Noise Reduction Methods for Heterogeneous Soil Background

The conventional background removal method can only deal with horizontal clutters, but it is not effective in removing inclined clutters, which significantly impacts root recognition. Capineri et al. used the Hough transform for straight line to remove the inclined clutter noise [34]. Other noise reduction method such as wavelet method [43], deconvolution method [44] and K distribution method [45] may also increase the signal-noise ratio of the GPR data and improve the performance of recognition. In addition, an algorithm to recover missing traces is also helpful to improve the completeness of reflection signals when some traces were missed in radargrams [46].

4.3.2. Combination of Several Advanced Algorithms to Deal With Complex Reflection of Roots

As mentioned before, it is difficult for the RHT algorithm to identify the incomplete and interfering reflections of roots in GPR radargrams. Other advanced target recognition algorithms, such as the genetic algorithm (GA) [47] or iterated RHT [48], can be combined with RHT to address this problem. The GA-based algorithm can search for the target curves more efficiently than RHT-based algorithm in the presence of multiple imperfect curves [47]. The iterated RHT updates the ROI to locate the target curves, which may detect interfering reflections of roots more accurately than the original RHT. To updates the ROI, an improved RHT algorithm to select the contributing points to hyperbolas may be useful [49]. Incorporating the advantages of these advanced algorithms into RHT may yield improvements in the automatic recognition of root objects in GPR images. It is also possible to develop a fusion method that combines the recognition results from different algorithms to make use of the advantage of each method in the future.

5. Conclusions

The application of a randomized Hough transform (RHT)-based algorithm for the automatic recognition of root signals in GPR images has been evaluated and analyzed in both controlled and in situ experiments. An acceptable accuracy was obtained for most of the datasets with a recognition rate of approximately 80% and a false alarm rate of less than 1.5/m. Most of the complete and obvious hyperbolic root signals could be recognized in the GPR images. The results suggest that it is feasible to apply the RHT algorithm in automatic recognition of root signals in most of the cases. Moreover, factors influencing the performance of the RHT method were analyzed in detail. A two-level framework of the limiting factors was proposed, including both root growth level factors and signal level factors. It was found that the root distribution and soil heterogeneity factors in the root growth level are crucial in the recognition of roots by RHT, because these factors lead to incomplete and interfering reflections. Suitable conditions are also proposed for root recognition by RHT algorithm. Further improvements are still required to address these specific limiting factors for root recognition.

Acknowledgments

This study was supported by the National Natural Science Foundation of China (Grant No. 41571404) and the State Key Laboratory of Earth Surface Processes and Resource Ecology at Beijing Normal University.

Author Contributions

Wentao Li, Xihong Cui and Li Guo designed the experiments. Wentao Li coded the algorithm and wrote the method and results of the paper. Xihong Cui wrote the introduction and discussion. Jin Chen, Xuehong Chen and Xin Cao supported the interpretation of the results.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Daniels, D.J. Surface-penetrating radar. Electron. Commun. Eng. J. 1996, 8, 165–182. [Google Scholar] [CrossRef]
  2. Jol, H.M. Ground Penetrating Radar: Theory and Application; Elsevier Science: Oxford, UK, 2009; pp. 4–5. [Google Scholar]
  3. Vore, S.L.D. Ground-penetrating radar: An introduction for archaeologists. Geoarchaeology 1997, 54, 527–528. [Google Scholar]
  4. Bassuk, N.; Grabosk, J.; Mucciardi, A.; Raffel, G. Ground penetrating radar accurately locates tree roots in two soil media under pavement. Arboric. Urban For. 2011, 37, 160–166. [Google Scholar]
  5. Čermák, J.; Ka, J.H.; Martinková, M.; Prax, A. Urban tree root systems and their survival near houses analyzed using ground penetrating radar and sap flow techniques. Plant Soil 2000, 219, 103–116. [Google Scholar] [CrossRef]
  6. Hruska, J.; Čermák, J.; Šustek, S. Mapping tree root systems with ground-penetrating radar. Tree Physiol. 1999, 19, 125–130. [Google Scholar] [CrossRef] [PubMed]
  7. Isaac, M.E.; Anglaaere, L.C.N. An in situ approach to detect tree root ecology: Linking ground-penetrating radar imaging to isotope-derived water acquisition zones. Ecol. Evol. 2013, 3, 1330–1339. [Google Scholar] [CrossRef] [PubMed]
  8. Stokes, A.; Fourcaud, T.; Hruska, J.; Cermak, J.; Nadyezdhina, N.; Nadyezhdin, V.; Praus, L. An evaluation of different methods to investigate root system architecture of urban trees in situ. I. Ground-penetrating radar. J. Arboric. 2002, 28, 2–10. [Google Scholar]
  9. Wu, Y.; Guo, L.; Cui, X.; Chen, J.; Cao, X.; Lin, H. Ground-penetrating radar-based automatic reconstruction of three-dimensional coarse root system architecture. Plant Soil 2014, 383, 155–172. [Google Scholar] [CrossRef]
  10. Butnor, J.R.; Doolittle, J.A.; Kress, L.; Cohen, S.; Johnsen, K.H. Use of ground-penetrating radar to study tree roots in the southeastern United States. Tree Physiol. 2001, 21, 1269–1278. [Google Scholar] [CrossRef] [PubMed]
  11. Cui, X.; Guo, L.; Chen, J.; Chen, X.; Zhu, X. Estimating tree-root biomass in different depths using ground-penetrating radar: Evidence from a controlled experiment. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3410–3423. [Google Scholar] [CrossRef]
  12. Cui, X.H.; Chen, J.; Shen, J.S.; Cao, X. Modeling tree root diameter and biomass by ground-penetrating radar. Sci. China Earth Sci. 2011, 5, 711–719. [Google Scholar] [CrossRef]
  13. Guo, L.; Lin, H.; Fan, B.; Cui, X.; Chen, J. Impact of root water content on root biomass estimation using ground penetrating radar: Evidence from forward simulations and field controlled experiments. Plant Soil 2013, 371, 503–520. [Google Scholar] [CrossRef]
  14. Hirano, Y.; Dannoura, M.; Aono, K.; Igarashi, T.; Ishii, M.; Yamase, K.; Makita, N.; Kanazawa, Y. Limiting factors in the detection of tree roots using ground-penetrating radar. Plant Soil 2009, 319, 15–24. [Google Scholar] [CrossRef]
  15. Stover, D.B.; Day, L.F.P.; Butnor, J.R.; Ke, B.G. Effect of elevated CO2 on coarse-root biomass in Florida scrub detected by ground-penetrating radar. Ecology 2007, 88, 1328–1334. [Google Scholar] [CrossRef] [PubMed]
  16. Chen, H.; Cohn, A. Probabilistic robust hyperbola mixture model for interpreting ground penetrating radar data. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Shanghai, China, 6–9 June 2010; pp. 1–8.
  17. Pasolli, E.; Melgani, F.; Donelli, M. Automatic Analysis of GPR Images: A Pattern-Recognition Approach. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2206–2217. [Google Scholar] [CrossRef]
  18. Maas, C.; Schmalzl, J. Using pattern recognition to automatically localize reflection hyperbolas in data from ground penetrating radar. Comput. Geosci. 2013, 58, 116–125. [Google Scholar] [CrossRef]
  19. Birkenfeld, S. Automatic detection of reflexion hyperbolas in GPR data with neural networks. In Proceedings of the 2010 World Automation Congress, Kobe, Japan, 19–23 September 2010; pp. 1189–1194.
  20. Janning, R.; Busche, A.; Horváth, T.; Schmidt-Thieme, L. Buried pipe localization using an iterative geometric clustering on GPR data. Artif. Intell. Rev. 2014, 42, 403–425. [Google Scholar] [CrossRef]
  21. Janning, R.; Horváth, T.; Busche, A.; Schmidt-Thieme, L. GamRec: A Clustering Method Using Geometrical Background Knowledge for GPR Data Preprocessing. In Proceedings of the Artificial Intelligence Applications and Innovations, Halkidiki, Greece, 27–30 September 2012; pp. 347–356.
  22. Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
  23. Paul, C.H. Method and Means for Recognizing Complex Patterns. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
  24. Xu, L.; Oja, E.; Kultanen, P. A new curve detection method Randomized Hough transform (RHT). Pattern Recognit. Lett. 1990, 11, 331–338. [Google Scholar] [CrossRef]
  25. Xu, L. A5 problem solving paradigm: A unified perspective and new results on RHT computing, mixture based learning, and evidence combination. In Proceedings of the 2005 IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; pp. 70–77.
  26. Xu, L.; Oja, E. Randomized Hough transform (RHT): Basic mechanisms, algorithms, and complexities. CVGIP Image Underst. 1993, 57, 131–154. [Google Scholar] [CrossRef]
  27. Simi, A.; Bracciali, S.; Manacorda, G. Hough transform based automatic pipe detection for array GPR: Algorithm development and on-site tests. In Proceedings of the Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6.
  28. Borgioli, G.; Capineri, L.; Falorni, P.L.; Matucci, S.; Windsor, C.G. The Detection of Buried Pipes From Time-of-Flight Radar Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2254–2266. [Google Scholar] [CrossRef]
  29. Windsor, C.; Capineri, L.; Falorni, P.; Matucci, S.; Borgioli, G. The estimation of buried pipe diameters using ground penetrating radar. Insight-Non-Destr. Test. Cond. Monit. 2005, 47, 394–399. [Google Scholar] [CrossRef]
  30. Falorni, P.; Capineri, L.; Masotti, L.; Pinelli, G. 3-D radar imaging of buried utilities by features estimation of hyperbolic diffraction patterns in radar scans. In Proceedings of the Tenth International Conference on Ground Penetrating Radar, Delft, The Netherlands, 21–24 June 2004; pp. 403–406.
  31. Song, W.L.; Yang, X.; Ke-Xin, L.I.; Jia, H.M. Tree root GPR target detection based on the gradient magnitude and modified Hough transform. J. For. Univ. 2013, 35, 108–112. [Google Scholar]
  32. Guo, L.; Wu, Y.; Chen, J.; Hirano, Y.; Tanikawa, T.; Li, W.; Cui, X. Calibrating the impact of root orientation on root quantification using ground-penetrating radar. Plant Soil 2015, 395, 289–305. [Google Scholar] [CrossRef]
  33. Tzanis, A. matGPR Release 2: A freeware MATLAB® package for the analysis & interpretation of common and single offset GPR data. FastTimes 2010, 15, 17–43. [Google Scholar]
  34. Capineri, L.; Grande, P.; Temple, J. Advanced image-processing technique for real-time interpretation of ground-penetrating radar images. Int. J. Imaging Syst. Technol. 1998, 9, 51–59. [Google Scholar] [CrossRef]
  35. Carlotto, M.J. Detecting buried mines in ground-penetrating radar using a Hough transform approach. In Proceedings of the Battlespace Digitization and Network-Centric Warfare, Orlando, FL, USA, 3–5 April 2002; pp. 251–261.
  36. Gamba, P.; Lossani, S. Neural detection of pipe signatures in ground penetrating radar images. IEEE Trans. Geosci. Remote Sens. 2000, 38, 790–797. [Google Scholar] [CrossRef]
  37. Guo, L.; Chen, J.; Cui, X.; Fan, B.; Lin, H. Application of ground penetrating radar for coarse root detection and quantification: A review. Plant Soil 2012, 362, 1–23. [Google Scholar] [CrossRef]
  38. Radzevicius, S.; Daniels, J. Ground penetrating radar polarization and scattering from cylinders. J. Appl. Geophys. 2000, 45, 111–125. [Google Scholar] [CrossRef]
  39. Der Kruk, J.; Streich, R. Towards true-amplitude imaging of GPR data using exact radiation patterns. In Proceedings of the 2010 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010; pp. 1–3.
  40. Tanikawa, T.; Hirano, Y.; Dannoura, M.; Yamase, K.; Aono, K.; Ishii, M.; Igarashi, T.; Ikeno, H.; Kanazawa, Y. Root orientation can affect detection accuracy of ground-penetrating radar. Plant Soil 2013, 373, 317–327. [Google Scholar] [CrossRef]
  41. Guo, L.; Lin, H.; Fan, B.; Cui, X.; Chen, J. Forward simulation of root’s ground penetrating radar signal: Simulator development and validation. Plant Soil 2013, 372, 487–505. [Google Scholar] [CrossRef]
  42. Mertens, L.; Persico, R.; Matera, L.; Lambot, S. Automated detection of reflection hyperbolas in complex GPR images with no a priori knowledge on the medium. IEEE Trans. Geosci. Remote Sens. 2015, 54, 580–596. [Google Scholar] [CrossRef]
  43. Delbo, S.; Gamba, P.; Roccato, D. A fuzzy shell clustering approach to recognize hyperbolic signatures in subsurface radar images. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1447–1451. [Google Scholar] [CrossRef]
  44. Van Kempen, L.; Sahli, H.; Brooks, J.; Cornelis, J. New results on clutter reduction and parameter estimation for land mine detection using GPR. In Proceedings of the Eighth International Conference on Ground Penetrating Radar, Gold Coast, Australia, 23–26 May 2000; pp. 872–879.
  45. Gurbuz, A. Determination of Background Distribution for Ground-Penetrating Radar Data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 544–548. [Google Scholar] [CrossRef]
  46. Safont, G.; Salazar, A.; Rodriguez, A.; Vergara, L. On Recovering Missing Ground Penetrating Radar Traces by Statistical Interpolation Methods. Remote Sens. 2014, 6, 7546–7565. [Google Scholar] [CrossRef]
  47. Yao, J.; Kharma, N.; Grogono, P. A multi-population genetic algorithm for robust and fast ellipse detection. Form. Pattern Anal. Appl. 2005, 8, 149–162. [Google Scholar] [CrossRef]
  48. Lu, W.; Tan, J. Detection of incomplete ellipses in images with strong noise by iterative randomized Hough Transform (IRHT). Pattern Recognit. 2008, 41, 1268–1279. [Google Scholar] [CrossRef]
  49. Windsor, C.G.; Capineri, L.; Falorni, P. A Data Pair-Labeled Generalized Hough Transform for Radar Location of Buried Objects. IEEE Geosci. Remote Sens. Lett. 2014, 11, 124–127. [Google Scholar] [CrossRef]
Remotesensing 08 00430 g001 1024
Figure 1. (a) Trench I for root orientation factor experiment in 2013. Diameters of the roots from R1 to R6 were 0.77, 2.22, 1.50, 1.32, 1.08, and 0.64 cm. Trenches II and III were similar to Trench I, but with roots of different vertical inclinations (30° and 45°, respectively); (b) Experiment for root depth factor. Diameters of the roots were between 1.1 and 1.3 cm; (c–e) The definition of the vertical inclination angle θ and the azimuth angle α.
Figure 1. (a) Trench I for root orientation factor experiment in 2013. Diameters of the roots from R1 to R6 were 0.77, 2.22, 1.50, 1.32, 1.08, and 0.64 cm. Trenches II and III were similar to Trench I, but with roots of different vertical inclinations (30° and 45°, respectively); (b) Experiment for root depth factor. Diameters of the roots were between 1.1 and 1.3 cm; (c–e) The definition of the vertical inclination angle θ and the azimuth angle α.
Remotesensing 08 00430 g001
Remotesensing 08 00430 g002 1024
Figure 2. An example of radargram processed by the recognition algorithm based on randomized Hough transform (RHT): (a) radargram after pre-processing; (b) binary image after edge extraction, each connected edge is considered as an ROI; (c) results of recognition using RHT. The apexes of the recognized curves are marked with green points; and (d) final recognized hyperbolas with scores higher than the threshold.
Figure 2. An example of radargram processed by the recognition algorithm based on randomized Hough transform (RHT): (a) radargram after pre-processing; (b) binary image after edge extraction, each connected edge is considered as an ROI; (c) results of recognition using RHT. The apexes of the recognized curves are marked with green points; and (d) final recognized hyperbolas with scores higher than the threshold.
Remotesensing 08 00430 g002
Remotesensing 08 00430 g003 1024
Figure 3. Flow chart of the automatic recognition algorithm based on randomized Hough transform (RHT).
Figure 3. Flow chart of the automatic recognition algorithm based on randomized Hough transform (RHT).
Remotesensing 08 00430 g003
Remotesensing 08 00430 g004 1024
Figure 4. (a) The GPR detection of a root; and (b) hyperbolic reflection in B-scan. This figure has been modified from that in Giovanni Borgioli [28].
Figure 4. (a) The GPR detection of a root; and (b) hyperbolic reflection in B-scan. This figure has been modified from that in Giovanni Borgioli [28].
Remotesensing 08 00430 g004
Remotesensing 08 00430 g005 1024
Figure 5. Results of recognition by RHT in controlled experiments for: (a) different root diameters; (b) different root depths; (c) a root with a diameter of 1.50 cm at azimuth angles of 90°, 60°, 45°, and 30° without vertical inclination; and (d) a root with a diameter of 1.85 cm at azimuth angles of 90°, 60°, 45°, and 30° and a vertical inclination of 30°. The roots correctly recognized by RHT were marked as green points and missed roots were marked as red circles. These radargrams were obtained using GPR with center frequency of 900 MHz. Figure 5a,b shows the corresponding results for experiments shown in Figure 1a,b.
Figure 5. Results of recognition by RHT in controlled experiments for: (a) different root diameters; (b) different root depths; (c) a root with a diameter of 1.50 cm at azimuth angles of 90°, 60°, 45°, and 30° without vertical inclination; and (d) a root with a diameter of 1.85 cm at azimuth angles of 90°, 60°, 45°, and 30° and a vertical inclination of 30°. The roots correctly recognized by RHT were marked as green points and missed roots were marked as red circles. These radargrams were obtained using GPR with center frequency of 900 MHz. Figure 5a,b shows the corresponding results for experiments shown in Figure 1a,b.
Remotesensing 08 00430 g005
Remotesensing 08 00430 g006 1024
Figure 6. Results of recognition by RHT for the four in situ cases with different center frequencies. Case I in Xilingol League with (a) 900 MHz and (b) 400 MHz; Case II in Jingbian with (c) 900 MHz and (d) 400 MHz; Case III in Wushen Banner with (e) 2 GHz and (f) 900 MHz; Case IV in Otog Front Banner with (g) 2 GHz and (h) 900 MHz. The roots correctly recognized by RHT are marked with green points. The missed roots are marked with red circles and the false alarms are marked with red triangles.
Figure 6. Results of recognition by RHT for the four in situ cases with different center frequencies. Case I in Xilingol League with (a) 900 MHz and (b) 400 MHz; Case II in Jingbian with (c) 900 MHz and (d) 400 MHz; Case III in Wushen Banner with (e) 2 GHz and (f) 900 MHz; Case IV in Otog Front Banner with (g) 2 GHz and (h) 900 MHz. The roots correctly recognized by RHT are marked with green points. The missed roots are marked with red circles and the false alarms are marked with red triangles.
Remotesensing 08 00430 g006
Remotesensing 08 00430 g007 1024
Figure 7. Receiver operating characteristic (ROC) curve for recognition results by RHT and ANN of the four in situ cases: (a) Case I in Xilingol League; (b) Case II in Jingbian; (c) Case III in Wushen Banner; and (d) Case IV in Otog Front Banner.
Figure 7. Receiver operating characteristic (ROC) curve for recognition results by RHT and ANN of the four in situ cases: (a) Case I in Xilingol League; (b) Case II in Jingbian; (c) Case III in Wushen Banner; and (d) Case IV in Otog Front Banner.
Remotesensing 08 00430 g007
Remotesensing 08 00430 g008 1024
Figure 8. Two levels of the limiting factors for the recognition algorithm based on RHT and the relationship between them.
Figure 8. Two levels of the limiting factors for the recognition algorithm based on RHT and the relationship between them.
Remotesensing 08 00430 g008
Table
Table 1. Experiment conditions of the four in situ cases.
Table 1. Experiment conditions of the four in situ cases.
CaseLocationPlant SpeciesDetected Root Depth (m)Soil Water Content (%)Center Frequency (MHz)Survey Line Layout
IXilingolC. microphylla0.2~1.04.94400/900Circular
IIJingbianPopulus simonii0.5~1.01.51400/900Circular
IIIWushen BannerC. korshinskii Kom.0.1~0.56.41900/2000Grid
IVOtog Front BannerC. korshinskii Kom.0.1~0.52.86900/2000Grid
Table
Table 2. Accuracy of the four in situ cases.
Table 2. Accuracy of the four in situ cases.
Case ICase IICase IIICase IV
Center frequency900 MHz400 MHz900 MHz400 MHz2000 MHz900 MHz2000 MHz900 MHz
Overall hyperbolas1411174038106110130157
RHTRR0.80.8030.6970.7220.8020.8090.9150.898
FAR1.51.3942.1422.041.411.4831.5111.397
Threshold1010151015201515
ANNRR0.710.740.6050.6110.7110.7270.6460.694
FAR1.9321.4163.7493.7492.4792.1561.862.428
Threshold0.70.650.70.70.70.50.650.5
RR: Recognition rate; FAR: False alarm rate, FA/meter.

Share and Cite

MDPI and ACS Style

Li, W.; Cui, X.; Guo, L.; Chen, J.; Chen, X.; Cao, X. Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform. Remote Sens. 2016, 8, 430. https://doi.org/10.3390/rs8050430

AMA Style

Li W, Cui X, Guo L, Chen J, Chen X, Cao X. Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform. Remote Sensing. 2016; 8(5):430. https://doi.org/10.3390/rs8050430

Chicago/Turabian Style

Li, Wentao, Xihong Cui, Li Guo, Jin Chen, Xuehong Chen, and Xin Cao. 2016. "Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform" Remote Sensing 8, no. 5: 430. https://doi.org/10.3390/rs8050430

APA Style

Li, W., Cui, X., Guo, L., Chen, J., Chen, X., & Cao, X. (2016). Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform. Remote Sensing, 8(5), 430. https://doi.org/10.3390/rs8050430

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop