Spatiotemporal Variability in Start and End of Growing Season in China Related to Climate Variability

Abstract

Satellite-derived vegetation phenophases are frequently used to study the response of ecosystems to climate change. However, limited studies have identified the common phenological variability across different climate and vegetation zones. Using NOAA/Advanced Very High Resolution Radiometer (AVHRR) Normalized Difference Vegetation Index (NDVI) dataset, we estimated start of growing season (SOS) and end of growing season (EOS) for Chinese vegetation during the period 1982–2012 based on the Midpoint method. Subsequently, the empirical orthogonal function (EOF) analysis was applied to extract the main patterns of phenophases and their annual variability. The impact of climate parameters such as temperature and precipitation on phenophases was investigated using canonical correlation analysis (CCA). The first EOF mode of phenophases exhibited widespread earlier or later SOS and EOS signals for almost the whole country. The attendant time coefficients revealed an earlier SOS between 1996 and 2008, but a later SOS in 1982–1995 and 2009–2012. Regarding EOS, it was clearly happening later in recent years, mainly after 1993. The preseason temperature contributed to such spatiotemporal phenological change significantly. The first pair of CCA patterns for phenology and preseason temperature was found to be similar and its time coefficients were highly correlated to each other (correlation coefficient >0.7). These results indicate that there is a substantial amount of common variance in SOS and EOS across different vegetation types that is related to large-scale modes of climate variability.

1. Introduction

Because plants are equipped with a phenotypic plasticity, they can grow and develop in changing environmental conditions as long as the conditions do not alter beyond the tolerances of the species [1]. Among various types of phenotypic plasticity (e.g., morphological, physiological, behavioral, phenological), phenology is particularly sensitive to small variations in environmental factors [2]. Recent meta-analyses showed that most time series of spring phenophases (e.g., flowering and leaf unfolding time of plants) arrived earlier in response to climate warming over the past several decades, and the magnitude of these advances are comparable across continents [3,4,5]. Regarding phenophases of plant senescence, the overall trend is towards later phenophases mainly due to the remarkable autumn warming, but the trends were less apparent and exhibited distinct regional difference [6]. Plant phenology not only responds to climate change, but also controls many feedbacks of vegetation to the climate system [7,8]. The change in plant phenology can change surface roughness length and albedo, further impacting sensible and latent heat flux as well as water flux from surface to the atmosphere [9]. In addition, extended growing season length may affect terrestrial carbon cycle and thus global temperature [10,11,12]. Therefore, plant phenology has attracted ever-increasing attention in the fields of ecology and climatology over the past few years.

There are two commonly used approaches to monitoring plant phenology [13]. Manual observation on the ground can provide phenological information about various phenophases of specific plant species with high temporal resolution, but it cannot cover continuously the entire geographic area [14]. Satellite-derived phenology offers important complementarity to ground observation because it can provide vegetation phenological information with full spatial coverage at the landscape level [15]. The seasonal pattern of variation in vegetated land surfaces based on satellite data was termed as remote sensing phenology [16] or land surface phenology (LSP) [17], which can offer several key phenological variables including the start of the growing season (SOS) and end of growing season (EOS). In contrast to the ground phenophases, SOS and EOS could represent spatially integrated date of green-up onset or dormancy onset for all plant species at each pixel. To date, most phenological studies at a regional or global scale are based on satellite data. For example, analyses from Advanced Very High Resolution Radiometer (AVHRR) Normalized Difference Vegetation Index (NDVI) data showed that green-up date was advanced and dormancy onset date was delayed in China from 1982 to 2010 [18,19]. In Europe, changes in the NDVI-derived EOS contributed more to the extension of growing season than changes in spring green-up date from 1982–2011 [20]. A similar conclusion was also found in North America [21]. In Africa, significant greening/browning trends for several regions were found, and could be attributed to both climatic and non-climatic drivers [22]. Furthermore, at the hemispheric or global scale, long-term trends of LSP have been detected using different satellite datasets [23,24,25].

The previous LSP studies mostly analyzed the temporal trends in phenological phases, and correlated the phenological metrics to climate variables for each pixel [23,25,26]. Furthermore, they also analyzed phenological trends or sensitivities to climate change for a group of pixels belonging to a given vegetation type or geographical region. Thus, lots of information about spatial difference in phenological responses had acquired. However, few studies have examined whether a common variability existed across geographical regions or ecosystems. It will reveal the answer if there is a general climate forcing for the observed interannual variability in phenology that is independent of geographic or vegetation zones at a large scale. Empirical orthogonal function (EOF) analysis is an effective method to address this question, since it could identify the most extensive spatial patterns of year-to-year variability in phenology. Thus far, EOF analysis has been applied to phenophases of several plants species based on ground phenological observations [27,28]. However, to our knowledge, few studies applied EOF analysis to LSP.

China is a suitable region to study the common variability in LSP since it encompasses a wide range of ecosystems and climate types along latitudinal and altitudinal gradients [29]. The objectives of this study are: (i) to examine whether different vegetation types have similar phenological variability across space; and (ii) to quantify the contribution of climate variables to spatial patterns of phenological variability. To that end, we assess the most important patterns of phenological variability in China from 1982 to 2012, and examine the linkage between phenophases and climate variables such as temperature and precipitation.

2. Materials and Methods

2.1. Data Sources

NDVI can be related to leaf area index and the absorption of photosynthetically active radiation by plant canopies [30]; it is thus widely used in studies about LSP [31,32]. In this study, an AVHRR NDVI dataset, developed by the global inventory modeling and mapping studies (GIMMS) group at NASA Goddard Space Flight Center, were used [33]. This dataset was called NDVI3g, which assembled NDVI time series from different AVHRR sensors, accounting for various deleterious effects, such as calibration loss, orbital drift, volcanic eruptions, etc. It has a spatial resolution of 1/12° and a 15-day temporal resolution, which is available from 1982 to 2012.

A 1:1,000,000 vegetation map was used for determining the vegetation type at each pixel in the NDVI3g dataset [34]. As shown on the map, the vegetations in China are categorized into 11 types: needleleaf forest, needleleaf and broadleaf mixed forest, broadleaf forests, scrub, grass-forb community, steppe, meadow, swamp, alpine vegetation, desert vegetation, and cultivated vegetation (Figure 1).

Regarding the climate data, we chose the China Meteorological Forcing (CMF) dataset [35], because it has comparable spatial resolution with the NDVI3g dataset. The CMF dataset was developed by the Data Assimilation and Modeling Center for Tibetan Multi-Spheres, Institute of Tibetan Plateau Research, Chinese Academy of Sciences. This dataset currently covers the period of 1979–2012. Its spatial resolution is 1/10°, and temporal resolution is 3 h. Two variables including surface temperature and precipitation were extracted from the dataset, and the original 3-h data were merged with monthly data. The climate parameters (temperature and precipitation) at each pixel in the NDVI3g dataset were extracted as the value at the nearest pixel of the CMF dataset.

2.2. Methods

2.2.1. Estimation of the Start and End of Growing Season

Prior to estimate SOS or EOS, we first removed cloud-contaminated points in the NDVI time series, which were marked by the highest 5% and the lowest 5% of values among all annual time series from 1982−2012 in each pixel. Furthermore, our analysis only included pixels whose multi-year median NDVI time series simultaneously met the following criteria:

(1)

Annual maximum NDVI > 0.15 and mean annual NDVI > 0.10 [36]. Such thresholds excluded deserts and sparsely vegetated areas, where the soil background would noticeably impact the spectral signals of vegetation.

(2)

The vegetation type should be natural vegetation, since the phenology of cultivated vegetation is strongly impacted by human activities [37].

(3)

The annual maximum NDVI occurred between June and September; mean NDVI of July to August >1.35 × NDVI of November to December; mean NDVI of July to August >1.35 × NDVI of January to February [36]. These criteria excluded the vegetation lack of seasonality, e.g., the evergreen vegetation over the humid tropics and subtropics, where aberrant NDVI fluctuation related to weather impact often occurred [37].

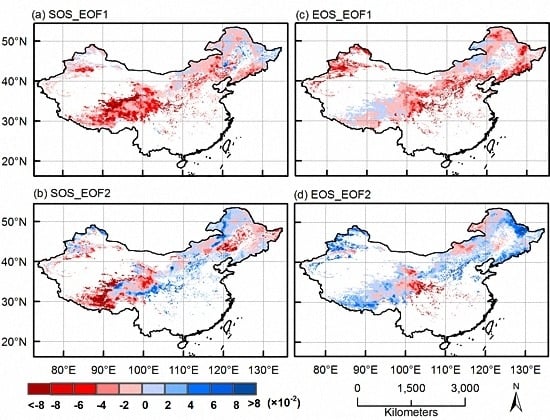
As a result, 34.0% of total pixels were included in the following analyses (

Table 1. Number of pixels and the percentage of pixels meeting the screening criteria for each vegetation type.

Code	Vegetation Types	Number of Pixels	Number of Pixels Analyzed	Percentage
1	Needleleaf forest	11,349	3882	34.2%
2	Alpine vegetation	4581	1892	41.3%
3	Cultivated vegetation	30,158	0	0.0%
4	Mixed forest	362	299	82.6%
5	Broadleaf forests	10,309	6405	62.1%
6	Scrub	12,361	4664	37.7%
7	Desert vegetation	18,379	2433	13.2%
8	Steppe	20,806	13,125	63.1%
9	Grass-forb community	3936	737	18.7%
10	Meadow	14,888	12,351	83.0%
11	Swamp	1131	1069	94.5%
12	Nonvegetated area	9466	0	0.0%
	Sum	137,726	46,857	34.0%

). All pixels from cultivated vegetation and nonvegetated areas, and most parts of desert vegetation and grass-forb communities were excluded.

For each pixel meeting the above criteria, we employed the Midpoint method to retrieve annual SOS and EOS. Although there are a number of methods to derive the SOS and EOS from NDVI time series [18,38], several studies found that the SOS derived from the Midpoint method was more closely related to ground-based spring phenophases of plants than other methods in North America [38], Europe [14] and China [39]. In this method, the multi-year median NDVI time series at each pixel is calculated (Figure 2), so as to eliminate the impact of extremely high or low NDVI values. Afterwards, a threshold is defined as the midpoint between the minimum and maximum NDVI value in the median NDVI time series. In each year, the first crossing of this threshold was marked as the SOS, and the last crossing of this threshold was marked as the EOS (Figure 2). Thus, in this method, the threshold for determining SOS and EOS is constant over time, but varies among different pixels.

Since the neighboring pixels were in very similar climate conditions, they would have similar SOS or EOS rather than abrupt changes. Therefore, we used a 7 × 7 median filter to remove noise in the derived SOS or EOS images. In addition, for the SOS or EOS time series in each pixel, the dates were considered as outliers if the estimated residuals of the linear models (between phenophases and years) were larger than or equal to 30 days [40]. These outliers were replaced with long-term mean (1982−2012) [28].

2.2.2. Empirical Orthogonal Function (EOF) Analysis

Prior to the EOF analysis, the SOS and EOS time series in each pixel were firstly transformed to anomalies through subtracting the multi-year average (1982–2012). The climate parameters during one or two months before the mean phenophases (also referred to as preseason) affect phenological events most markedly according to previous studies [4,41,42,43]. Therefore, the length of preseason was chosen to be two months. If the mean SOS or EOS occurred in the first half of the month, preseason was referred to the preceding two months; but if the mean SOS or EOS occurred in the latter half of the month, preseason was referred to the current month and previous month. In each pixel, preseason temperature and precipitation were then calculated as the average of daily temperature and sum of daily precipitation during the preseason period, respectively. Similar to the phenophases, the preseason temperature and precipitation were also transformed to anomalies through subtracting the multi-year average (1982–2012).

Subsequently, we used empirical orthogonal function (EOF) analysis to identify the most extensive and influential patterns of year-to-year variability in phenology and climate parameters [44]. Assuming that X_s,t denotes the climate matrix (preseason temperature or precipitation) and Y_r,t denotes the phenology matrix (SOS or EOS), where the subscripts s (s = 1,2,3,…,m) and r (r = 1,2,3,…,n) represent space, and subscript t represents time (t = 1,2,3,…,k), EOF analysis can be expressed as:

$$X_{s,t}=F_{s,s}^{}{T}_{s,t}^{}$$

(1)

$$Y_{r,t}=F_{r,r}^{}{T}_{r,t}^{}$$

(2)

where F_s,s and F_r,r represent EOF spatial modes of the climate and phenology matrices, respectively. T_s,t and T_r,t are their attendant time coefficients, which are also referred to as principal components (PCs). In this study, k equals 31 (the length of study period 1982−2012); m and n equal to 46,857 (the number of pixels meeting the above criteria).

2.2.3. Canonical Correlation Analysis (CCA)

EOF analysis can be only used to investigate the dominant modes of variability for each variable separately. Aiming to analyze the relationship between climate and phenological variables, we further applied the canonical correlation analysis (CCA), which was suitable for investigating the relationship between two multidimensional datasets [45]. Prior to the CCA, for simplicity, the original datasets were approximated by the first i-th EOF modes of the climate dataset (F_s,i, i < m) and the first j-th EOF modes of the phenology dataset (F_r,j, j < n):

$${\widehat{X}}_{s,t}=F_{s,i}^{}{T}_{i,t}^{}$$

(3)

$${\widehat{Y}}_{r,t}=F_{r,j}^{}{T}_{j,t}^{}$$

(4)

where ${\widehat{X}}_{s,t}$ and ${\widehat{Y}}_{r,t}$ are the approximation of the original datasets $X_{s,t}$ and $Y_{r,t}$, respectively. Since the first EOF mode of SOS and EOS can represent large-scale variability (see “Results” section), we set j = 1. Regarding the climate datasets, i was set as 5, because the climate pattern comparable to the phenological pattern may be identified through combination of several EOF modes.

In the next step, CCA was performed to calculate canonical vectors (C_i,q and D_j,q) and CCA time coefficients (U_q,t and V_q,t):

$$U_{q,t}=C_{i,q}^{\prime }{T}_{i,t}$$

(5)

$$V_{q,t}=D_{j,q}^{\prime }{T}_{j,t}$$

(6)

where U_q,t and V_q,t are CCA time coefficients of climate and phenology, respectively. q is equal to i or j, whichever is smaller (q = 1 here). U_q,t and V_q,t should meet the following conditions [46]: (1) correlations between any two rows of U_q,t are zero; correlations between any two rows of V_q,t are zero; correlations between any one row of U_q,t and any one row of V_q,t are zero if their row numbers are different; (2) the correlation between the first row of U_q,t and V_q,t is maximum; (3) the correlation between second row of U_q,t and V_q,t is the maximum under the constraints of (1) and (2). The correlations for the higher indexed pairs of coefficients satisfy similar constraints. The detailed algorithm to calculate C and D was described in von Storch [46].

Two new variables W and Z were introduced as the generalized inverse of matrix C and D, that is, W and Z satisfy the following equations:

$$W_{i,q}{C}_{i,q}^{\prime }=E_{i,i}$$

(7)

$$Z_{j,q}{D}_{j,q}^{\prime }=E_{j,j}$$

(8)

where E_i,i is i × i identity matrix and E_j,j is j × j identity matrix.

When following Equations (5) and (7), the time coefficients of climate (T_i,t) can be expressed as:

$$W_{i,q}{U}_{q,t}=T_{i,t}$$

(9)

Similarly, following Equations (6) and (8), the time coefficients of phenology (T_j,t) can be expressed as:

$$Z_{j,q}{V}_{q,t}=T_{j,t}$$

(10)

Finally, we could express ${\widehat{X}}_{s,t}$ and ${\widehat{Y}}_{r,t}$ by using CCA time coefficients (U_q,t and V_q,t). Following Equations (3) and (9),

$${\widehat{X}}_{s,t}=(F_{s,i}^{}{W}_{i,q})U_{q,t}$$

(11)

Following Equations (4) and (10),

$${\widehat{Y}}_{r,t}=(F_{r,j}^{}{Z}_{j,q})V_{q,t}$$

(12)

where F_s,iW_i,q is the CCA patterns for climate. The k-th column of F_s,iW_i,q represents the k-th CCA pattern of climate. U_q,t is the CCA coefficient of climate. The k-th row of U_q,t represents the time coefficient of the k-th CCA pattern. Similarly, F_r,jZ_j,q represents the CCA patterns of phenology and V_q,t is the corresponding CCA coefficient. In this study, we only analyzed the first EOF mode of phenology (i.e., j = q = 1). Therefore, the first CCA pattern of phenology is identical with the first EOF mode of phenology.

The above CCA was performed four times for each pair of phenology and climate dataset. The last step was analyzing the relationship between CCA time coefficients of phenology and climate. Meanwhile, similarities between CCA patterns of phenology and climate were examined.

3. Results

3.1. EOF Analyses

The EOF analyses on the phenology and the climate variables showed clear differences in the explained variances (

Table 2. Variance explained by the five leading EOF modes of phenology, preseason temperature and precipitation.

EOF Mode	Phenology	Temperature	Precipitation
Start of growing season
1	0.17	0.46	0.20
2	0.14	0.20	0.13
3	0.10	0.11	0.09
4	0.07	0.04	0.07
5	0.05	0.03	0.05
Sum	0.53	0.84	0.54
End of growing season
1	0.19	0.50	0.18
2	0.08	0.12	0.14
3	0.06	0.08	0.10
4	0.06	0.05	0.08
5	0.05	0.05	0.06
Sum	0.44	0.80	0.56

). The first EOF mode could explain 17% of the variance in the SOS data, while the five leading EOF modes together accounted for 53% of the year-to-year variance in the SOS. Regarding EOS, the dominance of the first EOF mode was a little more pronounced with 19% explained variability, while the five leading spatial patterns together explained 44% of the variance in the EOS.

With regard to preseason temperature of SOS and EOS, the first EOF mode could account for 46% and 50% of the variance, respectively (Table 2). For preseason precipitation of SOS and EOS, the dominance of the first EOF mode was less pronounced with only 20% and 18% explained variability, respectively.

3.2. Dominant Phenological Patterns and Their Time Evolutions

The leading EOF mode of SOS showed a relatively homogeneous structure with the strongest weights over the Tibetan plateau (Figure 3a). Except in a few pixels located in the Northeastern Plain, the EOF weights were almost consistently negative, suggesting an earlier or later SOS for the whole country, depending on the PC value. Thus, different vegetation types had similar variability of SOS across space. The yearly variations of the leading EOF mode are shown in Figure 4a. The time evolution of SOS experienced three stages. From 1982 to 1996, the SOS was on average 0.7 days later than the long-term mean. Between 1997 and 2008, the anomalies of SOS were negative, indicating an advance of 1.2 days. After 2008, the SOS occurred about 1 day later than the long-term mean. The overall linear trend found in the first EOF mode was 0.6 days per decade towards earlier SOS (Figure 4a).

In contrast to the first EOF mode of SOS, the second EOF mode revealed considerable regional patterns (Figure 3b). In the Northeastern Plain, the EOF weights changed from negative values in the north to positive values in the south. In addition, most pixels in the Tibetan Plateau showed negative EOF weights, while most pixels in the North China Plain showed positive weights (Figure 3b). Such North−South and altitude patterns seemed more pronounced in 2009–2012, as revealed in the PC time series (Figure 4b).

With regard to the EOS, the leading EOF mode represented a broad region of common variability with the strongest weights over Tianshan Mountains and the southeastern edge of the study area (Figure 3c). Only in a few pixels of the Greater Khingan Range and the northwestern Tibetan Plateau did the EOF weights show opposite phenological shifting. Generally, different vegetation types had common variability of EOS. The PC time series of the leading EOF is shown in Figure 4c. A clear change of direction in EOS occurred around 1993. During the period of 1982−1993, the EOS was about 0.8 days earlier than the long-term mean, which shifted to 0.5 days later than the long-term mean during the period of 1994−2012. Overall, the linear trend of EOS during the whole study period was 0.7 days per decade (Figure 4c).

The second EOF mode of EOS also revealed certain regional patterns (Figure 3d). Especially in the eastern edge of the Tibetan and Inner Mongolia Plateau, the direction of the change in EOS was contrary to the other parts of the country. According to the corresponding PC time series (Figure 4d), the second EOF mode of EOS revealed no considerable temporal trend.

3.3. CCA Patterns and Time Coefficients of Climate and Phenology

The first pair of derived CCA patterns for preseason temperature and SOS is shown in Figure 3a and Figure 5a, respectively. The first CCA pattern of temperature represented a mode of a ubiquitous warming across almost the whole country (Figure 5a), corresponding to the ubiquitous earlier SOS in the first CCA pattern of SOS (Figure 3a). Moreover, the CCA time coefficients of SOS were significantly correlated with that of temperature (Figure 5b, R = 0.71, p < 0.01), suggesting the interannual change in SOS pattern highly depended on the interannual change in temperature pattern.

Figure 3a and Figure 5c display the CCA patterns of preseason precipitation and SOS in the first canonical mode, respectively. In the southeastern part of the study area, precipitation anomalies revealed in the CCA pattern tended to be negative, while the precipitation anomalies tended to be positive in the northwestern part of the study area (Figure 5c). However, the CCA pattern of SOS revealed ubiquitous earlier SOS across the country (Figure 3a). These results suggested that the role of precipitation in regulating SOS varied among different geographical regions. Furthermore, the relationship between CCA time coefficients of SOS and precipitation was significant but weaker than temperature (Figure 5d, R = 0.58, p < 0.01).

The results of CCA between preseason temperature and EOS showed a relatively homogeneous structure in both temperature and phenological patterns. The negative temperature anomalies distributing uniformly almost over the entire area (Figure 6a, except a few pixels in northeastern China and Tibetan Plateau), is associated with an earlier EOS (Figure 3c). Additionally, significant correlation can be found between CCA time coefficients of EOS and temperature (Figure 6b, R = 0.79, p < 0.01).

Through canonical correlation analysis between preseason precipitation and EOS, the consequent CCA pattern of precipitation (Figure 6c) was more complex than that of EOS (Figure 3c). In most pixels of the Tibetan Plateau and the North China Plain, precipitation anomalies are negative, while precipitation anomalies are positive in other regions of China (Figure 6c). Although the CCA time coefficients of EOS were significantly associated with those of precipitation, the correlation was weaker than those with temperature (Figure 6d, R = 0.68, p < 0.01).

4. Discussion

Previous studies used EOF analysis to identify the most dominant pattern of year-to-year variability in spring phenophases based on species-level observation data. However, limited studies have applied it to satellite-derived phenology at the landscape level. The results of this study proved that the EOF analysis method was also able to diagnose the main spatial pattern in phenological variability at a larger spatial scale, despite the fact that the study area crossed various climate zones and vegetation types. The leading EOF modes of SOS and EOS in China revealed consistent advance or delay in phenophases over a broad region, which implied that there is synchronism among different vegetation types in phenological variation. This conclusion may be a result of phenological change at the species level, because many studies found that different individuals of the same or different species have the common variability of phenophases across geographical regions or ecosystems [47,48,49].

Although the SOS in China occurred relatively later from 2009 to 2012, the overall linear trend in SOS over the past 30 years still advanced at a rate of 0.6 days per decade. Similar shifts towards earlier SOS have also been reported by other phenological studies based on satellite data [18,50,51]. For example, Cong et al. [18] found that the vegetation green-up onset date advanced at the rate ranging from 0.4 to 1.9 days per decade (depending on the methods used) over temperate China in the period 1982–2010. In a recent meta-analysis of trends among Chinese plant phenophases, the spring phenophases of woody and herbaceous plants also advanced over the past several decades [3], suggesting that the variability of plant phenophases as seen from the ground is in accordance with the spatially integrated date of SOS observed from space.

Regarding the EOS, the PC of leading EOF mode was shown to be profoundly delayed in recent years, mainly after 1993, when a clear shift toward later EOS occurred. Few studies have focused on the change in autumn vegetation phenology at the landscape level in China. One earlier study indicated that the onset date of dormancy of China’s temperate vegetation was delayed in autumn by 3.7 days per decade from 1982 to 1999 [37]. Another study found that the autumn vegetation dormancy onset date over China’s temperate ecosystems was delayed by 0.13 days per year from 1982 to 2010 [19]. Therefore, the magnitudes of trends found in previous studies were stronger than our estimate (0.7 days per decade). The first reason for this is the impact of time periods on trend estimation [52], as our study extended the data series to 2012. In addition, trend values depended highly on phenophase retrieval methods [18]. In contrast to the Midpoint method applied in this study, Piao et al. [37] and Yang et al. [19] used polynomial function to reconstruct continuous NDVI series, and then determined the SOS or EOS threshold by the timing of the greatest relative change in multiyear averaged NDVI series. This discrepancy in method selection among different studies caused the difference in phenological trends.

The relationship between annual variability in the SOS and preseason climate variables was investigated through CCA. Similar to the results based on ground phenophase observation [53,54], the results of CCA revealed a strong correlation between large-scale temperature and SOS variability in China. Both the time evolution and the spatial pattern of the first CCA mode of temperature were very similar to those of the SOS. Across the whole country, higher spring temperature corresponds to earlier SOS, which was in accordance with the results of a great number of phenological studies [4,55,56,57]. Compared to temperature, precipitation plays a second role in modulating the SOS, as the correlation between CCA time coefficients of the SOS and precipitation was weaker than those with temperature. When comparing CCA patterns of the SOS and precipitation, we found that the role of precipitation in regulating SOS varied among different vegetation types. For steppe and meadow on the Inner Mongolia and the Tibetan Plateau, and desert vegetation in Northwestern China, more rainfall was associated with advanced SOS, as reflected in most pixels (70%). However, for other vegetation types, the response of SOS to precipitation was not so uniform. Such impact of precipitation on SOS in water-limited ecosystems can be anticipated because rainfall cues plant growth and development in arid and semiarid regions over the year [58,59,60].

The rapid climate change and its impacts on SOS of alpine ecosystems in the Tibetan Plateau are matters of global concern [50,61]. One recent study based on satellite-derived data pointed out that SOS is more sensitive to variations in preseason temperature in wetter than in dryer areas of the plateau [62]. Another study based on ground observation found that the correlation between preseason temperature and SOS was negative for most sites and species in the Tibetan Plateau, while the relationship between green-up dates and monthly precipitation series was less-pronounced and uncertain [63]. All these conclusions agreed with our results, i.e. warming would cause earlier SOS in the Tibetan Plateau, while increased preseason precipitation would promote the onset of green-up especially in arid areas. However, due to the fact that increased preseason precipitation may cause lower temperatures by accompanying deficient sunshine intensity and duration, later SOS may also be expected [62,64].

The interannual variance of EOS was associated with interannual change in temperature. The CCA patterns of EOS and temperature revealed that colder autumn temperatures were linked to earlier EOS in most areas of temperate China. In other words, higher temperature would lead to later EOS, which was consistent with other studies [12,19,65]. In comparison to temperature, preseason precipitation accounted for a smaller proportion of variance in EOS patterns. When comparing the CCA pattern of precipitation and EOS, it was found that less rainfall in autumn would lead to earlier EOS in northwestern China, where desert vegetation is distributed. Such a significant positive correlation between EOS of desert vegetation and precipitation was also reported by Piao et al. [37]. For other vegetation types, no consistent relationship was found between rainfall and EOS anomalies, which implied that rainfall was not a factor in regulating their EOS. Indeed, the leaf senescence process is mainly affected by two environmental factors: photoperiod and temperature, especially for vegetation under no drought stress [66,67].

5. Conclusions

In this study, we employed the empirical orthogonal function (EOF) analysis to assess the variability of satellite-derived growing season during the period of 1982−2012. The results showed that the first EOF mode was dominated by a relatively homogeneous structure, i.e. an earlier or later start of season (SOS) and end of season (EOS) for almost the whole country. The SOS times have become earlier since 1996, but began occurring later in the most recent four-year study period (2009−2012), whereas the EOS times have arrived later since 1993. Furthermore, the phenophases and climate variables (including preseason temperature and precipitation) were analyzed using canonical correlation analysis (CCA) to identify their common variance. The first pair of CCA patterns for phenological and preseason temperature were found to be very similar with the correlation coefficient between their time coefficients greater than 0.7. The impact of rainfall on SOS and EOS was of less importance, because correlation coefficients between CCA time coefficients of phenophases and preseason precipitation are weaker. Nonetheless, the role of rainfall in accelerating vegetation development was notable in water-limited areas. These results indicate that the large-scale variability in phenology could be explained to a great extent by the interannual variability of temperature and precipitation.

Overall, our results highlighted that natural vegetation in China exhibits a consistent signal of phenological shifts in its dominant EOF modes, even if the study regions were across various climate and vegetation zones. The similar CCA patterns and time coefficients between phenophases and preseason temperature indicate that land surface phenology (LSP) can serve as a reliable indicator for assessing the impact of climate change. Since the signal of phenological shifts was substantially inconsistent in other EOF modes, further research is needed to examine in detail the correlation between phenological metrics and other climate variables in specific climate or vegetation zones.