Detection of High-Density Crowds in Aerial Images Using Texture Classification

Abstract

Automatic crowd detection in aerial images is certainly a useful source of information to prevent crowd disasters in large complex scenarios of mass events. A number of publications employ regression-based methods for crowd counting and crowd density estimation. However, these methods work only when a correct manual count is available to serve as a reference. Therefore, it is the objective of this paper to detect high-density crowds in aerial images, where counting– or regression–based approaches would fail. We compare two texture–classification methodologies on a dataset of aerial image patches which are grouped into ranges of different crowd density. These methodologies are: (1) a Bag–of–words (BoW) model with two alternative local features encoded as Improved Fisher Vectors and (2) features based on a Gabor filter bank. Our results show that a classifier using either BoW or Gabor features can detect crowded image regions with 97% classification accuracy. In our tests of four classes of different crowd-density ranges, BoW–based features have a 5%–12% better accuracy than Gabor.

1. Introduction

1.1. Background and Motivation

During mass events with tens of thousands of people, security authorities and organizers need accurate information about crowded areas and potentially hazardous situations. Terrestrial cameras already provide the major part of this information as images and videos. In general, a lot of research has been done to process this huge amount of data automatically [1,2,3,4], and most often with the goal of crowd counting [5,6,7,8], person tracking [9,10], or behavior understanding [11,12]. However, all these methods are tested on benchmark datasets containing terrestrial images or videos, and do not consider aerial images for crowd counting.

For obvious reasons, terrestrial cameras can be installed more easily but might not always be sufficient while monitoring large events (e.g., street festivals, open-air concerts). In complex scenarios, terrestrial cameras cannot always provide all necessary visual information due to their limited field of view and limited availability, for example, terrestrial cameras cannot be mounted at every possible location. Low flying platforms like helicopters or small drones could help, but these are either very loud or not well accepted in public.

In contrast to that, a camera system installed on a high flying platform can leverage its elevated position and allows the monitoring of a complete city center or festival area with just a few images. It can be of great value if large groups gather spontaneously at new—otherwise not monitored—locations. The main challenges of crowd detection in aerial images, however, are the small object size of persons, the high density, and the nadir viewing angle. To be more specific, we use the term “aerial image” from now on for images with a spatial resolution of 10–20 cm, a covered area of 0.6–2.1 $\text{k}{\text{m}}^2$, and a viewing angle of $0–{32}^{\circ }$. In such images, one person only covers 6–24 pixels, and its appearance is hardly distinguishable from other objects with similar shape (e.g., light poles). In addition to the small object size of a person in an aerial image, the scenario gets even more challenging when many persons gather at certain “hot spots” in front of a concert stage or in a narrow street. The persons stand closer to each other and eventually form a dense crowd, where the surface they are standing on (the background) is no longer visible. Moreover, the viewing angle of the aerial images shows the person rather from the top than from the side. This perspective additionally reduces the number of covered pixels.

These three key characteristics, small object size of a person, mutual occlusion, and viewing angle lead to a different appearance of a person than in images so far mostly examined in the literature (Figure 1). We define these texture-like crowded regions as “crowd textures”. In this paper, we want to investigate methods for the detection of dense crowds in aerial images with these characteristics. We focus on crowded image regions with a crowd density so high that even manual counting is hardly possible.

1.2. Related Work

In general, the publications in the field of aerial crowd counting algorithms use images from two groups: visually distinguishable crowded images (VDC) and visually indistinguishable crowded images (VIC). This categorization depends on whether an interpreter or expert is able to clearly distinguish an individual person from other persons in the image or not. The category that an image belongs to depends on viewing angle, mutual occlusion, and spatial resolution. In the following, we review relevant works from these two categories.

In VDC images, an individual person is clearly distinguishable from other persons by a human expert looking at these images. One is able to count persons under the prevailing occlusion and resolution conditions of the respective image. In this way, a reference data set with an absolute number of persons and even a reference crowd density can be calculated. Then, this available reference data can be used for regression-based crowd detection methods.

Herrmann and Metzler [13] propose a system for crowd density estimation and people counting and apply it to one data set of 16 aerial VDC images. After preprocessing, the object size of each person is fixed at 256 pixels. This object size clearly allows a manual counting. A gradient boosted tree calculates the density function using a combination of frequency filters and adapted “Scale-Invariant Feature Transform” (SIFT) features. Then, a person model based on a Gaussian function is used for person counting. They evaluate the methodology by comparing it with a reference density map. Their evaluation yields promising results; however, their methodology is tailored for images shot at oblique viewing angles and with a much higher resolution than the images we investigate.

Perko et al. [14] estimate crowd density and crowd motion from video data in two different self-acquired test data sets. Their regression-based density estimation performs best when using a combination of dense SIFT features and an object detector introduced by Lempitsky and Zisserman [6]. The reported average height of a person of 90 pixels allows manual labeling and counting of the persons.

In contrast to that, the resolution and/or occlusion in VIC images do not allow a correct counting of all individual persons in an image by an expert. If a single person covers only ten to twenty pixels, there is not enough information to clearly state that this is a person. If the resolution is higher, but most body parts of the person are occluded, no counting is possible either. In other words, regression-based methods cannot be applied on VIC images because of missing reference data. The following rule proved to be quite useful while assembling the test data set. As soon as the surface the persons are standing on is no longer visible, the image can be considered as a VIC image. Figure 1 shows an example of a VIC image region: the low spatial resolution and the high crowd density in front of the stage do not allow a correct counting of all individual persons.

The method used by Hinz [15], applies regression on VIC images in a way that it uses the response of a Lawss filter convolved with a mask to get a two-dimensional density layer. The mask is created in a preceding step by applying a gray-level bounded region-growing approach. In the paper, some visualized results are shown to demonstrate that the method works in general; however, no quantitative results are given.

Sirmacek and Reinartz [16,17] calculate a density function which estimates the crowd density in 20-cm aerial images. This function is the result of convolving white blobs with a Gaussian kernel on image segments that have been extracted with mean shift segmentation. As one of the first publications in the field of aerial crowd monitoring, their method produces convincing results; however, some parameters (number of blobs per region, minimum area size, segmentation bandwidth) need careful tuning for every new data set.

Meynberg and Kuschk [18] focus on the detection of dense crowds in VIC images. Their method convolves image patches with a Gabor filter bank and classifies the filter responses with a Support Vector Machine (SVM). We include this approach in our evaluation and compare the results (Section 4).

In summary, VIC images represent a group of images which has been discussed in only a few crowd–monitoring publications. The applied methodologies focus on person counting, which naturally yield the best performance in image regions with a low crowd density. However, hazardous situations are more likely to occur in image regions where the crowd density is high and a robust detection of these densely crowded regions in a diverse range of VIC images is still missing in literature. Therefore, in this paper, we focus on high-density crowds in a variety of aerial images, where counting- or regression-based approaches would fail.

1.3. Contribution

The novelty of our contribution is the usage of texture-classification methods for the detection of dense crowds in aerial images.

• We concentrate on the potentially most hazardous regions in VIC images—the high-density crowds. We show that crowded regions in aerial images can indeed be regarded as a texture, and propose robust patch-based Bag-of-Words methods for the detection of these regions.
• We run extensive tests on a database that contains a wide variety of aerial image patches. These patches are categorized into four classes where the continuous crowd-density function is partitioned into four ranges of decreasing crowd density.
• Through the evaluation and comparison, we demonstrate that Bag-of-Words features with appropriate chosen local features perform significantly better than conventional Gabor texture features on the task of aerial crowd detection.

The remainder of this paper is organized as follows: In Section 2.1, we first describe our selection of methods for the BoW model and review the Gabor approach (Section 2.2). Then, we describe the test data and software tools to conduct the experiments in Section 3. The evaluation of the BoW and Gabor classifiers is done in Section 4. The results are discussed in Section 5, and final conclusions are drawn in Section 6.

2. Methodology

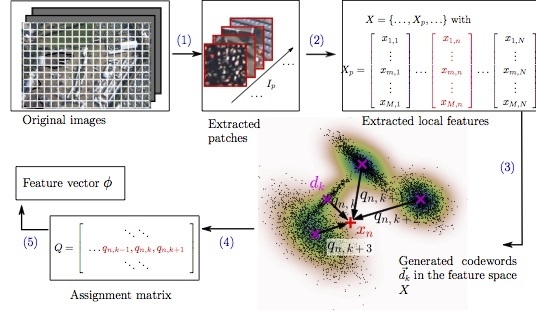
2.1. Crowd Features Using the Bag-of-Words Model

“Bag of Words” (BoW) is a state-of-the-art model in texture classification [19], and its development has been inspired by the original model used in natural language processing and document retrieval. The main idea behind this model is to disregard the word order and the grammar in the sentence and concentrate on the number of occurrences of specific words. In computer vision, these words can be seen as cluster centers in a feature space, leading to the BoW model. The BoW model has been widely used for texture classification [20,21,22,23] and also in remote sensing [24,25], however, never for the detection of a crowd in remotely sensed images.

There are three reasons why the BoW model is often used for texture classification: First, it does not depend on a specific type of local feature, so this can be chosen to fit the application. Second, building a histogram of the cluster centers (aka codewords) makes the model insensitive to local image perturbations. Third, a large margin classifier, such as an SVM, can directly use this histogram representation for classification. The BoW model itself is best understood as a framework of four general processing steps, which follow on the patch sampling shown in Figure 2. These steps are local feature extraction, codeword generation, feature encoding, and feature pooling.

2.1.1. Local Feature Extraction

An image patch ${\text{I}}_{\text{p}}$ can be extracted from the original aerial images in an either dense way (e.g., regular grid) or sparse way (e.g., keypoint detection or manual sampling). For each of these patches, a matrix ${\text{X}}_{\text{p}}=\left\{{\mathbf{x}}_{\mathbf{1}},\cdots ,{\mathbf{x}}_{\mathbf{n}},\cdots ,{\mathbf{x}}_{\text{N}}|{\mathbf{x}}_{\text{n}}\in {\mathbb{R}}^{\text{M}}\right\}$ of local feature descriptors is computed, where M is the dimension of each extracted ${\mathbf{x}}_{\text{n}}$ and N is the number of local features per patch. To detect crowded regions in an image, a local feature vector, and eventually ${\text{X}}_{\text{p}}$, should be principally insensitive to small changes in illumination, scale, intensity inversion, or rotation. Most of the commonly used local features work on a sparse set of points; however, the contrast and resolution of the crowd textures in this work are low, which would influence the performance of a sparse keypoint detector considerably. Therefore, we concentrare on two alternative texture features: (1) “Local Binary Pattern” (LBP) introduced by Ojala et al. [26] and (2) “Sorted Random Projections” (SRP) proposed by Liu et al. [27].

Local Binary Pattern (LBP)

The original LBP method creates a label from the 3 × 3-neighborhood of each pixel. This label is considered as an 8-digit binary number resulting in $2^8=256$ possible labels. The number of occurrences of each label represented in a 256-bin histogram can be used as a texture descriptor. A more advanced version further quantizes the number of labels in so called uniform patterns to improve the histogram statistic. Each uniform pattern has exactly one transition from 0 to 1 and one transition from 1 to 0. We use these quantized LBP on a number of cells with a fixed size in each patch. The quantized LBPs are then aggregated in each cell and normalized. The result is a matrix ${\text{X}}_{\text{p}}$ of local feature vectors ${\mathbf{x}}_{\text{n}}\in {\mathbb{R}}^{\text{M}}$, usually with $\text{M}=58$ in the case of “uniform” LBPs. N equals the number of cells. Furthermore, there are a number of different variants of LBP, such as [28,29].

Sorted Random Projections (SRP)

The SRP method extracts small subpatches in a sliding-window manner. Within each of these subpatches, rotation invariance is achieved through a sorting of pixel values by their intensity. From each subpatch, exactly one local feature vector ${\mathbf{x}}_{\text{n}}$ is calculated. The sorting within a subpatch can be performed on different neighborhood structures around the center pixel ${\text{x}}_{(0,0)}$. According to the performance evaluation in [27], we consider the proposed radial-diff neighborhood. This sorting scheme calculates the difference of two pixel values. The first lies on a concentric circle around the center pixel of the patch, and the second lies on the neighboring inner circle (see Figure 3). Formally, this radial difference is described in Equation (1).

The difference of two pixel values is calculated as ${\mathsf{▵}}_{\text{r},\text{i}}^{\text{Rad}}={\text{x}}_{\text{r},\text{i}}^{\text{C}}-{\text{x}}_{\text{r}-1,\text{i}·{\text{p}}_{\text{r}-1}/{\text{p}}_{\text{r}}}^{\text{C}}$, where ${\text{x}}_{\text{r},\text{i}}^{\text{C}}$ is the pixel value which lies on a concentric circle r with $1\le \text{r}\le \text{a}$ around the center. Each circle has i pixel values, with $0\le \text{i}<{\text{p}}_{\text{r}}$. Interpolation is used if ${\text{x}}_{\text{r},\text{i}}^{\text{C}}$ is not at a pixel center.

2.1.2. Codeword Generation

A randomly sampled subset X of all local features is used to generate the cluster centers in the local feature space. These cluster centers, also known as codewords, form a dictionary $\text{D}=[{\mathbf{d}}_1,...,{\mathbf{d}}_{\text{K}}]\in {\mathbb{R}}^{\text{M}\times \text{K}}$ with K codewords of the same dimension M as the local features. These codewords are calculated using a Gaussian Mixture Model (GMM). It takes a subset of X as input and yields a predefined number of cluster centers as output, stored in D. The GMM can be seen as a representative model of the whole feature space and is created using expectation maximization and a given number of modes. More specifically, let ${\text{u}}_{\mathsf{\lambda }}\left(\text{X}\right)$ be a GMM with K modes and the parameter set $\mathsf{\lambda }=\{{\mathsf{\pi }}_{\text{k}},{\mathsf{\mu }}_{\text{k}},{\mathsf{\Sigma }}_{\text{k}}|\text{k}=1,...,\text{K}\}$ which is trained on a large set of local features ${\mathbf{x}}_{\text{n}}\in {\mathbb{R}}^{\text{M}}$. ${\mathsf{\pi }}_{\text{k}}$, ${\mathsf{\mu }}_{\text{k}}$, and ${\mathsf{\Sigma }}_{\text{k}}$ are, respectively, the mixture coefficients, the mean vector, and the covariance matrix.

2.1.3. Feature Encoding

With a given GMM, each newly extracted matrix ${\text{X}}_{\text{p}}=[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_{\text{N}}]$ of an image patch is encoded using Improved Fisher Vectors (IFV) [30]. Now, the GMM can model a given descriptor ${\mathbf{x}}_{\text{n}}$ by weighting it with each mode K in the mixture with a posterior probability ${\text{q}}_{\text{nk}}$:

$${\text{q}}_{\text{nk}}=\frac{\text{exp}[-\frac{1}{2}{({\mathbf{x}}_{\text{n}}-{\mathbf{d}}_{\text{k}})}^{\text{T}}{\mathsf{\Sigma }}_{\text{k}}^{-1}({\mathbf{x}}_{\text{n}}-{\mathbf{d}}_{\text{k}})]}{{\sum }_{\text{j}=1}^{\text{J}}\text{exp}[-\frac{1}{2}{({\mathbf{x}}_{\text{n}}-{\mathbf{d}}_{\text{j}})}^{\text{T}}{\mathsf{\Sigma }}_{\text{j}}^{-1}({\mathbf{x}}_{\text{n}}-{\mathbf{d}}_{\text{j}})]}.$$

(2)

${\text{q}}_{\text{nk}}$ activates cluster centers with a weight and can be regarded as the influence of a mode K on the final feature encoding of a given local feature ${\mathbf{x}}_{\text{n}}$. It is an element of the assignment matrix that assigns a weight of every mode K to each feature descriptor ${\mathbf{x}}_{\text{n}}$. Modes with a small distance to a given descriptor ${\mathbf{x}}_{\text{n}}$ have a large weight ${\text{q}}_{\text{nk}}$, whereas modes which are far away in the feature space are very small or even negligible (Equation (2)). In this way, the encoding gets the more descriptive the better a new X fits to the GMM.

2.1.4. Feature Pooling

Feature pooling is done by computing the mean and covariance deviation of the distances of every local feature ${\mathbf{x}}_{\text{n}}$ to the nearest modes ${\mathbf{d}}_{\text{k}}$. The strength of ${\text{u}}_{\text{mk}}$ and ${\text{v}}_{\text{mk}}$ is substantially influenced by the weight ${\text{q}}_{\text{nk}}$, as can be seen in the Equations (3) and (4):

$${\text{u}}_{\text{mk}}=\frac{1}{\text{N}\sqrt{{\mathsf{\pi }}_{\text{k}}}}\sum _{\text{n}=1}^{\text{N}}{\text{q}}_{\text{nk}}\frac{{\text{x}}_{\text{mn}}-{\text{d}}_{\text{mk}}}{{\mathsf{\sigma }}_{\text{mk}}},$$

(3)

$${\text{v}}_{\text{mk}}=\frac{1}{\text{N}\sqrt{2{\mathsf{\pi }}_{\text{k}}}}\sum _{\text{n}=1}^{\text{N}}{\text{q}}_{\text{nk}}\left[{\left(\frac{{\text{x}}_{\text{mn}}-{\text{d}}_{\text{mk}}}{{\mathsf{\sigma }}_{\text{mk}}}\right)}^2-1\right].$$

(4)

${\text{d}}_{\text{mk}}$ and ${\mathsf{\sigma }}_{\text{mk}}$ are the Mth elements of the Kth mean vector and the Kth covariance matrix, respectively.

$\mathsf{\phi }\left({\text{X}}_{\text{p}}\right)$ is the concatenation of the mean vectors ${\mathbf{u}}_{\text{k}}$ and the variance vectors ${\mathbf{v}}_{\text{k}}$ for every mode k. Then, one has $\mathsf{\phi }\left({\text{X}}_{\text{p}}\right)\in {\mathbb{R}}^{2\text{MK}}$ with its dimension independent of N, leaving $\mathsf{\phi }\left({\text{X}}_{\text{p}}\right)$ constant if N should change, e.g., when changing the size of the patch ${\text{I}}_{\text{p}}$:

$$\mathsf{\phi }\left({\text{X}}_{\text{p}}\right)={\left[\cdots {\mathbf{u}}_{\text{k}}\cdots {\mathbf{v}}_{\text{k}}\cdots \right]}^{\text{T}}.$$

(5)

2.2. Crowd Features Using a Gabor Filter Bank

Because Gabor filter banks [31] are one of the standard methods in the field of texture classification, we create a feature representation that can be compared to a BoW feature representation. The general fitness of Gabor features for the classification of crowded and non–crowded patches has already been shown in [18]. Now, we want to investigate if their performance is comparable to the BoW approach in the case of a more challenging multi–class classification. Therefore, we briefly summarize the design of a Gabor feature for crowd detection. Unlike the BoW model, the filtering process does not require feature clustering and encoding steps. The image patches are directly convolved with a filter bank and each patch is eventually represented by one feature vector ϕ. In more detail, a Gabor filter encodes the orientation and scale of edges of the input image, resulting in a high filter response in a specific orientation and of a specific scale if the input image contains edges of buildings or other regular structures (Figure 4).

In contrast, an image patch containing a crowd exhibits no regular structures or patterns. The very detailed heterogenous texture of a crowd patch instead generates a high filter response in every direction. These characteristics of the Gabor filter create a feature space, which can be separated by a classifier.

We briefly show the key steps to build a Gabor feature: Let ${\text{I}}_{\text{p}}\in {\mathbb{N}}^{\text{R}\times \text{C}}$ be an image patch with a center pixel at position $(\text{m},\text{n})$. With a filter bank of Gabor functions ${\text{g}}_{\text{s},\text{k}}(\text{m},\text{n})$, the Gabor wavelet transform at that position can be written as:

$${\text{W}}_{\text{s},\text{k}}(\text{m},\text{n})={\text{I}}_{\text{p}}(\text{m},\text{n})*{\text{g}}_{\text{s},\text{k}}(\text{m},\text{n})=\sum _{\text{r}=0}^{\text{R}-1}\sum _{\text{c}=0}^{\text{C}-1}{\text{I}}_{\text{p}}\left(\text{r}-\frac{\text{R}}{2},\text{c}-\frac{\text{C}}{2}\right)·{\text{g}}_{\text{s},\text{k}}(\text{r},\text{c}),$$

(6)

where s indexes the scale ($\text{s}=0,\cdots ,\text{S}-1$) and K is the orientation angle of one filter ($\text{k}=0,\cdots ,\text{K}-1$).

In this work, the Gabor filter bank works with four scales and six orientations $(\text{S}=4,\text{K}=6)$. After the convolution of the whole filter bank, the final feature vector ϕ consists of the mean ${\mathsf{\mu }}_{(\text{s},\text{k})}$ and standard deviation ${\mathsf{\sigma }}_{(\text{s},\text{k})}$ values of the filters, concatenated into its final form:

$$\mathsf{\phi }\left({\text{I}}_{\text{p}}\right)={[{\mathsf{\mu }}_{(0,0)},{\mathsf{\sigma }}_{(0,0)},{\mathsf{\mu }}_{(0,1)},{\mathsf{\sigma }}_{(0,1)},\cdots ,{\mathsf{\mu }}_{(3,5)},{\mathsf{\sigma }}_{(3,5)}]}^{\text{T}}.$$

(7)

The methods that were presented in the previous section are evaluated by using an aerial image database that contains challenging scenes with different resolutions, viewing angles, and lighting conditions.

3. Test Data and Tools

In this study, we use a database containing 70,000 square patches extracted from aerial images. The images have been taken at two flight campaigns during open-air rock festivals in Germany. The two samples in Figure 5 exemplarily show the complexity of the scene that the proposed methods have to deal with.

The illumination conditions within an aerial image can vary from bright sunlight to dark shadowed regions caused by high buildings. In addition, different surface types can cause low contrast and a varying appearance of the crowded regions as festivals can take place at locations with muddy meadows or paved parking areas.

The images have been taken at viewing angles $0^{\circ }$ and ${32}^{\circ }$, due to the camera system’s design and mount configuration [32]. Each image has one of three spatial resolutions, namely 9 cm, 13 cm, or 17 cm. For the experiments in this work, we want to leave the covered area of one image patch constant, hence the size in pixels of one patch is deduced from its spatial resolution, so that each patch covers an area of 30 square meters. This size trades off the methods’ requirement to work reasonable on a certain patch size and the endeavor to create a boundary around the crowded regions as accurate as possible. To create a labeled reference for the classifier, each patch has been assigned manually to one of four classes, which are described in the following:

class 

1—dense crowd This class represents image patches which have at least covered 80% with a crowd density of two persons per square meter ($1.5\text{P}/{\text{m}}^2$) or more. Individuals in these areas can only walk slowly to other locations or cannot move at all. Because of the large number of patches and the small object size of one person in these images, the manual estimation of the actual crowd density is difficult. We assume that a density of $1.5\text{P}/{\text{m}}^2$ is reached as soon as the surface the persons are standing on is no longer visible.

class 

2—medium dense crowd In this class, the crowd density is between $0.5\text{P}/{\text{m}}^2$ and $1.5\text{P}/{\text{m}}^2$. If the whole patch is covered homogeneously with such a density, it can be assumed that the surface is visible at several spots in one patch, which gives enough space for the persons to walk around. If the patch happens to be covered with a class 1 crowd up to 80% and devoid regions otherwise, it is also considered as a patch of this class 2. This special case happens at festival barriers which often appear in this data set, naturally (e.g., Figure 6, row 1, column 4).

class 

3—sparse crowd A crowd with a density between $0.2\text{P}/{\text{m}}^2$ and $0.5\text{P}/{\text{m}}^2$ is defined as a “sparse crowd”. Here, single persons are able to roam freely, although groups of persons might still appear frequently.

class 

4—no crowd In image patches of this class, there are hardly any persons visible. Buildings, tree canopies, streets, and vehicles are the dominant objects in this class. A randomly sampled subset of these patches is used in the test runs as negative samples.

With these specifications, the database is structured as shown in Figure 6.

The SRP local features are implemented in C++. For the LBP local features, the GMM, and the feature encoding we use the VLFeat library, version 0.9.20 by Vedaldi et al. [33]. The quantized LBP features use local histograms with a cell size of 8 × 8 pixels. The fisher vectors are generated using the “Normalized” and “SquareRoot” options of the vl_fisher() function of their MATLAB interface. The SVM is based on a slightly modified version of libSVM version 3.20 by Chang and Lin, National Taiwan University [34] using a histogram intersection kernel [35]. The Gabor filter bank is implemented in MATLAB version R2015a without additional toolboxes.

4. Results

In the following, the BoW approach is evaluated and compared with a Gabor–filter–based crowd detection [18] through three experimental setups:

One-vs.-All 

This classification experiment tests the general ability of both Gabor and BoW classifiers to separate a class with a given crowd-density range from the other classes.

One-vs.-One 

This experiment clearly shows the ability of the two approaches to distinguish between adjacent crowd classes with only small differences in crowd density.

Multi-class 

Both BoW and Gabor classifiers are evaluated on all four available classes in a multi-class setup. This experiment is the desired use case for an operational “crowd detector”.

4.1. One-vs.-All Classification

In this section, we test the general ability of the proposed methods to detect crowded regions in aerial images and to discriminate patches with only small texture differences. For example, patches of class 1 have a high similarity to patches of the adjacent class 2. With a one-vs.-all classification, all possible combinations of the four classes are tested. Figure 7 shows the methods’ performance with an increasing number of training samples. In all tests, we compare the classification accuracy of an SVM trained with Gabor features with an SVM trained with BoW-LBP and BoW-SRP features. The BoW features are generated using a dictionary with 256 codewords. The dictionary has been created according to Section 2.1.1 using a feature space with several million points. Each test is conducted with 1000 sample patches of mixed resolution, viewing angle, and illumination conditions, and they are randomly selected for training or testing. The average classification accuracy and its standard deviation are calculated by using Monte Carlo cross-validation with 20 splits.

The simplest test case is the classification of patches without any persons on the one hand (class 4 “no crowd”) and crowded patches of classes 1 to 3 on the other hand. In Figure 7a, which shows this test case, the classification accuracy climbs above 90% using only 20 samples for training and 980 samples for testing. This test shows that the feature spaces of both Gabor and BoW-based methods are well separated and a decision boundary can be quickly found by the SVM classifier.

If the classifier takes class 3 “sparse crowd” as the positive class and all other samples as the negative class, then the achieved accuracy with 100 training samples or more is around 75% when using BoW features and around 65% when using Gabor features (Figure 7b).

With class 2 “medium dense” as the positive samples, the accuracies are 55% (Gabor), 60% (BoW-SRP), and 70% (BoW-LBP) if the classifier is trained with 100 samples or more. The reason for this drop in accuracy compared to the two previous tests is the strong visual similarity of class 1/class 2 and class2/class 3, which causes a large number of misclassifications (Figure 7c). Interestingly, BoW-LBP features are 10% more accurate than BoW-SRP features in this test.

The classification accuracy for class 1 “dense crowd” (Figure 7d) is generally higher than for the class 2 and the class 3 test. The highest accuracy can be achieved when using BoW-based features. While BoW-LBP features still perform better than BoW-SRP, the margin of 5% is only half as much as in the previous class 2 test.

4.2. One-vs.-One Classification

We compare the six possible combinations of a one-vs.-one classification test (Figure 8 and Figure 9). We show again the average accuracy depending on the number of training samples, calculated from 20 test runs on 1000 samples (500 samples per class).

When we compare the test series shown in Figure 8 and Figure 9, it becomes obvious that a test of class 4 against another class results in a much higher accuracy than the tests without a participation of class 4. Class 4 can be separated more easily from the other crowd classes 1, 2, and 3. This observation complies with the visual appearance and indicates that both Gabor and BoW-based features are a good choice for representing crowd features.

Interestingly, the Gabor features need less training samples than the BoW features when they are tested on class 4 samples (Figure 8a–c). The Gabor’s accuracy converges more quickly, but on the same level as the BoW features.

In the case of the intra-crowd-classes classification tests (Figure 9), the classifier has a lower accuracy in general. A possible explanation is again the strong visual similarity between these classes, causing the SVM to have difficulties finding the optimal decision boundary. However, in these cases, where the texture differences are small, the BoW features seem to be slightly more descriptive than the Gabor features (see Figure 9a,b).

Moreover, we can observe a superior classification accuracy of the BoW-LBP features in all three experiments shown in Figure 9. The margin between BoW-LBP and BoW-SRP is highest when the test includes class 2 ( Figure 9a,c).

4.3. Multi-Class Classification

In this experiment, we train multi–class SVMs with all four classes containing a subset (2440 patches) of the whole dataset. We used stratified sampling to prevent skewed classes. Since the crowded regions in an aerial image normally do not cover a large fraction of the whole image, the number of class four samples is highly over-represented. Therefore, we limit its number of samples and balance the test set of this experiment resulting in 610 randomly chosen samples per class. We use 440 samples for training (110 samples per class) and 2000 samples for testing (500 samples per class).

The prediction result of the SVM with Gabor features reaches an accuracy of 62.3%; with BoW-SRP features, it is 67.9%, and with BoW-LBP features, it is 74.2% . Figure 10 shows a confusion matrix for each feature type. The higher the diagonal values are, the better the performance of the classifier. The matrices’ cells are colored accordingly. Looking at the color distribution of the matrices, three aspects stand out. First, and most interestingly, the majority of the samples are classified correctly, hence the values on the diagonal of the matrices are high. This result shows the fundamental applicability of the chosen methodology on the dataset. Second, a considerably higher number of samples of the crowd classes 1, 2, and 3 are misclassified than in cases where class 4 takes part. These predictions of crowd samples often miss the actual class and are predicted as one of the other (neighboring) crowd classes. A possible explanation is the similarity of the crowd textures of classes 1, 2, and 3, and the dissimilarity of class 4 to the other classes. Third, in a comparison of the confusion matrices, the classification accuracy with BoW-based features is higher than the accuracy with Gabor features.

Now, we focus on the performance of the three crowd classes (classes one, two, three), as they seem to be hard to distinguish from each other. Therefore, we calculate the precision and recall scores, along with the ${\text{F}}_1$ scores, which are plotted in

Table 1. Precision, recall, and ${\text{F}}_1$ scores for the four–class classification experiments Gabor (left), BoW–SRP (center), and BoW–LBP (right).

	Cl-1	Cl-2	Cl-3	Cl-4	Cl-1	Cl-2	Cl-3	Cl-4	Cl-1	Cl-2	Cl-3	Cl-4
Precision	0.578	0.478	0.565	0.852	0.760	0.496	0.591	0.886	0.758	0.558	0.722	0.949
Recall	0.520	0.474	0.588	0.91	0.634	0.496	0.670	0.914	0.740	0.618	0.670	0.938
${\text{F}}_1$ Score	0.547	0.476	0.576	0.88	0.691	0.496	0.628	0.900	0.749	0.586	0.695	0.944

. Both the precision and recall scores should be as high as possible for each class, which is reflected in their harmonic mean, also known as the ${\text{F}}_1$ score. The ${\text{F}}_1$ score of each class has roughly the same value as the precision and the recall of that class, indicating a balanced training of the classifier. For class 1 (dense crowd), the ${\text{F}}_1$ score of the BoW-SRP and BoW-LBP features is 0.69 and 0.75, respectively, and the F1 score of the Gabor features is 0.55. Hence, the Gabor features perform not as well as the BoW features for class 1 predictions. The ${\text{F}}_1$ scores for class 2 (medium dense) are low for both BoW and Gabor features. Figure 10 shows that almost all false positives (FP) and false negatives (FN) are in the neighboring classes “dense crowd” and “sparse crowd”. The number of FP and FN in class “no crowd” are almost negligible. Accordingly, the classifiers have the highest ${\text{F}}_1$ Scores for class 4.

Finally, for getting a better visual impression, we show a prediction example in Figure 11 where the predicted four classes are displayed as an overlay of an aerial image. The original image (Figure 11a) contains crowd densities of all four classes, which is also shown as a visual comparison in Figure 11b .

5. Discussion

The experiments in Section 4 demonstrate the general ability of both Gabor and BoW features to detect crowded regions in VIC images. It further implies that the appearance of a crowd in VIC images is texture–like because the core methodologies of the two approaches have been originally designed for the task of texture classification.

When we consider the crowd detection as a binary classification task, the results in Figure 7a and Figure 8a show that both classifiers reach almost perfect performance with only a few training samples. Both Gabor and BoW-based features can be well separated in the feature space as the patches with crowd textures are different from the patches containing no crowd.

The experiments reveal that of all existing types of class 4 patches in the database, patches of tree canopies, meadows, and dumping grounds are often misclassified as false positives (see Figure 6, class 4 for examples). Interestingly, a number of colleagues have not been able to correctly label these patches either, when they were confronted with just that patch, and without information about the surroundings. Furthermore, both the Gabor and the BoW–based classifier predicted some false negatives in regions which lie in the shadow of a building (e.g., a stage) due to the extremely low contrast in these regions. Here, the difference in intensity which directly influences the values of the local features, is too low, which results in misclassifications. However, contrast enhancement methods should improve results.

In the experiments shown in Figure 7d and Figure 9a,b, the accuracy margin between BoW-based and Gabor-based features is the highest. As these experiments focus on the classification of high-density crowds, we can infer that samples of class 1 indeed can be regarded as textures, and their classification is done best with an approach specially designed for texture classification, which is the BoW model. As an interesting side effect, we observe the particular fitness of the BoW-LBP feature when predicting class 2 samples (Figure 7d and Figure 9c). Its accuracy is 5 to 10% higher than the BoW-SRP accuracy in these tests. We speculate that the local spatial pattern and the gray scale contrast of the medium-dense patches in class 2 can be well represented by LBP features.

The limits of the two texture-based classification approaches can be observed best when classifying the class 2 and class 3 samples (Figure 9c and in Figure 10). Class 2 and class 3 are visually very similar (Figure 6). As each class represents a crowd-density range, border cases between adjacent classes can really challenge a texture-based classifier because they do not count the individuals but classify a patch by its mere appearance. A counting-based approach in these most difficult cases might improve the results slightly. However, one should keep in mind, that even the manual labelling process for these classes requires careful counting of the individuals in each patch by an expert. An accurate dataset with a larger number of classes, i.e., a smaller range of crowd density per class, cannot be created without precise and synchronized reference data from another independent sensor source.

The engineering of the BoW features requires some careful design choices, like picking the best local-feature extraction and the best feature-encoding method. The used local features considerably influence the classification’s performance. Although we had to make these initial design choices, the parameters for every step in the BoW workflow needed to be tuned only once. The invariance of the BoW model to changes in illumination, scale, and viewing angle allow a once-only initialization. The clustering, as the most time-consuming step, is simply performed only once on all available data. Then, the learned Gaussian mixture model can be used on varying image data. The experiments also show that a trained SVM can be used for correctly detecting crowd patches taken at different conditions. This characteristic can be useful in a real-time environment when time is crucial and there is no time to re-initialize the whole system.

As the experiments have shown, the methodology is generally suited for deployment in an operational framework. An operational software module which estimates the crowd density will be trained on the image regions with highest crowd density. Therefore, a binary classification which regards class 1 or class 1 to 3 as the positive class is a practical design choice, which is essentially reflected by the tests shown in Figure 7a,d. The probability estimate for each patch, which is computed by the SVM, can be further used to highlight the most crowded (and potentially most hazardous) regions in an aerial image.

After all, one has to keep in mind that the proposed methodology classifies each patch independently. It does not take any holistic information into account as every expert would do. For example, an expert would recognize forest, buildings, and a stage at a festival and eventually use this information to identify the mass in front of the stage as a crowd. Without any knowledge of the environment and with only a single patch, an expert would have difficulties identifying crowd and no-crowd patches. To incorporate this kind of information into the crowd-detection workflow could be a key issue in this research field.

The images, which have been investigated in this work, have a spatial resolution of 9 cm or worse which leads to an object size of one person of roughly 30 pixels or less. Hence, an identification of a person is impossible with this kind of data, and the privacy of each individual is guaranteed by design.

6. Conclusions

In this work, we apply and compare texture classification methods for the detection of crowded regions in aerial images. The nature of the images used in this study does not allow a correct counting of individual persons, even by human experts. Therefore, we propose a multi-class texture classification to categorize crowd patches into four different classes. Each class represents a predefined range of crowd density.

We compare the performance of two different approaches: an SVM classification with patch-based Bag-of-Words features and an SVM with filter-based Gabor features. We test these two different methodologies on a dataset with 70,000 small image patches, and achieve 97% accuracy in both cases, when classifying dense crowd patches vs. no-crowd patches.

Moreover, we extend our evaluation and use the same features to categorize a patch just by its texture into one of four density-range classes. In this experiment, Bag-of-Words features achieve an accuracy of 74%, which is 12% higher than the accuracy achieved with Gabor features.

In conclusion, the results of our evaluation support the theory that a crowd in aerial images has a texture-like appearance and can be detected robustly by well-designed Bag-of-Words features. An operational system, based on the proposed methodology, could help security authorities to quickly identify high crowd densities and to prevent crowd disasters.